Kinetic analysis of low concentration CO detection by Au-loaded cerium oxide sensors†
Deblina Majumdera,
Aparna Dattab,
Manoj Kumar Mitrac and
Somenath Roy*a
aSensor and Actuator Division, CSIR-Central Glass and Ceramic Research Institute, 196, Raja S.C. Mullick Road, Kolkata 700032, West Bengal, India. E-mail: sroy@cgcri.res.in
bSchool of Materials Science and Nanotechnology, Jadavpur University, 188, Raja S.C. Mullick Road, Kolkata 700032, West Bengal, India
cDepartment of Metallurgical and Material Engineering, Jadavpur University, 188, Raja S.C. Mullick Road, Kolkata 700032, West Bengal, India
First published on 20th September 2016
Abstract
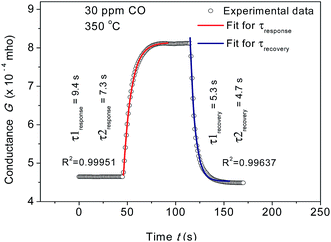
Owing to its high toxicity, even at very low concentration, early detection of carbon monoxide (CO) is imperative. We have fabricated sensors comprising gold nanoparticle-loaded cerium oxide (Au–CeO2). The morphology and elemental composition of the sensing material have been characterized using XRD, FESEM, TEM and XPS. The performance of the Au–CeO2 sensors has been studied for the detection of CO in the concentration range of 10–30 ppm in air. The response and recovery transients of conductance have been modeled using two-site Langmuir adsorption kinetics. In the presence of 30 ppm CO, the calculated response times for two energetically different adsorption sites, CeO2 surface and Au/CeO2 interface are 9 s and 7 s, respectively. Finally, an exponential correlation between the gas concentration and the time constants has been derived.
1. Introduction
Rare earth oxides, for example cerium oxide (CeO2), are widely explored for a gamut of applications primarily due to their unique properties arising from the existence of the 4f shell.1 In addition to its widespread usage in electronics, optics, and heterogeneous catalysis, ceria is a material of choice for the fabrication of gas sensors.2–8 Cerium oxide has abundant oxygen vacancies, a high oxygen storage capacity and a facile transition between Ce3+ and Ce4+, resulting in enhanced rates of the oxidation reaction.9 Either bare ceria or that in conjunction with noble metal catalysts has been used for the detection of target gases.10–14 For example, Izu et al. have reported efficient catalytic oxidation of CO using noble metal loaded CeO2.7 This is also in agreement with the report of Carrettin et al. who showed that CeO2 increases the activity of gold for CO oxidation by 2 orders of magnitude with respect to a conventional CeO2 support.15 The activity of gold as a catalyst for CO oxidation depends on several parameters like synthesis method, nature of the support, size of the gold nanoparticles (Au NP), as well as to the gold—support interactions and pre-treatment conditions.16 For example, the ability to supply reactive oxygen rendered an enhanced activity for CO oxidation in case of gold supported on a reducible transition metal oxide.17,18 Motivated by the above facts we have explored the potential of Au–CeO2 as an active material for detection of low-ppm CO. As mentioned previously, Izu and his co-workers have reported the use of Au-loaded CeO2 thick films for CO detection in the concentration range of 330–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm, which is impractically high as referred to the permissible exposure level (PEL) of this highly toxic gas. Furthermore, the response time was in the range of 46–49 s, which may not be deemed suitable for real-time CO detection. Additionally, though the detection of CO using Au–CeO2 has been mentioned in the literature, till date any comprehensive study on the adsorption/desorption kinetics of CO on CeO2 surface has not been reported.
000 ppm, which is impractically high as referred to the permissible exposure level (PEL) of this highly toxic gas. Furthermore, the response time was in the range of 46–49 s, which may not be deemed suitable for real-time CO detection. Additionally, though the detection of CO using Au–CeO2 has been mentioned in the literature, till date any comprehensive study on the adsorption/desorption kinetics of CO on CeO2 surface has not been reported.
In this article, we report the detection of CO down to 10 ppm, with discernible sensitivity and very fast response, using Au–CeO2 as a sensing material. Synthesis of CeO2 has been conducted in a catalyst-free and environmentally benign condition using a simple precipitation method. We further demonstrate how the sensor modules comprising Au–CeO2 detect CO gas in the concentration range of 10–30 ppm within a few seconds. The upper limit of CO detection has been determined following guidelines of Occupational Safety and Health Administration (OSHA, USA), which restricts the time-weighted average exposure limit of CO as 35 ppm for 8 h.19 The response and recovery transients of the sensors have been modeled using two-site Langmuir adsorption kinetics. Finally, we have conducted a selectivity study in which the cross sensitivity of the CO sensors has been tested in presence of interfering gases like ammonia and hydrocarbons.
2. Experimental section
2.1 Materials synthesis
Ammonium cerium(IV) nitrate [(NH4)2Ce(NO3)6, ≥98.5%], ethylene glycol (anhydrous, HOCH2CH2OH, ≥99.8%) and gold(III) chloride hydrate (HAuCl4·xH2O, 99.999%) were procured from Sigma-Aldrich. Ammonium bicarbonate (NH4HCO3, 98.5%) was purchased from Loba Chemie Pvt. Ltd., India. Ammonium cerium nitrate (4.4 g) was added in 30 ml isopropanol followed by the addition of 20 ml ethylene glycol under vigorous stirring and the mixture was heated under reflux condition at 190 °C for 4 h. Subsequently, the mixture was centrifuged and the precipitate was washed with deionized water and dried overnight in vacuum. For loading of gold, 50 mg CeO2 was dispersed in 50 ml of NH4HCO3 aqueous solution (1 M), in which HAuCl4 was added drop-wise, followed by 1 h heating at 90 °C. Size of the Au NP on CeO2 was tuned by varying HAuCl4 concentration from 5 to 15 mM. For each case, the mixture was centrifuged and washed with DI water. Finally, the collected Au-loaded ceria (Au–CeO2) samples were calcined at 600 °C for 6 h.2.2 Characterization of materials
The structural morphology of the synthesized materials was examined using high resolution transmission electron microscope (HRTEM, model: TECNAI G2 30ST; manufacturer: FEI Company, The Netherlands) and field emission scanning electron microscope (FESEM, model: Supra 35VP; manufacturer: Carl Zeiss, Germany). Crystallographic studies of the materials were done using X-ray diffractometer with Cu Kα line (model: D8 Advance; manufacturer: Bruker Corporation, MA, USA) and X-ray Photoelectron Spectroscopy (XPS, model: PHI 5000 Versa probe II XPS system having a source of Al Kα and charge neutralizer at room temperature. The base pressure was maintained at 6 × 10−10 mbar with an energy resolution of 0.6 eV).2.3 Fabrication of sensors
Each Taguchi-type thick film sensor consisted of an insulating cylindrical substrate with terminal electrodes, a coaxial heating element and sensing material coated on top of it. For substrate preparation, alumina tubes were cut into specific dimensions (length 4 mm, outer diameter 2 mm, and inner diameter 1 mm) and both the edges of the tubes were polished. The tubes were cleaned with HCl, distilled water and finally with acetone. Then gold electrodes were deposited on the alumina substrates using gold paste and cured at 950 °C for 1 h. Platinum lead wires were attached to the gold electrodes at the terminals of the tubular substrates and mounted on to a 6-pin holder by spot-wielding. Gold-loaded ceria powder was mixed with a small amount of isopropyl alcohol to make a thick paste. The thick paste was then coated over the substrate. The viscosity of the paste and the coating parameters were optimized to get a final coating of around 50–60 μm thickness. The thick film coated alumina substrates were cured at 400 °C for 1 h. Basically, the curing process stabilizes the coating in terms of its microstructure and electrical properties. For sensor packaging, the electrical leads protruding out of the thick film coated tubular substrate and the terminals of the coaxial heating element were spot-welded on nickel pins fixed on polymer sensor heads. The top part of the sensor housing contained a double stainless steel mesh (Fig. S1, ESI†).2.4 Gas sensing measurement
The sensor modules with Au–CeO2 as the sensing element were exposed to CO in air in the concentration range of 10–30 ppm. The operating temperature of the sensors was varied by changing the current driven through the Ni–Cr wire inserted in the hollow alumina tube. A series of mass flow controllers were deployed for dispensing a desired concentration of the target gas diluted in a carrier gas.The mixing of the target and the carrier gas was carried out in a pre-mixing chamber before delivering on to the sensor head. Sensors under test were exposed to the target gas at 1 atmospheric pressure and at a flow rate of 50 sccm. The change in resistance of the active metal oxide layer in presence of gas was measured using an Agilent B2901A source-meter and was recorded using a LabView-based graphical user interface (GUI) system.
3. Results and discussion
3.1 Crystallographic and morphological analysis
The X-ray diffraction pattern of the synthesized ceria is presented in Fig. 1(a). The characteristic peaks correspond to a face-centered cubic (FCC) phase of ceria (JCPDS card no. 34-1394). No diffraction peak of any impurity could be traced from the XRD spectrum. The XRD analyses were also performed on CeO2, loaded with Au NPs of different sizes viz. 5, 17 and 32 nm (hereinafter termed as AC1, AC2 and AC3, respectively) as presented in Fig. S2, ESI.† Though the characteristic peaks of FCC phase of CeO2 were recorded, no discernible peak for Au could be found for AC1, likely due to the fact that small Au NPs were sparingly dispersed on the surface of CeO2.20 The distinctive peaks of Au NP at 38.3° and 44.6° were found in both the cases of AC2 and AC3 along with the mentioned peaks of FCC CeO2.21 Morphological analyses of AC1 were done using FESEM showed obelisk type of hierarchical structures of ceria, with a mean length of 5 μm and diameter (at the center) of 1 μm [Fig. 1(b)]. From the magnified image (inset), the surface decoration of CeO2 with Au NP is clearly visible. The presence of the Au NPs on the surface of ceria could be confirmed from the energy-dispersive X-ray spectroscopy (EDAX), which is included in the ESI [Fig. S3, ESI].† The TEM image of AC1 [Fig. 1(c)] reveals that the obelisk-like superstructures are composed of small ceria nanoparticles. The particles show a very narrow size distribution with an average diameter of ∼4 nm [inset of Fig. 1(c)]. The selected area diffraction (SAED) pattern [inset of Fig. 1(c)] confirms the polycrystallinity of CeO2. In-depth microstructural investigation was done for the Au NP loaded CeO2 materials using high resolution transmission electron microscopy (HRTEM). Fig. 1(d)–(f) reveal the lattice fringes with the d-spacing of 0.32 nm, which could be indexed to the (111) plane of ceria in AC1, AC2 and AC3 respectively.22 This is in agreement with the fast Fourier transform (FFT) and SAED calculations. In the HRTEM image, Au NPs are manifested by high contrast. The Brunauer–Emmett–Teller (BET) surface area, pore volume and pore radius of ceria were found to be 67.5 m2 g−1, 0.101 cm3 g−1 and 20.03 Å, respectively.3.2 X-ray photoelectron spectroscopy analysis
The high oxygen vacancies of CeO2 could be confirmed by XPS results. It is well known that the oxygen vacancies in CeO2 arise due to its +3 oxidation state as they create defects in CeO2 lattice. In Fig. 2(a), the core level Ce 3d spectrum shows the characteristic peaks of Ce3+ at 885.7, 899 and 904.3 eV. The other distinguishable peaks at 882.2, 901.1 and 916.1 eV correspond to +4 oxidation state of ceria which proves the mix valence of the material.23 Another signature of prominent oxygen vacancies in ceria could be observed from the O 1s spectrum [Fig. 2(b)], where the characteristic peak is found at 532.1 eV.243.3 Gas sensing characteristics
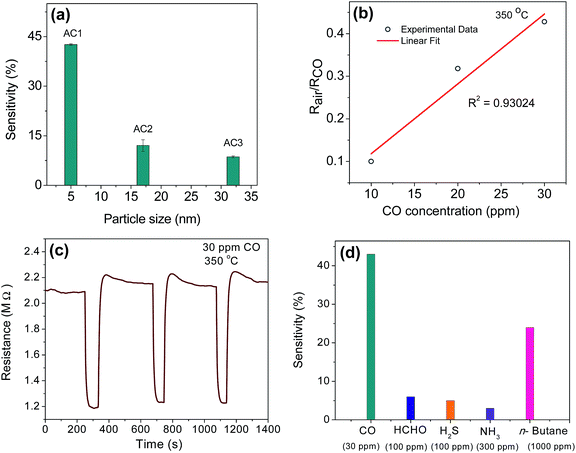
Gold-loaded CeO2 sensors were deployed for detection of low-ppm carbon monoxide in air. We have studied the influence of the size of Au NPs on the CO response pattern. Fig. 3(a) delineates the comparative CO response recorded for AC1, AC2 and AC3 samples. A gradual decrease in sensitivity was observed with an increase in size of the Au NPs. The efficacy of Au NP as a catalyst depends on the coordination number of the Au atoms, which make bonds with the reactive species (O2, O, or CO). In fact, the binding energy declines approximately linearly with decreasing coordination number.25 For smaller nanoparticles, low-coordinated Au atoms are located in abundance at the edges and, in particular, at the corners of the particles. Since these low-coordinated Au atoms are active sites for binding of CO and oxygen, the catalytic activity scale with the number of low-coordinated atoms in the Au NP, and not with the surface area. The above fact explains the observed increase in CO sensitivity with decreasing Au particle size.The normalized resistance values of the AC1, when exposed to CO concentrations in the range of 10–30 ppm, are presented in Fig. 3(b). In the calibration plot, Rair and RCO denote sensor resistances in air and in presence of CO, respectively. A linear trend could be obtained over the entire measurement range. At a CO concentration of 30 ppm, we obtained an average sensitivity of 43%. The lower limit of detection (LOD) of our sensor, which is 10 ppm, is comparable or superior to the commercial sensors in the same genre. The dynamic response characteristics of the sensors were recorded in presence of a series of gas pulses. Fig. 3(c) depicts such a representative curve, which was obtained for a pulse train of 30 ppm CO in air and at an operating temperature of 350 °C. A nominal shift in the baseline resistance could be observed. Selectivity of any chemical sensor is one of the most important parameters to be considered for field deployment. Fig. 3(d) reflects the degree of selectivity achieved with our AC1 sensors when operated at 350 °C. A closer look at the bar chart reveals that even a 3-fold higher concentration of formaldehyde and hydrogen sulphide (indoor air pollutants), a 10-fold higher concentration of ammonia or even a 30-fold higher concentration of a hydrocarbon (n-butane) resulted in lower sensor responses compared to that obtained for 30 ppm CO in air.
Further, the response and recovery transients of the AC1 sensors were analyzed using Langmuir adsorption kinetics. In conformity with the conventional theory of solid state gas sensors, at elevated temperatures (>100 °C), oxygen molecules (from air) are dissociatively or non-dissociatively adsorbed on the metal oxide surface in a delocalized manner, trapping electrons from the conduction band and forming charged molecular (O2−ads) and atomic (O−ads and O2−ads) oxygen species. These adatoms are electrostatically stabilized in the vicinity of the metal cations at the surface of the material. Reducing gases, like CO, reacts with these oxygen adatoms and setting the trapped electrons free to the conduction band. This phenomenon happens in the temperature range of 100–450 °C, which is the usual operating temperature of the metal-oxide sensors and can be attributed to the wide band-gap of the metal-oxides. Initially, physisorption takes place, in which oxygen is adsorbed on to the semiconductor surface atoms via dipole bonding. At this stage, electrons are removed from this high oxygen vacancy containing semiconductor surface via a charge transfer mechanism and subsequently a chemical bond is established with the semiconductor surface atoms (chemisorption). The chemisorbed surface oxygen species may be of atomic or molecular origin depending on the temperature of adsorption. Now, when the sensor is exposed to the reducing gas (CO in this case), the CO molecules get chemically adsorbed on the CeO2 surface as well as at the Au/CeO2 interface and react with the surface adsorbed oxygen species. The elementary steps for CO oxidation on Au/CeO2 sensor surface are depicted below:26
| 1/2O2 + * ↔ O* | (1) |
| CO + * ↔ CO* | (2) |
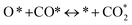 | (3) |
 | (4) |
Among the CO oxidation steps delineated above, the adsorption of oxygen and carbon monoxide on the CeO2 surface and Au/CeO2 interfaces (eqn (1) and (2)) is rather fast. Hence the adsorption transients are determined by the reaction between surface-adsorbed oxygen and carbon monoxide, which is the rate limiting factor. Now, according to Langmuir adsorption model, the transient conductance of the sensor G(t) at a constant temperature and at any given instant of time t can be presented as
| G(t) = G0 + G1[1 − exp(−t/τ1response)] + G2[1 − exp(−t/τ2response)] | (5) |
| G′(t) = G′0 + G′1[exp(−t/τ1recovery)] + G′1[exp(−t/τ2recovery)] | (6) |
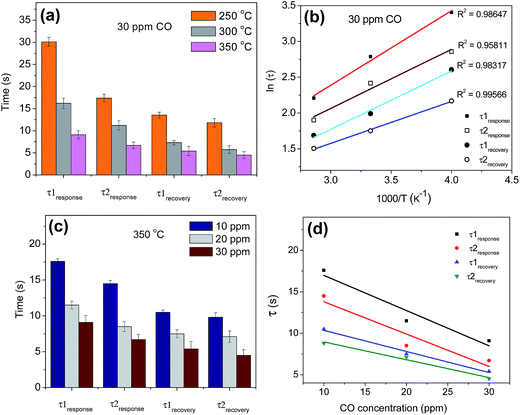
The transient conductance during response and recovery for exposure to 30 ppm CO, measured at various temperatures, was also fitted using eqn (5). As can be seen from Fig. 5(a), the response and recovery time for both the adsorption sites decrease with an increase in temperature. Usually, at a high operating temperature (>200 °C), the response transient is governed by the following equation.29
τ = τo![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[(EA + Q)/2kT] exp[(EA + Q)/2kT]
| (7) |
The time constants do not only depend on the energetics of the adsorption sites, they do vary with the concentration of the target gas being analyzed (CO in this case). Response and recovery time, calculated by fitting the transient conductance, was plotted as a function of CO concentration at a fixed temperature of 350 °C [Fig. 5(c)]. An exponential relationship between the time constant and CO concentration could be observed which may be expressed by the following equation:
| τ = τoC−β | (8) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ = log τ = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τo − β τo − β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C C
| (9) |
When log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C is plotted against log
C is plotted against log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ, we get a linear plot [Fig. 5(d)], the slope of which determines the value of β. For response characteristics, the values of power factor turned out be β1response = 0.425 and β2response = 0.399, corresponding to τ1response and τ2response, respectively. While, for recovery, the corresponding values are β1recovery = 0.255 and β2recovery = 0.215.
τ, we get a linear plot [Fig. 5(d)], the slope of which determines the value of β. For response characteristics, the values of power factor turned out be β1response = 0.425 and β2response = 0.399, corresponding to τ1response and τ2response, respectively. While, for recovery, the corresponding values are β1recovery = 0.255 and β2recovery = 0.215.
4. Conclusion
Gold-loaded cerium oxide has been explored as an active material for detection of low-ppm CO in air. Following the suggested permissible exposure limit of the regulatory authorities, we have calibrated the sensors in presence of CO in the concentration range of 10–30 ppm. A discernible sensitivity as well as a fast response has been observed. The sensors have exhibited high selectivity in presence of potentially interfering gases. Further, we have modeled the response and recovery transients of conductance using two-site Langmuir adsorption kinetics. The performance of our sensors, especially in terms of detection limit (LOD = 10 ppm) and response time (as low as 8 s) are comparable or superior to the commercially available solid state CO sensors.Acknowledgements
The present research was partially funded by Council of Scientific and Industrial Research (CSIR), Government of India, through the 12th five year plan network project ‘MULTIFUN’ (Grant number: CSC-0101). The author DM gratefully acknowledges the INSPIRE fellowship from Department of Science and Technology (DST), Government of India. The facility of DST-CSIR Sensor Hub, Kolkata has been partially utilized for this study.References
- Y. Chang, J. Teo and H. C. Zeng, Langmuir, 2005, 21, 1074–1079 CrossRef CAS PubMed.
- Catalytic Science Series, Catalysis by Ceria and Related Materials, ed. A. Trovarelli and G. J. Hutchings, Imperial College Press, London, 2002, vol. 2 Search PubMed.
- Y. Liu, Y. Ding, L. Zhang, P. X. Gao and Y. Lei, RSC Adv., 2012, 2, 5193–5198 RSC.
- N. Izu, I. Matsubara, T. Itoh, T. Akamatsu and W. Shin, Sensors, 2013, 13, 3252–3261 CrossRef CAS PubMed.
- N. Izu, S. Nishizaki, T. Itoh, M. Nishibori, W. Shin and I. Matsubara, Sens. Actuators, B, 2009, 136, 364–370 CrossRef CAS.
- S. M. A. Durrani, M. F. Al-Kuhaili, I. A. Bakhtiari and M. B. Haider, Sensors, 2012, 12, 2598–2609 CrossRef CAS PubMed.
- N. Izu, W. Shin, N. Murayama and S. Kanzaki, Sens. Actuators, B, 2002, 87, 95–98 CrossRef CAS.
- L. Liao, H. X. Mai, Q. Yuan, H. B. Lu, J. C. Li, C. Liu, C. H. Yan, Z. X. Shen and T. Yu, J. Phys. Chem. C, 2008, 112, 9061–9065 CAS.
- P. G. Harrison, I. K. Ball, W. Azelee, W. Daniel and D. Goldfarb, Chem. Mater., 2000, 12, 3715–3725 CrossRef CAS.
- D. Tibiletti, A. Amieiro- Fonseca, R. Burch, Y. Chen, J. M. Fisher, A. Goguet, C. Hardacre, P. Hu and D. Thompsett, J. Phys. Chem. B, 2005, 109, 22553–22559 CrossRef CAS PubMed.
- M. Haruta, Chem. Rec., 2003, 3, 75–87 CrossRef CAS PubMed.
- G. C. Bond and D. T. Thompson, Gold Bull., 2000, 33, 41–50 CrossRef CAS.
- T. Fujitani, I. Nakamura, T. Akita, M. Okumura and M. Haruta, Angew. Chem., Int. Ed., 2009, 48, 9515–9518 CrossRef CAS PubMed.
- N. Izu, W. Shin, N. Murayama and S. Kanzaki, Sens. Actuators, B, 2002, 87, 95–98 CrossRef CAS.
- S. Carrettin, P. Concepcion, A. Corma, J. M. L. Nieto and V. F. Puntes, Angew. Chem., Int. Ed., 2004, 43, 2538–2540 CrossRef CAS PubMed.
- D. L. Trimm, Appl. Catal., A, 2005, 296, 1–10 CrossRef CAS.
- A. Fonseca, J. Fisher, D. Ozkaya, M. Shannon and D. Thompsett, Top. Catal., 2007, 44, 223–235 CrossRef CAS.
- O. H. Laguna, F. Romero Sarria, M. A. Centeno and J. A. Odri-ozola, J. Catal., 2010, 276, 360–370 CrossRef CAS.
- https://www.osha.gov/dts/sltc/methods/inorganic/id209/id209.htm.
- P. Sudarsanam, P. R. Selvakannan, S. K. Soni, S. K. Bhargava and B. M. Reddy, RSC Adv., 2014, 4, 43460–43469 RSC.
- M. Y. M. Abdelrahim, S. R. Benjamin, L. M. Cubillana-Aguilera, I. Naranjo-Rodríguez, J. L. Hidalgo-Hidalgo de Cisneros, J. J. Delgado and J. M. Palacios-Santander, Sensors, 2013, 13, 4979–5007 CrossRef CAS PubMed.
- S. Kar, C. Patel and S. Santra, J. Phys. Chem. C, 2009, 113(12), 4862–4867 CAS.
- M. Chena, X. Wanga, Y. H. Yua, Z. L. Peib, X. D. Baib, C. Sunb, R. F. Huangb and L. S. Wenb, Appl. Surf. Sci., 2000, 158, 134–140 CrossRef.
- J. Zhang, S. Ohara, M. Umetsu, T. Naka, Y. Hatakeyama and T. Adschiri, Adv. Mater., 2007, 19, 203–206 CrossRef CAS.
- N. Lopez, T. V. W. Janssens, B. S. Clausen, Y. Xu, M. Mavrikakis, T. Bligaard and J. K. Nørskov, J. Catal., 2004, 223, 232–235 CrossRef CAS.
- G. Djega-Mariadassou and M. Boudart, J. Catal., 2003, 216, 89–97 CrossRef CAS.
- J. J. Stephan and V. Ponec, J. Catal., 1976, 42, 1–9 CrossRef CAS.
- N. Ta, J. Liu, S. Chenna, P. A. Crozier, Y. Li, A. Chen and W. Shen, J. Am. Chem. Soc., 2012, 134, 20585–20588 CrossRef CAS PubMed.
- G. Korotcenkov, V. Brinzari, V. Golovanov and Y. Blinov, Sens. Actuators, B, 2004, 98, 41–45 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra18547a |
| This journal is © The Royal Society of Chemistry 2016 |