The growth modes of graphene in the initial stage of a chemical vapor-deposition process

Abstract

Using first-principles techniques, the growth modes of carbon clusters including chain and island structures on the Ni (111) surface are investigated, which is crucial to understand the graphene growth in the initial stage. One of the interesting findings is that both the chains and islands of carbon have higher mobility than the single carbon atom on the Ni substrate. More importantly, it is found that there exists two different growth modes, i.e., the bonding of the carbon cluster with a carbon atom, and the bonding between two clusters. The former corresponds to the preferred growth mode of a one-dimensional carbon chain; and the latter tends to happen between two-dimensional carbon island clusters. In addition, we discussed the relationship between the strong migration ability of grapheme islands and the defect formation according to our simulation results. At last, based on the calculated Brønsted–Evans–Polanyi relation, the catalytic properties of Ni substrate for graphene growth can be well described quantitatively.

---

1 Introduction

Graphene has aroused much attention in various fields. It is important to prepare high-quality graphene over large areas. Large-scale synthesis methods like chemical vapor-deposition (CVD)^1,2 and epitaxial growth³ on metal and other substrates have been developed. The Ni (111) surface is often used as a substrate because its lattice is in almost perfect correspondence with that of free-standing graphene.⁴ Additionally, the Ni (111) surface has flat terraces and no grain boundaries through epitaxial growth of a Ni monolayer on top of MgO (111),⁵ thus representing a novel way of producing graphene in very mild and controlled conditions. In the process of graphene growth by CVD, the carbon species decomposed from methane first diffuses into the Ni substrate, and then these small C species nucleate on the Ni (111) surface. Next, the nuclei grow to island and then become domains (grains) that cover the metal surface in its entirety,^6,7 where a domain (grain) is defined as the area of graphene grown from one nucleus, and the domain size is depended on the specific growth conditions. In spite of arousing some attention on the mechanism of graphene nucleation and growth,^8–10 little has been revealed about the growth kinetics. Especially, the growth details have not been understood completely. Therefore, it is necessary to study further the microscopic growth process at atomic and molecular level.

On the other hand, the irrationality of the growth parameters and imperfection of the growth processes will induce the structural defects in graphene samples.¹¹ These defects have a strong influence on the electronic, optical, thermal, and mechanical properties of graphene.¹² Importantly, some of the extraordinary properties can only be observed at an extremely low defect concentration. Therefore, controlling the production of graphene and obtaining high-quality graphene with fewer defects are an ultimate goal that experimenters have been pursuing, which also requires a fundamental understanding on the mechanism of graphene growth and defect formation.

In experiments, lots of efforts have been made to clarify the reason on the formation of structural defects in graphene growth, and some important results have been presented. For instance, the so-called interdomain defects between submicron sized domains have got much attention. Raman imaging studies clearly display that these interdomain defects are formed at the joints of large domains as neighboring islands grow continuously and then connect to each other.¹³ However, compared to the interdomain defects, it is difficult for experimenters to study the formation of the defects in smaller nanometer level. Especially, the factors determining the defects are still not understood completely. First-principles simulations can supply a favorable way to learn about the graphene growth world.¹⁴

In this work, based on the first-principles techniques, the possible growth models of carbon clusters on the Ni (111) surface are investigated in details. A mechanism about the graphene defect formation at the nanoscale is further proposed, which is helpful to understand some previous experimental results.

2 Models and method

The projector augmented wave (PAW) method^15,16 is used to treat the electron–ion interactions, and the Perdew–Becke–Ernzerhof (PBE) functional¹⁷ is used to describe the exchange and correlation interaction among electrons at the level of the generalized gradient approximation (GGA). Kohn–Sham orbitals are expanded in a plane-wave basis set with a cutoff energy of 400 eV in the Vienna Ab Initio Simulation Package (VASP).^18,19 The Monkhorst–Pack k-point mesh of 2 × 2 × 1 is used in Brillouin zone (BZ) sampling for a 5 × 5 supercell model of the Ni (111) surface, and that of 1 × 2 × 1 is used for a 8 × 4 supercell model. Structural optimization of all systems is performed until the atomic forces drop below 0.02 eV Å⁻¹. The minimum energy path for different reactions is identified by using the nudged elastic band method (NEB)^20–22 which can give activation energies of the reactions and diffusion of the adsorbates on surfaces, and the spring force between adjacent images is set to 5.0 eV Å⁻¹.

A slab model, including a four atomic Ni layers slab and a vacuum layer of 12 Å along the z direction, is used to simulate the Ni (111) surface. The two bottom layers of the slab are fixed to simulate the Ni bulk. Two types of C_n clusters (carbon chains and graphene flake) are considered. To make sure the distance between two neighboring C_n clusters large enough, the surface supercells are made of 5 × 5 and 8 × 4 unit cells of the (111) surface of cubic metal Ni, respectively. In this work, the formation energy of a given carbon cluster supported on Ni surface is defined as

E_f = E_Cn/_Ni(111) − n × ε_{adsorbed single C} − E_Ni(111) (1)

where E_Cn/Ni(111) is the total energy of the C_n/Ni(111) adsorption system, ε_{adsorbed single C} is the energy of one C atom adsorbed on Ni (111) surface, and E_Ni(111) is the energy of the Ni substrate. Additionally, the binding energy between C_n and the Ni substrate is defined by the equation:

E_binding = E_Cn/Ni(111) − E_Cn − E_Ni(111) (2)

where E_Cn is the energy of a relaxed free C_n cluster in the same supercell by removing the Ni substrate, and E_Ni(111) is the energy of the clean substrate.

3 Results and discussion

It was reported that carbon clusters on Ni (111) surface have two sorts of stable configurations.²³ According to the definition given by eqn (1), one-dimensional carbon chains are energetically preferred as C atom number is less than 12. Increasing the atom number to 12 or larger, the most stable configurations are transformed to two-dimensional graphene sp² network (graphene island).²³ In the present work, we use the most stable structures of C₅ and C₁₂ clusters as the typical samples to study the migration of carbon clusters, which have the chain and island configurations, respectively. The growth of the two sorts of carbon clusters are studied systematically by simulating the combination of two carbon species, such as C + C_n and C_m + C_n (n, m > 1).

3.1 The migration of carbon species

On Ni (111) surface, single carbon atom is steadily adsorbed on the three-fold hollow sites, as shown in Fig. 1(a). For the C₅ cluster, various adsorption patterns on Ni(111) surface are considered. It is found that a C₅ chain prefers to bond with Ni along the 〈110〉 orientation of Ni surface, as displayed in Fig. 1(b). The most stable C₁₂ on Ni surface has a sp² network structure, which includes two hexagons and one pentagon, as shown in Fig. 1(c). The formation energy of this island is lower than that of the chain structure by 0.21 eV according to our calculations. Other isomers of C₁₂ with island structure are not discussed due to the relative low stability.

Fig. 1 The stable configurations of (a) C, (b) C₅, and (c) C₁₂ on Ni (111) surface. Yellow and gray spheres represent Ni and C atoms, respectively.

Considering the dynamics of the growth process, the mobility of carbon clusters plays an important role in the graphene catalytic synthesis. Therefore, the migration of carbon species is a crucial step, which can help us to understand the details of the growth mechanism. Using the NEB method, the diffusion pathways of carbon clusters on Ni (111) surfaces are explored. The migration barriers for C (single atom), C₅ with a chain, and C₁₂ with a network structure are calculated, respectively. The results are shown in Fig. 2(a)–(c). The corresponding configurations are displayed in Fig. 2(d).

Fig. 2 The migration of single C atom, C₅ chain and C₁₂ flake on Ni (111). (a) The calculated diffusion barriers of C atom as a function of the supercell size; (b) the comparison of diffusion barriers between C atom and C₅ on Ni (111); (c) the comparison of diffusion barriers between C atom and C₁₂ on Ni (111); (d) the structures of IS, MS, and FS for the C, C₅ and C₁₂ migration.

3.1.1 The migration of single C atom. As far as the single C is concerned, there exist two stable adsorption sites (hcp and fcc) that belong to three-fold hollow sites on (111) surface. The migration process of hcp → fcc → hcp forms a cycle of C moving on the Ni (111) surface, and therefore reflects the surface migration ability of single C atom.

The rate determining step of migration corresponds to the process from hcp to fcc site. Interestingly, the diffusion energy barriers are a little different for different coverage of C atoms, as shown in Fig. 2(a).

3.1.2 The migration of carbon clusters. For the carbon chain of C₅ on a 5 × 5 supercell, the average coverage of C atoms is 20%. The stable adsorption states along 〈110〉 orientation of Ni (111) surface have two nonequivalent configurations since there exist two sorts of three-fold hollow sites (hcp and fcc). One diffusion cycle is shown in the second column of Fig. 2(d), which is similar to the case of single C atom. Along the reaction pathway, the initial state, intermediate state and final state are marked by IS, MS and FS, respectively. The calculated energy barrier is only 0.27 eV, less than that of a single C atom at the similar coverage (0.48 eV on a 2 × 2 surface with 25% coverage), as shown in Fig. 2(b). Of even greater concern is the migration of the sp² network because it could represent the main process of graphene growth in the initial stage. For the C₁₂ on the 5 × 5 supercell with about 50% coverage, the entire migration cycle is also composed of two diffusion steps, shown in third column of Fig. 2(d). The calculated energy barrier of the rate determining step is 0.35 eV, which is also less than that of a single C atom at the similar coverage (0.38 eV on 1 × 2 surface supercell with 50% coverage), shown in Fig. 2(c). These results suggest that the carbon clusters including both chain structures and network structures have the higher flexibility and advantage of mobility as compared with the single C atom, which is interesting and significant to understand the dynamic process of graphene growth.

In general, it is expected that the single C atom would be more flexible to migrate than the carbon islands (or chains) on the Ni surface. Additionally, the adsorption of the carbon cluster such as C₁₂ on Ni (111) is stronger than that of the single C atom. The former has a binding energy of 11.1 eV, larger than that of the later (6.7 eV), which also seems to indicate that single C atom would be more flexible. However, our results on diffusion barriers suggest that the migration of the carbon clusters are even more flexible on Ni surface. Therefore, it is necessary to give an explanation to these abnormal phenomena. Firstly, the detailed difference of the migration processes should be taken into account between single C atom and carbon cluster. The migration of single C atom is relatively simple because there is no structural strain of the adsorbate. But for a carbon cluster, structural strain in the adsorbate is quite important. And the energy of the structural strain will be changed significantly in the migration process. We take the C₁₂ diffusion as a sample to investigate the energy changes induced by the structural strain during the migration. To this end, we calculate the energies of the isolated C₁₂ with pseudomorphic structures as those in ISs and the transition state (TSs). Interestingly, the energy of C₁₂ in transition state is lower than that in IS by 0.48 eV, meaning that the structural strain of C₁₂ is released in the transition state due to weaker interaction between the adsorbate and substrate. The decrease of the strain energy of C₁₂ can lead to a lower energy of the C₁₂/Ni (111) system in the transition state, and is thus responsible for a small diffusion barrier. From the IS to the TS, the weakening of the interaction between C₁₂ and Ni substrate is a factor to increase the system energy in TS; meanwhile, the release of the structural strain of C₁₂ to some extent in the TS is a factor to decrease the system energy. The two factors determine the migration energy barrier of the carbon cluster. Thus we propose that, for C_n cluster, the relaxation of the structural strain in TS plays an important role for a relative small diffusion barrier. The discussions would be helpful to study the diffusion and migration of other clusters adsorbed on surfaces. Additionally, some experimental work has indeed shown that graphene domains on metal surfaces have high mobility.²⁴

As for the graphene growth in the initial stage, we are interested in the process that a carbon nanocluster grows to a larger one. At this point, an intuitional picture is that the carbon atoms dispersing on Ni surface migrate flexibly and randomly, then a larger nanocluster is formed by incorporating C atoms continuously. However, our calculated results present a novel picture for the carbon cluster growth, i.e., the small graphene islands may move easily on the Ni substrate and catch the dispersing carbon atoms, forming larger graphene flakes eventually.

3.2 The growth of carbon clusters

3.2.1 The bonding of carbon clusters and carbon atoms. In order to figure out the details that carbon atoms are caught by carbon clusters, we calculate the bonding between C atoms and carbon clusters. The corresponding reaction heats are listed in Table 1, and the configurations of IS and FS are displayed in Fig. 3.

Table 1 The reaction heats (in eV) and the forward (reverse) barriers (in eV) for the bonding between a C atom and carbon clusters, C_n (n = 1, 5, 12, 13)

Reaction hybridization	C + C → C2	C5 + C → C6		C12 + C → C13	C13 + C → C14
	sp	sp	sp^2	sp^2	sp
Reaction heat	−0.86	−0.81	0.07	−0.87	−0.52
Reaction barrier	0.76 (1.56)	0.63 (1.43)	1.00 (0.8)	0.72 (1.59)	0.64 (1.18)

---

Fig. 3 The configurations of ISs and FSs of the reactions listed in Table 1.

The results in Table 1 suggest that the growth of carbon cluster on Ni (111) is an exothermic process with a reaction heat of about 0.5–0.8 eV to form a C–C bond by sp or sp² hybridization. For the small carbon cluster such as C₅, the calculated results indicate that the sp² hybridization is not energetically preferred, which corresponds to an endothermic process with a forky structure formed, as shown in the third column of Fig. 3; while the sp hybridization is strongly exothermic, by which the C₅ chain turns into C₆ chain, as shown in the second column of Fig. 3. However, for the growth of network structures such as C₁₂, the calculated reaction heats suggest that the formation of the sp² bonds is energetically preferred with a strong exothermicity. The reaction barriers of the cluster growth are also given in the Table 1, in which the values in brackets are the reverse energy barriers, describing the dissociation process. If we ignore the unstable forked C₆, the energy barrier that the carbon cluster (C₅, C₁₂, and C₁₃) catches a C atom is always lower than that of the bonding between two C atoms, indicating the carbon cluster has stronger ability to catch other carbon atoms than a single C on Ni surface. In addition, the formation barriers of the carbon clusters (C₂, C₆ (chain), C₁₃, and C₁₄) are always lower than the reverse (dissociation) barriers, suggesting that the growth process of the carbon clusters is energetically preferred.

3.2.2 The bonding between two carbon clusters. Along with the growth of carbon clusters, more clusters are formed with the number of C atoms decreased, and then the bonding between carbon clusters will dominate. Therefore, the special growth mode through the bonding of two small carbon clusters is studied in detail. Firstly, we study the formation of the C_n with a chain structure. Taking the C₆ as an example, as shown in Table 1, three possible growth modes are considered, including C + C₅, C₂ + C₄, and C₃ + C₃ modes.

As shown in Table 2, both the C₂ + C₄ and C₃ + C₃ bonding modes have larger reaction barriers and less heat release than the C + C₅ mode shown in Table 1, which suggests that the formation of carbon chains (C_n) mainly depends on the bonding between the carbon cluster and C atoms, and the bonding between two carbon chains is not a preferred growth mode. However, for the large cluster with a sp² network structure, the trend is reversed. For instance, here we consider the bonding of two C₁₂ flakes. The calculated reaction heat is 1.43 eV, larger than that of the bonding between C₁₂ clusters and C atoms (0.87 eV). In this process two sp-hybridized carbon atoms turn into the sp²-hybridized carbon atoms with a C–C bond formed, as shown in the third column of Fig. 4, which is responsible for the large reaction heat. More significantly, the corresponding activation energy is only about 0.1 eV, which is much smaller than the barriers of the bonding between C₁₂ cluster and C atom (0.72 eV, as shown in Table 1), indicating that the joint of carbon clusters will be the leading growth mode as the coverage of carbon clusters is large enough. In addition, the very high migration rate of carbon cluster also supports this growth mode, as mentioned above.

Table 2 The reaction heats (in eV) and forward (reverse) barriers (in eV) for the bonding between two carbon clusters

Reaction	C2 + C4 → C6	C3 + C3 → C6	C12 + C12 → C24
Reaction heat	−0.4	−0.76	−1.43
Reaction barrier	1.1 (1.5)	0.98 (1.74)	0.1 (1.5)

---

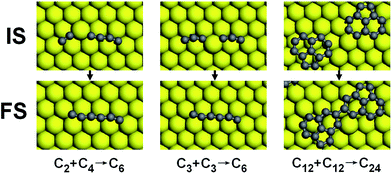Fig. 4 The configurations of ISs and FSs of the reactions listed in Table 2.

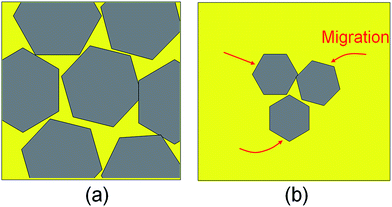
In experiments, structural defects do exist in graphene and can dramatically alter its properties. In fact, many characteristics of graphene-based materials such as the conductance and the mechanical strength are governed by the defects. Studying the formation mechanism of defects is thus very meaningful for graphene synthesis. In general, researchers tend to attribute the formation of structural defects to the high-density graphene islands. In this case the islands grow to the larger grains, and the merging of grains inevitably occurs, as shown by the sketch in Fig. 5(a).

Fig. 5 Sketch of the formation mechanism of interdomain defects in graphene growth: (a) the case of high nucleation density; (b) the case of low nucleation density. Gray hexagons represent graphene islands or grains.

The grain boundary would be formed in this growth process as these flakes have different crystal orientations, which is responsible for the formation of the structural defects of graphene in CVD synthesis. Therefore, experimenters always attempt to decrease the nucleation density for the synthesis of high-quality graphene.^25,26 However, the present work suggests that, even for the graphene islands with relative low-density, the bonding between islands is also a possible growth mode due to the high migration rate and low activation energy, and there still exist structural defects in graphene synthesis, as shown by the sketch in Fig. 5(b). Therefore, we highlight that, besides the nucleation density, the migration capability of the graphene islands is also an important aspect affecting the defect formation in graphene. In experiments, it is worth considering how to inhibit the islands migration to reduce the merging of graphene islands for the growth of perfect graphene crystals. For example, it is considerable to modify the properties of Ni substrates by introducing the metal or nonmetal dopants. Our investigations not only give a basic understanding on the universal existence of structural defects in graphene fabricated by the CVD method, but also provide the proposal that can guide the synthesis of single crystal graphene films by carefully engineering the substrate surface and selecting growth conditions.

3.2.3 The Brønsted–Evans–Polanyi (BEP) relationship in graphene growth on Ni substrates. Previous studies have suggested that metal substrates play an important role for graphene nucleation.^27,28 The different transition metal substrates have different effects on graphene synthesis. Therefore, it is meaningful to build a fitting description of substrates' properties based on first-principles calculations. In this section, we will give a discussion about these issues.

A number of dissociative reactions of gas molecules on metal surfaces show a linear BEP relation between the activation energy and the reaction energy.²⁹ It could be generalized as a rule for other types of surface catalytic reactions. In this work, we analyze the relationship between activation energies and reaction energies for plenty of reaction processes of the carbon clusters formation. Similarly, we can get the BEP relationship of graphene growth on Ni substrates, as shown in Fig. 6.

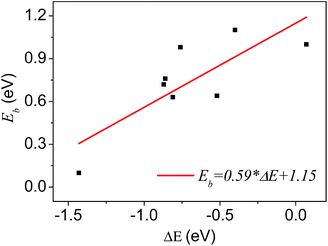Fig. 6 The BEP relationship in graphene growth on Ni substrates. The datas come from Tables 1 and 2. Each point represents a reaction related to the graphene growth, plotted by reaction heats on the horizontal axis and activation energies on the vertical.

It displays roughly a linear relationship between the activation energies and reaction heats in the growth process. The slope and intercept of the straight line are given in Fig. 6. Though, we get the linear relationship and the corresponding parameters (slope and intercept) by fitting datas of all reactions, it is the substrate properties that are responsible for these two parameters, and diverse substrates will give different parameters.¹⁴ From this base, we propose that, for the graphene growth, the catalytic properties of metal substrates can be depicted quantitatively by these two parameters (slope and intercept). Thus we could be able to get the characteristic parameters for each metal, such as Cu, Ir, Ru, and Ag, etc. In order to compare with Ni substrates, we simulated dimerization process of C atoms on pure Cu and Cu–Ni alloy substrates. On Cu surface the calculated reaction heat and activity energies of dimerization are 2.7 and 0.93 eV respectively, clearly different from those on Ni surface (0.86 and 0.76 eV). On Cu–Ni alloy surface with a ratio of 1 : 1, the reaction heat and activity energies of dimerization are 1.1 and 0.74 eV, which suggest alloying can tune both reaction heat and activity energy. These results are instructive and meaningful to study the alloying of substrate for excellent graphene synthesis.

4 Conclusions

The graphene growth in the initial stage of the CVD process is studied based on the density functional theory. Firstly, the migration of carbon clusters on Ni substrates is simulated. It is found that both the chain and the sp² network forms of clusters have higher flexibility and advantage of mobility as compared to the single carbon atom. This conclusion would offer a new understanding on the dynamics process of graphene growth. Next, two different growth modes of graphene are investigated systematically. In the first mode, i.e., the bonding of the carbon cluster with a carbon atom, the carbon chain prefers to the sp hybridization with the carbon atom and grows into a longer chain, while the sp² hybridization is not preferred in the carbon chain growth. For the carbon flake growth, the sp² hybridization between the cluster and C atoms is preferred with a large heat release. The second growth mode concerns the bonding between two clusters. The results suggest that the carbon chain growth does not prefer to take this mode because the bonding of two chains has relative large activation energy. However, the carbon flake of the sp² network would mainly take this growth mode with quite low activation barriers. For the one-dimensional carbon chain clusters and the two-dimensional carbon island clusters, the preferred growth modes are entirely different in the process of graphene growth. In addition, we propose that the second growth mode is significant even for the case with low-density graphene grains due to their high migration rate, which can help to understand the formation mechanism of structural defects in graphene growth. The conclusions in the present work are instructive to synthesize high-quality graphene in large scale.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant no. 11304084 and U1304109) and the High Performance Computing Centre of Henan Normal University.

Notes and references

1. S. Bae, H. Kim, Y. Lee, X. Xu, J.-S. Park, Y. Zheng, J. Balakrishnan, T. Lei, H. R. Kim and Y. I. Song, Nat. Nanotechnol., 2010, 5, 574–578.
2. K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J.-H. Ahn, P. Kim, J.-Y. Choi and B. H. Hong, Nature, 2009, 457, 706–710.
3. B. Kiraly, E. V. Iski, A. J. Mannix, B. L. Fisher, M. C. Hersam and N. P. Guisinger, Nat. Commun., 2013, 4, 2804.
4. S. Helveg, C. Lopez-Cartes, J. Sehested, P. L. Hansen, B. S. Clausen, J. R. Rostrup-Nielsen, F. Abild-Pedersen and J. K. Nørskov, Nature, 2004, 427, 426–429.
5. T. Iwasaki, H. J. Park, M. Konuma, D. S. Lee, J. H. Smet and U. Starke, Nano Lett., 2010, 11, 79–84.
6. X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang and R. Piner, Science, 2009, 324, 1312–1314.
7. M. P. Levendorf, C. S. Ruiz-Vargas, S. Garg and J. Park, Nano Lett., 2009, 9, 4479–4483.
8. P. Wu, H. Jiang, W. Zhang, Z. Li, Z. Hou and J. Yang, J. Am. Chem. Soc., 2012, 134, 6045–6051.
9. G. Barcaro, B. Zhu, M. Hou and A. Fortunelli, Comput. Mater. Sci., 2012, 63, 303–311.
10. D. Cheng, G. Barcaro, J.-C. Charlier, M. Hou and A. Fortunelli, J. Phys. Chem. C, 2011, 115, 10537–10543.
11. A. K. Geim, Science, 2009, 324, 1530–1534.
12. F. Banhart, J. Kotakoski and A. V. Krasheninnikov, ACS Nano, 2010, 5, 26–41.
13. X. Li, W. Cai, L. Colombo and R. S. Ruoff, Nano Lett., 2009, 9, 4268–4272.
14. Z. Fu, Y. Zhang and Z. Yang, Phys. Lett. A, 2015, 379, 1361–1365.
15. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
16. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
17. K. Schwarz, P. Blaha and G. Madsen, Comput. Phys. Commun., 2002, 147, 71–76.
18. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
19. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
20. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Phys. Chem., 2000, 113, 9901–9904.
21. G. Henkelman and H. Jonsson, J. Chem. Phys., 2000, 113, 9978–9985.
22. T. Zhu, J. Li and S. Yip, Phys. Rev. Lett., 2004, 93, 025503.
23. J. Gao, Q. Yuan, H. Hu, J. Zhao and F. Ding, J. Phys. Chem. C, 2011, 115, 17695–17703.
24. X. Li, C. W. Magnuson, A. Venugopal, J. An, J. W. Suk, B. Han, M. Borysiak, W. Cai, A. Velamakanni and Y. Zhu, Nano Lett., 2010, 10, 4328–4334.
25. Y. Hao, M. Bharathi, L. Wang, Y. Liu, H. Chen, S. Nie, X. Wang, H. Chou, C. Tan and B. Fallahazad, Science, 2013, 342, 720–723.
26. Q. Yu, L. A. Jauregui, W. Wu, R. Colby, J. Tian, Z. Su, H. Cao, Z. Liu, D. Pandey and D. Wei, Nat. Mater., 2011, 10, 443–449.
27. J. Gao, J. Yip, J. Zhao, B. I. Yakobson and F. Ding, J. Am. Chem. Soc., 2011, 133, 5009–5015.
28. Q. Yuan, J. Gao, H. Shu, J. Zhao, X. Chen and F. Ding, J. Am. Chem. Soc., 2012, 134, 2970–2975.
29. T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217.

---