Complexation of NpO2+ with (2-hydroxyethyl)ethylenediaminetriacetic acid (HEDTA) in aqueous solutions: thermodynamic studies and structural analysis†
Abstract
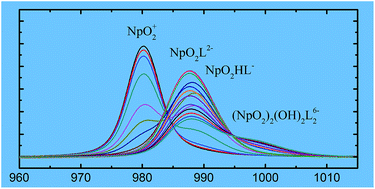
Complexation of Np(V) with N-(2-hydroxyethyl)ethylenediaminetriacetic acid (HEDTA) was studied in aqueous solution (I = 1.0 mol L−1 NaClO4, t = 25 °C) by spectrophotometry, microcalorimetry and Extended X-ray absorption fine structure (EXAFS) spectroscopy. Equilibrium constants for the formation of three complexes, NpO2L2−, NpO2(HL)−, and (NpO2)2(OH)2L26−, were determined to be (6.91 ± 0.06), (4.28 ± 0.03) and −(4.93 ± 0.03), respectively. The enthalpies of complexation were determined to be −(8.0 ± 2.0) kJ mol−1 for NpO2L2− and −(2.2 ± 2.0) kJ mol−1 for NpO2(HL)−. Thermodynamic data of the complexation of Np(V) with HEDTA were compared to those of Np(V) with other aminopolycarboxylic acids, gaining insight into the possible coordination modes of the complexes. The EXAFS studies provided further structural information on those modes. In both NpO2L2− and NpO2(HL)− complexes, HEDTA coordinates to Np(V) in a tridentate mode through two oxygens of two carboxylic groups and one nitrogen of the amine group. In the (NpO2)2(OH)2L26− complex, two Np(V) atoms are bridged by two hydroxides and each HEDTA maintains the tridentate coordination mode.
- This article is part of the themed collection: RSC Advances Editors' collection: f Block Chemistry


 Please wait while we load your content...
Please wait while we load your content...