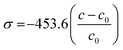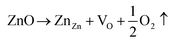Understanding the origin of ferromagnetism in Er-doped ZnO system

Abstract

The present study reports the structural, optical and magnetic properties of ZnO with doping of Er ions in low concentrations (0 ≤ x ≤ 0.05). X-ray diffraction (XRD) pattern shows that most Er ions are incorporated in the ZnO matrix when x ≤ 0.03, whereas few of them are present at interstitial sites. At higher concentrations, substitutional sites are occupied; therefore, Er ions form clusters at the interstitial sites of ZnO lattice or segregate on the surface, leading to lattice deformation. The lattice parameters and crystallite size initially decrease on doping with Er up to 3%, and increases for the highest dopant concentration (i.e., 5%). The surface morphology (particle size and porosity) changes with the introduction of Er ions into the host lattice. Magnetization follows the same trend as that of the structural parameters. The saturation magnetization first increases up to 3% of Er and then decreases thereafter. Such variations are understood on the basis of HRTEM, thermogravimetric (TGA), photoluminescence (PL) measurements and are then correlated with the results of X-ray photoelectron spectroscopy (XPS). PL results imply that the defect band edge is increased significantly for doping levels of 3% and a reduction is seen for 5%. TGA measurements reveal that there is a reduction in weight loss % with Er content from 0% to 3%, whereas a slight increase is noticed for Er 5%. XPS measurements show that Zn 2p edge is not altered after doping with Er, whereas there is a change in the peak intensity of oxygen 1s edge. Based on the results of PL, TGA and XPS, it is inferred that defects related to oxygen vacancies are mainly responsible for the magnetism in the present system.

---

1. Introduction

A wide variety of potential applications in advanced optoelectronic and spintronic devices have been demonstrated using ZnO owing to its wide band gap (∼3.3 eV), high exciton binding energy (60 meV) and the availability of lattice-matched substrates.^1–3 It is also non-toxic in nature, inexpensive and chemically stable. Although ZnO has been a well-studied material in last two decades, there has been renewed interest in the modification of its physical properties with the incorporation of rare earth ions. It has now been well established that the physical and chemical properties of ZnO can be dramatically altered simply by incorporating foreign ions in the host lattice and varying their concentrations.^4–7 Semiconductors doped with rare earth (RE) ions (Gd, Y, Er and Yb) have enabled promising applications in the field of optoelectronic devices owing to the involvement of intra-4f shell transitions.^8–12 It has been reported that the band gap of the host lattice can be reduced by doping with Ce.¹³ Relatively high photonic efficiencies and improved photocatalytic activity have been achieved by doping La in ZnO by Anandan et al.¹⁴ Doping with Er in ZnO films has resulted in modulation of their optical band gap and improvements in luminescence and optical properties. Apart from optoelectronic applications, recent studies have demonstrated that RE ions can induce magnetism in oxide semiconductors, which is an important phenomenon for spintronic device applications. However, the origin of ferromagnetic (FM) ordering is still not resolved and many researchers are working in this direction. Recent reports have shown that oxygen vacancies are mainly responsible, whereas others claim that Zn vacancies play a key role in ferromagnetic ordering.^5,15–17 A report by Straumal et al.¹⁸ explained that the presence of ferromagnetism is associated with grain boundaries and related vacancies. In order to be ferromagnetically aligned, the magnetic spins of the dopant should be distributed uniformly in the host lattice. Shi et al.¹⁹ examined the structural and magnetic properties of ZnO doped with RE ions (Gd and Nd) and concluded that coupling between RE ions in nearest neighboring sites gave rise to ferromagnetism. Another report on ZnO implanted with Gd established that indirect magnetic coupling leads to the development of room-temperature ferromagnetism (RTFM) and Gd/Zn clusters were found to be responsible for the observed behavior.²⁰ FM ordering in ZnO samples doped with Er was also found to be related to several factors such as bound magnetic polarons, Zn vacancies, Er clusters,^21,22 etc. However, there is still a lack of true understanding of FM ordering caused by RE dopants in wide-band-gap semiconductors. In the present study, we have focused on understanding the origin of RTFM in ZnO doped with Er. Samples were synthesized with different Er concentrations by solid-state reaction method and then examined for their structural, optical and magnetic properties.

2. Experimental details

ZnO samples doped with Er (0%, 1%, 3% and 5%, hereafter referred as Er-0, Er-1, Er-3 and Er-5) were synthesized using solid-state reaction method from ZnO and Er₂O₃ powders (Alfa Aesar, 99.995% purity). These powders were mixed and ground for 2 hours to obtain a uniform mixture, calcined at 800 °C for 6 h and then sintered at same temperature for the same duration to obtain a stable crystalline phase. X-ray diffraction (XRD) was carried out with a Panalytical X'Pert Pro X-ray diffractometer using Cu K_α radiation (1.54 Å) and the surface morphology was investigated with field emission scanning electron microscope (FEI Nova NanoSEM 450). An STR 500 confocal micro-Raman spectrometer (532 nm DPSS laser) and Microsense EV-9 vibrating sample magnetometer were used, respectively, for Raman spectroscopy and magnetic measurements of the samples. Thermogravimetric analysis (TGA) was carried out with Perkin Elmer simultaneous thermal analyzer (STA 6000) instrument from 30 °C to 900 °C at a heating rate of 3° min⁻¹ in an air ambient environment. The electronic properties were investigated using XPS from Oxford Instruments (with Al K_α source) at Materials Research Centre, MNIT, Jaipur.

3. Results and discussion

3.1 X-ray diffraction

Fig. 1 shows the XRD patterns of ZnO compounds doped with Er and all the diffraction peaks observed for ZnO are indexed to wurtzite phase with hexagonal structure (JCPDS file 36-1451). The incorporation of small amounts of Er₂O₃ into the host lattice resulted in additional peaks (marked as *) along with the diffraction peaks of ZnO. It is worth mentioning here that incorporating Er³⁺ ions into the ZnO host lattice does not guarantee that doped Er ions will be able to replace Zn²⁺ ions in the host lattice to form a solid solution of Zn_1−xEr_xO (uniformly distributed). In the present case, most of the Er atoms substitute Zn sites, as is evident from the shift in (101) diffraction peak, and very few of them occupy interstitial sites up to an Er doping level of 3%. A shift towards higher angles usually occurs when a dopant with larger ionic radius is substituted in the place of host with a smaller ionic radius. This strongly depends upon the synthesis method, annealing temperature and dopant concentration. At higher Er concentrations, cluster formation takes place and different behaviour is exhibited when compared with that of ZnO doped with low concentrations of Er.

Fig. 1 XRD patterns of ZnO doped with Er (0 ≤ x ≤ 0.05). The inset shows a magnification of the most intense (101) peak and * indicates a peak related to Er₂O₃.

It has been found that the intensity of the diffraction peaks decreases gradually with Er doping. In order to analyze the lattice parameters, strain and crystallite size of the samples, the raw data for the ZnO (100), ZnO (002) and ZnO (101) peaks were fitted and the exact values of the diffraction angle (2θ) and FWHM for ZnO (002) were calculated. The values of the a- and c-axis lattice parameters of ZnO were found to be 3.289 Å and 5.189 Å, respectively. The analysis of peaks revealed a small shift towards higher angles in the diffraction peaks for ZnO doped with Er (up to a doping of 3%) and a shift towards lower angles for 5% Er. The shifts in the diffraction peaks first toward higher and then lower angles resulted in changes in lattice parameters, are shown in Table 1. These changes in the lattice parameters are because of the difference in ionic radii of Er and Zn ions. The reverse trend at higher dopant concentrations is attributed to the solubility limit of Er in the ZnO lattice. At lower dopant concentrations (≤3%), Er ions occupies the substitutional sites and few of them are present at interstitial sites, whereas segregation/accumulation on the surface occurs at 5% Er, which distorts the ZnO crystal structure. Earlier reports on Mg doped ZnO, Y doped ZnO, C ion implanted ZnO and CeO₂ doped with Mn showed similar behavior (i.e., a non-uniform distribution of dopant ions above a certain limit of dopant concentration).^2,5,23–25

Table 1 Lattice parameters, stress and crystallite sizes obtained from XRD along with saturation magnetization

Sample	Lattice parameter (Å)		Stress (GPa)	Crystallite size (nm)	Dislocation density	Magnetization (emu g^−1)
	a-axis	c-axis			δ = 1/D^2 (m^−2) × 10^−14
Er-0	3.289	5.189	1.48	54.72	3.33	2.92
Er-1	3.283	5.174	2.79	53.07	3.55	4.44
Er-3	3.276	5.163	3.75	44.00	5.16	8.11
Er-5	3.295	5.193	1.13	52.35	3.65	3.64

---

It is expected that the substitution of larger Er³⁺ ions for Zn²⁺ ions produces local structural distortion in the lattice, which in turn causes stress in the system. The biaxial stress along the c-axis has been calculated using the following formula:²⁶

here, c and c₀ are the values of lattice parameters obtained from XRD measurements and JCPDS card 36-1451, respectively. The minus sign indicates compressive stress, whereas plus sign represents the tensile nature of the stress. Vijayalakshmi et al.²⁷ have reported that tensile stress is associated with the presence of oxygen vacancies, whereas compressive stress is likely to be attributed to the presence of Zn interstitials. The stress produced in the host lattice is responsible for the modification of various physical properties, in particular magnetic properties. The positive value in the present case indicates tensile stress (Table 1). The estimated value of tensile stress for pure ZnO sample was found to be ∼1.48 GPa and increased up to Er of 3% (∼3.75 GPa). A reduction in this parameter was observed at 5% in the host lattice (∼1.13 GPa).

The Scherrer equation (D = 0.89λ/β cos θ, where λ is the wavelength of X-rays, β is the FWHM and θ is Bragg angle) was used to calculate the crystallite size. A change in the crystallite size was observed owing to doping with Er. The FWHM of the peak increased on doping with Er, which resulted in a reduction in crystallite size up to doping of 3%. However, this decreases for highest Er doping (5%), as shown in Table 1. The calculated crystallite size of ZnO is 54.72 nm and decreases to 44.0 nm for ZnO doped with 3% Er. The obtained results have shown that the incorporation of Er³⁺ ions in Zn sites led to reduction in crystallite size up to x = 0.03. The XRD pattern implies that the decrease in crystallite size occurred owing to the difference between Er and Zn atoms. The addition of larger Er atom (0.88 Å) at Zn (0.74 Å) site in ZnO lattice would create tensile stress. The developing stress restricted the growth of grains, as a result of which the grain size decreases with an increase in Er concentration. Similar results have been obtained for ZnO doped with Er and Gd^7,28. However, for the Er-5 sample, the increase in crystallite size appears to be related to the segregation of ions on the surface.

For Er-5, Er atoms are unable to substitute Zn sites completely owing to segregation/clustering over the surface. This results in a relaxation of stress, as is evident from Table 1. Such a relaxation of stress enables the growth of grains and hence an increase in grain size.

3.2 Raman spectroscopy

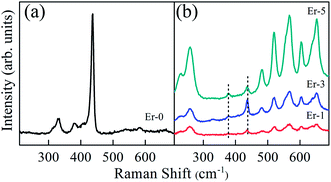
Raman spectroscopy provides complementary information related to the crystal structure, mainly the phase of materials. Fig. 2 shows the Raman spectra of pure and Er-doped ZnO samples. As discussed in the XRD section, ZnO crystallizes in wurtzite phase, having hexagonal crystal structure with space group P6₃mc (4 atoms per unit cell). According to group theory, the lattice vibrational modes of wurtzite ZnO at the Γ point of Brillouin zone are predicted from Γ_opt = A₁ + 2B₁ + E₁ + 2E²₂. Among these, the polar A₁ and E₁ vibrational modes (both Raman- and infrared-active) split into longitudinal optical (LO) and transverse optical (TO) phonons. The B₁ modes are silent in Raman scattering because these are infrared- and Raman-inactive. The non-polar E₂ modes are Raman-active and possess two frequencies, namely, E₂ (high) and E₂ (low), respectively. The E₂ (high) mode is associated with the motion of O atoms, whereas the E₂ (low) mode corresponds to the Zn sublattice.²⁹ The Raman spectrum of pure ZnO consists of peaks at ∼330 cm⁻¹, ∼380 cm⁻¹, 410 cm⁻¹, 437 cm⁻¹, 582 cm⁻¹ and 660 cm⁻¹. The most intense optical phonon E₂ (high) mode, which is located at ∼437 cm⁻¹, corresponds to the band that is characteristic of the wurtzite crystal structure. The strong E₂ (high) mode demonstrates that pure ZnO sample has a highly crystalline hexagonal structure, in accordance with the XRD results. The three weak peaks at ∼380 cm⁻¹, 410 cm⁻¹ and 582 cm⁻¹ are attributed to the A₁ (TO), E₁ (TO) and A₁ (LO) modes, respectively.

Fig. 2 Raman spectra of (a) ZnO and (b) Er-doped ZnO.

The occurrence of TO modes reflect the strength of polar lattice bonds, whereas LO modes signify the presence of long-range electrostatic order in the system.³⁰ The other two peaks at ∼330 cm⁻¹ and ∼660 cm⁻¹ are assigned to multiple-phonon scattering processes corresponding to E₂ (high)–E₂ (low) and 2E₂ (high)–2E₂ (low) modes, respectively.³¹ The profile and peak positions are related to the degree of crystallization, residual stress, structural disorder and defects, which can be tailored. The substitution of Er modifies the peak intensity with the generation of new additional bands. XRD results have shown the presence of additional peaks corresponding to Er₂O₃ along with ZnO peaks. Er₂O₃ crystallizes in the cubic structure with the space group la3(T⁷_h). In accordance with the XRD results, the Raman spectra also display some additional bands and their intensities vary depending upon the Er concentration. The intensity of additional peaks continues to increase with Er concentration.

3.3 Scanning electron microscopy

Pure and Er-doped ZnO samples were examined by FESEM and HRTEM to obtain information related to their surface morphology and microstructure. The SEM images (shown in Fig. 3) show the formation of well-defined crystals for all samples. The samples have a wide range of particle size distributions with an average particle size of 120–130 nm. Small agglomerations are visible at the highest Er concentration (5%), which is attributed to the fact that Er ions were accumulated/segregated over the surface for this composition. Chemical analysis by energy dispersive X-ray spectroscopy (EDX) technique in SEM was performed to confirm the composition of the samples. An increase in the Er with a simultaneous decrease in Zn content (not shown here) was noticed with Er in ZnO.

Fig. 3 SEM images of Er-doped ZnO showing variations in the morphology.

3.4 Transmission electron microscopy

TEM analysis of pure and Er-doped ZnO nanoparticles was performed (Fig. 4) on samples prepared over a TEM grid. The preparation included sonication for 2 h and then drying for more than 15 h. The crystallographic planes of ZnO and Er-doped ZnO were determined using fast Fourier transform (FFT) and inverse FFT analysis of the high-resolution transmission electron micrograph. The HRTEM images of ZnO and Er-doped ZnO showed agglomerated polycrystalline structures. The lattice spacings were found to be 2.82 Å and 2.49 Å, respectively, corresponding to (100) and (101) planes of ZnO, which confirmed the wurtzite structure of the nanocrystallites.²⁶ These results confirm that the particles are composed of several grains and exhibit anisotropy in the shape of different grains corresponding to different planes.

Fig. 4 HRTEM images with corresponding SAED patterns (insets) of Er-doped ZnO samples. In this figure, () represents ZnO planes whereas [] corresponds to Er₂O₃ planes.

The sample with Er of 3% also displays a polycrystalline structure with the presence of Er₂O₃ [211] and [222] planes. There is negligible variation in the lattice constants with Er doping of 5% for both ZnO (100) and (101) planes. The corresponding selected-area electron diffraction (SAED) patterns, which are shown in the insets of Fig. 4, indicate the polycrystalline structure of the samples. The results from TEM analysis are consistent with XRD data. The crystallographic information indicates preferential growth of ZnO (101) plane compared with other (100) and (002) planes. For Er₂O₃, the growth occurs in the [222] and [211] planes, as can be seen clearly from HRTEM image of ZnO doped with 3% Er. Furthermore, elemental mapping performed via STEM EDX demonstrated that Zn, O and Er ions (Fig. 5d–f) are distributed homogeneously throughout the structure and are clearly seen in both ZnO and Er-doped ZnO.

Fig. 5 Elemental image mapping from TEM for ZnO: (a) Zn, (b) O, and (c) Zn and O; ZnO doped with 3% Er: (d) Zn, (e) O and (f) Er ions.

3.5 Magnetic properties

Magnetization is very sensitive to the microstructure, defect structure and dimensions of samples. A curve of magnetization versus magnetic field (M–H curve) is the main method of evaluating the magnetic properties of any material. Fig. 6 shows the magnetization hysteresis loops of the Er-doped ZnO samples.

Fig. 6 M–H curves at 300 K for Er-doped ZnO. An increase in the saturation magnetization is observed up to Er 3% and the magnetization decreases thereafter.

All the samples exhibit FM ordering and the saturation magnetization for ZnO was found to be ∼2.92 × 10⁻³ emu g⁻¹. In the present case, the order of magnetization was less than that of samples grown using chemical methods, e.g., sol–gel techniques (nanoparticles) and physical methods (RF sputtering/pulsed laser deposition), as the solid-state reaction method does not involve any chemical treatment. FM ordering in ZnO has been observed by various groups and attributed to the presence of intrinsic defects (such as d⁰-FM mediated by oxygen vacancies) in the host lattice.^5,32 A similar mechanism is responsible for the presence of FM in the samples under investigation and can be associated with intrinsic defects (most probably oxygen vacancies). It can be seen that the saturation magnetization (M_s) does not vary monotonically with an increase in Er concentration. It is clear that the ZnO sample doped with 3% Er exhibited the highest magnetization of ∼8.11 × 10⁻³ emu g⁻¹. As is evident, the magnetic properties of oxide semiconductors are determined by the localized magnetic moments associated with the dopant and their interaction with the host semiconductor. In RE dopants, 4f electrons are responsible for the induced magnetic moments. The 4f electrons are localized and there are indirect exchange interactions among them. Owing to their indirect exchange interactions and high orbital momentum, 4f electrons have a high total magnetic moment per atom compared with that of 3d TM electrons.³³ Different models have been proposed for the magnetic ordering in ZnO doped with Er, which has been attributed to several factors such as Er clusters,³⁴ bound magnetic polarons²¹ and the presence of defects such as O and Zn vacancies. Coey et al.³⁵ have proposed a model known as the bound magnetic polaron (BMP) model to understand the origin of magnetism in ZnO doped with TM ions and rare earths. In this model, FM is mediated via various types of intrinsic defects such as O vacancies (V_O), Zn vacancies (V_Zn), Zn interstitials (Zn_i), and O interstitials (O_i). When a trivalent ion is incorporated in the ZnO matrix, O vacancies occur naturally to maintain charge neutrality. In this case, there will be an interaction between Er ions via O vacancies (Er³⁺–V_O–Er³⁺). Electrons are locally trapped in the oxygen vacancy by occupying an orbital that overlaps with the 4f shells of the neighbouring Er atoms and forming BMPs that lead to long-range FM ordering. However, the exact relationship between these defects and magnetism in ZnO-based DMS materials is still in question. A similar kind of variation has been reported for Er, as well as other ZnO samples doped with RE.²² These results indicate that for lower Er contents (up to x = 0.03), the ferromagnetic character is enhanced; however, further increase in Er (x = 0.05) leads to reduction in magnetization. This means 3% Er in ZnO is a critical point above which various physical properties are altered. The incorporation of larger amount of Er ions (5%) leads to the reduction in FM ordering (∼3.64 × 10⁻³ emu g⁻¹). This is related to the fact that at higher concentrations, antiferromagnetic interactions among the Er ions predominate over the magnetic ordering caused by the presence of defects. Also, at higher concentrations, Er ions reach saturation and appear at interstitial sites. The density of V_O (O ratio) initially increases on doping with Er and then decreases at x = 0.05, which implies that Er interstitials may suppress the formation of V_O. In order to discover the type of defects responsible for the observed magnetic coupling, photoluminescence, TGA and XPS measurements were performed on these samples.

3.6 Thermogravimetric analysis

Fig. 7 shows the loss in weight percentage with temperature from 30 to 900 °C. The TGA curve shows a small reduction in weight percentage for all samples. It is well known that the vapor pressure of oxygen is much higher compared with that of Zn; therefore, oxygen evaporates first at elevated temperatures, according to this equation:³⁶

Fig. 7 TGA curves for Er-doped ZnO (0 ≤ x ≤ 0.05) showing the reduction in weight percentage with temperature caused by oxygen vacancies.

The reduction in weight percentage with an increase in temperature is related to the evaporation of oxygen from the samples. The maximum loss takes place in the temperature range of 200–450 °C. Furthermore, it is noted that the weight loss was greater for Er contents of 3%, whereas the variation was less for the highest concentration. It has already been stated that an increase in the loss in weight percentage is directly related to oxygen vacancies. The addition of trivalent Er ions at Zn sites creates oxygen vacancies to maintain the charge neutrality. The presence of large number of oxygen vacancies in the composition with Er content of 3% is responsible for the maximum magnetization.

3.7 X-ray photoelectron spectroscopy

XPS measurements provide information on the chemical composition and electronic structure and enable the type of defects in a system to be determined. XPS spectra of pure and Er-doped ZnO samples are shown in Fig. 8A–D and consist of peaks corresponding to C, O, Zn and Er. The binding energy scale was corrected by considering the carbon correction (C 1s peak at 284.6 eV). The Zn 2p spectrum (Fig. 8A) for pure ZnO consists of two strong peaks at ∼1021.1 eV and 1044.3 eV, which correspond to Zn 2p_3/2 and Zn 2p_1/2 states, respectively. The difference between the binding energies for these two peaks was found to be 23.2 eV, which is in close agreement with the reported value.⁵ The positions of both peaks and the difference in their binding energies reveal that Zn ions in the +2 oxidation state are bound to oxygen in the ZnO matrix.⁵ The Zn 2p spectra show that the spectra for all samples closely resemble each other. This indicates that doping with Er does not affect the electronic states of Zn; therefore, the presence of Zn interstitials/vacancies is neglected. The spectral feature for ZnO doped with 3% Er (Fig. 8B) at a binding energy of ∼169.4 eV is attributed to the 4d levels of Er³⁺ ions forming a multiplet via an interaction with an unfilled shell.

Fig. 8 XPS spectra of (a) Zn 2p core-level spectra of pure, 3% and 5% Er-doped ZnO; (b) Er 4d core-level spectra of 3% and 5% Er-doped ZnO, and O 1s core-level spectra of (c) pure and (d) 3% Er-doped ZnO.

Further analysis of the O K-edge spectra infers that the feature can be deconvolved into two peaks at ∼530.4 eV and ∼532.8 eV, respectively, for pure ZnO. The peak positioned at ∼530.4 eV (lower binding energy) is ascribed to the wurtzite structure of hexagonally arranged Zn²⁺ ions in the metal oxide. The other peak present at higher binding energy (532.8 eV) might be related to different components such as oxygen vacancies and absorbed oxygen and hydroxyl groups.^37,38 On the basis of existing literature, it is inferred that the presence of peak at higher binding energy is associated with oxygen vacancies in the system.^38,39 With the introduction of Er ions in ZnO lattice, the intensity of the peak at higher binding energy is increased, indicating an increase in oxygen vacancies, which in turn is responsible for the enhanced saturation magnetization with Er.

3.8 Photoluminescence measurements

To identify the defects responsible for the magnetism observed in these materials, PL measurements were carried out and the results are shown in Fig. 9. These spectra consist of near band edge (NBE) emission in the UV region and deep-level emission (DLE) band in the visible region.² According to the existing literature, NBE band originates owing to the recombination of free electrons in the conduction band and holes in the valence band.^5,40,41 This band is associated with the most preferred (002) orientation (c-axis) of ZnO.

Fig. 9 PL spectra of Er-doped ZnO showing the change in the peak intensity of NBE and DLE bands with Er doping.

The band gap of pure ZnO has been found to be ∼3.20 eV. With the incorporation of Er ions, the band edge displays a small red shift. However, the intensity of this band is significantly reduced, which is well correlated with the reduction in intensities of diffraction peaks observed by XRD. It was mentioned above that the NBE emission is related to the most preferred (002) orientation (c-axis) of ZnO; therefore, the decrease in the NBE peak implies a reduction in crystallinity, as evidenced by XRD. Similar kinds of results have also been observed by Asikuzun et al. and Dakhel et al. for ZnO doped with Er as well as Gd.^7,28

Apart from NBE band, DLE band provides information related to intrinsic site defects that are present in the system and was found to be dominant for samples doped with Er. The DLE band in the visible region consists of violet, green, and orange-red regions, which correspond to defect levels for zinc interstitials (Zn_i), oxygen vacancies (V_O), and oxygen interstitials (O_i), respectively.⁵ The PL spectra of Er-doped ZnO samples consist of broad band centered at ∼530 nm (∼2.34 eV). The peak intensity of this band was found to increase significantly with Er ions up to 3%. Therefore, PL measurements confirm that the substitution of Er creates large numbers of V_O. This is in agreement with the fact that these vacancies are responsible for increase in saturation magnetization. Now, the question arises about the type of defects that mainly contributes to the magnetization in the present system. Both V_O and V_Zn exist as native vacancies in pure ZnO. In n-type ZnO, V_O defects act as donors and their concentration is higher when compared with that of the dominant acceptor (V_Zn).^42–44 Based on PL measurements, it is quite difficult to distinguish V_Zn from V_O owing to a slight difference in their emission centers. The enhanced green emission band is normally attributed to the increase in O vacancies with the introduction of foreign ions into the host lattice. The presence of tensile stress (as observed via XRD) is indicative of the presence of O vacancies. The TGA results imply that an increase in the Er concentration leads to a reduction in the content of oxygen ions and generates oxygen vacancies. Furthermore, XPS measurements confirm the presence of oxygen vacancies in the pure as well as in Er-doped ZnO.

On the basis of current observations and the existing literature, it can be inferred that V_O defects are mainly responsible for the FM in pure and Er-doped ZnO. V_O defects exist in three different charge states: F⁰ (doubly occupied), F⁺ (singly occupied), and F²⁺ (unoccupied).⁴⁵ Zhan et al.⁴² have shown that the peak at ∼580 nm arises owing to F²⁺ vacancies, whereas the peak in the region of 510–535 nm (∼530 nm in the present case) is attributed to F⁺ vacancies. Furthermore, Coey et al.³⁵ have found that F⁰ and F²⁺ vacancies have spin-zero ground states and are not able to induce a magnetic signal in the lattice. Therefore, the magnetic contribution mainly originates owing to singly ionized (F⁺) oxygen vacancies, which are paramagnetic in nature. The F⁺ charge state can activate BMPs in dilute magnetic semiconductors.⁴² In this model, a defect (oxygen vacancy) could capture a mobile electron to form a hydrogen-like orbital of a certain radius. When the defect concentration reaches a certain level, narrow impurity band is formed with the overlap of orbitals. The doped magnetic ions within this radius are associated with the electrons in the impurity band to become ferromagnetic. In the present case, oxygen vacancies are generated by the substitution of Er ions in the ZnO lattice and their presence is confirmed with the help of versatile techniques such as PL, TGA and XPS. Thus, whenever the concentration of surface defects is greater than the percolation threshold, surface defects overlap with dopants as well as with adjacent defects, resulting in the formation of Er³⁺–V_O–Er³⁺ groups, which indicates ferromagnetic coupling among dopant spins.⁴⁶ Therefore, we can speculate that FM originates owing to Er³⁺ ions and are mediated via oxygen vacancies along with a very small contribution from Er₂O₃.

4. Conclusion

Dilute concentrations of Er ions were doped in ZnO using solid-state reaction method and samples were investigated for variations in their physical properties, mainly structural, optical and magnetic properties. XRD results show reduction in lattice parameters as well as crystallite size for Er concentrations up to x = 0.03, whereas the values of these parameters increase at higher Er concentrations (5%). It can be concluded based on these observations that x = 0.03 is a critical value for providing modified physical properties, mainly optical and magnetic properties. The saturation magnetization was found maximum at this concentration and then decreases for 5% Er. This variation in magnetic behavior is explained on the basis of the concentration and nature of defects, as revealed by PL, TGA and XPS measurements. PL measurements imply that oxygen vacancies are the dominant defects in the crystal structure and increase up to the critical concentration of 3% and then decreases at higher dopant concentration of 5%. A loss in weight percentage occurs on heating the samples and explained in terms of oxygen vacancies, which can be matched with the magnetization results. Based on these various characterizations and close observations, our results suggest that the FM originates owing to the substitution of Er³⁺ ions and are mediated via oxygen vacancies along with a very small contribution from the Er₂O₃ phase.

Acknowledgements

PK would like to acknowledge the Department of Science and Technology for providing the financial support under the DST-Inspire Faculty Scheme [No. DST/INSPIRE/04/2015/003149] and MRC, MNIT Jaipur for the experimental support.

References

1. T. H. Flemban, M. C. Sequeira, Z. Zhang, S. Venkatesh, E. Alves, K. Lorenz and I. S. Roqan, J. Appl. Phys., 2016, 119, 065301.
2. P. Kumar, J. P. Singh, Y. Kumar, A. Gaur, H. K. Malik and K. Asokan, Curr. Appl. Phys., 2012, 12, 1166–1172.
3. A. Kumar, P. Kumar, K. Kumar, T. Singh, R. Singh, K. Asokan and D. Kanjilal, J. Alloys Compd., 2015, 649, 1205–1209.
4. P. Kumar, H. K. Malik, A. Ghosh, R. Thangavel and K. Asokan, Appl. Phys. Lett., 2013, 102, 221903.
5. P. Kumar, H. K. Malik and K. Asokan, Europhys. Lett., 2015, 110, 67006.
6. P. Kumar, R. Joshi, A. Gaur, L. Kumar and K. Asokan, Mater. Res. Express, 2015, 2, 045901.
7. E. Asikuzun, O. Ozturk, L. Arda, A. T. Tasci, F. Kartal and C. Terzioglu, Ceram. Int., 2016, 42, 8085–8091.
8. A. K. Pradhan, L. Douglas, H. Mustafa, R. Mundle, D. Hunter and C. E. Bonner, Appl. Phys. Lett., 2007, 90, 072108.
9. E. Alves, E. Rita, U. Wahl, J. G. Correia, T. Monteiro, J. Soares and C. Boemare, Nucl. Instrum. Methods Phys. Res. B, 2003, 206, 1047–1051.
10. A. Layek, S. Banerjee, B. Manna and A. Chowdhury, RSC Adv., 2016, 6, 35892–35900.
11. K. C. Verma and R. K. Kotnala, Phys. Chem. Chem. Phys., 2016, 18, 17565–17574.
12. I. Bantounas, V. Singaravelu, I. S. Roqan and U. Schwingenschlogl, J. Mater. Chem. C, 2014, 2, 10331–10336.
13. J. Iqbal, X. Liu, H. Zhu, C. Pan, Y. Zhang, D. Yu and R. Yu, J. Appl. Phys., 2009, 106, 083515.
14. S. Anandan, A. Vinu, K. L. P. Sheeja Lovely, N. Gokulakrishnan, P. Srinivasu, T. Mori, V. Murugesan, V. Sivamurugan and K. Ariga, J. Mol. Catal. A: Chem., 2007, 266, 149–157.
15. I. Lorite, B. Straube, H. Ohldag, P. Kumar, M. Villafuerte, P. Esquinazi, C. E. Rodríguez Torres, S. Perez de Heluani, V. N. Antonov, L. V. Bekenov, A. Ernst, M. Hoffmann, S. K. Nayak, W. A. Adeagbo, G. Fischer and W. Hergert, Appl. Phys. Lett., 2015, 106, 082406.
16. M. Venkatesan, C. B. Fitzgerald, J. G. Lunney and J. M. D. Coey, Phys. Rev. Lett., 2004, 93, 177206.
17. M. Khalid, M. Ziese, A. Setzer, P. Esquinazi, M. Lorenz, H. Hochmuth, M. Grundmann, D. Spemann, T. Butz, G. Brauer, W. Anwand, G. Fischer, W. A. Adeagbo, W. Hergert and A. Ernst, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 035331.
18. B. B. Straumal, A. A. Mazilkin, S. G. Protasova, A. A. Myatiev, P. B. Straumal, G. Schütz, P. A. van Aken, E. Goering and B. Baretzky, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205206.
19. H. Shi, P. Zhang, S.-S. Li and J.-B. Xia, J. Appl. Phys., 2009, 106, 023910.
20. K. Potzger, S. Zhou, F. Eichhorn, M. Helm, W. Skorupa, A. Mücklich, J. Fassbender, T. Herrmannsdörfer and A. Bianchi, J. Appl. Phys., 2006, 99, 063906.
21. J. Qi, Y. Yang, L. Zhang, J. Chi, D. Gao and D. Xue, Scr. Mater., 2009, 60, 289–292.
22. P. P. Murmu, J. Kennedy, B. J. Ruck and J. Leveneur, Nucl. Instrum. Methods Phys. Res. B., 2015, 359, 1–4.
23. P. Kumar, Y. Kumar, H. K. Malik, S. Annapoorni, S. Gautam, K. H. Chae and K. Asokan, Appl. Phys. A: Mater. Sci. Process., 2014, 114, 453–457.
24. P. Kumar, V. Singh, V. Sharma, G. Rana, H. K. Malik and K. Asokan, Ceram. Int., 2015, 41, 6734–6739.
25. P. Kumar, P. Kumar, A. Kumar, R. C. Meena, R. Tomar, F. Chand and K. Asokan, J. Alloys Compd., 2016, 672, 543–548.
26. P. Kumar, J. P. Singh, H. K. Malik, S. Gautam, K. H. Chae and K. Asokan, Superlattices Microstruct., 2015, 78, 183–189.
27. K. Vijayalakshmi, A. Renitta and K. Karthick, Ceram. Int., 2014, 40, 6171–6177.
28. A. A. Dakhel and M. El-Hilo, J. Appl. Phys., 2010, 107, 123905.
29. V. E. Kaydashev, E. M. Kaidashev, M. Peres, T. Monteiro, M. R. Correia, N. A. Sobolev, L. C. Alves, N. Franco and E. Alves, J. Appl. Phys., 2009, 106, 093501.
30. L. Bergman, J. L. Morrison, X.-B. Chen, J. Huso and H. Hoeck, Appl. Phys. Lett., 2006, 88, 023103.
31. L. Chun, F. Guojia, X. Sheng, Z. Dongshan and Z. Xingzhong, Nanotechnology, 2006, 17, 5367.
32. J. M. D. Coey, Solid State Sci., 2005, 7, 660–667.
33. R. John and R. Rajakumari, Nano-Micro Lett., 2012, 4, 65–72.
34. H.-M. Chen, X.-C. Liu, S.-Y. Zhuo, Z. Xiong, R.-W. Zhou, F. Li and E.-W. Shi, AIP Adv., 2014, 4, 047121.
35. J. M. D. Coey, M. Venkatesan and C. B. Fitzgerald, Nat. Mater., 2005, 4, 173–179.
36. Z. Q. Chen, S. Yamamoto, M. Maekawa, A. Kawasuso, X. L. Yuan and T. Sekiguchi, J. Appl. Phys., 2003, 94, 4807–4812.
37. G. Gaggiotti, A. Galdikas, S. Kačiulis, G. Mattogno and A. Šetkus, J. Appl. Phys., 1994, 76, 4467–4471.
38. F. Li, X.-C. Liu, R.-W. Zhou, H.-M. Chen, S.-Y. Zhuo and E.-W. Shi, J. Appl. Phys., 2014, 116, 243910.
39. X. Q. Wei, B. Y. Man, M. Liu, C. S. Xue, H. Z. Zhuang and C. Yang, Phys. B, 2007, 388, 145–152.
40. B. Lin, Z. Fu and Y. Jia, Appl. Phys. Lett., 2001, 79, 943–945.
41. B. J. Jin, H. S. Woo, S. Im, S. H. Bae and S. Y. Lee, Appl. Surf. Sci., 2001, 169–170, 521–524.
42. P. Zhan, W. Wang, C. Liu, Y. Hu, Z. Li, Z. Zhang, P. Zhang, B. Wang and X. Cao, J. Appl. Phys., 2012, 111, 033501.
43. F. Tuomisto, V. Ranki, K. Saarinen and D. C. Look, Phys. Rev. Lett., 2003, 91, 205502.
44. S. Lany and A. Zunger, Phys. Rev. Lett., 2007, 98, 045501.
45. D. Pan, G. Xu, L. Lv, Y. Yong, X. Wang, J. Wan, G. Wang and Y. Sui, Appl. Phys. Lett., 2006, 89, 082510.
46. D. Arora, K. Asokan, A. Mahajan, H. Kaur and D. P. Singh, RSC Adv., 2016, 6, 78122–78131.

---