The implications of various molecular interactions on the dielectric behavior of cimetidine and cimetidine hydrochloride
M. Rams-Baron*ab,
Z. Wojnarowskaab,
A. Jedrzejowskaab,
A. Swiety-Pospiechab and
M. Paluchab
aInstitute of Physics, University of Silesia, Uniwersytecka 4, 40-007 Katowice, Poland. E-mail: marzena.rams-baron@us.edu.pl
bSilesian Center for Education and Interdisciplinary Research, 75 Pulku Piechoty 1a, 41-500 Chorzow, Poland
First published on 14th November 2016
Abstract
Herein, we employed broadband dielectric spectroscopy to characterize the molecular dynamics of the two related materials, cimetidine base and cimetidine hydrochloride, with similar structural skeletons but involving different molecular interactions (ionic vs. non-ionic). BDS experiments performed at ambient and elevated pressures, combined with rheology and temperature-modulated calorimetry studies, revealed significant discrepancies in the supercooled dynamics of both samples. The strong electrostatic interactions resulted in slower dynamics of the ionic counterparts, manifested by a higher Tg value. However, the samples exhibited some similarities in the glassy dynamics. The dielectric response of cimetidine hydrochloride revealed features similar to those previously observed for the other molten hydrochloride salts, wherein decoupling between the timescales of the structural and ionic displacements affirms the universal character of the behavior presented herein.
Introduction
Molecular dynamics studies have attracted significant attention of the scientific community since they can provide answers to the questions that have long been unresolved. Experimental and theoretical efforts were addressed to investigate the various glass-forming materials (i.e. van der Waals liquids, polymers, metallic glasses, and ionic liquids) with diverse dynamic behavior patterns. It is believed that the systematic search for the common features will help to elucidate the nature of glass transitions and even to reach a definitive theory of this fascinating phenomenon. However, only a deep understanding of the fundamental problems may result in significant advancement in the use of glass-forming materials in various industrial areas in the future.It is widely known that the dynamics of glass-forming liquids do not depend only on the chemical structure, but are also governed by the interplay of the intermolecular attractions involved. Hence, finding a quantitative correlation between the relaxation properties and existing interactions remains the prime goal of the ongoing research activity. The most universal way to describe the potential between the two interacting neutral particles relies on the application of an empirical Lennard-Jones (LJ) equation:1
 | (1) |
In the past two decades, ionic liquids (ILs) have attracted growing interest, and nowadays, they find outstanding roles in applied science. This is due to the fact that these liquid-state salts may cover a wide range of properties that are attractive with regard to a multitude of daily and industrial applications. Among ILs, protic ionic liquids (PILs), obtained by the proton transfer from a Brønsted acid to Brønsted base, create a distinctive group with unique features arising from their ability to enhance the proton transfer through a hydrogen-bonded network.4 Due to the increasing interest in the properties of PILs, the amount of research dedicated to a better understanding of their proton transport behavior has systematically grown. At the same time, significant progress has been made with respect to the theoretical and computational approaches, shedding more light on the crucial structure–property relationships.5 Investigations dealing with ionic materials in relation to their non-ionic counterparts have been particularly insightful, providing an excellent survey of the interplay of various molecular factors governing their unique features. However, a limited number of analogous experimental investigations have been reported. This may be due to the specificity of each class of such systems, which may cause their shared experimental characteristics to be challenging at times. However, this may be overcome by using broadband dielectric spectroscopy (BDS), a method being designed to explore the dynamic processes with a distinct molecular origin.
Herein, we present dielectric relaxation studies on cimetidine (CIM) base and cimetidine hydrochloride (CIM HCl). Both materials are pharmaceutically relevant since they are histamine H2-receptor antagonists that inhibit the production of acid in the stomach. Although the structural cores of both materials are similar (see Fig. 1), the course and character of the molecular attractions involved are totally different. CIM HCl belongs to the PILs class, whereas CIM base can be considered as a van der Waals liquid. In the present study, we use the BDS method to get an insight into their dynamics over a broad range of frequencies, temperatures, and pressures. Since the selected materials are characterized by the opposite, neutral, and ionic natures, it is obvious that each of them will possess unique dynamic features. Herein, we focus on verifying how the variations in the intramolecular potentials will be reflected in the parameters describing (i) the many-body cooperative dynamics in a supercooled liquid regime, (ii) faster local dynamics observed below Tg, and (iii) the sensitivity of the dynamics to the applied pressure. To achieve a complete insight into the issues raised, the dielectric investigations were supported by rheological and temperature-modulated differential scanning calorimetry experiments.
Materials and methods
Investigated materials
Crystalline cimetidine base (CIM) and cimetidine hydrochloride (CIM HCl) were purchased from Sigma-Aldrich as crystalline powders. Both materials were characterized with purity greater than 98%. The amorphous forms of both the samples were prepared by quench cooling of the melt. The crystalline powder was placed on a heating block until complete melting was achieved. After that, the sample was quickly transferred to a very cold metal plate. The melting temperatures, determined by means of DSC, were Tm = 414 K and Tm = 461 K for CIM base and CIM HCl, respectively. Since it is well known that glasses have history-dependent properties, therefore, considering this, we precisely controlled the conditions for the sample preparation and performed the analogous preparation routes for both materials.Dielectric measurements at ambient and elevated pressures
Dielectric measurements were performed under atmospheric pressure using a Novocontrol GMBH Alfa analyzer with frequency values limited to 106 Hz. The temperature was precisely controlled with a Quatro temperature controller using a nitrogen gas cryostat (accuracy better than 0.1 K). During the measurements, the tested samples were placed between the steel electrodes of a capacitor (15 mm diameter), with a fixed distance between the electrodes (0.1 mm) provided by fused silica spacer fibers. The same experimental setup was used in time-dependent dielectric measurements.The pressure-dependent dielectric measurements were performed using an automatic high-pressure system developed by Unipress. As above mentioned, the investigated sample was placed between the steel electrodes of the capacitor (diameter 15 mm; gap 0.1 mm; Teflon spacer). Then, the capacitor was placed inside a Teflon ring and sealed. The tested sample, which was not in contact with the compression medium, was fixed to a pressure chamber filled with silicon oil.
Temperature-modulated differential scanning calorimetry (TMDSC)
Stochastic temperature-modulated differential scanning calorimetry (Mettler-Toledo) was used to determine the structural relaxation times. The quenched samples were analyzed at a heating rate of 0.5 K min−1. In the experiment, a temperature amplitude of 0.5 K for the pulses was selected at a switching time range with minimum and maximum values of 15 and 30 s, respectively. The relaxation times, τα = 1/2πf, were determined from the temperature dependences of the real part of the complex heat capacity c′p(T), obtained at different frequencies in the glass transition region.Rheological (RH) measurements
The rheological measurements were carried out using an ARES-G2 rheometer (TA Instruments), in which the sample was placed between two 8 mm diameter parallel circular plates with a controlled gap distance. During the experiments, we measured the dynamic shear modulus G*(f) by applying an oscillatory strain and measuring the resultant stress. The strain was produced by rotating the bottom plate, whereas the stress was determined from the torque, required to hold the top plate in its position. The frequency dependences of G′ and G′′ were measured for various temperatures in the frequency range 0.1–100 rad s−1.Results and discussion
Many-body cooperative dynamics in the supercooled liquid regime
The application of the BDS spectroscopy offers tremendous opportunities to get an insight into the molecular dynamics of the various types of glass formers. Moreover, its advantage over other techniques arises from the possibility to characterize the materials over a wide range of frequencies, temperatures, and what seems the most beneficial, pressures. Another convenience results from the free choice of representation, which can be applied during data analysis. Although all attainable formalisms are related to each other, the proper conversion between one representation to another may give a valuable insight into the different features of the analyzed experimental data. Thus, using the BDS technique, one can easily study the processes of distinct origin, such as those resulting from ion diffusion or local molecular motions. In general, the dielectric data can be presented by means of three different formalisms: the complex permittivity ε*(f) = ε′(f) − iε′′(f), the complex conductivity σ*(f) = σ′(f) + iσ′′(f), and the complex electric modulus M*(f) = M′(f) + iM′′(f). The susceptibility formalism is favored in the case of non-conductive samples, wherein reorientations of the permanent dipoles give rise to distinctive frequency-dependent features of the permittivity dielectric loss spectra. The other representations assume greater importance in the studies of ion-containing systems, such as CIM HCl, investigated in this work.The dielectric spectra of CIM base, covering seven decades in frequencies (10−1 to 106 Hz), are presented in Fig. 2 in the permittivity representation. The well-resolved maximum in the frequency dependence of the imaginary part of the dielectric permittivity ε′′(f) corresponds to the characteristic time required for the reorientation of molecular dipoles, i.e. the α-relaxation time. When the system cools down, this maximum shifts toward the lower frequencies, indicating an increase in the time scale of such cooperative motions. Finally, when the structural relaxation time exceeds τα = 1000 s, the global mobility becomes frozen in the glassy state and the dielectric spectra become dominated by the secondary modes.
 | ||
| Fig. 2 Dielectric spectra of the CIM base measured at an ambient pressure above and below the glass transition temperature. | ||
Since the intramolecular potential inherently determines the dynamics of the investigated materials, the main dielectric characteristics, such as the shape of the dielectric curves or dielectric strength, should clearly reflect their properties. Recently, Paluch et al. instigated a universality in the dielectric behavior of the various glass-formers, expressed as a correlation between the dielectric strength (Δε = ε0 − ε∞ ≈ Nμ2, where ε0 denotes the dielectric permittivity of vacuum and N is the number of relaxing dipoles, whereas μ corresponds to the value of the permanent dipole moment) and the broadening of the dielectric response.6 The higher the dipole moment of the investigated system, the larger the observed βKWW value (or equivalently narrower α-relaxation peak). The value of the βKWW parameter, an exponent in the Kohlrausch–Williams–Watts function:7
| φ(t) = exp[−(t/τα)βKWW] | (2) |
To thoroughly analyze the temperature dependence of the relaxation times, we applied the Havriliak–Negami (HN) function, which is widely used to parametrize the relaxation behaviour of various glass formers:10
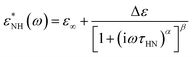 | (3) |
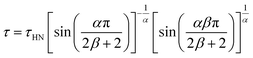 | (4) |
The logarithm of the determined relaxation times as a function of inverted temperature is depicted in a so-called relaxation map (Fig. 4, right panel) illustrating all the key dynamic features of the material under study. Using the map, one can easily find the relaxation time corresponding to log10(τα) = 3, indicating the glass transition temperature, which for CIM base was equal to Tg = 312 K. At this point, it should be clarified that the same strategy was also applied to characterize the secondary relaxations. In this case, the parameter β in eqn (4) was equal to one that was equivalent to the transformation of the HN equation into the Cole–Cole function. In addition, the following peculiarity, τ = τHN, is, therefore, true. As observed in Fig. 2, two secondary modes (assigned as β and γ) were found for CIM base; however, their plausible nature has been discussed later. Now, we would focus on the character of their temperature dependencies. The secondary relaxation modes observed in the glassy state usually obey the Arrhenius law. However, when the material is heated above the glass transition temperature (defined by η = 1012 Pa s and τα = 1000 s) its properties, such as viscosity, diffusion coefficients, relaxation times, begin to change suddenly in a way characteristic for particular substance. The rapidity of the change in τα near the glass transition defines the material ‘fragility’.12 In most cases, the cooperative dynamics of the supercooled liquid state have been well parametrized by the empirical Vogel–Fulcher–Tammann (VFT) equation:13–15
 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ∞ = −14.9s ± 0.1, D = 11.8 ± 0.2, and T0 = 242 ± 1 K). The D value, known as the strength parameter, is helpful in classifying the glass formers as so-called strong (with large D-values) or fragile (with small D, typically D < 10), as was reported by Angell.16 According to this nomenclature, CIM base should be categorized as an intermediate glass-former since its calculated D value is within the range 10 < D < 100. An alternative way of estimating the ‘fragility’ involves the determination of steepness index m, being defined as follows:17
τ∞ = −14.9s ± 0.1, D = 11.8 ± 0.2, and T0 = 242 ± 1 K). The D value, known as the strength parameter, is helpful in classifying the glass formers as so-called strong (with large D-values) or fragile (with small D, typically D < 10), as was reported by Angell.16 According to this nomenclature, CIM base should be categorized as an intermediate glass-former since its calculated D value is within the range 10 < D < 100. An alternative way of estimating the ‘fragility’ involves the determination of steepness index m, being defined as follows:17
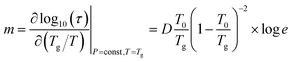 | (6) |
 | ||
| Fig. 4 Relaxation map obtained for CIM base. Relaxation times assessed from BDS – τα–M′′ and τα (circles), TMDSC – τTOPEM (asterisks), RH – τη (pentagons), and τG′′max (tringles) techniques are depicted. To properly compare the BDS and RH data, τα−M′′ values were determined from M′′ data. Open stars denote the aging relaxation times obtained from eqn (12). The secondary relaxation times – τβ and τγ are shown together with the calculated values of activation energies. Solid and dashed lines denote VFT and Arrhenius fit functions, respectively. | ||
For various glass formers, the value of m may change within a broad range, from about 17 (strong glass formers) to about 200 (fragile one).18 The value obtained for CIM base, m = 80 (for τα = 1000 s), falls roughly in the middle of this range. Moreover, the m value is also governed by the intramolecular potential. The results of a simulation performed by Bordat et al. clearly show that by adjusting the properties of the theoretical potential, in particular by increasing its value and anharmonicity, an increase in the fragility is observed. This is an effect of density growth resulting in stronger intramolecular coupling.18
The dielectric spectra of the ionic CIM HCl sample are shown in Fig. 5 in all the aforementioned formalisms. It can be observed that the loss peak in the ε′′(f) spectra is almost completely covered by the conductivity contribution originating from the translational motions of the cations and anions in the investigated sample. The only recognizable features appear below Tg as secondary modes. Thus, a detailed analysis of CIM HCl behavior in the supercooled regime was performed for data in the electric modulus and conductivity representation. From the imaginary part of the complex modulus function M′′(f), the conductivity relaxation time was calculated as τσ = 1/2πfmax with fmax corresponding to the maximum of the M′′ peak. It was observed that upon cooling, this maximum is shifted to a low frequency due to a decrease in the ion mobility. Simultaneously, the downturn of the ion displacement was disclosed as a decrease in the value of dc-conductivity (σdc), assigned from the frequency-independent plateau-like region of the real part of the complex conductivity σ′ (see Fig. 5).
 | ||
| Fig. 5 Representative dielectric spectra for CIM HCl at an ambient pressure above and below the glass transition temperature presented in various representations. | ||
After thorough observation of the registered spectra M′′(f), an interesting feature can be observed: above a certain temperature, the interval between the succeeding spectra is decreasing, although the same temperature step is maintained. Such behavior, known as ‘decoupling’ in the field of ionic liquids, denotes separation between the time-scales of ion diffusion and structural dynamics.19 Moreover, this phenomenon has been reflected in the temperature characteristics of the conductivity relaxation times, as depicted in Fig. 6. One can easily see that for log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τσ = 0.74, a crossover in the dynamic behavior of CIM HCl occurs. Then, the temperature dependence of the conductivity relaxation times shows a visible departure from the VFT-like into the Arrhenius-like behavior. Usually, for conventional glass-formers, such crossovers can be observed for much longer relaxation times, i.e. as large as hundreds or thousands of seconds. To compare the timescales of the conductivity and structural relaxation times, we assessed structural relaxation times using temperature-modulated differential scanning calorimetry (TMDSC). Although these measurements were performed for both CIM base and CIM HCl, only in the former, the agreement between the τ values determined from both the methods was observed.
τσ = 0.74, a crossover in the dynamic behavior of CIM HCl occurs. Then, the temperature dependence of the conductivity relaxation times shows a visible departure from the VFT-like into the Arrhenius-like behavior. Usually, for conventional glass-formers, such crossovers can be observed for much longer relaxation times, i.e. as large as hundreds or thousands of seconds. To compare the timescales of the conductivity and structural relaxation times, we assessed structural relaxation times using temperature-modulated differential scanning calorimetry (TMDSC). Although these measurements were performed for both CIM base and CIM HCl, only in the former, the agreement between the τ values determined from both the methods was observed.
As obvious from the relaxation map, at the crossover temperature, the structural relaxation time for CIM HCl reached approximately 1000 s. However, the corresponding conductivity relaxation time was much shorter, corresponding to the decoupling index,20 Rτ(Tg) = log[τα(Tg)/τσ(Tg)], being equal to 3. For comparison, the Rτ(Tg) values found for other protic ionic conductors were equal to 3 for procaine HCl, procainamide HCl,21 and sumatriptan succinate,22 3.5 for phosphoric acid, and 7 for lidocaine di-(dihydrogen phosphate).23
Another approach shedding more light on the decoupling phenomenon is the application of the rheological measurements to probe the mechanical relaxation in the tested materials. In this study, we investigated the dynamic shear modulus by applying an oscillatory strain and measuring the resultant stress. The determined viscosity values (η) were then converted into the relaxation times (τη) according to the Maxwell relation,24 i.e. η = G∞τη. The infinite frequency shear modulus (G∞), determined as the high-frequency asymptote of G′(f), was found to be G∞ = 2.3 × 108 Pa for CIM base and G∞ = 2.7 × 108 Pa for CIM HCl. The real G′(f) and imaginary G′′(f) parts of the shear modulus spectra for both materials are presented in Fig. 7. One can see that the frequency dependence of the G′′ is characterized by a single peak, which moves to the higher frequency on heating. From the maximum of the G′′(f) peak, we determined the mechanical relaxation times, defined as τG′′max = 1/2πfmax. These relaxation times, together with the dielectric data, are depicted in the left panel of Fig. 4 for CIM base and Fig. 6 for CIM HCl. To properly compare the relaxation data obtained from the different spectroscopic methods, it is necessary to analyze the data in the analogous representations. We can decide whether we choose the dynamic susceptibilities (i.e. dielectric ε* or mechanical compliance J*) or the dynamic modulus (M* or G*). Note that, because the former refers to a retardation process and the latter to relaxation, the resultant characteristic relaxation time may be different. In our study, we applied modulus representation and thus we had to convert the dielectric data for CIM base from dielectric susceptibility to modulus representation according to the following relation: ε* = 1/M*. At this point, it should be noted that this conversion can affect the shape of the relaxation peak. This is particularly important for the molecules with high conformational freedom and a diverse pattern of secondary processes. Then, changes in the magnitude of particular modes associated with the data transformation may artificially broaden the relaxation peak.
 | ||
| Fig. 7 The frequency dependence of the real G′ and imaginary part G′′ of the shear modulus measured for CIM base (upper panels) and CIM HCl (bottom panels). The rightmost panels show the masterplots obtained by the horizontal shifting of the normalized G′′(f) spectra, registered at different temperatures, together with the value of the βKWW parameter (from eqn (2)). | ||
The τη(T) and τG′′max(T) relationships (see Fig. 4 and 6) have non-Arrhenius characteristics over the whole investigated range of temperatures. In the case of CIM base, the temperature dependences of the mechanical and dielectric relaxation times have parallel courses and significantly overlap with each other. However, a different behavior was observed for CIM HCl, where mechanical data were significantly shifted, indicating the existence of decoupling between the viscosity and conductivity relaxation.
To quantify the extent of decoupling, the Stokes–Einstein relation can be applied, where τση−s = const. Then, the slope assigned from log(τσ) vs. log(η) corresponds to the decoupling parameter, s.25 The values obtained here were 0.79 and 0.98 for CIM HCl and CIM base, respectively. The degree of decoupling is related to the efficiency of proton hopping, which seems to increase when the Grotthuss mechanism is involved.26 In CIM HCl, decoupling can be further enhanced by tautomerization. However, the privileged mechanism of proton transfer will be dependent on the PIL chemical structure and, essentially, on the number of proton-donor and proton-acceptor sites that may be used to create a hydrogen-bonded network. Hence, the outstanding properties of the PILs will be conditioned by the balance between the columbic forces and dispersion forces, such as the abovementioned hydrogen bonds.27 It is experimentally proven that the overall potential of the ionic conductors can be reinforced by the proper selection of its constituent anions and cations. As reported in an insightful FTIR and DFT study by Ludwig, depending on the composition, the contribution of hydrogen bonding to the intramolecular potential may vary from a small fraction to more than 50%, for aprotic [C4C1mim][BF4] and protic ionic liquid [PrAm][NO3], respectively.28
Since the dielectric response of an ionic sample is dominated by the conductivity contribution, a comparison of the structural relaxation data for CIM base and CIM HCl was not possible. However, we analyzed the τη values determined from the mechanical response of both samples. To quantify τη(T) dependencies, we used the VFT equation. We obtained the following fitting parameters: log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ∞ = −15.7s ± 0.2, D = 11.7 ± 0.4, and T0 = 243 ± 1 K for CIM base and log
τ∞ = −15.7s ± 0.2, D = 11.7 ± 0.4, and T0 = 243 ± 1 K for CIM base and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ∞ = −16.7s ± 0.1, D = 21 ± 0.4, and T0 = 233 ± 1 K for CIM HCl. This parameterization leads to the glass transition temperatures (determined for τη = 1000 s) being equal to Tg,η = 309 K for CIM base and Tg,η = 340 K for its ionic counterpart. Moreover, the corresponding fragility values were m = 80 and m = 64 for the non-ionic and ionic forms, subsequently. Regardless of the assessment method, the Tg value found for CIM HCl was higher in comparison to that for CIM base, indicating slower dynamics of the ionic sample. In recent years, the development of powerful computational approaches, in particular, finding a proper force field that will appropriately describe the interactions between atoms in ILs, has led to an improvement in the understanding of the basic phenomena governing ILs dynamics.29 The excellent comparison reported by Shirota and Castner revealed that the stronger ion–ion interactions lead to higher densities of the ionic samples in relation to their neutral counterparts.30 However, a theoretical study reported by Roy for the idealized ionic liquids modeled on [Im41][PF6] showed that the IL behavior is mainly driven by the structural rigidity of the electrostatic coupling, leading to high viscosities and consequently, inhibited the dynamics observed in ILs.31 A comparison of the mechanical data revealed another interesting fact, i.e. lower fragility and lower βKWW values for the ionic sample. This result may be discussed in terms of differences in dynamic heterogeneities in both materials. The breakthrough in quantifying the dynamic heterogeneities occurred when Berthier et al. proposed an approach that enabled an easy calculation of the number of dynamically correlated molecules, Nc, directly from the accessible experimental parameters, i.e.:32,33
τ∞ = −16.7s ± 0.1, D = 21 ± 0.4, and T0 = 233 ± 1 K for CIM HCl. This parameterization leads to the glass transition temperatures (determined for τη = 1000 s) being equal to Tg,η = 309 K for CIM base and Tg,η = 340 K for its ionic counterpart. Moreover, the corresponding fragility values were m = 80 and m = 64 for the non-ionic and ionic forms, subsequently. Regardless of the assessment method, the Tg value found for CIM HCl was higher in comparison to that for CIM base, indicating slower dynamics of the ionic sample. In recent years, the development of powerful computational approaches, in particular, finding a proper force field that will appropriately describe the interactions between atoms in ILs, has led to an improvement in the understanding of the basic phenomena governing ILs dynamics.29 The excellent comparison reported by Shirota and Castner revealed that the stronger ion–ion interactions lead to higher densities of the ionic samples in relation to their neutral counterparts.30 However, a theoretical study reported by Roy for the idealized ionic liquids modeled on [Im41][PF6] showed that the IL behavior is mainly driven by the structural rigidity of the electrostatic coupling, leading to high viscosities and consequently, inhibited the dynamics observed in ILs.31 A comparison of the mechanical data revealed another interesting fact, i.e. lower fragility and lower βKWW values for the ionic sample. This result may be discussed in terms of differences in dynamic heterogeneities in both materials. The breakthrough in quantifying the dynamic heterogeneities occurred when Berthier et al. proposed an approach that enabled an easy calculation of the number of dynamically correlated molecules, Nc, directly from the accessible experimental parameters, i.e.:32,33
 | (7) |
Dynamic sensitivity to increasing pressure
To gain a deeper insight into the impact of the molecular attractions on the dynamics of both systems, i.e. CIM base and CIM HCl, we performed molecular dynamics studies at various pressures. It is well known that the application of pressure through altering interatomic distances will reinforce the molecular interactions, as it was observed for some H-bonded systems.36 In the case of materials consisting of ions, such pressure-induced changes in the distances between an equally and oppositely charged particles will modify the nature of the repulsive and attractive forces in the system under study.37 The question is how the effect of compression will be reflected in the dielectric properties of the materials selected to study, which are entirely different from the viewpoint of the interactions determining their overall properties. Fig. 8a shows the dielectric spectra registered during the compression of CIM base at T = 333 K. By isothermal squeezing, we obtained an effect analogous to that obtained during isobaric cooling, i.e. slowing down of the sample dynamics being reflected in the shifting of the maxima of the dielectric loss spectra towards the low frequencies. The spectra registered for several different temperatures (from T = 333 K to T = 373 K) and pressures up to p = 410 MPa were analyzed, and the α-relaxation times were calculated. These values of τα as a function of pressure are presented in Fig. 8b. Basically, there are several models that may be used to describe the pressure dependence of τα. We chose the pressure version of the VFT equation, which provided an excellent description of the obtained experimental data. The obtained pVFT parameterization was then used to find out the pressure value, Pg, corresponding to τα = 100 s, being an indicator of the glass transition. We chose such a relaxation time, instead of the previously adopted τα = 1000 s, to avoid an excessive data extrapolation. The pressure dependence of Tg is presented in the inset to Fig. 8b. One can see that the Tg(Pg) dependence reveals a nonlinear character that can be well described by the empirical relation proposed by Andersson and Andersson:38
 | (8) |
The fitting parameters k1, k2, and k3 were found to be equal to k1 = 315.6 ± 0.2, k2 = 5.5 ± 0.1, and k3 = 2188.5 ± 31. At first glance, one can see that after the compression, Tg value increases; as the higher pressure is applied, the gradient dTg/dP is decreasing, indicating dwindling Tg(P) dependency. The effect of pressure on the glass transition temperature has been investigated for miscellaneous classes of glass-forming materials covering various molecular architectures and a wide spectrum of the physical properties. These valuable findings clearly show that the manner in which the Tg value varies with the pressure is characteristic for a given material and essentially reflects the nature of the molecular attractions involved. In general, van der Waals liquids are characterized by the significant sensitivity to the applied pressure.39 Systems with extended hydrogen-bonded structures behave in the opposite way. In the latter, the reinforcing of the supramolecular network under pressure may give rise to deviations from the commonly observed behavior.40 When we look at the chemical structure of CIM base, we will notice the presence of NH groups that can act as hydrogen bond donors. Moreover, nitrogen atoms can potentially accept a hydrogen atom, leading to intra- or intermolecular N⋯HN attractions. However, according to reports, CIM base is not an example of a strongly associated liquid.41,42 On the other site, its remarkable ability for an intramolecular proton transfer, i.e. tautomerization, is repeatedly stressed.43 A diverse form of cimetidine tautomers, formed by the conversion within the imidazole ring or guanidine moiety, has been anticipated in several theoretical studies.44,45 However, only the form corresponding to the structure presented in Fig. 1 was found in the crystalline cimetidine.
To quantify the pressure sensitivity of Tg, we determined the pressure coefficient of the glass transition temperature, dTg/dP, taken in a limit of low pressure according to the following relationship:36
 | (9) |
The calculated value, equal to 0.149 K MPa−1, indicates a rather moderate sensitivity to pressure, comparable to those reported for diisobutyl phthalate (0.15 K MPa−1).46 This is lower than that observed for van der Waals liquids (usually more than 0.20 K MPa−1), but at the same time is higher than those observed for strongly hydrogen-bonded systems, such as glycerol (0.04 K MPa−1) or m-fluoroaniline (0.081 K MPa−1).36
At this point, the following question naturally arises: how will change the pressure sensitivity of the material in which coulombic interactions between the constituted charged particles govern intramolecular potential? To investigate this issue, we performed isothermal measurements for the CIM HCl sample at elevated pressures. The M′′(f) dielectric spectra of CIM HCl registered at T = 352 K for pressures varying from 10 MPA to 410 MPa are presented in Fig. 9a. The logarithms of conductivity relaxation times as a function of pressure are presented in Fig. 9b. It is easy to recognize, starting from a certain pressure, that the character of the pressure dependence of the conductivity relaxation times changes apparently indicating decoupling phenomenon. Moreover, one can see that the relaxation time corresponding to this dynamic crossover is reduced after compression, indicating that decoupling, i.e. separation between the timescales of the structural and ionic motions, is enhanced with the increase in pressure. To express the sensitivity of decoupling to pressure, a parameter that is a derivative of the decoupling index (Rτ), has been calculated using the following formula:47
 | (10) |
The obtained value dlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Rτ/dp = 0.00268 MPa−1 is similar to that obtained for carvedilol HCl (0.0029 MPa−1) or lidocaine hemisuccinate (0.0029 MPa−1).19
Rτ/dp = 0.00268 MPa−1 is similar to that obtained for carvedilol HCl (0.0029 MPa−1) or lidocaine hemisuccinate (0.0029 MPa−1).19
Returning to the question concerning the sensitivity of the glass transition temperature to the pressure, let us look again at the data shown in Fig. 9b. As reported for many ionic glass-formers, the data points, for which the crossover is observed, correspond to the iso-viscosity line (for η = 1012 Pa s) and can be satisfactorily applied to determine the Tg(Pg) values.26 Therefore, we used these values to designate the pressure coefficient of the glass transition temperature, as was previously done for CIM base. The calculated value of 0.139 K MPa−1 (see Fig. 9c) was only slightly lower than those obtained for the non-ionic counterpart. A very similar value was reported for lidocaine hemisuccinate (0.127 K MPa−1) and lidocaine docusate (0.132 K MPa−1).23 The dTg/dp values mentioned in the reports for other ionic glass formers were usually slightly higher i.e. carvedilol dihydrogen phosphate (0.170 K MPa−1), carvedilol hydrochloride (0.152 K MPa−1),48 verapamil hydrochloride (0.208 K MPa−1),49 lidocaine hydrochloride (0.170 K MPa−1),50 procainamide hydrochloride (0.150 K MPa−1).51 An insufficient number of reports, especially those regarding comparative analysis of ionic samples and their neutral counterparts, does not allow the formulation of general rules regarding the high pressure behavior of the ionic liquid in relation to the corresponding non-charged form. In the case of the carvedilol salts both abovementioned ionic materials possessed a higher pressure coefficient of the glass transition temperature when compared to their non-ionic analogue (0.137 K MPa−1).48 In the case of CIM base and HCl, the values determined for the pressure coefficients were roughly similar and indicated rather moderate Tg susceptibility to the applied pressure.
Glassy dynamics
When we look closer at the dielectric spectra of CIM base and CIM HCl, we will see similarities in the patterns of their secondary relaxation behavior. Also, according to reports, the secondary relaxations, being a fingerprint of glassy dynamics, in ionic glasses share features common to those observed in the molecular glasses. However, it is hard to find reports comparing the glassy dynamics of ionic conductors and their non-ionic counterparts. Nonetheless, recently, several papers on the glassy dynamics of various PILs have been published, shedding more light on their complex dynamics below the Tg.52,53 Basically, in molecular glasses, the origin of secondary processes may be twofold: one can reflect the local internal rearrangements, whereas another may involve the motions of all the atoms in a molecule.54,55 The latter, due to its intramolecular cooperative nature and contribution to the glass transition, gained recognition as being particularly important. From their discovery by Johari and Goldstein, the so-called JG relaxations determined the course of the discussion on the glassy dynamics for the next few decades. Note that both types of motions were found for various PILs. However, according to previous reports, being rather rare, they may have either a bipolar or ionic origin. Moreover, in some cases, an extra feature can be observed, such as nearly constant loss (NCL) regions reflecting ionic motions restricted by cages formed by the surrounding molecules.56–58Returning to our results, the dielectric spectra of CIM base revealed two easily distinguishable secondary modes, assigned as β and γ, both showing the Arrhenius behavior with activation energies Eβ = 56 ± 2 kJ mol−1 and Eγ = 30 ± 1 kJ mol−1. To decide whether the observed processes have an intrinsic nature or rather a JG character, we performed detailed investigations using pressure as a variable. This is a widespread approach to use pressure sensitivity as a reliable factor to directly determine whether the analyzed process has an intramolecular nature.59,60 According to a classification proposed by Ngai and Paluch, depending on the response to increasing compression, secondary modes can be categorized as strongly sensitive (true-JG) or indifferent to densification by pressure (non-JG). The third group includes processes weakly sensitive to pressure, sometimes described as pseudo-JG.59 In such cases, it is necessary to perform additional tests to reliably verify the origin of the analyzed process. The dielectric spectra of CIM base at T = 333 K registered for increasing pressures are presented in Fig. 8. Also, in ambient pressure experiments, two secondary modes were found, although under the applied thermodynamic conditions, the γ-process was only partially visible in the experimental window. However, this does not preclude the assessment of its pressure sensitivity. The presented results indicate that the γ-process was totally insensitive to compression, whereas for the β-process, pressure sensitivity, with ΔV = 11.61 cm3 mol−1 (see Fig. 10), was observed. To remove the resulting uncertainty and determine the origin of the slightly pressure-sensitive β-process, we calculated the primitive relaxation time (τ0), which, based on the assumptions of the Coupling Model (CM), can rationally predict the position of true JG-relaxation. We use the well-known relationship to calculate τ0:61,62
| τ0 = (τc)1−βKWW(τα)βKWW | (11) |
As mentioned in the beginning of this section, the comparison of the dielectric spectra registered for CIM base and CIM HCl revealed many similarities (see Fig. 10). As in the non-ionic sample, two secondary modes were found for CIM HCl. We assigned these as β′ and γ′, with activation energies Eβ′ = 48 ± 1 kJ mol−1 and Eγ′ = 35 ± 1 kJ mol−1, respectively. These secondary modes were visible in both ε′′(f) and M′′(f) spectra and thus we assumed their bipolar nature. The previously reported results for other PILs with the analogous Cl− anion but different cations, i.e. lidocaine,53 procaine, and procainamide hydrochlorides,21 revealed the presence of secondary processes of ionic nature, which were described as β-conductivity relaxations. However, in CIM HCl as well as in the previously investigated chlorpromazine hydrochloride, both the secondary modes were due to dipolar cation relaxations.52 The questions concerning their JG or non-JG nature remains open. The performed experiments verifying the CIM HCl response to compression did not bring decisive results. Within these measurements the γ′-process was out of the accessible frequency range, whereas the β′-process seems to be pressure-sensitive with ΔV = 10.95 cm3 mol−1. Almost the same effect was observed for CIM base. Contrary to the non-conductive sample, decision-making calculations based on CM were not possible in this case since the structural relaxations were completely covered by the conductivity contribution, making it impossible to assess the width of the structural relaxation peak. On the other hand, in the discussion on the origin of secondary processes in CIM HCl, we can appeal to undeniable similarities in the chemical structure of CIM base and its cation. In fact, they only differ in the presence of one proton, which may be irrelevant with respect to the dipole moment of a material. Since both processes found in CIM base reflect the local internal rearrangements, due to their similar structural skeleton, they should also appear in CIM base. To determine which part of a molecule is responsible for a particular mode, theoretical calculations in the framework of density functional theory (DFT) must be performed. Such results will also be helpful in determining whether the β′-process in CIM HCl is true-JG or not. It interesting is that the results presented herein clearly show that intramolecular forces govern the dynamics of the investigated samples to a greater extent in the supercooled liquid state. This is directly related to its cooperative and many-body character.
It is well known that when the liquid is quenched below the glass transition temperature, it deviates from the equilibrium and starts to relax towards more energy-favorable states.63 The deeper the material kept in the glassy state, the longer the time required for the structural rearrangement into the equilibrium configuration. This time evolution of glass properties is called physical aging and can be investigated by monitoring the dielectric, mechanical, or thermal responses of the materials. This is possible because aging affects the various features of glassy materials, i.e. density, rate of stress, strain, enthalpy, and volume.64 Aging is a general phenomenon, observed for all glasses regardless of their ionic or non-ionic nature. The undeniable fundamental and practical importance of history-dependent and time-evolving properties of glassy materials stimulated experimental and theoretical efforts to improve the understanding of their non-equilibrium behavior.65,66 To shed more light on this problem, we performed time-dependent dielectric experiments and investigated the effects associated with the isothermal aging of CIM base and CIM HCl. The representative dielectric spectra registered in a time-dependent manner and analyzed in the framework of permittivity formalism are presented in Fig. 11. With time, the right slope of the α-process moves to lower frequencies, reducing its contribution to the β-process. These data clearly show that the gradual decline in the amplitude of β-relaxation peak is the most prominent hallmark of the ongoing aging process. The dielectric loss ε′′ values at fixed frequency plotted as a function of aging time are presented in Fig. 11. To their quantification, we applied the equation proposed by Lunkenheimer et al.67
ε′′(t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−[t/τage]β) + ε′′∞ exp(−[t/τage]β) + ε′′∞
| (12) |
 | ||
| Fig. 11 Shift of dielectric loss peak during physical aging of CIM base at T = 298 K and CIM HCl at T = 308 K. The inset panels present the normalized dielectric loss ε′′ values at fixed frequency plotted as a function of aging time for indicating temperatures (open circles), as well as the fits of eqn (12) to the experimental data (solid lines). | ||
Conclusions
The aim of our study assumed the comparison of the dielectric responses of two systems with a similar chemical backbone but totally distinct molecular interactions involved. As an object of our research, we chose CIM base and CIM HCl. The CIM base represents a van der Waals liquid, whereas CIM HCl belongs to the class of protic ionic conductors. While the dynamic properties of the former can be well described by the Lennard-Jones potential, in the latter, the long-range electrostatic interactions between the positively and negatively charged ions dominate over the short-range components. In our study, we address the vital problem related to the search for a relationship between the relaxation characteristics and the pattern of attractions involved. We confirmed that strong electrostatic interactions between the ions affect the material fluidity and leads to slowing of molecular dynamics, indicated by a higher Tg obtained for the conductive counterpart. Besides Tg, there are other characteristics attainable from dielectric loss spectra that can reflect the properties of the intramolecular potential. As shown for CIM base, its polar nature was indicated by a high Δε value and a narrow α-relaxation peak. This is related to the large value of the attractive part of the overall intramolecular force. This additional contribution originates from the interactions among the permanent dipoles in cimetidine base and is proportional to μ4/kT. We show that the careful analysis of the dielectric spectra above Tg can depict much valuable information about the nature of the molecular interactions governing the properties of the materials under study. On the contrary, below Tg, some similarities were found in the dynamic behavior of both samples. A comparison of the effects observed after the sample compression revealed another similarities, such as moderate pressure sensitivities of both materials. We showed that the BDS spectroscopy is a convenient method of choice for the comparative analysis of samples with distinct dynamic behavior, together with the TMDSC technique and rheology, enabling a detailed comparison of the relaxation features of ionic and non-ionic materials.CIM HCl, investigated here, is an another representative of a protic ionic liquid explored by our group. It is a succeeding example of a molecule in which decoupling is accelerated due to compression, which confirms the assumption that fast proton hopping is probably involved in its conductivity mechanism. Previously, we investigated PILs with the same monoatomic Cl− anion and various molecular cations, i.e. lidocaine, procaine and procainamide, chlorpromazine, and carvedilol. These results, together with the outcome of the present study, make a huge contribution to the study on establishing a universal pattern of PIL behavior, also including the interplay between the intramolecular factors affecting their behavior. This is necessary for a further successful implementation of PILs in various industrial areas.
Acknowledgements
The authors highly acknowledge the financial support received from the National Science Centre within the framework of the Opus8 project (Grant DEC-2014/15/B/ST3/04246).Notes and references
- D. Chandler, J. D. Weeks and H. C. Andersen, Science, 1983, 220(4599), 787–794 CAS.
- K. Dong and S. Zhang, Chem.–Eur. J., 2012, 18, 2748–2761 CrossRef CAS PubMed.
- H. Weingrtner, Angew. Chem., Int. Ed., 2008, 47, 654–670 CrossRef PubMed.
- L. T. Greaves and C. J. Drummond, Chem. Rev., 2015, 115, 11379–11448 CrossRef PubMed.
- E. J. Maginn, J. Phys.: Condens. Matter, 2009, 21, 373101 CrossRef CAS PubMed.
- M. Paluch, J. Knapik, Z. Wojnarowska, A. Grzybowski and K. L. Ngai, Phys. Rev. Lett., 2016, 116(2), 025702 CrossRef CAS PubMed.
- G. Williams and D. C. Watts, Trans. Faraday Soc., 1970, 66, 80–85 RSC.
- P. Lunkenheimer, in Habilitation, Augsburg, 1999 Search PubMed.
- Y. Sun, H. Xi, M. D. Ediger, R. Richert and L. Yu, J. Chem. Phys., 2009, 131, 074506 CrossRef PubMed.
- S. Havriliak and S. Negami, Polymer, 1967, 8, 161–210 CrossRef CAS.
- F. Kremer and A. Schönhals, Broadband Dielectric Spectroscopy, Springer Verlag, Berlin, 2003 Search PubMed.
- D. Saha, Y. M. Joshib and R. Bandyopadhyay, Soft Matter, 2014, 10, 3292 RSC.
- H. Vogel, Phys. Z., 1921, 22, 645–646 CAS.
- G. S. Fulcher, J. Am. Ceram. Soc., 1925, 8, 339–355 CrossRef CAS.
- G. Tammann and W. Hesse, Z. Anorg. Allg. Chem., 1926, 156, 245–257 CrossRef.
- C. A. Angell, in Relaxations in complex systems, ed. K. L. Ngai and G. B. Wright, NRL, Washington, DC, 1985, pp. 3–11 Search PubMed.
- R. Bohmer, K. L. Ngai, C. A. Angell and D. J. Plazek, J. Chem. Phys., 1993, 99, 4201 CrossRef.
- P. Bordat, F. Affouard, M. Descamps and K. L. Ngai, Phys. Rev. Lett., 2004, 93(10), 105502 CrossRef PubMed.
- Z. Wojnarowska and M. Paluch, J. Phys.: Condens. Matter, 2015, 27(7), 073202 CrossRef PubMed.
- F. S. Howell, R. A. Bose, P. B. Macedo and C. T. Moynihan, J. Phys. Chem., 1974, 78, 639–648 CrossRef CAS.
- Z. Wojnarowska, A. Swiety-Pospiech, K. Grzybowska, L. Hawelek, M. Paluch and K. L. Ngai, J. Chem. Phys., 2012, 136, 164507 CrossRef CAS PubMed.
- Z. Wojnarowska, J. Knapik, M. Rams-Baron, A. Jedrzejowska, M. Paczkowska, A. Krause, J. Cielecka-Piontek, M. Jaworska, P. Lodowski and M. Paluch, Mol. Pharm., 2016, 13, 1111–1122 CrossRef CAS PubMed.
- Z. Wojnarowska, K. J. Paluch, E. Shoifet, C. Schick, L. Tajber, J. Knapik, P. Wlodarczyk, K. Grzybowska, S. Hensel-Bielowka, S. P. Verevkin and M. Paluch, J. Am. Chem. Soc., 2015, 137, 1157–1164 CrossRef CAS PubMed.
- R. D. Deegan, R. L. Leheny, N. Menon, S. R. Nagel and D. C. Venerus, J. Phys. Chem. B, 1999, 103, 4066–4070 CrossRef CAS.
- T. Psurek, S. Hensel-Bielowka, J. Ziolo and M. Paluch, J. Chem. Phys., 2002, 116, 9882 CrossRef CAS.
- Z. Wojnarowska, Y. Wang, K. J. Paluch, A. P. Sokolov and M. Paluch, Phys. Chem. Chem. Phys., 2014, 16, 9123 RSC.
- T. L. Greaves and C. J. Drummond, Chem. Rev., 2015, 115, 11379–11448 CrossRef CAS PubMed.
- K. Fumino, A. Wulfa and R. Ludwig, Phys. Chem. Chem. Phys., 2009, 11, 8790–8794 RSC.
- F. Dommert, K. Wendler, R. Berger, L. Delle Site and C. Holm, ChemPhysChem, 2012, 13(7), 1625–1637 CrossRef CAS PubMed.
- H. Shirota and E. W. Castner, J. Phys. Chem. A, 2005, 109(42), 9388–9392 CrossRef CAS PubMed.
- D. Roy, N. Patel, S. Conte and M. Maroncelli, J. Phys. Chem. B, 2010, 114, 8410–8424 CrossRef CAS PubMed.
- L. Berthier, G. Biroli, J. P. Bouchaud, L. Cipelletti, D. El Masri, D. L'Hote, F. Ladieu and M. Pierno, Science, 2005, 310, 1797–1800 CrossRef CAS PubMed.
- S. Capaccioli, G. Ruocco and F. Zamponi, J. Phys. Chem. B, 2008, 112, 10652–10658 CrossRef CAS PubMed.
- K. Grzybowska, A. Grzybowski, Z. Wojnarowska, J. Knapik and M. Paluch, Sci. Rep., 2015, 5, 16876 CrossRef CAS PubMed.
- K. Ueno, Z. Zhao, M. Watanabe and C. A. Angell, J. Phys. Chem. B, 2012, 116, 63–70 CrossRef CAS PubMed.
- C. M. Roland, S. Hensel-Bielowka, M. Paluch and R. Casalini, Rep. Prog. Phys., 2005, 68, 1405–1478 CrossRef CAS.
- Y. Zhao, X. Liu, X. Lu, S. Zhang, J. Wang, H. Wang, G. Gurau, R. D. Rogers, L. Su and H. Li, J. Phys. Chem. B, 2012, 116, 10876–10884 CrossRef CAS PubMed.
- A. Andersson and O. Andersson, Macromolecules, 1998, 31(9), 2999–3006 CrossRef.
- K. Koperwas, A. Grzybowski, S. N. Tripathy, E. Masiewicz and M. Paluch, Sci. Rep., 2015, 5, 17782 CrossRef CAS PubMed.
- C. M. Roland, R. Casalini, R. Bergman and J. Mattsson, Phys. Rev. B: Solid State, 2008, 77, 012201 CrossRef.
- W. A. Bueno and E. G. Sobrinho, Spectrochim. Acta, 1995, 51(2), 287–292 CrossRef.
- M. Barańska and L. M. Proniewicz, J. Mol. Struct., 1999, 511–512, 153–162 CrossRef.
- H. Tecle, L. Robichaud and C. F. Schwender, J. Med. Chem., 1981, 24, 1095–1097 CrossRef CAS PubMed.
- G. Karpińska, J. C. Dobrowolski and A. P. Mazurek, J. Mol. Struct., 2003, 645, 37–43 CrossRef.
- N. L. Calvo, S. O. Simonetti, R. M. Maggio and T. S. Kaufman, Anal. Chim. Acta, 2015, 875, 22–32 CrossRef CAS PubMed.
- M. Sekula, S. Pawlus, S. Hensel-Bielowka, J. Ziolo, M. Paluch and C. M. Roland, J. Phys. Chem. B, 2004, 108, 4997–5003 CrossRef CAS.
- A. Swiety-Pospiech, Z. Wojnarowska, S. Hensel-Bielowka, J. Pionteck and M. Paluch, J. Chem. Phys., 2013, 138(20), 204502 CrossRef CAS PubMed.
- Z. Wojnarowska, Y. Wang, J. Pionteck, K. Grzybowska, A. P. Sokolov and M. Paluch, Phys. Rev. Lett., 2013, 111, 225703 CrossRef CAS PubMed.
- Z. Wojnarowska, M. Paluch, A. Grzybowski, K. Adrjanowicz, K. Grzybowska, K. Kaminski, P. Wlodarczyk and J. Pionteck, J. Chem. Phys., 2009, 131, 104505 CrossRef.
- A. Swiety-Pospiech, Z. Wojnarowska, J. Pionteck, S. Pawlus, A. Grzybowski, S. Hensel-Bielowka, K. Grzybowska, A. Szulc and M. Paluch, J. Chem. Phys., 2012, 136, 224501 CrossRef CAS PubMed.
- Z. Wojnarowska, C. M. Roland, A. Swiety-Pospiech, K. Grzybowska and M. Paluch, Phys. Rev. Lett., 2012, 108, 015701 CrossRef CAS PubMed.
- S. Hensel-Bielowka, K. L. Ngai, A. Swiety-Pospiech, L. Hawelek, J. Knapik, W. Sawicki and M. Paluch, J. Non-Cryst. Solids, 2015, 407, 81–87 CrossRef CAS.
- Z. Wojnarowska, K. Grzybowska, L. Hawelek, A. Swiety-Pospiech, E. Masiewicz, M. Paluch, W. Sawicki, A. Chmielewska, P. Bujak and J. Markowski, Mol. Pharm., 2012, 9, 1250 CrossRef CAS PubMed.
- G. P. Johari and M. Goldstein, J. Chem. Phys., 1970, 53, 2372 CrossRef CAS.
- S. Capaccioli, D. Prevosto, M. Lucchesi, P. A. Rolla, R. Casalini and K. L. Ngai, J. Non-Cryst. Solids, 2005, 351, 2643–2651 CrossRef CAS.
- C. M. Roland, M. J. Schroeder, J. J. Fontanella and K. L. Ngai, Macromolecules, 2004, 37, 2630–2635 CrossRef CAS.
- J. C. Dyre, P. Maass, B. Roling and D. L. Sidebottom, Rep. Prog. Phys., 2009, 72, 046501 CrossRef.
- S. N. Tripathy, Z. Wojnarowska, J. Knapik, H. Shirota, R. Biswas and M. Paluch, J. Chem. Phys., 2015, 142, 184504 CrossRef PubMed.
- K. L. Ngai and M. Paluch, J. Chem. Phys., 2004, 20(2), 857–873 CrossRef PubMed.
- K. L. Ngai and S. Capaccioli, J. Phys.: Condens. Matter, 2008, 20, 244101 CrossRef.
- K. L. Ngai, J. Phys.: Condens. Matter, 2003, 15, S1107–S1112 CrossRef CAS.
- K. L. Ngai, J. Chem. Phys., 1998, 109, 6982 CrossRef CAS.
- R. Casalini and C. M. Roland, Phys. Rev. Lett., 2009, 102, 035701 CrossRef CAS PubMed.
- I. M. Hodge and A. R. Berens, Macromolecules, 1982, 15, 762–770 CrossRef CAS.
- R. Xiao, J. Choi, N. Lakhera, C. M. Yakacki, C. P. Frick and T. D. Nguyen, J. Mech. Phys. Solids, 2013, 61, 1612–1635 CrossRef.
- R. Xiao and T. D. Nguyen, J. Mech. Phys. Solids, 2015, 82, 62–81 CrossRef CAS.
- P. Lunkenheimer, R. Wehn, U. Schneider and A. Loidl, Phys. Rev. Lett., 2005, 95, 055702 CrossRef CAS PubMed.
- M. Paluch, Z. Wojnarowska and S. Hansel-Bielowka, Phys. Rev. Lett., 2013, 110, 015702 CrossRef CAS PubMed.
- Z. Wojnarowska, C. M. Roland, K. Kolodziejczyk, A. Swiety-Pospiech, K. Grzybowska and M. Paluch, J. Phys. Chem. Lett., 2012, 3, 1238 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |






