Molecular-level insight of hindered phenol AO-70/nitrile-butadiene rubber damping composites through a combination of a molecular dynamics simulation and experimental method
Xiuying Zhaoab,
Geng Zhanga,
Feng Lua,
Liqun Zhangb and
Sizhu Wu*ab
aState Key Laboratory of Organic–Inorganic Composites, Beijing University of Chemical Technology, Beijing 100029, P. R. China. E-mail: wusz@mail.buct.edu.cn; Fax: +86-10-64433964
bEngineering Research Center of Elastomer Materials Energy Conservation and Resources, Ministry of Education, Beijing University of Chemical Technology, Beijing 100029, China
First published on 5th September 2016
Abstract
Through a combination of a molecular dynamics (MD) simulation and experimental method, in this work we have methodically expatiated the essential mechanism of the observably enhanced damping performance of nitrile-butadiene rubber (NBR) ascribed to the introduction of hindered phenol AO-70. The computed results revealed that four types of hydrogen bonds (H-bonds), namely, type A (AO-70) –OH⋯NC– (NBR), type B (AO-70) –OH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C– (AO-70), and type C (AO-70) –OH⋯OH– (AO-70), type D (AO-70) –OH⋯O–C– (AO-70) were formed in the AO-70/NBR composites, where type A was the most stable. Meanwhile, the AO-70/NBR composite with AO-70 content of 109 phr had the largest number of H-bonds, highest binding energy, and smallest fractional free volume (FFV), demonstrating a good compatibility between NBR and AO-70 and the best damping property of the composites. The experimental results were highly consistent with the MD simulation results, which means the combining methods can provide a new attempt for the design of optimum damping materials.
C– (AO-70), and type C (AO-70) –OH⋯OH– (AO-70), type D (AO-70) –OH⋯O–C– (AO-70) were formed in the AO-70/NBR composites, where type A was the most stable. Meanwhile, the AO-70/NBR composite with AO-70 content of 109 phr had the largest number of H-bonds, highest binding energy, and smallest fractional free volume (FFV), demonstrating a good compatibility between NBR and AO-70 and the best damping property of the composites. The experimental results were highly consistent with the MD simulation results, which means the combining methods can provide a new attempt for the design of optimum damping materials.
1. Introduction
At present, noise pollution is increasingly influencing our work and fitness levels, therefore it has attracted growing attention.1,2 Viscoelastic polymers have a remarkable characteristic for weakening disagreeable noise and preventing vibration fatigue failure, therefore a large portion of them have been used as damping materials.3 The damping mechanism is essentially connected with the internal friction.4 When the polymer received alternating stress effect, the motion of molecular chains needed to overcome the internal friction resistance, the strain usually lagged behind the stress, hysteresis effect can convert sound and mechanical energy to heat energy and then dissipated.5 As a classic representative of viscoelastic polymer, damping rubbers are widespreadly used in multitudinous fields including vessel, construction, aviation and aerospace industries.6,7 In general, the damping property reaches the most optimal condition around glass transition temperature (Tg), at which the polymer chain segments can obtain sufficient mobility, but can not follow the vibration frequency thoroughly.8Nitrile-butadiene rubber (NBR) has a preferable damping property on account of the high polarity of the nitrile groups (–CN) and widely applied in all sorts of fields.9 However the loss peak of NBR appears in a low temperature and the range of temperature is narrow. In order to achieve a more prominent loss peak over an extensive range, all kinds of modification methods have been adopted, for instance, blending modification,10 co-polymerization modification,11 gradient polymers,12 interpenetration network (IPN) polymers,13 and the core content of the paper: through hydrogen bonds (H-bonds) to design a damping composite, which can significantly improve damping performance of NBR.
Commonly, functional organic nanofillers can form strong intermolecular interactions with the polar rubber. The H-bonds which can ameliorate the damping performances of composites are the uppermost part in the strong intermolecular interactions.14 In the previous studies, Xu et al.15 investigated the essential mechanism of the ameliorative damping property of poly(vinyl acetate) (PVAc) caused by the addition of hindered phenol triethylene glycol-bis-[3-(3-tert-butyl-4-hydroxy-5-methyl phenyl)propionyloxy] (AO-70), and discovered that the intermolecular H-bonds formed between PVAc and AO-70 were the primary cause for the ameliorative damping property of the composites. Xu et al.16 also prepared a polyurethane (TPU)/AO-70 composite with improved high damping property.
The H-bond that was an especial intermolecular interaction between the electron-deficient hydrogen atom and the atom with high electron density,17 and it is a topical subject of science studies and has drawn the extensive attention of numerous fields.18–20 For instance, Kim et al.18 revealed that the H-bonding of urea groups on the hydrophobic blocks of polymer can improve the micelle assemblies for drug transmission. Yang et al.19 prepared hindered phenol exterminated hyperbranched polyester (mHBP)/NBR composites, elucidating that the intermolecular H-bonding between mHBP and NBR can dramatically improve the damping and mechanical performances of the composites. Fu et al.20 studied a series of H-bonds in four proteins, obtaining a better understanding of the contribution of the polar groups and hydrogen bonds to the conformational stability of proteins. It is well known that the existence of H-bonds can influence the vibrational behaviors of functional groups,21 and the deshielding effect of proton gradually enhances with increasing H-bonds strength, which gives rise to 1H downfield shifts that are concerned with the length of the H-bond.22 Thus Fourier transform infrared (FTIR) spectroscopy and 1H-nuclear magnetic resonance (1H-NMR) both become the standard means to estimate H-bonds, what's more, temperature-dependent FTIR can be used as a valid means for analysing the influence of temperature on the stability of H-bonds.23
With the ever-increasing computational technology, molecular simulation has provided an attractive complementary method to comprehend the structural and dynamic properties of materials at the molecular level.24 What's more, molecular simulation not only can act as an effective tool to investigate materials beyond experimental level in the harsh environmental conditions such as extreme high or low temperature and pressure,25 but also can reduce the endeavor in experiment such as synthesis and characterization.26 Typical three representative simulation methods of molecular scale are the Molecular Mechanics (MM) simulation based on Born–Oppenheimer approximation theory,27 the Monte Carlo (MC) simulation based on bond-fluctuation model28,29 and the molecular dynamics (MD) simulation based on bead-spring model.30,31 MD simulation can be used to simulate the static structure and dynamic behavior of molecules such as small molecules diffusion,32 adsorption on the surface of materials33 and the bending movement of molecular chains34 when the chosen time scale is relatively short in the process of simulation. Thus, MD simulation has an irreplaceable advantage in investigating the intermolecular interactions between small molecules and polymers. Zhu et al.35 investigated the microstructure and H-bonds network of polybenzimidazole by means of MD simulation. Topf et al.36 also used the MD method to study the stability of serine protease tetrahedron structure.
In this paper, with constructing the amorphous cells for different mass ratios AO-70/NBR composites, the micro-properties of AO-70/NBR composites were investigated from the molecular level. Then, by establishing the correlation between experiment and MD simulation, the objective of this work was to: (1) to investigate the relationship between the characteristics of H-bonds and damping mechanism in AO-70/NBR composites and (2) try to design the optimum ratio of AO-70/NBR composite with the highest damping performance and compare to the experimental results.
2. Experimental
2.1 Materials and sample preparation
NBR (N220S) with the acrylonitrile mass fraction of 41% was provided by Japan Synthetic Rubber Co., Ltd. (Tokyo, Japan). Hindered phenol AO-70, in the powder form, was provided from Beijing Jointek Technology Corp. (Beijing, China). The chemical structure of NBR and AO-70 are shown in Fig. 1(a) and (b) respectively.The AO-70/NBR composites preparation method is shown below: (1) firstly, the as-received NBR matrix was kneaded on a Φ 152.4 mm two-roll mill at room temperature for 4 min, in order to guarantee the consistency of the experiment and simulation, AO-70 was added to the NBR in the mass ratios of 0/100, 22/100, 44/100, 66/100, 88/100 and 109/100, respectively. Then, these mixtures were hot sheared in a Haake Banbury mixer (Greeloy, Shanghai) at a rotor speed of 60 rpm for 8 min at 100 °C with the addition of 5.0 phr of zinc oxide and 2.0 phr of stearic acid to guarantee the homogeneous dispersion of AO-70 molecules in the NBR matrix, which formed the first-stage AO-70/NBR composites (called AO-70/NBR(a) composites). (2) Secondly, the AO-70/NBR(a) composites were blended with the vulcanizing and accelerating agents including 0.2 phr of tetramethylthiuram disulfide, 0.5 phr of diphenyl guanidine, 0.5 phr of dibenzothiazole disulfide, and 2.0 phr of sulfur, the composites were then kneaded on the two-roll mill for 10 min and made triangle bag about eight times to guarantee the favourable mixing between AO-70 molecules and NBR matrix. (3) Lastly, under the pressure of 15 MPa, the composites were hot-pressed and vulcanized to form cross-linked composites at 160 °C, and then cooled down spontaneously to room temperature.
2.2 Characterization
Infrared measurements were performed on a Nicolet 8700 FTIR spectrometer (Thermo Fisher Scientific Inc. USA). AO-70 samples were firstly grated into powder and then pressed into ultra-thin films combined with anhydrous potassium bromide (KBr). Through the attenuated total reflection (ATR) technique, the FTIR spectra of AO-70/NBR composites were acquired from specimens (prepared by hot-pressing and vulcanizing) with a thickness of approximately 1 mm. A total of 128 scans were accumulated with a resolution of 2 cm−1 in the wavenumber range of 400 cm−1 to 4000 cm−1 for the FTIR spectral measurement.1H-NMR spectra was acquired on a Bruker Advance spectrometer manipulating at 400.13 MHz. CDCl3 was used to dissolve the uncross-linked materials before the NMR measurements.
The thermal properties of samples (5 mg) were acquired using a TGA/DSC calorimeter (Mettler-Toledo Co. Switzerland). Firstly, the sample was heated from room temperature to 120 °C at a heating rate of 20 °C min−1 to eliminate heat history. Secondly, the sample was cooled to −80 °C at a cooling rate of 20 °C min−1 and heated again to 120 °C at a heating rate of 10 °C min−1. All the heating and cooling procedures were operated under a nitrogen atmosphere. The melting temperature (Tm) of AO-70 was acquired from the first-heating scan, the Tg was acquired from the inflection point in the second-heating scan.
Temperature-dependent FTIR spectra were obtained on a Perkin Elmer 100 FTIR spectrometer conjunct with heating equipment. In nitrogen atmosphere, the thin samples were heated at a rate of 10 °C min−1, the temperature is set at 22 °C, 40 °C, 60 °C, 100 °C, 150 °C and 200 °C respectively.
DMA spectra were acquired in a tension mode by means of a VA 3000 dynamic mechanical analyzer (Rheometric Scientific Inc. USA). The samples with sizes of 20 mm (length) × 10 mm (width) × 2 mm (thickness) were heated from −80 °C to 100 °C at a heating rate of 3 °C per minute and a constant frequency of 10 Hz, a deformation of 0.1%.
3. MD simulation strategies and results
3.1 Simulation strategies for AO-70/NBR composites
To implement all MD simulation on the AO-70/NBR composites, the analog modules of Forcite, Discover and Amorphous cell (Accelrys, Inc., SanDiego, CA) with the commercial molecular simulation program Material Studio 7.0 were used. The ab initio condensed-phase optimized molecular potentials for atomistic simulation studies (COMPASS) force field was used for computing intramolecular and intermolecular interactions in that it can acquire a far-ranging coverage in organic and inorganic systems.15 The temperature was controlled by means of the Andersen method,37 the non-bonded Coulomb and van der Waals interactions were disposed using the standard Ewald and Atom-Based simulation methods, respectively.38 The Atom-Based simulation was applied for the van der Waals interactions with a cutoff distance, a buffer width and a spline width are 15.5 Å, 0.5 Å and 1 Å, respectively.The amorphous polymer models were built by using the Maxwell–Boltzmann profiles at 298 K under 3D periodic boundary conditions.39 Each cell consisting of 4 NBR chains with 50 repeat units and different AO-70 molecules. Table 1 exhibits the details of the MD simulation formulations, which comprises the number of NBR and AO-70 molecules as well as AO-70/NBR mass ratios. To regulate the repeat units of the molecular chains, three criteria should be adopted: (1) to control the repeat cell size and keep the computing time in a controllable scope, (2) to guarantee adequate movement of chain segments, and (3) to promote calibrated calculation scale.40
| No. of NBR molecules | No. of AO-70 molecules | Mass ratios of AO-70 |
|---|---|---|
| 4 × 50 | 0 | 0/100 |
| 4 × 50 | 4 | 22/100 |
| 4 × 50 | 8 | 44/100 |
| 4 × 50 | 12 | 66/100 |
| 4 × 50 | 16 | 88/100 |
| 4 × 50 | 20 | 109/100 |
3.2 Construction procedure of the AO-70/NBR cells
Fig. 2 shows the procedure of construction of the AO-70/NBR composites amorphous cells. The acrylonitrile repeat units (Fig. 2(a)) and butadiene repeat units (Fig. 2(b)) were first random copolymerized as a NBR polymer chain (Fig. 2(c)) with an acrylonitrile mass fraction of 41%. Secondly, four NBR polymer chains and several AO-70 small molecules (Fig. 2(d)) were built in a 3D periodic cell (Fig. 2(e)). Then, the cell was energy-minimized with the “Smart Minimizer” algorithm (including conjugate gradient, steepest descent, and the Newton method) at 298 K for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps to equilibrate the conformation until the energy convergence threshold of 1.0 × 10−4 cal mol−1 was reached. After the completion of energy minimization, in order to eliminate the internal stress, an annealing process was performed with the annealing cycle of 5 and the temperature ranged from 200 K to 400 K for 200 ps. Lastly, NVT (constant number of particles, volume, and temperature) as well as NPT (constant number of particles, pressure, and temperature) were accomplished at 298 K and followed by the total simulation time of 1000 ps (Fig. 2(f)). Eventually, the optimized cell can be used to determine the numbers and types of H-bonds (Fig. 2(g)) and to calculate the fractional free volume (FFV) (Fig. 2(h)), binding energy (Ebinding) as well as radial distribution function (RDF). In Fig. 2(g), the red dashed line represents an H-bond between NBR polymer chains and AO-70 small molecules. Fig. 2(h) shows the free volume (the space in blue) of the cell.
000 steps to equilibrate the conformation until the energy convergence threshold of 1.0 × 10−4 cal mol−1 was reached. After the completion of energy minimization, in order to eliminate the internal stress, an annealing process was performed with the annealing cycle of 5 and the temperature ranged from 200 K to 400 K for 200 ps. Lastly, NVT (constant number of particles, volume, and temperature) as well as NPT (constant number of particles, pressure, and temperature) were accomplished at 298 K and followed by the total simulation time of 1000 ps (Fig. 2(f)). Eventually, the optimized cell can be used to determine the numbers and types of H-bonds (Fig. 2(g)) and to calculate the fractional free volume (FFV) (Fig. 2(h)), binding energy (Ebinding) as well as radial distribution function (RDF). In Fig. 2(g), the red dashed line represents an H-bond between NBR polymer chains and AO-70 small molecules. Fig. 2(h) shows the free volume (the space in blue) of the cell.
3.3 Solubility parameters of AO-70 and NBR and analysis of the density of AO-70/NBR composites
As defined by Hildebrand and Scott, the solubility parameter (δ) is simply the square root of the cohesive energy density (CED) and it characterizes the strength of attractive interactions.41 When the two parts have a closer solubility parameter (usually δNBR − δAO-70 < 1 (cal cm−3)0.5), demonstrating a better compatibility between fillers and polymer matrix.
 | (1) |
Through MD simulation we calculated the solubility parameters of AO-70 and NBR (shown in Table 2), it is revealed that NBR and AO-70 have very close solubility parameters (δNBR − δAO-70 < 0.5 (cal cm−3)0.5) both in simulated and experimental results which is an indication of good compatibility. The deviation between simulation and experimental δ could mainly ascribe to two reasons: (1) compared to real samples, the polymers used in simulation were relatively shorted, and (2) the force field is unable to cover all the detailed interactions.
| Components | Solubility parameter ((cal cm−3)0.5) | ||
|---|---|---|---|
| Simulation | Experimental | Difference | |
| NBR | 9.28 | 9.64 | 0.36 |
| AO-70 | 9.64 | 9.90 | 0.26 |
Molecular dynamics simulation models of polymers are particularly sensitive to the change in tiny cell density. Thus the density should be confirmed exactly and can be approximately replace the real materials.42 As is seen in Table 3, the simulated densities reasonably in agreement with the experimental values (ρMD − ρExp < 0.1 g cm−3), which reveals that the valid optimization of intermolecular interactions have been acquired and the simulative structure is close to reality.
| AO-70/NBR | 0/100 | 22/100 | 44/100 | 66/100 | 88/100 | 109/100 |
|---|---|---|---|---|---|---|
| Density ρMD (g cm−3) | 1.030 | 1.050 | 1.063 | 1.074 | 1.081 | 1.087 |
| Density ρExp (g cm−3) | 1.059 | 1.070 | 1.083 | 1.085 | 1.094 | 1.102 |
3.4 Radial distribution function research
In order to ulteriorly analyse the intermolecular interactions such as H-bonding in AO-70/NBR composites, we can utilize the radial distribution function (RDF, also known as pair correlation function, PCF43) which is the physical quantity has nothing to do with the time and represents the possibility of discovering a pair of atoms at a distance in an absolutely stochastic distribution. Intermolecular interactions can be divided into H-bonding, strong van der Waals' force and weak van der Waals' force which correspond to the distances between atoms of 2.6–3.1, 3.1–5.0 and above 5.0 Å respectively.44 In the process of computing RDF, firstly, the nitrogen atoms of NBR and the hydrogen atoms of AO-70 are marked with different colours, then, we analyse the RDF of H (AO-70) and N (NBR). Similarly, the RDF of H (AO-70) and O (AO-70) can be calculated. The RDF of H (AO-70) and N (NBR) are presented (shown in Fig. 3(a)) by calculating. It is revealed that a pointed peak appears for all components in the scope of 2.6–3.0 Å, demonstrating the high probability existence of type A (AO-70) –OH⋯NC– (NBR) H-bonds in AO-70/NBR composites. In Fig. 3(b), all components in the scope of 2.6–3.0 Å present a peak, suggesting that there is a moderate probability for type B (AO-70) –OH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C– (AO-70) H-bonds to form. Similarly, as is seen from Fig. 3(c) and (d), type C (AO-70) –OH⋯OH– (AO-70) and D (AO-70) –OH⋯O–C– (AO-70) H-bonds would potential appear in the AO-70/NBR composites with AO-70 content of 66 and 109 phr (parts per hundreds).
C– (AO-70) H-bonds to form. Similarly, as is seen from Fig. 3(c) and (d), type C (AO-70) –OH⋯OH– (AO-70) and D (AO-70) –OH⋯O–C– (AO-70) H-bonds would potential appear in the AO-70/NBR composites with AO-70 content of 66 and 109 phr (parts per hundreds).
 | ||
| Fig. 3 RDFs for (a) type A H-bonds, (b) type B H-bonds, (c) type C H-bonds and (d) type D H-bonds in the AO-70/NBR composites. | ||
3.5 Analysis of the stability of hydrogen bonds in AO-70/NBR composites
H-bond (X–H⋯Y) is a characteristic attractive interaction (X–H is the H-bond donator, however, Y is the H-bond acceptor), commonly, X and Y are high electronegative elements such as O, F, N atom.45 As mentioned above, we discovered that four different H-bonds were formed in the AO-70/NBR composites with the addition of AO-70 by discussing the RDF. As is shown in Fig. 4, the hindered phenol small molecules are randomly connected with the rubber matrix by this invertible interaction, forming a three-dimensional network structure.Bond length L and angle θ play a vital role in the formation as well as stability of the H-bonds.46 Generally speaking, a larger bond angle and a smaller bond length correspond to a more stable H-bonds, what's more, the electronegativity of atom which connected by electropositive H atom also influence the formation of H-bonds. As is seen in Table 4, although the oxygen atom on phenolic hydroxyl group in AO-70 has a high electronegativity, the steric hindrance effect of the tertiary butyl and methyl groups (shown in Fig. 5(a)) would impede the formation of type C H-bonds in the three-dimensional network structure. Compared with Fig. 5(b)–(d) can show that the length of a type A H-bond is shorter than that of a type B and D H-bonds (L3 < L1, L2), moreover, the bond angle of a type A H-bond is larger than that of a type B and D H-bonds (θ3 > θ1, θ2), making the formation of a type A H-bond easier than that of a type B and D.
| Atom (red represent the object of study) | Electronegativity |
|---|---|
| AO-70–OH | 0.410 |
| NBR–N | −0.428 |
AO-70–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
−0.450 |
| AO-70–O | −0.320 |
| AO-70–HO | −0.452 |
3.6 Number and types of hydrogen bonds in AO-70/NBR systems
As shown in Fig. 6, four types of H-bonds can be formed in the AO-70/NBR composites in accordance with the theoretical analysis of RDF.As is known to all, through MD simulation we can acquire the quantitative information about the H-bonds such as the number, bond length and bond angle in composites. The average number of H-bonds (listed in Table 5) in AO-70/NBR composites with different mass ratios were based on ten different frame cells. The number of total H-bonds almost increases linearly with the increasing of AO-70 content, type A H-bonds largely outnumber other three H-bonds, indicating that type A H-bonds are the most easily to form in the three-dimensional network structure, consistent with the analysis of the stability of H-bonds. While type B H-bonds overnumber type C and D H-bonds, which because the oxygen atom on carbonyl group in AO-70 has a high electronegativity and type B H-bond has a shorter bond length as well as a larger bond angle. Moreover, type C and D H-bonds only appear with the AO-70 content of 66 and 109 phr which is unanimous with the analysis of RDF, and they have little impact on the dynamic properties of the composites. Thus, the type A and type B H-bonds are mainly considered in the study of the effect of AO-70 content on the damping performances of AO-70/NBR composites.
| Mass ratio AO-70/NBR | 0/100 | 22/100 | 44/100 | 66/100 | 88/100 | 109/100 |
|---|---|---|---|---|---|---|
| Type A | 0 | 2 | 10 | 10 | 10 | 14 |
| Type B | 0 | 1 | 1 | 0 | 6 | 3 |
| Type C | 0 | 0 | 0 | 1 | 0 | 2 |
| Type D | 0 | 0 | 0 | 1 | 0 | 2 |
3.7 Fractional free volume in AO-70/NBR hybrids
In order to calculate the amount of mobilizable free space and the efficiency of chain packing in AO-70/NBR composites, usually, the fractional free volume (FFV) theory can be used to analyse the influence of the H-bonds on these composites.As is known to all, a common definition can be used to calculate FFV:47
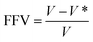 | (2) |
Through the positron annihilation lifetime spectroscopy (PALS) we can also observe the FFV of materials, which validates the results of MD simulation from the angle of the experiment. Commonly, the positron preferentially forms a quasi-bound state called positronium (Ps) with an electron around the mediums in polymer materials and annihilates subsequently. The Ps can be divided into two forms which are para positronium (anti-parallel electron and positron spins: p-Ps) and ortho positronium (parallel electron and positron spins: o-Ps) in the light of the different spin-coupling characteristics between electron and positron, moreover, the lifetimes of p-Ps and o-Ps in vacuum are 125 ns and 142 ns respectively.48,49 In consideration of the disorganized structure of amorphous polymer, the o-Ps probe is extraordinary free volume in situ probe on account of its extremely small size (0.106 nm) and electric neutrality, thus the probe has little influence on atomic vacancy and free volume. At present, the most frequently-used quantum mechanical model possesses homogeneous thickness electron layer, where o-Ps can be approximately regard as a particle which situates a spherical well with the radius R0 and given that an electron layer in the region R < r < R0, R is the mean free volume radius.50
The following semi-empirical equation provides a relationship between the o-Ps lifetime τ3 and free volume radius R:51
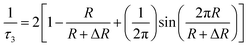 | (3) |
The relative FFV can be calculated with the following equation:
 | (4) |
As is shown in Table 6, the FFV and relative FFV of AO-70/NBR composites measured by MD simulation and PALS respectively. The relative FFV has the similar change tendency as FFV, which generally decreases with the increasing of AO-70 content in that AO-70 small molecules form sufficient H-bonds with NBR, causing the tight packing of molecular chains and impeding the chain segments from rotating allodially. While the AO-70/NBR composite with AO-70 content of 109 phr has the smallest FFV and relative FFV, indicating the strongest intermolecular H-bonds interaction. In conclusion, the PALS results are basically in agreement with those calculated by MD simulation.
| Mass ratio AO-70/NBR | 0/100 | 22/100 | 44/100 | 66/100 | 88/100 | 109/100 |
|---|---|---|---|---|---|---|
| FFV (%) by MD | 37.88 | 37.06 | 37.55 | 37.13 | 36.74 | 36.31 |
| Relative FFV (%) by PALS | 3.25 | 3.10 | 3.02 | 3.08 | 3.13 | 2.92 |
3.8 Binding energy in AO-70/NBR composites
Binding energy (Ebinding) is defined as the negative value of the interaction energy (Einter) and can forecast the compatibility of two components.52 The binding energy between AO-70 and NBR can be calculated by the following equation:| Ebinding = −Einter = −(Etotal − EAO-70 − ENBR) | (5) |
The Ebinding of the AO-70/NBR composites, the energy of AO-70 and NBR are presented in Table 7, ENBR is constant in theory because the number of NBR chains are fixed in the construction procedure of cells, however, actually the value of ENBR is variable contributed to the conformation change in the system. The Ebinding gradually increases and maintains positive value with the increasing of AO-70 content, demonstrating the growing intermolecular interactions and perfect compatibility in the system. The Ebinding of AO-70/NBR composite reaches the maximum with an AO-70 content of 109 phr, demonstrating the strongest interaction between NBR and AO-70 and corresponding to the maximum number of H-bonds. Next, experimental methods below will be used from the macroscopic point of view in order to further testify our microscopic analysis from MD simulation.
| Mass ratio AO-70/NBR | Etotal (kcal mol−1) | EAO-70 (kcal mol−1) | ENBR (kcal mol−1) | Ebinding (kcal mol−1) |
|---|---|---|---|---|
| 0/100 | 443.01 | 0 | 443.01 | 0 |
| 22/100 | 489.68 | 139.15 | 611.75 | 261.22 |
| 44/100 | 397.35 | 361.80 | 702.21 | 666.66 |
| 66/100 | 514.93 | 450.08 | 878.00 | 813.05 |
| 88/100 | 573.76 | 622.44 | 912.74 | 961.42 |
| 109/100 | 380.35 | 514.07 | 828.35 | 962.07 |
4. Experimental results and discussion
4.1 FTIR of AO-70/NBR composites
To investigate the origin of the intermolecular interaction between AO-70 and NBR, the FTIR measurements of pure AO-70 and AO-70/NBR composites (shown in Fig. 7) were performed. The telescopic vibration peak of hydroxyl group (–OH) is usually in the wavenumber range of 3125–3704 cm−1. As is shown in Fig. 7(a), there is a significant absorption peak in 3480 cm−1 correspond to hydroxyl groups with H-bonds, indicating that hydroxyl groups in the AO-70 principally formed H-bonds, the amount of free hydroxyl groups are very limited. In Fig. 7(b), there is almost no apparent absorption peak of the neat NBR in the wavenumber range of 4000–3200 cm−1, whereas the absorption peak of AO-70/NBR composites at 3482 cm−1 associated with H-bonded hydroxyl groups becomes more and more obvious and a red shift occurs with increasing of AO-70 content, which can be ascribed to H-bonding between the –OH groups of AO-70 and –CN groups of NBR as well as –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups of AO-70. In the wavenumber range of 2400–2050 cm−1 (shown in Fig. 7(c)), the absorption peak of the –CN groups are gradually weakened and a blue shift occurs with increasing of AO-70 content, demonstrating the H-bonds in the three-dimensional network structure have become stronger.
O groups of AO-70. In the wavenumber range of 2400–2050 cm−1 (shown in Fig. 7(c)), the absorption peak of the –CN groups are gradually weakened and a blue shift occurs with increasing of AO-70 content, demonstrating the H-bonds in the three-dimensional network structure have become stronger.
 | ||
| Fig. 7 FTIR/TR spectrum of AO-70 (a), and FTIR/ATR spectra of AO-70/NBR composites (b and c) at various components (the red and blue arrow indicates a red and blue shift respectively). | ||
4.2 1H-NMR of AO-70/NBR composites
In general, 1H-NMR can be served as an advantageous means to study the structure of polymer, thus we intend to further demonstrate the surmise of H-bonds of the AO-70/NBR composites through 1H-NMR measurement. Fig. 8 shows the 1H-NMR spectra of AO-70 and NBR, there is a spike at 4.68 ppm correspond to the characteristic peak of the hydrogen atom of phenolic hydroxyl of AO-70 (shown in Fig. 8(a)) and the characteristic peaks for five kinds of the hydrogen atoms of the methylene groups of AO-70 are at the scope of δ 2.5–4.5 ppm. Compared with the 1H-NMR spectra at δ 3.1–5.1 ppm of Fig. 8(a) and (b), it is revealed that there is no apparent peak of NBR, whereas there are some characteristic peaks of AO-70.Fig. 9 shows the effect of different AO-70 contents on 1H-NMR spectra. As is shown in Fig. 9, it is obvious that the characteristic peaks of AO-70 become more and more distinct in the spectra of the composites with increasing of AO-70 content.
Generally, the NMR peak will shift toward the direction of lower field in that the H-bonding association effect can induce the deshielding effect of protons. The higher the association effect, the greater the reduction of the electron cloud density of protons.53 Thus, we analysed the chemical shift of the proton of the phenolic hydroxyl of AO-70 and contrast the area ratio of the characteristic peaks between phenolic hydroxyl and methylene groups. It is conceivable that the area of the characteristic peak of methylene theoretically should be twice as large as that of the phenolic hydroxyl, while the area ratio of the peaks between phenolic hydroxyl and methylene were not constant as well as the chemical shift moving towards lower field with increasing of AO-70 content (shown in Fig. 10) which contributed to H-bonds interaction, agreed well with the FTIR results.
 | ||
| Fig. 10 Comparison of H (phenolic hydroxyl group, 4.68 ppm) with H (methane group) in 1H-NMR spectra of various AO-70/NBR composites. | ||
4.3 DSC analysis of AO-70/NBR composites
DSC was an effective tool to study the Tg variation and the compatibility in the composites. Fig. 11 shows the DSC traces of AO-70 and AO-70/NBR composites. The as-received AO-70 powder was crystalline and had a melting point about 81.3 °C measured by the first heating scan (shown in the red line of Fig. 11(a)). The amorphous AO-70 with a Tg of around 4.49 °C was obtained by the second heating scan (shown in the blue line of Fig. 11(a)). What's more, all the AO-70/NBR composites only have one glass transition temperature (shown in Fig. 11(b)), demonstrating the favourable compatibility between AO-70 and NBR, consistent with the analysis of solubility parameters of AO-70 and NBR in MD simulation. The glass transition temperature of AO-70/NBR composites increases with increasing of AO-70 content on the reason that the H-bonds which restrict the movements of polymer chains formed in the three-dimensional network structure.4.4 Temperature-dependent FTIR of AO-70/NBR composites
The topology structures and dynamics properties of transient molecular networks are extremely sensitive to environmental variables (peculiarly temperature) on account of the thermoreversibility of H-bonds. Therefore, in order to validate the stability of H-bonds in AO-70/NBR composites, temperature-dependent FTIR can be used as an ideal tool to analyse the formation and fracture of intermolecular and intramolecular H-bonds on the reason that the H-bonds are generally destroyed as the temperature increases. Fig. 12 shows the temperature-dependent FTIR spectra of AO-70/NBR (109/100) composite.As shown in Fig. 12, in the wavenumber range of 3800–3100 cm−1, the absorption peak of hydroxyl groups with H-bonds are gradually weakened and a blue shift occurs as well as the range of absorption peak gradually widened with increasing of the temperature, moreover, the characteristic peak for free hydroxyl groups at around 3610 cm−1 are increasingly apparent when the temperature exceeds 100 °C because the melting point of AO-70 is 81.3 °C, indicating that H-bonded hydroxyl groups are destroyed with increasing of the temperature. In general, in the wavenumber range of 2400–2100 cm−1, the absorption peak of nitrile groups with H-bonds are only faintly weakened and a red shift occurs with increasing of the temperature, demonstrating that the nitrile groups with H-bonds are not sensitive to temperature and more stable with increasing of the temperature. In conclusion, compared with other H-bonds, type A H-bonds are much more stable at high temperature and more difficultly destroyed, consistent with the analysis of the stability of H-bonds.
4.5 Dynamic mechanical properties of AO-70/NBR composites
As stated above, H-bonds play a crucial role in determining the damping performances of AO-70/NBR composites. In this study, DMA was a valid method to analyse the damping performances of the AO-70/NBR composites as well as validate the miscibility between AO-70 and NBR. The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is the ratio of the dissipated energy to the biggest stored energy in one deformation cycle, reflecting the internal and external friction.54 Therefore, a higher tan
δ is the ratio of the dissipated energy to the biggest stored energy in one deformation cycle, reflecting the internal and external friction.54 Therefore, a higher tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ, a better damping performance of the materials.
δ, a better damping performance of the materials.
In Fig. 13, the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak of AO-70/NBR shifts to higher temperature and the tan
δ peak of AO-70/NBR shifts to higher temperature and the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ value gradually increases with the increasing of AO-70 content which contributed to the strong H-bonds interactions between AO-70 and NBR reduce the motion of NBR chains and induce a distinct energy dissipation, suggesting that there is a favourable damping property of AO-70/NBR composites. Moreover, there is only one tan
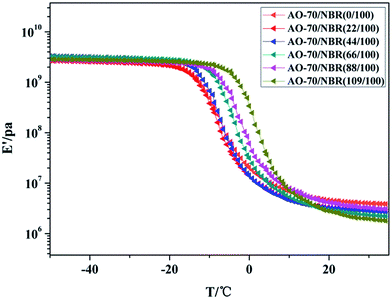
δ value gradually increases with the increasing of AO-70 content which contributed to the strong H-bonds interactions between AO-70 and NBR reduce the motion of NBR chains and induce a distinct energy dissipation, suggesting that there is a favourable damping property of AO-70/NBR composites. Moreover, there is only one tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ peak appears in each of the AO-70/NBR composite, demonstrating a favourable compatibility between the AO-70 and NBR in accordance with the DSC results mentioned above. In Fig. 14, the storage modulus E′ for NBR and AO-70/NBR composites curves show only one transition, and gradually shifts toward higher temperature, demonstrating no phase separation occurs and strong H-bonds interactions in the three-dimensional network structure.
δ peak appears in each of the AO-70/NBR composite, demonstrating a favourable compatibility between the AO-70 and NBR in accordance with the DSC results mentioned above. In Fig. 14, the storage modulus E′ for NBR and AO-70/NBR composites curves show only one transition, and gradually shifts toward higher temperature, demonstrating no phase separation occurs and strong H-bonds interactions in the three-dimensional network structure.
We summarize the DMA results of AO-70/NBR composites with different AO-70 contents in Table 8. Generally, the peak area (TA) which is the area under the tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ versus temperature curve at tan
δ versus temperature curve at tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ > 0.3 is used as an index of damping performance.55 As is seen in Table 8, as the AO-70 content increases from 0 phr to 109 phr, the loss peak value of AO-70/NBR composites gradually increases from 1.78 to 2.97. It is quite clear that the AO-70/NBR (109/100) composite has the largest tan
δ > 0.3 is used as an index of damping performance.55 As is seen in Table 8, as the AO-70 content increases from 0 phr to 109 phr, the loss peak value of AO-70/NBR composites gradually increases from 1.78 to 2.97. It is quite clear that the AO-70/NBR (109/100) composite has the largest tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ and TA (tan
δ and TA (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ > 0.3) value than other composites, indicating the optimized damping property.
δ > 0.3) value than other composites, indicating the optimized damping property.
| Mass ratio of AO-70/NBR | Maximum tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ δ |
Peak area for (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ > 0.3) δ > 0.3) |
|
|---|---|---|---|
| Value | At T (°C) | TA | |
| 0/100 | 1.78 | −3.60 | 21.45 |
| 22/100 | 2.08 | −4.35 | 24.07 |
| 44/100 | 2.42 | −3.60 | 26.80 |
| 66/100 | 2.57 | −0.50 | 28.67 |
| 88/100 | 2.71 | 0.70 | 27.03 |
| 109/100 | 2.97 | 5.15 | 33.30 |
5. Conclusions
In this article, molecular dynamic (MD) simulation and experimental combinative methods were used to systematically elucidate the microstructure of AO-70/NBR composites and the mechanism of the damping performance of NBR result from the addition of hindered phenol AO-70. Ultimately, we have drawn the following conclusions:(1) MD simulation results proved that four types of H-bonds were formed in the AO-70/NBR composites: type A (AO-70) –OH⋯NC– (NBR), type B (AO-70) –OH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C– (AO-70), and type C (AO-70) –OH⋯OH– (AO-70), type D (AO-70) –OH⋯O–C– (AO-70), what's more, type A H-bonds which were most stable and type B H-bonds were properly formed in the AO-70/NBR composites. The RDF showed type C H-bonds and type D H-bonds potential appeared in the AO-70/NBR composites with higher AO-70 content. The PALS result had the similar change tendency as FFV, which generally decreased with the increasing of AO-70 content in that the H-bonds impeded the movement and rotation of polymer chains. The Ebinding gradually increased and maintained positive value with the introduction of AO-70 content, demonstrating the growing intermolecular interactions and perfect compatibility in the composites.
C– (AO-70), and type C (AO-70) –OH⋯OH– (AO-70), type D (AO-70) –OH⋯O–C– (AO-70), what's more, type A H-bonds which were most stable and type B H-bonds were properly formed in the AO-70/NBR composites. The RDF showed type C H-bonds and type D H-bonds potential appeared in the AO-70/NBR composites with higher AO-70 content. The PALS result had the similar change tendency as FFV, which generally decreased with the increasing of AO-70 content in that the H-bonds impeded the movement and rotation of polymer chains. The Ebinding gradually increased and maintained positive value with the introduction of AO-70 content, demonstrating the growing intermolecular interactions and perfect compatibility in the composites.
(2) The temperature-dependent FTIR proved that the type A H-bond was most stable and would not change with temperature. DSC and DMA demonstrated that strong intermolecular H-bonds interaction formed in the three-dimensional network structure and the damping property of the composites got a noteworthy increase with the introduction of AO-70—max tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ increased by 66.9%. Both MD simulation and experimental results revealed that the AO-70/NBR (109/100) composite has the largest H-bonds and best damping performance.
δ increased by 66.9%. Both MD simulation and experimental results revealed that the AO-70/NBR (109/100) composite has the largest H-bonds and best damping performance.
In a word, our work has indicated that the availability of MD simulation help us expediently comprehend the damping mechanism of AO-70/NBR composite, and inspires us to sequentially research other polymer systems through this computational means.
Acknowledgements
The authors gratefully acknowledge the financial supports of the Ministry of Science and Technology of China (Grant No. 2014BAE14B01) and the National Natural Science Foundation of China (Grant No. 51473012, 51320105012 and 51521062).References
- N. Tucker and K. Lindsey, J. Eng. Mater. Technol., 2003, 18, 191 Search PubMed.
- J. L. Leblanc, J. Appl. Polym. Sci., 1997, 66, 2257–2268 CrossRef CAS.
- C. L. Lewis, K. Stewart and M. Anthamatten, Macromolecules, 2014, 47, 729–740 CrossRef CAS.
- S. P. Balch and R. S. Lakes, Funct. Mater. Lett., 2015, 5, 1550059 CrossRef.
- R. D. Friend and V. K. Kinra, J. Sound Vib., 2000, 1, 93–118 CrossRef.
- X. D. Mao, S. A. Xu and C. F. Wu, Polym.-Plast. Technol. Eng., 2008, 47, 209 CrossRef CAS.
- S. W. Kuo and F. C. Chang, Macromol. Chem. Phys., 2001, 202, 3112 CrossRef CAS.
- J. L. White and Y. M. Lin, J. Appl. Polym. Sci., 1973, 17, 3273–3292 CrossRef CAS.
- M. Song, X. Y. Zhao, Y. Li, L. Q. Zhang and S. Z. Wu, RSC. Adv., 2014, 4, 6719–6729 RSC.
- X. Y. Shi, W. N. Bi and S. G. Zhao, J. Appl. Polym. Sci., 2012, 124, 2234–2239 CrossRef CAS.
- C. Meiorin, M. I. Aranguren and M. A. Mosiewicki, Polym. Int., 2012, 61, 735–742 CrossRef CAS.
- Y. Q. Wang, Y. Wang, H. F. Zhang and L. Q. Zhang, Macromol. Rapid Commun., 2006, 27, 1162–1167 CrossRef CAS.
- X. F. Niu, X. G. Yang, P. Brochu, H. Stoyanov, R. Y. Sung, Z. B. Yu and Q. B. Pei, Adv. Mater., 2012, 24, 6513–6519 CrossRef CAS PubMed.
- X. Y. Zhao, J. N. Yang, D. T. Zhao, Y. L. Lu, W. C. Wang, L. Q. Zhang and T. Nishic, Int. J. Smart Nano Mater., 2015, 6, 239–250 CrossRef.
- K. M. Xu, F. S. Zhang, X. L. Zhang, J. W. Guo, H. Wu and S. Y. Guo, RSC Adv., 2015, 5, 4200–4209 RSC.
- K. M. Xu, F. S. Zhang, X. L. Zhang, Q. M. Hu, H. Wu and S. Y. Guo, J. Mater. Chem. A, 2014, 2, 8545–8556 CAS.
- M. Rossi, Choice, 1998, 35, 1017 Search PubMed.
- S. H. Kim, J. P. K. Tan, N. Fredrik, F. Kazuki, C. John, C. Yang, N. Alshakim, Y. Y. Yang and J. L. Hedrick, Biomaterials, 2010, 31, 8063–8071 CrossRef CAS PubMed.
- Y. Yang, Y. F. Zhao, M. S. Zhan, J. Y. Wang, C. Zhao, X. Y. Liu and J. H. Zhang, J. Appl. Polym. Sci., 2015, 132 DOI:10.1002/app.42605.
- C. N. Pace, H. L. Fu, K. L. Fryar, J. Landua, S. R. Trevino, D. Schell, R. L. Thurlkill, S. Imura, J. M. Scholtz, K. Gajiwala, J. Sevcik, L. Urbanikova, J. K. Myers, K. Takano, E. J. Hebert, B. A. Shirley and G. R. Grimsley, Protein Sci., 2014, 23, 652–661 CrossRef CAS PubMed.
- J. G. C. M. Van Duijneveldt-van De Rijdt, F. B. Van Duijneveldt, J. A. Kanters and D. R. Williams, J. Mol. Struct.: THEOCHEM, 1984, 109, 351–366 CrossRef.
- L. X. Wang, B. Q. Hu, J. F. Xiang, J. Cui, X. Hao, T. L. Liang and Y. L. Tang, Tetrahedron, 2014, 70, 8588–8591 CrossRef CAS.
- Q. Wei, X. N. Guo, Y. L. Wang and H. Yang, J. Mol. Liq., 2013, 177, 225–228 CrossRef CAS.
- M. Song, X. Y. Zhao, B. Qiao, H. Zou and S. Z. Wu, Asian J. Chem., 2013, 25, 5200–5202 Search PubMed.
- I. Ysrovsky and E. P. Eevans, Polymer, 2005, 46, 973–981 Search PubMed.
- J. C. Palmer and P. G. Debenedetti, AIChE J., 2015, 61, 370–383 CrossRef CAS.
- A. Witkowski, Mol. Phys., 2011, 109, 2423–2432 CrossRef CAS.
- J. Andreas, N. Jürgen and H. Gert, Macromol. Theory Simul., 2007, 16, 430–440 CrossRef.
- M. Wittkop, T. Hölzl, S. Kreitmeier and D. Göritz, J. Non-Cryst. Solids, 1996, 201, 199–210 CrossRef CAS.
- T. Davris and A. V. Lyulin, Polym. Compos., 2015, 36, 1012–1019 CrossRef CAS.
- S. S. James, B. Dmitry and D. S. Grant, Compos. Sci. Technol., 2003, 63, 1599–1605 CrossRef.
- Z. W. Wang, P. L. Wang and C. Y. Hu, Packag. Technol. Sci., 2010, 23, 457–469 CrossRef CAS.
- J. W. Shen, T. Wu, Q. Wang and H. H. Pan, Biomaterials, 2008, 29, 513–532 CrossRef CAS PubMed.
- E. Khurana, S. O. Nielsen and M. L. Klein, J. Phys. Chem. B, 2006, 110, 22136–22142 CrossRef CAS PubMed.
- W. Zhu, W. J. Xiao and X. H. Xiao, J. Hazard. Mater., 2010, 158, 211–217 Search PubMed.
- T. Maya, V. Peter and R. W. Graham, J. Am. Chem. Soc., 2002, 124, 14780–14788 CrossRef.
- M. E. Riley, M. E. Coltrin and D. J. Diestler, J. Chem. Phys., 1988, 88, 5934 CrossRef CAS.
- M. P. Allen, D. J. Tildesley and J. R. Banavar, Phys. Today, 1989, 42, 105–106 CrossRef.
- P. J. Skrdla and R. T. Robertson, J. Phys. Chem. B, 2005, 109, 10611–10619 CrossRef CAS PubMed.
- B. Qiao, X. Y. Zhao, D. M. Yue, L. Q. Zhang and S. Z. Wu, J. Mater. Chem., 2012, 22, 12339–12348 RSC.
- M. M. Coleman, C. J. Serman, D. E. Bhagwagar and P. C. Painter, Polymer, 1990, 31, 1187–1203 CrossRef CAS.
- M. Song, X. Y. Zhao, W. C. Tung, L. Q. Zhang and S. Z. Wu, Macromol. Theory Simul., 2015, 24, 41–51 CrossRef CAS.
- J. P. Zeng, Y. X. Zhang, Y. Dai and S. Chen, J. Mol. Liq., 2014, 198, 274–279 CrossRef CAS.
- A. Mattozzi, M. S. Hedenqvist and U. W. Gedde, Polymer, 2007, 48, 5174–5180 CrossRef CAS.
- S. J. Grabowski, J. Phys. Chem. A, 2011, 115, 12789–12799 CrossRef CAS PubMed.
- T. Steiner and G. R. Desiraju, Chem. Commun., 1998, 891–892 RSC.
- A. Morteza and S. A. Mousavi, J. Mol. Struct., 2015, 1100, 401–414 CrossRef.
- Y. C. Jean, P. E. Mallon and D. M. Schrader, Principles and application of positron and positronium chemistry, World Scientific, Singapore, 2003 Search PubMed.
- O. E. Mogensen, Positron annihilation in chemistry, Springer Verlag, New York, 1995 Search PubMed.
- M. L. Cheng, Y. M. Sun, H. M. Chen and Y. C. Jean, Polymer, 2009, 50, 1957–1964 CrossRef CAS.
- D. Bamford, G. Dlubek, G. Dommet, S. Höring and T. Lüpke, Polymer, 2006, 47, 3486–3493 CrossRef CAS.
- Y. H. Lan, D. H. Li, R. J. Yang, W. H. Liang, L. X. Zhou and Z. W. Chen, Compos. Sci. Technol., 2013, 88, 9–15 CrossRef CAS.
- L. H. Yu and H. J. Schneider, Eur. J. Org. Chem., 1999, 1619–1625 CrossRef CAS.
- E. Esmizadeh, G. Naderi, M. H. R. Ghoreishy and G. R. Bakhshandeh, J. Polym. Eng., 2011, 31, 83–92 CAS.
- M. R. Duncan, C. R. Wassgren and C. M. Krousgrill, J. Sound Vib., 2005, 286, 123–144 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |