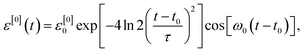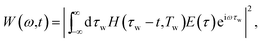DOI:
10.1039/C6RA16158H
(Paper)
RSC Adv., 2016,
6, 92962-92969
Sampling-based robust control in synchronizing collision with shaped laser pulses: an application in charge transfer for H+ + D → H + D+
Received
22nd June 2016
, Accepted 30th August 2016
First published on 1st September 2016
Abstract
In laser-assisted collisions, a control field may fail if we cannot precisely synchronize the colliding particles and the laser pulse. In this paper, we show that laser pulses that are robust in this situation can be obtained by a sampling-based method to achieve a desired charge transfer probability with limited sensitivity to the arrival time of the laser pulses. The time-dependent wave packet method and an adaptive target scheme are used in optimal control calculations based on an adiabatic two-state model of a H + D+ collision system. Several samples with different pulse arrival times are selected to construct robust fields at two different collision energies and the validity of these fields are examined by tests with additional samples. Excellent performance was obtained with the robust fields in both cases.
1 Introduction
For many decades, various spectroscopic methods have been used to carefully observe quantum systems at the atomic and molecular scale. A fascinating feature of quantum control is the ability to actively manipulate the course of physical and chemical processes, thereby providing a new means to explore quantum dynamics. For a specified control objective, and with restrictions imposed by many possible constraints, the time-dependent field required to manipulate the system in a desired way can be designed using Quantum Optimal Control Theory (QOCT).1,2 An optimally shaped laser pulse typically has a complex form, both temporally and spectrally. The phases and amplitudes of the available frequency components are optimized to excite an interference pattern among distinct quantum pathways, to best achieve the desired dynamics.3,4 Many monotonic QOCT algorithms have been developed.5–12 In particular, QOCT was recently applied to identify optimal sequences of RF pulses for the operation of NMR quantum information processors,13 phase control of a vibrational state qubit,14 photoassociation,15 stabilization of ultracold molecules,16,17 conversion of atoms into a molecular Bose–Einstein condensate,18 control of isomerization,19 field-free molecular orientation control of a thermal ensemble with near-single-cycle THz pulses,20 control of charge transfer,21 and control of inhomogeneous quantum ensembles.22 However, control performance may significantly decrease in the presence of unavoidable uncertainties such as control noise or environmental disturbances. Hence, control field robustness is a key issue in developing practical quantum technologies.23
Charge transfer processes are of considerable interest, both theoretically and experimentally, because of their fundamental role in the elementary processes of physics, chemistry and biology.24 For instance, charge transfer is the main mechanism for recombination, ionization, and excitation in astrophysical and laboratory plasmas.25 Laser fields have been considered for modifying electron transfer processes in ion-atom collisions.26–28 Symmetric collisions between protons and atomic hydrogen have been tested as a platform for the basic principles of laser-assisted electron transfer on account of their simplicity.29,30 In asymmetric ion-atom collisions, the charge exchange cross section may be strongly modified by a suitable laser field.31,32 Some recent numerical simulations showed that enhancement by a factor of ∼two was possible for proton-neon and proton-argon collisions, utilizing a moderate intensity laser field in contrast with field-free collisions.33 Even for a relatively weak laser intensity, a substantial increase in the charge transfer cross section has been observed.34,35 Optimal control theory can be applied to achieve a desired charge transfer outcome.21 However, the robustness of the field was not considered in the collision. The solution of the time-dependent Schrödinger equation depends on the initial condition and the Hamiltonian. Therefore, a control field is effective at a specific time, and the efficiency of charge transfer may decrease significantly without the precise arrival of the control laser pulse. Hence, synchronizing the control pulse and the collision plays a significant role, but this usually cannot be directly controlled. With this point in mind, the goal of this paper is to present a systematic study into achieving control pulses that are robust to synchronizing H+ + D charge transfer processes.
Several methods have been proposed for quantum system robust control design. For example, an H∞ method has been developed to formulate and solve this problem for linear quantum stochastic systems.36 Sliding mode control has been developed to enhance the robustness of quantum systems.37–39 In addition, the sampled-data feedback model of quantum systems has also been utilized for a risk-sensitive control problem.40 The present work considers constructing a robust field using a sampling-based method,22,41,42 synchronizing the asymmetric H+ + D(1s) collisional system with a two-state model.43,44 This scheme is realized by incorporating many samples with different pulse arrival times in combination with an optimal control algorithm. For the QOCT calculation we adopt the recently developed fast-kick-off algorithm12 based on the two-point boundary-value quantum control paradigm (TBQCP) method.10,11,20 Furthermore, we impose a zero-area constraint on the control algorithm to ensure that the laser field can be readily implemented experimentally.45 Our target is to maximize the average probability over selected samples when the transient HD+ complex dissociates into the designated outgoing channel at a large internuclear distance where the nonadiabatic coupling vanishes. Specifically, the target for each sample is a continuously adapting wave packet, adjusted according to the renormalized fragmentary yield in the exit channel from iteration to iteration during the optimization.21,46,47
The remainder of the paper is organized as follows. In Section 2, we present the theoretical model using the sampling-based control method for charge transfer in slow H+ + D collisions in the presence of a laser field. The TBQCP optimal control algorithm associated with the adaptive target scheme is also introduced. Detailed simulation results are presented in Section 3 and conclusions are drawn in Section 4. Atomic units (a.u.) are used throughout the paper.
2 General formulation
2.1 Two-state model
Fig. 1(a) shows the scenario of colliding H+ + D → H + D+ described by a one-dimensional two-state model based on an adiabatic representation developed by Esry and Sadeghpour.43 The zero point of energy is chosen as the asymptote of the 1sσ state. The left-pointing arrow (purple) refers to the incoming wave packet Φi0(R) having a Gaussian form| |
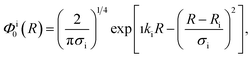 | (1) |
where R denotes the internuclear distance between the two atoms, σi is the width, Ri is the central position, ı is the imaginary unit, and ki is the momentum. The collision energy Ei associated with this incoming Gaussian wave packet is| | |
Ei = (ki2 + 1/σi2)/2m,
| (2) |
where m is the reduced mass of the collisional system. The right-pointing arrow (red) in Fig. 1 refers to the outgoing wave function.
 |
| | Fig. 1 (a) The scenario of charge transfer H+ + D → H + D+ represented by adiabatic potential curves of the 1sσ and 2pσ electronic states of the system. The left (purple) and right (red) pointing arrows denote the incoming and outgoing wave packets, respectively. The inset shows the shallow well on the 2pσ state and the energy difference between the dissociation limits of the two potentials. (b) The permanent dipole moments μgg and μee including the nuclear contributions and the transition dipole moment μge. (c) Peg, Qgg, and Qee versus internuclear distance R. The data above are from ref. 43. | |
We assume that the expected arrival time of the laser pulse is 0. The real time tδ when the laser pulse actually arrives is earlier or later than its expected arrival time, i.e., tδ ∈ [−Δt,Δt] with Δt ≥ 0. Thus, tδ can be regarded as the time deviation from the expected arrival time and Δt is the maximum time deviation. In this scenario, the state of the system ϕ(t = tδ) depends on the time shift, and ϕ(t = tδ) can be obtained by solving the field-free Schrödinger equation forward (tδ > 0) or backward (tδ < 0) from ϕ(t = 0) = Φi0. In order to find a robust laser pulse against the time deviation, we employ a sampling-based control design method developed in ref. 41. Here we evenly discretize tδ into N samples, thus, tδj = −Δt + 2(j − 1)Δt/(N − 1) for j = 1,…, N and N > 1. We let tδ = 0 when N = 1. We use ϕ(t = tδj) as the initial states in the optimal control calculations to construct a robust field arriving at time 0, which can drive each sample to a desired target state as best as possible.
The dynamics of an N-sample two-state model in the presence of the same laser field is governed by the time-dependent equation21
| |
 | (3) |
where the Hamiltonian of the system
Ĥ = diag[
Ĥ0,…,
Ĥ0] contains
N blocks
Ĥ0, and
ψ(
R,
t) = [
ψ1(
R,
t),…,
ψN(
R,
t)]
T is the associated nuclear wave packet. Here
ψj(
R,
t) = [
ψgj(
R,
t),
ψej(
R,
t)]
T (
j = 1,…,
N) denotes the wave packets of the
jth sample, and the subscripts g and e correspond to the electronic states 1sσ and 2pσ, respectively. The Hamiltonian
Ĥ0 of each sample is identical and can be expressed as
| |
 | (4) |
where
| |
 | (5) |
| |
 | (6) |
Here Vag(R) and Vae(R) are adiabatic potential curves, μge = μeg is the transition dipole moment, and μgg and μee are the permanent dipole moments, shown in Fig. 1(b). Moreover, Pge = −Peg, and Qgg and Qee account for non-adiabatic effects resulting from nuclear radial motion, shown in Fig. 1(c). In this paper, we only consider the uncertainty of the laser arrival time, and the laser field ε(t) is assumed to be linearly polarized along the molecular axis. We use the second-order split-operator method48–50 to solve eqn (3) by an adiabatic–diabatic transformation21 to obtain the wave packet ψ(R,t) of the jth sample with its initial condition Φi = [ϕ(t = tδ1),…, ϕ(t = tδN)].
2.2 Robust control scheme
We consider the laser-assisted charge transfer H+ + D → H + D+ of the jth sample with the associated initial state Φij(R) = ψgj(R,0) in the incoming channel 1sσ to a target state Φfj(R) = ψej(R,T) in the outgoing channel 2pσ at some final time T > 0. Here Φij(R < Rout) = 0 and Φfj(R < Rout) = 0, where Rout ≈ 26 a.u. and the non-adiabatic radial couplings and the transition dipole moment are negligible for R > Rout. The last two bound states of the two electronic states extend past Rout, but their contributions are negligible because the collision energies are much higher. The average probability over the selected samples in the charge transfer state at the final time T may be defined as| |
 | (7) |
which yields the probability of finding the system in the exit channel (for R ≥ Rout). Note that the same target time T is chosen for each member of the ensemble despite the varying arrival time of the field for each member. In this paper, we use an adaptive target scheme in which the target is updated according to the renormalized fragmentary yield in the exit channel at each iteration until an optimal control field is attained. Specifically, the target at the lth iteration is defined as21,46,47| |
 | (8) |
where |Ôψe,[l−1]j(T)|2 = 〈Ôψe,[l−1]j|Ôψe,[l−1]j〉, ψe,[0]j(R,T) is the nuclear wave packet of the jth sample associated with the trial field and ψe,[l−1]j(R,T), l ≥ 2, is the nuclear wave packet at the (l − 1)th iteration. The target projection operator Ô removes the inner portion of ψe,[l−1]j(R,T), R < Rout, where the non-adiabatic couplings and transition dipole moments are not negligible. Specifically, Ô acts as a unit step function such that Ô2 = Ô and Ôψe,[l−1]j(R < Rout,T) = 0. The normalized target function Φe,[l]j(R) only accounts for the portion of ψe,[l]j(R,T) lying at the internuclear distance R > Rout. The update of the objective function in eqn (8) aims to increase the push of the final wave packet into the desired product channel without specifically identifying an a priori form in the target state. In the numerical implementation, we approximate the target projection operator Ô by a smooth cutoff function| |
 | (9) |
where R′ and R′′ are some large internuclear distances chosen to be close to each other (in this work R′ = Rout = 26 a.u. and R′′ = 27 a.u.) such that  for any arbitrary function f(R).
for any arbitrary function f(R).
This work utilizes the monotonically convergent fast-kick-off TBQCP algorithm12 with zero-area constraint45 to search for an optimal control ε(t) to maximize the probability K[T]. Specifically, the optimal field is updated using the following recurrence relation10–12
| | |
ε[l](t) = ε[l−1](t) + ηS(t)[f[l]μ(t) − θAl−1], l = 1, 2,…
| (10) |
where
η > 0 is the step size of updating the field,
ε[l](
t) is the field of the
lth iteration, the index
l = 0 corresponds to the initial field,
S(
t) is the shape function which is usually chosen to be in the form of sine (cosine) square to enforce smooth switching on and off for the control pulse, and the last term
θAl ensures that the area of the updated pulse converges to zero. Here

is the area of
ε[l](
t) and
θ > 0 (we choose
θ = 10
−5 throughout the paper). Since there is no coupling between different samples,
f[l]μ(
t) for
l = 1, 2.… can be written as
| |
 | (11) |
where 0 ≤
α ≤ 1, with a faster kick-off rate at a larger value of
α and the fastest one corresponding to
α = 1. Here
χ[l−1]j(
R,
t) is the auxiliary wave function of the
jth sample, which is solved by
eqn (3) in the presence of the control field
ε[l−1](
t), satisfying the terminal condition
χ[l−1]j(
R,
T) =
Φfj(
R). The climbing rate depends on the control parameters
η and
α. In principle, the iteration step parameter
η in
eqn (10) may have any value, but in practice it needs to be sufficiently small in order to achieve monotonic convergence (stability).
5–12 Since our results are not very sensitive to
η and
α, in all the calculations in the paper, we set
η = 1.0/
N and
α = 1.0 throughout to obtain the fastest initial kick. The recurrence relation
eqn (10) will guarantee that the charge transfer probability increases from iteration to iteration.
3 Results and discussions
In the numerical calculations, the wave packets are discretized into 5120 evenly spaced grid points extending to 300a0 in order to prevent the wave packet from encountering the boundary. The time step size is chosen as 0.01 fs to ensure good accuracy. The eigenvalues and eigenvectors of the bound states for the 1sσ potential are calculated by the Fourier–Grid–Hamiltonian (FGH) method.51 The calculations are performed over the time interval [−200,200] fs. For the optimal control simulations below, we choose Ri = 35 a.u. and σi = 5.1 a.u. for the initial state. We aim to design robust fields to achieve a high probability charge transfer for two different collision energies with a time arrival uncertainty of tσ ∈ [−20,20] fs. Even though 20 fs is small physically, it is still a considerable portion of the reaction time.
We demonstrate the probability density distribution |ϕ(R,tδ)|2 of the initial state as a function of time deviation tδ from −20 fs to 20 fs in Fig. 2. The results show that the initial state significantly changes if the arrival time of the laser pulse is earlier or later than its expected arrival time of zero. A significant change of the probability density distribution of the initial state may intuitively have a deleterious effect on the performance of the control field, which will be proved in the following calculations.
 |
| | Fig. 2 Probability density distribution |ϕ(R,tδ)|2 as a function of time deviation tδ. | |
Table 1 shows the eigenvalues of 10 vibrational levels (from v = 12 to 21) of the 1sσ channel that are most relevant in the following optimal control simulations of the charge transfer reactions.
Table 1 Eigenvalues (cm−1) of vibrational levels v of the 1sσ state
| v |
Eigenvalue |
v |
Eigenvalue |
| 12 |
−4444.77 |
17 |
−999.56 |
| 13 |
−3577.97 |
18 |
−591.94 |
| 14 |
−2797.75 |
19 |
−287.45 |
| 15 |
−2103.10 |
20 |
−91.34 |
| 16 |
−1505.61 |
21 |
−9.78 |
First as a reference case, we neglect possible uncertainty in the arrival time of the laser pulse and perform the calculations with only one sample (Δt = 0 and N = 1) when the collision energy is Ei = 0.22 eV (1774.7 cm−1). The initial trial field ε[0](t) is chosen to have a Gaussian envelope shape
| |
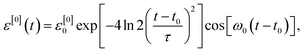 | (12) |
where
ε[0]0 = 1.94 × 10
−3 a.u. (≈10 MV cm
−1 or the intensity
I0 = 1.32 × 10
11 W cm
−2) is the peak amplitude,
τ = 56.6 fs is the full width at half maximum (FWHM),
ω0 = 2366.7 cm
−1 is the carrier frequency (the difference between the collision energy
Ei and the vibrational level
v = 18), and
t0 = 0 denotes the time corresponding to the peak amplitude. After 323 iterations, an optimal laser pulse is obtained, achieving a charge transfer probability of 0.995. In order to demonstrate the optimal field in both time and frequency domains, we introduce a windowed-Fourier transform
52,53| |
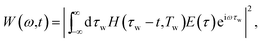 | (13) |
where
t and
ω denote the time and frequency, respectively, and the Blackman window function
H(
τw −
t,
Tw) is
| |
 | (14) |
with
Tw = 400 fs being the temporal resolution. The windowed-Fourier transform
W(
ω,
t) of this optimal laser pulse is shown in
Fig. 3(a). In order to better understand the distribution of the laser spectra,
Fig. 3(d) shows the time-dependent population (red dashed line) of each relevant vibrational level of a single sample by using the laser pulse in
Fig. 3(a) and the average time-dependent population (black solid line) of each relevant vibration level over eleven samples by using the robust pulse in
Fig. 3(b). In
Fig. 3(a), the major frequency components from 2250 cm
−1 to 2850 cm
−1 cover the transitions between the initial scattering state and
v = 18 (transition frequency 2366.7 cm
−1) and
v = 17 (transition frequency 2774.3 cm
−1), and their corresponding populations
versus time are shown in
Fig. 3(d). However, a weak peak appears between
ω = 4800 cm
−1 and 5100 cm
−1, corresponding to the transition between the initial scattering state and
v = 15 (transition frequency 5352.7 cm
−1). In comparison,
Fig. 3(b) demonstrates the windowed-Fourier transform
W(
ω,
t) of the robust laser pulse using
N = 11 samples for
Δt = 20 fs, achieving
K[
T] = 0.990 after 917 iterations. The optimal laser pulse in
Fig. 3(a) has been selected as the trial field for calculating the robust field. The robust field becomes stronger overall, having two peaks still at approximately
ω =
ω0 and
ω = 5000 cm
−1. However, a weaker peak appears in the vicinity of
ω ≈ 1850 cm
−1, which corresponds to the stronger transition between the initial scattering state and
v = 20 (transition frequency 1866.0 cm
−1). We evenly select 200 samples in the interval [−20,20] fs to test the robustness of the laser pulse in
Fig. 3(a). The charge transfer probabilities
P(
tδ)
versus the arrival time deviation
tδ of the laser pulse are shown in
Fig. 3(c) by the black solid line. The charge transfer probability
P(
tδ) drops rapidly as |
tδ| increases, from 0.995 at
tδ = 0 to 0.930 at
tδ = −20 fs and 0.936 at
tδ = 20 fs. The average charge transfer probability is 0.969. In contrast, we also calculate the charge transfer probabilities
Probust(
tδ) (red dashed line) with these 200 samples using the laser field in
Fig. 3(b). The two boundary probabilities are 0.977 at
tδ = −20 fs and 0.982 at
tδ = 20 fs, and at most points
Probust(
tδ) values are higher than their counterparts achieved using the laser pulse in
Fig. 3(a), showing better robustness of the laser pulse in
Fig. 3(b).
 |
| | Fig. 3 (a) Windowed-Fourier transform of the laser pulse using one sample (Δt = 0 and N = 1) when Ec = 0.22 eV. (b) Windowed-Fourier transform of the laser pulse using eleven samples when Ec = 0.22 eV for Δt = 20 fs, where the laser pulse in (a) is used as the trial field. The colors indicate the intensity of the spectrum in arbitrary units in (a) and (b). (c) Charge transfer probabilities versus arrival time deviation tδ using the optimal laser pulse in (a) (red dashed line) and the robust laser field in (b) (black solid line). (d) The red dashed line represents the time-dependent population of each relevant vibrational level by using only one sample under the action of the laser pulse in (a), and the black solid line represents the average time-dependent population of each relevant vibrational level over eleven samples under the action of the robust laser pulse in (b). | |
Notwithstanding the robust behaviour above, in the vicinity of the two boundary points at tδ = −20 and 20 fs, Probust(tδ) still has room for further enhancement. In order to avoid smaller yields at boundary points, we select N = 11 samples with a larger uncertainty bound Δt = 30 fs to calculate a field which is robust within tδ ∈ [−20,20] fs with the laser pulse in Fig. 3(a) as the trial field. K[T] reaches 0.992 after 3217 iterations, and the windowed-Fourier transform of the corresponding laser pulse is illustrated in Fig. 4(a). It is clear that the spectrum has six peaks, showing that more frequency components are required to construct a robust control field with a larger uncertainty bound on the arrival time of the laser pulse. These frequency components can be explained by plotting the average time-dependent population (black solid line) of each relevant vibration level over eleven samples by using the robust pulse in Fig. 4(a). The time-dependent population (red dashed line) of each relevant vibrational level of one sample by using the laser pulse in Fig. 3(a) is also drawn as a reference in Fig. 4(c). The frequency components mainly cover the transitions between the initial scattering state and v = 19, v = 18, v = 17, v = 14 and v = 13, as is reflected in Fig. 4(c). In Fig. 4(b), we also evenly select 200 samples to test its robustness. For comparison, we demonstrate the P(tδ) versus time deviation tδ under the action of the optimal laser pulse in Fig. 3(a) as a red dashed line. As is shown, large time deviations reduce the charge transfer probabilities to 0.92 at tδ = −20 fs and 0.93 at tδ = 20 fs. However, when the robust field (black solid line) is implemented, P(tδ) is always higher than 0.990 at each point with the highest being 0.995 at tδ = −3 fs.
 |
| | Fig. 4 (a) Windowed-Fourier transform of the robust laser pulse when Ec = 0.22 eV (the colors indicate the intensity of the spectrum in arbitrary units). (b) Charge transfer probabilities versus the arrival time deviation tδ by using the optimal laser pulse in Fig. 3(a) (red dashed line) and the robust field in (a) (black solid line). (c) The red dashed line represents the time-dependent population of each relevant vibrational level by using only one sample under the action of the laser pulse in Fig. 3(a), and the black solid line represents the average time-dependent population of each relevant vibrational level over eleven samples under the action of the robust laser pulse in (a). | |
We now reduce the collision energy Ec to 0.15 eV (1210 cm−1) and the corresponding frequency to ω0 = 1802 cm−1. The other parameters for the initial state and the trial field remain the same as those used in Fig. 3. Fig. 5(a) shows the windowed-Fourier transform of the optimal pulse with one sample involved (Δt = 0 and N = 1) where K[T] = 0.995 after 505 iterations, and the position of the strongest peak shows little deviation from ω0, corresponding to the transition between the initial scattering state and v = 18. Other frequency components appear at ω ≈ 1300 cm−1 corresponding to the transition between the initial state and v = 20 (transition frequency 1301.3 cm−1), and 3500 cm−1 corresponding to the transition between the initial state and v = 15 (transition frequency 3303.1 cm−1). Similarly, we calculate the robust field with N = 11 samples and Δt = 30 fs. The optimal control field in Fig. 5(a) is used as the trial field. After 1604 iterations, K[T] climbs up to 0.993. The windowed-Fourier transform of this robust field is shown in Fig. 5(b). Compared with the result in Fig. 5(a), the major difference appears to be that the peak around ω = 3500 cm−1 becomes stronger. In Fig. 5(c) we evenly select 200 samples for tδ ∈ [−20,20] fs to test the robustness of these two pulses. The red dashed line represents P(tδ) under the action of the optimal field in Fig. 5(a). It is clear that P(tδ) drops to as low as 0.95 at tδ = −20 fs and 0.96 at tδ = 20 fs, and the control performance decreases with increasing |tδ|. However, at almost each point P(tδ) is higher than its counterpart when Ec = 0.22 eV (shown in Fig. 4(b)). The black solid line represents Probust(tδ) associated with the robust field in Fig. 5(b). At tδ = −20 and 20 fs, Probust(tδ) reaches 0.994. Probust(tδ) is higher than 0.990 at ∀tδ ∈ [−20,20] fs, showing strong robustness of this field within [−20,20] fs.
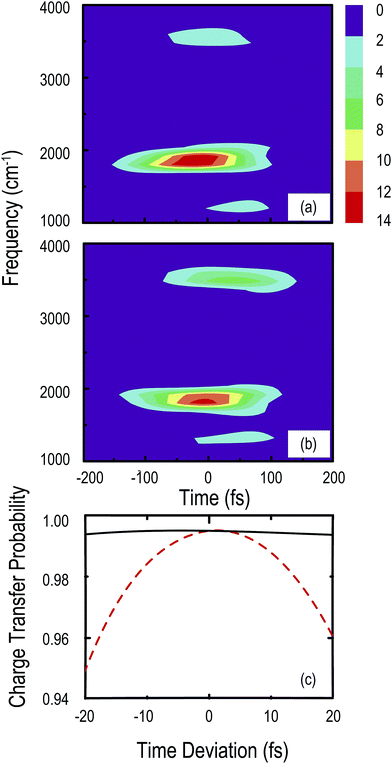 |
| | Fig. 5 (a) Windowed-Fourier transform of the laser pulse using one sample (Δt = 0 and N = 1) when Ec = 0.15 eV. (b) Windowed-Fourier transform of the robust laser pulse when Ec = 0.15 eV. The laser pulse in (a) has been used as the trial field. The colors indicate the intensity of the spectrum in arbitrary units in (a) and (b). (c) Charge transfer probabilities versus time deviation tδ under the action of the optimal laser pulse in (a) (red dashed line) and using the robust laser pulse in (b) (black solid line). | |
4 Conclusions
Since the synchronization of the colliding particles and the arrival of a laser pulse at the expected time plays an important role in effective laser-assisted collision, we combine the sampling-based method with the optimal control algorithm to construct robust fields which make the control still effective even when a limited deviation from the expected arrival time of the control field exists. The H + D+ charge transfer system is selected as an example to demonstrate the proposed method. The optimal control simulations are conducted using the time-dependent wave packet method with an adaptive target scheme based on an adiabatic two-state model. The robust fields are constructed by incorporating a number of samples with different pulse arrival times in two different collision energies, and their validity is examined using additional samples. We compare the performance between the robust field using the proposed approach and that with the optimal field using traditional optimal control simulations. The optimal laser pulses without the time uncertainty considered are more inclined to lose their robustness with the increase in collision energy. In comparison, robust fields calculated by the sampling-based method retain their robustness in both cases. In our current work, we focus on a one-dimensional system by fixing the collision direction parallel to the dipole direction, and we realise that the uncertainty in this will rise in a three-dimensional gas sample and the axis might even change during the collision. Notwithstanding this situation, our current work paves the way for extending our future studies involving three-dimensional systems using the sampling-based method.
Acknowledgements
This work was supported by the Australian Research Council (DP130101658, FL110100020). H. R. acknowledges the support from the Army Research Office (W911NF-13-1-0237).
References
- S. A. Rice and M. Zhao, Optimal Control of Molecular Dyanmics, New York, Wiley, 2000 Search PubMed.
- H. Rabitz, M. Hsieh and C. Rosenthal, Science, 2004, 303, 1998 CrossRef CAS PubMed.
- H. Rabitz and W. S. Zhu, Acc. Chem. Res., 2000, 33, 572 CrossRef CAS PubMed.
- J. Werschnik and E. K. U. Gross, J. Phys. B: At., Mol. Opt. Phys., 2007, 40, R175 CrossRef CAS.
- J. Somlói, V. A. Kazakov and D. J. Tannor, Chem. Phys., 1993, 172, 85 CrossRef.
- J. Palao and R. Kosloff, Phys. Rev. A, 2003, 68, 062308 CrossRef.
- G. G. Balint-Kurti, S. Zou and A. Brown, Adv. Chem. Phys., 2008, 138, 43 CrossRef CAS.
- W. Zhu and H. Rabitz, J. Chem. Phys., 1998, 109, 385 CrossRef CAS.
- W. Zhu and H. Rabitz, J. Chem. Phys., 1999, 110, 7142 CrossRef CAS.
- T.-S. Ho and H. Rabitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 026703 CrossRef PubMed.
- T.-S. Ho, H. Rabitz and S.-I. Chu, Comput. Phys. Commun., 2011, 182, 14 CrossRef CAS.
- S.-L. Liao, T.-S. Ho, S.-I. Chu and H. Rabitz, Phys. Rev. A, 2011, 84, 031401(R) CrossRef.
- C. A. Ryan, C. Negrevergne, M. Laforest, E. Knill and R. Laflamme, Phys. Rev. A, 2008, 78, 012328 CrossRef.
- M. Zhao and D. Babikov, J. Chem. Phys., 2006, 125, 024105 CrossRef PubMed.
- E. F. de Lima, T.-S. Ho and H. Rabitz, Chem. Phys. Lett., 2011, 501, 267 CrossRef CAS.
- M. Ndong and C. P. Koch, Phys. Rev. A, 2010, 82, 043437 CrossRef.
- W. Zhang, T. Xie, Y. Huang, G.-R. Wang and S.-L. Cong, Chin. Phys. B, 2013, 22, 013301 CrossRef.
- T. Hornung, S. Gordienko, R. de Vivie-Riedle and B. J. Verhaar, Phys. Rev. A, 2002, 66, 043607 CrossRef.
- Y. Kurosaki, M. Artamonov, T.-S. Ho and H. Rabitz, J. Chem. Phys., 2009, 131, 044306 CrossRef PubMed.
- S.-L. Liao, T.-S. Ho, H. Rabitz and S.-I. Chu, Phys. Rev. A, 2013, 87, 013429 CrossRef.
- W. Zhang, C.-C. Shu, T.-S. Ho, H. Rabitz and S.-L. Cong, J. Chem. Phys., 2014, 140(140), 094304 CrossRef PubMed.
- C. Chen, D. Dong, R. Long, I. R. Petersen and H. A. Rabitz, Phys. Rev. A, 2014, 89, 023402 CrossRef.
- M. A. Pravia, N. Boulant, J. Emerson, E. M. Fortunato, T. F. Havel, D. G. Cory and A. Farid, J. Chem. Phys., 2003, 119, 9993–10001 CrossRef CAS.
- A. M. Kuznetsov, Charge Transfer in Physics, Chemistry and Biology: Physical Mechanisms of Elementary Processes and an Introduction to the Theory, Taylor & Francis, 1995 Search PubMed.
- A. Dalgarno, Nucl. Instrum. Methods Phys. Res., Sect. B, 1985, 9, 655 CrossRef.
- D. A. Copeland and C. L. Tang, J. Chem. Phys., 1976, 65, 3161 CrossRef CAS.
- T.-S. Ho, C. Laughlin and S.-I. Chu, Phys. Rev. A, 1985, 32, 122 CrossRef CAS.
- F. H. J. Hall, M. Aymar, N. Bouloufa-Maafa, O. Dulieu and S. Willitsch, Phys. Rev. Lett., 2011, 107, 243202 CrossRef PubMed.
- L. B. Madsen, J. P. Hansen and L. Kocbach, Phys. Rev. Lett., 2002, 89, 093202 CrossRef CAS PubMed.
- M. F. Ciappina and L. B. Madsen, Phys. Rev. A, 2008, 77, 023412 CrossRef.
- M. S. Pindzola, T. Minami and D. R. Schultz, Phys. Rev. A, 2003, 68, 013404 CrossRef.
- T. Niederhausen and U. Thumm, Phys. Rev. A, 2006, 73, 041404(R) CrossRef.
- T. Kirchner, Phys. Rev. A, 2007, 75, 025401 CrossRef.
- T. Kirchner, Phys. Rev. A, 2004, 69, 063412 CrossRef.
- F. Anis, V. Roudnev, R. Cabrera-Trujillo and B. D. Esry, Phys. Rev. A, 2006, 73, 043414 CrossRef.
- M. R. James, H. I. Nurdin and I. R. Petersen, IEEE Trans. Autom. Control, 2008, 53, 1787–1803 CrossRef.
- D. Dong and I. R. Petersen, New J. Phys., 2009, 11, 105033 CrossRef.
- D. Dong and I. R. Petersen, Automatica, 2012, 48, 725–735 CrossRef.
- D. Dong and I. R. Petersen, Automatica, 2012, 48, 3089–3097 CrossRef.
- M. R. James, Phys. Rev. A, 2004, 69, 032108 CrossRef.
- D. Dong, C. Chen, B. Qi, I. R. Petersen and F. Nori, Sci. Rep., 2015, 5, 7873 CrossRef CAS PubMed.
- D. Dong, M. A. Mabrok, I. R. Petersen, B. Qi, C. Chen and H. Rabitz, IEEE Transactions on Control Systems Technology, 2015, 23, 2155–2166 CrossRef.
- B. D. Esry and H. R. Sadeghpour, Phys. Rev. A, 1999, 60, 3604 CrossRef CAS.
- B. D. Esry, H. R. Sadeghpour, E. Wells and I. Ben-Itzhak, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, 5329 CrossRef CAS.
- D. Sugny, S. Vranckx, M. Ndong, N. Vaeck and O. Atabek, Phys. Rev. A, 2014, 90, 053404 CrossRef.
- R. de Vivie-Riedle, K. Sundermann and M. Motzkus, Faraday Discuss., 1999, 113, 303 CAS.
- C.-C. Shu, T. Rozgonyi, L. González and N. E. Henriksen, J. Chem. Phys., 2012, 136, 174303 Search PubMed.
- M. D. Feit and J. A. Fleck Jr, J. Chem. Phys., 1983, 78, 301 CrossRef CAS.
- M. D. Feit and J. A. Fleck Jr, J. Chem. Phys., 1984, 80, 2578 CrossRef CAS.
- R. Kosloff, J. Phys. Chem., 1988, 92, 2087 CrossRef CAS.
- C. C. Marston and G. G. Balint-Kurti, J. Chem. Phys., 1989, 91, 3571 CrossRef CAS.
- K. Hoki, Y. Ohtsuki, H. Kono and Y. Fujimura, J. Phys. Chem. A, 1999, 103, 6301 CrossRef CAS.
- W. Zhang, Z.-Y. Zhao, T. Xie, G.-R. Wang, Y. Huang and S.-L. Cong, Phys. Rev. A, 2011, 84, 053418 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. 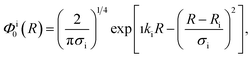








 for any arbitrary function f(R).
for any arbitrary function f(R).
 is the area of ε[l](t) and θ > 0 (we choose θ = 10−5 throughout the paper). Since there is no coupling between different samples, f[l]μ(t) for l = 1, 2.… can be written as
is the area of ε[l](t) and θ > 0 (we choose θ = 10−5 throughout the paper). Since there is no coupling between different samples, f[l]μ(t) for l = 1, 2.… can be written as