Can hyperelastic material parameters be uniquely determined from indentation experiments?†
Yihui Pana,
Yuexing Zhanb,
Huanyun Jib,
Xinrui Niu*b and
Zheng Zhong*a
aSchool of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, People's Republic of China. E-mail: zhongk@tongji.edu.cn
bCenter for Advanced Structural Materials (CASM), Department of Mechanical and Biomedical Engineering, City University of Hong Kong, Kowloon, Hong Kong SAR, People's Republic of China. E-mail: xinrui.niu@cityu.edu.hk
First published on 23rd August 2016
Abstract
Indentation experiments have been widely adopted to evaluate the hyperelastic material properties of soft polymers and biological tissues. However, due to the combination of constitutive, geometric and contact nonlinearities, the hyperelastic indentation problem has not been solved analytically. The hyperelastic parameters extracted from the indentation load–displacement curve are poorly defined. Even the uniqueness of these parameters remains unknown. This work determines the uniqueness of hyperelastic material parameters by conducting dimensional analysis based on different combinations of hyperelastic models (which include constitutive nonlinearity) and the shapes of indenters (which reflect geometric and contact nonlinearities). It is proved that the unique determination of hyperelastic material parameters depends on a simple criterion: whether the dimensionless hyperelastic parameters are coupled with indentation displacement or not. Furthermore, for the indentation problems in which unique hyperelastic material parameters cannot be guaranteed, a unique measure is constructed and validated by experiments on biomedical polymers.
1. Introduction
An indentation experiment is a popular engineering method to evaluate the mechanical properties of a material.1–4 By impressing an indenter into the surface of a solid material, an f–d curve is generated, where f and d denote the load applied and the indentation depth marched by the indenter, respectively. Mechanical properties of the material are then extracted from the curve with various mathematical and computational methods.3–7 Since the late 1990's3,8–12 till recently,13–17 the uniqueness of linear elastic and elasto-plastic material parameters obtained from indentation f–d curves has been investigated. It was proved that linear elastic parameters can be uniquely determined regardless of the shape of the indenter,18 whereas the unique determination of elasto-plastic parameters depends on the shape of the indenter.11,15,16In recent decades, accompanying the blossom of biomaterials research19 and soft robotics,20 indentation experiment has been widely adopted to determine material properties of biomedical polymers/gels21,22 and biological tissues.23,24 These materials are much softer than the traditional engineering materials and commonly exhibit hyperelastic constitutive behaviors, which include both nonlinear stress–strain relationship and finite elastic deformation. Combining with the nonlinearity introduced by the contact problem itself, it's challenging to determine hyperelastic material parameters from indentation f–d curve. To authors' knowledge, whether hyperelastic material parameters can be uniquely determined from indentation f–d curve has not yet been investigated. If this question is not answered, reliability of the parameters could be easily challenged.
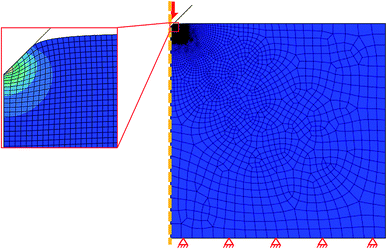
This work is aimed to determine the uniqueness of hyperelastic material parameters obtained from indentation f–d curve. Furthermore, for the hyperelastic indentation problems from which unique parameters are not able to be determined, a new measure will be defined. The work includes mathematical analysis, experimental validation and computational interpretation. Indentation problems in which a small indenter is impressed into a semi-infinite hyperelastic solid will be investigated (Fig. 1a–c). The hyperelastic solid is isotropic and incompressible. Shape of the rigid indenter could be conical, spherical or flat. Conical and spherical indenters are studied for their wide application on materials of all types. Flat indenter is for its popular usage on soft materials.25,26
 | ||
| Fig. 1 (a–c) Schematics of conical, spherical and flat indenters impressed into the surface of a semi-infinite hyperelastic solid. (d) Comparison of f–d curves obtained from experiments, FEA and fitting of eqn (2). Black line is the average of five individual f–d curves obtained from conical indentation experiments on PEGDA hydrogel (shown as inset). Colored hollow dots represent the f–d curves generated by FEA with different combinations of hyperelastic parameters (G0 and γ1) based on Arruda–Boyce model. The orange line is generated from the first equation of eqn (2). | ||
2. Material and methods
2.1. Material
A popular biomedical hydrogel, poly(ethylene glycol) diacrylate (PEGDA) hydrogel was fabricated with following procedure. First, 0.7 wt% of photoinitiator, 2-hydroxy-4′-(2-hydroxyethoxy)-2-methylpropiophenone (Sigma-Aldrich Co., St. Louis, MO, USA), was added into deionized (DI) water. The mixture was heated at 80 °C for 20 minutes in a sealed opaque bottle and cooled down to room temperature. 5 wt% of PEGDA (Sigma-Aldrich Co., St. Louis, MO, USA) was then added and stirred for uniform dispersion. The precursor was injected into Petri dish until filled up and cured by ultraviolet (UV) light. The cured PEGDA hydrogel sample has a diameter of 35 mm and a height of 10 mm. Samples were stored in DI water for one day before testing.2.2. Methods
3. Results and discussion
3.1. Exhibition of non-uniqueness
Black line in Fig. 1d shows the f–d curve generated by conical indentation experiment on PEGDA hydrogels. The hyperelastic material parameters based on Arruda–Boyce hyperelastic model27 were extracted by using finite element method (FEM). Shown as colored hollow dots in Fig. 1d, multiple pairs of hyperelastic material parameters could fit the same experimental data well, which indicates that the hyperelastic parameters obtained from the conical f–d curve are not unique and suggests that the investigation of uniqueness is necessary.3.2. Determination of uniqueness
Hyperelastic materials exhibit versatile constitutive behaviors. Some can be described by single-parameter model,29,30 whereas some have to be captured by multiple-parameter ones.26,31,32 Hence, people constructed many hyperelastic constitutive models which are distinct in both the number of parameters and the general form. Table 1 listed several classic models.27,33–36 In this work, we categorize the models by the number of parameters and unify the parameters of different models into a general parameter set {G0, γj}, where G0 is the initial hyperelastic shear modulus with a unit of Pascal and γj is a series of dimensionless hyperelastic parameters. The positive integer j takes the value from 1 to χ − 1 where χ is the total number of material parameters of a given hyperelastic model. For the single-parameter model, γj is eliminated. The unified parameters are also shown in Table 1.To determine the uniqueness of parameter set {G0, γj}, the f–d relationship obtained from dimensional analysis based on a multiple-parameter Ogden model relationship is shown as,
 | (1) |
For single-parameter hyperelastic materials, by eliminating dimensionless parameters γj in eqn (1), there is only one material parameter G0 to be determined. Hence, regardless of the shape of indenter, once given ρl, the sole material parameter G0 can be uniquely determined for all three shapes of indenters.
For multiple-parameter hyperelastic materials, the uniqueness depends on the shape of indenter. For conical indenter, observing the first equation in eqn (1), although only one is physically reasonable, infinite sets of {G0, γj} could satisfy the same equation. Hence, the hyperelastic material parameters G0 and γj cannot be uniquely determined. This conclusion was demonstrated in the previous section in Fig. 1d. For spherical or flat indenter, we transform the f–d relationships shown as the second and third equations in eqn (1) into a normalized form of Ψ − Δl (l = S or F), where Ψ denotes fS/rdd for spherical indenter and fF/ad for flat indenter. The f–d relationships of spherical and flat indenters are then rewritten as ΨOGl = G0ΠOGl(γ1, …, γ2N−1, Δl). The uniqueness depends on the form of ΠOGl function. If ΠOGl can be decoupled into the form of ΠlOG_γj(γ1, …, γ2N−1)ΠlOG_Δl(Δl), the material parameter set cannot be uniquely determined because there are infinite sets of {G0, γj} to constitute the same value of G0ΠlOG_γj(γ1, …, γ2N−1). In contrast, if γj and Δl are coupled in ΠOGl function, {G0, γj} is conditionally unique. This conclusion is explained in the Section II of ESI.†
Above analysis is schematically illustrated in Fig. 3a as a 3-layer binary tree, in which, the first layer considers the number of parameters, the second layer considers the shape of indenter, and the third layer considers whether γj and Δl are coupled in Π function or not. The layers are named as number (of parameter), shape (of indenters) and coupling (between γj and Δl). The “Number layer” suggests that, for an indentation experiment, if the hyperelastic material can be described by single-parameter hyperelastic model, the hyperelastic parameter can be uniquely determined no matter the indenter is conical, spherical or flat. The “Shape layer” suggests that, if the hyperelastic material has to be described by multiple parameters, the uniqueness of parameters depends on the shape of the indenter. If the indenter is conical, hyperelastic parameters can't be uniquely determined. The “Coupling layer” suggests that, if the indenter is spherical or flat, the uniqueness depends on whether γj and Δl are coupled in Π function. If yes, they could be uniquely determined but cannot be guaranteed (conditionally unique); otherwise, cannot be uniquely determined.
 | ||
| Fig. 3 (a) Analysis logic of the uniqueness question. (b) The unified criterion to determine uniqueness. | ||
3.3. A simple criterion to determine uniqueness
Although Fig. 3a has three layers, the criterion of unique determination could be unified as one simple question: whether γj and d are coupled in f–d relationship. This criterion obviously works for the coupling layer in Fig. 3a but needs a little explanation for the number and shape layers.For the shape layer in Fig. 3a, eqn (1) shows that γj and d are decoupled in conical solution which leads to non-unique sets of {G0, γj}. Meanwhile, they could be coupled for spherical and flat indenters which in turn provides the possibility to uniquely determine {G0, γj}. Therefore, the underneath criterion for the shape layer is still about the relationship between γj and d. For the number layer in Fig. 3a, absence of γj in the single-parameter model can be considered as a singular case for which γj is either coupled or decoupled with d. Because uniqueness is already been demonstrated, γj shall be treated as coupled with d.
The question whether the hyperelastic parameters could be uniquely determined from indentation f–d curve or not is finally answered with a simple criterion: whether γj and d are coupled in f–d relationship or not. As schematically shown in Fig. 3b, if the answer is yes, {G0, γj} could be uniquely determined (absolutely or conditionally); otherwise, cannot. Although the answer is derived based on given hyperelastic constitutive models, the analysis is mathematically general.
3.4. Construction of a new unique measure
Once the uniqueness question is answered, it's natural to raise following question: for the hyperelastic indentation problem from which set of {G0, γj} cannot be uniquely determined, is there another measure which is both unique and can govern the materials' hyperelastic behavior? Illustrated by Fig. 3a, the question could be rephrased as, for the situations shown as the two blue circles, can we define any unique measure?The two blue circles represent decoupled hyperelastic indentation problems based on the multiple-parameter model with conical, spherical and flat indenters. Eqn (1) is then rewritten as:
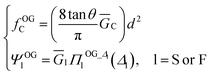 | (2) |
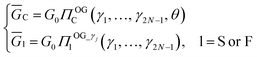 | (3) |
Eqn (3) shows that, the unit of Ḡl (l = C, S or F) is Pascal which agrees with that of the elastic modulus. Hence, it's reasonable to denote Ḡl as an equivalent hyperelastic shear modulus. The top-bar of Ḡl denotes its equivalency to shear modulus and the subscript l indicates that, for indenters with different shapes, conditions to define Ḡl are slightly different. For conical indenter, on top of the decoupling condition, θ needs to be given.
Then, observing eqn (2), following two conclusions are achieved. First, Ḡl can be uniquely determined from the f–d curve. Second, Ḡl is independent of the form of constitutive model.
Because closed-form solution is not available for the hyperelastic indentation problem, the hyperelastic material parameters can only be extracted with complex numerical methods such as inverse finite element method (FEM) (shown in Fig. 1d). To simplify the procedure, people either adopt point-wise parameters, which depend on the value of strain,37,38 or simply ignore hyperelasticity.39,40 Compared with the point-wise and approximate modulus, Ḡl shines for its uniqueness and model independency.
To demonstrate application of Ḡl, ḠC was evaluated by fitting the f–d curve obtained from conical indentation experiment with the first equation of eqn (2). The quadratic function (shown as orange line in Fig. 1d) fits the experimental data well and yields the value of 3.46 kPa. ḠC was also applied to a stiffer polymer polydimethylsiloxane (PDMS) which was fabricated and tested by Zhang and co-workers.41 The fitted ḠC is 1.62 MPa.
The above verification demonstrated that ḠC is effective in the modulus range from kPa to MPa, and could capture the difference between the stiffness of the two model materials PEGDA and PDMS. Compared with seeking help from FEM,42,43 polynomial fitting39,44 and phenomenological model,45 adoption of ḠC has following benefits. First, ḠC is mathematically simpler. Second, derivation of the first equation in eqn (2) is actually not depending on the uniqueness of {G0, γj}. Hence, ḠC is unique regardless of the uniqueness of {G0, γj}. Third, ḠC is a constant number describing the curvature of f–d curve, which allows it to capture the overall hyperelastic indentation response.
3.5. Identification of hyperelasticity
By comparing the powers of d in the f–d relationships of hyperelastic and linear elastic solutions, a useful criterion to identify hyperelasticity was obtained. For isotropic and incompressible linear elastic solids, the power of d is 2, 1.5 and 1 for conical, spherical and flat indenters, respectively. For hyperelastic indentations problems, as shown in eqn (1), it is 2 for conical indenter and indeterminate for spherical and flat indenters. Based on above knowledge, Fig. 4 is constructed. It suggests that, for the soft polymer or tissue, when people are not sure whether it is hyperelastic or linear elastic, a flat indentation experiment shall be carried out. If the obtained f–d curve is not linear, the material is hyperelastic.Spherical indenter also produces f–d curves with different powers of d but was not preferred to provide judgement for following two reasons. First, its power of d for linear elastic material is 1.5 which is not easy to be identified. Second, ΔS is bounded by 1 which limits the value of deformation and, in turn, weakens the exhibition of hyperelasticity.
3.6. Discussion
Main objective of this work is to determine the uniqueness of hyperelastic parameters obtained from indentation f–d curves. Uniqueness is often related with posedness, an important mathematical feature of nonlinear inverse problem. To provide a comprehensive perspective to readers, we would like to briefly discuss the implication of this work on the posedness of hyperelastic indentation problem.As defined by Jacques Hadamard,46 a well-posed inverse problem shall fulfill following conditions: (i) there exists a solution to the problem (existence), (ii) the solution is unique (uniqueness), and (iii) the solution continuously depends on the data (stability). This work shows, for hyperelastic indentation problems, the 1st condition was naturally satisfied and the 2nd condition could be determined. Based on the determination of the 2nd condition, we can conclude that the hyperelastic indentation problems without unique solution are ill-posed. Whether those with unique solution are well-posed needs assessment on the 3rd condition – stability.
Generally speaking, stability has always been an issue for hyperelastic problems. Due to the complex constitutive behavior of hyperelastic material, even the hyperelastic parameters extracted from uniaxial tensile tests can be easily influenced by experimental error.47,48 For hyperelastic indentation problem, the difficulty exaggerated. Zhang et al.49 investigated the stability of hyperelastic parameters extracted from spherical indentation test, and suggested that the stability of the initial shear modulus and parameters of the Π function depend on the value of ΔS and material parameters such as locking stretch.
For the hyperelastic indentation problems with unique solutions, if the material could be described by the single-parameter constitutive model, the conditional number of the sole parameter stays as 1 for displacement-controlled experiment (proved in the Section III of ESI†). The stability of the parameter is, therefore, ensured for all three types of indenters. The problem is then determined as well-posed. If the material has to be described by two- or multiple-parameter constitutive model, the stability needs to be assessed, most likely, with the help of complex numerical methods, which could be a meaningful future study. The posedness of indentation problems due to different combinations of indenter shapes and hyperelastic models are summarized in ESI Table S2.†
4. Conclusion
In summary, combing mathematical analysis, experimental validation and computational interpretation, this work determines the uniqueness of hyperelastic parameters obtained from indentation f–d curve with a simple criterion (Fig. 3b): whether γj and d are coupled in f–d relationship or not. If the answer is yes, the parameters could be uniquely determined (absolutely or conditionally); otherwise, cannot.To facilitate the practical usage of this criterion, the uniqueness of parameters due to different combinations of indenter shapes and hyperelastic models are summarized in Table 2. It's clear to see that, for single-parameter hyperelastic models, the uniqueness is ensured for all three types of indenters. For two- and multiple-parameter hyperelastic models, conical indentation leads to non-unique sets of hyperelastic parameters; the situations of spherical and flat indentations are indeterminate.
| Indenter shape | No. of parameter | ||
|---|---|---|---|
| Single-parameter | Two-parameter | Multiple-parameter | |
| Conical | Unique | Non-unique | Non-unique |
| Spherical | Unique | Indeterminate: depends on whether γj and Δl are coupled in Π function. If yes, conditionally unique; otherwise, non-unique | |
| Flat | Unique | ||
Furthermore, for the hyperelastic indentation problems from which unique parameters are not able to be determined, a new unique measure Ḡl is defined and demonstrated its effectiveness by applying to the conical indentation tests on two types of polymers.
In addition, a useful criterion to identify hyperelasticity via indentation test was also obtained and illustrated in Fig. 4.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 11572227) and Hong Kong Research Grant Council Early Career Scheme Fund (No. CityU138713).References
- M. Liu, C. Lu, K. A. Tieu, C. T. Peng and C. Kong, Sci. Rep., 2015, 5, 15072 CrossRef CAS PubMed.
- J. L. Bucaille, S. Stauss, E. Felder and J. Michler, Acta Mater., 2003, 51, 1663–1678 CrossRef CAS.
- W. C. Oliver and G. M. Pharr, J. Mater. Res., 1992, 7, 1564–1583 CrossRef CAS.
- W. D. Nix and H. Gao, J. Mech. Phys. Solids, 1998, 46, 411–425 CrossRef CAS.
- W. C. Oliver and G. M. Pharr, J. Mater. Res., 2004, 19, 3–20 CrossRef CAS.
- A. Raman, S. Trigueros, A. Cartagena, A. Stevenson, M. Susilo, E. Nauman and S. A. Contera, Nat. Nanotechnol., 2011, 6, 809–814 CrossRef CAS PubMed.
- J. Du, X. Niu, N. Rahbar and W. Soboyejo, Acta Biomater., 2013, 9, 5273–5279 CrossRef CAS PubMed.
- G. Pharr, W. Oliver and F. Brotzen, J. Mater. Res., 1992, 7, 613–617 CrossRef CAS.
- M. F. Doerner and W. D. Nix, J. Mater. Res., 1986, 1, 601–609 CrossRef.
- C. M. Cheng and Y. T. Cheng, Appl. Phys. Lett., 1997, 71, 2623–2625 CrossRef CAS.
- Y. T. Cheng and C. M. Cheng, J. Mater. Res., 1999, 14, 3493–3496 CrossRef CAS.
- A. Giannakopoulos and S. Suresh, Scr. Mater., 1999, 40, 1191–1198 CrossRef CAS.
- J. Phadikar, T. Bogetti and A. M. Karlsson, Int. J. Solids Struct., 2013, 50, 3242–3253 CrossRef.
- M. Zhao, N. Ogasawara, N. Chiba and X. Chen, Acta Mater., 2006, 54, 23–32 CrossRef CAS.
- Y. P. Cao and J. Lu, Acta Mater., 2004, 52, 4023–4032 CrossRef CAS.
- Y. P. Cao and J. Lu, Acta Mater., 2004, 52, 1143–1153 CrossRef CAS.
- Y. P. Cao and J. Lu, J. Mech. Phys. Solids, 2005, 53, 49–62 CrossRef CAS.
- I. N. Sneddon, Int. J. Eng. Sci., 1965, 3, 47–57 CrossRef.
- J. Malda, J. Visser, F. P. Melchels, T. Jüngst, W. E. Hennink, W. J. Dhert, J. Groll and D. W. Hutmacher, Adv. Mater., 2013, 25, 5011–5028 CrossRef CAS PubMed.
- D. Rus and M. T. Tolley, Nature, 2015, 521, 467–475 CrossRef CAS PubMed.
- S. Fakhouri, S. B. Hutchens and A. J. Crosby, Soft Matter, 2015, 11, 4723–4730 RSC.
- N. Gavara and R. S. Chadwick, Nat. Nanotechnol., 2012, 7, 733–736 CrossRef CAS PubMed.
- T. P. Prevost, G. Jin, M. A. De Moya, H. B. Alam, S. Suresh and S. Socrate, Acta Biomater., 2011, 7, 4090–4101 CrossRef PubMed.
- M. Lekka, Nat. Nanotechnol., 2012, 7, 691–692 CrossRef CAS PubMed.
- S. T. Choi, S. R. Lee and Y. Y. Earmme, Acta Mater., 2008, 56, 5377–5387 CrossRef CAS.
- T. Kaster, I. Sack and A. Samani, J. Biomech., 2011, 44, 1158–1163 CrossRef CAS PubMed.
- E. M. Arruda and M. C. Boyce, J. Mech. Phys. Solids, 1993, 41, 389–412 CrossRef CAS.
- E. Buckingham, Phys. Rev., 1914, 4, 345–376 CrossRef.
- A. Livne, E. Bouchbinder, I. Svetlizky and J. Fineberg, Science, 2010, 327, 1359–1363 CrossRef CAS PubMed.
- C. Haller, W. Buerzle, A. Kivelio, M. Perrini, C. Brubaker, R. Gubeli, A. Mallik, W. Weber, P. Messersmith and E. Mazza, Acta Biomater., 2012, 8, 4365–4370 CrossRef CAS PubMed.
- J. Bergström, S. Kurtz, C. Rimnac and A. Edidin, Biomaterials, 2002, 23, 2329–2343 CrossRef.
- M. Wissler and E. Mazza, Sens. Actuators, A, 2005, 120, 184–192 CrossRef CAS.
- R. Rivlin, Philos. Trans. R. Soc. London, Ser. A, 1948, 241, 379–397 CrossRef.
- M. Mooney, J. Appl. Phys., 1940, 11, 582–592 CrossRef.
- Y. Fung, Am. J. Physiol., 1967, 213, 1532–1544 CAS.
- R. W. Ogden, Non-linear elastic deformations, Courier Corporation, 1997 Search PubMed.
- K. D. Costa, A. J. Sim and F. C. Yin, J. Biomech. Eng., 2006, 128, 176–184 CrossRef PubMed.
- H. J. Butt, B. Cappella and M. Kappl, Surf. Sci. Rep., 2005, 59, 1–152 CrossRef CAS.
- M. Sato, K. Nagayama, N. Kataoka, M. Sasaki and K. Hane, J. Biomech., 2000, 33, 127–135 CrossRef CAS PubMed.
- M. Troyon and S. Lafaye, Philos. Mag., 2006, 86, 5299–5307 CrossRef CAS.
- M. G. Zhang, J. Chen, X. Q. Feng and Y. Cao, J. Appl. Mech., 2014, 81, 091011 CrossRef.
- B. R. Donohue, A. Ambrus and S. R. Kalidindi, Acta Mater., 2012, 60, 3943–3952 CrossRef CAS.
- Y. Fu and C. Chui, J. Biomech., 2014, 47, 2430–2435 CrossRef CAS PubMed.
- S. Sen, S. Subramanian and D. E. Discher, Biophys. J., 2005, 89, 3203–3213 CrossRef CAS PubMed.
- D. Lin, E. Dimitriadis and F. Horkay, eXPRESS Polym. Lett., 2007, 1, 576–584 CrossRef.
- J. Hadamard, Lectures on Cauchy's problem in linear partial differential equations, Courier Corporation, 2014 Search PubMed.
- D. De Tommasi, D. Ferri, G. Marano and G. Puglisi, Eur. Polym. J., 2016, 78, 302–313 CrossRef CAS.
- R. Ogden, G. Saccomandi and I. Sgura, Comput. Mech., 2004, 34, 484–502 CrossRef.
- M.-G. Zhang, Y.-P. Cao, G.-Y. Li and X.-Q. Feng, Biomech. Model. Mechanobiol., 2014, 13, 1–11 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra15747e |
| This journal is © The Royal Society of Chemistry 2016 |