A theoretical study of methylation and CH/π interactions in DNA intercalation: methylated 1,10-phenanthroline in adenine–thymine base pairs

Abstract

The study of CH/π interactions in DNA model intercalated systems has been carried out with the popular intercalator 1,10-phenanthroline (phen) and several methyl derivatives, changing number and position, and the adenine–thymine tetramers (AT/TA) where thymine also contains a methyl group. Density Functional Theory (DFT) was used for the calculations, by means of improved functionals including dispersion effects. Our results given by the AIM analysis confirm the existence of these CH/π interactions and the energy decomposition analysis shows a perfect direct correlation between the number of CH/π interactions found and their ΔE_int. Moreover, despite the important role of dispersion energy in the systems with more methyl groups, it is not yet enough to compensate the Pauli repulsion term, ΔE_Pauli, and the orbital contribution, ΔE_orb, and the electrostatic contribution, ΔE_elstat, become crucial for the stabilization of the structures in the intercalation process.

---

Introduction

Despite being among the weakest interactions in the family of hydrogen bonds and in a grey area considered by some authors to be between the hydrogen bond and the London van der Waals interaction,¹ the CH/π interaction^2,3 has been shown to be important in several chemical and biochemical processes. For the last three decades, several experimental³ and theoretical studies,^4–10 which support the existence of such an attractive molecular force, have been reported. Being a “donor–acceptor” interaction between a soft acid (CH) and a soft base (π-system),^2,11 it can be considered a hydrogen bond, as demonstrated by experiments on the electronic effect of a substituent on stereoselectivity,^12–15 conformational equilibrium,¹⁶ crystal packing,¹⁷ enantioselectivity,^18,19 and coordination chemistry.¹² Moreover, statistical analyses of crystal structures show that the C–H bond tries to point toward the π system.²⁰Ab initio calculations of the benzene clusters with small hydrocarbon molecules^8,21–23 confirmed this preference and the role of weak electrostatic interactions in stabilizing this orientation. Nevertheless, while electrostatic forces play a major role in conventional hydrogen bonds,^24,25 the CH/π interaction has been mainly attributed to the dispersion forces,^8,20,26–37 namely when aliphatic or aromatic CH groups are involved. Electrostatic contributions may become more relevant for species involving strong CH donors such as chloroform or acetylenic CH. Thus, the interaction energy depends on the nature of the molecular fragments, CH as well as π-groups: the stronger the proton donating ability of the CH group, the larger the stabilizing effect. The dual nature of the interaction, with electrostatic and dispersion terms, is the basis for the ubiquitous existence of this molecular force in chemistry, responsive to surrounding circumstances, especially when it operates cooperatively.

Directionality is a requisite for the CH/π hydrogen bond, distinguishing it from the classic London dispersion force. Nevertheless, in general, the CH/π interaction is a very weak interaction and its limited directionality comes from dipole/quadrupole and charge–transfer interactions,³⁸ while the conventional hydrogen bonds are stronger interactions with strong directionality.³⁹ Dependence of an interacting system often follows the order of the strength: the stronger the bond, the stronger the trend for the linearity.^39,40 Thus, the different nature shows that the roles of CH/π interactions in controlling structures of molecular assemblies should not be discussed in complete analogy with the hydrogen bond.

As said above, these CH/π interactions become important in several chemical and biochemical systems and several experimental and theoretical studies showed their key role for controlling crystal packing,^20,41–46 organic reactions,^47,48 conformational analysis,^49,50 and molecular recognition processes^51–61 mainly owing to their cooperative effect, and their importance in chemistry has been well recognized.^38,62 Moreover, CH/π interactions are also important in the stability of biological structures^63,64 because they include dispersion and polarization contributions and persist in both highly polar and apolar environments such as those found in the interior of proteins.⁶⁵ This is of paramount importance in the consideration of the effect in biochemistry. Thus, some authors highlighted the role of CH/π interactions in the stability of proteins,^66–68 the binding of carbohydrates to proteins,^69,70 and the packing of the adenine ring⁷¹ or guanine nucleotide⁷² in protein structures. In addition, CH/π contacts of the methyl group of thymine or the backbone sugars with DNA or proteins have been also described.^73–75 Moreover, several theoretical calculations^{8,22,23,31,33–35,37} and gas phase spectroscopic measurements of the CH/π interactions have been reported^{22,23,33,35,76–78} and it is expected that such CH/π interactions are able to play an important role in drug design.

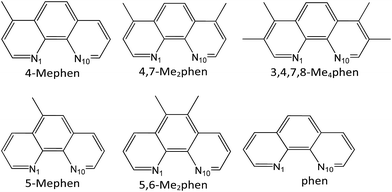
The aim of this study is the analysis of the CH/π interactions between different methylated derivatives, in number and position, of the 1,10-phenanthroline (phen) intercalator drug (see Scheme 1) and the adenine–thymine (AT) base pairs, taking into account that thymine also contains a methyl group, which is able to interact with the intercalators by means of CH/π interactions.

Scheme 1 Phen and methylated phen structures analyzed in this work.

We focused our study on phen methylated derivatives because it was shown that both phen and its organometallic complexes have significant antitumoral activity.^79–83 In particular, its Mo(II) complexes were effective in vitro against different human tumor cell lines.⁷⁹ Viscosity, linear dichroism, NMR and NOESY spectra experiments showed that cytotoxic phen methylated derivatives intercalate between DNA base pairs and the efficiency depends on the number and position of methyl groups.^84,85 Several reviews on drugs based on intercalation have appeared recently,^86–90 showing how the growing interest in the use of these systems for a range of medical applications prompted a renewed need for a structural understanding of their interactions with bases of DNA.⁹¹ The development of a strategy to quantify this process and calculate the relevant energy terms would be very useful. In this work we carry out the study of the intercalation of methylated phen systems between AT/TA stacked base pairs of DNA by DFT methods with selected functionals that take into account dispersion forces, which are crucial for the study of the intercalation and CH/π interactions, to calculate the contributions to the energy and the nature of the interaction between the active cytotoxic intercalator and base pairs.

As far as we know, this is the first study addressing the important role of CH/π interactions in intercalated systems by means of DFT methods including dispersion contribution. The knowledge of intrinsic molecular interactions constitutes an important prerequisite to understand the role of intercalators between nucleobases in DNA structure. Therefore, we expect that this work will help to understand how methylated phen ligands behave in biological processes of intercalation, and to interpret the results of several experimental techniques.

Computational details

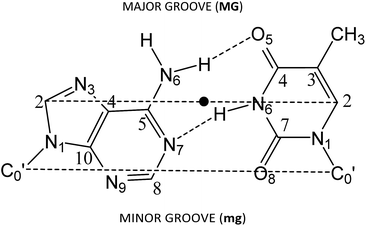
Several approaches reported in the literature may be used to model the intercalation of ligands in DNA.^92–112 Large systems (DNA chains from decamers to pentadecamers including the intercalators) have been modelled at low level of theory by using force fields in molecular mechanics (MM) or classical molecular dynamics (MD).^{92,93,95–98,113} On the other hand, small systems (models consisting in just one base pair and the intercalator – three-body model) have been treated at high level of theory by means of HF, MP2 or DFT level of calculation.^99–105 Finally, other approximations have been found in the bibliography between the treatment of a DNA sequence of various steps and the intercalator at low level of theory and the treatment of the three body systems with the base pair and the intercalator at high level of theory. That is, the use of a model consisting of the intercalator and two base pairs (either including – ring model – or not considering – sandwich model – the phosphate backbone and sugars) at HF, MP2 and dispersion corrected DFT levels of theory, at DF-SAPT0 level or at QM/MM level.^94,106–112 Here we shall use these last models with two base pairs and the intercalator and DFT methods including dispersion corrections.

To build the models, we used the optimized geometries of AT/TA (θ = 36°) described in our previous work,¹¹⁴ which correspond to Watson–Crick base pairing described in DNA. For such structures, we increased the distance between the two base pairs (z coordinate) to twice the initial value. Then the intercalator was inserted manually to be equidistant from both base pairs and to achieve maximum overlap with them. Only two different orientations were taken into account for the model systems (intercalator + two DNA base pairs). In one, the intercalation takes place from the minor groove. This situation is reproduced when the N₁ and N₁₀ atoms of the intercalator (Scheme 1) are close to the minor groove. The localization of the side corresponding to the minor groove in the base pairs is shown in Fig. 1. In the other orientation, the intercalation takes place from the major groove side (N₁ and N₁₀, see Scheme 1, close to the major groove; see Fig. 1 for the localization of the side corresponding to the major groove in the base pairs). The structures corresponding to these two orientations were called (AT/intercalator/TA)mg (intercalation from minor groove) and (AT/intercalator/TA)MG (intercalation from major groove). The intercalator can be phen, 4-Mephen, 5-Mephen, 4,7-Me₂phen, 5,6-Me₂phen or 3,4,7,8-Me₄phen. Full geometry optimizations were performed using a DFT approach¹¹⁵ with the M06-2X functional,^116,117 which includes some dispersion effects, and the 6-31+G(d,p) basis set.¹¹⁸ We already used with success this functional to study the stacking of AT/TA base pairs and the role of CH/π interactions in a previous study.¹¹⁴ Moreover M06-2X functional and its precursor M05-2X were used by other authors to study intercalated systems^110,112 to avoid the use of the more time consuming MP2 method, which had been extensively used^{99,100,102–107,110} before the appearance of DFT methods including dispersion. Because we are not studying excitation/decay processes as fluorescence, phosphorescence, etc. we do not take into account multireference methods. In fact, we tested the stability of the wavefunction for different systems and the wavefunction was stable at our M06-2X/6-31+G(d,p) level of calculation.

Fig. 1 Scheme of the adenine–thymine base pairs AT. The dashed line C₂–C₂ represents the long base-pair axis, which is roughly parallel to the C′₀–C′₀ line, where C′₀ stands for the sugar carbon atoms bonded to the bases. The twist angle (θ) is defined as the rotation around the midpoint of the C₂–C₂ axis (denoted by a dot).

The optimized geometries were characterized by the harmonic vibrational frequencies to verify that all frequencies are real and correspond to minima structures in the potential energy surface. The counterpoise (CP) method^119,120 was used to estimate the basis set superposition error (BSSE) in some calculations. These calculations were performed with the GAUSSIAN 09, Revision A.02 software.¹²¹ Net atomic charges were obtained using the natural population analysis of Reed et al.^122,123 by means of the NBO 5.0 software.¹²⁴ The localization of bond critical points¹²⁵ and topological analysis were carried out using AIM2000 program.¹²⁶

The Energy Decomposition Analysis (EDA) to partition the interaction energy between the fragments was performed using the ADF program.^127–129 In this analysis, the interaction energy is divided into orbital, Pauli and electrostatic terms following a Morokuma-type energy decomposition method.^130,131 These calculations were also performed with the M06-2X functional with an uncontracted triple-ζ basis set of Slater type orbitals augmented with a polarization function (TZP). Since the calculations with M06-2X functional gave some convergence problems, we also carried out the EDA with the B3LYP-D3 functional with the explicit Grimme's D3 correction to dispersion forces,^132–135 with the same basis set (see ESI†). Previous calculations on the intercalation of phen between base pairs showed that when comparing the EDAs obtained with M06-2X and B3LYP-D3 functionals the conclusions are very similar.⁹⁴ Moreover, we think that the discussion becomes simpler with an explicit term for dispersion (ΔE_disp).

Results and discussion

In the next sections we shall analyze the effect of methylation in phen, namely number and position of methyl groups, when intercalation occurs between AT/TA base pairs. First, we focus on the AIM analysis of the optimized geometries of the systems. We then analyze the energetics emphasizing the changes in the stability and in several energetic contributions. Finally, a global discussion of the results is given.

Geometries and AIM analysis

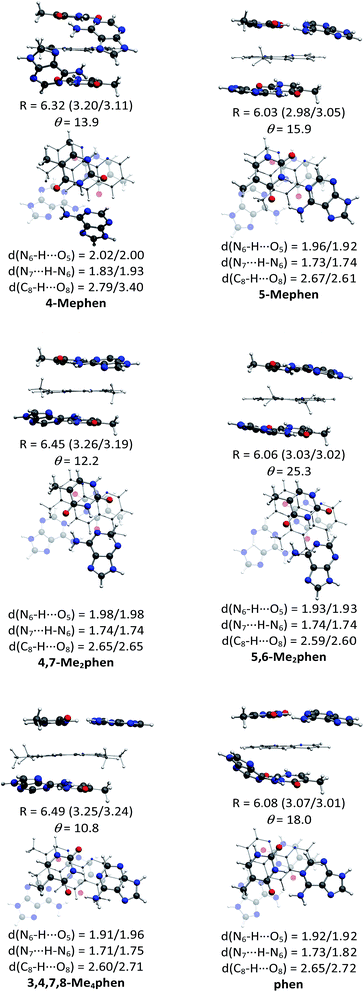
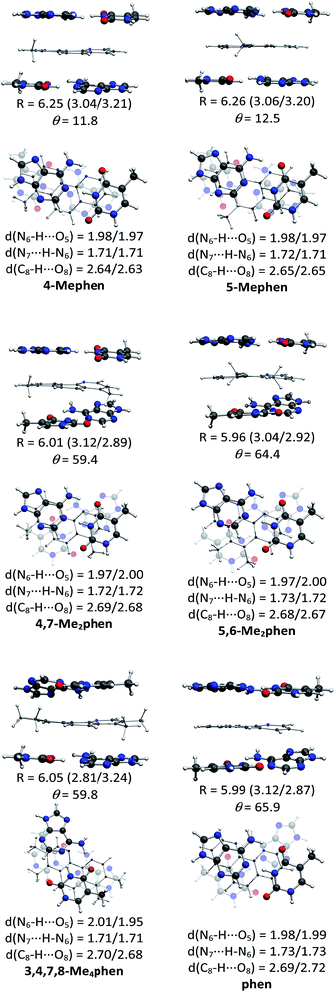
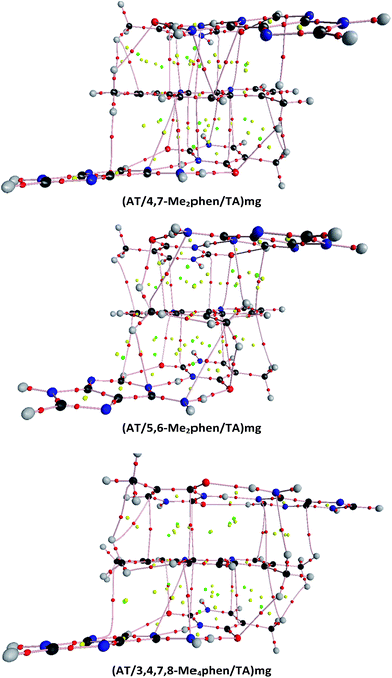
The structures of all the systems optimized at M06-2X/6-31+G(d,p) level are shown in Fig. 2 and 3 for the (AT/intercalator/TA)mg and (AT/intercalator/TA)MG systems, respectively. In all cases, a side view and a top view are shown. The Cartesian coordinates of the optimized structures are also available as ESI.† The values of θ and R (see ESI† for definition) together with the distance values between phen and base pairs, and the hydrogen bond lengths are also shown in Fig. 2 and 3. Distances associated to CH/π interactions are depicted in Tables 1 and 2 for (AT/intercalator/TA)mg and (AT/intercalator/TA)MG systems, respectively.

Fig. 2 Fully optimized structures of the (AT/intercalator/TA)mg systems at M06-2X/6-31+G(d,p) level of calculation. In each case, a side view (above) is presented to appreciate better the rise (R in Å) displacement of base pairs, and the intercalator···base pair distance (in parentheses) and a top view (below) is also shown to appreciate better the twist (θ in °) motion. Hydrogen bond distances between base pairs are also collected.

Fig. 3 Fully optimized structures of the (AT/intercalator/TA)MG systems at M06-2X/6-31+G(d,p) level of calculation. In each case, a side view (above) is presented to appreciate better the rise (R in Å) displacement of base pairs, and the intercalator···base pair distance (in parentheses) and a top view (below) is also shown to appreciate better the twist (θ in °) motion. Hydrogen bond distances between base pairs are also collected.

Table 1 Distances (Å) for the CH/π interactions found in the optimized (AT/intercalator/TA)mg systems at M06-2X/6-31+G(d,p) level

System	d(Y–CH3⋯Z(B))^a
a Y is the fragment with the CH3 group that produces the interaction (thymine, T, or the intercalator, I). Z is an atom of the fragment acting as π-system for which a bond path is associated, whereas B is the fragment (A for adenine, T for thymine and I for the intercalator).
(AT/phen/TA)mg	3.48 (Tup–CH3⋯N1(Adown))
	2.92 (Tdown–CH3⋯C8(I))
(AT/4-Mephen/TA)mg	2.83 (Tup–CH3⋯C4(I))
	2.63 (I–CH3⋯O5(Tup))
	2.57 (I–CH3⋯N9(Adown))
	2.87 (Tdown–CH3⋯C7(I))
(AT/5-Mephen/TA)mg	2.60 (I–CH3⋯O5(Tup))
	2.74 (I–CH3⋯N7(Adown))
	2.95 (Tdown–CH3⋯C8(I))
(AT/4,7-Me2phen/TA)mg	2.82 (Tup–CH3⋯C4(I))
	2.64 (I–CH3⋯O5(Tup))
	2.69 (I–CH3⋯N9(Adown))
	2.69 (I–CH3⋯N9(Aup))
	2.64 (I–CH3⋯O5(Tdown))
	2.83 (Tdown–CH3⋯C7(I))
(AT/5,6-Me2phen/TA)mg	2.90 (Tup–CH3⋯C4(I))
	2.50 (I–CH3⋯O5(Tup))
	2.66 (I–CH3⋯N7(Adown))
	2.66 (I–CH3⋯N7(Aup))
	2.50 (I–CH3⋯O5(Tdown))
	2.90 (Tdown–CH3⋯C7(I))
(AT/3,4,7,8-Me4phen/TA)mg	2.88 (I–CH3⋯C2(Tup))
	2.62 (I–CH3⋯N6(Aup))
	2.64 (I–CH3⋯O5(Tdown))
	2.71 (I–CH3⋯C10(Aup))
	2.81 (Tdown–CH3⋯C7(I))

---

Table 2 Distances (Å) for the CH/π interactions found in the optimized (AT/intercalator/TA)MG systems at M06-2X/6-31+G(d,p) level

System	d(Y–CH3⋯Z(B))^a
a Y is the fragment with the CH3 group that produces the interaction (thymine, T, or the intercalator, I). Z is an atom of the fragment acting as π-system for which a bond path is associated, whereas B is the fragment (A for adenine, T for thymine and I for the intercalator).
(AT/phen/TA)MG	2.80 (Tdown–CH3⋯C4(I))
(AT/4-Mephen/TA)MG	2.65 (I–CH3⋯N9(Aup))
	2.49 (I–CH3⋯O8(Tdown))
(AT/5-Mephen/TA)MG	2.82 (I–CH3⋯N9(Aup))
	2.45 (I–CH3⋯O8(Tdown))
(AT/4,7-Me2phen/TA)MG	2.68 (I–CH3⋯N9(Aup))
	2.88 (I–CH3⋯C3(Tdown))
	2.55 (I–CH3⋯O8(Tup))
	2.34 (I–CH3⋯O8(Tdown))
	2.79 (Tdown–CH3⋯C4(I))
(AT/5,6-Me2phen/TA)MG	2.64 (I–CH3⋯N9(Aup))
	2.33 (I–CH3⋯O8(Tup))
	2.77 (I–CH3⋯C2(Tdown))
	2.44 (I–CH3⋯O8(Tdown))
	2.76 (Tdown–CH3⋯C4(I))
(AT/3,4,7,8-Me4phen/TA)MG	2.52 (I–CH3⋯N9(Aup))
	2.33 (I–CH3⋯O8(Tup))
	2.83 (I–CH3⋯C3(Tup))
	2.76 (Tup–CH3⋯C7(I))
	2.80 (I–CH3⋯C2(Adown))
	2.67 (I–CH3⋯N9(Adown))
	2.55 (I–CH3⋯O8(Tdown))
	2.63 (I–CH3⋯C2(Tdown))

---

Several CH/π interactions are observed after optimization of the structures and for some of them, as (AT/phen/TA)mg and (AT/4-Mephen/TA)mg, reorganize drastically the geometry. In the case of (AT/phen/TA)mg system the adenine in the lower pair is extruded in order to form some CH/π interaction with the methyl group of the upper thymine and, in the case of (AT/4-Mephen/TA)mg, even folding of the adenines occurs to achieve this CH/π interaction now with the methyl group of the intercalator (see Fig. 2).

The identification of CH/π interactions was based on the AIM^125,136,137 topologies (see some examples in Fig. 4 and all the structures in the ESI† along with the values for the electronic density, ρ, and its laplacian (∇²ρ) at each bond critical point (BCP)). The length of CH/π interactions goes from 2.33 to 3.48 Å. The (AT/phen/TA)MG system has only one CH/π, whereas the system with more CH/π interactions is the (AT/3,4,7,8-Me₄phen/TA)MG system with 8 bond paths associated to the CH/π interactions (see Table 2, Fig. 4 and ESI†). As a general trend we find more CH/π interactions for the structures where intercalation is produced from the minor groove than from the major groove. The only exception is the above mentioned case of (AT/3,4,7,8-Me₄phen/TA)MG with 8 bond paths associated to CH/π interactions, whereas for the (AT/3,4,7,8-Me₄phen/TA)mg only 5 bond paths are found.

Fig. 4 Topologies of the (AT/4,7-Me₂phen/TA)mg, (AT/5,6-Me₂phen/TA)mg, and (AT/3,4,7,8-Me₄phen/TA)mg systems. Small red spheres correspond to bond critical points, yellow spheres to ring critical points, and green spheres to cage critical points. Bond paths connecting atoms are also shown.

CH/π interactions are characterized by values of ρ at the BCPs that go from 0.0044 a.u. to 0.0122 a.u. and a positive Laplacian (see from Tables S4–S15 of the ESI†). We found between 4 and 7 bond paths (BPs) associated to these CH/π interactions in all the systems that contain 4,7-Me₂phen, 5,6-Me₂phen or 3,4,7,8-Me₄phen intercalators and 2 BPs associated to CH/π interactions in the monosubstituted systems (see Fig. 4 and ESI†). The methyl group of thymine is also involved in CH/π interactions with the intercalator. The values of ρ in the associated BCPs go from 0.0062 a.u. to 0.0073 a.u. with a positive Laplacian. These CH/π interactions will favor in general the intercalation process and they go from 1 in the case of the (AT/phen/TA)MG to 8 for the (AT/3,4,7,8-Me₄phen/TA)MG. The importance of stabilizing CH/π interactions was already stressed for the methane/adenine systems.¹³⁸

Energetics

Table 3 collects in the second column the energies of formation, E_f of each structure from the separated fragments (the two optimized base pairs and the optimized intercalator in the case of the systems with intercalator or just the two optimized base pairs when the intercalator is not included in the system). The many-body analysis of the interaction energy is also depicted in Table 3. Thus, the third column corresponds to the interaction energy of the bodies, E_int(bod), which is calculated by subtracting from the total energy the energy of the isolated fragments (4 in the case of stacked base pairs without intercalator and 5 for the systems with intercalator) with the geometry they have in the final system. The other columns contain the analysis of the interaction energy, obtained by splitting it into different two-body and many-body interactions, all of them calculated with the geometries in the total system. E_HB is the two-body hydrogen-bonding interaction in each base pair, calculated as the difference between the energy of the base pairs and the sum of the energies of the two bases. E_S has the other four two-body interactions between the four bases: two intrastrand and two interstrand stacking interactions in the case of the systems without intercalator, the interstrand terms being usually repulsive and, in the case of the systems with the intercalator, the four two-body interactions between the four bases and the intercalator, all of them being attractive. Finally, E_MB is the multibody interaction energy which was calculated by substracting the two-body terms (E_HB and E_S) from the total interaction energy of the bodies, E_int(bod).

Table 3 Formation energy (E_f) and multi-body analysis of the interaction energies, in kcal mol⁻¹, for the free stacked base pairs AT/TA and including the intercalator at M06-2X/6-31+G(d,p) level of theory

System	E f	E int(bod) ^a	E HB ^b	E S	E MB
a Values with counterpoise (CP) correction are also given in italics. b The two values correspond to the upper and lower pair of bases (the sum is given in parentheses).
AT/TA	−19.7	−54.4 (−40.9)	−16.0/−16.4 (−32.4)	−22.6	0.5
Intercalation via minor groove (AT/intercalator/TA)mg
phen	−11.9	−65.9 (−58.6)	−16.4/−15.3 (−31.7)	−32.3	−2.0
4-Mephen	−21.4	−75.7 (−67.7)	−15.0/−13.7 (−28.7)	−36.2	−10.8
5-Mephen	−12.6	−68.1 (−60.6)	−16.2/−16.5 (−32.7)	−34.0	−1.4
4,7-Me2phen	−19.1	−74.9 (−67.2)	−16.2/−16.2 (−32.4)	−41.5	−1.0
5,6-Me2phen	−19.9	−75.8 (−67.9)	−16.5/−16.5 (−33.0)	−41.9	−0.8
3,4,7,8-Me4phen	−17.6	−73.4 (−65.3)	−16.5/−16.1 (−32.7)	−39.3	−1.5
Intercalation via major groove (AT/intercalator/TA)MG
phen	−12.7	−67.8 (−60.0)	−16.1/−15.8 (−31.9)	−34.0	−1.9
4-Mephen	−14.6	−69.3 (−61.4)	−16.2/−16.3 (−32.5)	−35.8	−1.0
5-Mephen	−13.8	−68.4 (−60.6)	−16.2/−16.3 (−32.6)	−35.2	−0.7
4,7-Me2phen	−18.3	−73.6 (−65.3)	−16.1/−15.9 (−32.0)	−39.8	−1.8
5,6-Me2phen	−16.9	−72.1 (−63.8)	−16.1/−15.8 (−32.0)	−38.4	−1.7
3,4,7,8-Me4phen	−20.9	−77.0 (−68.1)	−15.6/−16.2 (−31.8)	−43.4	−1.7

---

As expected E_int(bod) are more negative than E_f, because the deformation energy is not taken into account in E_int(bod). The behavior of E_f differs when comparing intercalation from the minor groove with the intercalation from the major groove. In the latter case E_f correlates with the number of methyl groups and the energies go from −12.7 to −20.9 kcal mol⁻¹. Also, the number of CH/π interactions increases (see Table 2, topologies of Fig. 4 and ESI†) with the number of methyl groups and it can be directly related to the stabilization of E_f when going from phen to 3,4,7,8-Me₄phen. On the other hand, when intercalation takes place from the minor groove, E_f energies go from −11.9 to −21.4 kcal mol⁻¹ and whereas they do not correlate with the number of methyl groups, they do with the number of CH/π interactions. This indicates that, more than by the number of methyl groups in the systems, the stabilization is determined by their capacity to form CH/π interactions. This correlation is only broken in the (AT/4-Mephen/TA)mg system, the most stabilized system but with only 4 CH/π interactions. We attribute this anomalous behavior of (AT/4-Mephen/TA)mg to the formation of strong N₆–H⋯N₃ hydrogen bonds (see Fig. 1, 2 and S3 of ESI†) between both extruded adenines, which can neither be formed for (AT/4,7-Me₂phen/TA)mg nor for (AT/3,4,7,8-Me₄phen/TA)mg structures. These systems have also a methyl group in position 4 but the adenines are not folded enough. E_int(bod) shows similar trends as E_f. Both values of E_f and E_int(bod) show that intercalation through the minor groove is favored for disubstituted systems and monosubstituted AT/4-Mephen/TA system, whereas intercalation through the major groove is favored for the most substituted AT/3,4,7,8-Me₄phen/TA system and the system without methyl groups AT/phen/TA. For (AT/5-Mephen/TA) the energies are very similar and no preference is observed for any. These trends can be associated to the number of CH/π interactions achieved. The structures that form more CH/π interactions when intercalate via minor groove will have more negative E_f and E_int(bod) than their counterparts intercalated through the major groove (4-Mephen, 4,7-Me₂phen, and 5,6-Me₂phen). The 3,4,7,8-Me₄phen structure, having the highest number of CH/π interactions for the intercalation via major groove, has the lowest E_f and E_int(bod) when intercalation is produced through this side. The influence of the CP correction in E_int(bod) was also calculated for these systems (see Table 3). The values go from 7.3 to 8.8 kcal mol⁻¹, which would be ∼11% of the E_int(bod). Thus, the effect of the BSSE does not change dramatically E_int(bod) at our level of calculation.

Let us now discuss the partition of the E_int(bod) into two-body and many-body terms (see Table 3). For all the systems there are two similar values of E_HB, which correspond to hydrogen bonds of the upper and lower pair of bases and the sum is given in parentheses. As a general trend, all the values of E_HB for methylated systems are very similar to those for the systems with non-methylated phen. Thus, methylation of phen does not affect the forces related to the hydrogen bonds, in agreement with the small changes observed in hydrogen bonds after methylation (compare values in Fig. 2 and 3).

The values of E_S are more negative than E_f because they do not contain the energy relaxation term. Such values of the E_S increase with the number of CH/π interactions and thus with the number of methyl groups when intercalation is produced via major groove. On the other hand, when intercalation takes place from the minor groove, the number of CH/π interactions is not proportional to the number of the methyl groups (see Table 1 and Fig. S3 and from Tables S4–S9 of the ESI†) but the stabilization of E_S is totally proportional to the number of effective CH/π interactions (compare the number of CH/π interactions in Table 1 and the values of E_S in Table 3). Thus, it can be concluded that the stabilization of E_S depends on the number of CH/π interactions in the structure.

Finally, the E_MB contribution is residual compared to E_HB and E_S with the exception of the (AT/4-Mephen/TA)mg system. For this structure the value of E_MB (−10.8 kcal mol⁻¹) is roughly 1/3 of the value for E_HB or E_S and such high value can be attributed to stabilizing N₆–H⋯N₃ hydrogen bond interactions between the extruded and folded adenines. Also, E_MB is cooperative (E_MB < 0) for all the systems.

The energy of the interaction between the rigid fragments can also be decomposed by the EDA into several contributions:

ΔE_int = ΔE_elstat + ΔE_Pauli + ΔE_orb (+ΔE_disp) (1)

ΔE_elstat corresponds to the classical electrostatic interaction between the unperturbed charge distributions of the rigid fragments, ΔE_Pauli comprises the destabilizing interactions between occupied orbitals, and the orbital interaction contribution ΔE_orb, accounts for charge transfer and polarization terms. The EDA provides another interpretation of the energy terms and was performed with ADF^127–129 (see the Computational details), using different functionals. As reported previously,^94,131,139 if an explicit correction term for dispersion interaction is employed, the results of the EDA remain unchanged and the dispersion contribution appears as an extra term, ΔE_disp. Otherwise, if dispersion contribution is part of the functional, then it will change the EDA values by weakening the repulsive ΔE_Pauli contribution. For all the systems we analyzed the EDA values obtained with the M06-2X functional used before. However, because this functional does not contain an explicit dispersion term and because it is more informative to take into account an explicit ΔE_disp term for dispersion we also carried out the EDA with the B3LYP-D3 functional including an explicit dispersion term and we present the results for this last functional in the subsequent paragraph. The values of the EDA for both functionals M06-2X and B3LYP-D3 can be found in the ESI.†

The trends for the EDA at B3LYP-D3/TZP level are shown by cumulative bar diagrams in Fig. 5. ΔE_disp values are around −50 kcal mol⁻¹. This ΔE_disp contribution is more important for 3,4,7,8-Me₄phen intercalator (−55.5 kcal mol⁻¹ and −60.1 kcal mol⁻¹), not surprisingly because 3,4,7,8-Me₄phen, with four methyl groups, has the highest value of polarizability (209.9 a.u.⁻³, see Table S3 of ESI†) and thus the strongest dispersion forces. ΔE_disp for (AT/4,7-Me₂phen/TA)MG has also a quite different value (about −55 kcal mol⁻¹) because this ligand with two methyl groups has also a high polarizability (179.0 a.u.⁻³, see Table S3 of ESI†). The ΔE_orb component is very similar for all the systems (between −12.4 and −17.0 kcal mol⁻¹), while ΔE_elstat ranges from −25.8 to −36.1 kcal mol⁻¹. This attractive contribution has a determining influence in the energy balance defining the total ΔE_int, as it accounts for roughly 1/3 of the attractive forces and parallels the behavior of ΔE_int. This was also observed in another work¹⁴⁰ addressing the role of electrostatics in stacked DNA base pairs and in our previous work on the intercalation of phen.⁹⁴ This term stabilized the ΔE_int since the ΔE_disp contribution is not sufficient to compensate the repulsive ΔE_Pauli term and ΔE_elstat provides the other considerable stabilizing contribution to ΔE_int. Also, the values of ΔE_elstat are more negative when intercalation takes place from the major groove with the only exception of (AT/4-Mephen/TA)MG (−29.5 kcal mol⁻¹), for which its counterpart (AT/4-Mephen/TA)mg has a more negative ΔE_elstat value (−31.2 kcal mol⁻¹).

Fig. 5 Cumulative bar diagram of the different contributions in the EDA at B3LYP-D3/TZP level. Bars proportional to the values of the energy contribution ΔE_int are included close to ΔE_elstat contribution to appreciate better the fitting of the ΔE_elstat to ΔE_int (energy contributions in kcal mol⁻¹).

ΔE_int has the smallest values (in absolute value) for the systems without methyl groups. On the other hand, the most negative values of ΔE_int correspond to the 3,4,7,8-Me₄phen intercalator for the intercalation via major groove (−38.9 kcal mol⁻¹) and to the 5,6-Me₂phen system when intercalation takes place from the minor groove (−37.7 kcal mol⁻¹). Also, the disubstituted 5,6-Me₂phen and 4,7-Me₂phen systems have more negative values than the monosubstituted intercalators. We notice again that the stabilization of the ΔE_int reflects the number of CH/π interactions and it increases with the number of methyl groups when intercalation is produced through the major groove. On the other hand, when intercalation takes place from the minor groove there are more CH/π interactions for dimethyl systems (6 CH/π interactions, see Table 1, Fig. 4 and ESI† about AIM results) than for the tetramethyl system (5 CH/π interactions) and the ΔE_int is more negative for dimethyl systems. Thus, in these and the other systems, there is a perfect and direct fit between ΔE_int and the number of CH/π interactions, highlighting the importance of these CH/π interactions for such biological processes.

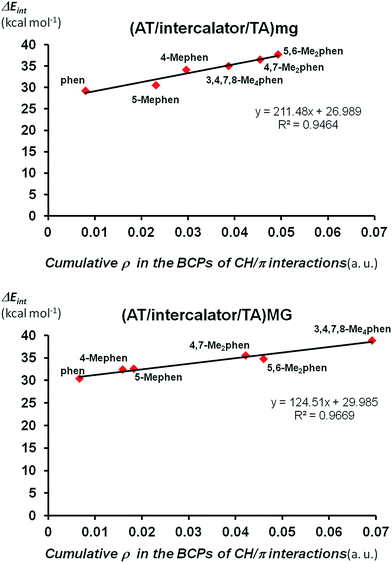
Finally we looked at the relation between the stabilization of the ΔE_int not only with the number of CH/π interactions but also with the strength of these CH/π interactions. We can quantify the strength of CH/π interactions by the values of the electronic density (ρ) at BCPs points associated to CH/π interactions.⁶² That is, as the value of ρ in the BCP increases, the strength of the CH/π increases. Thus, we can define the cumulative electronic density as the summation of all the values for ρ in each bond critical point associated to CH/π interactions of any structure and this cumulative electronic density can give us an idea about the total strength achieved by the sum the individual CH/π interactions in such structure. Thus, we plotted the cumulative electronic density ρ vs. the values of ΔE_int for (AT/intercalator/TA)mg and (AT/intercalator/TA)MG systems in Fig. 6 (see ESI† for the ρ values). Both plots show a perfect correlation between the stabilization of ΔE_int and the increasing value of ρ in the bond critical points associated to CH/π interactions.

Fig. 6 ΔE_int (in kcal mol⁻¹) at B3LYP-D3/TZP level (in absolute value for a better view) vs. cumulative ρ in the bond critical points (BCPs) associated to CH/π interactions (in a.u.) for (AT/intercalator/TA)mg and (AT/intercalator/TA)MG systems.

Discussion

In this exhaustive DFT study we analyzed the geometries, the energy of the bodies, the EDA, and the CH/π interactions of methylated phen systems intercalated between AT/TA stacked base pairs, which also contain methyl groups capable to interact with the π system of the intercalator. We showed the importance of the effective CH/π interactions, triggered by the methyl groups to stabilize the final intercalated structures. Indeed, CH/π interactions, mainly characterized by the AIM analysis and BCPs and bond paths, were shown to be present for the systems where the –CH₃ groups of the intercalator or of the thymine DNA base interacted with either π-system of the base pairs or the intercalator. We established a perfect fit between the number of CH/π interactions and the stabilization of E_f, E_int(bod), E_S or ΔE_int (see definition in the section corresponding to energetics). These terms reflect the stabilization of the final intercalated system. This result is very interesting because it suggests that, more than the number of methyl groups, it is the number of the effective CH/π interactions that rules the stability of the final intercalated system. For this reason, in the cases of (AT/4,7-Me₂phen/TA)mg and (AT/5,6-Me₂phen/TA)mg with 2 –CH₃ groups, these energy terms are more negative than for (AT/3,4,7,8-Me₄phen/TA)mg with 4 –CH₃ groups. This result is also derived from the EDA and the nature of the CH/π interactions. The latter are mainly influenced by dispersion, which is the main contribution to the ΔE_int. However, some non-negligible electrostatic and charge transfer terms contribute to the final ΔE_int, in agreement with the electrostatic component of the CH/π interactions and the low charge transfer through such kind of hydrogen interactions. In fact, as observed previously for phen,⁹⁴ dispersion forces are necessary but not sufficient to compensate the repulsive ΔE_Pauli contribution and the role of ΔE_elstat forces and ΔE_orb contribution becomes crucial to stabilize the intercalated final systems. Although the polarizability of the methylated systems is higher than that of phen intercalator, also in methylated systems is there a need for ΔE_elstat and ΔE_orb to compensate the repulsive ΔE_Pauli forces. The non-negligible importance of the ΔE_elstat can be associated to the high dipolar moments of the intercalators and base pairs, whereas the small charge transfer associated to the ΔE_orb is evidenced by the energies of frontier orbitals, and AIM analysis.

The present work was motivated by the previous works of McFayden et al.⁸⁴ and Brodie et al.⁸⁵ who reported the evidence of modulation of the cytotoxicity with methylation of phen in different number and position, but offered no explanation for these experimental findings. Here, we describe the direct correlation we found between the number of effective CH/π interactions and the stabilization of E_f, E_int(bod), E_S, and ΔE_int. If the cytotoxic effect of the intercalators depends on their time of residence between base pairs,¹⁴¹ then it can be enhanced by the formation of hydrogen bonds or electrostatic interactions. This was used by Snyder et al.¹⁴² to explain the cytotoxicity of Michler's ketone, which depended significantly on the position of the positively charged N-dimethyl groups. Thus, groups of the intercalator able of forming hydrogen bonds and/or electrostatic interactions dictating the residence time and biological activities of any drug will become essential for cytotoxicity.¹⁴³ Some authors even suggested a minimum value of electrostatic energy, setting the limit to hydrogen bond interactions yielding effective intercalation.¹⁴² This finding is similar to those of McFayden et al.⁸⁴ and Brodie et al.⁸⁵ now for neutral methyl groups. However, in the case of methylated phen systems, because methyl groups are neither cationic nor capable of forming charge assisted strong hydrogen bonds, the idea of defining a electrostatic threshold above which the species become cytotoxic is not realistic owing to the small energy amounts involved. Here, we emphasize the importance of these CH/π interactions and notice that the higher the number of CH/π interactions, the more stabilized E_f, E_int(bod), E_S and ΔE_int will be. Thus, the higher number of CH/π interactions contribute to an increased stability of the intercalation complex and we extrapolate that the systems able to form more CH/π interactions will be the most cytotoxic. In fact, the 5,6-Me₂phen system, which was the most cytotoxic system in the work of Brodie et al.⁸⁵ (in that case intercalated between GC/CG via minor groove) has the highest number (6) of CH/π interactions for the intercalation between AT/TA base pairs via minor groove.

We believe that quantification of intrinsic contributions to interaction energy in the intercalated systems can play an important role in favoring intercalation and thus, in discrimination the cytotoxicity of the intercalators. Of course, many other variables will govern the process of intercalation/de-intercalation of ligands in DNA aside from the intrinsic forces studied here, namely, solvation, entropy and steric effects as suggested by Sasikala et al.⁹² and Franco et al.¹¹³ Nevertheless, the intrinsic interactions that take place directly in the intercalation pocket must have a primary role and their comprehension and rationalization becomes fundamental.

Because the objective of our work was to give new and detailed insight on the nature of the intrinsic interactions that rule intercalation (ΔE_disp, ΔE_elstat, ΔE_orb, and ΔE_Pauli), we used a model in which the treatment at QM level with our technical resources was possible (two base pairs of DNA and the intercalator). Such interactions were studied in the seminal works of Bondarev et al.⁹⁹ and Řeha et al.¹⁰⁰ with three-body models (intercalator + one base pair) and this simplest of the models continued to be used for more than one decade^99–105 until the recent work of Hazarika et al.¹⁰⁴ Nevertheless, as stated by Hill et al.,¹⁰⁸ we need the other base-pair to have a better description of the role of the intrinsic forces that rule the intercalation. We understand that the presence of the phosphate backbone would also improve our results because we would have a more realistic model, but such systems cannot be treated at QM level with our technical resources. Despite this limitation, we believe that the main conclusion of this study, without taking into account the phosphate backbone, would remain. Indeed, more than the number of methyl groups, responsible for the increase in the polarizability of the molecule and thus, the dispersion forces, it is the effective number of CH/π interactions that governs the stability of the intercalation of methylated phen between AT/TA base pairs containing –CH₃ groups in thymine. Moreover, we also believe that the systems able to form more effective CH/π interactions will be also the most cytotoxic.

Conclusions

We carried out DFT optimizations on the stacked systems AT/TA incorporating methylated phen intercalators (4-Mephen, 5-Mephen, 4,7-Me₂phen, 5,6-Me₂phen, and 3,4,7,8-Me₄phen) by using the M06-2X functional, which includes the effect of dispersion, to determine the effect of intercalator methylation in the structure, energetics and bond properties of the DNA base pairs where intercalation is produced and to analyze the importance of the CH/π interactions in such systems.

The multibody energy analysis shows that the E_HB contribution does not change significantly with methylation in agreement with the lack of changes in lengths of the hydrogen bonds. On the other hand, the effect of methylation produces more negative E_S contributions, and these become more important than the E_HB. The E_MB term can be considered residual in all the analyzed structures with the exception of the folded (AT/4-Mephen/TA)mg system for which we obtained a value of −10.8 kcal mol⁻¹ (∼14% of the E_int(bod)). This increase is due to the formation of N₆–H⋯N₃ hydrogen bonds between the extruded and folded adenines and is unlikely to occur in the real systems.

The EDA supports the same conclusion we obtained in our previous work.⁹⁴ Even increasing the values of polarizability by methylating phen and thus the attractive ΔE_disp contribution to ΔE_int, this ΔE_disp term is necessary but not enough to balance the repulsive ΔE_Pauli contribution, so that ΔE_orb and specially, ΔE_elst contributions are crucial to achieve the stability of the intercalated system.

Finally, we found a perfect direct correlation between the number of effective CH/π interactions and the stabilization of E_f, E_int(bod), E_S, and ΔE_int. It suggests that the number of effective CH/π interactions which stabilize the intercalated final structure is more important than the number of methyl groups. In an attempt to build a bridge between our results and the cytotoxicity of the systems, we suggest that the structures in which more CH/π interactions are present will also lead to the most cytotoxic systems. We hope that our work will help to shed light on understanding these important intercalation processes, which are of the highest current interest.

Acknowledgements

The research was financially supported by the Fundação para a Ciência e a Tecnologia (FCT) by means of the postdoctoral grant SFRH/BPD/89722/2012 to A. G. and the grant UID/MULTI/00612/2013.

Notes and references

1. T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48.
2. Y. Kodama, K. Nishihata, M. Nishio and N. Nakagawa, Tetrahedron Lett., 1977, 2105.
3. M. Nishio, M. Hirota and Y. Umezawa, The CH/π Interaction Evidence, Nature and Consequences, Wiley-VCH, New York, 1998.
4. T. Takagi, A. Tanaka, S. Matsuo, H. Maezaki, M. Tani, H. Fujiwara and Y. Sasaki, J. Chem. Soc., Perkin Trans. 2, 1987, 1015.
5. S. Sakaki, K. Kato, T. Miyazaki, Y. Musashi, K. Ohkubo, H. Ihara and C. Hirayama, J. Chem. Soc., Faraday Trans., 1993, 89, 659.
6. M.-F. Fan, Z. Lin, J. E. McGrady and D. M. P. Mingos, J. Chem. Soc., Perkin Trans. 2, 1996, 563.
7. D. Philip and J. M. A. Robinson, J. Chem. Soc., Perkin Trans. 2, 1998, 1643.
8. S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2000, 122, 3746.
9. K. Sundararajan, K. Sankaran, K. S. Viswanathan, A. D. Kulkarni and S. R. Gadra, J. Phys. Chem. A, 2002, 106, 1504.
10. O. Takahashi, Y. Kohno and K. Saito, Chem. Phys. Lett., 2003, 378, 509.
11. M. Nishio and M. Hirota, Tetrahedron, 1989, 45, 7101.
12. M. Nakamura, H. Okawa and S. Kida, Bull. Chem. Soc. Jpn., 1985, 58, 3377.
13. R. Ehama, A. Yokoo, M. Tsushima, T. Yuzuri, H. Suezawa and M. Hirota, Bull. Chem. Soc. Jpn., 1993, 66, 814.
14. A. Arduini, G. Giorgi, A. Pochini, A. Secchi and F. Ugozzoli, Tetrahedron, 2001, 57, 2411.
15. G. Arena, A. Contino, E. Longo, G. Spoto, A. Arduini, A. Pochini, A. Secchi, C. Marsera and F. Ugozzoli, New J. Chem., 2004, 28, 56.
16. H. Suezawa, T. Hashimoto, K. Tsuchinaga, T. Yoshida, T. Yuzuri, K. Sakakibara, M. Hirota and M. Nishio, J. Chem. Soc., Perkin Trans. 2, 2000, 1243.
17. K. Kinbara, Y. Harada and K. Saigo, J. Chem. Soc., Perkin Trans. 2, 2000, 1339.
18. M. Yamakawa, I. Yamada and R. Noyori, Angew. Chem., Int. Ed., 2001, 40, 2818.
19. I. Yamada and R. Noyori, Org. Lett., 2001, 2, 3425.
20. Y. Umezawa, S. Tsuboyama, K. Honda, J. Uzawa and M. Nishio, Bull. Chem. Soc. Jpn., 1998, 71, 1207.
21. K. Shibasaki, A. Fujii, N. Mikami and S. Tsuzuki, J. Phys. Chem. A, 2006, 110, 4397.
22. K. Shibasaki, A. Fujii, N. Mikami and S. Tsuzuki, J. Phys. Chem. A, 2007, 111, 753.
23. A. Fujii, K. Shibasaki, T. Kazama, R. Itaya, N. Mikami and S. Tsuzuki, Phys. Chem. Chem. Phys., 2008, 10, 2836.
24. S. Tsuzuki and A. Fujii, Phys. Chem. Chem. Phys., 2008, 10, 2584.
25. A. Stone, J. Chem. Phys. Lett., 1993, 211, 101.
26. S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Phys. Chem. A, 1999, 103, 8265.
27. S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2000, 122, 11450.
28. P. Tarakeshwar, H. S. Choi and K. S. Kim, J. Am. Chem. Soc., 2001, 123, 3323.
29. F. Ugozzoli, A. Arduini, C. Massera, A. Pocchini and A. Secchi, New J. Chem., 2002, 26, 1718.
30. S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2002, 124, 104.
31. S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Phys. Chem. A, 2002, 106, 4423.
32. M. O. Sinnokrot and C. D. Sherryll, J. Am. Chem. Soc., 2004, 126, 7690.
33. E. C. Lee, B. H. Hong, J. Y. Lee, J. C. Kim, D. Kim, Y. Kim, P. Tarakeshwar and K. S. Kim, J. Am. Chem. Soc., 2005, 127, 4530.
34. S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and A. Fujii, J. Phys. Chem. A, 2006, 110, 10163.
35. S. Morita, A. Fujii, N. Mikami and S. Tsusuki, J. Phys. Chem. A, 2006, 110, 10583.
36. C. Ramos, P. R. Winter, J. A. Sterns and T. S. Zwier, J. Phys. Chem. A, 2003, 107, 10280.
37. S. Tsuzuki, K. Honda, A. Fujii, T. Uchimaru and M. Mikami, Phys. Chem. Chem. Phys., 2008, 10, 2860.
38. M. Nishio, Phys. Chem. Chem. Phys., 2011, 13, 13873.
39. G. R. Desiraju, The Weak Hydrogen Bond in Structural Chemistry and Biology, Oxford University Press, New York, 1999.
40. T. Steiner and G. R. Desiraju, Chem. Commun., 1998, 891.
41. M. Nishio, CrystEngComm, 2004, 6, 130.
42. Y. Umezawa, S. Tsuboyama, H. Takahashi, J. Uzawa and M. Nishio, Tetrahedron, 1999, 55, 10047.
43. A. Matsumoto, T. Tanaka, T. Tsubouchi, K. Tashiro, S. Saragai and S. Nakamoto, J. Am. Chem. Soc., 2002, 124, 8891.
44. S. Nagahama, K. Inoue, K. Sada, M. Miyata and A. Matsumoto, Cryst. Growth Des., 2003, 3, 247.
45. K. Saigo and Y. Kobayashi, Chem. Rec., 2007, 7, 47.
46. T. E. Clark, M. Makha, A. N. Sobolev, S. J. Dalgarno, J. L. Atwood and C. L. Raston, Cryst. Growth Des., 2007, 7, 2059.
47. M. Nishio, Tetrahedron, 2005, 61, 6923.
48. G. Ujaque, P. S. Lee, K. N. Houk, M. F. Hentemann and S. J. Danishef-sky, Chem.–Eur. J., 2002, 8, 3423.
49. J. Ribas, E. Cubero, F. J. Luque and M. Orozco, J. Org. Chem., 2002, 67, 7057.
50. O. Takahashi, Y. Kohno, K. Saito and M. Nishiro, Chem.–Eur. J., 2003, 9, 756.
51. U. Samanta, P. Chakrabarti and J. Chandrasekhar, J. Phys. Chem. A, 1998, 102, 8964.
52. S. Re and S. Nagase, Chem. Commun., 2004, 6, 658.
53. V. Spiwok, P. Lipopová, T. Skálová, E. Buchtelová, J. Hasek and B. Králová, Carbohydr. Res., 2004, 339, 2275.
54. A. L. Ringer, M. S. Figgs, M. O. Sinnokrot and C. D. Sherril, J. Phys. Chem. A, 2006, 110, 10822.
55. K. Kobayashi, Y. Asakawa, Y. Kato and Y. Aoyama, J. Am. Chem. Soc., 1992, 114, 10307.
56. D. B. Amabilino, P. R. Ashton, C. L. Brown, E. Cordova, L. A. Godinez, T. T. Goodnow, A. E. Kaifer, S. P. Newton, M. Pietraszkiewicz, D. Philp, F. M. Raymo, A. S. Reder, M. T. Rutland, A. M. Z. Slawin, N. Spencer, J. F. Stoddart and D. J. Williams, J. Am. Chem. Soc., 1995, 117, 1271.
57. A. Frontera, C. Garau, D. Quinonero, P. Ballester, A. Costa and P. M. Deya, Org. Lett., 2003, 5, 1135.
58. P. Sozzani, A. Comotti, S. Bracco and R. Simonutti, Chem. Commun., 2004, 768.
59. G. Toth, K. E. Kover, R. F. Murphy and S. Lovas, J. Phys. Chem. B, 2004, 108, 9287.
60. Y. Yamamoto, A. Yamamoto, S. Furuta, M. Horie, M. Kodama, W. Sato, K. Y. Akiba, S. Tsusuki, T. Uchimaru, D. Hashizume and F. Iwasaki, J. Am. Chem. Soc., 2005, 127, 14540.
61. P. S. Lakshmirarayanan, D. K. Kumar and P. Ghosh, J. Am. Chem. Soc., 2006, 128, 9600.
62. M. J. Calhorda and P. J. Costa, Weak Hydrogen Bonding, in Comprehensive Inorganic Chemistry, ed. J. Reedijk and K. Poeppelmeier, Elsevier, Amsterdam, 2nd edn, 2013, pp. 341–357.
63. F. A. Quiocho and N. K. Vyas, Nature, 1984, 310, 381.
64. N. K. Vyas, M. N. Vyas and F. A. Quiocho, Nature, 1987, 327, 635.
65. M. S. Weiss, M. Brandl, J. Sühnel, D. Pal and R. Hilgenfeld, Trends Biochem. Sci., 2001, 26, 521.
66. A. Jabs, M. S. Weiss and R. Hilgenfeld, J. Mol. Biol., 1999, 286, 291.
67. D. Pal and P. Chakrabarti, J. Mol. Biol., 1999, 294, 271.
68. M. Harigai, M. Kataoka and Y. Imamoto, J. Am. Chem. Soc., 2006, 128, 10646.
69. M. Muraki and K. Harata, Biochemistry, 2000, 39, 292.
70. M. Muraki, Protein Pept. Lett., 2002, 9, 195.
71. P. Chakrabarti and U. Samanta, J. Mol. Biol., 1995, 251, 9.
72. Y. Umezawa and M. Nishio, Bioorg. Med. Chem., 1998, 6, 493.
73. Y. Umezawa and M. Nishio, Bioorg. Med. Chem., 2000, 8, 2643.
74. Y. Umezawa and M. Nishio, Nucleic Acids Res., 2002, 30, 2183.
75. C. F. Matta, N. Castillo and R. Boyd, J. Phys. Chem. B, 2006, 110, 563.
76. J. R. Gord, A. W. Garrett, R. E. Bandy and T. S. Zwier, Chem. Phys. Lett., 1990, 171, 443.
77. A. J. Gotch, R. N. Pribble, F. A. Ensminger and T. S. Zwier, Laser Chem., 1994, 13, 187.
78. A. Fujii, S. Morita, M. Miyazaki, T. Ebata and N. Mikami, J. Phys. Chem. A, 2004, 108, 2652.
79. D. Bandarra, M. Lopes, T. Lopes, J. Almeida, M. S. Saraiva, M. V. Dias, C. D. Nunes, V. Félix, P. Brandão, P. D. Vaz, M. Meireles and M. J. Calhorda, J. Inorg. Biochem., 2010, 104, 1171.
80. O. F. Ikotun, E. M. Higbee, W. Ouellette and R. P. Doyle, J. Inorg. Biochem., 2009, 103, 1254.
81. X. Liang, X. Zou, L. Tan and W. Zhu, J. Inorg. Biochem., 2010, 104, 1259.
82. P. Prasad, P. K. Sasmal, R. Majumdar, R. R. Dighe and A. R. Chakravarty, Inorg. Chim. Acta, 2010, 363, 2743.
83. H.-L. Seng, S.-T. Von, K.-W. Tan, M. J. Maah, S.-W. Ng, R. N. Z. A. Rahman, I. Caracelli and C.-H. Ng, BioMetals, 2010, 23, 99.
84. W. D. McFayden, L. P. G. Wakelin, I. A. G. Roos and V. A. Leopold, J. Med. Chem., 1985, 28, 1113.
85. C. R. Brodie, J. Grant Collins and J. R. Aldrich-Wright, Dalton Trans., 2004, 1145.
86. B. M. Zeglis, V. C. Pierre and J. K. Barton, Chem. Commun., 2007, 44, 4565.
87. H. K. Liu and P. J. Sadler, Acc. Chem. Res., 2011, 44, 349.
88. D. R. Boer, A. Canals and M. Coll, Dalton Trans., 2009, 3, 399.
89. A. Mukherjee and W. D. Sasikala, Adv. Protein Chem. Struct. Biol., 2013, 92, 1.
90. A. V. Vargiu and A. Magistrato, ChemMedChem, 2014, 9, 1966.
91. C. Cordier, V. C. Pierre and J. K. Barton, J. Am. Chem. Soc., 2007, 129, 12287.
92. W. D. Sasikala and A. Mukherjee, Phys. Chem. Chem. Phys., 2013, 15, 6446.
93. A. Mukherjee, R. Lavery, B. Bagchi and J. T. Hynes, J. Am. Chem. Soc., 2008, 130, 9747.
94. A. Gil, M. Melle-Franco, V. Branchadell and M. J. Calhorda, J. Chem. Theory Comput., 2015, 11, 2714.
95. M. Trieb, C. Rauch, F. R. Wibowo, B. Wellenzohn and K. R. Liedl, Nucleic Acids Res., 2004, 32, 4696.
96. A. Robertazzi, A. V. Vargiu, A. Magistrato, P. Ruggerone, P. Carloni, P. de Hoog and J. Reedijk, J. Phys. Chem. B, 2009, 113, 10881.
97. A. V. Vargiu and A. Magistrato, Inorg. Chem., 2012, 51, 2046.
98. R. Galindo-Murillo, L. Ruíz-Azuara, R. Moreno-Esparza and F. Cortés-Guzmán, Phys. Chem. Chem. Phys., 2012, 14, 15539.
99. D. A. Bondarev, W. J. Skawinski and C. A. Venanzi, J. Phys. Chem. B, 2000, 104, 815.
100. D. Řeha, M. Kabeláč, F. Ryjaček, J. Šponer, J. E. Šponer, M. Elstner, S. Suhai and P. Hobza, J. Am. Chem. Soc., 2002, 124, 3366.
101. A. Kumar, M. Elstner and S. Suhai, Int. J. Quantum Chem., 2003, 95, 44.
102. T. M. El-Gogary and G. Koehler, J. Mol. Struct.: THEOCHEM, 2007, 808, 97.
103. T. M. El-Gogary and G. Koehler, J. Mol. Struct.: THEOCHEM, 2009, 895, 57.
104. P. Hazarika, B. Bezharuah, P. Das, O. K. Medhi and C. Medhi, J. Biophys. Chem., 2011, 2, 152.
105. S. Li, V. R. Cooper, T. Thonhauser, B. I. Lundqvist and D. C. Langreth, J. Phys. Chem. B, 2009, 113, 11166.
106. X. Xiao, S. Antony, Y. Pommier and M. Cushman, J. Med. Chem., 2005, 48, 3231.
107. K. M. Langner, P. Kedzierski, W. A. Sokalski and J. Leszczynski, J. Phys. Chem. B, 2006, 110, 9720.
108. J. Grant Hill and J. A. Platts, Chem. Phys. Lett., 2009, 479, 279.
109. D. Ambrosek, P.-F. Loos, X. Assfeld and C. Daniel, J. Inorg. Biochem., 2010, 104, 893.
110. A. Biancardi, T. Biver, A. Marini, B. Mennucci and F. Secco, Phys. Chem. Chem. Phys., 2011, 13, 12595.
111. E. G. Hohenstein, R. M. Parrish, C. D. Sherrill, J. M. Turney and H. F. Schaefer III, J. Chem. Phys., 2011, 135, 174107.
112. P. Deepa, P. Kolandaivel and K. Senthilkumar, Mater. Sci. Eng., C, 2012, 32, 423.
113. D. Franco, A. V. Vargiu and A. Magistrato, Inorg. Chem., 2014, 53, 7999.
114. A. Gil, V. Branchadell, J. Bertran and A. Oliva, J. Phys. Chem. B, 2009, 113, 4907.
115. R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989.
116. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157.
117. Y. Zaho and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
118. W. J. Hehre, L. Radom, P. V. R. Schleyer and J. A. Pople, Ab Initio Molecular Quantum Theory, Wiley, New York, 1986.
119. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
120. S. Simon, M. Duran and J. J. Dannenberg, J. Chem. Phys., 1996, 105, 11024.
121. M. J. Frish, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Kkene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. DApprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford, CT, 2009.
122. A. E. Reed, R. B. Weistock and F. Weinhold, J. Chem. Phys., 1985, 73, 735.
123. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.
124. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.0, Theoretical Chemistry Institute, University of Winsconsin, Madison, WI, 2001.
125. R. F. W. Bader, Atoms in Molecules. A Quantum Theory, Clarendon, Oxford, UK, 1990.
126. J. S. Friedrich Biegler-König, J. Comput. Chem., 2002, 23, 1489.
127. G. te Velde, F. M. Bickelhaupt, S. J. A. van Gisbergen, C. Fonseca Guerra, E. J. Baerends, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931.
128. C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391.
129. ADF, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2013, http://www.scm.com.
130. K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1975, 10, 325.
131. M. von Hopffgarten and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43.
132. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
133. B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200.
134. C. Lee, W. Yang and G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785.
135. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
136. R. F. W. Bader, Chem. Rev., 1991, 91, 893.
137. R. F. W. Bader and H. Essen, J. Chem. Phys., 1984, 80, 1943.
138. A. Gil, V. Branchadell, J. Bertran and A. Oliva, J. Phys. Chem. B, 2007, 111, 9372.
139. C. Acosta-Silva, V. Branchadell, J. Bertran and A. Oliva, J. Phys. Chem. B, 2010, 114, 10217.
140. G. Hill, G. Forde, N. Hill, W. A. Lester, A. W. Sokalski and J. Leszczynski, Chem. Phys. Lett., 2003, 381, 729.
141. R. D. Snyder, Mutat. Res., Fundam. Mol. Mech. Mutagen., 2007, 623, 72.
142. R. D. Snyder, J. McNulty, G. Zairov, D. E. Ewing and L. B. Hendry, Mutat. Res., Fundam. Mol. Mech. Mutagen., 2005, 578, 88.
143. R. D. Snyder and L. B. Hendry, Environ. Mol. Mutagen., 2005, 45, 100.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra15495f

---