A dynamical coarse-grained model to disclose allosteric control of misfolding β2-microglobulin†
O. Carrillo-Parramon*a,
G. Brancolini*b and
S. Cornib
aScuola Normale Superiore, Piazza Dei Cavalieri 7, 56126 Pisa, Italy. E-mail: oliver.carrillo@gmail.com; Tel: +39 059 2055333
bCNR Institute of Nanoscience, S3 Center, Via Campi 213/A, 41125 Modena, Italy. E-mail: giorgia.brancolini@nano.cnr.it
First published on 23rd September 2016
Abstract
We developed a Coarse-Grained (CG) model for β2-microglobulin using one CG bead per aminoacid residue. The CG model was parameterized using atomistic simulations with the aim of investigating the protein dynamical features related to its natural propensity to misfold and aggregate. The pathological self-aggregation of β2-microglobulin is related to dialysis-related amyloidosis. Despite decades of studies, the mechanism of misfolding and fibrillation of this protein remains controversial. To the best of our knowledge this is the first computational study applying a CG model to follow the structural dynamics of different portions of this amyloidogenic protein in response to external dynamical stimuli. Our results indicate that the propensity to detach the N- and C-terminal β-strands (previously suggested to be part of the fibril formation mechanism) of the protein strongly depend on the strengths of the local interactions between specific internal β-strands. The dynamical changes applied locally to the CG model are able to highlight cooperative rearrangements on selectively coupled regions of the protein, resembling allosteric events, which could provide hints to the understanding of the misfolding mechanism process.
Introduction
Coarse-grained (CG) methods have been shown to be useful tools to model biological systems.1 They simplify the structure of a protein by considering only those atoms or sets of atoms that are supposed to be fundamental in the behavior of the system, condensing them in the so called “coarse-grained beads”. The inter-atomic interactions are then mapped by the effective interactions between these CG beads. The reduction of the degrees of freedom, increases the speed of the simulation which allows the study of new relevant biological problems that were unconceivable some years ago by only considering classical atomistic MD.2,3 There are several ways to define the CG beads and compute their effective interactions. These ways depend on the systems to which they have to be applied. Literature is rich of different CG methods and different applications that extend to a huge variety of systems.1,4–6One of the less explored applications is the study of protein structure transitions. These transitions occur, for example, in the so called amyloidogenic proteins, which are characterized by the propensity to start misfolding, followed by protein self-aggregation and formation of fibrillar structures. Many human diseases are associated with this pathological protein aggregation and the consequent abnormal accumulation of amyloid fibrils in organs.
Very known examples are Alzheimer's disease, Parkinson's disease and prion disease7,8 although the exact role of fibrils in these diseases is still controversial. All amyloid assemblies share an elongated fibrillar morphology whose diameter is about 5–15 nm; their arrangement is maintained through β-sheet structures. Considerable progress has been made in order to understand the structure and properties of amyloid fibrils, however, little knowledge exists at the microscopic level, about the structure and dynamics of the initial oligomers from which they originate and about the “viable” intermediate state structures occurring in the transition from the native to the misfolded state.9–12
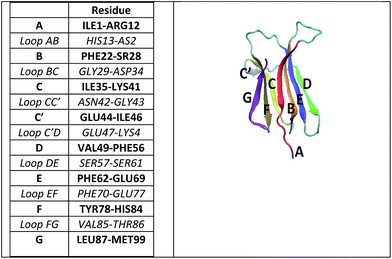
In this paper, we study the particular case of β2-microglobulin (β2m), a protein which is non-covalently bound to the major histocompatibility complex class I (MHC I).13 Native human β2m is a 99-residue-long, 11.9 kDa protein, stabilized by a single disulphide bridge between β-strands B and F. The protein folds into the classical β-sandwich motif of the immunoglobulin superfamily, i.e. seven antiparallel β-strands (A, B, …G) forming two facing sheets (ABED and CFG) (see Fig. 1).
D-strand and DE-loop regions are supposed to play a crucial role in the development of amyloid fibrils.14–17 These portion of the protein form non-covalent contacts in the MHC I bound state and their backbone dynamics is enhanced in the monomeric state of the protein. Dissociation of monomeric β2m from the MHC I occurs mainly in the kidney. As a consequence, the concentration of β2m in the blood of patients suffering from renal dysfunction increases, causing the formation of amyloid fibrils predominantly in the osteoarticular tissues which is accompanied by bone destruction. This process leads to what is known as Dialysis-Related Amyloidosis (DRA).18–20 However, the simple β2m concentration increase cannot be considered responsible for amyloid deposition, since solutions of the protein at physiological conditions can be stable for about a year even at concentration as high as 100–200 μM.21 An alternative mechanism of formation of fibrils has been reported22 which involves the interaction of the native protein with other biomolecules normally present in deposition districts i.e. osteoarticular tissues and/or during the dialysis treatment. Several species have been found to be able to enhance the aggregation of β2m such as collagen, glycosaminoglycans, lysophosphatidic acid, Cu2+ ions and non-esterified fatty acids,20–30 e.g. works in the literature reported that the direct interaction between collagen and D-strand and DE-loop of β2m can increase the propensity of terminal strands A (N-terminus) and G (C-terminus) to open, being a preliminary step for the self-aggregation process.31–35 In this view the monomeric state of the protein would act as the initial core for the β2m amyloid formation and the role of a straight D-strand conformation and the trans–cis conversion of the HIS31-PRO32 peptide bond of DE-loop, could be considered as important features favoring the amyloid structure nucleation.36–48
In this paper we investigate the environmental factors affecting the protein structure by means of one-bead coarse-grained model and Langevin dynamics simulations. We mimic external stimuli from such environment (e.g., interaction with other molecules) by apply changes at the interaction between specific protein portions i.e. the D and E strands, and we follow the protein structure response to those changes. We observe that weakening the interaction between D and E strands induce a correlated response of the protein at the AB- and FG-strands, resembling known allosteric events. Our results show that D-strand play an important role in the overall structure dynamics of β2m.
Methodology
Coarse-grained model
In order to study how protein atoms can change their motion due to internal factors, we used a flexible coarse-grained model that has shown to accurately describe protein motions and flexibility.49 The model relies on the assignment of one bead per amino acid and it is based on an harmonic-like potential U (eqn (1)) which connects each pair of beads and allows the structure to fluctuate around its native equilibrium position:
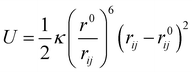 | (1) |
Langevin dynamics
Langevin dynamics simulations are performed to achieve this objective. They are based on the following evolution equation:
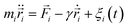 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i is the position of the atom/bead i, mi is the mass of each bead taken as the total mass of the residue it represents. A Verlet algorithm is used in order to simulate the system.46 A time step of 1 fs is used and gamma is set to 0.4 ps (as was considered in ref. 49) for all the simulations. The random parameter ξi is a zero-mean Gaussian number with autocorrelation47
i is the position of the atom/bead i, mi is the mass of each bead taken as the total mass of the residue it represents. A Verlet algorithm is used in order to simulate the system.46 A time step of 1 fs is used and gamma is set to 0.4 ps (as was considered in ref. 49) for all the simulations. The random parameter ξi is a zero-mean Gaussian number with autocorrelation47| 〈ξi(t)ξj(0)〉 = 2kBTγδijδ(t) | (3) |
Statistical tools for the analysis
The focus of the present work is to mimic the behaviour of β2m when one of its strands is modified by dynamical changes resembling the effect of environmental factors affecting the protein at specific regions connected to misfolding. Dynamical changes are here applied at DE-loop and D strand and the protein response to those changes are followed by means of a statistical CG model. Although this model is structurally stable and cannot undergo large configurational changes, normalized correlations between pairs of beads Cnm in eqn (4) can be used as a measure of how proteins behave when such dynamical modifications are induced:
 | (4) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) n =
n = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) n(t) −
n(t) − ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〈
〈![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) n〉. An increase/decrease of correlation in the motion of beads C(n, m) is expected when they increase/decrease their effective interaction, due to collective motion effects. This provide a hint towards the consequent structural evolution of the protein based on other experimental and/or theoretical results.51 However, bead–bead correlations are not sufficient to describe a possible structural transition. These sort of changes normally require large sets of atoms. That is why this measure need to be extended in order to compare the change of correlation between different parts of the structure. From the bead–bead correlations, the correlation between a set of NA beads A and a set of NB beads B can be computed as follows,
n〉. An increase/decrease of correlation in the motion of beads C(n, m) is expected when they increase/decrease their effective interaction, due to collective motion effects. This provide a hint towards the consequent structural evolution of the protein based on other experimental and/or theoretical results.51 However, bead–bead correlations are not sufficient to describe a possible structural transition. These sort of changes normally require large sets of atoms. That is why this measure need to be extended in order to compare the change of correlation between different parts of the structure. From the bead–bead correlations, the correlation between a set of NA beads A and a set of NB beads B can be computed as follows,
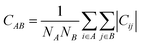 | (5) |
As well as correlation, similarity index γ (or Hess index) in eqn (6) (ref. 50) and β-factor in eqn (7), are be used in order to compare two different molecular dynamics X and Y. The similarity index γ compares two
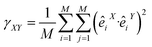 | (6) |
 | (7) |
γXY is expected to be zero when dynamics X and Y are unrelated and one when they describe the same motion. From previous studies based on the present method,49 indexes greater than 0.6 can be considered good enough to conclude that X and Y are mostly equivalent. Other important measurements are the total variance (i.e. the sum of all the eigenvalues of a dynamics) and the partial variance of k order (defined as the sum of the first k eigenvalues). The threshold M is the degree of accuracy to be used in order to properly describe both dynamics. M is normally considered as the order of the partial variance for which it is the 90% of the total variance. The sums in γXY are set up to a value smaller than the total amount of eigenvectors describing the total motions of the protein, being the initial eigenvector contributing the most.
Results and discussion
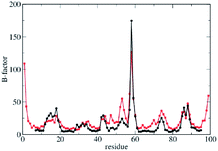
The quality of the CG model was firstly assessed through the comparison between MD and LD simulations results.48 Fully atomistic MD trajectories were collected for 50 ns for the free β2m in water (PDB code: 1JNJ) and the last 20 ns (where RMSD has reached a stable value) were compared with LD trajectories48 also based on the 1JNJ PDB structure. Both MD and LD were performed at 300 K. Previously performed enhanced sampling MD simulations47 showed that 50 ns MD simulation is a reasonable simulation time for this system (see Fig. 7SI†). MD simulations were performed with the Gromacs 4.5.5 package55,56 and after equilibration the trajectories were reasonably stable in terms of density, temperature and potential energy (see Fig. 1SI of ESI†). LD counterpart was run for the same system using a force constant of κ = 150 kcal mol−1 Å−2 between all pair of beads of the CG model. β-Factors of β2m (in Å2) are plotted for the two simulations, reporting values per residue type of MD (in black) and CG (in red), respectively. Both dynamics show similar behaviour for κ = 150 kcal mol−1 Å−2 of LD predicting the occurrence of the same peaks at the same positions along the chain indicating an equivalent flexibility pattern between the two cases (Fig. 2).Essential dynamics was also applied to both MD and LD simulations in order to extract the corresponding sets of eigenvectors (or modes) and eigenvalues characteristic of each dynamics. Eigenvectors, eigenvalues and similarity indexes were also analyzed providing an equivalent flexibility pattern between the two simulations (for more details see Table 1SI and Fig. 2SI in the ESI†).
Inspired by several experimental and computational evidences suggesting the importance of the polypeptide loop comprised between β-strands D and E of β2m for protein stability and its propensity to start aggregation, this work has been devoted to modifying our original Kovacs' CG model in order to mimic the effects on protein dynamics of different interaction strengths (κ values) between D and E strands.
Both experiments and molecular dynamics simulations have reported that the DE loop segment of the protein is the preferred interaction sites for the protein with external environmental factors such as protein–protein interactions,52,53 protein–collagen54 and protein–nanoparticles interactions.51 In all cases, a local attenuation of the NMR chemical shifts was observed and it was ascribed to the binding of the protein to external entities of the surrounding environment. Experiments on the substitution of residues belonging to the DE loop with two mutants, reinforced the hypothesis that conformational strain in the DE loop can affect β2m stability and amyloid aggregation properties.52 Experimental evidences suggested that by weakening the interaction between D and E strand through the inclusion of mutations at Trp60 it is possible to affect the strength of the interaction between F and G strands (Trp95) inducing allosteric type behaviour on the protein.57,58 The unfolding of the native structure would originate from the detachment of the G strand from F strand (PDB structure 2X89) being an important step towards the formation of fibrils via β-sheet interactions.59
Given those experimental and computational evidences57–61 and with the aim of exploring this hypotesis, we have devoted the present work to modify the original Kovacs' CG model to investigate the allosteric effects triggered in the protein dynamics by the incorporating different κ values (i.e. interaction strengths). In Fig. 3A correlation per pair of beads is computed in the presence of identical κ value between all the strands: κDE = 150 kcal mol−1 Å−2 for the “springs” connecting D and E strands is identical to the values of 150 kcal mol−1 Å−2, kept for all the other pair of strands.
The weaker attachment between D and E strand in the CG model was mimicked by lowering the value of κDE = 10 kcal mol−1 Å−2 for the “springs” connecting D and E strands while maintaining the same values of 150 kcal mol−1 Å−2 for all the other pair of strands. The assigned lower values allowed both D and E strands to maintain the original connectivity with the rest of the protein. As in the previously described cases, a 50 ns LD simulation has been performed and its corresponding bead–bead correlation map has been depicted Fig. 3B (with the same color code as in Fig. 3A).
Relevant differences can be noticed between maps in Fig. 3A and B, corresponding to correlated and uncorrelated strands, respectively. The weakening of the interaction between D and E strands has the effect of breaking the correlation pattern of other strands in the protein motions, being D and E relevant for maintenance of a properly folded structure. The map in Fig. 3B shows that the terminal residues of the protein at the C-terminus (corresponding to strands F and G) loose correlation with respect to the rest of the protein and even with respect to each other. Additionally, two strands at the N-terminal region (A and B strands) slightly decrease their own correlation. The present result clearly supports the initial hypothesis posted above that DE loop can affect β2m stability and amyloid aggregation properties. Similarly to the case of κDE = 10 kcal mol−1 Å−2, correlation maps for different values of κDE have been depicted and shown in Fig. 4.
The plots report the correlations between different portions of the protein, FG, DG, AB and AD strands respectively, as a function of different values of the κDE constant. In all cases, we register a decrease in the correlation between the selected pair of strands when κDE assumes small values, on the contrary, we observe a well maintained correlation between each strand's pair when κDE assumes large values. In Fig. 4, the correlation curves between strands AB, FG, AD and DG are presented in separate panels, for different values of κDE. It is worth noticing that for κDE values smaller than 150 kcal mol−1 Å−2 correlations between strands decrease but for larger κDE values correlations between strands reach a constant plateau. We searched for trends in the correlation between pair of strands as a function not only of κDE values but also of κAB, κCC′ and κFG values. The aim was to verify that the observed behaviour is indeed dependent on the selected pair of strands for which the κ is modified, and not a generic result associated with loosening of the structure. We have thus modified the interaction between strands AB, CC′ and FG and we have compared the correlations with those obtained for DE strands. The results are shown in Table 1, and indicate that the protein correlations are not affected by a change of the interactions between AB, CC′ or FG but only by a change of the DE interaction. In other words, changing the κ values in other localized region, different from DE portion, does not induce any modification in the conformational behavior of the system.
| CAB | CFG | CDE | CAD | CDG | |
|---|---|---|---|---|---|
| κAB | |||||
| 50 | 0.96 | 0.94 | 0.92 | 0.90 | 0.83 |
| 150 | 0.97 | 0.95 | 0.92 | 0.93 | 0.87 |
| 500 | 0.92 | 0.90 | 0.92 | 0.91 | 0.80 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| κCC′ | |||||
| 50 | 0.96 | 0.94 | 0.91 | 0.90 | 0.84 |
| 150 | 0.97 | 0.95 | 0.92 | 0.93 | 0.87 |
| 500 | 0.98 | 0.96 | 0.96 | 0.94 | 0.89 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| κDE | |||||
| 50 | 0.57 | 0.57 | 0.68 | 0.25 | 0.28 |
| 150 | 0.97 | 0.95 | 0.92 | 0.93 | 0.87 |
| 500 | 0.92 | 0.90 | 0.95 | 0.91 | 0.80 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| κFG | |||||
| 50 | 0.95 | 0.85 | 0.88 | 0.87 | 0.78 |
| 150 | 0.97 | 0.95 | 0.92 | 0.93 | 0.87 |
| 500 | 0.96 | 0.93 | 0.91 | 0.86 | 0.80 |
This proves that the structural dynamics of D and E strands correlate with the conformational flexibility of the protein and play a crucial role in maintaining the protein globular native state. We have also verified that the number of native contacts (defined as in ref. 62) is smaller in the simulation where the DE loop is more flexible (see Fig. 4SI†). On the contrary, we did not observe an increase in the hydrophobic Solvent Accessible Surface Area (SASA) in passing from the non-perturbed to the perturbed LD simulations (see Fig. 5SI†), which is not surprising since amyloidogenic mutants of β2m (such as ΔN6, PDB:2XKU) do not always have a hydrophobic SASA larger than wild-type β2m. It is remarkable that correlations between AD and DG are not affected by a change in κAB or κFG values. Their values, instead, are dramatically affected by a decrease of the κDE value. The present results together with the observation that no modification of κAB or κFG values is able to induce relevant changes in the correlations between strands DE, AB or FG, clearly suggest that the detachment between strand D and E by itself is a central step in the misfolding process.
These observations are even strengthened by the comparison with RMSD values computed for the individual A, B, D, F, G strands and for the whole protein atoms, as a function of κDE values. In Table 2 all the RMSD averages were computed using the LD native structure as a reference (i.e. native with initial homogeneous κ value set to 150 kcal mol−1 Å−2). The ranges of RMSD values, were larger for the G terminal strand than for the A strand. Therefore, according to the presented data, the overall effect of increasing the mobility of the D strand, is to change the flexibility of the terminal of selected strands (notably F and G) and not that of changing the flexibility of the protein as a whole. Considering the data in more details, we see that F and G strands (C-terminus) are more sensitive to the changes in the flexibility of D strand (κDE) than the A and B strands (N-terminus). For κDE = 50 kcal mol−1 Å−2 and κDE = 500 kcal mol−1 Å−2, the RMSD values of G strands deviate considerably with respect the RMSD of other portion the protein. All those observation reinforce the picture of an allosteric-like mechanism through which an interaction loosening the loop DE affect the conformation and the dynamics of other specific fragments of β2m.
| κDE | ALL | Strand A | Strand B | Strand D | Strand F | Strand G |
|---|---|---|---|---|---|---|
| 50 | 0.746 | 0.549 | 0.439 | 0.955 | 0.656 | 0.877 |
| 150 | 0.519 | 0.562 | 0.360 | 0.544 | 0.341 | 0.557 |
| 500 | 0.402 | 0.483 | 0.362 | 0.356 | 0.246 | 0.329 |
According the presented data, the strength of the interaction between D and E strands appear to be pivotal for the misfolding process and aggregation of β2m.47,48 For the sake of completeness, the GC results on protein structure were compared with our molecular mechanics characterization of the potential energy surface of an allosteric path in which the final dimer structure is characterized experimentally.63 Computed values for the protein distance between strand D and strand E along the allosteric path leading to the swapped dimer (PDB:2X89) are reported in Fig. 6SI,† confirming the crucial role played by D and E strands in the first allosteric transformation of an early amyloidogenic intermediate. This is in line with previous experimental evidences, in particular to experiments in which the protein was subjected to mutations at residue belonging to the DE loop, and revealing their effect on protein misfolding. More in details, structure 2Z9T57 and 3DHM58 were subjected to the mutations W60G and D59P, respectively. Experimental evidences57,58 suggested that these mutations included in the DE loop, were able to decrease the aggregation propensity and to avoid the misfolding process. On the basis of our CG model results, we suggest that the effect of such W60G mutation are related to a stronger stability of the D strand and consequently of the DE portion (i.e. larger κDE in the language of our model), revealed by experimental and atomistic computational data,57–61 notwithstanding the role of W60 in protein–protein contact.57 In fact, according to the presented data, such W60G mutation would result in a lower propensity of the protein to open A and G strands. A similar discussion can be done for D59P mutation, that was specifically conceived to increase the rigidity of the DE loop.58 Therefore, we believe that our CG model has the capability to disclose new molecular insights relevant for the understanding of β2m misfolding towards fibrillation.
As a further validation of our CG model we compared our CG results with fully atomistic simulations performed on β2m interacting with doxycycline (a drug known to inhibit fiber formation, see Fig. 3SI†).64 The docking between the protein and the drug revealed that the preferential site for the binding was localized on AB strands, which had the effect of sensibly reducing the protein fluctuations at this site. With our GC model we can mimic the effect of the protein binding to such drug by increasing the mutual interaction between the strands AB as the effect of the binding to the drug at this site. In order to check this, we changed κAB to 500 kcal mol−1 Å−2 by keeping κDE equal to 10 kcal mol−1 Å−2. Simulations confirmed that the correlation between FG increased from 0.25 (for κAB = 150 kcal mol−1 Å−2) to 0.96. According to this, correlation between strands F and G are very sensitive to the change in AB interactions. Therefore, the attachment of strands FG increases its rigidity as well as the rigidity of other portions of the protein. To conclude, the drug exerts what resemble an allosteric inhibition of the process of opening of the FG β-sheet, and thus it avoids the eventual formation of fibrils. The present case study represent a further evidence of the reliability of our CG method which offer a novel tool in addition to the already available,65 to follow the protein dynamics and to provide new insight into the experimental findings.
Conclusions
We have presented a novel use of the Kovacs' CG model to study the β2m protein dynamical features related to its natural propensity to misfold and start fibrillation. Even if one bead coarse-grained model cannot predict large conformational changes of the protein, it can indicate propensities in the deformation behavior of the protein via investigation of the proten motion correlations. The presented results reveal that the attachment/detachment of G and A terminal strands of the protein, strongly depend on the strengths of the local interactions between D and E strands. No other pair has such an extensive effects on the rest of the protein, inducing cooperative rearrangements on coupled regions of the protein, which resemble allosteric events. In particular, when the interaction between DE strands becomes weaker with respect to the homogeneous native interaction, the terminal strands A and G are getting more loosely bound to the protein and tend to fluctuate more freely, favoring the protein misfolding propensity. Nevertheless, our results clearly show that such a motion could cause the break of AB and FG parallel β-sheets leading to a structure prone to start aggregation. These theoretical results provide a possible explanation of several known experimental findings57–61 and of the interaction of the protein with the doxycycline drug.63 Finally, the present work extends the Kovac's coarse-grained model49 to a new class of problems, never considered before. This opens the door to other new and interesting applications and corroborate the use of the present CG approach as a tool to predict possible structural changes in proteins which have the potential to change their internal interaction pattern, or the way they interact with external agents. The evidence that the spatial structure of a protein largely determines its own motion is the ultimate principle that makes this approach working.Acknowledgements
Authors thank Alessandra Corazza, Gennaro Esposito, Federico Fogolari for useful discussions about β2-microglobulin aggregation, and Valentina Tozzini for discussions about coarse-grained models. Funding from MIUR under the project PRIN 2012A7LMS3_003 is gratefully acknowledged. Oak Ridge National Laboratory by the Scientic User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy is acknowledged for the supercomputing project CNMS2013-064. Facilities of the National Energy Research Scientific Computing Center (NERSC), which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231, are also acknowledged.References
- V. Tozzini, Acc. Chem. Res., 2009, 43, 220 CrossRef PubMed.
- V. Tozzini, Q. Rev. Biophys., 2010, 43, 333 CrossRef CAS PubMed.
- K. Voltz, J. Trylska, V. Tozzini, J. Kurkal-Siebert, J. Langowski and J. Smith, J. Comput. Chem., 2008, 29, 1429 CrossRef CAS PubMed.
- A. R. Atilgan, S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin and I. Bahar, Biophys. J., 2001, 80, 505 CrossRef CAS PubMed.
- D. Baker, Nature., 2000, 405, 39 CrossRef CAS PubMed.
- N. Koga and S. Takada, J. Mol. Biol., 2001, 313, 171 CrossRef CAS PubMed.
- J. D. Harper and P. T. Lansbury Jr, Annu. Rev. Biochem., 1997, 66, 385 CrossRef CAS PubMed.
- M. Stefani and C. M. Dobson, J. Mol. Med., 2003, 81, 678 CrossRef CAS PubMed.
- H. Krobath, S. G. Estácio, P. F. N. Faísca and E. I. Shakhnovich, J. Mol. Biol., 2012, 422, 705 CrossRef CAS PubMed.
- S. G. Estácio, C. S. Fernandes, H. Krobath, P. F. N. Faísca and E. I. Shakhnovich, J. Chem. Phys., 2012, 137, 085102 CrossRef PubMed.
- S. G. Estácio, E. I. Shakhnovich and P. F. N. Faísca, Int. J. Mol. Sci., 2013, 14, 17256 CrossRef PubMed.
- S. G. Estácio, H. Krobath, D. Vila-Viçosa, M. Machuqueiro, E. I. Shakhnovich, P. F. N. Faísca and G. Wei, PLoS Comput. Biol., 2014, 10, e1003606 Search PubMed.
- E. A. Hughes, C. Hammond and P. Cresswell, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 1896 CrossRef CAS.
- K. M. Paulsson, P. Wang, P. O. Anderson, S. Chen, R. F. Pettersson and S. Li, Int. Immunol., 2001, 13, 1063 CrossRef CAS PubMed.
- J. W. Becker and G. N. Reeke Jr, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 4225 CrossRef CAS.
- D. P. Smith and S. E. Radford, Protein Sci., 2001, 10, 1775 CrossRef CAS PubMed.
- H. Katou, T. Kanno, M. Hoshino, Y. Hagihara, H. Tanaka, T. Kawai, K. Hasegawa, H. Naiki and Y. Goto, Protein Sci., 2002, 11, 2218 CrossRef CAS PubMed.
- J. Floege and M. Ketteler, Kidney Int. Suppl., 2001, 78, S164 CrossRef CAS PubMed.
- J. J. Zingraff, L. H. Noel, T. Bardin, C. Atienza, B. Zins, T. B. Drueke and D. Kuntz, N. Engl. J. Med., 1990, 323, 1070 CrossRef CAS PubMed.
- C. J. Morgan, M. Gelfand, C. Atreya and A. D. Miranker, J. Mol. Biol., 2001, 309, 339 CrossRef CAS PubMed.
- A. Relini, C. Canale, S. De Stefano, R. Rolandi, S. Giorgetti, M. Stoppini, A. Rossi, F. Fogolari, A. Corazza and G. Esposito, et al., J. Biol. Chem., 2006, 281, 16521 CrossRef CAS PubMed.
- A. Relini, S. De Stefano, S. Torrassa, O. Cavalleri, R. Rolandi, A. Gliozzi, S. Giorgetti, S. Raimondi, L. Marchese and L. Verga, et al., J. Biol. Chem., 2008, 283, 4912 CrossRef CAS PubMed.
- N. A. Athanasou, B. Puddle and B. Sallie, Nephrol., Dial., Transplant., 1995, 10, 1672 CAS.
- T. Ookoshi, K. Hasegawa, Y. Ohhashi, H. Kimura, N. Takahashi, H. Yoshida, R. Miyazaki, Y. Goto and H. Naiki, Nephrol., Dial., Transplant., 2008, 23, 3247 CrossRef CAS PubMed.
- H. Pal-Gabor, L. Gombos, A. Micsonai, E. Kovacs, E. Petrik, J. Kovacs, L. Graf, J. Fidy, H. Naiki and Y. Goto, et al., Biochemistry, 2009, 48, 5689 CrossRef CAS PubMed.
- D. V. Blaho and A. D. Miranker, Biochemistry, 2009, 48, 6610 CrossRef CAS PubMed.
- K. Antwi, M. Mahar, R. Srikanth, M. R. Olbris, J. F. Tyson and R. W. Vachet, Protein Sci., 2008, 17, 748 CrossRef CAS PubMed.
- M. F. Calabrese and A. D. Miranker, J. Mol. Biol., 2007, 367, 1 CrossRef CAS PubMed.
- S. Giorgetti, A. Rossi, P. Mangione, S. Raimondi, S. Marini, M. Stoppini, A. Corazza, P. Viglino, G. Esposito and G. Cetta, et al., Protein Sci., 2005, 14, 696 CrossRef CAS PubMed.
- G. Esposito, A. Corazza, P. Viglino, G. Verdone, F. Pettirossi, F. Fogolari, A. Makek, S. Giorgetti, P. Mangione and M. Stoppini, et al., Biochim. Biophys. Acta, 2005, 1753, 76 CrossRef CAS PubMed.
- A. Corazza, E. Rennella, P. Schanda, M. C. Mimmi, T. Cutuil, S. Raimondi, S. Giorgetti, F. Fogolari, P. Viglino and L. Frydman, et al., J. Biol. Chem., 2010, 285, 5827 CrossRef CAS PubMed.
- T. R. Jahn, M. J. Parker, S. W. Homans and S. E. Radford, Nat. Struct. Mol. Biol., 2006, 13, 195 CAS.
- A. Kameda, M. Hoshino, T. Higurashi, S. Takahashi, H. Naiki and Y. Goto, J. Mol. Biol., 2005, 348, 383 CrossRef CAS PubMed.
- M. Rueda, P. Chacon and M. Orozco, Structure, 2007, 15, 565 CrossRef CAS PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, UK, 1989 Search PubMed.
- S. Ricagno, S. Raimondi, S. Giorgetti, V. Bellotti and M. Bolognesi, Biochem. Biophys. Res. Commun., 2009, 380, 543 CrossRef CAS PubMed.
- S. Ricagno, M. Colombo, M. de Rosa, E. Sangiovanni, S. Giorgetti, S. Raimondi, V. Bellotti and M. Bolognesi, Biochem. Biophys. Res. Commun., 2008, 377, 146 CrossRef CAS PubMed.
- C. Rosano, S. Zuccotti, P. Mangione, S. Giorgetti, V. Bellotti, F. Pettirossi, A. Corazza, P. Viglino, G. Esposito and M. Bolognesi, J. Mol. Biol., 2004, 335, 1051 CrossRef CAS PubMed.
- G. Esposito, S. Ricagno, A. Corazza, E. Rennella, D. Gumral, M. C. Mimmi, E. Betto, C. E. Pucillo, F. Fogolari and P. Viglino, et al., J. Mol. Biol., 2008, 378, 887 CrossRef PubMed.
- E. Rennella, A. Corazza, F. Fogolari, P. Viglino, S. Giorgetti, M. Stoppini, V. Bellotti and G. Esposito, Biophys. J., 2009, 96, 169 CrossRef CAS PubMed.
- E. Rennella, A. Corazza, S. Giorgetti, F. Fogolari, P. Viglino, R. Porcari, L. Verga, M. Stoppini, V. Bellotti and G. Esposito, J. Mol. Biol., 2010, 401, 286 CrossRef CAS PubMed.
- S. L. Myers, S. Jones, T. R. Jahn, I. J. Morten, G. A. Tennent, E. W. Hewitt and S. E. Radford, Biochemistry, 2006, 45, 2311 CrossRef CAS PubMed.
- G. Esposito, R. Michelutti, G. Verdone, P. Viglino, H. Hernandez, C. V. Robinson, A. Amoresano, F. Dal Piaz, M. Monti and P. Pucci, et al., Protein Sci., 2000, 9, 831 CrossRef CAS PubMed.
- V. Bellotti, M. Gallieni, S. Giorgetti and D. Brancaccio, Semin. Dial., 2001, 14, 117 CrossRef CAS PubMed.
- C. M. Eakin and A. D. Miranker, Biochim. Biophys. Acta, 2005, 1753, 92 CrossRef CAS PubMed.
- D. P. Smith, S. Jones, L. C. Serpell, M. Sunde and S. E. Radford, J. Mol. Biol., 2003, 330, 943 CrossRef CAS PubMed.
- R. S. Armen and V. Daggett, Biochemistry, 2005, 44, 16098 CrossRef CAS PubMed.
- F. Fogolari, A. Corazza, P. Viglino, P. Zuccato, L. Pieri, P. Faccioli, V. Bellotti and G. Esposito, Biophys. J., 2007, 92, 1673 CrossRef CAS PubMed.
- J. A. Kovacs, P. Chacon and R. Abagyan, Proteins, 2004, 56, 661 CrossRef CAS PubMed.
- A. Emperador, A. O. Carrillo, M. Rueda and M. Orozco, Biophys. J., 2008, 95, 2127 CrossRef CAS PubMed.
- A. Amadei, A. B. Linssen and H. J. Berendsen, Proteins, 1993, 17, 412 CrossRef CAS PubMed.
- B. Hess, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 8438 CrossRef CAS.
- G. Brancolini, A. Corazza, M. Vuano, F. Fogolari, M. C. Mimmi, V. Bellotti, M. Stoppini, S. Corni and G. Esposito, ACS Nano, 2015, 9, 2600 CrossRef CAS PubMed.
- S. Giorgetti, S. Raimondi, K. Pagano, A. Relini, M. Bucciantini, A. Corazza, F. Fogolari, L. Codutti, M. Salmona, P. Mangione, L. Colombo, A. De Luigi, R. Porcari, A. Gliozzi, M. Stefani, G. Esposito, V. Bellotti and M. Stoppini, J. Biol. Chem., 2011, 286, 2121 CrossRef CAS PubMed.
- F. Fogolari, A. Corazza, P. Viglino, P. Zuccato, L. Pieri, P. Faccioli, V. Bellotti and G. Esposito, Biophys. J., 2007, 92, 1673 CrossRef CAS PubMed.
- G. Esposito, A. Corazza and V. Bellotti, Subcell. Biochem., 2012, 65, 1917 Search PubMed.
- G. A. Kaminski, R. A. Friesner, J. Tirado-Rives and W. L. Jorgensen, J. Phys. Chem. B, 2001, 105, 6474 CrossRef CAS.
- D. Van der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701 CrossRef CAS PubMed.
- G. Esposito, S. Ricagno, A. Corazza, E. Rennella, D. Gumral, M. C. Mimmi and E. Betto, et al., J. Mol. Biol., 2008, 378, 885 CrossRef CAS PubMed.
- S. Ricagno, M. Colombo, M. de Rosa, E. Sangiovanni, S. Giorgetti, S. Raimondi, V. Bellotti and M. Bolognesi, Biochem. Biophys. Res. Commun., 2008, 337, 146 CrossRef PubMed.
- F. Fogolari, A. Corazza, N. Varini, M. Rotter, D. Gumral, L. Condutti, E. Rennella, P. Viglino, V. Bellotti and G. Esposito, Proteins, 2011, 79, 986 CrossRef CAS PubMed.
- R. B. Best, G. Hummer and W. A. Eaton, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 17874 CrossRef CAS PubMed.
- K. Domanska, S. Vanderhaegena, V. Srinivasana, E. Pardona, F. Dupeuxc, J. A. Marquez, S. Giorgetti, M. Stoppini, L. Wyns, V. Bellottid and J. Steyaerta, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1314 CrossRef CAS PubMed.
- C. Camilloni, B. M. Sala, P. Sormanni, R. Porcari, A. Corazza, M. De Rosa, S. Zanini, A. Barbiroli, G. Esposito and M. Bolognesi, et al., Sci. Rep., 2016, 6, 25559 CrossRef CAS PubMed.
- L. Nagel-Steger, M. C. Owen and B. Strodel, ChemBioChem, 2016, 17, 657 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra15491c |
| This journal is © The Royal Society of Chemistry 2016 |