DFT study on 1,7-octadiene polymerization catalyzed by a non-bridged half-titanocene system

Abstract

Polymerization of 1,7-octadiene catalyzed by the (η⁵-C₅Me₅)TiCl₂(O-2,6-ⁱPr₂C₆H₃)/MAO system exhibited unusual favorable selectivity of repeated insertion. However, the mechanism of selectivity of the insertion mode of non-conjugated dienes has not been reported previously as far as we know. By using the density functional theory (DFT) method, the insertion modes of 1,7-octadiene, especially the selectivity of repeated insertion and intramolecular cyclization, were explored in detail concerning the (η⁵-C₅Me₅)TiCl₂(O-2,6-ⁱPr₂C₆H₃)/MAO system. At the initiation stage, the 1,2-si-insertion is the optimal pathway among four insertion modes kinetically and thermodynamically. At the chain propagation stage, the competition between repeated insertion and intramolecular cyclization was discussed in detail, concerning the insertion into different growing chains. The computational results indicated that the repeated insertion of 1,7-octadiene showed more kinetically favorable than the intramolecular cyclization in three different situations, with free energy barrier differences between two insertion modes of 3.75 kcal mol⁻¹, 3.88 kcal mol⁻¹ and 7.43 kcal mol⁻¹ respectively. Moreover, the sequential insertion of seven-membered rings exhibited disadvantageous kinetically and thermodynamically, probably due to the steric repulsion effect between two cyclic rings. Those are in good agreement with the experimental data.

---

Introduction

The control of a monomer's insertion mode is one of the most important aspects for olefin polymerization.¹ Especially for polymerization of non-conjugated dienes, repeated insertion and cyclized insertion of a monomer will conduct the different structures of chain elements, which are cyclic units and vinyl groups respectively.² Polyolefins with cyclic units usually exhibit remarkable properties, such as high transparency, good mechanical properties, and high glass transition temperature, etc.,³ while the polyolefins with vinyl groups are able to produce functional polymers by using post-polymerization modification.⁴ Since Marvel and Stille successfully achieved polymerization of non-conjugated dienes by using heterogeneous Ziegler–Natta catalysts,⁵ a large number of transition metal catalysts have been reported for homo- and copolymerization of non-conjugated dienes, e.g. 1,5-hexadiene (HD),⁶ 1,6-heptadiene (HPD),⁷ and 1,7-octadiene (OD).⁸ However, most studies have resulted in the polymers with predominant cyclic groups, viz. cyclization of non-conjugated dienes is the primary reaction during the polymerization process. Only limited catalyst systems have been used for the repeated insertion of non-conjugated dienes efficiently.^9–14 The metallocene/methylaluminoxane (MAO) catalyst system was reported to carry out the co- and homopolymerization of non-conjugated dienes by Shiono.¹⁰ The fraction of vinyl group derived from OD was observed up to about 64% in the copolymer and up to 60% in the homopolymer. Upon activation with MMAO, the constrained-geometry catalyst, [Me₂Si(η⁵-C₅Me₄)(N^tBu)]TiCl₂, could conduct copolymerization of ethylene and OD with vinyl group about 30%.¹¹ The polymerization of HD catalyzed by the bis(phenoxyimine) titanium system gave the resultant polymer containing methylene-1,3-cyclopentane units and 3-vinyl tetramethylene units.¹² The resultant polymers with pendant vinyl groups could be modified by the post-polymerization cross metathesis strategy, resulting in the tailored random and block copolymers.^12b Recently, Li et al. reported that the pyridylamido-ligated hafnium catalyst could conduct the polymerization of asymmetric and symmetric Si-containing α,ω-diolefins.¹³ When the monomer is 4,4-diphenyl-4-sila-1,6-heptadiene, the resultant polymer contains about 20% pendant vinyl groups. Besides, the homo- and copolymers of OD with the moderate content of vinyl groups were also obtained by using the rare-earth metal catalysts.¹⁴

Non-bridged half-titanocenes bearing anionic ancillary donor ligands are the versatile catalysts for olefin polymerization. In 1998, Nomura et al. first reported that Cp′TiCl₂(OAr) (Cp′ = cyclopentadienyl group; OAr = aryloxy group, such as O-2,6-ⁱPr₂C₆H₃) exhibited not only remarkable catalytic activities for ethylene polymerization, but also efficient copolymerization of ethylene and α-olefins.¹⁵ Following the studies, this kind of catalyst system was developed for the homo- and/or copolymerization of different kinds of olefins, including styrene, cyclic olefins, HD, bulky substitutional olefins and functional olefins.¹⁶ Comparing to polymerization of HD,¹⁷ polymerization of OD exhibited favourable selectivity of repeated insertion by (η⁵-C₅Me₅)TiCl₂(O-2,6-ⁱPr₂C₆H₃)/MAO system, affording 74 to ≥92% content of terminal olefin unit.¹⁸ The resultant polymers showed high M_n values and narrow PDIs without cross-linking. What's more, the OD/1-octene copolymer could be modified by post-polymerization modification strategy to generate the functional polymers. In spite of the dramatic catalytic performance, the related mechanism and factors, taking the charge of the performance on favourable repeated insertion of OD by non-bridged half-titanocene system, remain unclear.

In the last two decades, computational chemistry has been widely and successfully used in study on the mechanism of olefin coordination polymerization by using various catalyst systems, such as group IV systems,¹⁹ late transition metal systems,²⁰ rare-earth metal systems²¹ etc. The computational results provide considerable insights into the experimental research on olefin polymerization. As for the non-bridged half-titanocene system, the polymerization mechanism of homo- and copolymerization of ethylene has been researched by combining theoretical and experimental methods.²² The results showed that the substituents on the cyclopentadienyl group could markedly influence the catalytic activity, the comonomer incorporation, the monomer sequence distribution etc.^22b,c In addition, comparing to the other olefin monomers, the computational study on the polymerization mechanism of non-conjugated dienes is very limited so far.²³ Especially, the investigation of the selectivity of insertion mode hasn't been reported as far as we know. Herein, we carried out a DFT study on the mechanism of polymerization of OD catalyzed by (η⁵-C₅Me₅)TiCl₂(O-2,6-ⁱPr₂C₆H₃)/MAO system. The selective competitions between repeated insertion and intramolecular cyclization were explored in detail by analyzing the structures and energies of π-complexes, transition states and products during the chain propagation.

Computational details

Density functional theory (DFT) was employed in the present study. Geometry optimizations of all the complexes were performed at the Becke3LYP (B3LYP) level.²⁴ The effective core potentials (ECPs) of Hay and Wadt with a double-ζ valence basis set (LanL2DZ)²⁵ were used to describe the 1s²2s²2p⁶ configuration of titanium the standard 6-31G** basis set was used for all other atoms. All geometries of local minima and transition state were fully optimized without any symmetry constraints. The transition state search was performed by using Opt = TS keyword using Berny algorithm²⁶ to optimize to a transition state rather than a local minimum. Each stationary point was verified by harmonic vibration frequencies (N_imag = 1 for transition state and N_imag = 0 for the local minimum). Connectivity of each transition state was determined by means of the intrinsic reaction coordinate (IRC) approach. Gibbs free energies and enthalpy correction obtained from analytic frequency calculation were added to the zero-point energy in this paper. The single-point calculations were performed with M06 functional²⁷ based on the optimized structures. Larger basis set 6-311G** was used for C, O and H atoms, and the Stuttgart/Dresden effective core potential (ECP) basis set²⁸ for the Ti atoms. The thermodynamic correction obtained from analytic frequency calculation was added to the single-point energy to estimate thermodynamic change. The potential energy surface (PES) was described by the relative free energies (ΔG, 298.15 K, 1 atm) computed in the gas phase. All the calculations were carried out by using Gaussian09 software package.²⁹

Results and discussion

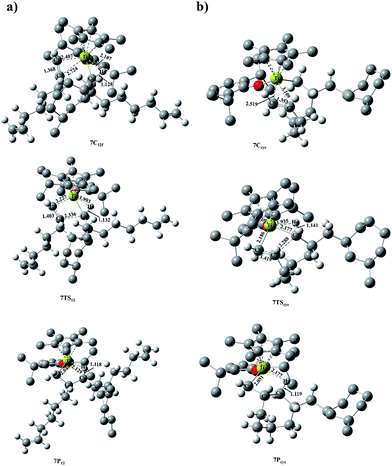
Upon activation with MAO, the monocationic titanium alkyl species [(η⁵-C₅Me₅)Ti(O-2,6-ⁱPr₂C₆H₃)Me]⁺ (1A) was constructed as the initial active species in present computational study (Fig. 1).^15b As the d0-metal complex, 1A is proposed to initiate the olefin insertion according to the modified Cossée–Arlman mechanism (Scheme 1a).³⁰ Comparing to the ethylene, the coordination mode of α-olefins is more complicated because of two non-equivalent sp² carbons. There are two manners with two enantio-faces: 1,2-insertion (primary insertion with re- and si-faces in transition state, respectively) and 2,1-insertion (secondary insertion with re- and si-faces in transition state, respectively) (Scheme 1b).³¹ Therefore, the coordination mode of the first insertion of OD was investigated primarily in this paper.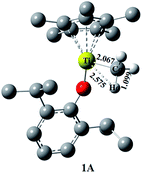

Fig. 1 Optimized structure (distances in Å) of active species 1A at chain initiation stage. Hydrogen atoms of the C₅Me₅ ligand and phenoxyl have been omitted for clarity.

Scheme 1 (a) Cossée–Arlman mechanism for α-olefin insertion; L = ligand; P = growing polymer chain; □ = open coordination site. (b) four possible transition states for α-olefin insertion.

The calculated energy profiles of four different insertions (1,2-re, 1,2-si, 2,1-re and 2,1-si) are shown in Fig. 2. It is showed that the energy barriers which 1,2-si, 1,2-re, 2,1-si, 2,1-re-insertions need to overcome are 8.88, 10.09, 13.96, 9.99 kcal mol⁻¹, respectively. The free energy barrier of 1,2-si-insertion is lowest than those of other three insertions. Furthermore, the 1,2-si-insertion process releases the maximum energy 24.43 kcal mol⁻¹, which is considered to be kinetically and thermodynamically favourable among the four different insertions. Further structural investigation shows that the vinyl of OD was activated well in 1TS_12si according to the elongated double bond (1.425 Å) (Fig. S2†). As well, the α-agostic interaction in 1TS_12si is relative strong (2.012 Å for Ti⋯Hα, 1.129 Å for Cα–Hα and 68.11° for Ti–Cα–Hα angle) to stabilize the transition state. Especially, following 1,2-si-insertion, the long chain of OD is able to extend favourably avoiding the C₅Me₅ and phenoxyl with bulky steric hindrance. Therefore, it is indicated that the first OD inserts into Ti–C bond in a 1,2-si-fashion based on structural and energetical advantage at chain initiation stage.

Fig. 2 The calculated energy profiles (energy in kcal mol⁻¹) for OD insertion at chain initiation stage.

After 1,2-si-insertion of the first OD, direct product 1P_12si containing γ-agostic interaction could rapidly rearrange to the β-agostic complex 1P′_12si through releasing energy 0.99 kcal mol⁻¹. The β-agostic interaction in 1P′_12si is stronger and more structurally favorable (2.000 Å for Ti⋯Hβ distance and 1.166 Å for Cβ–Hβ length) than the γ-agostic interaction in 1P_12si (Fig. S3†). The free energy barrier of transition state connecting 1P_12si and 1P′_12si is only 1.02 kcal mol⁻¹. Such a small energy barrier suggests that the transformation between γ-agostic and β-agostic is not a rate-determining step. Hence, it can be speculated that the β-agostic complex 1P′_12si is the secondary active species 2A for the further insertion process.³²

The proposed pathways for chain propagation process of OD are shown in Scheme 2. The competitions between repeated insertion and intramolecular cyclization were explored in three conditions, which are subsequent insertion into 2A (Path I vs. II), 3A (Path III vs. IV) and 7A (Path VI vs. VII) respectively.

Scheme 2 Possible scenarios of chain propagation process during polymerization of OD by non-bridged half-titanocene system; □ = open coordination site.

The first competition of insertions

To explore insertion selectivity of (η⁵-C₅Me₅)TiCl₂(O-2,6-ⁱPr₂C₆H₃)/MAO system, repeated insertion was investigated in the first place (Path I). Comparing to the first insertion, coordination and insertion of the second monomer are more complicated. It is assumed that the olefin monomer can insert into the central metal via front-side insertion (1,2-f- and 2,1-f-insertion) and back-side insertion (1,2-b- and 2,1-b-insertion) respectively, according to relative position between coordination direction and agostic bond (Fig. 3).¹ The calculated energy profiles of four different insertions (1,2-f-, 2,1-f-, 1,2-b- and 2,1-b-insertion) are shown in Fig. 4. According to the free energy barriers, the 1,2-insertions are superior to the 2,1-insertions with same insertion direction of OD respectively (2.21 kcal mol⁻¹ for 1,2-f-insertion vs. 9.39 kcal mol⁻¹ for 2,1-f-insertion, 9.49 kcal mol⁻¹ for 1,2-b-insertion vs. 19.05 kcal mol⁻¹ for 2,1-b-insertion). That could be attributed to the steric hindrance between C₅Me₅ ligand and growing chain. The free energy barrier of 1,2-f-insertion is much lower than that of 1,2-b-insertion. The strong α-agostic interaction, which is considered to be conducive to stabilizing the transition state, is observed in 2TS_12f, while relatively weak β-agostic interaction is in 2TS_12b (Fig. S4†).³³ Furthermore, the dihedral angle of Cα–Ti–C1–C2 in 2TS_12f is 4.32°, showing the better planarity of four-centered ring in 2TS_12f than in 2TS_12b (10.36° for dihedral angle of Cα–Ti–C1–C2). Therefore, 1,2-f-insertion is proved to be the most favorable than other three insertions due to the kinetic and geometric features during chain propagation. Namely, the second OD coordinates to the central Ti⁴⁺ from the side of the agostic bond and insert into Ti–C bond in a 1,2-fashion. However, this is in contrast to the chain propagation process of ethylene polymerization catalyzed by the non-bridged half-titanocene catalysts.^22c

Fig. 3 Optimized structure (distances in Å) of active species 2A for the second insertion process. Hydrogen atoms of the C₅Me₅ ligand and phenoxyl have been omitted for clarity.

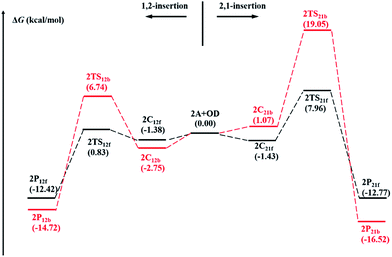Fig. 4 The calculated energy profiles of four different insertions (1,2-f-, 2,1-f-, 1,2-b-, 2,1-b-insertion) are shown.

In competition with repeated insertion of the second OD, the residual vinyl of the first OD monomer (C7=C8) in 2A could conduct intramolecular cyclization via a 1,2-fashion from the front-side attack, resulting in seven-membered ring units (Path II). The intramolecular cyclization was investigated through modeling the non-bonded interaction. There is no obvious agostic interaction in the π-complex 2C_cyc. But the strong α-agostic interaction (1.931 Å for Ti⋯Hα distance and 1.144 Å for Cα–Hα length) was observed to stabilize cyclization transition state 2TS_cyc (Fig. 5). The dihedral angle of Cα–Ti–C7–C8 is 3.58° in 2TS_cyc, demonstrating a good planarity of the four-centered ring. The cyclic structure in 2TS_cyc tends to be the twist-chair conformation, making the transition state stable. According to the calculated energy profiles (Fig. 6), the intramolecular cyclization of 2A needs to overcome a free energy barrier of 5.96 kcal mol⁻¹, which is higher than 1,2-repeated insertion via front-side attack (2.21 kcal mol⁻¹).

Fig. 5 Geometric structures (distance in Å) of OD 1,2-repeated insertion and intramolecular cyclization of 2A. Hydrogen atoms of the C₅Me₅ ligand and phenoxyl have been omitted for clarity. (a) 1,2-repeated insertion; (b) intramolecular cyclization.

Fig. 6 The calculated energy profiles (energy in kcal mol⁻¹) for 1,2-repeated insertion and the intramolecular cyclization of 2A.

However, the intramolecular cyclization process releases the energy 13.13 kcal mol⁻¹, which is a little bit more than the energy releasing of competitive repeated insertion process (12.42 kcal mol⁻¹). Summarily, the results indicate that 1,2-repeated insertion is kinetically favourable than the intramolecular cyclized insertion during the competitive insertion into 2A. The free energy barrier of intramolecular cyclization is 3.75 kcal mol⁻¹ higher than that of 1,2-repeated insertion.

The second competition of insertions

After the 1,2-repeated insertion, the direct product 2P_12f with γ-agostic interaction could isomerize into 2P′_12f with β-agostic interaction with releasing energy 1.42 kcal mol⁻¹. The 2P′_12f was considered as the further active species 3A, which would accomplish repeated insertion and cyclized insertion competitively. When repeated insertion of the third monomer accessed to 3A from the vacant site, the π-complex 3C₁₂ formed with releasing energy 2.69 kcal mol⁻¹ (Path III). The coordination of central Ti to C1 and C2 shows non-equivalent in 3C₁₂. The distance of Ti⋯C1 is 2.474 Å, while the distance of Ti⋯C2 is 3.871 Å (Fig. 7a). That is probably due to the bulky steric hindrance of long alkyl chains and the polarization of the π-orbital in OD toward the CH₂ group. Comparing to 3C₁₂, the strong α-agostic interaction can be observed in 3TS₁₂ according to the shortened Ti⋯Hα distance (from 2.613 to 1.954 Å) and the elongated Cα–Hα bond (from 1.101 to 1.142 Å). The typical four-centered ring in 3TS₁₂ shows a bit twisted with the dihedral angle of Cα–Ti–C1–C2 equal to 11.79°, larger than the dihedral angle of Cα–Ti–C1–C2 in 2TS_12f (4.32°). That might be supposed to result in the slightly higher free energy barrier of Path III (3.18 kcal mol⁻¹) than that of Path I (2.21 kcal mol⁻¹) (Fig. 6 and 8). It is found that the kinetic product 3P₁₂ with γ-agostic interaction (2.077 Å for Ti⋯Hγ).

Fig. 7 Geometric structures (distance in Å) of OD 1,2-repeated insertion and intramolecular cyclization of 3A. Hydrogen atoms of the C₅Me₅ ligand and phenoxyl have been omitted for clarity. (a) 1,2-repeated insertion; (b) intramolecular cyclization.

Fig. 8 The calculated energy profiles (energy in kcal mol⁻¹) for 1,2-repeated insertion and the intramolecular cyclization of 3A at chain propagation stage.

When the intramolecular cyclization occurred in 3A, the π-complex 3C_cyc formed with releasing energy 2.21 kcal mol⁻¹ (Path IV). The non-equivalent coordination of residual vinyl was observed (3.130 Å for Ti⋯C7 distance and 2.443 Å for Ti⋯C8 distance), similar to the process of the third monomer's insertion (Fig. 7b). The typical α-agostic interaction with 1.933 Å for Ti⋯Hα distance was observed in 3TS_cyc. The dihedral angle of Cα–Ti–C8–C7 in 3TS_cyc is 15.46°, a bit larger than that in 3TS₁₂ (11.79°), indicating relatively poorer planarity. That could be attributed to the steric hindrance and rigidity of the cyclic structure. It is found that the free energy barrier of this intramolecular cyclization to form 3TS_cyc is 7.05 kcal mol⁻¹, much higher than that of 3TS₁₂ (3.18 kcal mol⁻¹) (Fig. 8). The results indicated that the further repeated insertion of OD derived from 3A shows kinetically favorable than the intramolecular cyclization of 3A, with the gap of two free energy barriers of 3.87 kcal mol⁻¹. As well, the direct products 3P₁₂ and 3P_cyc with γ-agostic could both transform into the more stable β-agostic products 3P′₁₂ and 3P′_cyc respectively, with releasing energy.

The third competition of insertions

After cyclized insertion of the first OD, direct cyclization product 2P_cyc with γ-agostic could rapidly isomerize to more stable β-agostic product 2P′_cyc with releasing energy 0.14 kcal mol⁻¹. The 2P′_cyc with the cyclic growing chain was considered as the active species 4A for subsequent insertion. Then another OD coordinated to 4A from the front-side and inserted into Ti and cyclic growing chain (Path V). The free energy barrier of Path V is 10.21 kcal mol⁻¹, which is much higher than the free energy barrier of repeated insertion into 2A (2.21 kcal mol⁻¹) (Path I) (Fig. S5†). It indicates that after the intramolecular cyclization of the first OD, the repeated insertion of OD becomes more difficult. Furthermore, the analysis of energy (electronic energy, ΔE) decomposition was carried out in order to investigate the stability of two transition states 4TS and 2TS_12f.³⁴ The energies of the fragments including [(η⁵-C₅Me₅)Ti(O-2,6-ⁱPr₂C₆H₃)R]⁺ (X) and OD in the corresponding TSs were evaluated in single-point calculations. The energy of the TS, ΔE_TS, is evaluated with respect to the energy of the two separated fragments, according to the relation ΔE_TS = ΔE_int + ΔE_def(X) + ΔE_def(OD). In this relation, ΔE_int represents the interaction energy, which is estimated by the single-point energies of fragments and the energy of TS. ΔE_def(X) and ΔE_def(OD) represent the deformation energies of the two fragments respectively, which are estimated by the single-point energies of corresponding fragments and their energy in the optimal geometry. According to the analysis, it is found ΔE_int = −54.57 kcal mol⁻¹, ΔE_def(X) = 29.63 kcal mol⁻¹, ΔE_def(OD) = 12.24 kcal mol⁻¹, and therefore ΔE_TS = −12.70 kcal mol⁻¹ for 4TS, meanwhile, ΔE_int = −52.57 kcal mol⁻¹, ΔE_def(X) = 22.60 kcal mol⁻¹, ΔE_def(OD) = 13.24 kcal mol⁻¹, and therefore ΔE_TS = −16.73 kcal mol⁻¹ for 2TS_12f. The ΔE_TS value of −12.70 kcal mol⁻¹ for 4TS is significance larger than that for 2TS_12f (−16.73 kcal mol⁻¹) by 4.03 kcal mol⁻¹, which is similar to their difference (3.32 kcal mol⁻¹) in free energy (Part I and Part V). It is also showed that ΔE_def(X) value of 29.63 kcal mol⁻¹ in 4TS is significantly larger than that in 2TS_12f (22.60 kcal mol⁻¹) by 7.03 kcal mol⁻¹. The increased deformation energy of the fragment X could not be compensated by the ΔE_int and ΔE_def(OD) values in 4TS. Namely, the deformation of fragment X can account for the destabilization of 4TS in comparison with 2TS_12f.

The direct product 4P with γ-agostic could isomerize to 4P′ with β-agostic, which was considered as the subsequent active species 7A. If another OD coordinated to 7A via the 1,2-fashion, the complex 7C₁₂ formed, in which there was the obvious α-agostic interaction (Fig. 9a). Then, 7C₁₂ transferred into 7TS₁₂ very fast with overcoming the negligible free energy barrier of 0.36 kcal mol⁻¹ (Fig. 10). It is found the strong α-agostic interaction with 1.933 Å for Ti⋯Hα distance and 9.80° for dihedral angle Cα–Ti–C1–C2 in 7TS₁₂. With releasing energy, 7TS₁₂ transformed into 7P₁₂ with γ-agostic, which is 15.83 kcal mol⁻¹ more stable than 7A and OD. The steric interactions are minimized in 7P₁₂ through a ring-tilt, allowing the staggered orientation between long side-chain and seven-membered ring.

Fig. 9 Geometric structures (distance in Å) of OD repeated insertion into 7A and intramolecular cyclization of 7A at chain propagation stage. Hydrogen atoms of the C₅Me₅ ligand, phenoxyl and seven-membered ring of the growing chain have been omitted for clarity. (a) repeated insertion; (b) intramolecular ​cyclization.

Fig. 10 The calculated energy profiles (energy in kcal mol⁻¹) for the cyclization and repeated insertion into 7A at chain propagation stage.

Similar to the active species 3A, intramolecular cyclization of 7A took place via the vacant site. The π-complex 7C_cyc formed after coordination with absorbing energy 5.21 kcal mol⁻¹, indicating the coordination relatively tough. That might due to the steric hindrance between two cyclic structures. The α-agostic interaction with Ti⋯Hα distance 2.018 Å and Cα–Hα length 1.141 Å was observed in 7C_cyc (Fig. 9b). The transition state 7TS_cyc generated from 7C_cyc by overcoming the energy barrier of 7.79 kcal mol⁻¹ and the cyclization process completed by releasing energy 8.30 kcal mol⁻¹. Therefore, it is found that such an intramolecular cyclization (Path VII) is rather less favorable than the competitive repeated insertion (Path VI) kinetically and thermodynamically. Moreover, the cyclized insertion into the growing chain derived from repeated insertion (Path IV) shows energetically easier than into the cyclic growing chain (Path VII), probably due to the steric repulsion effect between two cyclic rings.

Conclusions

The selectivity of repeated insertion and cyclized insertion of OD in (η⁵-C₅Me₅)TiCl₂(O-2,6-ⁱPr₂C₆H₃)/MAO system was investigated by using DFT method. At chain initiation stage, the 1,2-si-insertion of the first OD showed kinetically and thermodynamically favourable than 1,2-si-, 2,1-re- and 2,1-si-insertions. At chain propagation stage, comparison and analysis of three insertion competitions show that this system tends to conduct repeated insertion of OD comparing to the competitive intramolecular cyclization kinetically, with the free energy barrier differences between two insertion modes of 3.75 kcal mol⁻¹, 3.88 kcal mol⁻¹ and 7.43 kcal mol⁻¹ respectively. Especially, the repeated insertion into 7A took place much more easily than intramolecular cyclization of 7A kinetically and thermodynamically, showing relatively fewer repeated cyclic units in the resultant polymer. That is due to the steric repulsion effect between two cyclic rings probably. The computational results are in good agreement with the experimental data, which is the resultant polymer containing predominant vinyl groups. This study could enrich the comprehension of the polymerization mechanism of non-bridged half-titanocene system, and help understand better the insertion selectivity of the polymerization of non-conjugated dienes.

Acknowledgements

We gratefully acknowledge Prof. Yi Luo for discussion of computational method and polymerization mechanism and Dr Yang Li for her suggestion for revision of the manuscript. This work was supported by the National Natural Science Foundation of China (No. 21404018, 21503030) and the China Postdoctoral Science Foundation (No. 2014M561233). G. He gratefully acknowledges the Chang Jiang Scholar Program (No. T2012049).

Notes and references

1. A. L. McKnight and R. M. Waymouth, Chem. Rev., 1998, 98, 2587.
2. I. Kim, in Stereoselective Polymerization with Sigle-Site Catalysts, ed. L. S. Baugh and J. A. M. Canich, CRC Press, Boca Raton, 2008, p. 489.
3. For cyclic olefin copolymers, see the selected reviews: (a) X. Li and Z. Hou, Coord. Chem. Rev., 2008, 252, 1842; (b) G. W. Coates, Chem. Rev., 2000, 100, 1223.
4. For modification of polyolefins, see the selected reviews: (a) S. B. Amin and T. J. Marks, Angew. Chem., Int. Ed., 2008, 47, 2006; (b) M. Jaymand, Polym. Chem., 2014, 5, 2663.
5. (a) C. S. Marvel and J. K. Stille, J. Am. Chem. Soc., 1958, 80, 1740; (b) C. S. Marvel and W. E. Garrison Jr, J. Am. Chem. Soc., 1959, 81, 4737.
6. (a) E. Ihara, M. Nodono, K. Katsura, Y. Adachi, H. Yasuda, M. Yamagashira, H. Hashimoto, N. Kanehisa and Y. Kai, Organometallics, 1998, 17, 3945; (b) K. C. Hultzsch, P. Voth, K. Beckerle, T. P. Spaniol and J. Okuda, Organometallics, 2000, 19, 228; (c) J. B. Edson and G. W. Coates, Macromol. Rapid Commun., 2009, 30, 1900; (d) F. Guo, M. Nishiura, H. Koshino and Z. Hou, Macromolecules, 2011, 44, 6335; (e) S. Han, E. Yao, W. Qin, S. Zhang and Y. Ma, Macromolecules, 2012, 45, 4054; (f) Y. Pan, T. Xu, Y.-S. Ge and X.-B. Lu, Organometallics, 2011, 30, 5687.
7. (a) D. Takeuchi, R. Matsuura, S. Park and K. Osakada, J. Am. Chem. Soc., 2007, 129, 7002; (b) D. Takeuchi, R. Matsuura and K. Osakada, Macromol. Rapid Commun., 2008, 29, 1932; (c) F. Guo, M. Nishiura, H. Koshino and Z. Hou, Macromolecules, 2011, 44, 2400; (d) K. E. Crawford and L. R. Sita, J. Am. Chem. Soc., 2013, 135, 8778.
8. W. Apisuk and K. Nomura, Macromol. Chem. Phys., 2014, 215, 1785.
9. Y. Doi, N. Tokuhiro and K. Soga, Macromol. Chem., 1989, 190, 643.
10. (a) N. Naga, T. Shiono and T. Ikeda, Macromolecules, 1999, 32, 1348; (b) N. Naga, T. Shiono and T. Ikeda, Macromol. Chem. Phys., 1999, 200, 1466.
11. N. Naga and A. Toyota, Macromol. Rapid Commun., 2004, 25, 1623.
12. (a) P. D. Hustad and G. W. Coates, J. Am. Chem. Soc., 2002, 124, 11578; (b) R. T. Mathers and G. W. Coates, Chem. Commun., 2004, 422.
13. B. Wang, Y.-X. Wang, J. Cui, Y.-Y. Long, Y.-G. Li, X.-Y. Yuan and Y.-S. Li, Macromolecules, 2014, 47, 6627.
14. F. Guo, R. Meng, Z.-H. Shi and R. Tan, Acta Polym. Sin., 2014, 1219.
15. (a) K. Nomura, N. Naga, M. Miki, K. Yanagi and A. Imai, Organometallics, 1998, 17, 2152; (b) K. Nomura, N. Naga, M. Miki and K. Yanagi, Macromolecules, 1998, 31, 7588.
16. For homo- and/or copolymerization of olefins by using non-bridged half-metallocene titanium complexes, see the selected reviews: (a) K. Nomura, J. Liu, S. Padmanabhan and B. Kitiyanan, J. Mol. Catal. A: Chem., 2007, 267, 1; (b) K. Nomura, Dalton Trans., 2009, 8811; (c) K. Nomura, J. Synth. Org. Chem., Jpn., 2010, 68, 1150; (d) K. Nomura and J. Liu, Dalton Trans., 2011, 40, 7666; (e) K. Nomura, Catalysts, 2013, 3, 157.
17. (a) K. Nomura, Y. Hatanaka, H. Okumura, M. Fujiki and K. Hasegawa, Macromolecules, 2004, 37, 1693; (b) K. Nomura, K. Nomura, Y. Hatanaka, H. Okumura, M. Fujiki, K. Hasegawa, Y. Hatanaka, H. Okumura, M. Fujiki and K. Hasegawa, Macromolecules, 2006, 39, 4009.
18. K. Nomura, J. Liu, M. Fujiki and A. Takemoto, J. Am. Chem. Soc., 2007, 129, 14170.
19. (a) L. Fan, D. Harrison, T. K. Woo and T. Ziegler, Organometallics, 1995, 14, 2018; (b) T. K. Woo, P. M. Margl, J. C. W. Lohrenz, P. E. Blöchl and T. Ziegler, J. Am. Chem. Soc., 1996, 118, 13021; (c) M. Linnolahti and T. A. Pakkanen, Macromolecules, 2000, 33, 9205; (d) G. Moscardi and L. Resconi, Organometallics, 2001, 20, 1918; (e) G. Minieri, P. Corradini, A. Zambelli, G. Guerra and L. Cavallo, Macromolecules, 2001, 34, 2459; (f) G. Lanza, I. L. Fragala and T. J. Marks, Organometallics, 2002, 21, 5594; (g) G. Guerra, P. Corradini and L. Cavallo, Macromolecules, 2005, 38, 3973; (h) S. H. Yang, J. Huh and W. H. Jo, Organometallics, 2006, 25, 1144; (i) T. de Bruin, P. Raybaud and H. Toulhoat, Organometallics, 2008, 27, 4864; (j) J. Saßmannshausen, Dalton Trans., 2009, 8993; (k) F. Sauriol, J. F. Sonnenberg, S. J. Chadder, A. F. Dunlop-Brière, M. C. Baird and P. H. M. Budzelaar, J. Am. Chem. Soc., 2010, 132, 13357; (l) G. Ciancaleoni, N. Fraldi, R. Cipullo, V. Busico, A. Macchioni and P. H. M. Budzelaar, Macromolecules, 2012, 45, 4046; (m) A. F. Dunlop-Brière, M. C. Baird and P. H. M. Budzelaar, J. Am. Chem. Soc., 2013, 135, 17514; (n) A. F. Dunlop-Brière, M. C. Baird and P. H. M. Budzelaar, Organometallics, 2015, 34, 2356; (o) A. F. Dunlop-Brière, M. C. Baird and P. H. M. Budzelaar, Organometallics, 2015, 34, 5245; (p) T. A. Manz, RSC Adv., 2015, 5, 48246; (q) L. Castro, E. Kirillov, O. Miserque, A. Welle, L. Haspeslagh, J.-F. Carpentier and L. Maron, ACS Catal., 2015, 5, 416; (r) G. Talarico and P. H. M. Budzelaar, Organometallics, 2016, 35, 47; (s) J. Tian, X. He, J. Liu, X. Deng and D. Chen, RSC Adv., 2016, 6, 22908.
20. (a) D. G. Musaev, R. D. J. Froese, M. Svensson and K. Morokuma, J. Am. Chem. Soc., 1997, 119, 367; (b) L. Deng, P. Margl and T. Ziegler, J. Am. Chem. Soc., 1997, 119, 1094; (c) R. D. J. Froese, D. G. Musaev and K. Morokuma, J. Am. Chem. Soc., 1998, 120, 1581; (d) S. Tobisch, J. Am. Chem. Soc., 2004, 126, 259; (e) R. Raucoules, T. de Bruin, P. Raybaud and C. Adamo, Organometallics, 2009, 28, 5358; (f) R. Raucoules, T. de Bruin, C. Adamo and P. Raybaud, Organometallics, 2011, 30, 3911.
21. (a) L. Perrin, Y. Sarazin, E. Kirillov, J.-F. Carpentier and L. Maron, Chem.–Eur. J., 2009, 15, 3773; (b) L. Perrin, E. Kirillov, J.-F. Carpentier and L. Maron, Macromolecules, 2010, 43, 6330; (c) Y. Luo, Y. Luo, J. Qu and Z. Hou, Organometallics, 2011, 30, 2908; (d) X. Kang, Y. Song, Y. Luo, G. Li, Z. Hou and J. Qu, Macromolecules, 2012, 45, 640; (e) X. Li, X. Wang, X. Tong, H. Zhang, Y. Chen, Y. Liu, H. Liu, X. Wang, M. Nishiura, H. He, Z. Lin, S. Zhang and Z. Hou, Organometallics, 2013, 32, 1445; (f) X. Kang, Y. Luo, G. Zhou, X. Wang, X. Yu, Z. Hou and J. Qu, Macromolecules, 2014, 47, 4596; (g) B. Liu, X. Wang, Y. Pan, F. Lin, C. Wu, J. Qu, Y. Luo and D. Cui, Macromolecules, 2014, 47, 8524; (h) X. Kang, A. Yamamoto, M. Nishiura, Y. Luo and Z. Hou, Organometallics, 2015, 34, 5540; (i) M. Zhang, Z. Liang, J. Ling, X. Ni and Z. Shen, Dalton Trans., 2015, 44, 11182; (j) F. Lin, X. Wang, Y. Pan, M. Wang, B. Liu, Y. Luo and D. Cui, ACS Catal., 2016, 6, 176; (k) G. Luo, Y. Luo, Z. Hou and J. Qu, Organometallics, 2016, 35, 778; (l) X. Kang, G. Zhou, X. Wang, J. Qu, Z. Hou and Y. Luo, Organometallics, 2016, 35, 913.
22. (a) C. Beddie, E. Hollink, P. Wei, J. Gauld and D. W. Stephan, Organometallics, 2004, 23, 5240; (b) W. Wang, T. Tanaka, M. Tsubota, M. Fujiki, S. Yamanaka and K. Nomura, Adv. Synth. Catal., 2005, 347, 433; (c) T.-J. Kim, S.-K. Kim, B.-J. Kim, J. S. Hahn, M.-A. Ok, J. H. Song, D.-H. Shin, J. Ko, M. Cheong, J. Kim, H. Won, M. Mitoraj, M. Srebro, A. Michalak and S. O. Kang, Macromolecules, 2009, 42, 6932; (d) T.-J. Kim, S.-K. Kim, B.-J. Kim, H.-J. Son, J. S. Hahn, M. Cheong, M. Mitoraj, M. Srebro, Ł. Piękoś, A. Michalak and S. O. Kang, Chem.–Eur. J., 2010, 16, 5630; (e) M. Srebro, Ł. Piękoś, A. Michalak, T.-J. Kim, S. O. Kang, M. Cheong and M.-A. Ok, Macromol. Res., 2010, 18, 960.
23. X.-C. Shi, Y.-X. Wang, J.-Y. Liu, D.-M. Cui, Y.-F. Men and Y.-S. Li, Macromolecules, 2011, 44, 1062.
24. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (b) A. D. Becke, J. Chem. Phys., 1986, 84, 4524; (c) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
25. (a) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270; (b) W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284; (c) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299.
26. H. B. Schlegel, J. Comput. Chem., 1982, 3, 214.
27. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
28. (a) M. Dolg, U. Wedig, H. Stoll and H. Preuss, J. Chem. Phys., 1987, 86, 866; (b) P. Schwerdtfeger, M. Dolg, W. H. E. Schwarz, G. A. Bowmaker and P. D. W. Boyd, J. Chem. Phys., 1989, 91, 1762.
29. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford CT, 2010.
30. (a) P. Cossée, J. Catal., 1964, 3, 80; (b) E. J. Arlman, J. Catal., 1964, 3, 89; (c) E. J. Arlman and P. Cossée, J. Catal., 1964, 3, 99; (d) M. Brookhart and M. L. H. Green, J. Organomet. Chem., 1983, 250, 395; (e) L. Fan, D. Harrison, T. K. Woo and T. Ziegler, Organometallics, 1995, 14, 2018.
31. L. Resconi, L. Cavallo, A. Fait and F. Piemontesi, Chem. Rev., 2000, 100, 1253.
32. For other isomerizations of active species, see: (a) J. C. W. Lohrenz, T. K. Woo and T. Ziegler, J. Am. Chem. Soc., 1995, 117, 12793; (b) R. D. J. Froese, D. G. Musaev, T. Matsubara and K. Morokuma, J. Am. Chem. Soc., 1997, 119, 7190; (c) S. F. Vyboishchikov, D. G. Musaev, R. D. J. Froese and K. Morokuma, Organometallics, 2001, 20, 309; (d) V. A. Karttunen, M. Linnolahti, T. A. Pakkanen, J. R. Severn, E. Kokko, J. Maaranen and P. Pitkanen, Organometallics, 2008, 27, 3390.
33. (a) M. H. Prosenc, C. Janiak and H. H. Brintzinger, Organometallics, 1992, 11, 4036; (b) R. H. Grubbs and G. W. Coates, Acc. Chem. Res., 1996, 29, 85.
34. K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra14867k

---