Colossal dielectric performance of pure barium titanate ceramics consolidated by spark plasma sintering
X. Yanga,
D. Lib,
Z. H. Ren*a,
R. G. Zengcd,
S. Y. Gonga,
D. K. Zhoua,
H. Tiand,
J. X. Lid,
G. Xu*a,
Z. J. Shen*b and
G. R. Hana
aSchool of Materials Science and Engineering, Zhejiang University, Hangzhou 310027, P. R. China. E-mail: renzh@zju.edu.cn; msegxu@zju.edu.cn; Fax: +86-571-87952341; Tel: +86-571-87952341
bDepartment of Materials and Environmental Chemistry, Arrhenius Laboratory, Stockholm University, S-106 91 Stockholm, Sweden. E-mail: shen@mmk.su.se
cScience and Technology on Surface Physics and Chemistry Laboratory, P. O. Box 718-35, Mianyang 621907, P. R. China
dCenter of Electron Microscopy, Zhejiang University, Hangzhou 310027, P. R. China
First published on 2nd August 2016
Abstract
A facile sol–gel-hydrothermal method was developed to prepare well-dispersed BaTiO3 (BT) nanocrystals with a size of about 20 nm. By using such nanopowder, dense BT nanoceramics were densified via spark plasma sintering (SPS). Dielectric measurements reveal that pure BT nanoceramics have an extremely high permittivity up to 6 × 104 and a low dielectric loss. On the basis of microstructure characterization and dielectric measurement, it was proposed that the polaron dipoles configured by oxygen vacancies and Ti3+ cations within the grains could contribute to the colossal dielectric permittivity of the ceramics. By using the thermally activated polaron hopping model, a large activation energy EA has been determined (0.135 eV) below the Curie temperature, possibly due to the coupling of polaron dipoles and intrinsic ferroelectric dipoles. This simple method offers the possibility to produce pure BT nanoceramics with a colossal permittivity.
Introduction
Owing to a high dielectric constant, ferroelectric barium titanate (BaTiO3, BT) has found many applications in various electronic devices, highly attractive for the usage in multilayer ceramic capacitors (MLCC).1 As the size of device is reduced, there is a growing demand for BT nanoceramics with a high dielectric constant. For example, the thickness of MLCC layers has been reduced to around 1 μm recently, and it is highly desirable to achieve several hundred nanometers.2 In recent years, there has been an increasing interest in developing BT ceramics with an average grain size well below 100 nm. However, it remains a great challenge to prepare BT ceramics with enhanced performance for MLCCs, and the difficulty arises from the fact that the ferroelectric and dielectric properties suffer degradation when the size of particles is reduced into nanoscale.To obtain high-performance BT nanoceramics, the key step is to prepare BT powders (the raw material) with controlled stoichiometry, uniformity and fine particle size. Currently, there are two prevailing methods to synthesize BT powders, i.e., solid phase3–6 and liquid phase methods.7–12 Traditional solid phase method requires high sintering temperatures that may cause serious agglomeration and coarse grains. The liquid phase routes include co-precipitation,7,8 microemulsion9 and hydrothermal methods.10–12 Among them, the first two methods still require a high sintering temperature, which will also result in large particle size. In contrast, the hydrothermal process combined with sol–gel method has been demonstrated to be an effective way to synthesize high purity, uniform, ultrafine, well-dispersed BT powder at low temperature, providing a prerequisite for preparing BT nanoceramics.13,14
Also, sintering is a critical processing step for obtaining dense ceramics with high performance. BT ceramics consolidated by conventional sintering approaches always have a low relative permittivity, with a range from 4000 to 6000.15,16 In comparison, spark plasma sintering (SPS) can produce well densified ceramics with fine microstructure due to a high heating rate, lower sintering temperature and shorter dwell time needed.17–21 The relative permittivity of SPSed BT ceramics is up to 3000–8000.22,23 To improve the permittivity of BT ceramics, several methods were developed, including the substitution of a small amount of lanthanum in the perovskite lattice,24,25 and fabricating core–shell architecture or a metallic layers on BT grain.26–29 However, the main drawback of them is the complexity and uncontrollability of the process that always leads to a large fluctuation in the overall performance of the material. Until now, pure-phase BT ceramics with colossal permittivity have been rarely reported.
In this work, well-dispersed BT nanoparticles with amorphous layer and a size of 10–40 nm were synthesized by a sol–gel-hydrothermal method. By using such nanopowders, dense BT nanoceramics were consolidated through SPS. The obtained BT ceramics showed extremely high permittivity up to 6 × 104, with relatively low dielectric below 0.058. Temperature dependence of dielectric properties and loss tangent at different frequencies were evaluated. A mechanism, based on the thermally activated hopping polaron dipoles and their coupling with intrinsic ferroelectric dipoles was proposed to explain the colossal dielectric permittivity.
Experimental procedures
The chemical reagents used in the work were barium acetate [Ba(CH3COO)2] (Shanghai Silian Chemical Co., Ltd.), tetrabutyl titanate [Ti(OC4H9)4] (Sinopharm Chemical Reagent Co., Ltd.), nitric acid (HNO3) (Zhejiang Zhongxing Chemical Reagent Co., Ltd.) and potassium hydroxide (KOH) (Sinopharm Chemical Reagent Co., Ltd.). All the chemicals have analytical grade purity and were used in their original forms without further purification. To synthesize BT nanoparticles, tetrabutyl titanate (0.005 mol), nitric acid (0.004 mol), hydrolysis inhibitor (0.002 mol) and deionized water (25 ml) were mixed together. The mixture was then incubated in a water bath (60 °C) with constantly vigorous stirring for 10 h and a homogeneous sol was formed. The obtained gel and barium acetate were used as the precursors to introduce the 0.015 mol Ba and 0.005 mol Ti cations into the solution. Potassium hydroxide was added as a mineralizer. The concentration of the KOH solution was 8 M. The hydrothermal treatment was performed in an autoclave at 200 °C for 6 h. The products were filtered and washed several times with distilled water and absolute ethanol and finally oven-dried in air at 80 °C for 12 h to obtain white powders for further characterization.Consolidation of the BaTiO3 nanopowders was carried out in a SPS apparatus (Dr Sinter 2050, Sumitomo Coal Mining Co., Tokyo, Japan). In a typical cycle, BaTiO3 nanopowder with a mass of 1.1 g was loaded in a cylindrical graphite die with an inner diameter of 12 mm. Four sintering regimes were performed, referred as BT-1, BT-2, BT-3 and BT-4, respectively. The temperature was automatically raised to 650 °C (BT-1) or 600 °C (BT-2, BT-3, and BT-4) over a period of 6 min (BT-1) or 3 min (BT-2, BT-3, and BT-4). Then the samples were heated to different sintering temperatures (950–1100 °C) with a heating rate of 50 °C min−1 and dwell time of 3 min and naturally cooled down to room temperature. A radiation pyrometer, focused on the bottom of a deep hole drilled on the wall of the graphite die that is only 2 mm away from the center of the powder compacts, was employed for monitoring the temperature. For all the experiments, a uniaxial pressure of 40–100 MPa was applied at room temperature and held constant from the beginning till the end of the sintering cycles. Finally, all the samples were annealed in air at 550 °C for 5 h in order to remove the residual carbon on the surfaces. The densitometer was employed to measure the relative density of BT ceramics (GH-120D, Xiamen qunlong Instrument Co. Ltd., China). The heating rate, sintering temperature mechanical pressure values and relative density are listed in Table 1.
| Sample name | BT-1 | BT-2 | BT-3 | BT-4 |
|---|---|---|---|---|
| Heating rate (°C min−1) | 50 | 50 | 50 | 50 |
| Sintering T (°C) | 950 | 1100 | 1050 | 1050 |
| Pressure (MPa) | 40 | 50 | 75 | 100 |
| Relative density | 95.4% | 94.3% | 96.8% | 96.4% |
Crystalline phase composition was determined by an X-ray diffractometer (XRD, D/max-RA, Rigaku Corporation, Japan) using CuKα radiation (λ = 1.5418 Å) over a 2θ range of 10–90° at room temperature. Microstructural investigations were conducted by using a scanning electron microscope (SEM, MODEL S-480, Hitachi, Japan) and a transmission electron microscope (TEM, F20, FEI, USA) with an accelerating voltage of 200 kV. Raman spectra were obtained by using a micro-Raman spectrometer (inVia, Renishaw, UK) with a Nd:YAG laser (532 nm). X-ray photoelectron spectroscopy (XPS) was carried out by Thermo ESCALAB 250Xi using a monochromatized Al Kα (hν = 1486.6 eV, 150 W) radiation. Scanning transmission electron microscopy (STEM) and electron energy loss spectroscopy (EELS) were obtained by using spherical aberration correction transmission electron microscope (FEI Titan G2 80-200 ChemiSTEM, FEI, USA). The BT-1 sample was polished by precision ion polishing system (PIPS, II 695, GATAN, USA).
The frequency spectra of complex permittivity of the materials were measured by a precision impedance analyzer (Agilent 4294 A) over the frequency range from 40 Hz to 110 MHz. Prior to it, the samples were well-polished and Ag electrodes were formed on both surfaces from Ag paint by heat-treated at 550 °C for 10 min.
Results and discussions
The XRD pattern of the as-synthesized powder is shown in Fig. 1a. All the diffraction peaks can be indexed to cubic BT (JCPDS 31-0174). No peaks from other phases are detected, implying a high purity of the single-phase BT powder. Fig. 1b shows a XRD pattern selected from literature30 as a comparison with that of BT powder in this work. On the basis of result in Fig. 1, the phase reported here agrees well with that of BaTiO3 powder in the literature.30 Fig. 1c shows SEM image of the BT powder. It can be observed that the powder consists of well-dispersed BT nanoparticles with a spherical morphology and a size of 10–40 nm. Fig. 1d and e are the HRTEM images of the BT nanoparticle. An amorphous layer can be observed clearly on the surface of the nanoparticle. In contrast, within the nanoparticle, the regular interplanar spacing of the observed lattice is 0.276 nm, as shown in Fig. 1e which is an enlarged image of the rectangular area in Fig. 1d. Index of this spacing confirmed the (110) plane of the cubic BT. | ||
| Fig. 1 Characterizations of the as-prepared BaTiO3 nanoparticles by a sol–gel-hydrothermal method, (a) XRD pattern, (c) SEM image, (d) and (e) HRTEM images of the BaTiO3 nanoparticles, (b) XRD pattern of the as-prepared BaTiO3 sample synthesized by the hydrothermal process at 200 °C for 6 h with 0.1 M KOH.30 | ||
The XRD patterns of our samples and standard PDF card of BT are together shown in Fig. 2. All peaks of the patterns can be indexed into tetragonal (JCPDF 05-0626) and cubic (JCPDF 31-0174) perovskite BT without any impurity. As shown in Fig. 2b, the enlarged peaks at 45–46° suggest a pseudo-cubic perovskite structure of the ceramics without the characteristic splitting of the tetragonal BT. This is due to the existence of a small spontaneous lattice strain in the ceramics in addition to the broadening effect related to the small grain size.31
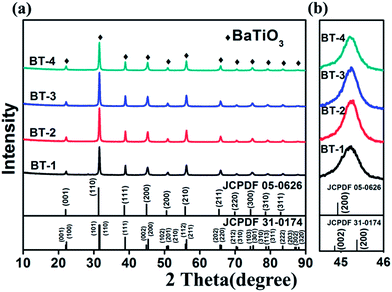 | ||
| Fig. 2 XRD patterns of (a) the as-sintered BaTiO3 ceramics and (the tetragonal (JCPDF 05-0626) and cubic (JCPDF 05-0626) PDF card of BaTiO3), (b) enlarged diffraction peak pattern at around 45.2°. | ||
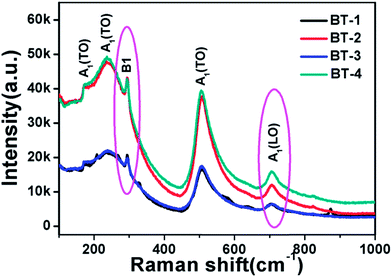
In order to verify the existence of tetragonal phase in BT ceramics, Raman spectroscopy was used to check the presence of Raman-active modes. As shown in Fig. 3, the Raman peaks at around 715 cm−1 and 298 cm−1 are identified as the characteristic peaks of tetragonal BT.32,33 The typical sharp band at around 298 cm−1 corresponds to the asymmetrical vibration mode of TiO6 octahedra.34 The peak at about 715 cm−1 is related to the highest frequency longitudinal optical mode (LO) of A1 symmetry of TiO6 octahedron, and is also an implication for the eventual Ba2+ defects in the BT lattice.35 These results reveal the existence of tetragonal distortion in the BT ceramics, which are in good agreement with the XRD patterns.
Table 1 lists the relative density values of the sintered samples, and the SEM images of their fracture surfaces are shown in Fig. 4. It can be seen that BT-3 and BT-4 possessed the highest sintered densities (96.8% & 96.4%), owing to the high sintering temperature and pressure applied. The high pressure also suppressed the grain growth as their grain size are estimated to be 10–50 nm for BT-3 and 10–20 nm for BT-4, the grain size in BT-3 and BT-4 is much smaller than that the average grain size was determined to be ∼300 nm in the literature.25 Sample BT-2 is the least dense one with a relative density of 94.3%. The highest sintering temperature (1100 °C) led to significantly coarser grains (80–500 nm) compared with others. The relative density of sample BT-1 is 95.4% with a grain size of 20 nm to 1 μm because of the lowest sintering temperature (950 °C). All the results show that the relative density and microstructure of the samples can be tuned by varying sintering parameters (temperature, pressure, etc.).
 | ||
| Fig. 4 SEM images of the fracture surfaces of the as-sintered BT ceramics. (a) BT-1, (b) BT-2, (c) BT-3, and (d) BT-4. | ||
The dielectric properties of the BT ceramics were measured and discussed. Fig. 5 shows the frequency dependence of dielectric permittivity (εr) for different samples at room temperature. All samples have a good stability of the permittivity in the wide frequency range from 40 Hz to 10 kHz, and the dielectric constant at low frequency is up to 104. For BT-1, BT-2, BT-3 and BT-4, the maximum values of the dielectric constant are 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700, 38
700, 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 58
000, 58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 and 35
400 and 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300, respectively. In comparison, the dielectric constants of these BT samples at 1 kHz are nearly 5–11 times higher than the previously reported values (3500, <1000, 5000, 3800 and 4000).36–40 To the best of our knowledge, the present values could be the highest among the reported for the pure-phase BT ceramics.
300, respectively. In comparison, the dielectric constants of these BT samples at 1 kHz are nearly 5–11 times higher than the previously reported values (3500, <1000, 5000, 3800 and 4000).36–40 To the best of our knowledge, the present values could be the highest among the reported for the pure-phase BT ceramics.
 | ||
| Fig. 5 Frequency dependence of permittivity (solid line) and loss tangent (dash line) for (a) BT-1, (b) BT-2, (c) BT-3 and (d) BT-4 at room temperature. | ||
Normally, the dielectric constants at low frequency (<1 kHz) increased with increasing relative density. However, the dielectric constant of sample BT-4 at low frequency is slightly lower than sample BT-2, which could be attributed to the smaller grain size of sample BT-4 compared with that of sample BT-2 (“size effect”).41 The results indicate that fine grain and high relative density should be beneficial for improving the dielectric constant. The relaxation frequency is about 100 kHz for BT-2 and BT-4, 300 kHz for BT-3, and 1 MHz for BT-1. The corresponding mechanism for sample BT-1 should be a typical ferroelectric dipole relaxation, whereas for other samples an additional relaxation mechanism such as defects is possible. At the same time, the corresponding dielectric losses (loss tangent, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) for different samples as a function of frequency at room temperature are also shown in Fig. 5. The dielectric loss peak frequency is consistent to the relaxation frequency. The minimum losses of BT-1, BT-2, BT-3, and BT-4 are 0.0379, 0.044, 0.04 and 0.058, respectively. It should be noted that the dielectric loss of all samples in the range of 50–1 kHz gradually decreased and thus grew at high frequency downward. Such phenomenon could be toughly related to the space charge relaxation due to oxygen defects and ferroelectric polarization relaxation.
δ) for different samples as a function of frequency at room temperature are also shown in Fig. 5. The dielectric loss peak frequency is consistent to the relaxation frequency. The minimum losses of BT-1, BT-2, BT-3, and BT-4 are 0.0379, 0.044, 0.04 and 0.058, respectively. It should be noted that the dielectric loss of all samples in the range of 50–1 kHz gradually decreased and thus grew at high frequency downward. Such phenomenon could be toughly related to the space charge relaxation due to oxygen defects and ferroelectric polarization relaxation.
Different mechanisms have been proposed to discuss the colossal dielectric performance of BT ceramics. Generally, grain boundaries (GB), domain walls and inhomogeneity are critical factors to influence the dielectric constants of the ceramics. Oyama et al.42 showed that the grain boundaries will limit the diffusion of oxygen vacancies, particularly in fine-grained ceramics. Oxygen vacancies associated with Ti3+ cations were present in the powders/ceramics and their localizations at grain boundaries have been suggested to be the key factor to control the dielectric properties.43 It is important to note that device fabrication with high-κ dielectrics favors amorphous layers.44 Recently, Jiang et al.45 found an increase in the dielectric constant as a function of decreasing the particle size of PbTiO3. The reason was the presence of an amorphous surface layer and surface energy associated with domain walls.46 In addition, the presence of an amorphous layer of SrTiO3 prepared hydrothermally resulted in the anomalous dielectric behavior of the SrTiO3 nanocrystals.47 Accordingly, we assumed that the amorphous layers of the as-sintered BT nanoparticles could facilitate the rapid formation of GB with fine grains. This offers the field for the numerous oxygen vacancies to be concentrated. These oxygen vacancies can act as blocking barriers against any further oxygen diffusion. Additionally, intrinsic ferroelectric dipole and defect dipole existing on the GB may also contribute to the colossal dielectric permittivity of the BT ceramics.
According to the results shown in Fig. 5, the dielectric property of BT-1 is the best among all the four samples, and thus was chosen for further characterization. Fig. 6a and b show HAADF-STEM images of BT-1, where grain boundaries are clearly observed and the grains grew up during the sintering process rather than aggregation by small nanoparticles. Electron energy loss spectra (EELS) of Ti across the grain boundary were collected along the area marked with green line (see Fig. 6b). Experimental EELS spectra of position located at 1, 2 and 3 were fitted by standard EELS spectra of Ti3+ (green curve) and Ti4+ (pink curve) (see Fig. 6c). The percentage of Ti4+, Ti3+ and Ti3+/Ti4+ ratio at 1, 2 and 3 are listed in Table 2. In addition, by the same method, the percentage of Ti3+, Ti4+ and Ti3+/Ti4+ ratio along the green line were depicted in Fig. 6d. According to the results in Table 2 and Fig. 6d, Ti3+ ions indeed exist within grain and at grain boundary. Particularly, large-scale Ti3+ ions are located within grain considering its size compared to that of grain boundary.
| Location | Ti3+ (%) | Ti4+ (%) | Ti3+/Ti4+ |
|---|---|---|---|
| 1 | 33.7 | 44.5 | 0.758 |
| 2 | 29.9 | 44.9 | 0.666 |
| 3 | 33.9 | 49.9 | 0.679 |
Moreover, X-ray photoelectron spectroscopy (XPS) was used to examine the valence state of the elements in BT ceramics. Fig. 7 shows the XPS narrow scanning spectra of Ba 3d and Ti 2p peaks of BT-1. All of the binding energies at various peaks were calibrated using that of C 1s (284.04 eV), and each component peak in the spectra was fitted with Lorentzian curves. As shown in Fig. 7a, the 5/2 and 3/2 spin–orbit doublet components of the Ba 3d photoelectron are located at about 780.97 eV and 796.31 eV, respectively. In Fig. 7b, the two peaks locating at 459.08 eV and 465.18 eV can be ascribed to Ti 2p peaks. The deconvolution of the slightly broad peak centered at 459.04 eV indicates the existence of an additional peak at around 457.86 eV. Similarly, the peak located at 463.64 eV is associated with the one at 465.18 eV. Both of them proved the co-existence of Ti3+ and Ti4+, which is in good agreement with the EELS results. Ti3+ species was also present in BT powder in the literature,48 two additional peaks located at 456.8 eV and 462.0 eV, which are ascribed to Ti3+ 2p3/2 and Ti3+ 2p1/2 peaks, are identified, suggesting the presence of Ti3+ species. In addition, the two peaks located at 457.9 eV and 463.6 eV can be assigned to the core levels of Ti4+ 2p3/2 and Ti4+ 2p1/2, respectively. The difference of binding energy for Ti 2p in our samples and the reported one is possibly due to the sample preparation and processing. The presence of Ti3+ probably give rise to the observed colossal permittivity, such as small polarons of electronic hopping of Ti3+/Ti4+ within the grain. It has also been found in Ba0.95La0.05TiO3−x ceramics.25
Temperature dependence of dielectric properties and loss tangent of the BT-1 at different frequencies are shown in Fig. 8. At the same temperature, the dielectric constant and loss tangent decreased with increasing frequency, and the corresponding dielectric peaks are gradually broadened with increasing frequency, indicating the occurrence of a diffuse phase transition.49 Generally, the degree of diffuse phase transition is enhanced with decreasing of grain size,50,51 which could be the reason for the enhanced diffusion of phase transition in our experiment. Generally, the temperature corresponding to the dielectric peak is considered to be the phase transition temperature. The phase transition temperature of sample BT-1 at different frequency is listed in Table 3. It shows that the phase transition temperature of BT-1 decreased with increasing frequency. At the frequency of 1 kHz, the Curie temperature of BT-1 is 144 °C, higher than the empirical value (120 °C). The increasing in Curie temperature may be caused by the smaller grain size.50 In the paraelectric region at 1 kHz, the permittivity of ceramics closely follows the Curie–Weiss (C–W) law at 143 °C. Two temperatures are very close, indicating that diffuse phase transition took place in the BT ceramics.
 | ||
| Fig. 8 Temperature dependence of (a) permittivity and (b) loss tangent measured at different frequencies for sample BT-1. | ||
| Frequency | 1 kHz | 5 kHz | 10 kHz | 50 kHz | 100 kHz |
| Temperature (°C) | 144 | 144 | 144 | 136 | 128 |
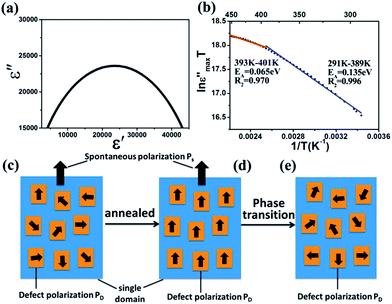
Furthermore, Fig. 9a shows the Cole–Cole diagram of BT-1. It provides the information of the dielectric relaxation in the BT ceramics.52 It is well known that the ideal Debye model of monodispersive relaxation corresponds to a standard semicircle, i.e., the circle center locates exactly on the ε′, whereas for a polydispersive process the circle center locates below the ε′ axis. In our case, there is a parabola above the ε′ axis in the sample, implying that the relaxation behavior exists and its character is a polydispersive relaxation rather than an ideal monodispersive Debye relaxation.53 The Debye relaxation time τ (the characteristic time that the dipoles response to an applied electric field) is calculated to be 1.0662 ×o10−7 s from the peak frequency fm of the Cole–Cole diagrams by equation τ = 1/(2πfm).
On the basis of the results in Fig. 6 and 7, the thermally activated polaron hopping model is used to get insight into the physical characteristics of the processes driving the relaxations. The maximum of the imaginary part of the relative permittivity (ε′′), is related to the number of hopping polarons (N) by54
 | (1) |
 | (2) |
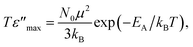 | (3) |
The ε′′max obtained for each temperature of BT-1, were then plotted in the Arrhenius form (ln(ε′′maxT) vs. 1/T) to calculate the activation energy for hopping polarization (Fig. 9b). The activation energy of the sample is calculated from the fitted line for high and low temperature region. The ε′′max increases as temperature increases, which confirms that thermally activated polarization, associated with polaronic dipoles, is a contribution polarization mechanism to the colossal permittivity of BT ceramics. The activation energy (EA) of 0.135 eV (291–389 K) and 0.065 eV (393–401 K) is obtained in the different temperature regions. The value of activation energy in the low temperature region is about 4 and 2 times larger than the values reported in the literature.54,56 The transition temperature for the activation energy is around 389 K, which could correspond to a ferroelectric phase transition temperature, as discussed in Fig. 8. One should note that the activation energy below Curie temperature range is much higher than that above the Curie temperature. We attempted to explain why the activation energy in the low temperature region is so high and a transition temperature exists by a simple model described in Fig. 9c–e. As revealed in defect BaTiO3 single crystal after aging, the defect symmetry in each domain followed the polar tetragonal crystal symmetry, and exhibited a defect dipole moment following the polarization direction of the residing domain.57 Encouraged by this work and considering the annealed treatment of the BT nanoceramics before our dielectric measurement, we proposed that defect dipoles tend to be aligned along the spontaneous polarization direction after annealing as shown in Fig. 9d. In contrast, before annealing, defect dipoles were randomly distributed within BaTiO3 single domain as shown in Fig. 9c. Below ferroelectric Curie temperature, the aligned defect dipoles coupled with Ps could be pinned, leading to the higher EA (291–389 K) for polaron hopping. Above the Curie temperature, PD was random distribution again, as shown in Fig. 9e, and the defect dipoles could be easily activated, thus the EA is lower (393–401 K).
Conclusions
In conclusion, BT nanoparticles with a size of ∼20 nm was synthesized via a sol–gel-hydrothermal method and subsequently densified by SPS. The average grain size of the sintered ceramics was less than 300 nm. The BT nanoceramics exhibited excellent behavior at room temperature as they combined both colossal permittivity (>35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) at low-frequency and very stable permittivity within a wide frequency range from 40 Hz to 10 kHz, while relaxation frequencies of all samples are larger than 100 kHz. At 1 kHz, the Curie temperature of BT-1 could be around 144 °C. On the basis of microstructure characterizations and dielectric measurement, it was proposed that the polaron dipoles configured by oxygen vacancies and Ti3+ cations within the grains could be attributed to the colossal dielectric permittivity of the ceramics. By using thermally activated polaron hopping model, large activation energy EA has been determined to be 0.135 eV below Curie temperature, probably due to a coupling of polaron dipoles and intrinsic ferroelectric dipoles. This simple method offers a possibility for the large-scale production of BT nanoceramics with a colossal permittivity.
000) at low-frequency and very stable permittivity within a wide frequency range from 40 Hz to 10 kHz, while relaxation frequencies of all samples are larger than 100 kHz. At 1 kHz, the Curie temperature of BT-1 could be around 144 °C. On the basis of microstructure characterizations and dielectric measurement, it was proposed that the polaron dipoles configured by oxygen vacancies and Ti3+ cations within the grains could be attributed to the colossal dielectric permittivity of the ceramics. By using thermally activated polaron hopping model, large activation energy EA has been determined to be 0.135 eV below Curie temperature, probably due to a coupling of polaron dipoles and intrinsic ferroelectric dipoles. This simple method offers a possibility for the large-scale production of BT nanoceramics with a colossal permittivity.
Acknowledgements
This work was financially supported by National Natural Science Foundation of China (51232006, 51472218, and 51102212), China Postdoctoral Science Foundation (2015M571866), and Fundamental Research Funds for the Central Universities (2016FZA4005).Notes and references
- R. Asiaie, W. D. Zhu, S. A. Akbar and P. K. Dutta, Chem. Mater., 1996, 8, 226–234 CrossRef CAS.
- M. Randall, D. Skamser, T. Kinard, J. Qazi, A. Tajuddin, S. Trolier-McKinstry, C. Randall, S. W. Ko and T. Dechakupt, Carts-conference, CARTS 2007 Symposium Proceedings, Albuquerque, NM, Components Technology Institute Inc. 2007, 27, p. 403 Search PubMed.
- T. T. Lee, C. Y. Huang, C. Y. Chang, I. K. Cheng, C. L. Hu, C. T. Lee and M. Fujimoto, J. Mater. Res., 2012, 27, 2495–2502 CrossRef CAS.
- C. Y. Chang, C. Y. Huang, Y. C. Wu, C. Y. Su and C. L. Huang, J. Alloys Compd., 2010, 495, 108–112 CrossRef CAS.
- M. T. Buscaglia, C. Harnagea, M. Dapiaggi, V. Buscaglia, A. Pignolet and P. Nanni, Chem. Mater., 2009, 21, 5058–5065 CrossRef CAS.
- M. T. Buscaglia, M. Bassoli, V. Buscaglia and V. Reinhard, J. Am. Ceram. Soc., 2008, 91, 2862–2869 CrossRef CAS.
- L. Simon-Seveyrat, A. Hajjaji, Y. Emziane, B. Guiffard and D. Guyomar, Ceram. Int., 2007, 33, 35–40 CrossRef CAS.
- S. K. Lee, T. J. Park, G. J. Choi, K. K. Koo and S. W. Kim, Mater. Chem. Phys., 2003, 82, 742–749 CrossRef CAS.
- C. Beck, W. Hartl and R. Hempelmann, J. Mater. Res., 1998, 13, 3174–3180 CrossRef CAS.
- Y. Yang, X. Wang, C. Sun and L. Li, J. Nanotechnol., 2009, 20, 55709 CrossRef PubMed.
- F. Maxim, P. Ferreira, P. M. Vilarinho and I. Reaney, Cryst. Growth Des., 2008, 8, 3309–3315 CAS.
- M. Oledzka, N. E. Brese and R. E. Riman, Chem. Mater., 1999, 11, 1931–1935 CrossRef CAS.
- W. W. Wang, L. X. Cao, W. Liu, G. Su and W. X. Zhang, Ceram. Int., 2013, 39, 7127–7134 CrossRef CAS.
- X. Yang, Z. H. Ren, G. Xu, C. Y. Chao, S. Jiang, S. Q. Deng, G. Shen, X. Wei and G. R. Han, Ceram. Int., 2014, 40, 9663–9670 CrossRef CAS.
- H. Han, D. Ghosh, J. L. Jones and J. C. Nino, J. Am. Ceram. Soc., 2013, 96, 485–490 CAS.
- G. Arlt, D. Hennings and G. de With, J. Appl. Phys., 1985, 58, 1619–1625 CrossRef CAS.
- Z. A. Munir, U. Anselmi-Tamburini and M. Ohyanagi, J. Mater. Sci., 2006, 41, 763–777 CrossRef CAS.
- Z. J. Shen, M. Johnsson, Z. Zhao and M. Nygren, J. Am. Ceram. Soc., 2002, 85, 1921–1927 CrossRef CAS.
- E. A. Olevsky and L. Froyen, J. Am. Ceram. Soc., 2009, 92, S122–S132 CrossRef CAS.
- D. Li, J. F. Hu, J. Z. Zhang, J. Ma and Z. J. Shen, Adv. Appl. Ceram., 2014, 113, 251–256 CrossRef CAS.
- D. Li, W. Li, C. Fasel, J. Shen and R. Riedel, J. Alloys Compd., 2014, 586, 567–573 CrossRef CAS.
- H. Maiwa, Jpn. J. Appl. Phys., 2008, 47, 7646–7649 CrossRef CAS.
- S. Yoon, J. Dornseiffer, Y. Xiong, D. Gruner, Z. J. Shen, S. Iwaya, C. Pithan and R. Waser, J. Eur. Ceram. Soc., 2011, 31, 1723–1731 CrossRef CAS.
- Z. Valdez-Nava, C. Tenailleau, S. Guillemet-Fritsch, N. El Horr, T. Lebey, P. Dufour, B. Durand and J. Y. Chane-Ching, J. Phys. Chem. Solids, 2011, 72, 17–23 CrossRef CAS.
- S. Guillemet-Fritsch, Z. Valdez-Nava, C. Tenailleau, T. Lebey, B. Durand and J. Y. Chane-Ching, Adv. Mater., 2008, 20, 551–555 CrossRef CAS.
- T. Ishii, M. Endo, K. Masuda and K. Ishida, Appl. Phys. Lett., 2013, 102, 062901 CrossRef PubMed.
- U. C. Chung, C. Elissalde, S. Mornet, M. Maglione and C. Estournes, Appl. Phys. Lett., 2009, 94, 072903 CrossRef.
- S. Jayanthi and T. R. N. Kutty, J. Mater. Sci.: Mater. Electron., 2005, 16, 269–279 CrossRef CAS.
- M. Valant, A. Dakskobler, M. Ambrozic and T. Kosmac, J. Eur. Ceram. Soc., 2006, 26, 891–896 CrossRef CAS.
- Y. G. Wang, G. Xu, L. L. Yang, Z. H. Ren, X. Wei, W. J. Weng, P. Y. Du, G. Shen and G. R. Han, Mater. Lett., 2009, 63, 239–241 CrossRef CAS.
- M. T. Buscaglia, M. Viviani, V. Buscaglia, L. Mitoseriu, A. Testino, P. Nanni, Z. Zhao, M. Nygren, C. Harnagea, D. Piazza and C. Galassi, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 0641114 CrossRef.
- C. H. Perry and D. B. Hall, Phys. Rev. Lett., 1965, 15, 700–702 CrossRef CAS.
- Y. Ma, E. Vileno, S. L. Suib and P. K. Dutta, Chem. Mater., 1997, 9, 3023–3031 CrossRef CAS.
- I. J. Clark, T. Takeuchi, N. Ohtori and D. C. Sinclair, J. Mater. Chem., 1999, 9, 83–91 RSC.
- M. F. Lin, V. K. Thakur, E. J. Tan and P. S. Lee, J. Mater. Chem., 2011, 21, 16500–16504 RSC.
- B. R. Li, X. H. Wang, M. M. Cai, L. F. Hao and L. T. Li, Mater. Chem. Phys., 2003, 82, 173–180 CrossRef CAS.
- W. L. Luan, L. Gao, H. Kawaoka, T. Sekino and K. Niihara, Ceram. Int., 2004, 30, 405–410 CrossRef CAS.
- B. R. Li, X. H. Wang, L. T. Li, H. Zhou, X. T. Liu, X. Q. Han, Y. C. Zhang, X. W. Qi and X. Y. Deng, Mater. Chem. Phys., 2004, 83, 23–28 CrossRef CAS.
- T. Takeuchi, C. Capiglia, N. Balakrishnan, Y. Takeda and H. Kageyama, J. Mater. Res., 2002, 17, 575–581 CrossRef CAS.
- M. T. Buscaglia, V. Buscaglia, M. Viviani, J. Petzelt, M. Savinov, L. Mitoseriu, A. Testino, P. Nanni, C. Harnagea, Z. Zhao and M. Nygren, Nanotechnology, 2004, 15, 1113–1117 CrossRef CAS.
- S. Yoon, J. Dornseiffer, Y. Xiong, D. Grüner, Z. J. Shen, S. Iwaya, C. Pithan and R. Waser, J. Eur. Ceram. Soc., 2011, 31, 1723–1731 CrossRef CAS.
- T. Oyama, N. Wada, H. Takagi and M. Yoshiya, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 134107 CrossRef.
- C. Voisin, S. Guillemet-Fritsch, P. Dufour, C. Tenailleau, H. Han and J. C. Nino, Int. J. Appl. Ceram. Technol., 2013, 10, E122–E133 CrossRef CAS.
- N. Izyumskaya, Y. Alivov and H. Morkoc, Crit. Rev. Solid State Mater. Sci., 2009, 34, 89–179 CrossRef CAS.
- B. Jiang, J. L. Peng, L. A. Bursill and W. L. Zhong, J. Appl. Phys., 2000, 87, 3462 CrossRef CAS.
- J. Varghese, R. W. Whatmore and J. D. Holmes, J. Mater. Chem. C, 2013, 1, 2618–2638 RSC.
- L. Q. Dong, K. Cheng, W. J. Weng and W. Q. Han, CrystEngComm, 2014, 16, 10750–10753 RSC.
- Q. Yu, D. Liu, R. Wang, Z. Feng, Z. Zuo, S. Qin, H. Liu and X. Xu, Mater. Sci. Eng., B, 2012, 177, 639–644 CrossRef CAS.
- H. C. Yu and Z. G. Ye, J. Appl. Phys., 2008, 103, 034114–034115 CrossRef.
- X. G. Tang, J. Wang, X. X. Wang and H. L. W. Chan, Solid State Commun., 2004, 131, 163–168 CrossRef CAS.
- W. H. Tzing, W. H. Tuan and H. L. Lin, Ceram. Int., 1999, 25, 425–430 CrossRef CAS.
- K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351 CrossRef CAS.
- H. B. Yang, H. Wang, L. He and X. Yao, Mater. Chem. Phys., 2012, 134, 777–782 CrossRef CAS.
- H. Han, C. Voisin, S. Guillemet-Fritsch, P. Dufour, C. Tenailleau, C. Turner and J. C. Nino, J. Appl. Phys., 2013, 113, 024102 CrossRef.
- S. Komine and E. Iguchi, J. Phys.: Condens. Matter, 2004, 16, 1061–1073 CrossRef CAS.
- O. Bidault, M. Maglione, M. Actis, M. Kchikech and B. Salce, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 4191–4197 CrossRef CAS.
- X. B. Ren, Nat. Mater., 2004, 3, 91–94 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |