Theoretical evaluation of some benzotriazole and phospono derivatives as aluminum corrosion inhibitors: DFT and molecular dynamics simulation approaches
Savaş Kaya*a,
Priyabrata Banerjeebc,
Sourav Kr. Sahabc,
Burak Tüzüna and
Cemal Kayaa
aCumhuriyet University, Faculty of Science, Department of Chemistry, 58140, Sivas, Turkey. E-mail: savaskaya@cumhuriyet.edu.tr
bSurface Engineering and Tribology Group, CSIR-Central Mechanical Engineering Research Institute, Mahatma Gandhi Avenue, Durgapur 713209, India
cAcademy of Scientific and Innovative Research (AcSIR), CSIR-CMERI Campus, Durgapur 713209, West Bengal, India
First published on 1st August 2016
Abstract
The adsorption and corrosion inhibition properties of some benzotriazole and phospono derivatives namely, 1-(2-pyrrolecarbonyl)-benzotriazole (PBTA), 1-(2-thienylcarbonyl)-benzotriazole (TBTA), 2-phosphonoacetic acid (PAA) and 4-phosphonobutyric acid (PBA) on the corrosion of aluminum were investigated by quantum chemical calculations and by molecular dynamics simulations. Global reactivity descriptors such as EHOMO, ELUMO, HOMO–LUMO energy gap (ΔE), chemical hardness (η), softness (σ), electronegativity (χ), proton affinity (PA), electrophilicity (ω) and nucleophilicity (ε) have been calculated and discussed. The analysis of the adsorption behavior of these mentioned inhibitors on the Al (111) surface was investigated using molecular dynamics simulations. The binding energies on the Al (111) surface of the studied compounds followed the order: PBTA > TBTA > PBA > PAA. The results obtained in this study are compatible with experimental data and it is proposed that the above mentioned molecules can be successfully used to prevent the corrosion of aluminum metal.
1. Introduction
Corrosion is a spontaneous destruction of a material in the environment by a chemical reaction. The prevention of corrosion using various methods is an important issue for industrial applications of materials. The use of corrosion inhibitors that are adsorbed on metallic surfaces is one of the most efficient methods used in order to prevent the corrosion of metal surfaces. The most effective inhibitors are π-conjugated systems and heterocyclic organic compounds.1–4 In many articles, it is stated that organic inhibitors containing nitrogen, oxygen, sulphur and aromatic rings in their molecular structure are highly effective against corrosion.Aluminum is a reactive metal and has remarkable industrial and economic importance because of its low cost and high conductivity. Although, aluminum is a corrosion resistant material by forming a preventive film on its surface upon its exposure to the atmosphere or aqueous solution, in some cases, this metal can be exposed to corrosion.5 For this reason, the synthesis and design of suitable inhibitors to prevent the corrosion of aluminum are quite momentous. It can be said that much research carried out in the prevention of corrosion of aluminum is available in the literature.6,7
Experimental methods used to determine the corrosion inhibition efficiencies of and to understand the inhibition mechanisms of chemical compounds such as weight loss, potentiodynamic polarization (PDP), Electrochemical Impedance Spectroscopy (EIS), Fourier transform infrared spectroscopy (FTIR) and Scanning Electron Microscopy (SEM) are generally expensive and time-consuming too. With the improvement of computational hardware and software, in recent times, theoretical methods like Density Functional Theory (DFT) and molecular dynamics simulation methods have been accepted as fast and powerful tools to predict the relative corrosion inhibition efficiencies of inhibitor molecules.8–14 Using molecular dynamic simulation methods, adsorption energy and binding energy between metal surface and corrosion inhibitors can be easily calculated. On the other hand, conceptual DFT15,16 is very popular in terms of the prediction of chemical properties such as HOMO–LUMO energy gap, chemical hardness,17,18 softness,19 electronegativity,20 chemical potential, proton affinity,21 electrophilicity22 and nucleophilicity of chemical species. In this theoretical approach evaluated quantum chemical parameters are considered in the prediction of chemical reactivity or stability. In the calculation of these mentioned chemical properties, Koopman's theorem23 in general provides great facilities to computational and theoretical chemists. According to this theory, ionization energy and electron affinity values of chemical species are associated with their HOMO and LUMO energy values, respectively.
In recent years, D. Gopi et al.24 have synthesized the some benzotriazole and phospono derivatives and investigated experimentally their inhibition performances on the corrosion of mild steel. The molecular structures of these molecules are given in Fig. 1. The objective of this study is to evaluate the corrosion inhibition performance of the molecules in Fig. 1 on the corrosion of aluminum using quantum chemical calculations and molecular dynamics simulations approach and also to theoretically predict the most effective corrosion inhibitor among them (Fig. 2).
 | ||
| Fig. 2 The optimized structures, HOMOs, LUMOs and electrostatic potential structures of studied inhibitors have been given in this figure. | ||
2. Computational details
2.1. Quantum chemical calculations
Density functional theory is certainly most widely used technique to ascertain the chemical reactivity of the studied molecules, cluster and solids. In view of above, the use of DFT methods for the evaluation of chemical reactivity has become very popular in recent times.25 In the present study, DFT calculations were carried out using Gaussian 9.0 Program package.26 The input files of studied molecules were prepared with Gauss View 5.0.8.27 A full optimization was performed up to a higher basis set denoted by 6-31G++ (d,p) because this basis set gives more accurate results in terms of the determination of geometries and electronic properties for a wide range of organic compounds. The calculations in both gaseous and aqueous phases were also carried out using other levels of theory such as HF and DFT/B3LYP methods with SDD, 6-31++G (d,p) and 6-31 G basis sets.Although, it is found in some cases that B3LYP does not give particularly accurate HOMO and LUMO energy levels due to the self interaction errors implicit to B3LYP. The hybrid B3LYP functional has also unsuccessful in some applications such as the polarizability of long chains, excitations using time dependent theory (TDDFT) for Rydberg states and charge transfer (CT) excitations.28–31 In this context, in recent times range separated functionals such as CAM-B3LYP, LC-BLYP, wB97XD is immerged as better functional for calculating accurate ground and excited state orbital energies.32–35
Range separated functionals is a new class of functionals for generalized Kohn–Sham theory that are very effective in order to predict ionization potentials and energy gaps for a wide range of molecules and solids. In contrast to the normal hybrid functionals, the range separated functionals mixes exchange densities nonuniformly by partitioning the electron repulsion operator into the short-range (first term) and long-range (second term) component as:
 | (1) |
DFT has provided significant contributions in the development of quantum chemistry. With the help of this theory, chemical indices such as chemical potential (μ), chemical hardness (η) and electronegativity (χ) have been defined as derivative of electronic energy (E) with respect to number of electron (N) at a constant external potential υ(r). Quantitative expressions related to these concepts are given as follows:36,37
 | (2) |
 | (3) |
Applying the finite differences method38 on the above equations the following, equations based on first vertical ionization energy and electron affinity values of chemical species for the calculation of chemical hardness, electronegativity and chemical potential have been derived.
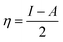 | (4) |
 | (5) |
Koopman's theorem23 provides an alternative method to determine the ionization energy and electron affinity values of chemical species. According to this theorem, the negative value of highest occupied and lowest unoccupied molecular orbital energy can be correlated with the ionization energy and electron affinity respectively (−EHOMO = I and −ELUMO = A). As a result of this theorem, chemical potential and chemical hardness can be expressed as.39
 | (6) |
 | (7) |
According to Pearson who introduced the chemical harness concept, global softness can be defined as the inverse of the global hardness. From the light of this information, softness is given as:40
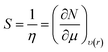 | (8) |
Electrophilicity22 and nucleophilicity concepts have important applications in organic chemistry and have been extensively used in the prediction of organic reaction mechanisms. The global electrophilicity index (ω) introduced by Parr41 could be defined via eqn (9). According to Parr, electrophilic power of a chemical compound is associated with its electronegativity and chemical hardness. Nucleophilicity (ε) is the inverse of the electrophilicity and it is given via eqn (10).
 | (9) |
| ε = 1/ω | (10) |
2.2. Molecular dynamics simulations
Adsorption process of the inhibitors compounds on the aluminum surface is investigated by MD simulation using Material Studio™ software 6.1 (from Accelrys Inc.).42 In this present investigation, we have chosen Al (111) surface for simulation. In this simulation process interaction between inhibitors and iron surface are carried out in a simulation box of (36.83 × 36.83 × 76.44 Å) with periodic boundary condition in order to avoid any arbitrary boundary effects. Here, we have used ten layers of aluminum atoms as it provides sufficient depth to overcome the issue related to cutoff radius in this case. In this investigation, simulation box is created by a three layer. The first layer contains Al slab and the second layer is the solution slab which contains 150 H2O and 1 inhibitor molecule and the remaining part of the box is the vacuum layer. After construction of the simulation box, dynamics simulation is carried out using the COMPASS (Condensed Phase Optimized Molecular Potentials for Atomistic Simulation Studies) force field. COMPASS is a highly accepted and authentic ab initio force field that enables accurate prediction of nature for a good many number of chemical entities. In general, the parameterization procedure can be divided in two phases: (i) ab initio parameterization, (ii) empirical optimization.43 The MD simulation is performed at 298.0 K using canonical ensemble (NVT) with a time step of 1.0 fs and a simulation time of 100 ps.The interaction energy (Einteraction) and binding energy (Ebinding) of the inhibitor molecule on the Al (111) surface are calculated by the following eqn (11) and (12).44
| Einteraction = Etotal − (Esurface+H2O + Einhibitor) | (11) |
The binding energy of the inhibitor molecule is negative value of interaction energy is as follows.45 Obviously, a larger value of Ebinding implies the corrosion inhibitor combines with the aluminum surface more easily and tightly, therefore higher and spontaneous inhibitive performance by the benzotriazole and phospono derivatives on the aluminum surfaces were observed.
| Ebinding = −Einteraction | (12) |
3. Results and discussion
The inhibition efficiencies of the benzotriazole and phospono derivatives on the corrosion of aluminum were investigated by quantum chemical and molecular dynamics simulation studies. The results obtained in the study demonstrated that these compounds considered are good inhibitors against corrosion of aluminum. Quantum chemical calculations and molecular dynamics simulations were carried out and the calculated binding energies of the studied molecules on the aluminum surface showed that these molecules are very effective against the corrosion of aluminum. The obtained results in the study are given in detail below.Chemical reactivity descriptors such as, EHOMO, ELUMO, ΔE (HOMO–LUMO energy gap), chemical hardness, softness, electronegativity, proton affinity, electrophilicity and nucleophilicity are important and useful tools to compare the corrosion inhibition performances of molecules. In the present study, calculated quantum chemical parameters using various methods and basis sets for protonated and non-protonated forms of studied molecules in both gas phase and aqueous phase are presented in Tables 1–4.
Analysis of frontier molecular orbitals presents important clues to us in terms of the prediction of chemical reactivity of molecules. There is a remarkable relationship between corrosion inhibition efficiency and HOMO energy level. The energy of HOMO is associated with the electron donating ability of a molecule. High energy value of HOMO state that the molecule is prone to donate electrons to appropriate acceptor molecules having low energy and empty molecular orbital. Another useful parameter to compare the electron donating or accepting abilities of molecules is LUMO energy level. LUMO energy level is an indicator of electron accepting abilities of molecules. It is important to note that the molecules that have lower LUMO energy value have more electron accepting ability. Considering calculated HOMO and LUMO energy levels given in Tables 1 and 2 for studied compounds, we can write the corrosion inhibition efficiency order as: PBTA > TBTA > PBA > PAA. This obtained corrosion inhibition efficiency ranking is compatible with the results obtained from molecular dynamic simulation approach.
| EHOMO | ELUMO | I | A | ΔE | η | σ | χ | PA | ω | ε | Energy | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HF/SDD level | ||||||||||||
| PBA | −11.98970 | 3.82867 | 11.98970 | −3.82867 | 15.81838 | 7.90919 | 0.12644 | 4.08052 | −2.56154 | 1.05261 | 0.95002 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 714.34658 714.34658 |
| PAA | −12.38182 | 3.34730 | 12.38182 | −3.34730 | 15.72912 | 7.86456 | 0.12715 | 4.51726 | −1.88250 | 1.29732 | 0.77082 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 592.11809 592.11809 |
| PBTA | −8.87942 | 1.29500 | 8.87942 | −1.29500 | 10.17442 | 5.08721 | 0.19657 | 3.79221 | −1.47436 | 1.41343 | 0.70750 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 413.91740 413.91740 |
| TBTA | −9.42202 | 0.91322 | 9.42202 | −0.91322 | 10.33524 | 5.16762 | 0.19351 | 4.25440 | −1.31030 | 1.75128 | 0.57101 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 732.54522 732.54522 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| HF/6-31G level | ||||||||||||
| PBA | −11.82480 | 3.62241 | 11.82480 | −3.62241 | 15.44721 | 7.72360 | 0.12947 | 4.10120 | −1.75692 | 1.08886 | 0.91839 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 711.01006 711.01006 |
| PAA | −12.30862 | 3.49914 | 12.30862 | −3.49914 | 15.80776 | 7.90388 | 0.12652 | 4.40474 | −1.86174 | 1.22736 | 0.81476 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589.01534 589.01534 |
| PBTA | −8.71778 | 1.60521 | 8.71778 | −1.60521 | 10.32299 | 5.16150 | 0.19374 | 3.55628 | −1.54933 | 1.22514 | 0.81623 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 411.52033 411.52033 |
| TBTA | −9.27181 | 1.17717 | 9.27181 | −1.17717 | 10.44898 | 5.22449 | 0.19141 | 4.04732 | −1.37753 | 1.56769 | 0.63788 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730.62643 730.62643 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| HF/6-31++G level | ||||||||||||
| PBA | −12.02970 | 0.65226 | 12.02970 | −0.65226 | 12.68197 | 6.34098 | 0.15770 | 5.68872 | −2.45697 | 2.55178 | 0.39188 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 711.70708 711.70708 |
| PAA | −12.46645 | 0.87077 | 12.46645 | −0.87077 | 13.33722 | 6.66861 | 0.14996 | 5.79784 | −1.78293 | 2.52039 | 0.39676 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589.67204 589.67204 |
| PBTA | −8.86636 | 1.02370 | 8.86636 | −1.02370 | 9.89006 | 4.94503 | 0.20222 | 3.92133 | −1.42379 | 1.55477 | 0.64318 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 412.10721 412.10721 |
| TBTA | −9.38583 | 0.84029 | 9.38583 | −0.84029 | 10.22612 | 5.11306 | 0.19558 | 4.27277 | −1.29093 | 1.78528 | 0.56014 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 731.16551 731.16551 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| B3LYP/SDD level | ||||||||||||
| PBA | −7.22713 | −0.93472 | 7.22713 | 0.93472 | 6.29241 | 3.14621 | 0.31784 | 4.08092 | −1.09758 | 2.64667 | 0.37783 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814.10643 814.10643 |
| PAA | −7.96184 | −1.61011 | 7.96184 | 1.61011 | 6.35173 | 3.17587 | 0.31487 | 4.78598 | −1.52557 | 3.60619 | 0.27730 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 676.28520 676.28520 |
| PBTA | −6.57079 | −2.46156 | 6.57079 | 2.46156 | 4.10922 | 2.05461 | 0.48671 | 4.51617 | −1.48810 | 4.96342 | 0.20147 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 535.78738 535.78738 |
| TBTA | −7.05297 | −2.78103 | 7.05297 | 2.78103 | 4.27195 | 2.13597 | 0.46817 | 4.91700 | −1.39566 | 5.65945 | 0.17670 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 864.28512 864.28512 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| B3LYP/6-31G level | ||||||||||||
| PBA | −7.03175 | −1.04874 | 7.03175 | 1.04874 | 5.98301 | 2.99151 | 0.33428 | 4.04024 | −1.06452 | 2.72832 | 0.36653 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810.47404 810.47404 |
| PAA | −7.84293 | −1.49827 | 7.84293 | 1.49827 | 6.34466 | 3.17233 | 0.31523 | 4.67060 | −1.52973 | 3.43825 | 0.29085 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 672.86100 672.86100 |
| PBTA | −6.38493 | −2.19325 | 6.38493 | 2.19325 | 4.19167 | 2.09584 | 0.47714 | 4.28909 | −1.66141 | 4.38877 | 0.22785 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 533.24998 533.24998 |
| TBTA | −6.88617 | −2.55190 | 6.88617 | 2.55190 | 4.33426 | 2.16713 | 0.46144 | 4.71904 | −1.54709 | 5.13797 | 0.19463 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 862.05043 862.05043 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| B3LYP/6-31++G level | ||||||||||||
| PBA | −7.49544 | −1.80168 | 7.49544 | 1.80168 | 5.69376 | 2.84688 | 0.35126 | 4.64856 | −0.85082 | 3.79523 | 0.26349 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 811.50868 811.50868 |
| PAA | −8.33355 | −1.76576 | 8.33355 | 1.76576 | 6.56779 | 3.28390 | 0.30452 | 5.04966 | −1.36398 | 3.88244 | 0.25757 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 673.73172 673.73172 |
| PBTA | −6.67637 | −2.54755 | 6.67637 | 2.54755 | 4.12882 | 2.06441 | 0.48440 | 4.61196 | −1.35598 | 5.15164 | 0.19411 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 534.03395 534.03395 |
| TBTA | −7.12781 | −2.86511 | 7.12781 | 2.86511 | 4.26270 | 2.13135 | 0.46919 | 4.99646 | −1.31672 | 5.85652 | 0.17075 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 862.77126 862.77126 |
| EHOMO | ELUMO | I | A | ΔE | η | σ | χ | PA | ω | ε | Energy | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| HF/SDD level | ||||||||||||
| PBA | −12.24522 | 3.91765 | 12.24522 | −3.91765 | 16.16287 | 8.08144 | 0.12374 | 4.16378 | −3.74121 | 1.07265 | 0.93227 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 715.46588 715.46588 |
| PAA | −12.64986 | 3.23900 | 12.64986 | −3.23900 | 15.88885 | 7.94443 | 0.12587 | 4.70543 | −3.73550 | 1.39350 | 0.71762 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 593.06451 593.06451 |
| PBTA | −8.93030 | 1.10751 | 8.93030 | −1.10751 | 10.03782 | 5.01891 | 0.19925 | 3.91140 | −3.26972 | 1.52414 | 0.65611 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 414.31110 414.31110 |
| TBTA | −9.42147 | 0.77036 | 9.42147 | −0.77036 | 10.19183 | 5.09592 | 0.19624 | 4.32556 | −2.99926 | 1.83583 | 0.54471 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 732.94709 732.94709 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| HF/6-31G level | ||||||||||||
| PBA | −12.14916 | 4.12637 | 12.14916 | −4.12637 | 16.27553 | 8.13777 | 0.12288 | 4.01140 | −3.74913 | 0.98868 | 1.01145 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 711.99270 711.99270 |
| PAA | −12.46808 | 3.54213 | 12.46808 | −3.54213 | 16.01022 | 8.00511 | 0.12492 | 4.46297 | −3.74059 | 1.24409 | 0.80380 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589.90780 589.90780 |
| PBTA | −8.78663 | 1.39133 | 8.78663 | −1.39133 | 10.17795 | 5.08898 | 0.19650 | 3.69765 | −3.33936 | 1.34335 | 0.74441 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 411.88535 411.88535 |
| TBTA | −9.29575 | 1.00656 | 9.29575 | −1.00656 | 10.30231 | 5.15116 | 0.19413 | 4.14460 | −3.03834 | 1.66736 | 0.59975 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 731.00146 731.00146 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| HF/6-31++G level | ||||||||||||
| PBA | −12.32903 | 1.10914 | 12.32903 | −1.10914 | 13.43818 | 6.71909 | 0.14883 | 5.60994 | −3.62943 | 2.34194 | 0.42700 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 712.75751 712.75751 |
| PAA | −12.65312 | 1.13119 | 12.65312 | −1.13119 | 13.78431 | 6.89215 | 0.14509 | 5.76097 | −3.64154 | 2.40772 | 0.41533 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590.58602 590.58602 |
| PBTA | −8.90826 | 1.04874 | 8.90826 | −1.04874 | 9.95700 | 4.97850 | 0.20086 | 3.92976 | −3.23089 | 1.55097 | 0.64476 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 412.48741 412.48741 |
| TBTA | −9.38800 | 0.69172 | 9.38800 | −0.69172 | 10.07972 | 5.03986 | 0.19842 | 4.34814 | −2.96843 | 1.87568 | 0.53314 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 731.54433 731.54433 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| B3LYP/SDD level | ||||||||||||
| PBA | −7.95694 | −0.79648 | 7.95694 | 0.79648 | 7.16046 | 3.58023 | 0.27931 | 4.37671 | −3.58698 | 2.67519 | 0.37380 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814.86841 814.86841 |
| PAA | −8.23967 | −1.45963 | 8.23967 | 1.45963 | 6.78004 | 3.39002 | 0.29498 | 4.84965 | −3.47422 | 3.46887 | 0.28828 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 676.94456 676.94456 |
| PBTA | −6.64534 | −2.65204 | 6.64534 | 2.65204 | 3.99330 | 1.99665 | 0.50084 | 4.64869 | −3.22895 | 5.41165 | 0.18479 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536.14171 536.14171 |
| TBTA | −7.08917 | −2.93586 | 7.08917 | 2.93586 | 4.15331 | 2.07665 | 0.48154 | 5.01251 | −3.04738 | 6.04947 | 0.16530 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 864.60456 864.60456 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| B3LYP/6-31G level | ||||||||||||
| PBA | −7.73000 | −0.50586 | 7.73000 | 0.50586 | 7.22414 | 3.61207 | 0.27685 | 4.11793 | −3.62633 | 2.34732 | 0.42602 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 811.10445 811.10445 |
| PAA | −8.06987 | −1.22289 | 8.06987 | 1.22289 | 6.84698 | 3.42349 | 0.29210 | 4.64638 | −3.50845 | 3.15305 | 0.31715 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 673.44175 673.44175 |
| PBTA | −6.45459 | −2.38047 | 6.45459 | 2.38047 | 4.07412 | 2.03706 | 0.49090 | 4.41753 | −3.32776 | 4.78989 | 0.20877 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 533.56194 533.56194 |
| TBTA | −6.92508 | −2.70538 | 6.92508 | 2.70538 | 4.21970 | 2.10985 | 0.47397 | 4.81523 | −3.12564 | 5.49480 | 0.18199 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 862.33579 862.33579 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| B3LYP/6-31++G level | ||||||||||||
| PBA | −8.21709 | −1.17064 | 8.21709 | 1.17064 | 7.04644 | 3.52322 | 0.28383 | 4.69386 | −3.30766 | 3.12674 | 0.31982 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 812.29177 812.29177 |
| PAA | −8.49056 | −1.79515 | 8.49056 | 1.79515 | 6.69541 | 3.34771 | 0.29871 | 5.14286 | −3.29471 | 3.95031 | 0.25314 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 674.44844 674.44844 |
| PBTA | −6.71365 | −2.71871 | 6.71365 | 2.71871 | 3.99493 | 1.99747 | 0.50063 | 4.71618 | −3.12904 | 5.56763 | 0.17961 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 534.38000 534.38000 |
| TBTA | −7.13243 | −3.00334 | 7.13243 | 3.00334 | 4.12909 | 2.06454 | 0.48437 | 5.06789 | −2.96934 | 6.22014 | 0.16077 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 863.08811 863.08811 |
| EHOMO | ELUMO | I | A | ΔE | η | σ | χ | ω | ε | Energy | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| HF/SDD level | |||||||||||
| PBA | −17.23583 | −0.75376 | 17.23583 | 0.75376 | 16.48207 | 8.24103 | 0.12134 | 8.99479 | 4.90875 | 0.20372 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 724.26812 724.26812 |
| PAA | −17.50522 | −0.97690 | 17.50522 | 0.97690 | 16.52833 | 8.26416 | 0.12100 | 9.24106 | 5.16672 | 0.19355 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 601.36059 601.36059 |
| PBTA | −12.74074 | −3.56581 | 12.74074 | 3.56581 | 9.17494 | 4.58747 | 0.21799 | 8.15328 | 7.24538 | 0.13802 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 422.75176 422.75176 |
| TBTA | −13.15626 | −4.09779 | 13.15626 | 4.09779 | 9.05847 | 4.52923 | 0.22079 | 8.62703 | 8.21614 | 0.12171 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 741.21552 741.21552 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| HF/6-31G level | |||||||||||
| PBA | −15.21482 | −1.20275 | 15.21482 | 1.20275 | 14.01207 | 7.00603 | 0.14273 | 8.20879 | 4.80901 | 0.20794 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720.12698 720.12698 |
| PAA | −17.45080 | −1.21881 | 17.45080 | 1.21881 | 16.23199 | 8.11600 | 0.12321 | 9.33480 | 5.36832 | 0.18628 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 598.23708 598.23708 |
| PBTA | −12.63897 | −3.36798 | 12.63897 | 3.36798 | 9.27099 | 4.63550 | 0.21573 | 8.00348 | 6.90925 | 0.14473 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420.42966 420.42966 |
| TBTA | −13.03626 | −3.93725 | 13.03626 | 3.93725 | 9.09901 | 4.54951 | 0.21980 | 8.48675 | 7.91569 | 0.12633 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 739.36396 739.36396 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| HF/6-31++G level | |||||||||||
| PBA | −17.24181 | −2.26537 | 17.24181 | 2.26537 | 14.97645 | 7.48822 | 0.13354 | 9.75359 | 6.35214 | 0.15743 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721.52405 721.52405 |
| PAA | −17.52699 | −2.78157 | 17.52699 | 2.78157 | 14.74542 | 7.37271 | 0.13564 | 10.1542 | 6.99264 | 0.14301 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 598.81497 598.81497 |
| PBTA | −12.70727 | −3.54975 | 12.70727 | 3.54975 | 9.15752 | 4.57876 | 0.21840 | 8.12851 | 7.21513 | 0.13860 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 420.89100 420.89100 |
| TBTA | −13.09177 | −4.07086 | 13.09177 | 4.07086 | 9.02092 | 4.51046 | 0.22171 | 8.58131 | 8.16313 | 0.12250 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 739.81644 739.81644 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| B3LYP/SDD level | |||||||||||
| PBA | −10.58286 | −6.49405 | 10.58286 | 6.49405 | 4.08882 | 2.04441 | 0.48914 | 8.53846 | 17.83041 | 0.05608 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 822.56401 822.56401 |
| PAA | −12.90701 | −6.13186 | 12.90701 | 6.13186 | 6.77514 | 3.38757 | 0.29520 | 9.51943 | 13.37531 | 0.07476 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685.17077 685.17077 |
| PBTA | −10.61525 | −7.06849 | 10.61525 | 7.06849 | 3.54676 | 1.77338 | 0.56389 | 8.84187 | 22.04225 | 0.04537 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544.63548 544.63548 |
| TBTA | −10.89280 | −7.43884 | 10.89280 | 7.43884 | 3.45397 | 1.72698 | 0.57904 | 9.16582 | 24.32340 | 0.04111 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873.04078 873.04078 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| B3LYP/6-31G level | |||||||||||
| PBA | −10.42939 | −6.74820 | 10.42939 | 6.74820 | 3.68119 | 1.84059 | 0.54330 | 8.58880 | 20.03905 | 0.04990 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 818.89856 818.89856 |
| PAA | −12.84905 | −6.36234 | 12.84905 | 6.36234 | 6.48670 | 3.24335 | 0.30832 | 9.60569 | 14.22439 | 0.07030 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 681.75073 681.75073 |
| PBTA | −10.46640 | −6.86739 | 10.46640 | 6.86739 | 3.59901 | 1.79950 | 0.55571 | 8.66689 | 20.87106 | 0.04791 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542.27139 542.27139 |
| TBTA | −10.59647 | −7.09134 | 10.59647 | 7.09134 | 3.50513 | 1.75256 | 0.57059 | 8.84391 | 22.31437 | 0.04481 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870.95752 870.95752 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| B3LYP/6-31++G level | |||||||||||
| PBA | −10.78913 | −7.01569 | 10.78913 | 7.01569 | 3.77343 | 1.88672 | 0.53002 | 8.90241 | 21.00287 | 0.04761 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 819.71950 819.71950 |
| PAA | −13.05477 | −6.59310 | 13.05477 | 6.59310 | 6.46167 | 3.23083 | 0.30952 | 9.82393 | 14.93572 | 0.06695 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 682.45570 682.45570 |
| PBTA | −10.66042 | −7.09406 | 10.66042 | 7.09406 | 3.56635 | 1.78318 | 0.56080 | 8.87724 | 22.09692 | 0.04526 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542.74993 542.74993 |
| TBTA | −10.89144 | −7.41353 | 10.89144 | 7.41353 | 3.47791 | 1.73896 | 0.57506 | 9.15249 | 24.08570 | 0.04152 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 871.44798 871.44798 |
| EHOMO | ELUMO | I | A | ΔE | η | σ | χ | ω | ε | Energy | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| HF/SDD level | |||||||||||
| PBA | −12.66727 | 3.32988 | 12.66727 | −3.32988 | 15.99716 | 7.99858 | 0.12502 | 4.66869 | 1.36254 | 0.73393 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 726.56709 726.56709 |
| PAA | −13.60444 | 3.35737 | 13.60444 | −3.35737 | 16.96181 | 8.48090 | 0.11791 | 5.12354 | 1.54763 | 0.64615 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 604.16001 604.16001 |
| PBTA | −9.51236 | −0.28763 | 9.51236 | 0.28763 | 9.22473 | 4.61237 | 0.21681 | 4.89999 | 2.60278 | 0.38420 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 424.94082 424.94082 |
| TBTA | −9.88353 | −0.72247 | 9.88353 | 0.72247 | 9.16106 | 4.58053 | 0.21832 | 5.30300 | 3.06971 | 0.32576 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 743.30635 743.30635 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| HF/6-31G level | |||||||||||
| PBA | −12.52795 | 3.04062 | 12.52795 | −3.04062 | 15.56857 | 7.78429 | 0.12846 | 4.74366 | 1.44537 | 0.69186 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 723.10183 723.10183 |
| PAA | −13.49505 | 3.16634 | 13.49505 | −3.16634 | 16.66139 | 8.33070 | 0.12004 | 5.16435 | 1.60074 | 0.62471 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 601.00839 601.00839 |
| PBTA | −9.42800 | −0.09606 | 9.42800 | 0.09606 | 9.33195 | 4.66597 | 0.21432 | 4.76203 | 2.43003 | 0.41152 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 422.58471 422.58471 |
| TBTA | −9.78175 | −0.58532 | 9.78175 | 0.58532 | 9.19643 | 4.59822 | 0.21748 | 5.18354 | 2.92168 | 0.34227 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 741.39980 741.39980 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| HF/6-31++G level | |||||||||||
| PBA | −12.72959 | 0.91458 | 12.72959 | −0.91458 | 13.64417 | 6.82208 | 0.14658 | 5.90750 | 2.55777 | 0.39097 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 723.74694 723.74694 |
| PAA | −13.62839 | 0.90560 | 13.62839 | −0.90560 | 14.53399 | 7.26699 | 0.13761 | 6.36139 | 2.78432 | 0.35915 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 601.58756 601.58756 |
| PBTA | −9.49739 | −0.26205 | 9.49739 | 0.26205 | 9.23534 | 4.61767 | 0.21656 | 4.87972 | 2.57832 | 0.38785 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 423.07830 423.07830 |
| TBTA | −9.83427 | −0.71594 | 9.83427 | 0.71594 | 9.11834 | 4.55917 | 0.21934 | 5.27510 | 3.05173 | 0.32768 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 741.87276 741.87276 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| B3LYP/SDD level | |||||||||||
| PBA | −8.04511 | −1.91515 | 8.04511 | 1.91515 | 6.12996 | 3.06498 | 0.32627 | 4.98013 | 4.04598 | 0.24716 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 825.81539 825.81539 |
| PAA | −8.90418 | −1.88685 | 8.90418 | 1.88685 | 7.01733 | 3.50866 | 0.28501 | 5.39552 | 4.14853 | 0.24105 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 687.77878 687.77878 |
| PBTA | −7.43230 | −3.83275 | 7.43230 | 3.83275 | 3.59955 | 1.79978 | 0.55562 | 5.63253 | 8.81371 | 0.11346 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 546.73066 546.73066 |
| TBTA | −7.66251 | −4.19358 | 7.66251 | 4.19358 | 3.46893 | 1.73447 | 0.57655 | 5.92805 | 10.13041 | 0.09871 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875.01194 875.01194 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| B3LYP/6-31G level | |||||||||||
| PBA | −7.81245 | −2.16632 | 7.81245 | 2.16632 | 5.64613 | 2.82307 | 0.35422 | 4.98938 | 4.40902 | 0.22681 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 822.09078 822.09078 |
| PAA | −8.74200 | −2.08114 | 8.74200 | 2.08114 | 6.66086 | 3.33043 | 0.30026 | 5.41157 | 4.39660 | 0.22745 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 684.31020 684.31020 |
| PBTA | −7.30006 | −3.63601 | 7.30006 | 3.63601 | 3.66404 | 1.83202 | 0.54585 | 5.46803 | 8.16022 | 0.12255 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544.24970 544.24970 |
| TBTA | −7.52455 | −4.01262 | 7.52455 | 4.01262 | 3.51193 | 1.75596 | 0.56949 | 5.76859 | 9.47530 | 0.10554 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 872.82143 872.82143 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||||||
| B3LYP/6-31++G level | |||||||||||
| PBA | −8.26933 | −2.46836 | 8.26933 | 2.46836 | 5.80097 | 2.90048 | 0.34477 | 5.36885 | 4.96892 | 0.20125 | −23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 822.95943 822.95943 |
| PAA | −9.14310 | −2.37285 | 9.14310 | 2.37285 | 6.77025 | 3.38512 | 0.29541 | 5.75797 | 4.89706 | 0.20420 | −21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 685.10315 685.10315 |
| PBTA | −7.48183 | −3.84527 | 7.48183 | 3.84527 | 3.63656 | 1.81828 | 0.54997 | 5.66355 | 8.82037 | 0.11337 | −19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 544.86904 544.86904 |
| TBTA | −7.67775 | −4.19957 | 7.67775 | 4.19957 | 3.47819 | 1.73909 | 0.57501 | 5.93866 | 10.13967 | 0.09862 | −28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 873.41745 873.41745 |
Chemical hardness is defined as the resistance towards the electron cloud polarization and deformation of chemical species.46 Hard and Soft Acids–Bases (HSAB)47,48 and Maximum Hardness (MHP)49 Principles based on chemical hardness concept are very useful in terms of estimating the directions of chemical reactions and understanding of the nature of chemical interactions. According to maximum hardness principle, a chemical system tends to arrange itself so as to achieve maximum hardness and chemical hardness can be considered as a measure of stability. As is given above, softness is the reciprocal of chemical hardness and it can be said that softness is a measure of the reactivity. Chemical hardness, softness and ΔE are quantum chemical parameters closely associated with each other. As it is well known, both softness and hardness are resulted based on HOMO and LUMO orbital energies as a theoretical outcomes of Koopman's theorem. Hard molecules which have high HOMO–LUMO energy gap cannot act as good corrosion inhibitor. However, soft molecules which have low HOMO–LUMO energy gap may be good corrosion inhibitor because those can easily donate the π-electrons to the metals. It is apparent that we can write the same corrosion inhibition ranking considering these aforementioned chemical properties. On the basis of the calculated chemical hardness, softness and energy gap given in the related tables, the corrosion inhibition efficiency ranking of studied chemical compounds can be written as: PBTA > TBTA > PBA > PAA. Pearson50 has classified as hard and soft the Lewis acids–bases. In this classification, sulfur containing molecules is located in the group of soft molecules. In this sense, it should be noted that the ranking given above is also compatible with theoretical expectations. Namely, TBTA containing sulfur atom should be more effective corrosion inhibitor among other molecules considered in this study.
Electronegativity is a key parameter used to estimate the electron transfer between metal and inhibitor. It is seen from the equation given below that electron transfer from the inhibitors to the metallic surfaces were decreases when the electronegativity of the inhibitors increases. According to Sanderson's electronegativity equalization principle,51,52 the electron transfer between metal and inhibitor continues until their electronegativity values become equal with each other. According to Pearson,47 the fraction of electrons transferred from corrosion inhibitor to metal (ΔN) can be calculated via following equation. It is important to note that this equation has been derived with the help of chemical hardness and electronegativity equalization principle.
 | (13) |
The partial atomic charges on atoms of the inhibitor molecules provide important clues about the identifying of reactive center.53 The constitute atoms with the highest negative charge represent the high tendency to be adsorbed of inhibitor molecule on the metal surface. The inhibitors can easily interact with the metal surface through such atoms. Proton affinity is a measure of basicity and it can be defined as the enthalpy of the reaction with H+ ion of a chemical species in gas phase.54 As can be understood from this definition, comparisons regarding proton affinities of molecules should be performed considering the results obtained in the gas phase. The presence of the heteroatoms such as oxygen, nitrogen and sulfur in the molecules of benzotriazole and phospono derivatives causes to high tendency for protonation in acidic medium. Thus, analysis of the protonated forms of studied compounds is important in terms of the calculation of the proton affinities of neutral inhibitors. It should be noted that a chemical compound with high proton affinity acts as a good corrosion inhibitor. If so, according to proton affinity values given in Table 1 of studied compounds, corrosion inhibition efficiencies follow the order: PAA > PBTA > TBTA > PBA. This ranking is not compatible with the results obtained from molecular dynamic simulation approach. It is important to note that only the ranking obtained at B3LYP/6-31-G level is consistent with the binding and adsorption energies presented in Table 5. Proton affinity values obtained have been calculated considering eqn (14) and (15).
| PA = E(pro) − (E(non-pro) + EH+) | (14) |
| EH+ = E(H3O+) − E(H2O) | (15) |
| Systems | Einteraction (kJ mol−1) | Ebinding (kJ mol−1) |
|---|---|---|
| Al + PBTA | −273.328 | 273.328 |
| Al + TBTA | −266.064 | 266.064 |
| Al + PBA | −264.531 | 264.531 |
| Al + PAA | −254.412 | 254.412 |
Electrophilicity (ω) and nucleophilicity are some of the parameters which are useful in their ability to help predict chemical behavior of molecules.55 Nucleophilicity (ε) is physically the inverse of electrophilicity (1/ω). Electrophilicity can be used to compare the tendency of the inhibitor molecule to accept the electrons. For this reason, it should be stated that a molecule that has large electrophilicity value is powerless in terms of the prevention of corrosion. On the other hand, a molecule that has large nucleophilicity value is a good corrosion inhibitor. Within framework of this information, we can write the corrosion inhibition efficiency ranking of the molecules as: PBA > PBTA > PAA > TBTA. A consistent ranking with the binding and adsorption energies presented in Table 5 has been obtained at HF/6-31++G level. This is well known that, HF/6-31++G level of basis set is one of the most trusted method in computational chemistry studies.56 In this basis all the theoretical outcomes obtained from this basis set are coincide with the experimental outcomes.
3.1. Molecular dynamic simulations
Nowadays, molecular dynamics (MD) simulation have considered as a modern tool to investigate the adsorption behavior of the inhibitor molecules on the concerned metallic surfaces. Recently Obot et al., Xia et al., Musa et al. and many other scientists are working on it to search the most adorable adsorption configuration of the corrosion inhibitors on the metallic surfaces.57–60 In this occasion, in order to finding out more suitable and adorable adsorption configuration of the studied inhibitors molecules, MD simulation is carried out in this present investigation.Among the different steps involved in the modeling approach, the first step in this computational study is the geometry optimization (i.e. energy minimization) of the investigated corrosion inhibitor. Optimization is carried out by employing a ‘smart’ algorithm, started with a steepest descent path then followed the conjugate gradient path and finally ended with the Newton's method.42 After the geometry optimization of the concern inhibitor, simulation box is constructed by the all concerned species (here water and inhibitor molecules). Followed by dynamic simulations are carried out. In this occasion the system tend towards the equilibrium when the temperature and energy of the system reached in their equilibrium state. After the system reached equilibrium Einteraction and Ebinding of the system were calculated by the above mentioned eqn (11) and (12) respectively. The obtained values are tabulated in the Table 5 and the best adorable adsorption configuration of the studied inhibitor molecules on the Al (111) surface are now depicted in Fig. 3. From Fig. 3 it can be seen that all the inhibitor molecules adsorb on the Al (111) surface with almost parallel or flat disposition. This is simply due to the formation of strong coordinate bond and back-bonding formation between the inhibitor molecule and Al-atom of metal surface. Higher the surface coverage by the inhibitors higher is the inhibition efficiency of the inhibitors. Herein, all the inhibitors adsorb in the flat orientation. Then the obvious question is coming if all the inhibitors adsorb in flat orientation why PBTA and TBTA behave as a good corrosion inhibitors in comparison to PBA and PAA. This phenomenon can be explained in terms of considering their molecular structure. It is well known that if the inhibitor molecules contain higher number of heteroatom with π-conjugated system it covers higher surface area on the metallic surfaces and thereby higher inhibition efficiency is obtained. From the structure of the inhibitor molecules it is seen that PBTA and TBTA contains good many number of heteroatom with conjugated aromatic rings in their structures. Therefore, higher inhibition efficiency is expected and it is obtained accordingly from the experimental investigation. In comparison to the above mentioned inhibitors, PBA and PAA contain only small aliphatic chain. Thus, not able to cover higher surface area on the metallic surfaces. Thus, lower inhibition efficiency is expected and obtained accordingly.
The calculated values of interaction energy of the adsorption systems are −273.328, −266.064, −264.531 and −254.412 kJ mol−1 for PBTA, TBTA, BPA and PAA respectively. These larger negative values of interaction energies can be ascribed due to the strong interaction between the studied inhibitors molecules and aluminum surfaces. It is also apparent from these interaction energy values that PBTA and TBTA have highest interaction energy value among the four inhibitors. As a result, higher is the corrosion protection capability. Moreover, the adsorption ability of the molecule on the iron surface can also be measured from the binding energy values. Higher is the binding energy, more stable will be the adsorption. The obtained binding energy values are also corroborated with the experimental findings. Therefore, it is concluded from the interaction energy as well as binding energy values that aromatic conjugated system with good many numbers of heteroatoms containing molecule have more corrosion protection capability than that of the small aliphatic chain containing molecules. Therefore, MD simulation results coincide with the quantum chemical calculations and previously reported experimental findings.
4. Conclusions
Hartree Fock (HF), density functional theory at B3LYP with different basis sets and molecular dynamic simulation approach were performed to evaluate the corrosion inhibition efficiencies of some benzotriazole and phospono derivatives at the molecular level. The neutral and protonated forms were considered in quantum chemical calculations in gas and aqueous phases. Based on the results obtained in this study, the following conclusions can be presented.(1) The results of both DFT approach and molecular dynamics simulations approach showed that the corrosion inhibition efficiency ranking of studied compounds can be given as: PBTA > TBTA > PBA > PAA.
(2) The binding energies obtained in the study using molecular dynamic simulations approach show that these benzotriazole and phospono derivatives are good corrosion inhibitors against corrosion of aluminum. In addition, it should be noted that the most effective inhibitor among them is PBTA.
(3) The theoretical results obtained in this study are important towards rational design new benzotriazole and phospono derivatives as corrosion inhibitor.
Acknowledgements
PB thanks Department of Science and Technology, Govt. of India for supporting a research project under Fast Track Scheme for Young Scientists (vide ref. no. SB/FT/CS-003/2012 and project no. GAP-183112). SKS would like to acknowledge DST, New Delhi, India for his DST INSPIRE Fellowship.References
- S. N. Raicheva, B. V. Aleksiev and E. I. Sokolova, Corros. Sci., 1993, 34, 343–350 CrossRef CAS.
- H. D. Leçe, K. C. Emregül and O. Atakol, Corros. Sci., 2008, 50, 1460–1468 CrossRef.
- I. B. Obot, D. D. Macdonald and Z. M. Gasem, Corros. Sci., 2015, 99, 1–30 CrossRef CAS.
- S. Kaya, B. Tuzun, C. Kaya and I. B. Obot, J. Taiwan Inst. Chem. Eng., 2016, 58, 528–535 CrossRef CAS.
- A. Y. El-Etre, Corros. Sci., 2001, 43, 1031–1039 CrossRef CAS.
- A. K. Maayta and N. A. F. Al-Ravashdeh, Corros. Sci., 2004, 46, 1129–1140 CrossRef CAS.
- A. Y. El-Etre, Corros. Sci., 2003, 45, 2485–2495 CrossRef CAS.
- S. Kr. Saha, P. Ghosh, A. Hens, N. C. Murmu and P. Banerjee, Phys. E, 2015, 66, 332–341 CrossRef CAS.
- T. Chakraborty, A. Hens, S. Kulashrestha, N. C. Murmu and P. Banerjee, Phys. E, 2015, 69, 371–377 CrossRef CAS.
- S. Kr. Saha, A. Hens, A. Roychowdhury, A. K. Lohar, N. C. Murmu and P. Banerjee, Can. Chem. Trans., 2014, 2, 489–503 Search PubMed.
- K. F. Khaled, Electrochim. Acta, 2008, 53, 3484–3492 CrossRef CAS.
- I. B. Obot, E. E. Ebenso and M. M. Kabanda, J. Environ. Chem. Eng., 2013, 1, 431–439 CrossRef CAS.
- M. M. Kabanda, I. B. Obot and E. E. Ebenso, Int. J. Electrochem. Sci., 2013, 8, 10839–10850 CAS.
- I. B. Obot and N. O. Obi-Egbedi, Corros. Sci., 2010, 52, 657–660 CrossRef CAS.
- P. Geerlings, F. D. Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874 CrossRef CAS PubMed.
- P. Geerlings and F. D. Proft, Phys. Chem. Chem. Phys., 2008, 10, 3028–3042 RSC.
- S. Kaya and C. Kaya, Mol. Phys., 2015, 113, 1311–1319 CrossRef CAS.
- S. Kaya and C. Kaya, Comput. Theor. Chem., 2015, 1060, 66–70 CrossRef CAS.
- W. Yang, C. Lee and S. K. Ghosh, J. Phys. Chem., 1985, 89, 5412–5414 CrossRef CAS.
- S. Kaya and C. Kaya, Comput. Theor. Chem., 2015, 1052, 42–46 CrossRef CAS.
- Z. S. Safi and S. Omar, Chem. Phys. Lett., 2014, 610–611, 321–330 CrossRef CAS.
- P. K. Chattaraj, U. Sarkar and D. R. Roy, Chem. Rev., 2006, 106, 2065–2091 CrossRef CAS PubMed.
- T. Koopmans, Physica, 1933, 1, 104–113 CrossRef CAS.
- D. Gopi, E. M. Sherif, V. Manivannan, D. Rajeswari, M. Surendiran and L. Kavitha, Ind. Eng. Chem. Res., 2014, 53, 4286–4294 CrossRef CAS.
- C. Adamo and D. Jacquemin, Chem. Soc. Rev., 2013, 42, 845–856 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman Jr, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03W, GaussianInc., Wallingford, CT, 2004 Search PubMed.
- R. D. Dennington, T. A. Keith and C. M. Millam, GaussView 5.0, Wallingford CT, 2009 Search PubMed.
- D. J. Tozer, R. D. Amos, N. C. Handy, B. O. Roos and L. Serrano-Andres, Mol. Phys., 1999, 97, 859–868 CrossRef CAS.
- A. Dreuw, J. L. Weisman and M. Head-Gordon, J. Chem. Phys., 2003, 119, 2943–2946 CrossRef CAS.
- L. Bernasconi, M. Sprik and J. Hutter, J. Chem. Phys., 2003, 119, 12417–12431 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- M. E. Foster and B. M. Wong, J. Chem. Theory Comput., 2012, 8, 2682–2687 CrossRef CAS PubMed.
- T. Körzdörfer, J. S. Sears, C. Sutton and J. L. Brédas, J. Chem. Phys., 2011, 135, 204107/1–204107/6 CrossRef PubMed.
- B. M. Wong and T. H. Hsieh, J. Chem. Theory Comput., 2010, 6, 3704–3712 CrossRef CAS PubMed.
- Z. Zheng, J. L. Bredas and V. Coropceanu, J. Phys. Chem. Lett., 2016, 7, 2616–2621 CrossRef CAS PubMed.
- H. Chermette, J. Comput. Chem., 1999, 20, 129–154 CrossRef CAS.
- R. G. Parr and P. K. Chattaraj, J. Am. Chem. Soc., 1991, 113, 1854–1855 CrossRef CAS.
- R. P. Iczkowski and J. L. Margrave, J. Am. Chem. Soc., 1961, 83, 3547–3551 CrossRef CAS.
- N. Islam and D. C. Ghosh, Int. J. Quantum Chem., 2011, 109, 917–931 CAS.
- W. Yang and R. G. Parr, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 6723–6726 CrossRef CAS.
- R. G. Parr, L. Sventpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- Materials Studio 6.1 Manual, Accelrys, Inc., San Diego, CA, 2007 Search PubMed.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- Z. Cao, Y. Tang, H. Cang, J. Xu, G. Lu and W. Jing, Corros. Sci., 2014, 83, 292–298 CrossRef CAS.
- S. K. Saha, A. Dutta, P. Ghosh, D. Sukul and P. Banerjee, Phys. Chem. Chem. Phys., 2015, 17, 5679–5690 RSC.
- G. Makov, J. Phys. Chem., 1995, 99, 9337–9339 CrossRef CAS.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS.
- R. G. Pearson, J. Chem. Educ., 1968, 45, 581–587 CrossRef CAS.
- R. G. Pearson, Acc. Chem. Res., 1993, 26, 250–255 CrossRef CAS.
- R. G. Pearson, Chemical Hardness: Applications from Molecules to Solids, Wiley-VCH, Weinheim, Germany, 1997 Search PubMed.
- R. T. Sanderson, Chemical Bond and Bond Energy, Academic Press, New York, 1976 Search PubMed.
- R. T. Sanderson, J. Chem. Educ., 1954, 31, 2–7 CrossRef CAS.
- N. O. Obi-Egbedi, I. B. Obot and M. I. El-Khaiary, J. Mol. Struct., 2011, 1002, 86–96 CrossRef CAS.
- C. Kaya, Inorganic Chemistry 1 and 2, Palme Publishing, Ankara, 2011 Search PubMed.
- A. A. El-Bindary, M. A. Hussein and R. A. El-Boz, J. Mol. Liq., 2015, 211, 256–267 CrossRef CAS.
- M. K. Awad, M. R. Mustafa and M. M. A. Elnga, J. Mol. Struct.: THEOCHEM, 2010, 959, 66–74 CrossRef CAS.
- I. B. Obot and Z. M. Gasem, Corros. Sci., 2014, 83, 359–366 CrossRef CAS.
- S. Xia, M. Qiu, L. Yu, F. Liu and H. Zhao, Corros. Sci., 2008, 50, 2021–2029 CrossRef CAS.
- L. Guo, S. Zhu and S. Zhang, J. Ind. Eng. Chem., 2015, 24, 174–180 CrossRef CAS.
- A. Y. Musa, R. T. T. Jalgham and A. B. Mohamad, Corros. Sci., 2012, 56, 176–183 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2016 |


