Potential thermoelectric materials CsMI₃ (M = Sn and Pb) in perovskite structures from first-principles calculations

Abstract

The thermoelectric properties of halide perovskites CsMI₃ (M = Sn and Pb) are investigated from a combination of first-principles calculations and semiclassical Boltzmann transport theory by considering both the electron and phonon transport. The electronic part is performed using a modified Becke and Johnson (mBJ) exchange potential, including spin–orbit coupling (SOC), while the phonon part is computed using generalized gradient approximation (GGA). It is found that SOC has remarkable detrimental effect on the n-type power factor, while it has a negligible influence on p-type doping, which can be explained by considering the effect of SOC on the conduction and valence bands. The calculated results show exceptionally low lattice thermal conductivities in CsSnI₃ and CsPbI₃, and the corresponding room-temperature lattice thermal conductivity is 0.54 W m⁻¹ K⁻¹ and 0.25 W m⁻¹ K⁻¹, which suggests that they may be potential thermoelectric materials. At 1000 K, the maximal figure of merit ZT is up to 0.63 and 0.64 for CsSnI₃ and CsPbI₃ with scattering time τ = 10⁻¹⁴ s, and the peak ZT is 0.49 and 0.41 with τ = 10⁻¹⁵ s. These results lead us to believe that CsMI₃ (M = Sn and Pb) in perovskite structures may be potential thermoelectric materials.

---

I. Introduction

Thermoelectric materials enable the direct conversion from heat to electricity, which may make an essential contribution to the energy crisis.^1,2 A good thermoelectric material should have high dimensionless figure of merit ZT = S²σT/(κ_e + κ_L), where S, σ, T, κ_e and κ_L are the Seebeck coefficient, electrical conductivity, absolute temperature, the electronic and lattice thermal conductivities, respectively. A high ZT material requires a high power factor (S²σ) and low thermal conductivity (κ = κ_e + κ_L). They generally influence each other, and a counteracting relationship between the electrical conductivity and thermal conductivity or Seebeck coefficient is often found. Excellent classic thermoelectric materials include bismuth–tellurium systems,^3,4 silicon–germanium alloys,^5,6 lead chalcogenides^7,8 and skutterudites.^9,10 For thermoelectric research, searching for potential high ZT materials with a classic common lattice structure, like a perovskite structure, is interesting and challenging.

The cubic perovskite structure SrTiO₃ has attracted growing attention for thermoelectric power generation.¹¹ The ZT value of undoped SrTiO₃ is less than 0.5 due to its high thermal conductivity,¹² which can be reduced by introducing point defects.^13,14 Searching other perovskites for more efficient thermoelectric applications is imperative and fruitful. The AMX₃ perovskites (A = Cs, CH₃NH₃; M = Sn, Pb; X = halide) have recently attracted a great deal of attention for solar cell designs, which can realize up to 15% energy conversion efficiencies.^15–18 A fair amount of theoretical works have been performed to investigate their electronic structures, phonons and optical properties.^19–24 The CsMI₃ (M = Sn and Pb) under reasonable hydrostatic pressure can turn into three-dimensional topological insulators, which has been predicted by first-principles calculations.^25,26

Here, we report on the thermoelectric properties of cubic CsMI₃ (M = Sn and Pb) in perovskite structures from a combination of first-principles calculations and semiclassical Boltzmann transport theory. The spin–orbit coupling (SOC) can produce obvious effects on the power factor of many thermoelectric materials,^27–34 so the SOC is included in our calculations of the electronic part. The calculated results show that SOC has a notably reduced influence on the n-type power factor. It is noteworthy that ultralow lattice thermal conductivities are attained for CsMI₃ (M = Sn and Pb), and the corresponding lattice thermal conductivities at 300 K are 0.54 W m⁻¹ K⁻¹ and 0.25 W m⁻¹ K⁻¹, which is comparable with the lattice thermal conductivity of 0.23 W m⁻¹ K⁻¹ in SnSe with an unprecedented ZT of 2.6 at 923 K.³⁵ Finally, the dimensionless thermoelectric figure of merit ZT is calculated with τ = 10⁻¹⁴ s or τ = 10⁻¹⁵ s, and can reach about 0.6 or 0.4 at high temperature with optimized doping.

The rest of the paper is organized as follows. In the next section, we shall describe computational details. In the third section, we shall present the electronic structures and thermoelectric properties of CsMI₃ (M = Sn and Pb). Finally, we shall give our discussions and conclusion in the fourth section.

II. Computational details

The electronic structures of CsMI₃ (M = Sn and Pb) are modelled using a full-potential linearized augmented-plane-waves method within the density functional theory (DFT),³⁶ as implemented in the WIEN2k package.³⁷ We employ Tran and Blaha's mBJ exchange potential plus local-density approximation (LDA) correlation potential for the exchange–correlation potential,³⁸ which has been known to produce more accurate band gaps than LDA and GGA for these materials.³⁹ Moreover, the computational time is nearly the same as those for LDA or GGA. The SOC was included self-consistently^40–43 due to containing heavy elements, which leads to band splitting, and produces important effects on the power factor. We use 5000 k-points in the first Brillouin zone for the self-consistent calculation, make harmonic expansion up to l_max = 10 in each of the atomic spheres, and set R_mt × k_max = 8. The self-consistent calculations are considered to be converged when the integration of the absolute charge-density difference between the input and output electron density is less than 0.0001|e| per formula unit, where e is the electron charge. Transport calculations, including Seebeck coefficient, electrical conductivity and electronic thermal conductivity, are performed through solving Boltzmann transport equations within the constant scattering time approximation (CSTA) as implemented in BoltzTrap,⁴⁴ and reliable results have been obtained for several materials.^45–47 To obtain accurate transport coefficients, we use 140 000 k-points in the first Brillouin zone for the energy band calculation. The lattice thermal conductivities are calculated within the linearized phonon Boltzmann equation by using Phono3py + VASP codes.^48–51 For the third-order force constants, 2 × 2 × 2 supercells are built, and reciprocal spaces of the supercells are sampled by 3 × 3 × 3 meshes. To compute lattice thermal conductivities, the reciprocal spaces of the primitive cells are sampled using the 20 × 20 × 20 meshes.

III. Main calculated results and analysis

CsMI₃ (M = Sn and Pb) belong to the family of perovskite semiconductors, which consists of a network of corner-sharing MI₆ octahedra. The perovskites undergo a series of structural transitions from high temperature to low temperature due to the rotations and rearrangements of the MI₆ octahedra; they change from the cubic phase to the tetragonal phase, and then to the orthorhombic phase. To attain the lattice thermal conductivity relatively easily (calculating lattice thermal conductivity is very time consuming, especially for a low-symmetry structure), we investigate cubic CsMI₃ (M = Sn and Pb), and the schematic crystal structure is shown in Fig. 1. Based on the experimental structures, the electronic structures of CsMI₃ (M = Sn and Pb) are investigated using mBJ and mBJ + SOC, and the energy band structures are plotted in Fig. 2. Both mBJ and mBJ + SOC show that the CsMI₃ (M = Sn and Pb) species are direct-gap semiconductors, with the conduction band minimum (CBM) and valence band maximum (VBM) at the R point. The mBJ and mBJ + SOC energy band gap values are 0.52 eV (1.69 eV) and 0.17 eV (0.50 eV) for CsSnI₃ (CsPbI₃), respectively. The conduction bands are dominated by M-6p states, and the CBM is threefold degenerate in the absence of SOC. The VBM is a mixture of I-p and M-s states, which is nondegenerate. The SOC can remove band degeneracy, and lead to a spin–orbital splitting value of 0.43 eV and 1.49 eV for CsSnI₃ and CsPbI₃ at CBM. It is clearly seen that, near the Fermi level, the SOC has a more obvious influence on the conduction bands than on the valence bands. The related data are shown in Table 1, and the mBJ gaps are larger than GGA or LDA ones, but are smaller than GW or HSE ones.^19,21–24

Fig. 1 The crystal structure of CsMI₃ (M = Sn and Pb). The largest blue ball represent the Cs atom, the medium green balls M, and the smallest red balls I.

Fig. 2 The energy band structures of CsMI₃ (M = Sn and Pb) using mBJ (left) and mBJ + SOC (right).

Table 1 The experimental lattice constant a (Å); the calculated energy band gap values with mBJ E₁ (eV) and mBJ + SOC E₂ (eV); E₁ − E₂ (eV); spin–orbit splitting Δ (eV) at the CBM

Name	a	E1	E2	E1 − E2	Δ
CsSnI3	6.22	0.52	0.17	0.35	0.43
CsPbI3	6.29	1.69	0.50	1.19	1.49

---

Next, we calculate semi-classic transport coefficients using CSTA Boltzmann theory. The rigid band approach is used to mimic the doping effects by shifting the Fermi level, which is reasonable, when the doping level is low.^52–54 The semi-classic transport coefficients, such as the Seebeck coefficient S, electrical conductivity with respect to scattering time σ/τ and power factor with respect to scattering time S²σ/τ, as a function of doping level at room temperature using mBJ and mBJ + SOC are plotted in Fig. 3. Due to electrical thermal conductivity κ_e = LσT (Lorenz number L = π²k_B²/3e², where k_B is the Boltzmann constant, e is the charge of an electron), the electrical thermal conductivity has a similar outlines to the electrical conductivity. The Fermi level moves into the conduction bands, which means n-type doping (negative doping levels) with the negative Seebeck coefficient. The p-type doping (positive doping levels) with the positive Seebeck coefficient can be achieved by shifting the Fermi level into the valence bands. Although the Seebeck coefficient is very large, when the Fermi level is in the middle of band gap, the low electrical conductivity leads to very small power factor. Upon shifting the Fermi level into the conduction bands or valence bands, the Seebeck coefficient (absolute value) decreases, while the electrical conductivity increases, which leads to a maximum of the power factor at certain doping level.

Fig. 3 At room temperature, transport coefficients of CsSnI₃ (top panel) and CsPbI₃ (bottom panel) are plotted as a function of doping level (N): Seebeck coefficient S, electrical conductivity with respect to scattering time σ/τ and power factor with respect to scattering time S²σ/τ calculated with mBJ (black solid lines) and mBJ + SOC (red dashed lines). The N means electrons (minus value) or holes (positive value) per unit cell.

It has been proved that SOC has very important effects on the power factor in many thermoelectric materials containing heavy elements.^27–34 The calculated results show that SOC has an obviously reduced influence on S and σ/τ in n-type doping for both CsSnI₃ and CsPbI₃, but weak effects for p-type. The large slope of the density of states (DOS) near the energy band gap can induce a large Seebeck coefficient in narrow-gap semiconductors. This can be understood by the following formula: ,⁵⁵ where n(E) and μ(E) are the energy dependent carrier density and mobility, respectively. It is found that the slope of the DOS using mBJ near the energy band gap is larger than that using mBJ + SOC for the conduction bands, while they are nearly the same for the valence bands. Band degeneracy, namely band convergence, can induce a larger slope of DOS. The SOC can reduce the slope of DOS by removing band degeneracy. The SOC effects on energy bands can explain SOC influences on S. The SOC-induced reduced S and σ/τ for n-type lead to a very remarkable detrimental influence on the power factor, especially for CsPbI₃. However, the SOC has weak effects on p-type power factor. For CsPbI₃, at the absence of SOC, the best n-type power factor is larger than that in p-type doping. However, including SOC, it is opposite in the considered doping range. Similar SOC-induced switch of best power factor between n-type and p-type can be achieved in Mg₂Sn.³² Therefore, including SOC is very important in the theoretical prediction of thermoelectric properties of CsMI₃ (M = Sn and Pb).

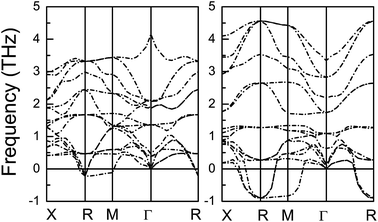
The power factor and electronic thermal conductivity with respect to scattering time (S²σ/τ and κ_e/τ) of CsSnI₃ and CsPbI₃ as a function of doping level with temperature from 200 K to 1000 K using mBJ + SOC are shown in Fig. 4. For CsSnI₃, n-type doping has larger power factor than p-type doping, while the p-type power factor is larger than that of the n-type for CsPbI₃. If we assume the scattering time is constant, in the considered doping and temperature range, the best power factor of CsSnI₃ is nearly four times larger than that of CsPbI₃, and about two times larger for electronic thermal conductivity. The lattice thermal conductivity is an important factor, which significantly affects thermoelectric performance. The phonon band structures and lattice thermal conductivities κ_L as a function of temperature of CsMI₃ (M = Sn and Pb) are shown in Fig. 5 and 6, respectively. The calculated results show imaginary frequency modes for CsMI₃ (M = Sn and Pb), which reflect the instability of the cubic crystal structures at low temperatures. These are in agreement with previous theoretical and experimental results.^20,56 The calculated results show ultralow lattice thermal conductivities in CsMI₃ (M = Sn and Pb). The lattice thermal conductivity can be assumed to have weak dependence on doping level, and typically proceeds as 1/T. The corresponding room-temperature lattice thermal conductivity is 0.54 W m⁻¹ K⁻¹ and 0.25 W m⁻¹ K⁻¹ for CsSnI₃ and CsPbI₃. The imaginary frequencies may produce some errors in the lattice thermal conductivities of CsMI₃ (M = Sn and Pb) at low temperature. The major cause is that they undergo structural transition from high temperature to low temperature. However, CsMI₃ (M = Sn and Pb) should possess low lattice thermal conductivities with low-symmetry crystal structures, because the structural transition is only due to rotations and rearrangements of MI₆ octahedra, and the basic framework of perovskites still remains. Theoretically, ultralow lattice thermal conductivities in many compounds have been predicted, such as PbRbI₃ (0.10 W m⁻¹ K⁻¹), PbIBr (0.13 W m⁻¹ K⁻¹), K₂CdPb (0.45 W m⁻¹ K⁻¹) and Cs₂[PdCl₄]I₂ (0.31 W m⁻¹ K⁻¹).⁵⁷ Many compounds composed of these elements (Pb, Cs, I, Br and Cl) show lower lattice thermal conductivities,⁵⁷ which supports our results of ultralow lattice thermal conductivities in CsMI₃ (M = Sn and Pb). It is found that the lattice thermal conductivity of CsSnI₃ is nearly two times larger than that of CsPbI₃.

Fig. 4 The power factor with respect to scattering time S²σ/τ and electronic thermal conductivity with respect to scattering time κ_e/τ of CsSnI₃ (top panel) and CsPbI₃ (bottom panel) as a function of doping level with temperature being 200, 400, 600, 800 and 1000 (unit: K) using mBJ + SOC.

Fig. 5 Phonon band structure of CsSnI₃ (left) and CsPbI₃ (right) using GGA.

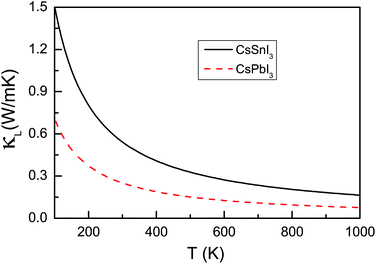Fig. 6 The lattice thermal conductivities κ_L of CsMI₃ (M = Sn and Pb) as a function of temperature using GGA.

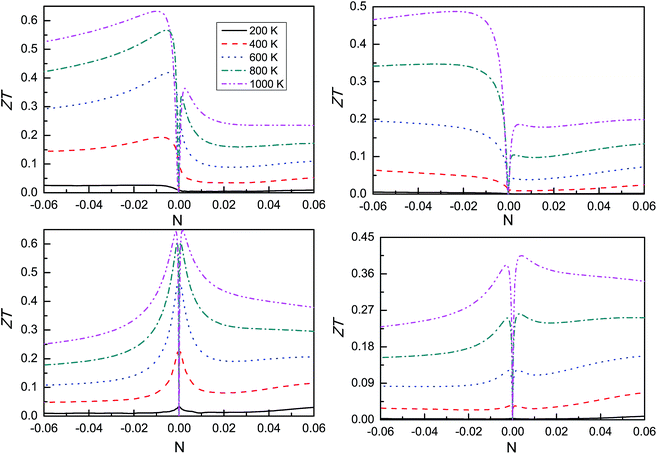
Due to the complexity of various carrier scattering mechanisms, it is difficult to calculate the scattering time τ from first principles. To estimate the thermoelectric conversion efficiency, the thermoelectric figure of merit ZT is calculated with hypothetical τ = 10⁻¹⁴ and τ = 10⁻¹⁵ s, and plotted in Fig. 7. The peak ZT and corresponding doping concentrations for both n- and p-type at 1000 K are summarized in Table 2. For CsSnI₃, the n-type doping has a larger ZT than p-type doping, which is mainly due to the larger n-type Seebeck coefficient. However, the ZT between n- and p-type are nearly the same for CsPbI₃ due to almost the same Seebeck coefficient. According to Fig. 4 and 6, the total thermal conductivity κ is dominated by the lattice thermal conductivity κ_L in the very low doping level, but the electronic thermal conductivity κ_e becomes much larger than lattice thermal conductivity κ_L in the slightly high doping region. These leads to a very low doping concentration for peak ZT. Therefore, the electronic thermal conductivity of CsMI₃ (M = Sn and Pb) is a fatal disadvantage to obtain a higher ZT value.

Fig. 7 The ZT of CsSnI₃ (top panel) and CsPbI₃ (bottom panel) as a function of doping level with temperature being 200, 400, 600, 800 and 1000 (unit: K), and the scattering time τ is 1 × 10⁻¹⁴ s (left) and 1 × 10⁻¹⁵ s (right).

Table 2 Peak ZT for both n- and p-type at 1000 K with τ = 10⁻¹⁴ s and τ = 10⁻¹⁵ s, and the corresponding doping concentrations. The doping concentration equals 4.16 × 10²¹ cm⁻³ (4.02 × 10²¹ cm⁻³) × doping level for CsSnI₃ (CsPbI₃)

Name	τ = 10^−14 s				τ = 10^−15 s
	n (×10^19 cm^−3)	ZT	p (×10^19 cm^−3)	ZT	n (×10^19 cm^−3)	ZT	p (×10^19 cm^−3)	ZT
CsSnI3	4.16	0.63	1.08	0.36	9.78	0.49	1.88	0.19
CsPbI3	0.53	0.64	0.60	0.65	1.14	0.38	1.53	0.41

---

IV. Discussions and conclusion

The CBM of CsMI₃ (M = Sn and Pb) is dominated by a giant spin–orbit coupling (SOC), especially for CsPbI₃. The SOC removes the band degeneracy of CBM by spin–orbit splitting, which leads to obvious effects on the n-type Seebeck coefficient, and further affects the power factor. The larger spin–orbit splitting Δ leads to a more obvious detrimental influence on the n-type power factor, which can be observed from Fig. 4. The similar SOC-induced detrimental influence on the power factor has been observed in Mg₂Sn and half-Heusler ANiB (A = Ti, Hf, Sc, Y; B = Sn, Sb, Bi).^28,32 Therefore, it is very important for the electronic part of the thermoelectric properties of CsMI₃ (M = Sn and Pb) to include SOC.

CsMI₃ (M = Sn and Pb) have been predicted to be three-dimensional topological insulators under reasonable hydrostatic pressure using a tight-binding analysis and first-principles calculations,^25,26 which means that the electronic structures of CsMI₃ (M = Sn and Pb) are easily tuned by pressure. The pressure-induced enhanced power factor has been predicted in Mg₂Sn³² and BiTeI⁵⁸ by first-principles calculations. Experimentally, it is possible to tune the thermoelectric properties of CsMI₃ (M = Sn and Pb) by pressure.

To attain accurate gaps, an improved mBJ exchange potential is used to investigate the electronic structures and thermoelectric properties of CsMI₃ (M = Sn and Pb), which is superior to GGA and LDA. However, the gaps are still far below the experimental values for lead halide perovskites. Recently, Jishi, Ta and Sharif considered a new set of values for the parameter of mBJ exchange potential (JTS-mBJ), and the calculated band gaps of all six lead halide compounds CH₃NH₃PbI₃, CH₃NH₃PbBr₃, CsPbX₃ (X = Cl, Br, I) and RbPbI₃ agree well with the experimental results.³⁹ Here, the JTS-mBJ is used to investigate electronic structures of CsMI₃ (M = Sn and Pb), and the energy band structures using mBJ + SOC and JTS-mBJ + SOC are shown in Fig. 8. The band gap of CsSnI₃ using JTS-mBJ + SOC is 0.18 eV, which is very close to 0.17 eV using mBJ + SOC. For CsPbI₃, the JTS-mBJ + SOC gap is 1.01 eV, which is larger than 0.50 eV with mBJ + SOC, and agrees well with previous value of 1.07 eV with JTS-mBJ + SOC.³⁹ The JTS-mBJ can accurately calculate the band gaps of lead halide semiconductors, but it may be inappropriate for tin halide semiconductors. The outlines of energy band structures using JTS-mBJ + SOC have observable changes with respect to those with mBJ + SOC, especially for valence bands, which can produce obvious effects on transport coefficients. The room-temperature power factors with respect to scattering time S²σ/τ of CsMI₃ (M = Sn and Pb) as a function of doping level using mBJ + SOC and JTS-mBJ + SOC are plotted in Fig. 9. In n-type doping, the power factor of CsMI₃ (M = Sn and Pb) with JTS-mBJ + SOC is larger than that with mBJ + SOC. For p-type, the peak value of the power factor using JTS-mBJ + SOC is smaller than that using mBJ + SOC, and the corresponding doping level moves toward a higher level. The difference of transport coefficients between JTS-mBJ + SOC and mBJ + SOC is mainly due to the difference of their outlines of energy band structures rather than energy band gaps.

Fig. 8 The energy band structures of CsSnI₃ (left) and CsPbI₃ (right) using mBJ + SOC (black lines) and JTS-mBJ + SOC (red lines).

Fig. 9 At room temperature, the power factor with respect to scattering time S²σ/τ of CsSnI₃ (top panel) and CsPbI₃ (bottom panel) are plotted as a function of doping level (N) calculated with mBJ + SOC (black lines) and JTS-mBJ + SOC (red lines).

In summary, mBJ and mBJ + SOC are chosen to investigate the electronic structures and electronic part of the thermoelectric properties of halide perovskites CsMI₃ (M = Sn and Pb). The strength of SOC’s influence on CBM is very large, especially for CsPbI₃, which gives rise to an obvious detrimental influence on n-type power factor. The lattice thermal conductivities of CsMI₃ (M = Sn and Pb) are performed with GGA, and ultralow lattice thermal conductivities are predicted, which is key for providing high thermoelectric performance. At 1000 K, with a low doping level, the figure of merit ZT reaches about 0.6 with τ = 10⁻¹⁴, and about 0.4 with τ = 10⁻¹⁵. The present work provides a platform to search for potential thermoelectric materials from perovskite compounds.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant No. 11404391). We are grateful to the Advanced Analysis and Computation Center of CUMT for the award of CPU hours to accomplish this work.

References

1. Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Nature, 2011, 473, 66–69.
2. L. E. Bell, Science, 2008, 321, 1457.
3. W.-S. Liu, Q. Zhang, Y. Lan, S. Chen, X. Yan, Q. Zhang, H. Wang, D. Wang, G. Chen and Z. Ren, Adv. Energy Mater., 2011, 1, 577–587.
4. D.-K. Ko, Y. Kang and C. B. Murray, Nano Lett., 2011, 11, 2841–2844.
5. M. Zebarjadi, G. Joshi, G. Zhu, B. Yu, A. Minnich, Y. Lan, X. Wang, M. Dresselhaus, Z. Ren and G. Chen, Nano Lett., 2011, 11, 2225–2230.
6. B. Yu, M. Zebarjadi, H. Wang, K. Lukas, H. Wang, D. Wang, C. Opeil, M. Dresselhaus, G. Chen and Z. Ren, Nano Lett., 2012, 12, 2077–2082.
7. Y. Z. Pei, X. Y. Shi and A. Lalonde, et al., Nature, 2011, 473, 66.
8. J. He, J. R. Sootsman, S. N. Girard, J.-C. Zheng, J. Wen, Y. Zhu, M. G. Kanatzidis and V. P. Dravid, J. Am. Chem. Soc., 2010, 132, 8669–8675.
9. A. C. Sklad, M. W. Gaultois and A. P. Grosvenor, J. Alloys Compd., 2010, 505, L6.
10. X. Shi, J. Yang and J. R. Salvador, J. Am. Chem. Soc., 2011, 133, 7837.
11. T. Okuda, K. Nakanishi, S. Miyasaka and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 113104.
12. H. Muta, K. Kurosaki and S. Yamanaka, J. Alloys Compd., 2005, 392, 306.
13. S. Ohta, T. Nomura, H. Ohta and K. Koumoto, J. Appl. Phys., 2005, 97, 034106.
14. H. C. Wang, C. L. Wang, W. B. Su, J. Liu, Y. Sun, H. Peng and L. M. Mei, J. Am. Ceram. Soc., 2011, 94, 838.
15. J. Burschka, N. Pellet, S.-J. Moon, R. Humphry-Baker, P. Gao, M. K. Nazeeruddin and M. Grätzel, Nature, 2013, 499, 316.
16. M. Liu, M. B. Johnston and H. J. Snaith, Nature, 2013, 501, 395.
17. K. Wojciechowski, M. Saliba, T. Leijtens, A. Abate and H. J. Snaith, Energy Environ. Sci., 2014, 7, 1142.
18. G. Hodes, Science, 2013, 342, 317.
19. P. Umari, E. Mosconi and F. De Angelis, Sci. Rep., 2014, 4, 4467.
20. L. Y. Huang and W. R. L. Lambrecht, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 195201.
21. L. Y. Huang and W. R. L. Lambrecht, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 165203.
22. J. Even, L. Pedesseau, J. M. Jancu and C. Katan, Phys. Status Solidi RRL, 2014, 8, 31.
23. J. Even, L. Pedesseau, J. M. Jancu and C. Katan, J. Phys. Chem. Lett., 2013, 4, 2999.
24. L. Lang, J. H. Yang, H. R. Liu, H. J. Xiang and X. G. Gong, Phys. Lett. A, 2014, 378, 290.
25. K. Yang, W. Setyawan, S. Wang, M. B. Nardelli and S. Curtarolo, Nat. Mater., 2012, 11, 614.
26. H. Jin, J. Im and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 121102.
27. K. Kutorasinski, B. Wiendlocha, J. Tobola and S. Kaprzyk, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 115205.
28. S. D. Guo, J. Alloys Compd., 2016, 663, 128.
29. P. Larson, S. D. Mahanti and M. G. Kanatzidis, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 8162.
30. T. J. Scheidemantel, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding and J. O. Sofo, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125210.
31. S. J. Youn and A. J. Freeman, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 085112.
32. S. D. Guo and J. L. Wang, RSC Adv., 2016, 6, 31272.
33. S. D. Guo, RSC Adv., 2016, 6, 47953.
34. N. Singh and U. Schwingenschlögl, Phys. Status Solidi RRL, 2014, 08, 805.
35. L. D. Zhao, S. H. Lo and Y. S. Zhang, et al., Nature, 2014, 508, 373.
36. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
37. P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, an Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties, Karlheinz Schwarz Technische Universität Wien, Austria, 2001.
38. F. Tran and P. Blaha, Phys. Rev. Lett., 2009, 102, 226401.
39. R. A. Jishi, O. B. Ta and A. A. Sharif, J. Phys. Chem. C, 2014, 118, 28344.
40. A. H. MacDonald, W. E. Pickett and D. D. Koelling, J. Phys. C: Solid State Phys., 1980, 13, 2675.
41. D. J. Singh and L. Nordstrom, Plane Waves, Pseudopotentials and the LAPW Method, Springer, New York, 2nd edn, 2006.
42. J. Kunes, P. Novak, R. Schmid, P. Blaha and K. Schwarz, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 153102.
43. D. D. Koelling and B. N. Harmon, J. Phys. C: Solid State Phys., 1977, 10, 3107–3114.
44. G. K. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71.
45. B.-L. Huang and M. Kaviany, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125209.
46. L. Xu, Y. Zheng and J.-C. Zheng, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 195102.
47. J. J. Pulikkotil, D. J. Singh, S. Auluck, M. Saravanan, D. K. Misra, A. Dhar and R. C. Budhani, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 155204.
48. G. Kresse, J. Non-Cryst. Solids, 1995, 192–193, 222–229.
49. G. Kresse and J. Furthmller, Comput. Mater. Sci., 1996, 6, 15–50.
50. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
51. A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306.
52. T. J. Scheidemantel, C. Ambrosch-Draxl, T. Thonhauser, J. V. Badding and J. O. Sofo, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 125210.
53. G. K. H. Madsen, J. Am. Chem. Soc., 2006, 128, 12140.
54. X. Gao, K. Uehara, D. Klug, S. Patchkovskii, J. Tse and T. Tritt, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 125202.
55. W. Liu, X. Tan, K. Yin, H. Liu, X. Tang, J. Shi, Q. Zhang and C. Uher, Phys. Rev. Lett., 2012, 108, 166601.
56. I. Chung, J. H. Song, J. Im, J. Androulakis, C. D. Malliakas, H. Li, A. J. Freeman, J. T. Kenney and M. G. Kanatzidis, J. Am. Chem. Soc., 2012, 134, 8579.
57. A. Seko, A. Togo, H. Hayashi, K. Tsuda, L. Chaput and I. Tanaka, Phys. Rev. Lett., 2015, 115, 205901.
58. S. D. Guo and J. L. Wang, J. Phys. D: Appl. Phys., 2016, 49, 215107.

---

Footnote

† PACS numbers: 72.15.Jf, 71.20.-b, 71.70.Ej, 79.10.-n.

---