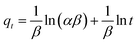Preparation and characterization of a composite based on polyaniline, polypyrrole and cigarette filters: adsorption studies and kinetics of phenylbutazone in aqueous media
Tienne Aparecida Nascimentoa,
Flávia Viana Avelar Dutraa,
Bruna Carneiro Piresa,
César Ricardo Teixeira Tarleybc,
Valdir Manoa and
Keyller Bastos Borges *a
*a
aDepartamento de Ciências Naturais, Universidade Federal de São João del-Rei, Campus Dom Bosco, Praça Dom Helvécio 74, Fábricas, 36301-160, São João del-Rei, Minas Gerais, Brazil. E-mail: keyller@ufsj.edu.br
bDepartamento de Química, Universidade Estadual de Londrina, Campus Universitário, Rod. Celso Garcia Cid, PR 445 km 380, Londrina, PR CEP 86051-990, Brazil
cInstituto Nacional de Ciência e Tecnologia (INCT) de Bioanalítica, Universidade Estadual de Campinas (UNICAMP), Instituto de Química, Departamento de Química Analítica, Cidade Universitária Zeferino, Vaz s/n, CEP 13083-970 Campinas, SP, Brazil
First published on 20th June 2016
Abstract
Understanding the adsorption mechanisms of drugs on the surfaces of solid materials is important for determining the fate of these compounds in aqueous samples during water or wastewater treatment. A composite based on polyaniline (PAni), polypyrrole (PPy) and cigarette filters (CFs), PAni–PPy–CFs, was prepared, characterized by FTIR, TGA and SEM and applied in the investigation of the adsorption of a non-steroidal anti-inflammatory, phenylbutazone (PBZ), from aqueous solution. A group of experiments were conducted, and four kinetic models and five isotherm models were used to describe the adsorption process. The experimental kinetic data fitted very well with the second-order kinetic model, indicating that PBZ adsorption involves chemical adsorption at different binding sites, which could control the reaction rate. The equilibrium adsorption data were best fitted with the dual-site Langmuir–Freundlich isotherm, with a maximum adsorption capacity of 100.22 mg g−1; this indicates the existence of two kinds of adsorption sites on the polymer composite surface. Finally, this composite may act as a excellent adsorbent for environmental and analytical processes, such as a stationary phase in separation processes.
1. Introduction
Phenylbutazone (PBZ) is a non-steroidal anti-inflammatory drug (NSAID) that has powerful analgesic and anti-inflammatory action in the treatment of acute and chronic rheumatoid arthritis. In humans, the pharmacokinetics of PBZ is characterized by slow release, and absorption is almost complete after oral dosing. 3 h after a 300 mg dosage of the drug is administered, it reaches a maximum concentration of 35 to 50 μg mL−1 in plasma. However, after repeated dosing, the plasma concentration of PBZ is 95 μg mL−1 to 45 μg mL−1 for its metabolite, oxyphenbutazone. Additionally, just 1% of PBZ is excreted in urine as the original drug; up to 72% is excreted in urine as metabolites and 10% is excreted in bile as metabolites.1,2 The use of PBZ in human medicine is limited because of increased risks of several diseases such as agranulocytosis, aplastic anemia, hematemesis, perforation of peptic ulcer, hepatotoxicity, and renal failure.3–5PBZ is frequently found in the environment, leading to long term exposure and resulting in adverse effects on humans and wildlife. Thus, it is desirable to monitor this pharmaceutical and to develop analytical methodologies to detect and control its presence in very different kinds of samples, including urine, serum or plasma, and waste water; most of these have very complex matrices.6,7 Some studies have been performed to determine PBZ in various matrices, such as bovine, equine and porcine muscle tissues, using SPE cartridges packed with magnesium–silica gel;8 animal urine, using liquid extraction with chloroform;9 urine and blood, using continuous solid-phase extraction in a sorbent column (Oasis HLB);10 equine plasma, using molecularly imprinted solid-phase extraction;11 and aqueous medium, using a C8 stationary phase and a phosphatidylcholine-modified microemulsion mobile phase.12
Conducting polymers and their composites have been extensively studied due to their interesting chemical and physical properties in addition to their wide range of potential applications, such as sensors,13 thermoelectric applications,14 electrodes,15 and supercapacitors.16 Among this class of polymers, polypyrrole (PPy) and polyaniline (PAni) have drawn the attention of many scientists because they are considered to be two of the most promising materials for potential applications due to their relatively high electrical conductivity, easy preparation and relatively low cost.17 Additionally, PPy and PAni have been applied in separation science18 as filling materials in solid phase extraction (SPE),19,20 solid phase micro-extraction (SPME)21–24 and magnetic solid phase extraction (MSPE).25 Therefore, PAni–PPy composites have attracted a great deal of attention in the field of adsorption due to their multifunctional properties, including hydrophobicity, acid–base character, π–π interactions, polar functional groups, ion exchange properties, hydrogen bonding and electroactivity. Furthermore, their high surface area, good stability and, mainly, their extraction capability for different analytes in different matrices are some of the advantages of using this composite in the extraction process; examples include organochlorine pesticides in seawater,26,27 heavy metals,28,29 several esters30 and Congo red31 from aqueous solution, organic analytes from biological fluids32 and parabens from water, milk and fruit juice samples.33
In addition, cellulose acetate is also reported in the literature as an excellent material with a high capacity for the adsorption of different analytes because its surface can be modified by simple chemical and low cost processes.34–38 Cigarette filters (CFs) are alternative materials derived from cellulose acetate with great potential for the adsorption and preconcentration of different analytes of several matrices; CFs are widely used in the field of separation.39–44
The use of the adsorption process for the determination of different analytes in different matrices is a good alternative due to the availability of a large range of adsorbents as well as their properties, including high surface area, good adsorption capacity and reusability. In this sense, the aim of this work was to prepare an adsorbent for the adsorption of PBZ in aqueous medium, which also could be applied to many other analytes and matrices. PAni–PPy–CFs was synthesized by chemical oxidation polymerization in a triple-phase interface system, where the composite is prepared in the presence of oxidation in the middle aqueous phase. The capacity of the material for PBZ adsorption and the effects of different parameters, such as the pH of the solution and the reaction time, were investigated; also, the sorption kinetics and isotherm models were studied. This is the first time that PAni–PPy–CFs composite has been synthetized and used as an adsorbent with enhanced capacity for PBZ adsorption.
2. Materials and methods
2.1. Reagents
All reagents used in the experiments were of analytical grade. Pyrrole (98%) and aniline (99.5%) monomers were acquired from Sigma-Aldrich (St. Louis, MO, USA) and were purified by vacuum distillation and stored in a refrigerator prior to use. Hydrochloric acid (HCl, 37%) was purchased from Vetec (Rio de Janeiro, Brazil). Ammonium persulfate (APS – (NH4)2S2O8, 98%) was obtained from Synth (Diadema, Brazil). Tetrachloromethane (CCl4) was acquired from ÊxodoCientífica (Hortolândia, Brazil). Toluene (C7H8) was purchased from Qhemis – Hexis (Jundiaí, Brazil). Phenylbutazone (81.78%) was obtained from the United States Pharmacopeia (USP) Reference Standard. Water was distilled and purified using a Millipore Milli-Q Plus system (Bedford, MA, USA).2.2. Synthesis of PAni–PPy–CFs composite
PAni–PPy–CFs composite was prepared by a static one-step triple-phase interfacial reaction in the temperature range from 0 to 5 °C. At the bottom of the beaker, an organic phase was obtained by dissolving 14.9 mmol of pyrrole in 75 mL cooled CCl4. Then, 600 mL cooled HCl aqueous solution (1.0 mol L−1) containing 40 mmol APS and 2.84 g dispersed cigarette filters were used as the middle aqueous phase. Finally, another organic phase at the top of the beaker was prepared by dissolving 14.9 mmol of aniline in 75 mL cooled toluene. The molar ratio of the pyrrole and aniline monomers was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which corresponds to 1.45 and 1.39 g, respectively, for a total of 2.84 g. Therefore, the mass ratio of conducting polymers and cigarette filters in the composite was 1
1, which corresponds to 1.45 and 1.39 g, respectively, for a total of 2.84 g. Therefore, the mass ratio of conducting polymers and cigarette filters in the composite was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Subsequently, the reaction system was placed in an ice bath to maintain the temperature below 5 °C for 24 h. The resulting black precipitate was obtained and suction-filtered in a vacuum pump, washed with distilled water and dried in 60 °C under vacuum overnight. A schematic of the synthesis of PAni–PPy–CFs composite by a one-step triple-phase interfacial method, as well as a photographic illustration, are shown in Fig. 1.
1. Subsequently, the reaction system was placed in an ice bath to maintain the temperature below 5 °C for 24 h. The resulting black precipitate was obtained and suction-filtered in a vacuum pump, washed with distilled water and dried in 60 °C under vacuum overnight. A schematic of the synthesis of PAni–PPy–CFs composite by a one-step triple-phase interfacial method, as well as a photographic illustration, are shown in Fig. 1.
 | ||
| Fig. 1 (a) Schematic of the synthesis of the PAni–PPy–CFs composite; (b) schematic of the formation of the PAni–PPy–CFs composite. | ||
2.3. Effect of pH on the adsorption of PBZ
To study the effect of pH on the adsorption of PBZ onto PAni–PPy–CFs composite, a 0.5 mg mL−1 stock solution of PBZ was prepared by dissolving 6.11 mg PBZ in 10 mL methanol. This solution was used to prepare an aqueous solution with a concentration of 0.01 mg mL−1. All these solutions were stored at 5 °C in the absence of light. Then, 5.0 mL of PBZ solution with a concentration of 0.01 mg mL−1 in a wide pH range (pH 2, 4, 6, 8 and 10, respectively) was stirred in a horizontal shaker at 150 rpm for 20 min with 25.0 mg of the polymer composite. After stirring, the mixture was centrifuged (2000 rpm) for 2 min and the residual PBZ in the supernatant was analyzed by UV-vis spectrophotometry.2.4. Adsorption kinetics
The dependence of the contact time on the adsorption of PBZ onto PAni–PPy–CFs composite was evaluated by varying the stirring time of 5.0 mL of PBZ solution with a concentration of 0.01 mg mL−1 at pH 6.0 from 1 to 30 min at 150 rpm at room temperature. The mixture was centrifuged at 2000 rpm for 2 min, and the supernatant was used for the determination of PBZ that was not retained in the polymer. Eqn (1) was used to determine the amount of PBZ adsorbed onto PAni–PPy–CFs, where Ci and Cf are the initial and final concentrations of PBZ, respectively (mg L−1), determined by UV-vis; V is the volume of solution (mL); and m is the mass of the polymer composite (g).
 | (1) |
The experimental kinetic data were further fitted to the common adsorption kinetic models, including pseudo-first-order, pseudo-second order, Elovich, and intraparticle diffusion.45–47
2.5. Adsorption isotherm studies
For the adsorption isotherm studies, a 5 mg mL−1 stock solution of PBZ was prepared by dissolving 305 mg in 50 mL methanol. This stock solution was used in a dilution series, resulting in a concentration range of 0.003 to 1.5 mg L−1 of PBZ, and 5.0 mL of these solutions were used with 25 mg of PAni–PPy–CFs. The mixture was stirred for 30 min under the same conditions as previously described for the kinetic studies. The amounts of PBZ adsorbed (mg g−1) were calculated according to eqn (1), and the adsorption isotherms were plotted. The data were analyzed using the Langmuir, Freundlich, Langmuir–Freundlich, single-site Langmuir–Freundlich and dual-site Langmuir–Freundlich isotherm models.48,492.6. Apparatus
The remaining concentration of PBZ in the solution after adsorption by PAni–PPy–CFs composite was determined by molecular absorption spectroscopy in the visible region using a Varian-Agilent Cary 5000 Probe UV-vis spectrophotometer (Agilent Technologies, Palo Alto, CA, USA) and a square quartz cuvette, optical path 10 mm. The data were acquired at 265 nm. The infrared spectra of the polymer composite were obtained in the 4000 to 400 cm−1 region with a Fourier transform infrared spectrometer (Bomem Hartmann & Braun, MB series, Quebec, Canada) using the KBr pellet method. Thermogravimetric analyses (TGA) were performed in a thermobalance (2950 Thermal Analysis Instrument, TA Instrument, New Castle, DE, USA) with a heating rate of 10 °C min−1, under flowing nitrogen (50 mL min−1), from 25 to 1000 °C. The morphology of the material was evaluated by scanning electron microscopy (SEM) using a Hitachi Analytical Table Top Microscope TM3000 with voltage acceleration varying between 5 kV and 15 kV.3. Results and discussion
3.1. Characterization of the PAni–PPy–CFs composite by FTIR, TGA and SEM
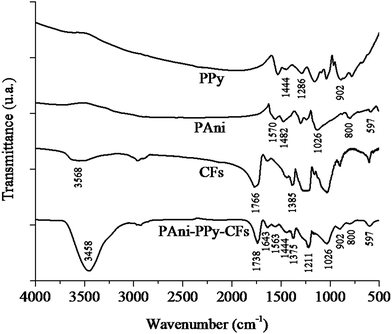
Fig. 2 shows the FTIR spectra of PAni, PPy, CFs and PAni–PPy–CFs; the fundamental vibration bands of the functional groups of each component are indicated by arrows. Furthermore, these bands in the composite are presented in Table 1.| Wavenumber (cm−1) | Attribution |
|---|---|
| 1444 | C–C vibration – PPy |
| 1211 | C–N vibration – PPy |
| 902 | C–H out of plane vibration – PPy |
| 1643 | Quinonoid ring vibration – PAni |
| 1563 | Benzenoid ring vibration – PAni |
| 1026 | C–N vibration of secondary aromatic amines – PAni |
| 800 | Quinonoid ring deformation – PAni |
| 597 | Benzenoid ring deformation – PAni |
| 3458 | O–H vibration – CFs |
| 1738 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibration – CFs O vibration – CFs |
| 1375 | C–O–H vibration of primary alcohols – CFs |
In the case of the FTIR spectrum of PAni, the fundamental vibrations centered at 1570 and 1482 cm−1 were ascribed to the quinonoid and benzenoid ring vibrations; peaks at 800, 597 and 1026 cm−1 were also observed for PAni, corresponding to the deformation of the quinonoid rings, the deformation of the benzenoid rings and the C–N vibration of the secondary aromatic amines, respectively. As for PPy, the fundamental vibrations of the pyrrole ring, centered at 1444 and 1286 cm−1, were ascribed to the C–H and C–N vibrations, respectively, and the out of plane vibration of C–H was observed at 902 cm−1. The fundamental bands of CFs, centered at 3568, 1766 and 1385 cm−1, are ascribed to O–H vibration, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibration and the C–O–H vibration of primary alcohols. The FTIR spectrum of PAni–PPy–CFs composite reflected the mutual influences of PAni, PPy and CFs and the fundamental vibration of these components on the composite. The spectroscopic differences in the peak intensity and position of each separate component and also in the composite demonstrated that there was an interaction between PAni, PPy and CFs instead of a simple mixture of these components.50–55
O vibration and the C–O–H vibration of primary alcohols. The FTIR spectrum of PAni–PPy–CFs composite reflected the mutual influences of PAni, PPy and CFs and the fundamental vibration of these components on the composite. The spectroscopic differences in the peak intensity and position of each separate component and also in the composite demonstrated that there was an interaction between PAni, PPy and CFs instead of a simple mixture of these components.50–55
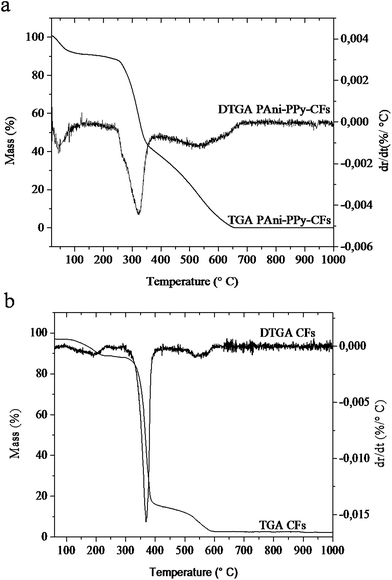
The TGA and DTGA curves for PAni–PPy–CFs composite and neat CFs are presented in Fig. 3. It can be seen that in the composite, there is a weight loss of 11% up to 100 °C, related to the evaporation of some residual water or solvent. From 247 to 350 °C a weight loss of 45% occurs, showing the typical CFs degradation process, which can be confirmed by the DTGA of neat CFs, Fig. 3(b). From 350 to 650 °C a weight loss of 44% is observed, related to the polymers, PAni and PPy, in the composite.54,56 Therefore, the composite is stable up to about 322 °C, a relatively high temperature, since this work and most of the adsorption experiments are performed at room temperature.
Fig. 4 shows the morphology of the polymer composite under magnifications of 1000× and 2000×. As can be seen, the composite PAni–PPy–CFs exhibits fibrous domains with a diameter of 27.4 μm due to the cigarette filter fibers, in which heterogeneous particles of PPy and PAni are aggregated. It is possible to infer that the material presents a heterogeneous surface and is slightly porous, which explains the strong adsorption power of the material.
3.2. Effect of pH on the adsorption of PBZ
The influence of pH on the adsorption of PBZ was studied in the 2.0 to 10 range; Fig. 5(a) shows that the adsorption of the drug occurs in the overall pH range evaluated without significant differences, thus indicating robustness with regard to pH during adsorption. However, above pH 4.0, PAni–PPy–CFs is negatively charged,52 as is PBZ, as presented in Fig. 5(b), where the red curve shows that as the pH of the medium increases, the concentration of negatively charged PBZ also increases; at pH 6.0, almost all of the drug is in anionic form. On the other hand, at pH values below 4, the predominant form of PBZ is molecular, as indicated by the blue curve.57 Therefore, at pH 6 to 12, considering a mechanism involving Coulomb forces (attraction of charges), the percentage of adsorption would be expected to decrease due to charge repulsion. Thus, the results can be attributed to different interactions related to the analyte and the aromatic rings of the polymers, involving intermolecular forces of dipole–dipole, hydrogen bonding and π–π interactions, which justifies the adsorption in a wide pH range. Taking into account the comments and the natural pH of the water samples, all further adsorption studies were carried out at pH 6.0.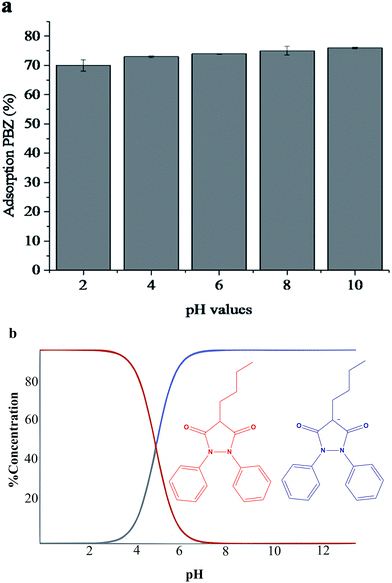 | ||
| Fig. 5 (a) Effect of pH on the adsorption of PBZ; (b) distribution chart of PBZ as a function of pH. | ||
3.3. Adsorption kinetics
The study of adsorption kinetic models provides an important role in understanding the adsorption process and the rate-controlling steps. According to the experimental data shown in Fig. 6(a), the adsorption of PBZ on PAni–PPy–CFs composite increased in the first 10 min, indicating that the polymer composite presents low resistance to mass transfer. In addition, the time of 30 min was adopted as the optimal conditions for the isotherm studies. This result was analyzed in an attempt to describe the adsorption kinetics of the drug by the polymer composite. Thus, kinetic parameters from the application of the pseudo-first order, pseudo-second order, Elovich and intraparticle diffusion models are shown in Table 2, while Fig. 6 graphically shows the linearized forms of the models.46,58,59 | ||
| Fig. 6 (a) Kinetics adsorption of PBZ by PAni–PPy–CFs, and kinetic models (b) pseudo-first order, (c) pseudo-second order, (d) Elovich, (e) intraparticle diffusion. | ||
| Pseudo-first order | Pseudo-second order | ||||||
|---|---|---|---|---|---|---|---|
| ln(qe − qt) = ln(qe) − k1t | |||||||
| k1 (min−1) | qe (mg g−1) | qe,exp (mg g−1) | R2 | k2 (g mg−1 min−1) | qe (mg g−1) | qe,exp (mg g−1) | R2 |
| a k1—rate constant of the pseudo-first order adsorption process; k2—rate constant of the pseudo-second order adsorption process; β is related to the extent of surface coverage and activation energy for chemisorption; α—initial sorption rate constant; Kd—internal diffusion coefficient; C—constant related to the thickness of the boundary layer; R2—determination coefficient. | |||||||
| 0.091 | 0.46 | 2.0 | 0.983 | 0.689 | 2.0 | 2.0 | 0.999 |
The pseudo-first order or Lagergren's kinetic model describes the adsorption rate based on the adsorption capacity and the approximation of the number of unoccupied adsorptive sites and indicates that this model is described by physical adsorption. Eqn (2) presents this model in its final form:60,61
| ln(qe − qt) = ln(qe) − k1t | (2) |
In this work, the value of qe was estimated on the basis of the pseudo-second order kinetic model, which is based on the notion that the adsorption should relate to the squared product of the difference between the number of equilibrium adsorptive sites available on an adsorbent and the number of occupied sites. Moreover, the analyte can bind to two active sites with different binding energies; this model assumes that the rate-limiting step is chemisorption and predicts the behavior over the whole range of adsorption.64,65 This model, in its final form, can be expressed in eqn (3),
 | (3) |
The Elovich equation, similarly to the pseudo-second order model, assumes that the adsorbent surface is energetically heterogeneous and considers an adsorption process of a chemical nature.68 Elovich's model is defined by eqn (4),
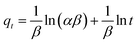 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) t enables the determination of the kinetic constants α and β by the slope and y-intercept values, respectively.69–71
t enables the determination of the kinetic constants α and β by the slope and y-intercept values, respectively.69–71
Intraparticle diffusion, namely the Morris–Weber kinetic model, is also used to describe the adsorption kinetics mathematically when the process is influenced by a diffusion phenomenon. Moreover, this model has been widely used to check the influence of mass transfer resistance on the binding of an analyte to an adsorbent. This model is represented by eqn (5), as follows:
| qt = kdt1/2 + C | (5) |
From the results presented in Table 2, the pseudo-second-order model shows a better adjustment to the experimental kinetic data, based on the better determination coefficient (R2 = 0.999), as well as on comparing the amount of experimental PBZ adsorbed at equilibrium (qe,exp = 2.0 mg g−1) with the amounts achieved from kinetic models; the qe value obtained from the pseudo-second order model (qe = 2.0 mg g−1) is equal to the experimental value. The Elovich model provides a reasonable fit due to the reasonable determination coefficient (R2 = 0.954). Therefore, this model assumes that the adsorbent surface is energetically heterogeneous and confirms the chemical nature of the PBZ adsorption. The presence of multilinearity in the intraparticle diffusion model characterizes different adsorption stages, which may be due to external mass transfer followed by intraparticle diffusion into the pores. According to Table 2 and Fig. 6(e), the first linear portion showed better fit, indicating that the PBZ was transported to the outer surface of PAni–PPy–CFs. In addition, the intercept C values of the intraparticle diffusion curve (1.588 and 1.781 mg g−1) suggest that the transport of PBZ toward the outer surface of PAni–PPy–CFs plays an important role in comparison with the spread of the analyte to the internal part of the material.
3.4. Adsorption isotherms
The experimental data of the adsorption isotherm were fitted to several isotherm models, as shown in Fig. 7. The aims of this fitting are to estimate the maximum adsorption capacity and describe the equilibrium between PBZ and PAni–PPy–CFs, as well as to supply different binding sites and affinities in the adsorbent, and often, to provide some general insight into the adsorption mechanism. The fits of the Langmuir, Freundlich, Sips, single-site Langmuir–Freundlich and dual-site Langmuir–Freundlich isotherm models are presented in Table 3.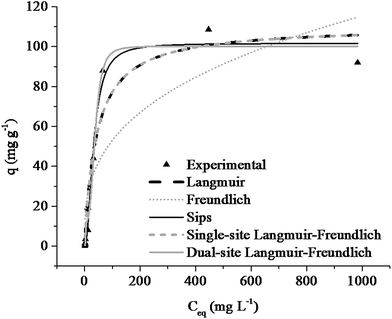 | ||
| Fig. 7 Isotherms of adsorption of PBZ on PAni–PPy–CFs fitted to the Langmuir, Freundlich, Sips, single-site Langmuir–Freundlich, and dual-site Langmuir–Freundlich models. | ||
| Model | Equation | Parameter | Value |
|---|---|---|---|
| a KL: Langmuir constant (L g−1); KF: Freundlich constant (mg g−1) (L g−1), related to the affinity adsorbent–adsorbate parameters; Q1,2: constant related to the maximum adsorption capacity (mg g−1); n1,2: constant related to the adsorption intensity or degree of adsorption. | |||
| Langmuir |  |
KL | 0.023 |
| Q | 110.4 | ||
| R2 | 0.929 | ||
| Freundlich |  |
KF | 11.19 |
| n | 2.961 | ||
| R2 | 0.975 | ||
| Sips |  |
KS | 6.236 × 10−4 |
| Q | 101.6 | ||
| n | 2.109 | ||
| R2 | 0.976 | ||
| Single-site Langmuir–Freundlich | 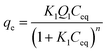 |
K1 | 0.830 |
| Q1 | 3.086 | ||
| n | 0.028 | ||
| R2 | 0.919 | ||
| Dual-site Langmuir–Freundlich |  |
K1 | 0.026 |
| Q1 | 87.96 | ||
| n1 | 3.402 | ||
| K2 | 0.249 | ||
| Q2 | 12.26 | ||
| n2 | 4.435 | ||
| R2 | 0.972 | ||
The Langmuir model is perhaps the most straightforward non-linear isotherm model; it was developed originally for the adsorption process of a single layer of solute on the surface of a sorbent. Thus, this model describes the adsorption of an adsorbate on a homogeneous adsorbent surface, and each adsorptive site can be occupied only once. It can be represented by eqn (6), as follows:
 | (6) |
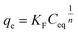 | (7) |
The Sips isotherm combines the Langmuir and Freundlich models and supposes that interactions may occur with different affinities. It is expected that the Sips model describes heterogeneous surfaces much better. At low analyte concentrations, it reduces to a Freundlich isotherm, while at high concentrations it transforms into the Langmuir model. The Sips model takes the form of eqn (8):
 | (8) |
Eqn (9) shows another way of representing the Sips equation, denoted the single-site Langmuir–Freundlich equation.
 | (9) |
The dual-site Langmuir–Freundlich isotherm model overcomes some limitations of the single-site and Sips models, such as heterogeneity of the solid phase sites in the adsorption process. Thus, this model assumes that adsorption can occur on both homogeneous and heterogeneous sites of a composite; this is the case for PAni–PPy–CFs, which possibly has different types of adsorption sites with different affinities.81–84 This corroborates the pseudo-second order model from the kinetic data. The dual-site Langmuir–Freundlich model is represented by eqn (10).
 | (10) |
According to the results shown in Table 3, the dual-site Langmuir–Freundlich isotherm model presented the best fit to the experimental data, presenting an R2 value of 0.972 with a maximum adsorption capacity of 100.22 mg g−1. It should be mentioned that there are no reports in the literature about isotherm adsorption studies involving adsorbents for PBZ that can be compared with the PAni–PPy–CFs composite; some similar studies have been published involving polymer composites, but for other analytes, especially heavy metals and dyes in wastewater,85,86 as shown in Table 4.
It should be noted that the composite PAni–PPy–CFs studied in this work showed a large sorption capacity when compared to some adsorbents in the literature. It can be inferred that PAni–PPy–CFs is a promising material for drug adsorption studies that is easily applicable in the field of separation science in general and may possibly be employed in the adsorption of other analytes, such as heavy metals.
4. Conclusions
PAni–PPy–CFs was successfully synthesized by a simple methodology; thus, the preparation of this material for use as an adsorbent is extremely viable. Despite reports concerning the effects of indiscriminate use of non-steroidal anti-inflammatory drugs on human health, only a few studies concerning the development of new adsorbent materials for drug determination have been reported in the literature. Adsorption kinetics and adsorption isotherms are vitally important to understanding the mechanism and the interactions of PBZ with the different binding sites of PAni–PPy–CFs. Thus, the proposed polymer composite exhibits remarkable properties as an adsorbent for PBZ, including a high surface area, a heterogeneous surface and slight porosity, due to the fibrous domains of the CFs and the aggregated PAni–PPy particles. Furthermore, a maximum adsorption capacity of 100.22 mg g−1 was obtained, which shows this material may be suitable for use in environmental and analytical studies. Thus, we conclude the material has good thermal stability at high temperatures and good resistance to leaching, since it can be used both in basic and acidic media. These are important characteristics for materials with potential applications as stationary phases in separation processes.Acknowledgements
The authors would like to thank the Brazilian agencies CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico), CAPES (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior) and FAPEMIG (Fundação de Amparo à Pesquisa do Estado de Minas Gerais) for their financial support. This study is also part of a project involving the Rede Mineira de Química (RQ-MG) supported by FAPEMIG (Project: REDE-113/10; Project: CEX – RED-0010-14).References
- J. J. Burns, R. K. Rose, T. Chenkin, A. Goldman, A. Schulert and B. B. Brodie, J. Pharmacol. Exp. Ther., 1953, 109, 346–357 CAS.
- P. Lees and P. L. Toutain, Vet. J., 2013, 196, 294–303 CrossRef CAS PubMed.
- K. G. Ishak, J. P. Kirchner and J. K. Dhar, Dig. Dis. Sci., 1977, 22, 611–617 CrossRef CAS.
- S. B. Benjamin, K. G. Ishak, H. J. Zimmerman and A. Grushka, Hepatology, 1981, 1, 255–263 CrossRef CAS PubMed.
- I. Manov, H. Motanis, I. Frumin and T. C. Iancu, Acta Pharmacol. Sin., 2006, 27, 259–272 CrossRef CAS PubMed.
- A. I. Olives, V. G. Ruiz and M. A. Martín, Anti-Inflammatory Anti-Allergy Agents Med. Chem., 2012, 11, 65–95 CrossRef CAS.
- N. Aljuhani, R. M. Whittal, S. R. Khan and A. G. Siraki, Chem. Res. Toxicol., 2015, 28, 1476–1483 CrossRef CAS PubMed.
- P. E. A. Asea, K. D. Souster and C. D. C. Salisbury, J. Liq. Chromatogr. Relat. Technol., 2004, 27, 3013–3027 CrossRef CAS.
- C. Igualada and F. Morague, Anal. Chim. Acta, 2005, 529, 235–238 CrossRef CAS.
- A. Azzouz and E. Ballesteros, J. Chromatogr. B: Anal. Technol. Biomed. Life Sci., 2012, 891, 12–19 CrossRef PubMed.
- V. Meucci, M. Minunni, M. Vanni, M. Sgorbini, M. Corazza and L. Intorre, Bioanalysis, 2014, 6, 2147–2158 CrossRef CAS PubMed.
- X. Xuan, L. Xu, L. Li, C. Gao and N. Li, Int. J. Pharm., 2015, 490, 258–264 CrossRef CAS PubMed.
- A. Sultan, S. Ahmad, T. Anwer and F. Mohammad, RSC Adv., 2015, 5, 105980–105990 RSC.
- C. Gao and G. Chen, Compos. Sci. Technol., 2016, 124, 52–70 CrossRef CAS.
- L. Mao, M. Li, J. Xue and J. Wang, RSC Adv., 2016, 6, 2951–2957 RSC.
- W. Zheng, S. Li, X. Lu, C. Chen, H. Huang, Y. Huang and L. Li, Mater. Res. Bull., 2016, 80, 303–308 CrossRef CAS.
- B. D. Malhotra, A. Chaubey and S. P. Singh, Anal. Chim. Acta, 2006, 578, 59–74 CrossRef CAS PubMed.
- X. Li, Y. Wang, X. Yang, J. Chen, H. Fu and T. Cheng, Trends Anal. Chem., 2012, 39, 163–179 CrossRef CAS.
- H. Bagheri and M. Saraji, J. Chromatogr. A, 2001, 910, 87–93 CrossRef CAS PubMed.
- F. Qi, X. Li, B. Yang, F. Rong and Q. Xu, Talanta, 2015, 144, 129–135 CrossRef CAS PubMed.
- H. Minjia, T. Chao and Z. Qunfang, J. Chromatogr. A, 2004, 1048, 257–262 CrossRef PubMed.
- J. K. Schubert, W. Miekisch, P. Fuchs, N. Scherzer, H. Lord, J. Pawliszyn and R. G. Mundkowski, Anal. Chim. Acta, 2007, 385, 57–62 CrossRef PubMed.
- A. Mehdinia, F. Roohi, A. Jabbari and M. R. Manafi, Anal. Chim. Acta, 2011, 683, 206–211 CrossRef CAS PubMed.
- H. Amanzadeh, Y. Yamini and M. Moradi, Anal. Chim. Acta, 2015, 884, 52–60 CrossRef CAS PubMed.
- Q. Gao, D. Luo, M. Bai, Z. W. Chen and Y. Q. Feng, J. Agric. Food Chem., 2011, 59, 8543–8549 CrossRef CAS PubMed.
- R. Ansari, N. K. Fahim and A. F. Dellavar, J. Iran. Chem. Res., 2009, 2, 163–171 Search PubMed.
- A. Mehdinia, J. Braz. Chem. Soc., 2014, 25, 2048–2053 CAS.
- M. Bhaumik, A. Maity, V. V. Srinivasu and M. S. Onyango, Chem. Eng. J., 2012, 181, 323–333 CrossRef.
- H. Javadian, J. Ind. Eng. Chem., 2014, 20, 4233–4241 CrossRef CAS.
- S. Zhao, M. Wu, F. Zhao and B. Zeng, Talanta, 2013, 117, 146–151 CrossRef CAS PubMed.
- M. Bhaumik, R. McCrindle and A. Maity, Chem. Eng. J., 2013, 228, 506–515 CrossRef CAS.
- A. A. Asgharinezhad, H. Ebrahimzadeh, F. Mirbabaei, N. Mollazadeh and N. Shekari, Anal. Chim. Acta, 2014, 844, 80–89 CrossRef CAS PubMed.
- H. Asiabi, Y. Yamini, S. Seidi, A. Esrafili and F. Rezaei, J. Chromatogr. A, 2015, 1397, 19–26 CrossRef CAS PubMed.
- D. Goveia, F. A. Lobo, U. P. Rodrigues, N. L. Dias, L. F. Fraceto and A. H. Rosa, Quim. Nova, 2010, 33, 1135–1140 CrossRef CAS.
- H. A. Magosso, N. Fattori, L. T. Arenas and Y. Gushikem, Cellulose, 2012, 19, 913–923 CrossRef CAS.
- J. Ju, Z. Duan, W. Zhao, Y. Liu, L. Zhang and Y. Li, Biochem. Eng. J., 2013, 79, 144–152 CrossRef CAS.
- P. D. Bhalara, D. Punetha and K. Balasubramanian, Int. J. Environ. Sci. Technol., 2015, 12, 3095–3106 CrossRef CAS.
- Y. B. Wu, J. Bi, T. Lou, T. B. Song and H. Q. Yu, Int. J. Miner., Metall. Mater., 2015, 22, 437–445 CrossRef CAS.
- X. P. Yan, Y. Li and Y. Jiang, Anal. Chem., 2003, 75, 2251–2255 CrossRef CAS PubMed.
- L. M. Dong, J. Chromatogr. A, 2014, 1036, 119–125 CrossRef.
- H. D. Liang, D. M. Han and X. P. Yan, J. Chromatogr. A, 2006, 1103, 9–14 CrossRef CAS PubMed.
- B. Chen, W. Wang and Y. Huang, Talanta, 2012, 88, 237–243 CrossRef CAS PubMed.
- W. Du, L. J. Tang, J. H. Wen, K. J. Zhong, J. H. Jiang, H. Wang, B. Chen and R. Q. Yu, Talanta, 2015, 131, 499–504 CrossRef CAS PubMed.
- R. T. Andrade, R. C. Santos, A. C. Pereira and K. B. Borges, Anal. Methods, 2015, 7, 7279 RSC.
- W. Plazinski and W. Rudzinski, J. Phys. Chem. C, 2007, 111, 15100–15110 Search PubMed.
- W. Plazinski, W. Rudzinski and A. Plazinski, Adv. Colloid Interface Sci., 2009, 152, 2–13 CrossRef CAS PubMed.
- H. Qiu, L. LV, B. C. Pan, Q. J. Zhang, W. M. Zhang and Q. X. Zhang, J. Zhejiang Univ., Sci., A, 2009, 10, 716–724 CrossRef CAS.
- K. Y. Foo and B. H. Hameed, Chem. Eng. J., 2010, 156, 2–10 CrossRef CAS.
- D. N. Clausen, I. Pires and C. R. T. Tarley, Mater. Sci. Eng. C., 2014, 44, 99–108 CrossRef CAS PubMed.
- N. V. Blinova, J. Stejskal, M. Trchová, J. Prokes and M. Omastová, Eur. Polym. J., 2007, 43, 2331–2341 CrossRef CAS.
- D. P. Dubal, S. V. Patil, G. S. Gund and C. D. Lokhande, J. Alloys Compd., 2013, 552, 240–247 CrossRef CAS.
- H. Javadian, F. Z. Sorkjrodi and B. B. Koutenaei, J. Ind. Eng. Chem., 2014, 20, 3678–3688 CrossRef CAS.
- V. Vickakaite and V. Ciuvasovaite, Cent. Eur. J. Chem., 2007, 5, 727–738 Search PubMed.
- B. Liang, Z. Qin, J. Zhao, Y. Zhang, Z. Zhou and Y. Lu, J. Mater. Chem. A, 2014, 2, 2129–2135 CAS.
- W. Lei, P. He, S. Zhang, F. Dong and Y. Ma, J. Power Sources, 2014, 266, 347–352 CrossRef CAS.
- A. Q. Zhang, Y. Zhang, L. Z. Wang and X. F. Li, Polym. Compos., 2011, 32, 1–5 CrossRef CAS.
- http://www.chemicalize.orghttp://www.chemicalize.org, accessed 12, 2015.
- Y. S. Ho and G. McKay, Process Biochem., 1999, 34, 451–465 CrossRef CAS.
- S. Azizian, J. Colloid Interface Sci., 2004, 276, 47–52 CrossRef CAS PubMed.
- Y. S. Ho, Scientometrics, 2004, 59, 171–177 CrossRef CAS.
- Y. S. Ho, J. Hazard. Mater., 2006, 36, 681–689 CrossRef PubMed.
- Y. S. Ho and G. McKay, Trans. Inst. Chem. Eng., 1998, 76, 1883–2191 Search PubMed.
- W. Rudzinski and W. Plazinski, J. Phys. Chem. C, 2007, 111, 15100–15110 CAS.
- W. Rudzinski and W. Plazinski, J. Phys. Chem. B, 2006, 110, 16514–16525 CrossRef CAS PubMed.
- F. C. Wu, R. L. Tseng, S. C. Huang and R. S. Juang, Chem. Eng. J., 2009, 151, 1–9 CrossRef CAS.
- Y. S. Ho and G. McKay, Chem. Eng. J., 1998, 70, 115–124 CrossRef CAS.
- Y. S. Ho and G. Mckay, Water Res., 2000, 34, 735–742 CrossRef CAS.
- ed. C. Aharoni, F. C. Tompkins, D. D. Eley, H. Pines and P. B. Weisz, Kinetics of adsorption and desorption and the Elovich equation, Academic Press, New York, 1970, vol. 21 Search PubMed.
- W. Rudzinski and T. Panczyk, J. Phys. Chem. B, 2000, 104, 9149–9162 CrossRef CAS.
- J. D. F. Bayo, R. Nogales and E. Romero, J. Agric. Food Chem., 2008, 56, 5266–5272 CrossRef PubMed.
- F. C. Wu, R. L. Tseng and R. S. Juang, Chem. Eng. J., 2009, 150, 366–373 CrossRef CAS.
- W. J. Weber and J. C. Morris, J. Sanit. Eng. Div., Am. Soc. Civ. Eng., 1963, 89, 31–60 Search PubMed.
- W. Rudzinski and W. Plazinski, Environ. Sci. Technol., 2008, 42, 2470–2475 CrossRef CAS PubMed.
- F. C. Wu, R. L. Tseng and R. S. Juang, Chem. Eng. J., 2009, 153, 1–8 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1916, 38, 1361–1403 Search PubMed.
- G. Ertl, Surf. Sci., 1994, 299, 742–754 CrossRef.
- H. M. F. Freundlich, J. Phys. Chem., 1906, 57, 385–470 CAS.
- W. J. Weber, P. M. McGinley and L. E. Katz, Water Res., 1991, 25, 499–528 CrossRef CAS.
- R. Sips, J. Chem. Phys., 1948, 16, 490–495 CrossRef CAS.
- A. Gunay, E. Arslankaya and I. Tosun, J. Hazard. Mater., 2007, 146, 362–371 CrossRef PubMed.
- R. Sips, J. Chem. Phys., 1950, 18, 1024–1026 CrossRef CAS.
- K. M. Diniz, M. G. Segatelli and C. R. T. Tarley, React. Funct. Polym., 2013, 73, 838–846 CrossRef CAS.
- E. Galunin, J. Ferreti, I. Zapelini, I. Vieira, C. R. T. Tarley, T. Abraão and M. J. Santos, J. Hazard. Mater., 2014, 265, 280–287 CrossRef CAS PubMed.
- R. J. Fonseca, M. G. Segatelli, K. B. Borges and C. R. T. Tarley, React. Funct. Polym., 2015, 93, 1–9 CrossRef.
- Y. Huang, J. Li, X. Chen and X. Wang, RSC Adv., 2014, 4, 62160–62178 RSC.
- H. N. M. E. Mahmud, A. K. O. Huq and R. B. Yahya, RSC Adv., 2016, 6, 14778–15791 RSC.
- X. Guo, G. T. Fei, H. Su and L. D. Zhang, J. Phys. Chem. C, 2011, 115, 1608–1613 CAS.
- M. Bhaumik, A. Maity, V. B. Srinivasu and M. S. Onyango, Chem. Eng. J., 2012, 181, 323–333 CrossRef.
- W. Yao, C. Shen and Y. Lu, Compos. Sci. Technol., 2013, 87, 8–13 CrossRef CAS.
- V. M. O. Medina, P. E. D. Flores, H. M. Gutierrez, L. A. M. Ruiz, I. D. A. Carmona and M. H. Ordoñez, Polym. Compos., 2014, 35, 186–193 CrossRef.
- B. Y. Yang, Y. Gao, F. F. Qi, X. Qing and Q. Xu, Nanoscale Res. Lett., 2015, 10, 2–13 CrossRef PubMed.
- K. Parashar, N. Ballav, S. Debnath, K. Pillay and A. Maity, J. Colloid Interface Sci., 2016, 476, 103–118 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |