Structural and micro-Raman studies of DyMnO₃ with potassium substitution at the Dy site

Abstract

Observation of colossal magnetoresistance at ferromagnetic and metal insulator transitions in manganites is considered to be closely related to a double exchange interaction between trivalent and tetravalent Mn ions combined with Jahn–Teller (JT) distortions produced by Mn³⁺ ions in MnO₆ octahedra. The rare earth manganite, DyMnO₃ has only Mn³⁺ ions which are JT active. This compound is antiferromagnetic involving Dy spins at low temperature (∼3 K) with weak magnetic interactions around 40 K due to Mn spins. When any aliovalent ion is substituted at the Dy site, tetravalent Mn ions are created for charge neutrality. With an aim to induce ferromagnetism by diluting the Dy sublattice to reduce super-exchange interactions and to provide mixed valent Mn ions to favor double exchange interactions in the DMO compound, we have undertaken monovalent potassium substitution at the Dy site. In this paper, for the first time we report the synthesis of a new series of compounds, Dy_1−xK_xMnO₃ (x = 0.1, 0.2 & 0.3) along with their structural and vibrational properties. All the compounds were found to crystallize in an orthorhombic structure. Structural analysis was performed using Rietveld refinement of X-ray powder diffraction data with the GSAS program. Refinement results revealed that MnO octahedra become more regular with potassium substitution as compared to the pristine compound. Raman spectroscopy studies showed that a 30 at% compound with less octahedral distortions exhibited sharp modes compared to other compounds with large distortions. From the vibrational spectra, Raman modes corresponding to stretching, bending and tilting of metal–oxygen polyhedra have been identified. The mixed valence state of the Mn ion for potassium substituted DyMnO₃ is investigated using XPS. The ratios of Mn³⁺/Mn⁴⁺ suggested that the production of holes is increased with potassium concentration.

---

1. Introduction

Rare earth manganites (RMnO₃) have attracted attention due to their diverse magnetic properties leading to a variety of technological applications.^1,2 Depending on the ionic size and synthesis temperature, RMnO₃ crystallizes either in an orthorhombic or in a hexagonal structure.^3–6 Hole doping at the R site in RMnO₃ has been found to give different low temperature ordered/disordered structures^7,8 depending on the rare earth ion in contrast to the phenomenon observed in LaMnO₃ due to the substitution of Ca/Sr at the La site.^9–11 The origin for such ground states was traced to the interplay between the 4f–3d orbitals of the R and Mn ions respectively.^12–14 Among RMnO₃, DyMnO₃ (DMO) was found to be interesting because it can adopt either a GdFeO₃-type distorted orthorhombic structure or a hexagonal structure depending on the synthesis temperatures.^15–17 Moreover, DMO has a very complex magnetic phase diagram at low temperatures.¹⁸ In the literature, structural,¹⁹ magnetic,²⁰ vibrational²¹ properties have been reported in both orthorhombic and hexagonal structures. Feyerherm et al.²² from their magnetic scattering experiments reported antiferromagnetic ordering of Dy spins around 5 K in DMO. Extensive research has been carried out in the DMO compound and structure–property correlations due to various ionic sizes at Dy site have been studied for Sr,²³ Ca,²⁴ Ho²⁵ and Y²⁶ substitutions at the Dy site. In view of the above, we have undertaken monovalent substitution at Dy site. Normal modes are closely associated to the lattice distortions hence, it is important to probe phonons involved in these compounds. We report here our structural and spectroscopic properties of these new compounds along with the pristine compound, DMO.

2. Experimental

Bulk compounds of Dy_1−xK_xMnO₃ (x = 0, 0.1, 0.2 and 0.3) were prepared using solid state technique. Hereafter, these compounds will be referred to as K0, K1, K2 and K3 corresponding to x = 0, 0.1, 0.2 and 0.3 respectively. Stoichiometric ratios of 4 N purity oxides, Dy₂O₃, K₂CO₃ and MnO₂ were mixed thoroughly using an agate mortar and pestle then calcined at 1000 °C for 12 hours. The mixture was once again ground well and heated at 1300 °C for 12 hours. All the heat treatments were carried out in alumina crucibles in air. Then phase identification was checked by powder X-ray diffraction technique with STOE (Germany) diffractometer, Cu K_α radiation (1.5406 Å). Initial crystal structure was arrived at orthorhombic unit cell using index and refine subroutine of WinXPow software that was provided along with STOE diffractometer. Later, diffraction data for refinement were collected in the angular range of 20° to 90° with an equal interval of 0.05° and a step size of 50 s per step in Bragg–Brentano para-focusing geometry at ambient temperature. X-ray generator was operated at 40 kV and 30 mA. Si(911) single crystal wafer²⁷ was used to hold the sample powder for XRD measurements. This sample holder gives low background intensity in the whole 2θ range. During data collection, divergence and receiving slits were fixed to 0.4 mm. Refinement of whole powder diffraction pattern was carried out using GSAS software.²⁸ Compositional homogeneity was verified using Scanning Electron Microscopy (SEM), CamScan 3200 (England) combined with Energy Dispersive X-ray (EDX) facility, INCAPenta FETX3 (Oxford instruments). Vibrational properties are closely linked to structural parameters hence; Raman spectroscopy measurements were performed to complement structural studies. Raman spectra were recorded using Renishaw spectrometer at room temperature in the backscattering geometry. An excitation wavelength of 514.5 nm with a laser power of 2 mW was used for all the compounds. Binding energies of manganese were calculated from X-ray Photoelectron Spectroscopy (XPS) (SPECS Surface Nano Analysis GmbH, Germany) measurements performed using a PHOIBOS 150 spectrometer equipped with a monochromatic Al K_α (1486.7 eV) X-ray source.

3. Results and discussion

3.1. Structural studies

Preliminary characterization with X-ray diffraction technique showed that all the compounds under study crystallize in orthorhombic structure. No impurity peaks were found within the detection limit of the diffractometer. All the diffraction peaks were indexed to Pnma space group of orthorhombic structure using Rietveld refinement by GSAS package. None of the compounds showed preferred orientation. Linear interpolation function (function 7) was used to fit the background while pseudo-Voigt (type 2 in GSAS) function was used to represent the diffraction peaks fairly well. Steps in the refinement were as per the sequence given in the GSAS manual. At the final cycles of refinement, fractional occupancies were refined but this did not improve either the R-factors or the visual fit hence occupancy parameters were unchanged. Fig. 1a shows experimental X-ray diffraction pattern of DMO along with the results of fitting. Lattice constants of DMO from the final refinement are a = 5.794 Å, b = 7.3883 Å and c = 5.2756 Å which follow the relation b/(√2) < c < a. These lattice parameters of DMO are in agreement with those published in ICDD database.²⁹ In the distorted perovskite, the unit cell is larger than the simple cubic unit cell and the distortions resemble that of GdFeO₃-type perovskite (space group Pnma and Z = 4). Due to smaller ionic size of Dy (1.027 Å), polyhedra in all directions tilt in order to fill the space created by the smaller ion (Dy) in an otherwise cubic unit cell adopted by an ideal perovskite (space group Pm3m and Z = 1). As a consequence, displacement of Dy and oxygen ions produces orthorhombic distortions such as Mn–O–Mn bond bending and octahedral tilts. This can be inferred from the decrease of the 〈Mn–O–Mn〉 angle to 144.713° in contrast to 180° in the undistorted cubic structure. DMO has only Mn³⁺ ions which are JT active and hence additional distortions are produced in the Mn–O bond lengths. Consequently, Mn³⁺ splits the six equal bond angles into three pairs of unequal lengths. Each Mn³⁺ site has a distribution of four short bonds and two long bonds showing elongation in the ac plane. In DMO, Dy is 8-fold coordinated due to its small size as compared to La where La is 12-fold coordinated with oxygen ions.³⁰ 8-Fold coordination was arrived at based on our refinement results. The same exercise of refinement was performed for the potassium substituted compounds and X-ray diffraction patterns corresponding to all the compounds are also shown in separate panels in the Fig. 1. Lattice constants, fractional atomic coordinates along with Wyckoff positions for all the compounds after the final refinement are summarized in Table 1. Reliability factors viz., the goodness of fit χ², structure factor R(F²), profile factor R_p, weighted profile factor R_wp and Durbin and Watson statistical parameter DWd for the refinement²⁷ are also included in the same table. Substitution of larger size, monovalent potassium (1.55 Å – 12-fold coordination) for smaller size Dy³⁺ ion (1.027 Å – 8-fold coordination) partially converts some of the JT active trivalent manganese ions (0.645 Å) to tetravalent manganese ions (JT inactive) of smaller size (0.58 Å) to preserve the total charge balance in the samples. The average ionic size at Dy size increases from 1.027 Å for x = 0.0 to 1.211 Å for x = 0.3 while the average ionic size at Mn reduces from 0.645 Å for x = 0 to 0.576 Å for x = 0.3. As a result of this, we see that for initial concentration of 10 at% K, volume of the unit cell increases and subsequent substitution brings down the volume because the number of smaller Mn⁴⁺ ions increases. However, distortions in bond lengths are much more distinctive when x = 0 as expected due to the presence of active JT Mn³⁺ ions. Table 2 lists some of the relevant inter atomic distances together with bond angles derived from the diffraction data with standard deviations in parenthesis. Although there are octahedral tilts which increase with x, coordination of manganese and dysprosium ions is preserved. With substitution, changes in the JT distortion of the oxide octahedron around Mn³⁺ cation are evident from the Mn–O bond distances. However, the distortions within Mn–oxygen octahedra are also reducing since concentration of JT ion (Mn³⁺) is decreasing with K. Dy_0.7K_0.3MnO₃ shows more regular octahedra as compared to the pristine compound. The apical bond length (Mn–O1) increases and approaches the one (the longer) of the axial Mn–O2 bond distances for K3 which indicates that the distortions within the octahedra are small as compared to the parent compound. The suppression of distortions for large K content is remarkable as compared to that of DMO, and this may be inferred to be due to the presence of less no. of JT active ions, Mn³⁺. This can also be verified with D_JT parameter which estimates the deformation of MnO₆ octahedra from the bond lengths and is calculated using the relation:
here Δd_Mn–O2 is the change in the axial bond distances and 〈d_Mn–O2〉 is the average bond distance in the ac plane. D_JT is 0.101 for x = 0.3 in contrast to 0.103 for x = 0. While some of the Dy–O distances decrease and others increase as seen from the Fig. 2d. All the parameters that influenced the polyhedral distortions in the structure with substitution are plotted against K content in Fig. 2.

Fig. 1 Diffraction patterns of Dy_1−xK_xMnO₃. (a) x = 0.0, (b) x = 0.1, (c) x = 0.2 and (d) x = 0.3. Experimental data are presented by closed circles and calculated intensity is plotted by solid lines. The difference between the experimental and calculated is also included by a solid line below the patterns. Vertical blue color lines correspond to Bragg reflection positions as per the lattice constants with Pnma space group.

Table 1 Structural parameters from the refined data for Dy_1−xK_xMnO₃. Dy, K and O(1) are at (4c) position: (x, 1/4, z), Mn is in a special position (4b): (0, 0, 1/2) and O(2) is in a general position (8d): (x, y, z)

Parameters			Composition, x
			0.0	0.1	0.2	0.3
Space group			Pnma
Lattice parameters (Å)		a	5.783993	5.792277	5.757226	5.744169
		b	7.388287	7.386155	7.403611	7.405681
		c	5.275582	5.276251	5.279975	5.278595
Unit cell volume (Å^3)			225.446	225.732	225.054	224.549
Fractional atomic coordinates	Dy/K	x	0.080109	0.080687	0.077851	0.077467
		z	0.983761	0.983401	0.983576	0.983449
	O1	x	0.469045	0.482108	0.461613	0.457863
		z	0.11002	0.115660	0.123688	0.132861
	O2	x	0.180673	0.179024	0.177344	0.179894
		y	0.548879	0.548430	0.551833	0.558297
		z	0.195885	0.204968	0.202080	0.197239
Reliability factors		χ^2	2.962	2.254	3.923	4.343
		R(F^2)	9.24	5.98	8.71	7.69
		Rp	10.04	9.26	11.70	12.20
		wRp	13.37	12.86	16.01	16.30
		Dwd	1.270	1.168	0.982	0.922

---

Table 2 Inter atomic distances (Å) and bond angles (°) in Mn–O octahedron for Dy_1−xK_xMnO₃ with standard deviations in parenthesis

Parameters	Composition, x
	0.0	0.1	0.2	0.3
dMn–O1	1.94479 (3)	1.94752 (3)	1.97139 (4)	1.99110 (4)
dMn–O2	1.94179 (2)	1.90434 (3)	1.91487 (4)	1.94872 (4)
dMn–O2	2.15187 (3)	2.18036 (3)	2.17317 (5)	2.15592 (5)
∠Mn–O1–Mn	143.521 (1)	142.936 (1)	139.730 (1)	136.822 (1)
∠Mn–O2–Mn	145.905 (0)	147.029 (0)	145.593 (0)	143.670 (0)

---

Fig. 2 Comparison of the refined structural parameters for all the compounds.

Due to changes in the ionic sizes of Dy and Mn, atomic positions of Dy, Mn and oxygen are changed giving rise to more complicated oxygen ion environment. The most prominent distortion from the ideal cubic perovskites is in the tilting of the polyhedra along b-axis and bending of Mn–O2–Mn in the ac plane in the Pnma symmetry. EDX spectra of K1, K2 and K3 shown in Fig. 3 reveal the presence of all the cations present in the studied compounds without loss of elements during high temperature synthesis.

Fig. 3 Energy dispersive X-ray spectra corresponding to the potassium substituted compounds revealing the presence of all the elements.

3.2. Vibrational properties

DyMnO₃ has an orthorhombic structure with space group Pnma, D¹⁶_2h(mmm) with four formula units per unit cell – 24 Raman active modes are expected. Raman active modes using SAM module of Bilbao crystallographic server³¹ normal modes at the zone centre are enumerated and are listed in Table 3.

Table 3 Irreducible representations for Raman active modes in the orthorhombic structure with Pnma space group

Atoms	Wyckoff position	Site symmetry	Ag	B1g	B2g	B3g
Dy & O1	4c	Cs	2	1	2	1
Mn	4b	Ci	—	—	—	—
O2	8d	C1	3	3	3	3

---

The irreducible representation, Γ for Pnma is given by:

Γ_Raman(Pnma) = 7A_g + 5B_1g + 7B_2g + 5B_3g

Mn atoms occupying a special position (0, 0, 1/2) with site symmetry C_i do not contribute to Raman modes (Table 3). Only dysprosium and oxygen ions give rise to Raman active modes. Hence Raman modes are due to oxygen polyhedral vibrations and translations of oxygen atoms in the unit cell. Peak centers of the Raman mode frequencies have been obtained by fitting the Raman spectra using Lorentzian function. Raman spectrum of DMO (Fig. 4a) exhibits fourteen vibrational modes in the range 50 to 1000 cm⁻¹ as shown in Table 4 and they are consistent with those reported in the literature.^21,32,33 Six external modes appear below 200 cm⁻¹. These low wave number modes could be assigned to the vibrations of heavier rare earth ion shifts. Remaining modes could not be detected either due to weak intensity or accidental degeneracy. Line widths of all bands are high due to polyhedral distortions and spin-phonon coupling.³⁴ Assignment of vibrational modes to their respective atomic motions/polyhedral units was carried out following Cai et al.³⁵ Out of the four pure modes, the Raman band at 614 cm⁻¹ is attributed to a symmetric stretching (SS) of the basal oxygen ions of the octahedra. Asymmetric stretching mode associated with distortions produced due to JT Mn³⁺ ions is observed at 488 cm⁻¹. The vibrational modes arising from polyhedral tilts and bending correspond to 372 cm⁻¹ and 522 cm⁻¹ respectively. With increasing potassium content, (i.e., reduction in Mn³⁺ concentration) (Fig. 2a), the intensity of the band at 488 cm⁻¹ which denotes JT distortions reduces. This can be understood from the reduction in the dispersion of octahedral bond lengths (Fig. 2c). Also atomic vibrations giving rise to a bending mode which appears as a shoulder to the JT mode gets decoupled and shifts to a higher frequency for K3. Frequency of the SS mode remains unchanged with x except for K3; where a mode hardening is observed. This is followed by an intensity reversal between SS and JT modes. Frequency of the Raman band corresponding to octahedral tilt remains the same but its intensity reduces gradually. The remaining bands arise due to coupled vibrations of Dy and O1 in the xz plane and along the y-axis. Raman spectra for the substituted compounds are shown in Fig. 4b–d. The overall features of the spectra of the substituted compounds are similar to those of the parent compound except for K3 where sharp peaks are observed. All six bands below 200 cm⁻¹ are preserved. Fig. 5 displays the dependence of mode frequencies on potassium composition (x). There is a slight upward shift in some of the Raman frequencies with increasing K content, which is attributed to lattice contraction upon replacement of Dy by K. It is worth noting here that the line width of the Raman bands for K3 has reduced which may facilitate magnetic interactions among Mn ions. Frequency of the bending mode increases showing hardening with x. Asymmetric mode found at 488 cm⁻¹ increased to 494 cm⁻¹ for K3. However, local symmetry might have changed as new peaks appear for x = 0.3. A remarkable feature is the large intensity of the low energy band for K3. K3 showed a high intense Raman band along with a small shoulder at 216 cm⁻¹. Since the bond distances do not change abruptly across the solid solution range studied, Raman band frequency changes are small except for the bands discussed above. In order to investigate valency state of Mn for substitution of potassium in DyMnO₃, X-ray photoelectron spectroscopy has been used. The Fig. 6 displays the normalized satellite peaks of 2p_3/2, 2p_1/2 of Mn ion for different concentration of potassium. In the parent compound DyMnO₃, only Mn ion is found in trivalent state with binding energies 641.8 eV for 2p_3/2 and 653.9 eV for 2p_1/2. This Mn ion is transferred into mixed valency states i.e., Mn³⁺ and Mn⁴⁺ ions when potassium is substituted at Dy site. Using XPS PEAKS 4.1 software,³⁶ the satellite peaks of Mn ion in potassium substituted DyMnO₃ are fitted and binding energies of Mn³⁺, Mn⁴⁺ are found and are given in Table 5. The binding energy difference of Mn³⁺ and Mn⁴⁺ is calculated and included in the Table 5. This difference is not exceeding 1.5 eV. The ratio of Mn³⁺/Mn⁴⁺ is calculated³⁷ and the reduction in their ratio suggested that JT active Mn³⁺ ion is decreased with potassium concentration. Therefore, we can conclude that as potassium concentration increases in material, holes generation increases.

Fig. 4 Unpolarized, room temperature Raman spectra for Dy_1−xK_xMnO₃ displaying Raman active phonon modes with respect to potassium content, x = 0, 0.1, 0.2 & 0.3. λ_exc. = 514.4 nm. Mode assignment has been done following Cai et al.³⁵ * indicates new Raman lines for K3.

Table 4 Comparison of experimental Raman frequencies corresponding to the vibrational modes in Dy_1−xK_xMnO₃. New peaks observed for K3 are also included in the table and marked with *. SS – Symmetric Stretching mode; B – bending mode; JT/ASS – Jahn–Teller/Anti Symmetric Stretching mode; T – tilting mode

S. no.	Composition, x
	0.0	0.1	0.2	0.3
1	61	60	59	60
2	75	74	74	73
3	94	96	91	93
4	111	113	112	109
5	141	141	139	144
6	163	163	161	177
				216*
7	274	283	278	238*
				302*
8	320	320	314	326
				336*
9	372	381	375	350
10	384	387	385	385
				416*
				454*
11	488	490	488	494
12	522	521	529	539
13	614	614	615	624
14	642	642	650	688

---

Fig. 5 Comparison of Raman modes for the solid solution, Dy_1−xK_xMnO₃.

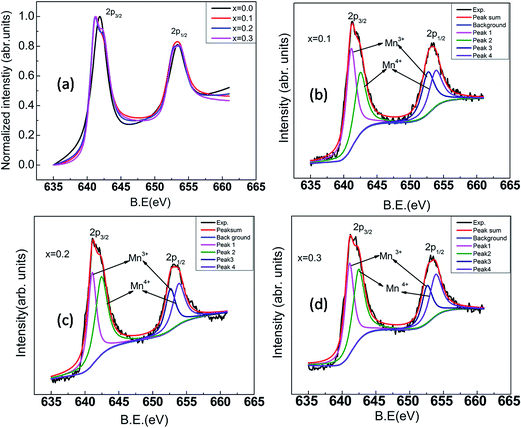Fig. 6 XPS spectra of Mn ion for Dy_1−xK_xMnO₃ (x = 0.0–0.3 : 0.1) (a) normalized XPS spectra of Mn ion (b–d) XPS spectra for x = 0.1, 0.2 and 0.3 respectively.

Table 5 Binding energies of Mn³⁺ and Mn⁴⁺ ions along with their energy difference and ratio

Dy1−xKxMnO3	2p3/2 (eV)				2p1/2 (eV)
	Mn^3+	Mn^4+	Mn^4+–Mn^3+		Mn^3+	Mn^4+	Mn^4+–Mn^3+
x = 0.0	641.8				653.4
x = 0.1	641.1	642.5	1.3	4	652.8	653.9	1.1	4
x = 0.2	641.1	64.4	1.3	1.5	652.7	654.3	1.6	1.5
x = 0.3	641.1	642.5	1.4	0.6	652.7	653.9	1.2	0.6

---

4. Conclusions

Bulk compounds of Dy_1−xK_xMnO₃ (x = 0–0.3 : 0.1) were synthesized using ceramic method. Rietveld analysis confirmed the single phase formation in orthorhombic structure with Pnma space group. Structural distortions in DyMnO₃ resemble that of GdFeO₃-type structure. These distortions were caused due to the presence of smaller Dy ion and active JT Mn³⁺ ions. Although ionic size of K is larger than Dy, for each potassium substitution, two tetravalent manganese ions (whose ionic size is smaller than Mn³⁺) are generated for charge compensation. As a consequence, unit cell volume decreases with increasing x. Furthermore, concentration of JT ion reduces with increasing K, leading to a reduction in octahedral bond deformations. This was evident from a comparison of equatorial and axial bond lengths of Mn–O octahedra in the case of K3. Moreover, decoupling of some of the Raman bands corroborates this conclusion. The primary results described in this report are that the Mn–O octahedra are distorted for x = 0 sample and these distortions are reduced for high K content, x = 0.3. Raman band frequencies increase with potassium substitution which involves stretching vibrations of Dy–O, Mn–O–Mn bending and octahedral tilts. EDX analysis reveals that the cationic composition of the compounds is close to the nominal one. The XPS results show evidence for Mn ion which is in the mixed oxidation states and holes production increases with increasing of potassium concentration.

Acknowledgements

We acknowledge UGC-DAE-CSR Centre and Dr R. Rajaraman, MSG, IGCAR for Raman scattering measurements and Ms N. Sreevidya and Mr Nandagopal, MMG, IGCAR for EDX and XPS measurements.

References

1. T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T. Arima and Y. Tokura, Nature, 2003, 426, 55.
2. Colossal Magnetoresistance, Charge Ordering and Related Properties of Manganese Oxides, ed. C. N. R. Rao and B. Raveau, World Scientific, Singapore, 1998.
3. Y. Chen, H. Yuan, G. Li, G. Tian and S. Feng, J. Cryst. Growth, 2007, 305, 242.
4. S. Harikrishnan, S. Robler, C. M. Naveen Kumar, H. L. Bhat, U. K. Robler, S. Wirth, F. Steglich and S. Elizabeth, J. Phys.: Condens. Matter, 2009, 21, 096002.
5. V. Y. Ivanov, A. A. Mukhin, A. S. Prokhorov, A. M. Balbashov and L. D. Iskhakova, Phys. Solid State, 2006, 48, 1726.
6. H. L. Yakel, W. C. Koehler and E. F. Bertaut, et al., Acta Crystallogr., 1963, 16, 957.
7. Y. Tokura, Rep. Prog. Phys., 2006, 69, 797.
8. Y. Moritomo, A. Asamitsu and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 16491.
9. R. Mahendiran, S. K. Tiwary, A. K. Raychaudhuri, T. V. Ramakrishnan, R. Mahesh, N. Rangavittal and C. N. R. Rao, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 3348.
10. G.-L. Liu, J.-S. Zhou and J. B. Goodenough, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 144414.
11. G. Biotteau, M. Hennion, F. Moussa, J. Rodriguez-Carvajal, L. Pinsard, A. Revcolevschi, Y. M. Mukovskii and D. Shulvatev, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 104421.
12. X. Fabreges, I. Mirebeau, P. Bonville, S. Petit, G. Lebras-Jasmin, A. Forget, G. Andre and S. Pailhes, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 214422.
13. F. Hong, Z. Cheng and X. Wang, Appl. Phys. Lett., 2011, 99, 192503.
14. C. Wehrenfennig, D. Meier, T. Lottermoser, T. Lonkai, J. U. Hoffmann, N. Aliouane, D. N. Argyriou and M. Fiebig, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 100414.
15. S. Harikrishnan Nair and S. Elizabeth, J. Cryst. Growth, 2013, 362, 24.
16. M. Pękała, F. Wolff-Fabris, J.-F. Fagnard, P. Vanderbemden, J. Mucha, M. M. Gospodinov, V. Lovchinov and M. Ausloos, J. Magn. Magn. Mater., 2013, 335, 46.
17. S. Mansouri, S. Jandl, J. Laverdière, P. Fournier, A. A. Mukhin, V. YuIvanov and A. M. Balbashov, J. Phys.: Condens. Matter, 2013, 25, 066003.
18. T. Kimura, S. Ishihara, H. Shintani, T. Arima, K. T. Takahashi, K. Ishizaka and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 060403.
19. T. Mori, K. Aoki, N. Kamegashira, T. Shishido and T. Fukuda, Mater. Lett., 2000, 42, 387.
20. S. Harikrishnan, C. M. Naveen Kumar, S. S. Rao, H. L. Bhat, S. V. Bhat and S. Elizabeth, J. Appl. Phys., 2008, 104, 023902.
21. M. N. Iliev, M. V. Abrashev, J. Laverdiere, S. Jandl, M. M. Gospodinov, Y.-Q. Wang and Y.-Y. Sun, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 064302.
22. R. Feyerherm, E. Dudzik, N. Aliouane and D. N. Argyriou, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 180401.
23. S. Harikrishnan, C. M. Naveen Kumar, H. L. Bhat, S. Elizabeth, U. K. Robler, K. Dorr, S. Robler and S. Wirth, J. Phys.: Condens. Matter, 2008, 20, 275234.
24. K. Yoshii, Y. Hiramitsu, Y. Yoneda, Y. Okajima, Y. Nishihata, J. Mizuki and N. Ikeda, Ferroelectrics, 2009, 379, 183.
25. N. Zhang, S. Dong, Z. Fu, Z. Yan, F. Chang and J. Liu, Sci. Rep., 2014, 4, 1.
26. C. Abughayada, B. Dabrowski, M. Avdeev, S. Kolesink, S. Remsen and O. Chmaissem, J. Solid State Chem., 2014, 217, 127.
27. G. V. Narasimha Rao, V. S. Sastry, H. S. G. K. Murthy, V. Seshagiri and T. S. Radhakrishnan, Powder Diffr., 1996, 11, 200.
28. B. H. Toby, EXPGUI, a graphical user interface for GSAS, J. Appl. Crystallogr., 2001, 34, 210.
29. JCPDS card no. 25-0330.
30. J. B. Goodenough, Localized to itinerant electronic transition in perovskite oxides, Springer, 2001.
31. http://www.cryst.ehu.es/rep/sam.html.
32. L. M. Carrón, A. de Andrés, M. J. M. Lope, M. T. Casais and J. A. Alonso, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174303.
33. J. Laverdiere, S. Jandl, A. A. Mukhin, V. Yu. Ivanov, V. G. Ivanov and M. N. Iliev, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 214301.
34. M. Viswanathan, P. S. Anil Kumar, V. S. Bhadram, C. Narayana, A. K. Bera and S. M. Yusuf, J. Phys.: Condens. Matter, 2010, 22, 346006.
35. X. Cai, L. Shi, S. Zhou, J. Zhao, Y. Guo and C. Wang, J. Appl. Phys., 2014, 116, 103903.
36. R. Kwok, XPSPEAK V4.1, 2000, http://www.phy.cuhk.end.hkl/Surface/XPSPEAK/.
37. M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2011, 257, 2717.

---