Theoretical study of electronic and mechanical properties of Fe2B
Shiyu Denga,
Jiashi Zhaob,
Shubo Weia,
Chunye Zhua,
Jian Lv*a,
Quan Li*a and
Weitao Zhenga
aCollege of Materials Science and Engineering and State Key Laboratory of Superhard Materials, Jilin University, Changchun, 130012, China. E-mail: liquan777@jlu.edu.cn; lvjian@calypso.cn
bSchool of Computer Science and Technology, Changchun University of Science and Technology, Changchun 130022, China
First published on 20th July 2016
Abstract
The structural, electronic, and mechanical properties of the Fe2B with the I4/mcm structure were investigated using first principles calculations. The dynamical stability and mechanical stability of the I4/mcm phase were confirmed, according to the calculated phonon dispersion and elastic constant. The theoretical band structure and density of states showed I4/mcm Fe2B to be metallic. The microscopic mechanism of the structural deformation of I4/mcm Fe2B was examined by calculating ideal strength values at large levels of strain. Our theoretical results demonstrated the failure mode in I4/mcm Fe2B to be dominated by shear, with the lowest pure shear peak stress calculated to be 20.0 GPa.
Introduction
The popularity and versatility of superhard and ultrahard materials originate not only from their superior hardness (with Vickers hardness values of over 40 GPa) but also from their wide range of mechanical properties. These materials have been adapted by various means to numerous industrial applications, such as abrasives, coatings, cutting, polishing tools, etc. Apart from traditional superhard or ultrahard materials such as (nano)diamonds and cubic boron nitride (c-BN), which require expensive high-temperature and high-pressure synthesis conditions, a distinct category of potential superhard materials consisting of small, light covalent elements (B, C, N, O) and large, electron-rich transition metals (Cr, Mn, Ru, W, Re, Os, Fe) provide less expensive alternatives.1–23 Therefore, experimental efforts devoted to Fe–B compounds should continue to be encouraged due to the potential capacity of these compounds to form superhard or hard materials. For example, the kinetic studies of boron diffusion in the paste boriding process during the growth of FeB and Fe2B layers were motivated by their practical and industrial applications as hard protective coatings.1,2 As reported most recently, Fe2B nanosheets have been synthesized for the purpose of producing potential magnetic recording media and electrode materials for Li-ion batteries and supercapacitors.3 As the latest experimental phase diagram4 verified, FeB and Fe2B are the only reproducible low-temperature phases that can be crystallized in the oP8 (or the related oS8) and tI12 configurations, respectively. In contrast, apart from the observation of a metastable FeB49 intercalation compound5 and syntheses of possibly amorphous6 and AlB2-type7 iron diborides, less is known about the boron-rich ordered phases. Yet, previous modeling work on Fe–B compounds predicted new candidate ground states of Fe–B compounds with Fe to B ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, 1
4, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, and 1
2, and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 via a combination of ab initio high-throughput and evolutionary searches.8 FeB4 was recently reported to be successfully synthesized and displayed a measured Vicker hardness value of over 60 GPa,9 much greater than those (20–30 GPa) of other known Fe–B compounds and other transition-metal borides, such as ReB2, WB4, and CrB4.9 However, the theoretical ideal strength10 and Vickers calculations11 showed that FeB4 is unlikely to be superhard.
1 via a combination of ab initio high-throughput and evolutionary searches.8 FeB4 was recently reported to be successfully synthesized and displayed a measured Vicker hardness value of over 60 GPa,9 much greater than those (20–30 GPa) of other known Fe–B compounds and other transition-metal borides, such as ReB2, WB4, and CrB4.9 However, the theoretical ideal strength10 and Vickers calculations11 showed that FeB4 is unlikely to be superhard.
Though it is commonly expected that the ideal strength of transition metal borides would increase with rising boron content,12–19 recent cases have shown the ideal strength of some materials to improve little or to even detectably decline with increasing boron content.20 Moreover, recent theoretical studies showed Mo2B,21 Ti2B,22 and W2B23 with their long-assumed I4/mcm space group to be dynamically unstable, and a new energetically more stable phase with tetragonal I4/m symmetry was predicted to be a candidate structure for these compounds. Many efforts have been devoted to the study of borides.24,25 Therefore, an interesting task would be to understand the stability and the mechanical properties of the compounds with the low boron content of Fe2B. In the current work, we selected the tetragonal Fe2B with the I4/mcm space group as the representative of the iron-rich Fe–B compounds, to compare its ideal strength with that of the boron-rich phase of FeB4. Here, first principles calculations were carried out to study the structural stability and ideal strength of I4/mcm Fe2B. The mechanical analyses showed the I4/mcm Fe2B to be dynamically stable and to display a relatively high simulated hardness, with a high bulk modulus, yet with a relatively low shear modulus, demonstrating the character of a low-compressible liquid.
Computational methods
We carried out ab initio structural relaxations and electronic properties calculations within the framework of density functional theory (DFT) using the Vienna Ab Initio Simulation Package (VASP) code.26 The Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA)27 was implemented for the exchange-correlation functional. The electron-ion interaction was described by applying the projector augmented-wave method (PAW)28 with 3d64s2 and 2s22p1 as the valence electrons for Fe and B atoms, respectively. The total energy of the structure was minimized by relaxing the structural parameters using a conjugate gradient optimization method.29,30 We chose an energy cutoff of 500 eV and Monkhorst–Pack31 k-point grids of 8 × 8 × 8 for the I4/mcm Fe2B structure, with more condensed Monkhorst–Pack k-point grids of 10 × 10 × 10 for the calculation of the elastic modulus and hardness. The energy convergence was found to be about 1 meV per atom, with residual stresses and forces in the fully relaxed structures less than 0.1 GPa and 0.001 eV Å−1, respectively. Recent advances in theoretical calculations make it possible to calculate the stress–strain relations of a perfect crystal under various tensile and pure shear strain directions. In the current work, the stress–strain relation was obtained by calculating the stress response to structural deformation along specific loading paths using a quasi-static relaxation method that simulates various loading conditions and determines the corresponding ideal strength and deformation modes.32–34Results and discussion
The crystal structure of the ground state of Fe2B with the I4/mcm space group under ambient pressure is shown in Fig. 1(a). The cell parameters and atomic positions of I4/mcm Fe2B were fully optimized by performing first principles calculations. The calculated structural parameters were determined to be a = b = 4.9498 Å and c = 4.2026 Å, and the volume of the unit cell was thus determined to be 102.9644 Å3, which are consistent with the previous experimental35 and theoretical data.36 Specifically, the calculated equilibrium lattice parameter in the c direction of I4/mcm Fe2B matched—quite well, while the values in the a and b directions deviated a little from—. Such deviations in the a and b directions may be caused by our choice to perform the calculations using DFT, and can be minimized by using the vdW-corrected DFT (DFT-D) method.37 Yet, there is merely a 3.1% lower and a 2.3% higher deviation of— from the experimental35 and theoretical values,36 respectively. Therefore, the obtained results based on the DFT method can still be considered reliable. The calculated phonon spectrum of I4/mcm Fe2B at ambient pressure in Fig. 1(b) illustrates no imaginary phonon frequency across the entire Brillouin zone, supporting its dynamical stability. Further analysis of the electronic properties of I4/mcm Fe2B identified it as a metallic phase with several energy bands crossing its Fermi surface, as shown in Fig. 2, where the calculated electronic bands are plotted along the corresponding high-symmetry directions. Accordingly, the density of state (DOS) was found to be relatively high around its Fermi energy. | ||
| Fig. 1 The crystal structure (a) and calculated phonon spectrum (b) for I4/mcm Fe2B. The Fe atoms are represented as large purple spheres, while B atoms are represented as small green spheres. | ||
 | ||
| Fig. 2 The electronic band plot along high-symmetry directions (left) and electronic density of states (right) for I4/mcm Fe2B. The E-Fermi level is the red line. | ||
We then explored the mechanical properties of the tetragonal phase of Fe2B based on the calculated elastic constants, listed as C11 = 455 GPa, C33 = 302 GPa, C44 = 96 GPa, C66 = 129 GPa, C12 = 231 GPa, and C13 = 274 GPa. Referring to the mechanical stability criteria38 of the tetragonal phase, I4/mcm Fe2B is mechanically stable under ambient conditions, with positive values for the evaluated elastic constants. Since calculated elastic constants are effective at estimating the hardness of materials, we compared the hardness of iron-rich Fe2B and boron-rich FeB4. The simulated Vickers hardness value of tetragonal Fe2B was calculated to be 11.5 GPa, while the Vickers indentation strength value of orthorhombic FeB4 was previously shown to be 16.6 GPa.11 Considering that boron makes up only 8.82% wt of Fe2B, while it makes up 43.64% of FeB4, the hardness value of Fe2B is indicative of a good performance. The bulk modulus of I4/mcm Fe2B was calculated to be 301 GPa, only a bit improved relative to that (B = 284 GPa) of FeB4,11 whereas the shear modulus (G = 87 GPa) of Fe2B was found to be much lower than that (G = 197 GPa) of FeB4.10 The high bulk modulus is due to the strong covalent bonding between Fe 3d and B 2p states and the high density of valence electrons in Fe2B. These properties make this material behave like a low-compressibility liquid, specifically difficult to compress when applying hydrostatic pressure (as indicated by its high bulk modulus), but flexible under uniaxial or shear strain conditions (as indicated by its low shear modulus).
Apart from considering elastic properties, we have also checked the ideal strength.39,40 Though a macroscopic material suffers deformation or fracture far below its ideal strength when being loaded in most cases, the ideal strength is nonetheless a crucial theoretical parameter, which sets an upper bound on the mechanical strength of the material and characterizes the nature of the chemical bonding in the crystal.41,42 Here, we calculated the ideal strength of tetragonal Fe2B in various tensile and pure shear deformation directions. The magnitude of ideal strength for different crystals depends on the direction of the applied load: tensile strength depends on the direction of tension strain, while pure shear strength depends on the plane in which the shear strain occurs and on the direction of the shear strain.43 Generally, the lowest peak stress in the stress–strain curves defines the corresponding ideal strength.43–50 If this minimum peak stress is applied and maintained, fracture or deformation will result in a perfect crystal structure.
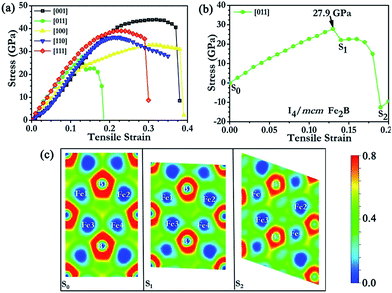
Fig. 3 shows the stress responses of I4/mcm Fe2B along various tensile strain directions. Fe2B displayed relatively strong stress responses along the [001], [110] and [111] directions with the peak tensile stresses ranging from 36.3 to 43.9 GPa. The weakest tensile direction was found to be along the [011] direction, indicating that I4/mcm Fe2B would cleave in the [011] direction with an ideal tensile strength of 27.9 GPa. From Fig. 3(b), we observed a creeplike behaviour, which is typically seen in metals but seldom observed in strong covalent solids. To examine the intrinsic mechanism of the bonding states, ideal strength and fracture behaviour for I4/mcm Fe2B under tensile strain, we carried out a detailed analysis of atomistic structural deformation modes in Fe2B, utilizing the plotted two-dimensional electron localization function (ELF) isosurfaces at several key points of strain along the weakest peak tensile stress direction [Fig. 3(c)]. B was clearly indicated to carry the negative charges for I4/mcm Fe2B, with positive charges shared by the surrounding Fe atoms. From the calculated ELF data, Fe was shown to introduce a high density of valence electrons into the compounds to resist compression while the B atoms were shown to help form a strong covalent bonding network to enhance structural integrity and to function as barriers to dislocations during deformation, enabling I4/mcm Fe2B to be harder than pure iron. Additionally, these electrons, which are not localized between particular atoms, directly contribute to other physical properties of Fe2B over FeB4, e.g., Fe2B is an excellent conductor of electricity (and heat), displays good ductility and is not transparent to visible light.
Though the shear strength of Fe2B was found to be lower than its tensile strength, ranging from 27.9 to 43.9 GPa, Fe2B was found to withstand a greater shear strain (ε = 0.29) before deformation or fracture at the critical point than the critical tensile strain (ε = 0.13). Below we describe the analysis of the atomistic deformation mode with the lowest stress peak along the shear deformation direction (011)[11−1]. The corresponding two-dimensional ELF plots at several key points of strain are shown in Fig. 4(c). When Fe2B was being loaded, it was the Fe–B bond that displayed the most obvious deformation tendency with increasing pure shear strain values along the (011)[11−1] shear direction. The reduced pure shear strength of Fe2B (20.0 GPa), compared to that of FeB4 (24.1 GPa), resulted from the relatively flexible Fe–B bonds in Fe2B and absence of strong B–B covalent bonds. The ELF plots indicated the electrons to be densely and uniformly dispersed in the crystal, occupying void spaces instead of being specifically attached to iron atoms. Such electride-like51 behavior may contribute to Fe2B performing well under high pressure, and possessing a relatively high bulk modulus. Additionally, the transformation of boron vacancies during deformation or under pressure may affect the spin density of Fe2B, thus affecting the magnetism.52 Therefore, further investigation of the properties of Fe2B is merited; however, the mechanical properties are not sensitive to the consideration of magnetism,11 and the studies of magnetism are beyond the scope of this work.
Conclusions
From the obtained phonon dispersion curves and elastic constants, the tetragonal Fe2B with I4/mcm space group was substantiated to be dynamically and mechanically stable. I4/mcm Fe2B was found to be metallic with several bands crossing the Fermi level. A high bulk modulus of 301 GPa was predicted for I4/mcm Fe2B, higher than that of FeB4 (284 GPa), while the shear modulus (87 GPa) of Fe2B was calculated to be much lower than that of FeB4 (197 GPa). I4/mcm Fe2B was therefore shown to be ultra-incompressible under static pressure but rather flexible under uniaxial or shear strain conditions, with these properties attributed to the strong covalent bonding and the high density of valence electrons, and making the material behave like a low-compressible liquid. The ideal strength of I4/mcm Fe2B was calculated to be 20.0 GPa, appearing in the (011)[11−1] shear direction, with this value of ideal strength being a little lower than that (24.1 GPa) of FeB4 in the (110)[001] shear direction. The current results are expected to stimulate further investigations into the intrinsic hard nature of other transition metal borides.Acknowledgements
This work was supported by the China 973 Program (2011CB808200); the Natural Science Foundation of China under No. 11474125, 51202084, 51372095 and 11534003; the 2012 Changjiang Scholars Program of China; and Changjiang Scholar and Innovative Research Team in University (IRT1132). Some of the calculations were performed in the High-Performance Computing Center of Jilin University.References
- I. Campos, J. Oseguera, U. Figueroa, J. A. Garcia, O. Bautista and G. Kelemenis, Mater. Sci. Eng. A, 2003, 352(1), 261–265 CrossRef.
- S. Sen, U. Sen and C. Bindal, Vacuum, 2005, 77(2), 195–202 CrossRef CAS.
- G. V. Loyola, M. C. Pereira, E. C. Passamani, P. S. Moscon, C. Larica, A. Y. Takeuchi and A. L. Rossi, RSC Adv., 2015, 5(87), 71341–71344 RSC.
- T. Van Rompaey, K. H. Kumar and P. Wollants, J. Alloys Compd., 2002, 334(1), 173–181 CrossRef CAS.
- K. Balani, A. Agarwala and N. B. Dahotre, J. Appl. Phys., 2006, 99(4), 044904 CrossRef.
- K. Moorjani, T. O. Poehler, F. G. Satkiewicz, M. A. Manheimer, D. J. Webb and S. M. Bhagat, J. Appl. Phys., 1985, 57, 3444–3446 CrossRef CAS.
- L. G. Voroshnin, L. S. Lyakhovich, G. G. Panich and G. F. Protasevich, Met. Sci. Heat Treat., 1970, 12(9), 732–735 CrossRef.
- A. N. Kolmogorov, S. Shah, E. R. Margine, A. F. Bialon, T. Hammerschmidt and R. Drautz, Phys. Rev. Lett., 2010, 105(21), 217003 CrossRef CAS PubMed.
- H. Gou, N. Dubrovinskaia, E. Bykova, A. A. Tsirlin, D. Kasinathan, W. Schnelle and D. Batuk, Phys. Rev. Lett., 2013, 111(15), 157002 CrossRef PubMed.
- M. Zhang, M. Lu, Y. Du, L. Gao, C. Lu and H. Liu, J. Appl. Phys., 2014, 140(17), 174505 Search PubMed.
- B. Li, H. Sun and C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(1), 014106 CrossRef.
- R. Mohammadi, A. T. Lech, M. Xie, B. E. Weaver, M. T. Yeung, S. H. Tolbert and R. B. Kaner, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(27), 10958–10962 CrossRef CAS PubMed.
- M. Xie, R. Mohammadi, Z. Mao, M. M. Armentrout, A. Kavner, R. B. Kaner and S. H. Tolbert, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(6), 064118 CrossRef.
- Q. Gu, G. Krauss and W. Steurer, Adv. Mater., 2008, 20(19), 3620–3626 CrossRef CAS.
- X. Cheng, W. Zhang, X. Q. Chen, H. Niu, P. Liu, K. Du, G. Liu, D. Li, H. Cheng, H. Ye and Y. Li, Appl. Phys. Lett., 2013, 103(17), 171903 CrossRef.
- M. Wang, Y. Li, T. Cui, Y. Ma and G. Zou, Appl. Phys. Lett., 2008, 93(10), 101905 CrossRef.
- Q. Tao, D. Zheng, X. Zhao, Y. Chen, Q. Li, Q. Li, C. Wang, T. Cui, Y. Ma, X. Wang and P. Zhu, Chem. Mater., 2014, 26(18), 5297–5302 CrossRef CAS.
- M. Xie, R. Mohammadi, C. L. Turner, R. B. Kaner, A. Kavner and S. H. Tolbert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(10), 104104 CrossRef.
- X. Li, Y. Tao and F. Peng, J. Alloys Compd., 2016, 6(687), 579–585 CrossRef.
- Q. Li, D. Zhou, W. Zheng, Y. Ma and C. Chen, Phys. Rev. Lett., 2015, 115(18), 185502 CrossRef PubMed.
- D. Zhou, Y. Liu, B. Shen, X. Zhao, Y. Xu and J. Tian, Phys. Chem. Chem. Phys., 2016, 18(11), 7927–7931 RSC.
- Q. Li, D. Zhou, W. Zheng, Y. Ma and C. Chen, Phys. Rev. Lett., 2013, 110(13), 136403 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186 CrossRef CAS.
- F. A. La Porta, L. Gracia, J. Andrés, J. R. Sambrano, J. A. Varela and E. Longo, J. Am. Ceram. Soc., 2014, 97(12), 4011–4018 CrossRef CAS.
- B. Xiao, J. D. Xing, J. Feng, C. T. Zhou, Y. F. Li, W. Su, X. J. Xie and Y. H. Cheng, J. Phys. D: Appl. Phys., 2009, 42(11), 115415 CrossRef.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(11), 6671 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979 CrossRef.
- M. P. Teter, M. C. Payne and D. C. Allan, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40(18), 12255 CrossRef.
- D. M. Bylander, L. Kleinman and S. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42(2), 1394 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13(12), 5188 CrossRef.
- R. H. Telling, C. J. Pickard, M. C. Payne and J. E. Field, Phys. Rev. Lett., 2000, 84(22), 5160 CrossRef CAS PubMed.
- Y. Zhang, H. Sun and C. F. Chen, Phys. Rev. Lett., 2004, 93(19), 195504 CrossRef PubMed.
- Z. C. Pan, H. Sun and C. F. Chen, Phys. Rev. Lett., 2007, 98(13), 135505 CrossRef PubMed.
- Z. C. Pan, H. Sun, Y. Zhang and C. F. Chen, Phys. Rev. Lett., 2009, 102(5), 055503 CrossRef PubMed.
- E. E. Havinga, H. Damsma and P. Hokkeling, J. Less-Common Met., 1972, 27(2), 169–186 CrossRef CAS.
- C. T. Zhou, J. D. Xing, B. Xiao, J. Feng, X. J. Xie and Y. H. Chen, Comput. Mater. Sci., 2009, 44(4), 1056–1064 CrossRef CAS.
- Q. Wu, C. Li, L. Tan, Z. Hang and W. Zhu, RSC Adv., 2016, 6(54), 48489–48497 RSC.
- J. F. Nye, Physical Properties of Crystals, (Oxford University Press, Oxford, 1985) Search PubMed.
- T. Li, J. W. Morris Jr, N. Nagasako, S. Kuramoto and D. C. Chrzan, Phys. Rev. Lett., 2007, 98(10), 105503 CrossRef PubMed.
- J. Pokluda, M. Černý, P. Šandera and M. Šob, J. Comput.-Aided Mol. Des., 2004, 11(1), 1–28 CrossRef.
- S. Ogata, J. Li and S. Yip, Science., 2002, 298(5594), 807–811 CrossRef CAS PubMed.
- S. Ogata, J. Li, N. Hirosaki, Y. Shibutani and S. Yip, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(10), 104104 CrossRef.
- D. M. Clatterbuck, D. C. Chrzan and J. W. Morris, Acta Mater., 2003, 51(8), 2271–2283 CrossRef CAS.
- D. Roundy, C. R. Krenn, M. L. Cohen and J. W. Morris Jr, Phys. Rev. Lett., 1999, 82(13), 2713 CrossRef CAS.
- S. Ogata, J. Li and S. Yip, Science, 2002, 298(5594), 807–811 CrossRef CAS PubMed.
- Y. Zhang, H. Sun and C. F. Chen, Phys. Rev. Lett., 2005, 94(14), 145505 CrossRef PubMed.
- Y. Zhang, H. Sun and C. F. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73(14), 144115 CrossRef.
- Y. Zhang, H. Sun and C. F. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(14), 144101 CrossRef.
- J. Yang, H. Sun and C. F. Chen, J. Am. Chem. Soc., 2008, 130(23), 7200 CrossRef CAS PubMed.
- M. Zhang, M. Lu, Y. Du, L. Gao, C. Lu and H. Liu, J. Chem. Phys., 2014, 140(17), 174505 CrossRef PubMed.
- M. S. Miao and R. Hoffmann, J. Am. Chem. Soc., 2015, 137(10), 3631–3637 CrossRef CAS PubMed.
- Y. Zhang, J. Wang, M. P. K. Sahoo, T. Shimad and T. Kitamura, Phys. Chem. Chem. Phys., 2015, 17(40), 27136–27144 RSC.
| This journal is © The Royal Society of Chemistry 2016 |