Room-temperature spin transport in InAs nanowire lateral spin valve
Zhicheng Wanga,
Dong Panb,
Le Wang*c,
Tingwen Wanga,
Bing Zhaoa,
Yong Wua,
Ming Yanga,
Xiaoguang Xu*a,
Jun Miaoa,
Jianhua Zhaob and
Yong Jianga
aState Key Laboratory for Advanced Metals and Materials, School of Materials Science and Engineering, University of Science and Technology Beijing, 100083, Beijing, China. E-mail: xgxu@ustb.edu.cn
bState Key Laboratory of Superlattices and Microstructures, Institute of Semiconductors, Chinese Academy of Sciences, Beijing, 100083, China
cDepartment of Physics, Renmin University of China, Beijing, 100872, China. E-mail: le.wang@ruc.edu.cn
First published on 28th July 2016
Abstract
With its strong spin–orbital interaction, indium arsenide (InAs) is a potential candidate material for spintronic devices. Owing to the reduced scale and quasi one-dimensional confinement, InAs nanowires are expected to show novel physics property compared with InAs two-dimensional electron gas. In this work, we report room-temperature local measurement of spin transport in an InAs nanowire synthesized from the bottom-up paradigm by molecular beam epitaxy. Due to the advantage of Co/MgO barrier contact, a large spin signal of up to 35 kΩ is observed, and long spin diffusion length (about 1.9 μm) in the unintentionally doped InAs nanowire is achieved by analysing the spin signal using the transfer matrix method.
1. Introduction
Electrical spin injection into semiconductors is fundamental to realize spintronic devices using the electron spin degree of freedom instead of, or in addition to, the charge.1 Among many spin-based device concepts,2–6 the Datta–Das spin field-effect transistor (spin-FET)4 is the most classical scheme, comprising a ferromagnetic spin injector and detector, while the injected spins in the semiconductor channel are manipulated by a gate electric field. Due to the high conductance mismatch between the ferromagnetic metal (FM) and semiconductor (SC), however, spin polarization of the injected current across the FM/SC interface has been predicted theoretically less than 0.1%7 and has been verified to be slightly higher at 1.3%.8Recently, there has been considerable progress in achieving successful spin injection into semiconductors by employing Schottky9,10 or oxide tunnel contacts,11–15 an effective solution to the conductance mismatch problem proposed by Rashba.16 All-electrical spin injection and detection have been achieved in a variety of materials such as silicon (Si),12,17,18 indium arsenide (InAs),2,19 germanium (Ge),20,21 gallium arsenide (GaAs),14,15,22 doped-SrTiO3,23 graphene11,24,25 and carbon nanotube.26 Semiconductor nanowires (NWs) are ideal building blocks for future spin-based integrated circuits owing to their quasi one-dimensional confined channel and the bottom-up growth mode, avoiding complex fabrication steps. However, only a few works related to spin injection in semiconductor NWs, e.g., gallium nitride (GaN),27 indium nitride (InN),28 indium antimonide (InSb),29 Ge,30 and Si17,31,32 have been reported. Because most of them are of weak spin–orbital interaction, research on NWs with strong spin–orbital interaction is essential for achieving the spin-FET. III–V compound semiconductors, such as InSb and InAs, have received a great deal of interest so far due to their high electron mobility and narrow band gap.33–35 However, there has been no publication associated with spin injection into InAs NW to date. Also, it is reported that spin relaxation in III–V semiconductors can be significantly suppressed by reducing the channel width.36 Owing to the reduced scale and quasi one-dimensional confinement, InAs NWs are expected to show novel physics property (e.g. longer spin diffusion length, lsf) compared with InAs two-dimensional electron gas (2DEG) for future nanoscale spintronic devices. Nonlocal measurement is reported as a convincing method for effective detection of the spin signal ΔR (the difference in resistance measured when the magnetizations of FM electrodes are parallel and antiparallel), while local measurement is commonly considered unreliable for proving spin injection.31 However, the ΔR obtained by nonlocal measurement can hardly exceed a few hundred ohms; it is generally a few tens of ohms or less. Aiming at future application of spintronic devices, both a large ΔR and a large magnetoresistance (MR, the spin signal normalized by the device resistance) are desirable to discriminate them from background and spurious signals and to circumvent unpractical four-terminal device geometries.
Here, we show our measurements of efficient spin information transport and large spin signals in InAs NW-based lateral spin valve geometry with Co/MgO contact at room temperature.
2. Experiment
The InAs NWs under investigation were grown in a catalyst-free manner on n-type Si (111) substrates by molecular-beam epitaxy. The growth was performed at a temperature of 505 °C, with a V/III beam equivalent pressure ratio of 120 and growth time of 120 min. The NW morphology and crystal structure were characterized by scanning electron microscopy (SEM) and transmission electron microscopy (TEM). As shown in Fig. 1(a), the InAs NWs were vertically grown on the Si (111) substrate, and the diameter varied from ∼40 to 120 nm. As shown in Fig. 1(b), high-resolution TEM image of the InAs NW indicates that the NW has a mixture of wurtzite and zinc-blende crystal structure. After the growth, the NWs were mechanically transferred on a p-type Si (100) substrate covered with a 300 nm-thick SiO2 layer. For each NW, two contact regions were defined using electron beam lithography after locating individual wires. Prior to the deposition of electrodes, the sample was etched in buffered hydrofluoric acid to remove the native oxide layer on the NW, followed by a (NH4)2Sx solution passivation to avoid any re-oxidation of the contact area. For typical back-gate measurement, Cr/Pt (20 nm/60 nm) electrodes were deposited by magnetron sputtering and a subsequent lift-off process, as shown in Fig. 1(c). For spin transport measurement, however, 1.5 nm MgO oxide barrier, 100 nm Co and 20 nm Au capping layer were fabricated by electron beam evaporation (Fig. 1(d)). Finally, this sample was annealed at 350 °C for 30 minutes. It should be noted that the width of the two FM electrodes is 200 nm and 500 nm, respectively, and the channel length L is 650 nm.3. Results and discussion
Fig. 2(a) and (b) show the typically measured room-temperature transfer and output curves of an InAs NW transistor, indicating the stable FET characteristics. We calculated the field effect mobility as37| μFE = gmLG2/CVds | (1) |
 | (2) |
 when tox ≫ a. We then calculated the μFE to be 380 cm2 V−1 s−1; this small value may be due to the large contact resistance induced by the residual oxide layer on the surface of InAs NW. Using the expression
when tox ≫ a. We then calculated the μFE to be 380 cm2 V−1 s−1; this small value may be due to the large contact resistance induced by the residual oxide layer on the surface of InAs NW. Using the expression  , we obtain the two-dimensional carrier concentration of 9.4 × 1011 cm−2, comparable to the previously reported value of InAs NW devices with similar crystal structure.38 The inset of Fig. 2(a) shows that the Ion/Ioff ratio is over 103. It should be noted that the nanowire device exhibits hysteresis in the transfer curve, which can be attributed to the large number of traps in the InAs NW surface amorphous layer.39
, we obtain the two-dimensional carrier concentration of 9.4 × 1011 cm−2, comparable to the previously reported value of InAs NW devices with similar crystal structure.38 The inset of Fig. 2(a) shows that the Ion/Ioff ratio is over 103. It should be noted that the nanowire device exhibits hysteresis in the transfer curve, which can be attributed to the large number of traps in the InAs NW surface amorphous layer.39
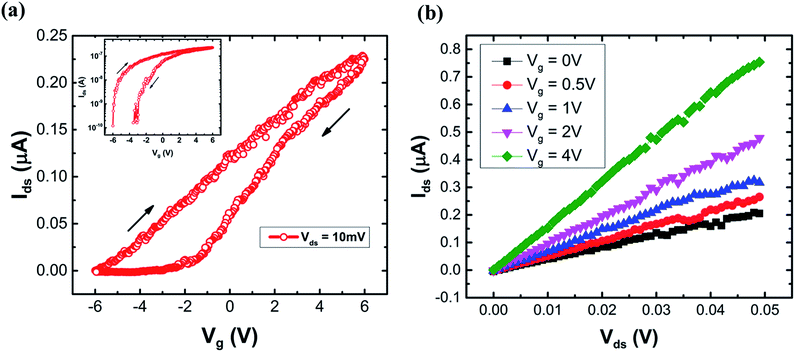 | ||
| Fig. 2 (a) Room-temperature transfer curve of an InAs NW back-gate device at Vds = 10 mV. The inset is the logarithmic Ids vs. Vg. (b) Output curves of the same device at different gate voltages. | ||
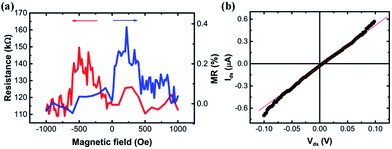
We then performed the local measurement on the two-terminal devices with two ferromagnetic electrodes. The resistance (R) was measured as a function of external magnetic field (H) while applying a fixed injection current (150 nA) between the two electrodes. Direction of the applied magnetic field was along the easy axes of the electrodes (parallel to the long axes of FM electrodes). Fig. 3(a) shows the measured R–H curve. While sweeping the magnetic field between ±1000 Oe, we can observe pronounced resistance change. At H = 1000 Oe, the magnetization of two electrodes are both aligned along the positive magnetic field direction. When the field decreases to ∼−200 Oe, the magnetization of the wider electrode changes its direction to the negative magnetic field direction and becomes antiparallel to the narrower one, causing an increase of resistance. With further decreasing H to ∼−600 Oe, the magnetization of the narrower electrode also changes its direction to the negative magnetic field direction and again becomes parallel to the wider electrode, causing a decrease in resistance. Sweeping the field reversely results in a similar procedure. Anisotropy magnetoresistance (AMR) curves of the two electrodes were carried out in order to estimate their coercive fields. From Fig. 4(a) and (b), we can clearly see that the switching fields are about 230 Oe and 540 Oe for the wider and narrower FM electrodes, respectively, which agree with the R–H curves in Fig. 3(a).
Fig. 3(b) shows the I–V curve of this device. The nonlinear I–V behavior indicates the tunneling nature of the contacts. The overall resistance of the two-terminal device is much larger than that of the InAs channel (a few kΩ), proving that the transport behavior is dominated by the tunnel barrier.
When the magnetizations of the two FM electrodes are in parallel alignment, the device resistance (Rp) is ∼115 kΩ. The resistance difference between parallel and antiparallel states (ΔR) is ∼35 kΩ, a rather large spin signal, almost two orders of magnitude greater than previously reported spin injection devices. This large spin signal can hardly be explained by spurious effects such as AMR, local Hall effect (LHE)40 or magneto-Coulomb effect (MCE).41 As in Fig. 3(a) and (b), the signals of AMR for the two FM electrodes are all quite small and less than 1 Ω. The LHE signal is generally induced by the strong fringe field near the edge of an FM electrode in a nanoscaled semiconducting system. In our case, the LHE signal should be significantly reduced because the InAs NW is far away from the edge of two FM electrodes. Besides, MCE should play a role in two-terminal devices only at low temperature rather than room temperature. Also considering the fact that all the signals originated from these spurious effects generally cannot exceed 1 kΩ, which are far below the observed signal ΔR, then we attribute the large signal to spin transport instead of from spurious effects.
Our experiment results can be analyzed by employing eqn (3)42
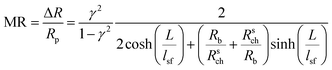 | (3) |
In Fig. 5, we show the simulated Rb dependence of ΔR using eqn (4) with typical parameters of our device (L = 650 nm, ρ = 0.01 Ω cm), γ = 0.55 for Co/MgO tunnel barrier and different lsf. It is found that the observation of spin signal ΔR above 10 kΩ requires not only very large lsf (typically above 1 μm) but also a high contact resistance (>30 kΩ). If both conditions are not satisfied, ΔR is limited to only a few hundred ohms.
 | (4) |
 | ||
| Fig. 5 Calculated spin signal ΔR vs. tunnel barrier resistance Rb by using eqn (4) with different lsf. | ||
4. Conclusions
In summary, we have fabricated the two-terminal InAs NW-based lateral spin valve with Co/MgO tunnel contacts. The R–H measurement shows a large spin signal of up to 35 kΩ and MR of 30.4% at room temperature. The SDL in the unintentionally doped InAs NW is calculated to be 1.9 μm. We believe that these results open a practical way to design InAs NW-based spintronic devices to realize more reliable, faster and less energy-consuming information processing.Acknowledgements
This work was supported by the National Basic Research Program of China (Grant No. 2012CB932702, 2015CB921502), the National Science Foundation of China (Grant No. 51371024, 51325101, 51271020, 51471029, 61504133, 11304381).Notes and references
- I. Žutić, J. Fabian and S. D. Sarma, Rev. Mod. Phys., 2004, 76, 323 CrossRef.
- H. C. Koo, J. H. Kwon, J. Eom, J. Chang, S. H. Han and M. Johnson, Science, 2009, 325, 1515–1518 CrossRef CAS PubMed.
- M. Tanaka and S. Sugahara, IEEE Trans. Electron Devices, 2007, 54, 961–976 CrossRef CAS.
- S. Datta and B. Das, Appl. Phys. Lett., 1990, 56, 665–667 CrossRef CAS.
- T. Schäpers, J. Nitta, H. Heersche and H. Takayanagi, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 125314 CrossRef.
- A. Fert, J. M. George, H. Jaffres and R. Mattana, IEEE Trans. Electron Devices, 2007, 54, 921–932 CrossRef CAS.
- G. Schmidt, D. Ferrand, L. Molenkamp, A. Filip and B. Van Wees, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R4790 CrossRef CAS.
- W. Han, K. Pi, W. Bao, K. McCreary, Y. Li, W. Wang, C. Lau and R. Kawakami, Appl. Phys. Lett., 2009, 94, 222109 CrossRef.
- Y. Ando, K. Kasahara, S. Yamada, Y. Maeda, K. Masaki, Y. Hoshi, K. Sawano, M. Miyao and K. Hamaya, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 035320 CrossRef.
- A. Spiesser, H. Saito, R. Jansen, S. Yuasa and K. Ando, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 205213 CrossRef.
- W. Han, K. Pi, K. McCreary, Y. Li, J. J. Wong, A. Swartz and R. Kawakami, Phys. Rev. Lett., 2010, 105, 167202 CrossRef PubMed.
- B. T. Jonker, G. Kioseoglou, A. T. Hanbicki, C. H. Li and P. E. Thompson, Nat. Phys., 2007, 3, 542–546 CrossRef CAS.
- K. R. Jeon, B. C. Min, Y. H. Jo, H. S. Lee, I. J. Shin, C. Y. Park, S. Y. Park and S. C. Shin, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 165315 CrossRef.
- S. Liang, T. Zhang, P. Barate, J. Frougier, M. Vidal, P. Renucci, B. Xu, H. Jaffres, J.-M. George and X. Devaux, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 085310 CrossRef.
- S. H. Shim, H. J. Kim, H. C. Koo, Y. H. Lee and J. Chang, Appl. Phys. Lett., 2015, 107, 102407 CrossRef.
- E. Rashba, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R16267 CrossRef CAS.
- O. Van'tErve, A. Friedman, E. Cobas, C. Li, J. Robinson and B. Jonker, Nat. Nanotechnol., 2012, 7, 737–742 CrossRef PubMed.
- S. P. Dash, S. Sharma, R. S. Patel, M. P. de Jong and R. Jansen, Nature, 2009, 462, 491–494 CrossRef CAS PubMed.
- W. Y. Choi, H. J. Kim, J. Chang, S. H. Han, H. C. Koo and M. Johnson, Nat. Nanotechnol., 2015, 10, 666–670 CrossRef CAS PubMed.
- Y. Zhou, W. Han, L. T. Chang, F. Xiu, M. Wang, M. Oehme, I. A. Fischer, J. Schulze, R. K. Kawakami and K. L. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 125323 CrossRef.
- K. Kasahara, Y. Fujita, S. Yamada, K. Sawano, M. Miyao and K. Hamaya, Appl. Phys. Express, 2014, 7, 033002 CrossRef.
- T. Saito, N. Tezuka, M. Matsuura and S. Sugimoto, Appl. Phys. Express, 2013, 6, 103006 CrossRef.
- W. Han, X. Jiang, A. Kajdos, S. H. Yang, S. Stemmer and S. S. Parkin, Nat. Commun., 2013, 4, 2134 Search PubMed.
- N. Tombros, C. Jozsa, M. Popinciuc, H. T. Jonkman and B. J. Van Wees, Nature, 2007, 448, 571–574 CrossRef CAS PubMed.
- B. Dlubak, M.-B. Martin, C. Deranlot, B. Servet, S. Xavier, R. Mattana, M. Sprinkle, C. Berger, W. A. De Heer and F. Petroff, Nat. Phys., 2012, 8, 557–561 CrossRef CAS.
- L. E. Hueso, J. M. Pruneda, V. Ferrari, G. Burnell, J. P. Valdes-Herrera, B. D. Simons, P. B. Littlewood, E. Artacho, A. Fert and N. D. Mathur, Nature, 2007, 445, 410–413 CrossRef CAS PubMed.
- H. Kum, J. Heo, S. Jahangir, A. Banerjee, W. Guo and P. Bhattacharya, Appl. Phys. Lett., 2012, 100, 182407 CrossRef.
- S. Heedt, C. Morgan, K. Weis, D. Bürgler, R. Calarco, H. Hardtdegen, D. Grützmacher and T. Schapers, Nano Lett., 2012, 12, 4437–4443 CrossRef CAS PubMed.
- S. Bandyopadhyay, M. Hossain, H. Ahmad, J. Atulasimha and S. Bandyopadhyay, Small, 2014, 10, 4379–4385 CAS.
- E.-S. Liu, J. Nah, K. M. Varahramyan and E. Tutuc, Nano Lett., 2010, 10, 3297–3301 CrossRef CAS PubMed.
- S. Zhang, S. A. Dayeh, Y. Li, S. A. Crooker, D. L. Smith and S. Picraux, Nano Lett., 2013, 13, 430–435 CrossRef CAS PubMed.
- J. Tarun, S. Huang, Y. Fukuma, H. Idzuchi, Y. Otani, N. Fukata, K. Ishibashi and S. Oda, Appl. Phys. Express, 2012, 5, 045001 CrossRef.
- D. Pan, D. Fan, N. Kang, J. Zhi, X. Yu, H. Xu and J. Zhao, Nano Lett., 2016, 16, 834–841 CrossRef CAS PubMed.
- N. Guo, W. Hu, L. Liao, S. Yip, J. C. Ho, J. Miao, Z. Zhang, J. Zou, T. Jiang and S. Wu, Adv. Mater., 2014, 26, 8203–8209 CrossRef CAS PubMed.
- D. Zheng, J. Wang, W. Hu, L. Liao, H. Fang, N. Guo, P. Wang, F. Gong, X. Wang and Z. Fan, Nano Lett., 2016, 16, 2548–2555 CrossRef CAS PubMed.
- A. Holleitner, V. Sih, R. Myers, A. Gossard and D. Awschalom, Phys. Rev. Lett., 2006, 97, 036805 CrossRef CAS PubMed.
- S. A. Dayeh, D. P. Aplin, X. Zhou, P. K. Yu, E. T. Yu and D. Wang, Small, 2007, 3, 326–332 CrossRef CAS PubMed.
- C. Blömers, T. Grap, M. Lepsa, J. Moers, D. Grützmacher, H. Lüth and T. Schäpers, Appl. Phys. Lett., 2012, 101, 152106 CrossRef.
- X. Zhang, M. Fu, X. Li, T. Shi, Z. Ning, X. Wang, T. Yang and Q. Chen, Sens. Actuators, B, 2015, 209, 456–461 CrossRef CAS.
- F. Monzon, D. Patterson and M. Roukes, J. Magn. Magn. Mater., 1999, 195, 19–25 CrossRef CAS.
- F. Zwanenburg, D. Van der Mast, H. Heersche, L. Kouwenhoven and E. Bakkers, Nano Lett., 2009, 9, 2704–2709 CrossRef CAS PubMed.
- H. Jaffrès, J. M. George and A. Fert, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 140408 CrossRef.
- C. Kant, O. Kurnosikov, A. Filip, P. LeClair, H. Swagten and W. de Jonge, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 212403 CrossRef.
- T. Ishikura, L. K. Liefeith, Z. Cui, K. Konishi, K. Yoh and T. Uemura, Appl. Phys. Express, 2014, 7, 073001 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |