Heat transfer performance of water-based tetrahydrofurfuryl polyethylene glycol-treated graphene nanoplatelet nanofluids

Abstract

In order to improve the colloidal stability of graphene nanoplatelets (GNPs) in aqueous media, GNPs were first functionalized with tetrahydrofurfuryl polyethylene glycol in a quick electrophilic addition reaction method. To assess this, surface functionalization of the GNPs was analyzed by FTIR and Raman spectroscopy, and thermogravimetric analysis. In addition, the morphology of treated samples was investigated by transmission electron microscopy (TEM). As the second phase of the study, the thermophysical properties of samples were experimentally investigated. The third phase of the study involved experimentally measuring and numerically simulating the convective heat transfer coefficient and pressure drop of water-based TFPEG-treated GNP nanofluids (TGNP/water) at various weight concentrations and comparison with the base fluid in an annular heat exchanger. The results suggest that the addition of TGNP into the water improved the convective heat transfer coefficient dramatically. The pressure drop of prepared samples illustrated an insignificant variation as compared with the base fluid. The steady-state forced convective heat transfer experiments and simulation have confirmed the promising cooling capabilities of TGNP/water.

---

1 Introduction

Nanofluids are nanoscale colloidal suspensions containing nanometer-sized materials (nanoparticles, nanotubes, nanorods) with diameter sizes in the order of 1 to 100 nanometers suspended in working fluids. Nanofluids have been found to possess enhanced thermophysical properties such as thermal conductivity, thermal diffusivity, viscosity, and convective heat transfer coefficients as compared to those of base fluids like oil or water. The thermal conductivity of heat transfer fluids is a fundamental issue for determining the efficiency of heat exchange systems. Since the size of heat exchange systems can be reduced with highly efficient heat transfer fluids, the enhancement of the thermal conductivity will contribute to the miniaturization of devices.

The annular heat exchangers are the common and unique geometry in industrial applications and specially heat transfer equipment. They attracted a large number of scientists and have been employed in different equipment such as electronic devices, air condition and ventilation systems, turbo machinery, nuclear reactors, gas turbines, double pipe heat exchanger etc. So, the investigation of heat transfer in annular heat exchangers and introducing a novel method for improving their performance play a vital role in energy-saving.^1–3 Abu-Nada et al.³ investigated heat transfer rate of annular heat exchanger in the presence of Al₂O₃-based water nanofluid with single phase method. They considered different thermal conductivity and viscosity models to evaluate heat transfer improvement in the annular heat exchanger. Izadi et al.² have also simulated laminar forced convection of Al₂O₃-based water nanofluid in a two dimensional annular heat exchanger with the single-phase method.

Almost 24% maximal reduction of thermal resistance in gold–water and titanium dioxide–water nanofluids was presented by Buschmann and Franzke.⁴ Shanbedi et al.⁵ investigated the performance of two-phase closed thermosyphon (TPCT) and multiwalled carbon nanotubes (MWCNT). They reported that presence of functionalized MWCNT leads to 11% improvement in the thermal efficiency of the TPCT. The researchers besides reported that the thermo-physical properties such as thermal conductivity of nanoparticles play the key roles in the heat transfer applications.^6–8 Graphene nanoparticles (GNP) has promising thermal conductivity as compared to the other carbon allotropes such as diamond, SWNT and MWNT as well as seems more cost-effective.⁹ To address this issue, GNP has attracted numerous researchers in various scientific fields for manufacturing some equipment like sensors and batteries and providing high-conductive polymers or coolants. A majority of these usages, on the other hand, cannot completely be realized due to insignificant interaction among GNP and other materials. Thus, in order to increase the interactivity of carbon nanostructures, covalent (aminoacids) and non-covalent (GA) functionalizations were proposed as the common solutions elsewhere.¹⁰ Covalent and non-covalent functionalizations are two promising approaches to enhance the GNP dispersibility in aqueous/organic solvents. Non-covalent functionalization of carbon nanostructures is performed by engaging several surfactants.^10–14 In order to enhance the dispersibility of carbon nano-structures in aqueous media, four common surfactants of Triton X-100, sodium dodecyl benzene sulphonate (SDBS), sodium dodecyl sulphonate (SDS) and gum arabic (GA) are commonly applied. SDBS and Triton X-100 have a benzene function, which produce powerful π–π interaction with the surface of carbon nanostructures. It is noteworthy that SDBS has higher dispersibility than that of Triton X-100.¹⁵ This is attributed to the steric hindrance tip chains in Triton X-100, which resulted in low concentration of Triton on the carbon nanostructures surface.¹⁶ By contrary, GA can provide better condition for dispersion of carbon nanostructures in comparison with SDBS and Triton X-100, it significantly increases the viscosity of mixture, which may cause numerous problems including increase in pressure drop in thermal equipment.⁵

The main problem with applying surfactants are the reduction of specific surface area of carbon nanostructures, implying a significant decrease in thermal properties of nanofluids. So, to avoid this issue and removing foaming in the flow-systems, covalent functionalization was suggested. However, most of the covalently functionalization procedures are complex and multi-step.¹⁷ As some new studies in this field, Sun et al.¹⁸ and our group¹⁹ employed in situ diazonium formation procedure to functionalize thermally expanded graphite with 4-bromophenyl. They reported higher solubility for the chemically-assisted exfoliated graphene sheets than pristine graphene without any stabilizer additive. Sarsam et al.²⁰ also reported a novel synthesis procedure for preparing triethanolamine-treated graphene nanoplatelets with different specific areas (SSAs). Using ultrasonication, the covalently functionalized graphene nanoplatelets with different weight concentrations and SSAs were dispersed in distilled water to prepare a new version of nanofluids.

Here, a quick and efficient covalent route is employed to synthesize tetrahydrofurfuryl polyethylene glycol-treated graphene nanoplatelets (TGNP). To prove functionalization, the TGNP sample was subjected to morphological and chemical characterization. The treated sample was then added to the pure water as a base fluid to investigate the thermophysical properties. Finally, the convective heat transfer coefficient and pressure drop of the prepared supercoolants were studied in an annular heat exchanger.

2 Experimental study

2.1 Functionalization procedure and preparation of coolants

To synthesize TGNP, the pristine GNP (7 g) and AlCl₃ as a Lewis acid (129.8 g) were poured into an agate mortar and were grounded for several minutes. This mentioned mixture and 400 mL TFPEG were then poured into a vessel and stirred for 30 min at room temperature until a homogeneous suspension was produced. Then, 0.5 mL concentrated hydrochloric acid were added drop by drop. The mixture was then sonicated at 100 °C for 36 h. The resulting mixture was then cooled to the room temperature, centrifuged withy ethanol, methanol and water 9 times to remove any unreacted materials, following by drying at 60 °C.

To synthesize the TGNP/water coolant, the given amount of TGNP was sonicated with water as a base-fluid for 10 min at power of 480 W. The TGNP/water coolants were synthesized at the weight concentrations of 0.025%, 0.05%, 0.075% and 0.1%.

The mechanism of the reaction can be summarized as follows:

With a Lewis acid (AlCl₃) as a catalyst and a trifle amount of concentrated hydrochloric acid (HCl) to protonate tetrahydrofurfuryl polyethylene glycol, electrophilic addition reactions were carried out between tetrahydrofurfuryl polyethylene glycol and GNPs through a sonication method. The reaction resulted in the attachment of tetrahydrofurfuryl polyethylene glycol and hydroxyl groups to the surface of the GNP.²¹

2.2 Functionalization and morphology

Raman characterization is a strong measurement for analyzing structure and sp² and sp³ hybridized carbon atoms in carbon-based materials and functionalization by following alterations in holes. The Raman spectra of the pristine GNP, and TGNP are presented in Fig. 1 panel (a). While the pristine GNP is weak in terms of D band intensity, the fairly strong D band in the TGNP sample can be seen at 1343 cm⁻¹. The ratio of the intensities of the D-band to that of the G-band (I_D/I_G) was considered to be the amount of disordered carbon (sp³-hybridized carbon) relative to graphitic carbon (sp²-hybridized carbon). In functionalization studies of GNP, the higher intensity ratio of I_D/I_G indicates a higher disruption of aromatic π–π electrons, implying partial damage of the graphitic carbon produced by covalent functionalization. The I_D/I_G ratio of TGNP is relatively higher than that of pristine GNP, which confirmed the successful functionalization via an electrophilic addition reaction under microwave irradiation. A significant increase in I_D/I_G can also confirm that the present method is completely successful for functionalization of GNP without acid-treatment phase.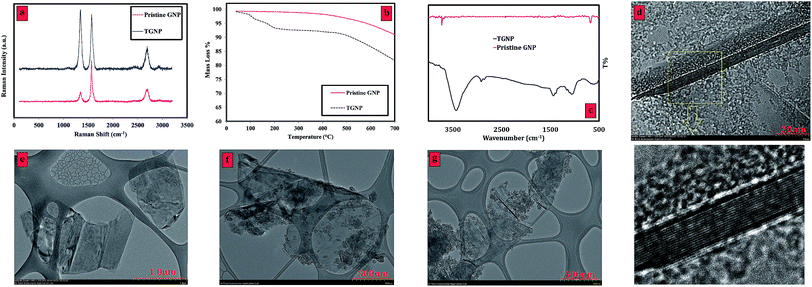

Fig. 1 (a) Raman spectra, (b) TGA trace, (c) FTIR spectra of the pristine GNP and TGNP, TEM images of (d and e) pristine GNP and (f and g) TGNP.

We have also calculated the in-plane crystallite size (L_a) (Table 1) from the spectra taken with the 514 nm Raman spectroscopy from functionalized GNPs samples, using the following general equation:²²

Table 1 In-plane crystallite sizes, L_a of functionalized samples along with I_D/I_G

Sample	ID/IG	La (nm)
Pristine GNP	0.236283	71
TGNP	1.051884	16

---

Results from Table 1 show that TGNP sample presents lower L_a values than that of pristine GNP. L_a as an average interdefect distance can be a superior indicator to show the density of defects on the surface and edges of GNP.²² The lower average interdefect distance means the higher density of defect on the surface, representing higher degree of functionalization in our work. Considering L_a as an indicator for degree of functionalization, one could see fewer defects in pristine GNP flakes. Instead it seems that functionalization, probably, also created along the edges of the new surfaces during the electrophilic addition reaction.

As further evidence, thermogravimetric analysis (TGA) was conducted to investigate functionalization of GNP with tetrahydrofurfuryl polyethylene glycol. TGA is a technique of thermal analysis in which alterations in the structure of materials are measured as a function of temperature. Fig. 1 panel (b) presents the TGA curve of the pristine GNP and TGNP. It can be seen that the TGA results of the pristine sample illustrate no mass loss up to 600 °C. However, there is an obvious weight loss in the temperature range of 100–200 °C in the TGNP curve. This mass loss was attributed to the functionality of tetrahydrofurfuryl polyethylene glycol as an unstable organic part on the surface of the GNP.

Fig. 1c illustrates the FT-IR spectra of TGNP and pristine GNP in transmittance (%) vs. wavenumber (cm⁻¹). In contrast to the pristine sample, the TGNP demonstrates the cues of tetrahydrofurfuryl polyethylene glycol molecules on the GNP structures. A detailed list of the main infrared peaks along with their assigned bonds is given in Table 2. According to Fig. 1c, TGNP shows significant peaks of C–O, CH₂, and C–H bonds. The mentioned bonds correspond to attaching tetrahydrofurfuryl polyethylene glycol on the GNP surface. It is noteworthy that the TGNP sample represents a specific peak in the range of 3000 to 3500 cm⁻¹, which confirms the presence of –OH groups on the surface of GNP.

Table 2 Fourier transform infrared interpretation of the TGNP

Peak (cm^−1)	Interpretation
3000–3500	–OH stretching vibration
2850–2950	C–H stretching vibration and asymmetric stretching of CH3
1384	CH2 bending vibration
1162	C–C stretching vibration
1065	C–O stretching vibration

---

Fig. 1 panels d, e, f and g depict the TEM images of pristine GNP as well as TGNP. First, the multi-layer structure of the GNP is obvious (almost 14 layers) in the TEM images of pristine GNP (Fig. 1d), which has almost smooth surface (Fig. 1e). Although HRTEM images are not able to distinguish minute functional groups, any change in morphology and surface deterioration can be considered as an evidence in TEM images. Pristine sample (Fig. 1d and e) shows a GNP flake with relatively smooth layers' surface and edge. Unlike pristine sample, the TGNP (Fig. 1f and g) provide edges as well as surface with highly defects. Such higher roughness indicates the partial damage of graphitic carbon, in effect of our severe functionalization under electrophilic addition reaction with sonication. Also, the lines seen in the HRTEM images of TGNP can be wrinkles on the GNP surface, is due to the inherent instability of 2D structures. The obtained increase of such lines after functionalization can be attributed to the enhancement of wrinkles (waviness) during the reaction procedures, resulting from appropriate flexibility of GNP flakes after treatment and surface functionalization. Undoubtedly, TGNP can increase the wettability of GNP layer's surface, implying higher tendency for wrinkling during ultrasonication and/or drying process in preparing TEM samples. Consequently, higher dispersion stability was obtained as a result of higher wettability of the GNP layer's surface, which will be discussed in UV-Vis study in depth.

2.3 Experimental apparatus

In the field of heat transfer, the heat transfer coefficient (h) plays a key role in the rate of heat transfer and the performance of thermal equipment. The experimental setup for this work is shown in Fig. 2. It contains of a flow loop, measuring instruments, a cooling part, a heating unit and a control unit. The flow loop includes a reservoir tank, a pump, a magnetic flow meter, a differential pressure transmitter, and an annulus test section. The nanofluids were pumped from a 7 liter capacity stainless steel jacketed tank by a Cole–Parmer magnetic drive pump at a flow rate of 0–8 liter per min, and the pump flow was controlled by a Hoffman Muller inverter. The flow rate and the pressure loss were measured using a magnetic flow meter and a differential pressure transmitter, respectively.

Fig. 2 (a) Schematic diagram of the experimental setup (b) experimental test section for the measurement of the convective heat transfer coefficient.

A straight stainless horizontal annulus formed with a length of 900 mm between an inner heat generating solid circular cylinder and an outer adiabatic cylindrical boundary with diameters of 15 mm and 26.7 mm, respectively (Fig. 3). The test section was heated using an ultra-high-temperature heater (Omega, USA) at a maximum power of 3000 W, which was linked to a Variac transformer and a watt/amp meter. Three type K thermocouples (Omega, Singapore) were fixed at the outer surface of the inner heat generating tube.

Fig. 3 Geometrical configuration and boundary conditions of the present study.

To measure the cold and hot nanofluid temperatures, two RTD (PT-100) sensors (Omega, Singapore) were inserted to measure the bulk temperature at the inlet and outlet of the test section.

2.4 Data processing

Convective heat transfer coefficient is calculated from the measured temperature of surface and bulk by placing in eqn (2), which is the Newton's cooling law:where q, T_b and T_w, are heat flux, bulk temperature and wall temperature, respectively. Heat flux can be found using eqn (3) as follows:where V and I are, respectively, the voltage and current. Internal surface area of the tube is defined as A = πDL. Three input powers (VI) were used for current study are 800, 1000 and 1200 W. Also, the temperature profile between the thermocouple and the fluid inside the circular pipe and the bulk temperature are calculated by the Wilson plot method.²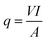³

3 Numerical study

The present numerical simulation employs the mixture model by assuming that two phases are interpenetrating, meaning there is a velocity vector field of the primary phase and also a velocity vector field of the secondary phase, within any control volume each phase has its own volume fraction, and the connection between phases is strong, so nanoparticles closely follow the base-fluid flow. The mixture method applications and its accuracy in calculation for nanofluids has been showed by several researchers such as Lotfi et al.,²⁴ Bianco et al.,²⁵ Akbarinia and Laur;²⁶ Mirmasoumi and Behzadmehr and his research group.^27–29

As an alternative for applying the governing equations for each phase, the continuity, momentum and fluid energy equations for the mixture are employed. By looking at the forced convection heat transfer in the turbulent region for incompressible and Newtonian fluid, the governing equations can be written as follow:³⁰

(a) Continuity equation:

∇·(ρ_effV̄) = 0 (4)

(b) Momentum equations:

(c) Conservation of energy:

∇·(ρ_effC_p,effV̄T̄) = ∇·((k_eff + k_t)∇T̄) (6)

In the eqn (4)–(6), the symbols V̄, P̄ and T̄ represent the time averaged flow variables, while the symbol v′ represents the fluctuations in the velocity. The term of 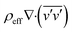in the momentum equations illustrate the turbulent shear stress. The terms of k_eff and k_t represent the effective molecular conductivity and the turbulent thermal conductivity, respectively.

For modeling flow in turbulent regime, the standard k–ε model can be employed based on the Launder and Spalding study,³¹ which is as follow:

C_μ = 0.09, σ_k = 1.00, σ_ε = 1.30, C_1ε = 1.44, C_2ε = 1.92 (10)

where μ_eff and μ_t are the effective viscosity of nanofluid and coefficient of viscosity in turbulent regime, respectively.

3.1 Numerical implementation

Herein, the numerical method available in the commercial CFD package of ANSYS-Fluent, V15 has been used. Fluent uses a finite volume approach to convert the governing partial differential equations into a system of discrete algebraic equations. Based on the discretization methods, a second-order upwind scheme is selected for the momentum, turbulent kinetic energy and turbulent dissipation rate equations, whereas the second order upwind for energy equation is selected. For two-phase calculations, the phase momentum equations with the shared pressure are solved in a coupled and segregated fashion. The phase coupled SIMPLE (PC-SIMPLE) algorithm is employed for the pressure–velocity coupling. PC-SIMPLE is an extension of the SIMPLE algorithm to multiphase flows. The scaled residuals for the velocity components and energy are set equal to 10⁻⁸ and 10⁻⁹, respectively.

A structured non-uniform grid distribution has been used to discretize the computational domain as shown in Fig. 4. Finer grids have been used close to the inner wall where the temperature gradients are high. Several different grid distributions have been tested to ensure that the calculated results are grid independent. It is shown in Fig. 5 that increasing the grid numbers does not change significantly the Nusselt numbers. Therefore, the total grid points and the elements employed in the whole tube are 147 358 and 395 977, respectively.

Fig. 4 Mesh configuration of the present study.

Fig. 5 Comparison of Nusselt numbers versus Reynolds numbers for base-fluid at three different grid distributions.

4 Results and discussion

4.1 Dispersibility

The UV-Vis spectrum for the water-based TGNP nanofluids with different weight concentrations is presented in Fig. 6a, from which it can be realized that the peak value of absorbance for all samples due to the presence of TGNP lies almost at 268 nm. Photometric analysis of the UV-Vis spectrometer was used to track the weight concentration of all the samples that were prepared at different times for 30 days. To this end, a standard curve was prepared for each nanofluid sample relating its weight concentration with the value of absorbance. Also, Fig. 6b shows the quantitative analysis of the dispersion state and the long-term stability of the TGNP/water coolants in UV-Vis spectroscopy for different weight fractions. It can be seen that the relative concentration of TGNP/water nanofluid decrease insignificantly over time. As a result, the maximum sediment of about 15% was obtained for highest weight concentration of 0.1, which confirmed the suitable dispersibility of TGNP in water as the basefluid.

Fig. 6 (a) UV-Vis absorbance spectrum for the four different weight concentration of the water-based TGNP nanofluids and (b) colloidal stability of the TGNP/water as a function of time at different volume fractions.

4.2 Physical properties

Thermophysical properties of coolants such as thermal conductivity, viscosity, density and specific heat are the most important characteristics in the field of heat transfer. The prepared TGNP/water nanofluid was characterized in terms of thermo-physical properties. The prepared samples are studied with a differential scanning calorimeter (Perkin Elmer Diamond DSC) for measuring the specific heat capacities of samples. The thermal conductivity of TGNP/water samples at different concentrations were obtained by a KD2 Pro-thermal analyzer (Decagon Devices, USA). Also, the rheological properties of samples were measured on a shear-rate controlled Anton Paar rotational rheometer (model Physica MCR301, Anton Paar GmbH). The densities of water and nanofluids were measured experimentally by Mettler Toledo DE-40 density meter. The accuracy of density measurement is 10 g cm⁻³. For each temperature and sample, the measurements were recorded 3 times.

Experimental results about thermophysical properties of TGNP/water were compared with pure water, which are shown in Fig. 7–10. Fig. 7–10 show the experimental data of the density, specific heat, viscosity and thermal conductivity at different temperatures of 20 to 60 °C, respectively. Density is one of the thermophysical properties of fluids that can affect the convective heat transfer rate. Experimental density of the GNP/water nanofluids for different weight concentrations as well as basefluid is shown in Fig. 7 for different temperatures. The results show that the density of prepared coolants increases with temperature and concentration, and expectedly are higher than that of the basefluid.

Fig. 7 Densities of the TGNP/water and water for different weight concentrations (kg m⁻³).

As another thermo-physical property, the specific heat capacity plot of TGNP as the functions of temperature and weight concentration of TGNP is illustrated in Fig. 8. The results suggest that an increase in the weight concentration of TGNP leads a drop in the specific heat capacity. Also, the specific heat capacity of all samples increases gradually with the temperature, which is sharper in coolants including TGNP. It is noteworthy the drop in the specific heat capacity of nanofluids is due to the lower specific heat capacity of TGNP than that of the basefluid.

Fig. 8 Specific heat capacity of the TGNP/water and water for different weight concentrations (J kg⁻¹ K⁻¹).

Viscosity is a crucial parameter in the dynamic design of nanofluids for heat transfer applications as well, especially in the systems including pressure drop. By loading nanoparticles into the water, viscosity increases commonly (Fig. 9). With increasing concentration, the viscosity of nanofluids increases and opposite trend obtains for increasing temperature. In all temperatures and concentrations, the highest viscosity was for the nanofluid with highest weight concentration (0.1%).

Fig. 9 Dynamic viscosity of the TGNP/water and water as the functions of temperature and weight concentration at shear rate of 140 s⁻¹ (mPa s).

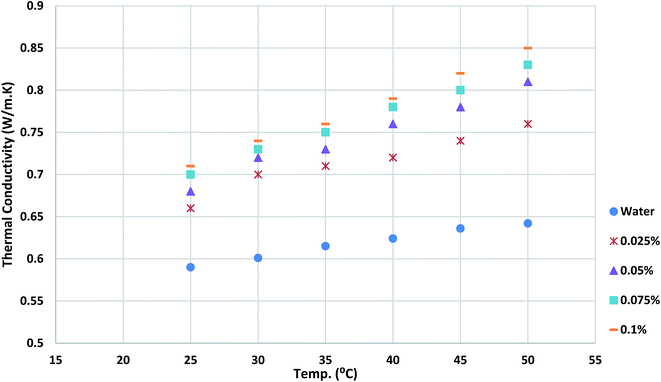
Thermal conductivity of working fluids is one of the key parameters in evaluating heat transfer rate of heat exchanger. It can be seen in Fig. 10 that the thermal conductivity of nanofluids is obtained measured and reported. The results show that the thermal conductivity of nanofluids improves with loading TGNP in basefluid as compared with water. Also, as the temperature increases, thermal conductivity increases, which is more significant for higher concentration.

Fig. 10 Thermal conductivity of TGNP/water and pure water (W m⁻¹ K⁻¹).

4.3 Thermal analysis

4.3.1 Accuracy. To evaluate the accuracy and reliability of the experimental system before conducting systematic experiments with TGNP/water nanofluids and pure water were tested as the working fluids and compared with the reported equation. Fig. 11 panels (a) to (c) show a comparison between the Nusselt numbers obtained experimentally for distilled water and that calculated using theoretically validated equation e.g. the Dittus–Boelter correlation, which is shown in eqn (11).

Nu_D = 0.023Re_D^4/5Pr⁴ (11)

Fig. 11 Comparison of the experimental Nusselt numbers for distilled water in relation to obtained by the Dittus–Boelter correlation at (a) 800 W, (b) 1000 W and (c) 1200 W.

The deviation between the present predictions obtained from eqn (11), experimental and numerical values are found to be less than 5% and 8%, respectively. This indicates that the present test facility is in good condition and can be used to evaluate the heat transfer characteristics of TGNP/water nanofluid.

4.3.2 Heat transfer. TGNP/water was tested for the Reynolds numbers range of 2220 ± 20 to 4760 ± 20, three weight concentrations (0.025, 0.05, 0.075 and 0.1%) and three input powers in the test section (800, 1000 and 1200 W). Fig. 12a–c shows the heat transfer coefficient plots of TGNP/water as the functions of Reynolds number and weight concentration. It is realized that the enhancement of heat transfer coefficient of TGNP/water remarkably exceed those of the thermal conductivity improvements for different weight concentrations in both numerical and experimental results. The maximum heat transfer coefficient at concentration of 0.1%, Reynolds number of 4766 and input power of 1200 W is 25.6%. According to recent studies,^32,33 applying a simple analogy that the connective heat transfer is proportional to k/δ_t, where δ_t is the thickness of thermal boundary layer. Therefore, increasing k and/or decreasing δ_t lead to an increase in the heat transfer coefficient. Noticeably, as reported by ref. 33 and 34, carbon nanomaterials such as graphene and CNTs decrease thickness of thermal boundary layer. As a result, convective heat transfer coefficient of prepared nanofluid improves significantly as compared to that of the basefluid.

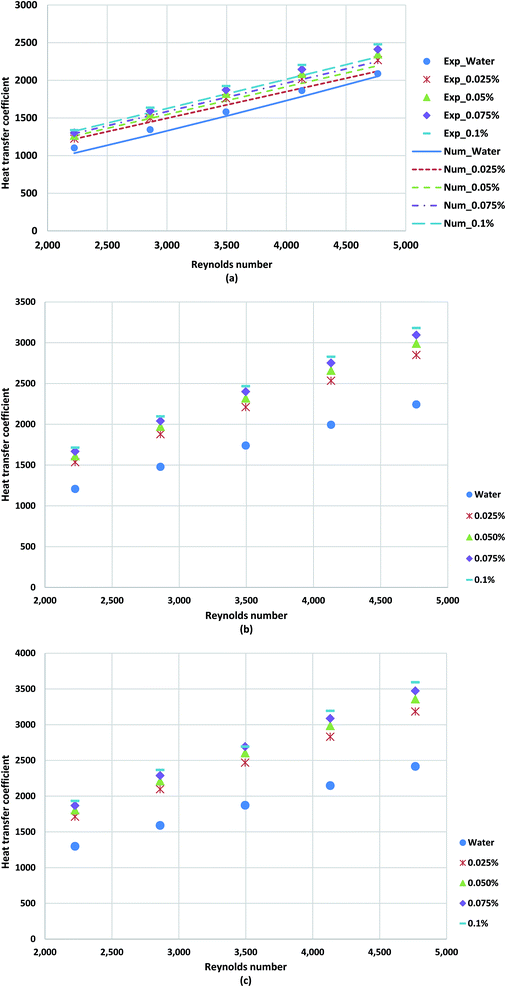Fig. 12 Comparison of the heat transfer coefficient obtained for distilled water and TGNP/water for different weight concentrations at (a) 800 W, (b) 1000 W and (c) 1200 W.

Fig. 13a–c shows the average Nusselt numbers of GNP/water nanofluid for various weight concentrations and Reynolds numbers. To evaluate the ratio of convective to conductive heat transfer of GNP/water coolants, Nusselt number plots have been employed. The results suggest that the Nusselt number increases remarkably in the presence of treated samples in comparison to the applied base-fluid. The TGNP loading in base-fluid improves the thermal conductivity of base-fluid, which leads to the lower temperature difference between the bulk fluid and wall tube, indicating higher Nusselt numbers and subsequently heat transfer rate. The comparison between the measurements and the predicted results are illustrated in Fig. 13a. The experimental results were in a good agreement with numerical with a deviation percentage of 4.58%.

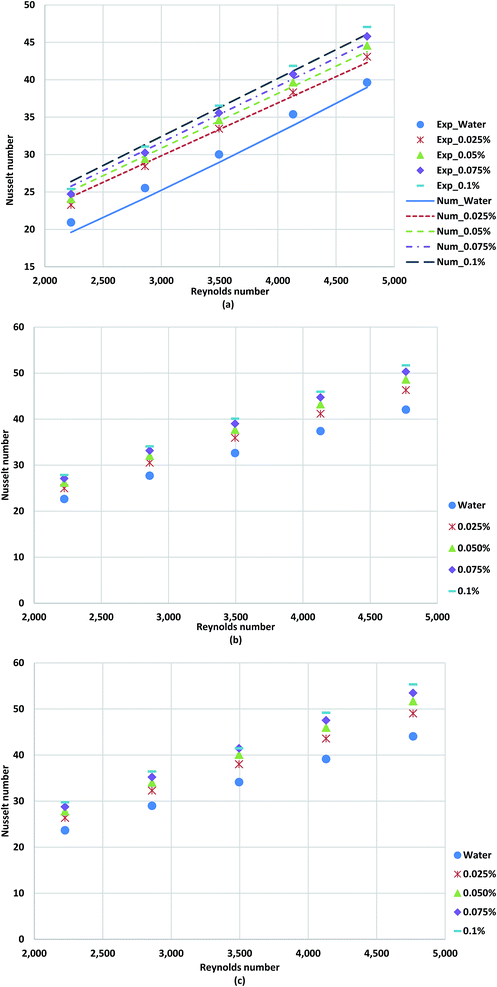Fig. 13 Comparison of Nusselt numbers obtained for distilled water and TGNP/water for different weight concentrations at (a) 800 W, (b) 1000 W and (c) 1200 W.

Fig. 14 illustrates heat transfer performance of the TGNP/water coolant at different heat fluxes for constant weight concentration of 0.1%, which obviously increasing temperature condition leads to increase of heat transfer performance of working fluid.

Fig. 14 Comparison of Nusselt numbers of TGNP/water for different heat fluxes at 0.1% weight concentration.

Fig. 15 Test section pressure gradient versus Reynolds number for all samples at input water of 800 W.

4.3.3 Pressure drop. The pressure gradient between inlet and outlet of the pipe is depicted in Fig. 15. The pressure drop increases dramatically with the increment of the Reynolds number in both numerical and experimental results. The increasing rate of the pressure drop at the concentration of 0.1% with respect to the concentration of 0.0% appears nearly 39.3% higher at Reynolds number of 4760 and input water of 800 W. This value is considerably low in comparison with the increasing rate of the heat transfer.

In order to evaluate influence of temperature on pressure drop of TGNP/water coolants, experiments are performed for different input powers (800, 1000 and 1200 W) at constant the weight concentration of 0.1% in a range of inlet velocities and the pressure drops are evaluated and presented in Fig. 16. This figure shows that for the TGNP/water coolants the pressure drop decreases significantly by increase in circulation temperature. It is also noteworthy that the pressure drop and viscosity curves exhibit similar trends, which can be attributed to the direct relationship between pressure drop and viscosity.

Fig. 16 Test section pressure gradient versus Reynolds number for three different hear fluxes at concentration of 0.1%.

5 Conclusion

The present study is abstracted in introducing a promising, potentially industrially scalable, cost-effective functionalization approach for preparing TGNP/water nanofluids and followed by measuring the thermophysical properties of the synthesized samples experimentally for different weight concentrations. Thermal and flow behaviors of the prepared nanofluids through an annular tube in an inner heat generating solid circular rod have been investigated within transition regime for three different heat fluxes. It is indicated that this new kind of working fluid can be an effective coolant for annular heat exchangers in terms of overall thermal properties and energy saving.

The following results can be considered as the fundamental points.

• Thermal parameters obtained experimentally and numerically showed that the value and the position of maximum Nu is depending on Reynolds number and weight fraction of nanoparticles in the transition regime.

• Pressure drop results showed that the higher concentration of TGNP in TGNP/water coolant led to the greater pressure drops, which considered as a negative factor.

• The thermal conductivity, viscosity, and density of all samples were increased with TGNP loading in base-fluid. On the other hand, the specific heat capacity decreases significantly.

• The convective heat transfer coefficient and Nusselt numbers of TGNP/water were shown the significant enhancements as compared with basefluid.

• The promising features of rapid method for synthesizing TGNP, long-term stability, no acidic environments, and high heat transfer coefficient would enable the TGNP/water as superior coolants for applying in the annular heat exchangers.

Acknowledgements

The authors gratefully acknowledge University of Malaya Research Grant (UMRG: RP012A-13AET), High Impact Research Grant (UM.C/625/1/HIR/MOHE/ENG/45) and Faculty of Engineering, University of Malaya, Malaysia for support to conduct this research work.

References

1. E. Abu-Nada and H. F. Oztop, Effects of inclination angle on natural convection in enclosures filled with Cu–water nanofluid, Int. J. Heat Fluid Flow, 2009, 30(4), 669–678.
2. M. Izadi, A. Behzadmehr and D. Jalali-Vahida, Numerical study of developing laminar forced convection of a nanofluid in an annulus, Int. J. Therm. Sci., 2009, 48(11), 2119–2129.
3. E. Abu-Nada, Z. Masoud and A. Hijazi, Natural convection heat transfer enhancement in horizontal concentric annuli using nanofluids, Int. Commun. Heat Mass Transfer, 2008, 35(5), 657–665.
4. M. H. Buschmann and U. Franzke, Improvement of thermosyphon performance by employing nanofluid, Int. J. Refrig., 2014, 40, 416–428.
5. M. Shanbedi, et al., Optimization of the thermal efficiency of a two-phase closed thermosyphon using active learning on the human algorithm interaction, Numer. Heat Transfer, Part A, 2014, 66(8), 947–962.
6. A. Amiri, et al., Microwave-assisted direct coupling of graphene nanoplatelets with polyethylene glycol and 4-phenylazophenol molecules for preparing stable-colloidal system, Colloids Surf., A, 2015, 487, 131–141.
7. M. Shanbedi, et al., Thermal performance prediction of two-phase closed thermosyphon using adaptive neuro-fuzzy inference system, Heat Transfer Eng., 2015, 36(3), 315–324.
8. K. Solangi, et al., A comprehensive review of thermo-physical properties and convective heat transfer to nanofluids, Energy, 2015, 89, 1065–1086.
9. A. Amiri, et al., Toward improved engine performance with crumpled nitrogen-doped graphene based water–ethylene glycol coolant, Chem. Eng. J., 2016, 289, 583–595.
10. A. Amiri, et al., Highly dispersed multiwalled carbon nanotubes decorated with Ag nanoparticles in water and experimental investigation of the thermophysical properties, J. Phys. Chem. C, 2012, 116(5), 3369–3375.
11. H. K. Arzani, et al., Experimental and numerical investigation of thermophysical properties, heat transfer and pressure drop of covalent and noncovalent functionalized graphene nanoplatelet-based water nanofluids in an annular heat exchanger, Int. Commun. Heat Mass Transfer, 2015, 68, 267–275.
12. C. A. Silvera-Batista, et al., A mechanistic study of the selective retention of SDS-suspended single-wall carbon nanotubes on agarose gels, J. Phys. Chem. C, 2011, 115(19), 9361–9369.
13. M. Suttipong, et al., Role of surfactant molecular structure on self-assembly: aqueous SDBS on carbon nanotubes, J. Phys. Chem. C, 2011, 115(35), 17286–17296.
14. J. J. Brege, C. Gallaway and A. R. Barron, Fluorescence quenching of single-walled carbon nanotubes in SDBS surfactant suspension by metal ions: quenching efficiency as a function of metal and nanotube identity, J. Phys. Chem. C, 2007, 111(48), 17812–17820.
15. A. Amiri, et al., Performance dependence of thermosyphon on the functionalization approaches: an experimental study on thermo-physical properties of graphene nanoplatelet-based water nanofluids, Energy Convers. Manage., 2015, 92, 322–330.
16. M. Islam, et al., High weight fraction surfactant solubilization of single-wall carbon nanotubes in water, Nano Lett., 2003, 3(2), 269–273.
17. H. Zare-Zardini, et al., In vitro and in vivo study of hazardous effects of Ag nanoparticles and Arginine-treated multi walled carbon nanotubes on blood cells: Application in hemodialysis membranes, J. Biomed. Mater. Res., Part A, 2015, 103(9), 2959–2965.
18. Z. Sun, et al., Soluble graphene through edge-selective functionalization, Nano Res., 2010, 3(2), 117–125.
19. A. Amiri, et al., Microwave-assisted synthesis of highly-crumpled, few-layered graphene and nitrogen-doped graphene for use as high-performance electrodes in capacitive deionization, Sci. Rep., 2015, 5, 17503.
20. W. S. Sarsam, et al., Stability and thermophysical properties of water-based nanofluids containing triethanolamine-treated graphene nanoplatelets with different specific surface areas, Colloids Surf., A, 2016, 500, 17–31.
21. R. Tian, et al., An efficient route to functionalize singe-walled carbon nanotubes using alcohols, Appl. Surf. Sci., 2008, 255(5), 3294–3299.
22. T. Ong and H. Yang, Effect of atmosphere on the mechanical milling of natural graphite, Carbon, 2000, 38(15), 2077–2085.
23. J. Fernandez-Seara, et al., A general review of the Wilson plot method and its modifications to determine convection coefficients in heat exchange devices, Appl. Therm. Eng., 2007, 27(17), 2745–2757.
24. R. Lotfi, Y. Saboohi and A. Rashidi, Numerical study of forced convective heat transfer of nanofluids: comparison of different approaches, Int. Commun. Heat Mass Transfer, 2010, 37(1), 74–78.
25. V. Bianco, et al., Numerical investigation of nanofluids forced convection in circular tubes, Appl. Therm. Eng., 2009, 29(17), 3632–3642.
26. A. Akbarinia and R. Laur, Investigating the diameter of solid particles effects on a laminar nanofluid flow in a curved tube using a two phase approach, Int. J. Heat Fluid Flow, 2009, 30(4), 706–714.
27. S. Mirmasoumi and A. Behzadmehr, Effect of nanoparticles mean diameter on mixed convection heat transfer of a nanofluid in a horizontal tube, Int. J. Heat Fluid Flow, 2008, 29(2), 557–566.
28. S. Mirmasoumi and A. Behzadmehr, Numerical study of laminar mixed convection of a nanofluid in a horizontal tube using two-phase mixture model, Appl. Therm. Eng., 2008, 28(7), 717–727.
29. A. Behzadmehr, M. Saffar-Avval and N. Galanis, Prediction of turbulent forced convection of a nanofluid in a tube with uniform heat flux using a two phase approach, Int. J. Heat Fluid Flow, 2007, 28(2), 211–219.
30. T. M. Shih, Numerical heat transfer, CRC Press, 1984.
31. B. E. Launder and D. Spalding, The numerical computation of turbulent flows, Comput. Meth. Appl. Mech. Eng., 1974, 3(2), 269–289.
32. S. J. Aravind, et al., Investigation of structural stability, dispersion, viscosity, and conductive heat transfer properties of functionalized carbon nanotube based nanofluids, J. Phys. Chem. C, 2011, 115(34), 16737–16744.
33. A. Amiri, et al., Laminar convective heat transfer of hexylamine-treated MWCNTs-based turbine oil nanofluid, Energy Convers. Manage., 2015, 105, 355–367.
34. Y. Ding, et al., Heat transfer of aqueous suspensions of carbon nanotubes (CNT nanofluids), Int. J. Heat Mass Transfer, 2006, 49(1), 240–250.

---