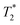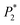DOI:
10.1039/C6RA13128J
(Paper)
RSC Adv., 2016,
6, 80946-80954
Strain tunability of the downward effective polarization of mechanically written domains in ferroelectric nanofilms
Received
20th May 2016
, Accepted 9th August 2016
First published on 9th August 2016
Abstract
Nano 180° domains written by local mechanical force via the flexoelectric effect have recently attracted great attention since they may enable applications in which memory bits are written mechanically. Downward effective polarization (DEP), i.e., the net downward-pointing polarization in the zone underneath the pressure-surface contact area, is expected to be large for clear storage and readout of the memory bits. Here, the strain tunability of the DEP of mechanically written domains is investigated by using a multi-field coupling model of the flexoelectric effect. The DEP of mechanically written domains in PbTiO3 films grown on five different substrates is examined. It is found that, when the mechanical force is not large enough for the mechanical writing process with the largest tensile misfit strain to reach a steady state, the DEP of the mechanically written domain increases as the misfit strain changes from being compressive to tensile. In contrast, when the mechanical force applied is sufficiently large for the writing process with the largest compressive misfit strain to reach a steady state, the effect of misfit strain on the DEP is opposite. In the latter case, the reduction of the DEP is mainly ascribed to the decrease of the flexoelectric field, which is reflected by the asymmetry of the polarization-electric field hysteresis loops under local mechanical force. Our work suggests that misfit compressive strains and sufficiently large mechanical force are useful for improving the DEP.
1. Introduction
Owing to their low power consumption, high reading and writing speed, high endurance, and non-volatility, ferroelectric memories (FMs) have attracted a great deal of attention and have became one of the most promising and advanced nonvolatile memory technologies in usage nowadays.1,2 Previous studies revealed that the macro properties of FMs are closely related to domain/polarization switching in ferroelectric films.3–5 Thus, understanding the key factors that determine the domain behavior and then controlling them to obtain desirable physical properties is an essential step in designing and optimizing the electrical properties of FMs.
Electromechanical coupling, the interaction between electrical and mechanical properties6 is considered to be one of the most important factors that govern domain behavior. The coupling between strain and polarization (piezoelectricity) has been studied extensively.7–9 Strain engineering, with an appropriate choice of substrate, has been proved to be a useful tool to optimize properties of ferroelectric thin films.10 Recently, an increasing amount of attention has been paid to a high order electromechanical coupling behavior, flexoelectricity, which describes the generation of an electric field by a strain gradient (the direct flexoelectric effect) or the mechanical response induced by an electric field gradient (the converse flexoelectric effect):11,12
| |
 | (1a) |
| |
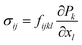 | (1b) |
here,
Ei,
σij,
εkl,
Pk and
xj are electric field, stress, strain, polarization and position coordinate, respectively.
fijkl are components of the flexoelectric tensor. Some failure problems were ascribed to the flexoelectric effect, such as imprint,
13,14 dead layer effect,
15 lowering of permittivity
16 and so on. On the other hand, flexoelectricity also provides opportunities to tune the physical properties of thin films. Lu
et al.17 demonstrated that the stress gradient generated by the AFM tip can mechanically switch the polarization in the nanoscale volume of a ferroelectric film
via flexoelectricity. This result opens up a way to switch polarization in ferroelectric thin films using mechanical force and may enable applications in which memory bits are written mechanically and read electrically. Compared with traditional electrically written domain patterns, mechanically written domains possess unique excellent properties.
17 For example, domains maintain longer and are electrically erasable, besides, the mechanically written domains are nanoscopic, and no damage to the sample surface is found after a high switching mechanical force. In order to meet the demand of higher density storage, strong enough electric signals in a smaller area are required. If the mechanically written domain is used as memory bits, the downward effective polarization (DEP) which is also referred to as the net downward-pointing polarization in the zone right underneath the tip-surface contact area is expected to be as large as possible for this purpose. Therefore, finding out the key factors that determine the DEP is crucial for the application of the mechanically written domain. Lu
et al.17 revealed in their experiments that the DEP increases with the external mechanical load growing. Jiang
et al.18 further found that the DEP will cease to increase and reach a steady state when the mechanical force is large enough.
a domain, which was formed during the mechanical writing process and existed around the newly formed
c domain, is a main factor affecting the magnitude of DEP. A smaller area of
a domains in the zone right underneath the tip-surface contact area corresponds to a larger DEP. Compressive substrate constraint has been successfully used to tune the mechanical threshold force for polarization reversal.
19 This holds a strong potential for reducing the area of
a domains and heightening the DEP.
In this study, we employed a multi-field coupling model of flexoelectric18,20,21 to understand the interfacial misfit strain effect on the DEP of the mechanically written domain. It is found that variation trend of DEP with the misfit strain depends on the magnitude of the mechanical force. Our modeling suggests that compressive misfit strain and large enough mechanical force are favorable for a big DEP. This study may provide some guides on the practical application of mechanical switching.
2. The multi-field coupling model of flexoelectric effect and its finite element implementation
Since the mechanical written domain is produced by local mechanical force via flexoelectricity, a finite element based multi-field coupling model of flexoelectric effect18 is employed to simulate the mechanical writing process. It should be noted that the multi-field coupling model proposed in our previous study is developed based on the phase field method18,20–28 and Mindlin's strain gradient theory,21,29,30 and is solved by using the finite element method,25,31–33 it can effectively predict the flexoelectric switching behavior induced by complex electromechanical loads. Three sets of equations should be included to establish the multi-field coupling model, and they are described below.18
2.1 Thermodynamic potential
Three physical fields, namely the polarization field, electric field and displacement field are required to describe the electromechanical coupling behavior of ferroelectric materials under electrical and mechanical loadings.25,34 The quantities utilized to depict these three physical fields are displacement (u), stress (σ), strain (ε), double stress (t), strain gradient (∇ε), electric potential (φ), electric field (E), electric displacement (D), polarization (P) and polarization gradient (∇P). Among them, ε, E, P, ∇P and ∇ε are chosen as independent variables for the finite element implementations. The corresponding thermodynamic potential density for this set of independent variables is electric enthalpy. To extend the convention phase field model to include the flexoelectric contributions, a Lifshitz invariant35 should be inserted to the electric enthalpy density, i.e.,| | |
h = hLD + helas + hcoup + hp_grad + helec + hflexo
| (2a) |
with
| |
 | (2b) |
| |
 | (2c) |
| |
 | (2d) |
| |
 | (2e) |
| |
 | (2f) |
| |
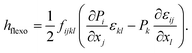 | (2g) |
Unless otherwise stated, the indices run from 1 to 3, repeating indices imply summation, and commas imply differentiation. hLD, which is given based on the Landau–Devonshire theory of ferroelectrics,36 represents the Landau free energy density, where αij, βijkl, γijklmn are the phenomenological Landau–Devonshire coefficients. helas denotes the elastic energy density of the system, in which cijkl are the elastic constants. hcoup refers to the coupling energy density between the polarizations and the strains, where qijkl are the electrostrictive coefficients. hp_grad, the polarization gradient energy density, is related to the domain wall energy, in which gijkl are the gradient coefficients. The gradient energy density gives the energy penalty for spatially inhomogeneous polarization. helec stands for the electric energy due to the presence of an electric field, where εb is the dielectric constant of the background reference. hflexo denotes the flexoelectric coupling energy density, where fijkl are components of the flexocoupling tensors. εij, Ei, and Pi,j are defined as
| |
 | (3a) |
| |
 | (3b) |
| |
 | (3c) |
2.2 Constitutive equation of each physical field when considering flexoelectricity
Based on the electric enthalpy density defined in eqn (2), the constitutive equations can be derived.| |
 | (4a) |
| |
 | (4b) |
| |
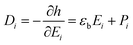 | (4c) |
| |
 | (4d) |
| |
 | (4e) |
here, ηi are the effective local electric forces, Λij can be taken as higher order local electric force. tijk, the double stress tensors, work-conjugate with the strain gradient tensor:
2.3 The balance laws for each physical field
Unlike the existing phase field methods with considering of flexoelectric effect6,37 which use classic mechanical governing equation to characterize the deformation behavior, the present model uses a higher order equilibrium equation to describe the displacement field. The higher-order equilibrium equation is given based on the Mindlin's theory of strain gradient elasticity.29,30 The main feature of the higher-order equilibrium equation is the existence of higher-order stresses which depend on different components of the strain gradient. That is| | |
(σik − tijk,j)i + bk = 0, in V
| (6) |
where bk are the components of a body force per unit volume.
The electric field is governed by the Maxwell's (or Gauss') equation.
here,
ζ is the volume charge density.
The temporal evolution of the polarization field is described by the time dependent Ginzburg–Landau equations22,25,38–41
| |
 | (8) |
where
L is the kinetic coefficient.
The boundary conditions for polarization field are
| |
Pi = ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) i, on SP i, on SP
| (9) |
Since the governing equation for polarization field is one order in time, one initial condition is needed, i.e.
| | |
P(x, 0) = P0(x), in V
| (10) |
here
P0(
x) denotes the polarization of the initial time.
The model equations are solved by using a FEM-based numerical method through the weak form PDE (partial differential equation) interface of the finite element commercial software package, COMSOL Multiphysics. Weak form of the proposed phase field model is needed in the weak form PDE interface. Using the variation or principle of virtual work, the weak form of governing equations can be obtained as
| |
 | (11) |
To reduce the computation cost, dimensionless treatment is conducted to simplify the coefficients and variables, details of the dimensionless treatment can be found in ref. 18 and 25.
3. Simulation results and discussion
The lead titanate PbTiO3 is taken as an example in the present simulations. Values of its material parameters including the flexoelectric coefficients fijkl and the electrostrictive coefficients qijkl are the same with those in Jiang et al.18 The material coefficients and variables in eqn (2)–(8)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 are nondimensionalized with P0 = 0.757 C m2, g110 = 1.73 × 10−10 C2 m4 N and α0 = 1.725 × 108 C2 m2 N. For simplicity, two dimensional (2D) finite element simulations were conducted in the present work under the plane strain condition along the x3 axis, although the theoretical framework described in Section 2 can be applied to three dimensional simulations. Fig. 1 shows a schematic illustration of the simulated ferroelectric film subjected to concurrent local mechanical and electrical loads.
18 are nondimensionalized with P0 = 0.757 C m2, g110 = 1.73 × 10−10 C2 m4 N and α0 = 1.725 × 108 C2 m2 N. For simplicity, two dimensional (2D) finite element simulations were conducted in the present work under the plane strain condition along the x3 axis, although the theoretical framework described in Section 2 can be applied to three dimensional simulations. Fig. 1 shows a schematic illustration of the simulated ferroelectric film subjected to concurrent local mechanical and electrical loads.
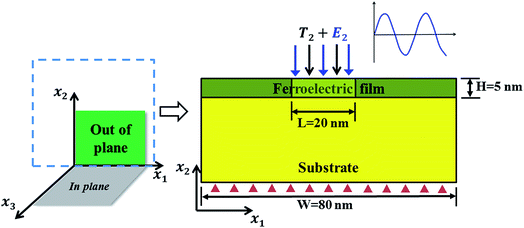 |
| | Fig. 1 Computational model for the mechanical switching of ferroelectric polarization, where ‘‘W’’ and ‘‘H’’ denote the length and the thickness of ferroelectric film, respectively. Arrows in black simulate the local mechanical force that an AFM sharp tip imposes on the surface of the film, while blue arrows denote the applied external alternating electric field. | |
The boundary conditions of each field are set as follows:
To mimic a ferroelectric film, periodic boundary conditions for the polarization field, displacement field, and electric field along the x1 direction are applied. The bottom surface of the substrate is fixed. Considering that the contact area of an atomic force microscope tip and film is almost flat, we use a uniform mechanical stress to simulate the local stress that an atomic force microscope tip applied on the film surface. Maybe a more realistic stress distribution, such as that of a spherical indenter or a flat punch, will be closer to the experimental results. However, Gu et al.42 found that AFM tip geometry is not important comparing to the magnitude of stress in the mechanical switching process. Under the premise that our model can reproduce and predict the experimental results correctly, we hope that our model can be as simple and convenient as possible. In the absence of compressive load, the top surface of the film is assumed to be stress free. Due to the dissimilar a-axis lattice constants of PbTiO3 thin film and substrate, there is a misfit strain ε11 at the interface. The value of the misfit strain εmisfit is given by
| |
 | (12) |
where
asub and
aPTO are the effective lattice parameters of the substrate and ferroelectric film, respectively. To conduct a comprehensive study of the strain tunability of the polarization switching behavior of mechanically written domain, five kinds of substrates which are frequently used in the strain engineering are considered here. They are PbTiO
3, Pb(Mg
1/3Nb
2/3)
0.72Ti
0.28O
3(PMN-PT), Pt, SrTiO
3 and LaAlO
3, the lattice constants and misfit strain of which are listed in
Table 1.
Table 1 Lattice constant of substrate and the ferroelectric thin film, and the corresponding interfacial misfit strain
| |
asub (Å) |
aPTO (Å) |
Misfit strain (%) |
| PbTiO3 (ref. 43) |
3.94 |
3.94 |
0 |
| PMN-PT (ref. 19) |
4.022 |
3.94 |
0.021 |
| Pt (ref. 44) |
3.97 |
3.94 |
0.008 |
| SrTiO3 (ref. 45) |
3.905 |
3.94 |
−0.009 |
| LaAlO3 (ref. 19) |
3.79 |
3.94 |
−0.038 |
Note that the displacement boundary conditions used here is different from those employed in ref. 46–48. The reason why we don't use those boundary conditions is that complicated external loads including local stress on the top surface and strain on the bottom surface were applied to the boundary. To solve equations with complicated boundary conditions effectively, we choose finite element method, in which mechanical load can be applied directly to boundaries. It is important to notice that Cao et al.49 also directly applied a stress to the center of the top surface of the ferroelectric film and set the rest of the top surface be traction free in their phase field model of flexoelectrical writing.
The boundary conditions for the electric field are grounded on the bottom interface of the film. A local electric potential which results in a local electric field changing as sine function  is applied to the center of the top surface of the ferroelectric film. The dimensionless time step is set as Δt* = 0.05 and total time is t* = 2500.
is applied to the center of the top surface of the ferroelectric film. The dimensionless time step is set as Δt* = 0.05 and total time is t* = 2500.
About the polarization boundary conditions, it is worthy to note that there are two ways to take the surface effect into consideration: one is to add the surface effect energy into total energy,47,48,50–53 the other is to set a proper polarization boundary condition, i.e., dP/dn = −P/δ, where n denotes a unit length in the outward normal direction of the surface, δ is the so-called extrapolation length induced to describe the difference in polarizations between the surface and the interior of the material.54–57 We adopted the later one in our model for simplicity and set δ = 0, i.e.,  , meaning that polarizations are completely suppressed at the surface. This approximate but simple zero boundary condition has been successfully used to explain some experimental observation.58 We have also obtained the domain structures for the first way in which a surface effect energy term is added to the total energy. It is found out that dissimilar way of considering surface effect leads to little difference in domain structure.
, meaning that polarizations are completely suppressed at the surface. This approximate but simple zero boundary condition has been successfully used to explain some experimental observation.58 We have also obtained the domain structures for the first way in which a surface effect energy term is added to the total energy. It is found out that dissimilar way of considering surface effect leads to little difference in domain structure.
In the simulations, quintic order Argyris finite element is used to construct the shape function. We use 8836 plane triangular elements with five degrees of freedom (mechanical displacement u1 and u2; polarization P1 and P2; electric potential φ) per node to discretize the ferroelectric domain. We use 1600 quadrilateral elements to discretize the substrate with an element size of  , which corresponds to real element size of Δx1 = Δx2 = 1 nm.
, which corresponds to real element size of Δx1 = Δx2 = 1 nm.
Before presenting the strain tunability of polarization switching behavior of mechanically written domain, we first study the effect of local stress on the polarization–electric field (P–E) hysteresis loops to test the effectiveness of the proposed model. Note that the interfacial misfit strain between ferroelectric film and the substrate is not taken into account here. Fig. 2 shows the P–E hysteresis loop of the ferroelectric domain written by a local stress of  . Obviously, there is a shift of the hysteresis loop towards the positive bias. The positive and negative coercive field are, respectively,
. Obviously, there is a shift of the hysteresis loop towards the positive bias. The positive and negative coercive field are, respectively,  and
and  , implying that it is easier for the polarization to switch from the upward-pointing state to the downward-pointing state. The local compressive vertical stress generates a polar bias via flexoelectricity.
, implying that it is easier for the polarization to switch from the upward-pointing state to the downward-pointing state. The local compressive vertical stress generates a polar bias via flexoelectricity.
 |
| | Fig. 2 P–E hysteresis loop of the ferroelectric domain written by a local stress of  . .  is the mean magnitude of the second component of the polarization vector in the zone right underneath the tip-surface contact area. is the mean magnitude of the second component of the polarization vector in the zone right underneath the tip-surface contact area. | |
Then, polarization responses of ferroelectric domain written by different local stresses are investigated. As shown in Fig. 3, the hysteresis loops become narrow and increasingly asymmetric under increasing load. We define the offset bias as the shift of the center of the hysteresis loop, which is half the sum of positive and negative coercive electric fields:  . We then define the coercivity as the half-width of the hysteresis loop, measured as the difference between positive and negative coercive electric fields divided by two:
. We then define the coercivity as the half-width of the hysteresis loop, measured as the difference between positive and negative coercive electric fields divided by two: 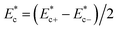 . The offset and coercivity for the films under increasing load is listed in Table 2. There is a monatonical shift of the hysteresis loops towards positive values as the load is increased, implying an increasing flexoelectric field.17 The negative coercive field is decreased while the positive coercive field does not. The above observations are well in agreement with the experiment results in ref. 17 and calculation results in ref. 49. Thus, the correctness of our model is verified.
. The offset and coercivity for the films under increasing load is listed in Table 2. There is a monatonical shift of the hysteresis loops towards positive values as the load is increased, implying an increasing flexoelectric field.17 The negative coercive field is decreased while the positive coercive field does not. The above observations are well in agreement with the experiment results in ref. 17 and calculation results in ref. 49. Thus, the correctness of our model is verified.
 |
| | Fig. 3 P–E hysteresis loops of nanodomains written by different loading forces. Note that the imprint behavior becomes serious and the remnant polarization reduces as the load increases. | |
Table 2 The positive and negative coercive fields, the offset bias of the ferroelectric nanodomain written by different external local load
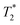
|

|

|

|

|
| 0 |
−0.656 |
0.717 |
0.0305 |
0.6865 |
| −30 |
−0.614 |
0.736 |
0.061 |
0.675 |
| −50 |
−0.555 |
0.706 |
0.075 |
0.630 |
| −100 |
−0.357 |
0.733 |
0.188 |
0.545 |
| −150 |
−0.166 |
0.690 |
0.262 |
0.428 |
Next, the dependence of DEP on the interfacial misfit strain is studied. Fig. 4 shows the domain structures of the ferroelectric thin films with identical external vertical force  at the center of the upper surface and different misfit strain at the interface. No 180° domain is formed when the film is under misfit compressive strain. When the misfit strain is zero, the newly formed 180° domain is equal to the original 180° domain, resulting in a zero DEP. As the misfit strain turns to be tensile, the DEP grows with increasing tensile misfit strain. The raise of the DEP is intrinsically associated with a drop of the mechanical threshold force. As shown by Fig. 4(a), two small a domains that enjoy opposite directions are formed underneath both sides of the tip-surface contact area. This result indicates that, when the interfacial misfit strain is εmisfit = −0.038, the external mechanical force
at the center of the upper surface and different misfit strain at the interface. No 180° domain is formed when the film is under misfit compressive strain. When the misfit strain is zero, the newly formed 180° domain is equal to the original 180° domain, resulting in a zero DEP. As the misfit strain turns to be tensile, the DEP grows with increasing tensile misfit strain. The raise of the DEP is intrinsically associated with a drop of the mechanical threshold force. As shown by Fig. 4(a), two small a domains that enjoy opposite directions are formed underneath both sides of the tip-surface contact area. This result indicates that, when the interfacial misfit strain is εmisfit = −0.038, the external mechanical force  is slightly greater than the threshold value for 90° switching and much smaller than the threshold value for 180° switching. With the same magnitude of mechanical force, when the interfacial misfit strain is −0.009, newly formed a domain has a greater size (see Fig. 4(b)), denoting that
is slightly greater than the threshold value for 90° switching and much smaller than the threshold value for 180° switching. With the same magnitude of mechanical force, when the interfacial misfit strain is −0.009, newly formed a domain has a greater size (see Fig. 4(b)), denoting that  is much greater than the threshold value for 90° domain switching and approaches the threshold value for 180° domain switching. Obviously, the critical value for 90° domain switching decreases with a decreasing compressive misfit strain at the interface. For ferroelectric film with no misfit strain at the interface as shown in Fig. 4(c), 180° domain switching occurred in the center of the thin film on a small scale, indicating that
is much greater than the threshold value for 90° domain switching and approaches the threshold value for 180° domain switching. Obviously, the critical value for 90° domain switching decreases with a decreasing compressive misfit strain at the interface. For ferroelectric film with no misfit strain at the interface as shown in Fig. 4(c), 180° domain switching occurred in the center of the thin film on a small scale, indicating that  is larger than the threshold value for 180° domain switching. As shown in Fig. 4(d) and (e), 180° domain switching appears on a larger scale when the interfacial misfit strain turns to be tensile and becomes larger, implying that the tensile misfit strain makes 180° mechanical switching easier to achieve. Note that, under
is larger than the threshold value for 180° domain switching. As shown in Fig. 4(d) and (e), 180° domain switching appears on a larger scale when the interfacial misfit strain turns to be tensile and becomes larger, implying that the tensile misfit strain makes 180° mechanical switching easier to achieve. Note that, under 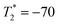 , mechanical writing process in none of the films reach a steady state. Comparing the domain structures of films with these five interfacial misfit strains, we have a rough conclusion that the mechanical threshold forces for 180° domain switching with different misfit strain have the following relationship:
, mechanical writing process in none of the films reach a steady state. Comparing the domain structures of films with these five interfacial misfit strains, we have a rough conclusion that the mechanical threshold forces for 180° domain switching with different misfit strain have the following relationship: 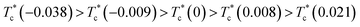 . Here, we define the mechanical threshold force for 180° domain switching as the value at which
. Here, we define the mechanical threshold force for 180° domain switching as the value at which  in the zone right underneath the tip-surface contact area equals to zero. With our model,
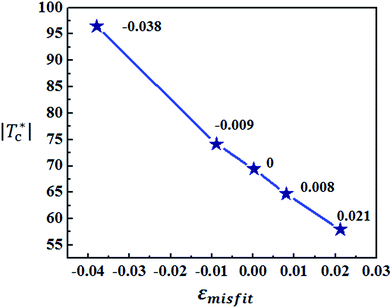
in the zone right underneath the tip-surface contact area equals to zero. With our model,  for film with misfit strain εmisfit = −0.038, εmisfit = −0.009, εmisfit = 0, εmisfit = 0.008 and εmisfit = 0.021 are quantitatively calculated as shown in Fig. 5.
for film with misfit strain εmisfit = −0.038, εmisfit = −0.009, εmisfit = 0, εmisfit = 0.008 and εmisfit = 0.021 are quantitatively calculated as shown in Fig. 5. 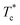 decreases from −96 to −58 when the interfacial misfit strain changes from the compressive strain εmisfit = −0.038 to the tensile strain εmisfit = 0.021. The finding that the mechanical threshold force decreases with the reduction of the compressive misfit strain agrees well with the experimental observations.19 The main cause of the reduction of mechanical threshold force is that the misfit tensile strain induces a decrease of tetragonality of the film and thus cutting down the potential barrier of the polarization switching. This is supported by the free-energy calculation of the PbTiO3 thin film epitaxially clamped on the substrate and simultaneously subjected to a vertical local compressive stress.59,60 With a vertical mechanical load but no misfit strain, a flexoelectric bias generated by local mechanical load via flexoelectricity destabilizes the upward-pointing polarization of the double well and forces the polarization switch to the downward-pointing polarization state. The double well of the free energy curve therefore becomes asymmetric, as shown by the black curve in Fig. 6. The energy barrier required to switch from the stable downward state to the upward state, Wdown→up, is far larger than that required to switch from the upward state to the downward state, Wup→down. With a tensile misfit strain and a local vertical mechanical load on the interface and top surface of the film, respectively, both of the energy barriers, Wdown→up and Wup→down, decrease (see the red curve in Fig. 6). With a compressive misfit strain and a local vertical mechanical load on the interface and top surface of the film, respectively, both of the energy barriers, Wdown→up and Wup→down, increase (see the blue curve in Fig. 6).
decreases from −96 to −58 when the interfacial misfit strain changes from the compressive strain εmisfit = −0.038 to the tensile strain εmisfit = 0.021. The finding that the mechanical threshold force decreases with the reduction of the compressive misfit strain agrees well with the experimental observations.19 The main cause of the reduction of mechanical threshold force is that the misfit tensile strain induces a decrease of tetragonality of the film and thus cutting down the potential barrier of the polarization switching. This is supported by the free-energy calculation of the PbTiO3 thin film epitaxially clamped on the substrate and simultaneously subjected to a vertical local compressive stress.59,60 With a vertical mechanical load but no misfit strain, a flexoelectric bias generated by local mechanical load via flexoelectricity destabilizes the upward-pointing polarization of the double well and forces the polarization switch to the downward-pointing polarization state. The double well of the free energy curve therefore becomes asymmetric, as shown by the black curve in Fig. 6. The energy barrier required to switch from the stable downward state to the upward state, Wdown→up, is far larger than that required to switch from the upward state to the downward state, Wup→down. With a tensile misfit strain and a local vertical mechanical load on the interface and top surface of the film, respectively, both of the energy barriers, Wdown→up and Wup→down, decrease (see the red curve in Fig. 6). With a compressive misfit strain and a local vertical mechanical load on the interface and top surface of the film, respectively, both of the energy barriers, Wdown→up and Wup→down, increase (see the blue curve in Fig. 6).
 |
| | Fig. 4 Domain structures of PbTiO3 with different interfacial misfit strain when the external force is  for εmisfit = (a) −0.038, (b) −0.009, (c) 0, (d) 0.008 and (e) 0.021. Here, it is important to notice that this figure just show region underneath and near the vertical pressure since the polarization switching process is highly localized. The magnitude and orientation of polarization are presented by the length and direction of arrows in the plots. Distribution of the second component of the polarization for εmisfit = (a) −0.038, (b) −0.009, (c) 0, (d) 0.008 and (e) 0.021. Here, it is important to notice that this figure just show region underneath and near the vertical pressure since the polarization switching process is highly localized. The magnitude and orientation of polarization are presented by the length and direction of arrows in the plots. Distribution of the second component of the polarization  of the ferroelectric film is presented by colors. of the ferroelectric film is presented by colors. | |
 |
| | Fig. 5 The mechanical threshold force for 180° domain switching in PTO with different misfit strain εmisfit = (a) −0.038, (b) −0.009, (c) 0, (d) 0.008 and (e) 0.021. | |
 |
| | Fig. 6 Free-energy curves of the PbTiO3 thin film under the same local mechanical load but with interface misfit strain εmisfit > 0 (red curve), εmisfit = 0 (black curve) and εmisfit < 0 (blue curve). | |
Based on the analysis above, we can ascertain that: (a) film subjected to the largest tensile misfit strain εmisfit = 0.021 demands the lowest mechanical threshold force for 180° switching and accordingly the lowest mechanical force for the mechanical writing process to reach a steady state; (b) when the mechanical force utilized to write 180° domains is not large enough for the writing process with the largest tensile misfit strain εmisfit = 0.021 to reach a steady state, the DEP of the mechanically written domain increases as the interfacial misfit strain changes from the compressive strain εmisfit = −0.038 to the tensile strain εmisfit = 0.021. Here, it should be pointed out that there exists difference on formation of c domain in film with tensile misfit strain between our simulation result and those in ref. 61 and 62. Our simulation showed that downward c domain still formed at the area far away from the contact area when the misfit tensile strain is 0.021. However, Li et al.62 showed that c domain will not form when the misfit tensile strain reaches up to 0.012. Pertsev et al.61 concluded that c domain will not form when the misfit tensile strains are about 0.001 in BaTiO3 and 0.01 in PbTiO3. Obviously, tensile misfit strain in our paper possesses a relative weaker impact on the formation of a domain. Two factors should be responsible for this difference. Firstly, different from the models in references, a giant compressive stress which will produce large c domains via flexoelectric effect is applied at the centre of the film surface. Compared with the huge compressive stress, the interfacial misfit strain which usually makes c domains be unstable plays a relatively weak role on domains. Therefore, even at a misfit tensile strain as large as 0.021, two times larger than 0.01, newly formed c domain possesses a dominant position in the zone underneath the pressure-surface contact area. a domains just form near the interface and at the surrounding area of compressive zone. Secondly, unlike the references in which the misfit strain at the interface is approximated by a uniform strain field within the thin film, this paper makes no approximation and the misfit strain is applied directly to the interface. It is worthy to emphasize that applying misfit strain directly to the interface is closer to the actual situation. Since the misfit strain is just applied at the interface, the effect of interfacial misfit strain on domains decreases rapidly with the increasing distance from the interface. Therefore, interfacial misfit strain that uniform distributed in the film has a larger effect on polarization.
When the mechanical force applied is sufficient large for all films with the five misfit strains mentioned in this paper to reach a steady state, variation trend of the DEP of the mechanically written domain with the interfacial misfit strain is opposite. Fig. 7 demonstrates the stable domain structures of ferroelectric films with different misfit strains. Here,  . Underneath the load-surface contact area, the newly written −x2 oriented 180° domain shrinks when the interfacial misfit strain changes from compressive to tensile, while the −x1/x1 oriented 90° domains that surround the −x2 oriented 180° domain expand. Shrink of 180° domain and expansion of 90° domain lead to a decline of DEP. There are two reasons for the decline of DEP. Firstly, it is because the interfacial misfit tensile strain makes the electric dipole in c domains more unstable. In order to stabilize the c domain, larger size of a domain which results in a lower DEP, will appear around the unstable c domain.63,64 Secondly, it may result from a reduction of the flexoelectric field, which is supported by shift of P–E hysteresis loops under vertical compressive pressure. To explain the second reason in detail, Fig. 8 gives the P–E hysteresis loops of films under different misfit strains but identical vertical compressive pressure. For clearly comparison, only the largest tensile strain εmisfit = −0.038 and compressive strain εmisfit = 0.021 are considered. From Fig. 8, it can be seen that, when the interfacial misfit strain turns to be tensile, the hysteresis loop becomes narrower and more symmetric. These two changes can be quantified by
. Underneath the load-surface contact area, the newly written −x2 oriented 180° domain shrinks when the interfacial misfit strain changes from compressive to tensile, while the −x1/x1 oriented 90° domains that surround the −x2 oriented 180° domain expand. Shrink of 180° domain and expansion of 90° domain lead to a decline of DEP. There are two reasons for the decline of DEP. Firstly, it is because the interfacial misfit tensile strain makes the electric dipole in c domains more unstable. In order to stabilize the c domain, larger size of a domain which results in a lower DEP, will appear around the unstable c domain.63,64 Secondly, it may result from a reduction of the flexoelectric field, which is supported by shift of P–E hysteresis loops under vertical compressive pressure. To explain the second reason in detail, Fig. 8 gives the P–E hysteresis loops of films under different misfit strains but identical vertical compressive pressure. For clearly comparison, only the largest tensile strain εmisfit = −0.038 and compressive strain εmisfit = 0.021 are considered. From Fig. 8, it can be seen that, when the interfacial misfit strain turns to be tensile, the hysteresis loop becomes narrower and more symmetric. These two changes can be quantified by  and
and  , respectively. Fig. 9 displays the influence of misfit strain on
, respectively. Fig. 9 displays the influence of misfit strain on  and
and  . The coercive fields
. The coercive fields  are 0.4335, 0.41125, 0.354, 0.3355 and 0.31285 when the misfit strains εmisfit are −0.038, −0.009, 0, 0.008 and 0.021, respectively. The monotone decreasing coercive fields reflects the reduction of the tetragonal characteristic of the ferroelectric thin film as the misfit strain turns from compressive to tensile. Lateral offset of the electric fields
are 0.4335, 0.41125, 0.354, 0.3355 and 0.31285 when the misfit strains εmisfit are −0.038, −0.009, 0, 0.008 and 0.021, respectively. The monotone decreasing coercive fields reflects the reduction of the tetragonal characteristic of the ferroelectric thin film as the misfit strain turns from compressive to tensile. Lateral offset of the electric fields  are 0.1305, 0.12625, 0.089, 0.0845, 0.0812 when interfacial misfit strain are −0.038, −0.009, 0, 0.008 and 0.021, respectively. Increasing symmetry of the ferroelectric hysteresis loop as the misfit strain turns to be tensile implies that ferroelectric thin film with tensile interfacial misfit strain possesses a lower flexoelectric field.
are 0.1305, 0.12625, 0.089, 0.0845, 0.0812 when interfacial misfit strain are −0.038, −0.009, 0, 0.008 and 0.021, respectively. Increasing symmetry of the ferroelectric hysteresis loop as the misfit strain turns to be tensile implies that ferroelectric thin film with tensile interfacial misfit strain possesses a lower flexoelectric field.
 |
| | Fig. 7 Distribution of  of stable domain structures in PbTiO3 thin film with five different misfit strains: εmisfit = (a) −0.038, (b) −0.009, (c) 0, (d) 0.008 and (e) 0.021. Area in blue, green, and red respectively denotes the mechanically written 180° domain, mechanically written 90° domain, and originally x2 oriented 180° domain. Here, the mechanical pressure of stable domain structures in PbTiO3 thin film with five different misfit strains: εmisfit = (a) −0.038, (b) −0.009, (c) 0, (d) 0.008 and (e) 0.021. Area in blue, green, and red respectively denotes the mechanically written 180° domain, mechanically written 90° domain, and originally x2 oriented 180° domain. Here, the mechanical pressure  . . | |
 |
| | Fig. 8 P–E hysteresis loops of films with the largest compressive misfit strain, εmisfit = −0.038, and the largest tensile misfit strain, εmisfit = 0.021. Here, the mechanical pressure  . . | |
 |
| | Fig. 9  and and  vs. εmisfit when the mechanical pressure vs. εmisfit when the mechanical pressure  . . | |
To sum up, depending on the magnitude of the external mechanical force, DEP of the mechanical writing domain increases or decreases as the misfit strain changes from being compressive to tensile. This is because misfit tensile strain can affect the domain structures from two aspects: (1) making the a domains stable and c domains unstable;61,62 (2) cutting down the potential barrier of the polarization switching.65,66 When the external force is small, only the area that very close to the external force gets the chance to obtain energy to overcome the potential barrier. If the potential barrier becomes lower, more polarization vectors will get the chance to switch. Potential barrier is the dominant factor that determines the magnitude of DEP. Thus, a larger tensile strain corresponds to a higher DEP in this case. When the external force is large enough for all the polarizations in the compressive zone to overcome the potential barrier, the unstability of c domain becomes the dominant factor that determine the magnitude of DEP. Therefore, a larger tensile strain corresponds to a lower DEP.
4. Conclusion
We have used a multi-field coupling model of flexoelectric to investigate the strain tunability of the downward effective polarization of mechanically written domains. The simulation results reveal that the downward effective polarization of the mechanically written domain increases/decreases with increasing tensile/compressive misfit strain when the external mechanical pressure is not large enough for the mechanical writing process of film with the largest tensile strain to reach a steady state. Once the mechanical load is sufficient for the mechanical writing process with the largest compressive strain to reach a steady state, variation trend of the DFP with misfit strain is opposite. In the latter case, the magnitude of the DFP is related to the flexoelectric field and is reflected by the asymmetry of the P–E hysteresis of film with mechanical pressure. Our simulation suggests that, in order to write a domain that has a large DEP, the following two points should be satisfied: first, ferroelectric film with a compressive interfacial misfit strain is favorable; second, a sufficient large mechanical load should be used to ensure that the mechanical written process approaches the steady state.
Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grant No. 11502224, 11032010, 11372266, 11402221, 11172257 and 11202054).
References
- J. F. Scott, Science, 2007, 315, 954 CrossRef CAS PubMed.
- B. H. Park, B. S. Kang, S. D. Bu, T. W. Noh, J. Lee and W. Jo, Nature, 1999, 401, 682 CrossRef CAS.
- P. Gao, C. T. Nelson, J. R. Jokisaari, Y. Zhang, S. H. Baek, C. W. Bark, E. Wang, Y. M. Liu, J. Y. Li, C. B. Eom and X. Q. Pan, Adv. Mater., 2012, 24, 1106 CrossRef CAS PubMed.
- H. Q. Fan and H. E. Kim, Jpn. J. Appl. Phys., Part 1, 2002, 41, 6768 CrossRef CAS.
- Z. Y. Wang, H. Q. Fan, K. H. Su and Z. Y. Wen, Polymer, 2010, 51, 3575 CrossRef.
- R. Ahluwalia, A. K. Tagantse, P. Yudin, N. Setter, N. Ng and D. J. Srolovitz, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 174105 CrossRef.
- D. G. Schlom, L. Q. Chen, C. B. Eom, K. M. Rabe, S. K. Streiffer and J. M. Triscone, Annu. Rev. Mater. Res., 2007, 37, 589 CrossRef CAS.
- C. B. Long, H. Q. Fan and P. R. Ren, Inorg. Chem., 2013, 52, 5045 CrossRef CAS PubMed.
- H. Q. Fan, Mater. Sci. Eng., B, 2005, 120, 114 CrossRef.
- K. J. Choi, M. Biegalski, Y. L. Li, A. Sharan, J. Schubert, R. Uecker and L. Q. Chen, Science, 2004, 306, 1005 CrossRef CAS PubMed.
- V. Indenbom, E. Lo ginov and M. Osipov, Kristallografiya, 1981, 26, 1157 CAS.
- D. Yu, M. Zhao, C. Wang, L. Wang, W. Su, Z. Gai and J. Zhang, RSC Adv., 2016, 6, 1182 RSC.
- D. Lee, A. Yoon, S. Y. Jang, J. G. Yoon, J. S. Chung, M. Kim and T. W. Noh, Phys. Rev. Lett., 2011, 107, 057602 CrossRef CAS PubMed.
- A. Gruverman, B. J. Rodriguez, A. Kingon, R. Nemanich, A. Tagantsev, J. Cross and M. Tsukada, Appl. Phys. Lett., 2003, 83, 728 CrossRef CAS.
- M. Majdoub, R. Maranganti and P. Sharma, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115412 CrossRef.
- G. Catalan, B. Noheda, J. McAneney, L. Sinnamon and J. Gregg, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 020102 CrossRef.
- H. Lu, C. W. Bark, D. Esque de los Ojos, J. Alcala, C. B. Eom, G. Catalan and A. Gruverman, Science, 2012, 336, 59 CrossRef CAS PubMed.
- L. M. Jiang, J. Y. Tang, Y. C. Zhou, Q. Yang, Y. Zhang, L. L. Guo and X. L. Zhong, Comput. Mater. Sci., 2015, 108, 309 CrossRef CAS.
- E. J. Guo, R. Roth, S. Das and K. Dörr, Appl. Phys. Lett., 2014, 105, 012903 CrossRef.
- B. Li, J. B. Wang, X. L. Zhong, F. Wang and Y. C. Zhou, J. Appl. Phys., 2010, 107, 014109 CrossRef.
- L. M. Jiang, Y. C. Zhou, Y. Zhang, Q. Yang, Y. J. Gu and L. Q. Chen, Acta Mater., 2015, 90, 344 CrossRef CAS.
- L. Q. Chen, J. Am. Ceram. Soc., 2008, 91, 1835 CrossRef CAS.
- J. Wang, Appl. Phys. Lett., 2010, 97, 192901 CrossRef.
- H. H. Wu, J. Wang, S. G. Gao and T. Y. Zhang, Appl. Phys. Lett., 2013, 102, 232904 CrossRef.
- J. Wang and M. Kamlah, Smart Mater. Struct., 2009, 18, 104008 CrossRef.
- Y. Cao, J. Shen, C. A. Randall and L. Q. Chen, Appl. Phys. Lett., 2014, 104, 182905 CrossRef.
- H. H. Wu, J. Wang, S. G. Cao, L. Q. Chen and T. Y. Zhang, Smart Mater. Struct., 2014, 23, 025004 CrossRef.
- H. H. Wu, J. Wang, S. G. Cao, L. Q. Chen and T. Y. Zhang, J. Appl. Phys., 2013, 114, 164108 Search PubMed.
- R. D. Mindlin, Int. J. Solids Struct., 1965, 1, 417 CrossRef.
- D. C. C. Lam, F. Yang, A. C. M. Chong, J. Wang and P. Tong, J. Mech. Phys. Solids, 2003, 51, 1477 CrossRef.
- L. M. Jiang, Y. C. Zhou, H. X. Hao, Y. G. Liao and C. S. Lu, Mech. Mater., 2010, 42, 908 CrossRef.
- C. P. Tsangarides, A. K. Yetisen, F. da Cruz Vasconcellos, Y. Montelongo, M. M. Qasim, T. D. Wilkinson and H. Butt, RSC Adv., 2014, 4, 10454 RSC.
- L. M. Jiang, Y. C. Zhou, Y. G. Liao and C. Q. Sun, Mater. Sci. Eng., A, 2008, 487, 228 CrossRef.
- Y. Su and C. M. Landis, J. Mech. Phys. Solids, 2007, 55, 280 CrossRef CAS.
- E. M. Lifshitz and L. D. Landau, Statistical Physics (Course of Theoretical Physics), 1984, p. 5 Search PubMed.
- A. F. Devonshire, The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1949, vol. 40, p. 1040 Search PubMed.
- Y. J. Gu, M. L. Li, A. N. Morozovska, Y. Wang, E. A. Eliseev, V. Gopalan and L. Q. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 174111 CrossRef.
- F. Xue, J. J. Wang, G. Sheng, E. Huang, Y. Cao, H. H. Huang and L. Q. Chen, Acta Mater., 2013, 61, 2909 CrossRef CAS.
- J. Wang, M. Kamlah and T. Y. Zhang, Acta Mech., 2010, 214, 49 CrossRef.
- J. Wang, S. Q. Shi, L. Q. Chen, Y. Li and T. Y. Zhang, Acta Mater., 2004, 52, 749 CrossRef CAS.
- J. Wang and T. Y. Zhang, Acta Mater., 2007, 55, 2465 CrossRef CAS.
- Y. J. Gu, Z. J. Hong, J. Britson and L. Q. Chen, Appl. Phys. Lett., 2015, 106, 022904 CrossRef.
- R. Nelmes and W. Kuhs, Solid State Commun., 1985, 54, 721 CrossRef CAS.
- J. Häglund, A. F. Guillermet, G. Grimvall and M. Körling, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 11685 CrossRef.
- S. Howard, J. Yau and H. Anderson, J. Appl. Phys., 1989, 65, 1492 CrossRef CAS.
- A. S. Yurkov, JETP Lett., 2011, 94, 455 CrossRef CAS.
- A. N. Morozovska, E. A. Eliseev, S. V. Kalinin, L. Q. Chen and V. Gopalan, Appl. Phys. Lett., 2012, 100, 142902 CrossRef.
- W. J. Chen, Y. Zheng, X. Feng and B. Wang, J. Mech. Phys. Solids, 2015, 79, 108 CrossRef CAS.
- Y. Cao, Q. Li, L. Q. Chen and S. V. Kalinin, Appl. Phys. Lett., 2015, 107, 202905 CrossRef.
- R. Kretschmer and K. Binder, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 20, 1065 CrossRef CAS.
- K. Ishikawa and T. Uemori, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 11841 CrossRef CAS.
- W. J. Chen, Y. Zheng and B. Wang, Appl. Phys. Lett., 2011, 98, 222902 CrossRef.
- W. J. Chen, Y. Zheng, B. Wang, D. C. Ma and C. M. Wu, J. Appl. Phys., 2014, 115, 094101 CrossRef.
- J. Wang and T. Y. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 144107 CrossRef.
- J. Wang, Theor. Appl. Mech. Lett., 2011, 1, 011003 CrossRef.
- J. Wang and M. Kamlah, Eng. Fract. Mech., 2010, 77, 3658 CrossRef.
- J. Wang, M. Kamlah and T. Y. Zhang, J. Appl. Phys., 2009, 105, 014104 CrossRef.
- W. Kanzig, Phys. Rev., 1955, 98, 549 CrossRef CAS.
- A. Y. Emelyanov, N. A. Pertsev and A. L. Kholkin, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 214108 CrossRef.
- Y. Zhang, X. L. Zhong, M. Vopson, J. B. Wang and Y. C. Zhou, J. Appl. Phys., 2012, 112, 014112 CrossRef.
- N. A. Pertsev, A. G. Zembilgotov and A. K. Tagantsev, Phys. Rev. Lett., 1998, 80, 1988 CrossRef CAS.
- Y. L. Li, S. Y. Hu, Z. K. Liu and L. Q. Chen, Acta Mater., 2002, 50, 395 CrossRef CAS.
- A. Gruverman, A. Kholkin, A. Kingon and H. Tokumoto, Appl. Phys. Lett., 2001, 78, 2751 CrossRef CAS.
- Z. Hong, J. Britson, J. M. Hu and L. Q. Chen, Acta Mater., 2014, 73, 75 CrossRef CAS.
- S. Choudhury, Y. L. Li, L. Q. Chen and Q. X. Jia, Appl. Phys. Lett., 2008, 92, 142907 CrossRef.
- J. Wang, Y. F. Xia, L. Q. Chen and S. Q. Shi, J. Appl. Phys., 2011, 110, 114111 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. 
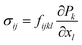





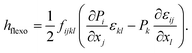





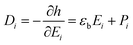



![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) i, on SP
i, on SP

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18 are nondimensionalized with P0 = 0.757 C m2, g110 = 1.73 × 10−10 C2 m4 N and α0 = 1.725 × 108 C2 m2 N. For simplicity, two dimensional (2D) finite element simulations were conducted in the present work under the plane strain condition along the x3 axis, although the theoretical framework described in Section 2 can be applied to three dimensional simulations. Fig. 1 shows a schematic illustration of the simulated ferroelectric film subjected to concurrent local mechanical and electrical loads.
18 are nondimensionalized with P0 = 0.757 C m2, g110 = 1.73 × 10−10 C2 m4 N and α0 = 1.725 × 108 C2 m2 N. For simplicity, two dimensional (2D) finite element simulations were conducted in the present work under the plane strain condition along the x3 axis, although the theoretical framework described in Section 2 can be applied to three dimensional simulations. Fig. 1 shows a schematic illustration of the simulated ferroelectric film subjected to concurrent local mechanical and electrical loads.

 is applied to the center of the top surface of the ferroelectric film. The dimensionless time step is set as Δt* = 0.05 and total time is t* = 2500.
is applied to the center of the top surface of the ferroelectric film. The dimensionless time step is set as Δt* = 0.05 and total time is t* = 2500. , meaning that polarizations are completely suppressed at the surface. This approximate but simple zero boundary condition has been successfully used to explain some experimental observation.58 We have also obtained the domain structures for the first way in which a surface effect energy term is added to the total energy. It is found out that dissimilar way of considering surface effect leads to little difference in domain structure.
, meaning that polarizations are completely suppressed at the surface. This approximate but simple zero boundary condition has been successfully used to explain some experimental observation.58 We have also obtained the domain structures for the first way in which a surface effect energy term is added to the total energy. It is found out that dissimilar way of considering surface effect leads to little difference in domain structure. , which corresponds to real element size of Δx1 = Δx2 = 1 nm.
, which corresponds to real element size of Δx1 = Δx2 = 1 nm. . Obviously, there is a shift of the hysteresis loop towards the positive bias. The positive and negative coercive field are, respectively,
. Obviously, there is a shift of the hysteresis loop towards the positive bias. The positive and negative coercive field are, respectively,  and
and  , implying that it is easier for the polarization to switch from the upward-pointing state to the downward-pointing state. The local compressive vertical stress generates a polar bias via flexoelectricity.
, implying that it is easier for the polarization to switch from the upward-pointing state to the downward-pointing state. The local compressive vertical stress generates a polar bias via flexoelectricity. . We then define the coercivity as the half-width of the hysteresis loop, measured as the difference between positive and negative coercive electric fields divided by two:
. We then define the coercivity as the half-width of the hysteresis loop, measured as the difference between positive and negative coercive electric fields divided by two: 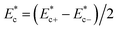 . The offset and coercivity for the films under increasing load is listed in Table 2. There is a monatonical shift of the hysteresis loops towards positive values as the load is increased, implying an increasing flexoelectric field.17 The negative coercive field is decreased while the positive coercive field does not. The above observations are well in agreement with the experiment results in ref. 17 and calculation results in ref. 49. Thus, the correctness of our model is verified.
. The offset and coercivity for the films under increasing load is listed in Table 2. There is a monatonical shift of the hysteresis loops towards positive values as the load is increased, implying an increasing flexoelectric field.17 The negative coercive field is decreased while the positive coercive field does not. The above observations are well in agreement with the experiment results in ref. 17 and calculation results in ref. 49. Thus, the correctness of our model is verified.
 at the center of the upper surface and different misfit strain at the interface. No 180° domain is formed when the film is under misfit compressive strain. When the misfit strain is zero, the newly formed 180° domain is equal to the original 180° domain, resulting in a zero DEP. As the misfit strain turns to be tensile, the DEP grows with increasing tensile misfit strain. The raise of the DEP is intrinsically associated with a drop of the mechanical threshold force. As shown by Fig. 4(a), two small a domains that enjoy opposite directions are formed underneath both sides of the tip-surface contact area. This result indicates that, when the interfacial misfit strain is εmisfit = −0.038, the external mechanical force
at the center of the upper surface and different misfit strain at the interface. No 180° domain is formed when the film is under misfit compressive strain. When the misfit strain is zero, the newly formed 180° domain is equal to the original 180° domain, resulting in a zero DEP. As the misfit strain turns to be tensile, the DEP grows with increasing tensile misfit strain. The raise of the DEP is intrinsically associated with a drop of the mechanical threshold force. As shown by Fig. 4(a), two small a domains that enjoy opposite directions are formed underneath both sides of the tip-surface contact area. This result indicates that, when the interfacial misfit strain is εmisfit = −0.038, the external mechanical force  is slightly greater than the threshold value for 90° switching and much smaller than the threshold value for 180° switching. With the same magnitude of mechanical force, when the interfacial misfit strain is −0.009, newly formed a domain has a greater size (see Fig. 4(b)), denoting that
is slightly greater than the threshold value for 90° switching and much smaller than the threshold value for 180° switching. With the same magnitude of mechanical force, when the interfacial misfit strain is −0.009, newly formed a domain has a greater size (see Fig. 4(b)), denoting that  is much greater than the threshold value for 90° domain switching and approaches the threshold value for 180° domain switching. Obviously, the critical value for 90° domain switching decreases with a decreasing compressive misfit strain at the interface. For ferroelectric film with no misfit strain at the interface as shown in Fig. 4(c), 180° domain switching occurred in the center of the thin film on a small scale, indicating that
is much greater than the threshold value for 90° domain switching and approaches the threshold value for 180° domain switching. Obviously, the critical value for 90° domain switching decreases with a decreasing compressive misfit strain at the interface. For ferroelectric film with no misfit strain at the interface as shown in Fig. 4(c), 180° domain switching occurred in the center of the thin film on a small scale, indicating that  is larger than the threshold value for 180° domain switching. As shown in Fig. 4(d) and (e), 180° domain switching appears on a larger scale when the interfacial misfit strain turns to be tensile and becomes larger, implying that the tensile misfit strain makes 180° mechanical switching easier to achieve. Note that, under
is larger than the threshold value for 180° domain switching. As shown in Fig. 4(d) and (e), 180° domain switching appears on a larger scale when the interfacial misfit strain turns to be tensile and becomes larger, implying that the tensile misfit strain makes 180° mechanical switching easier to achieve. Note that, under 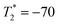 , mechanical writing process in none of the films reach a steady state. Comparing the domain structures of films with these five interfacial misfit strains, we have a rough conclusion that the mechanical threshold forces for 180° domain switching with different misfit strain have the following relationship:
, mechanical writing process in none of the films reach a steady state. Comparing the domain structures of films with these five interfacial misfit strains, we have a rough conclusion that the mechanical threshold forces for 180° domain switching with different misfit strain have the following relationship: 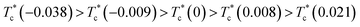 . Here, we define the mechanical threshold force for 180° domain switching as the value at which
. Here, we define the mechanical threshold force for 180° domain switching as the value at which  in the zone right underneath the tip-surface contact area equals to zero. With our model,
in the zone right underneath the tip-surface contact area equals to zero. With our model,  for film with misfit strain εmisfit = −0.038, εmisfit = −0.009, εmisfit = 0, εmisfit = 0.008 and εmisfit = 0.021 are quantitatively calculated as shown in Fig. 5.
for film with misfit strain εmisfit = −0.038, εmisfit = −0.009, εmisfit = 0, εmisfit = 0.008 and εmisfit = 0.021 are quantitatively calculated as shown in Fig. 5. 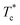 decreases from −96 to −58 when the interfacial misfit strain changes from the compressive strain εmisfit = −0.038 to the tensile strain εmisfit = 0.021. The finding that the mechanical threshold force decreases with the reduction of the compressive misfit strain agrees well with the experimental observations.19 The main cause of the reduction of mechanical threshold force is that the misfit tensile strain induces a decrease of tetragonality of the film and thus cutting down the potential barrier of the polarization switching. This is supported by the free-energy calculation of the PbTiO3 thin film epitaxially clamped on the substrate and simultaneously subjected to a vertical local compressive stress.59,60 With a vertical mechanical load but no misfit strain, a flexoelectric bias generated by local mechanical load via flexoelectricity destabilizes the upward-pointing polarization of the double well and forces the polarization switch to the downward-pointing polarization state. The double well of the free energy curve therefore becomes asymmetric, as shown by the black curve in Fig. 6. The energy barrier required to switch from the stable downward state to the upward state, Wdown→up, is far larger than that required to switch from the upward state to the downward state, Wup→down. With a tensile misfit strain and a local vertical mechanical load on the interface and top surface of the film, respectively, both of the energy barriers, Wdown→up and Wup→down, decrease (see the red curve in Fig. 6). With a compressive misfit strain and a local vertical mechanical load on the interface and top surface of the film, respectively, both of the energy barriers, Wdown→up and Wup→down, increase (see the blue curve in Fig. 6).
decreases from −96 to −58 when the interfacial misfit strain changes from the compressive strain εmisfit = −0.038 to the tensile strain εmisfit = 0.021. The finding that the mechanical threshold force decreases with the reduction of the compressive misfit strain agrees well with the experimental observations.19 The main cause of the reduction of mechanical threshold force is that the misfit tensile strain induces a decrease of tetragonality of the film and thus cutting down the potential barrier of the polarization switching. This is supported by the free-energy calculation of the PbTiO3 thin film epitaxially clamped on the substrate and simultaneously subjected to a vertical local compressive stress.59,60 With a vertical mechanical load but no misfit strain, a flexoelectric bias generated by local mechanical load via flexoelectricity destabilizes the upward-pointing polarization of the double well and forces the polarization switch to the downward-pointing polarization state. The double well of the free energy curve therefore becomes asymmetric, as shown by the black curve in Fig. 6. The energy barrier required to switch from the stable downward state to the upward state, Wdown→up, is far larger than that required to switch from the upward state to the downward state, Wup→down. With a tensile misfit strain and a local vertical mechanical load on the interface and top surface of the film, respectively, both of the energy barriers, Wdown→up and Wup→down, decrease (see the red curve in Fig. 6). With a compressive misfit strain and a local vertical mechanical load on the interface and top surface of the film, respectively, both of the energy barriers, Wdown→up and Wup→down, increase (see the blue curve in Fig. 6).
 . Underneath the load-surface contact area, the newly written −x2 oriented 180° domain shrinks when the interfacial misfit strain changes from compressive to tensile, while the −x1/x1 oriented 90° domains that surround the −x2 oriented 180° domain expand. Shrink of 180° domain and expansion of 90° domain lead to a decline of DEP. There are two reasons for the decline of DEP. Firstly, it is because the interfacial misfit tensile strain makes the electric dipole in c domains more unstable. In order to stabilize the c domain, larger size of a domain which results in a lower DEP, will appear around the unstable c domain.63,64 Secondly, it may result from a reduction of the flexoelectric field, which is supported by shift of P–E hysteresis loops under vertical compressive pressure. To explain the second reason in detail, Fig. 8 gives the P–E hysteresis loops of films under different misfit strains but identical vertical compressive pressure. For clearly comparison, only the largest tensile strain εmisfit = −0.038 and compressive strain εmisfit = 0.021 are considered. From Fig. 8, it can be seen that, when the interfacial misfit strain turns to be tensile, the hysteresis loop becomes narrower and more symmetric. These two changes can be quantified by
. Underneath the load-surface contact area, the newly written −x2 oriented 180° domain shrinks when the interfacial misfit strain changes from compressive to tensile, while the −x1/x1 oriented 90° domains that surround the −x2 oriented 180° domain expand. Shrink of 180° domain and expansion of 90° domain lead to a decline of DEP. There are two reasons for the decline of DEP. Firstly, it is because the interfacial misfit tensile strain makes the electric dipole in c domains more unstable. In order to stabilize the c domain, larger size of a domain which results in a lower DEP, will appear around the unstable c domain.63,64 Secondly, it may result from a reduction of the flexoelectric field, which is supported by shift of P–E hysteresis loops under vertical compressive pressure. To explain the second reason in detail, Fig. 8 gives the P–E hysteresis loops of films under different misfit strains but identical vertical compressive pressure. For clearly comparison, only the largest tensile strain εmisfit = −0.038 and compressive strain εmisfit = 0.021 are considered. From Fig. 8, it can be seen that, when the interfacial misfit strain turns to be tensile, the hysteresis loop becomes narrower and more symmetric. These two changes can be quantified by  and
and  , respectively. Fig. 9 displays the influence of misfit strain on
, respectively. Fig. 9 displays the influence of misfit strain on  and
and  . The coercive fields
. The coercive fields  are 0.4335, 0.41125, 0.354, 0.3355 and 0.31285 when the misfit strains εmisfit are −0.038, −0.009, 0, 0.008 and 0.021, respectively. The monotone decreasing coercive fields reflects the reduction of the tetragonal characteristic of the ferroelectric thin film as the misfit strain turns from compressive to tensile. Lateral offset of the electric fields
are 0.4335, 0.41125, 0.354, 0.3355 and 0.31285 when the misfit strains εmisfit are −0.038, −0.009, 0, 0.008 and 0.021, respectively. The monotone decreasing coercive fields reflects the reduction of the tetragonal characteristic of the ferroelectric thin film as the misfit strain turns from compressive to tensile. Lateral offset of the electric fields  are 0.1305, 0.12625, 0.089, 0.0845, 0.0812 when interfacial misfit strain are −0.038, −0.009, 0, 0.008 and 0.021, respectively. Increasing symmetry of the ferroelectric hysteresis loop as the misfit strain turns to be tensile implies that ferroelectric thin film with tensile interfacial misfit strain possesses a lower flexoelectric field.
are 0.1305, 0.12625, 0.089, 0.0845, 0.0812 when interfacial misfit strain are −0.038, −0.009, 0, 0.008 and 0.021, respectively. Increasing symmetry of the ferroelectric hysteresis loop as the misfit strain turns to be tensile implies that ferroelectric thin film with tensile interfacial misfit strain possesses a lower flexoelectric field.
 .
.