The electronic structure and spin–orbit-induced spin splitting in antimonene with vacancy defects

Abstract

We study the geometric, electronic properties, and spin splitting in monovacancy (MV) and divacancy (DV) antimonene with five different models using first-principles calculations. Meanwhile the influence of spin–orbit coupling (SOC) is included. Different vacancies cause different geometric structures with or without inversion symmetry and influence the electronic structures. MV antimonene shows metallic character, however, four DV antimnoene models preserve the semiconducting character narrowing the band gap. The inversion asymmetry and SOC lead to the spin splitting in MV and two DV models. Zeeman-type spin splitting appears with out-of-plane spin polarization along M–K–Γ. Rashba and Dresselhaus effects induced spin splitting occurs at Γ and M points in MV.

---

Introduction

Recently, V-family elements have been more and more investigated, especially the two dimensional (2D) material phosphorene after exfoliation from bulk black phosphorus, which has been applied in field-effect transistors.^1,2 Zhang et al.³ firstly predicted semiconductors of antimonene and arensene, which are monolayer antimony and arsenic, respectively. Antimonene has a buckled structure, which is different from planar graphene, silylene and puckered phosphorene. It can transform from an indirect band gap to direct gap semiconductor under external strain. Its high stability and indirect wide band gap of 2.28 eV may pave the way for optoelectronic devices working under blue or UV light and mechanical sensors based on new 2D crystals.³ Antimonene as a new 2D semiconductor gets lots of attention and researches about the stability, influence of strain and adatoms.^4,5 Recently, it has been successfully grown on Sb₂Te₃ and Bi₂Te₃ substrates.⁶

The atomic-scale defects and vacancies, generated usually by ion or electron irradiations can strongly influence electronic and mechanical properties of 2D materials.^7–9 Vacancy is one of the most common defects in crystalline solids and affects profoundly the physical properties of the solids, especially 2D semiconductors. These defects are believed to be the predominant defects on irradiated graphite surfaces.^7–9 Therefore, understanding possible formation of these intrinsic vacancies as well as their effects on the system's electronic and magnetic properties is of fundamental interest. A number of theoretical calculations have also been performed to study the vacancy in graphene, MoS₂, and phosphorene, which leads to interesting effects and potential applications.^10–13 So it is necessary to study the influence of vacancies on antimonene, which will have a guiding role in the future experiment based on antimonene. On the other hand, the spin–orbit interaction has effect on the band structure of graphene, MoS₂ and metal surfaces.^14–19 Spin–orbit coupling (SOC) manifests itself by lifting the spin degeneracy in the electronic structures, such as the magnetic anisotropy in magnetic systems and the band splitting of surface states when the systems lack the inversion symmetry. 2D materials MX₂ (M = Mo, W and X = S, Se) exhibit a giant spin splitting along Γ–K induced by SOC up to 456 meV (WSe₂)²⁰ at valance band maximum (VBM) due to the lack of inversion symmetry in monolayer. Especially the spin splitting induced by Rashba SOC always results in some interesting effects such as spin Hall and spin-galvanic effects.^21–23

Therefore in this work, we include SOC in calculations to study the influence vacancies on the geometric, electronic properties in monovacancy and divacancy antimonene. It is found that the vacancies result in the vanishing of inversion symmetry and modifying the electronic property. Meanwhile the SOC induces the spin splitting and spin polarization in the systems which lack the inversion symmetry, which is possible to have guiding significance in future experiment based on antimonene.

Calculation details and models

We carry out spin-polarized first-principles calculations using Vienna ab initio Simulation Package²⁴ code with the generalized gradient approximation (GGA)²⁵ of Perdew, Burke and Ernzernhof (PBE)²⁶ methods. DFT-D2 correction is employed to consider the van der Waals interaction²⁷ and SOC is included. An energy cutoff of 500 eV is employed in a plane-wave basis set. The atoms are relaxed until residual force on each atom is less than 0.01 eV Å⁻¹, and total energy is converged to 1 × 10⁻⁵ eV. Γ-Centered 5 × 5 × 1 k-mesh is set and a 15 Å vacuum layer vertical to surface is adopted to avoid the interaction between adjacent layers. We define the formation energy as E_f = E − N × E_Sb, where E represents the total energy of defective antimonene, N is Sb atom number in defective antimonene, and E_Sb is the energy per Sb in pristine antimonene. The smaller E_f means more stable.

Results and discussion

The pristine antimonene has inversion symmetry structure with P3̄m1 (D_3d³) space group, as shown in Fig. 1. Defective antimonene includes one monovacancy model (MV) and five divacancy antimonene models (DV), from DV-1 to DV-5, considering the relative distance between the two vacancies shown in Fig. 2. The different vacancies result in different symmetry structure and the corresponding space groups are shown in Table 1. It is notable that the MV, DV-2 and DV-4 become P3m1 (C_3v¹) and P3̄m1 (D_3d³), respectively. These three models lack the inversion symmetry, thus producing a spin splitting when including SOC discussed later. The lattice constants decrease for all defective antimonene models compared with pristine antimonene. Furthermore, the lattice constants of DVs are smaller than MV except for DV-1 antimonene where the two vacancies are nearest neighboring. The MV defect is formed most easily due to its smallest formation energy of 1.79 eV. In MV, the three Sb atoms around the vacancy form a triangle with edges of 3.67 Å, while the distance between the three Sb atoms is 4.05 Å in pristine antimonene. Therefore it is easy to understand the decreasing of the lattice constants of the defective antimonene. The bond length d between the Sb1 and Sb2 atoms is 3.67 and 3.86 Å in MV and DV-5, respectively. It is ranging 2.94–3.04 Å in other DV models, which is shorter than MV and DV-5. These are consistent with the change of the lattice constants in defective antimonene. The most stable DV antimonene is DV-1 with formation energy of 1.98 eV, which defect is common in graphene²⁸ and silylene.²⁹ However, the difference of the formation energy between other DVs is smaller.

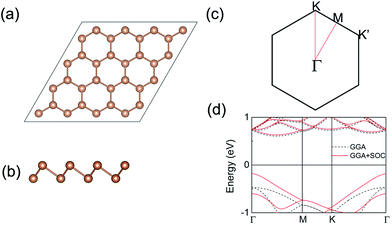Fig. 1 The (a) top and (b) side view of pristine antimonene. (c) The first Brillouin zone of antimonene. (d) The band structure with GGA and GGA + SOC method.

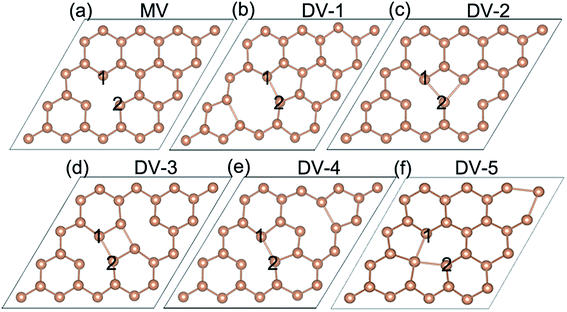Fig. 2 The models of defective antimonene of (a) MV model with single vacancy and (b)–(f) DV-1–DV-5 models with two vacancies.

Table 1 The calculated lattice constants a and b (Å), bond angle(degree) α, β, and γ, the bond length d (Å) between Sb1 and Sb2 atoms, space group and formation energy E_f (eV) of pristine and defective antimonene

System	a	b	α	β	γ	d	Space group	Ef
Pristine	16.18	16.18	90	90	120	4.05	P3̄m1 (D3d^3)	—
MV	15.99	15.99	90	90	120	3.67	P3m1 (C3v^1)	1.79
DV-1	16.12	16.12	91.35	91.35	122.81	3.04	C2/m (C2h^3)	1.98
DV-2	15.93	15.63	89.63	90.00	120.64	3.09	Cm (Cs^3)	3.10
DV-3	15.81	15.81	89.13	89.13	81.59	2.96	C2/m (C2h^3)	3.09
DV-4	15.91	15.91	88.60	88.63	121.73	2.94	Cm (Cs^3)	3.12
DV-5	15.57	15.57	90.42	90.42	118.50	3.86	C2/m (C2h^3)	3.11

---

In the calculations without SOC included, pristine antimonene is an indirect-band-gap semiconductor of 1.06 eV with conduction band minimum (CBM) at Γ, and valence band maximum (VBM) between Γ–M. The MV antimonene shows metallization with two defective energy bands (upper defective band UDB and lower defective band LDB in band gap) crossing E_f. However, all DVs preserve semiconducting characters, except for DV-5, which shows metallic character. The distance of two vacancies is too far in DV-5 model, which is close to the situation about two isolated single vacancy in antimonene, such as MV. In general, the band gap for DVs antimonene decreases from 0.75 to 0.23 eV with the increase of the distance between the two vacancies. The VBM in DV-1 locates at Γ point, and CBM is halfway between Γ–M with an indirect gap of 0.75 eV. In DV-2, CBM shifts to K point with an indirect band gap of 0.23 eV. For DV-3, both VBM and CBM locate at M, forming a direct band gap of 0.29 eV. In DV-4, CBM is still at M, but VBM locates at Γ with a band gap of 0.37 eV with VBM along Γ–M extremely flat, leading to a giant effective mass of holes. It can be seen that the vacancy can modify the electronic structure of antimonene, such as narrowing the band gap and even the transformation from indirect-band gap to direct-band gap. It is not only vacancies result in the direct band gap but also the biaxial tensile strain of 7–12% on antimonene leads to the direct band gap with CBM and VBM at Γ, and the band gap decreases with the increased tensile strain (1.96–0.9 eV at the HSE06 level).³

The charge densities of UDB and LDB in MV and DV-5 are shown in Fig. 3(a) and (b). It can be seen that the charge on defective bands comes from Sb atoms around vacancies. It is possible caused by the unpaired electrons around the Sb atoms neighboring the single vacancy in MV. The bonding states at VBM are exhibited in DV-1 and DV-3. The charge at CBM locates around the atom neighboring the vacancy, representing the anti-bonding states in DV-1–DV-4. In a word, the vacancy has important influence on the geometric and electronic structures, but it does not induce the magnetism in defective antimonene.

Fig. 3 The top and side view of partial charge density of UDB and LDB (a) in MV and (b) DV-5. (c)–(f) The partial charge density of VBM and CBM in DV-1, DV-2, DV-3 and DV-4, respectively.

According to Kramer's theorem, periodic bands of solids with inversion and time-reversal symmetries in momentum space are spin degenerate.³⁰ Time reversal symmetry always preserves the Kramer's degeneracy at any point of Brillouin zone as depicted of E(k,↑) = E(−k,↓). Inversion symmetry can preserve E(k,↑) = E(−k,↑) and E(k,↓) = E(−k,↓). If both time reversal symmetry and inversion symmetry coexist, the band structure should satisfy to the condition E(k,↑) = E(k,↓).^15,20 Therefore, SOC effects are especially noticeable without inversion symmetry, and cause the obvious spin splitting.

Electronic band structures of pristine antimonene with and without SOC are shown in Fig. 1(d). The VBM is fourfold degenerated (including spin) at M and K points without considering SOC. But the VBM becomes twofold degenerated at Γ point considering SOC. The p_x and p_y orbitals split at Γ (VBM) caused by spin–orbit interaction, which narrows the band gap from 1.06 to 0.79 eV. Meanwhile, the uppermost valance band is more dispersive, leading to a less effective mass of electrons. However, the spin splitting does not appear due to the existence of time reversal and inversion symmetry. From pristine to MV antimonene, the space group is reduced from P3̄m1 (D_3d³) to P3m1 (C_3v¹) with explicit breaking of inversion symmetry. The spin–orbit interaction causes spin splitting except for M and Γ with special symmetry in Brillouin zone in Fig. 4(a). We agree the spin degeneracy at Γ is preserved by time reversal symmetry alone. The combination of time reversal and translational symmetry leads to zero splitting at M.²⁰ The similar spin splitting appears in DV-2 and DV-4 without the inversion symmetry. In other DVs, which preserve the inversion symmetry with space group C2/m (C_2h³), the spin–orbit interaction does not lift spin degeneracy. Therefore, the spin splitting is caused by both SOC and its asymmetry. Meanwhile this material exhibits different spin splitting along the path in Brillouin zone in Fig. 5(a)–(c).

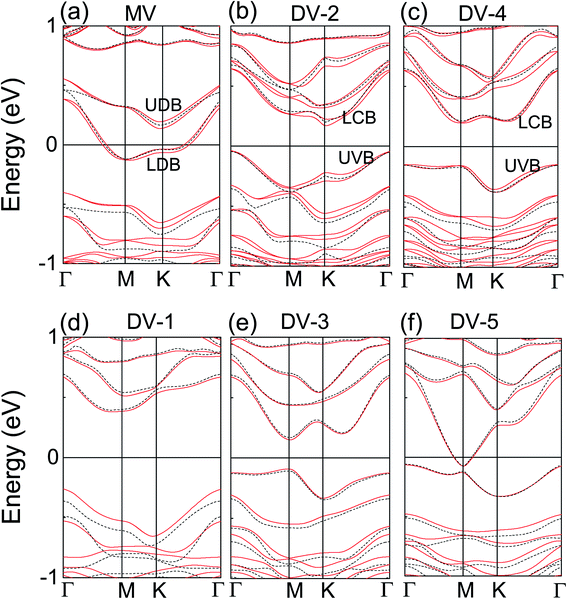Fig. 4 The band structure of (a) monovacancy (b)–(f) divacancy antimonene. Red solid line and black dash line represent the system with and without SOC. E_F is set at zero.

Fig. 5 The spin splitting as a function of k: UDB and LDB in (a) MV, LVB and UCB in (b) DV-2 and (c) DV-4, respectively. The Rashba and Dresselhaus induced spin splitting around M: (d) UDB and (g) LDB in MV, LVB and UCB in (e) and (h) DV-2, and in (f) and (i) DV-4. The red and blue rows represent spin up and spin down, respectively. E_F is set at zero.

In MV, DV-2 and DV-4, two types of spin splitting coexist. Zeeman type spin splitting along M–K–Γ path, where the spin polarized band shifts upward and downward, is mentioned and studied in WSe₂ slabs in previous report.³¹ The other is Rashba and Dresselhaus effects induced spin splitting around M and Γ with the band shifting in the momentum space in opposite directions³² in Fig. 5(a)–(c). In connection with the Rashba and Dresselhaus SOC effects, the corresponding effects will induce effective Rashba and Dresselhaus pseudomagnetic fields, which give the contribution to the net magnetic field and then induce the spin splitting. However, the Rashba and Dresselhaus effects are phenomenologically inseparable, so the extraction of their individual parameters is not simple.³³

Spin splitting Δ (it is defined as the difference between the energy band with opposite spin) is strongly depend on k for UDB and LDB in MV, the uppermost valance band (UVB) and lowermost conduction band (LCB) in DV-2 and DV-4 along Γ–M–K–Γ in Fig. 5. The signal of the spin splitting changes from path Γ–M to M–K in MV, DV-2 and DV-4, representing the change of spin direction. It is also concluded that the spin polarization is strongly dependent on Brillouin zone path. In MV, Δ rises continuously with the maximum of 58 meV between M–K, and decreases continuously along K–Γ for UDB and the maximum of Δ is 49 meV between Γ–M for LDB. In DV-2, Δ of LCB and UVB has almost same change trend but different magnitude along M–K–Γ. The maximum Δ for LVB is 43 meV between K–Γ and 59 meV between Γ–M. In DV-4, Δ reaches the maximum at K for both UVB (76 meV) and LCB (63 meV).

In order to understand the spin polarization, we calculate the band with spin projected along z direction (out of plane) in MV, DV-2 and DV-4. It can be seen that no spin polarization exists out of plane along Γ–M but appears along M–K–Γ where Zeeman-like spin splitting appears in Fig. 6(a). This means that the out-of-plane and in-plane component spin polarization exist along different pathes in MV. If we tune Fermi level between −518 and −583 meV by gating or the hole doping, as labeled by black dashed line in Fig. 6(a), spin polarization is merely out of plane around K and K′ points with opposite signal in Fig. 6(b), similar with Zeeman-like splitting in previous report.²⁷

Fig. 6 The band structure with spin projected along z direction in (a) MV, (c) DV-2 and (d) DV-4 antimonene considering SOC. (b) Spin texture of the MV antimonene. Here, we assume that the Fermi level is located between −583 and −518 meV (black dashed line in (a)). Fermi pockets that resulted from Zeeman type spin splitting can clearly be seen at the K point. The red filled circles are spins pointing out of the plane and blue circles are spins pointing inward. E_F is set at zero.

In DV-2, if Fermi level is tuned to CBM (161–213 meV) by gating or electron doping, the longitudinal transport will be spin-polarized. The spin-polarized carriers flow along one direction due to the SOC, then the transverse carrier accumulation and transverse potential difference generate in anomalous Hall effect.³⁴ SOC is the essential factor that can cause the spin-Hall effect, although the magnitude of this effect might not be large. However, the theory can be proposed for such spin splitting systems and be possible to apply on the spintronic devices. Meanwhile, the symmetry can be broken by magnetic field or other magnetic impurities, and then produce the spin polarization and control the spin. Herewith, we offer a method that the vacancy can break the inversion symmetry in some layer materials, and have further influence on spin.

Conclusion

In summary, the geometric and electronic properties of monovacancy and divacancy antimonene are studied by first-principles calculations. Different vacancies can result in different geometries and electronic structures, which offer a method to control the properties of antimonene. Monovacancy antimonene show metallic character and divacancy antimonene preserve semiconductor with different band gaps, which are dependent on the distance of the two vacancies. Meanwhile, the spin–orbit interaction has a large influence to the band structure of specific defective antimonene with vacancies. The in-plane asymmetry and SOC cause the spin splitting in MV, DV-2 and DV-4. The Zeeman type splitting occurs along M–K–Γ with an out-of-plane spin polarization. The Rashba and Dresselhaus induced spin splitting appears at Γ and K in MV. These features may seem to be promising in applications on spintronic devices, such as spin filter or spin field effect transistor based on antimonene.

Acknowledgements

This work is supported by Program for New Century Excellent Talents in University, State Education Ministry of China (NCET-13-0409). It is also supported by High Performance Computing Center of Tianjin University, China.

References

1. H. Liu, A. T. Neal, Z. Zhu, X. Xu, D. Tomanek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041.
2. L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372–377.
3. S. L. Zhang, Z. Yan, Y. F. Li, Z. F. Chen and H. B. Zeng, Angew. Chem., Int. Ed., 2015, 54, 3112–3115.
4. G. X. Wang, R. Pandey and S. P. Karna, ACS Appl. Mater. Interfaces, 2015, 7, 11490.
5. O. Üzengi Aktürk, E. Aktürk and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 035450.
6. T. Lei, C. Liu, J. L. Zhao, J. M. Li, Y. P. Li, J. O. Wang, R. Wu, H. J. Qian, H. Q. Wang and K. Ibrahim, J. Appl. Phys., 2016, 119, 015302.
7. C. P. Ewels, R. H. Telling, A. A. El-Barbary, M. I. Heggie and P. R. Briddon, Phys. Rev. Lett., 2003, 91, 025505.
8. A. J. Lu and B. C. Pan, Phys. Rev. Lett., 2004, 92, 105504.
9. M. Sammalkorpi, A. Krasheninnikov, A. Kuronen, K. Nordlund and K. Kaski, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 245416.
10. O. V. Yazyev and L. Helm, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 125408.
11. B. Wang and S. T. Pantelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 165438.
12. P. Srivastava, K. P. S. S. Hembram, H. Mizuseki, K. R. Lee, S. S. Han and S. Kim, J. Phys. Chem. C, 2015, 119, 6530–6538.
13. S. Najmaei, Z. Liu, W. Zhou, X. Zou, G. Shi, S. Lei, B. I. Yakobson, J. C. Idrobo, P. M. Ajayan and J. Lou, Nat. Mater., 2013, 12, 754–759.
14. S. LaShell, B. A. McDougall and E. Jensen, Phys. Rev. Lett., 1996, 77, 3419–3422.
15. Y. M. Koroteev, G. Bihlmayer, J. E. Gayone, E. V. Chulkov, S. Blügel, P. M. Echenique and P. Hofmann, Phys. Rev. Lett., 2004, 93, 046403.
16. C. R. Ast, D. Pacilé, L. Moreschini, M. C. Falub, M. Papagno, K. Kern, M. Grioni, J. Henk, A. Ernst, S. Ostanin and P. Bruno, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 081407.
17. O. Krupin, G. Bihlmayer, K. Starke, S. Gorovikov, J. E. Prieto, K. Döbrich, S. Blügel and G. Kaindl, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 201403.
18. C. R. Ast, J. Henk, A. Ernst, L. Moreschini, M. C. Falub, D. Pacilé, P. Bruno, K. Kern and M. Grioni, Phys. Rev. Lett., 2007, 98, 186807.
19. M. Hoesch, M. Muntwiler, V. N. Petrov, M. Hengsberger, L. Patthey, M. Shi, M. Falub, T. Greber and J. Osterwalder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 241401.
20. Z. Y. Zhu, Y. C. Cheng and U. Schwingenschlögl, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 153402.
21. S. Murakami, N. Nagaosa and S. C. Zhang, Science, 2003, 301, 1348–1351.
22. S. D. Ganichev, E. L. Ivchenko, V. V. Bel’kov, S. A. Tarasenko, M. Sollinger, D. Weiss, W. Wegscheider and W. Prettl, Nature, 2002, 417, 153–156.
23. S. J. Gong, C. G. Duan, Y. Zhu, Z. Q. Zhu and J. H. Chu, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 035403.
24. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
25. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115.
26. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
27. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
28. F. Banhart, J. Kotakoski and A. V. Krasheninnikov, ACS Nano, 2011, 5, 26–41.
29. J. Gaoab, J. Zhang, H. Liu, Q. Zhang and J. Zhao, Nanoscale, 2013, 5, 9785.
30. H. A. Kramers, Proc. - Acad. Sci. Amsterdam, 1930, 33, 959.
31. H. T. Yuan, M. S. Bahramy, K. Morimoto, S. F. Wu, K. Nomura, B. J. Yang, H. Shimotani, R. Suzuki, M. L. Toh, C. Kloc, X. D. Xu, R. Arita, N. Nagaosa and Y. Iwasa, Nat. Phys., 2013, 9, 563–569.
32. K. Agnieszka and H. Thomas, Chem. Soc. Rev., 2015, 44, 2603.
33. Y. H. Park, H. Kim, J. Chang, S. H. Han, J. Eom, H. J. Choi and H. C. Koo, Appl. Phys. Lett., 2013, 103, 252407.
34. N. Nagaosa, J. Sinova, S. Onoda, A. H. MacDonald and N. P. Ong, Rev. Mod. Phys., 2010, 82, 1539.

---