Novolac-derived carbon aerogels pyrolyzed at high temperatures: experimental and theoretical studies†
Abstract
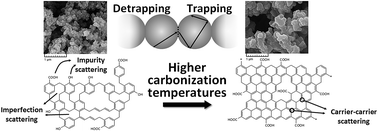
Microstructural characteristics of carbon aerogels dictate the conductance performance of these materials, as carrier transport in a porous carbon media highly depends on the carrier scattering rate. Here, we explore the influences of the carbonization temperature on the microstructural and textural characteristics of the novolac-derived carbon aerogels. A high-temperature carbonization process leads to the elimination of –OH groups from the molecular structure of the novolac-derived carbon aerogels, which in turn results in a reduction of the impurity scattering rate along the carrier transport pathway. Although, the density of the novolac-derived carbon aerogels increases with carbonization temperature, the content of micropores grows at higher temperatures, as the extent of –OH groups leaving the structure of carbon aerogels in the form of volatile gases increases at the higher pyrolysis temperatures. Moreover, the size and perfection of the nanocrystallite sites increase with carbonization temperature and hence, the imperfection scattering effect reduces at higher pyrolysis temperatures. As the carrier scattering rates decrease, the electrical conductivity and thermal conductivity of the novolac-derived carbon aerogels enhance with the pyrolysis temperature. In addition, an analytical modified series-parallel thermal conductivity model is presented here, and this model is used successfully for predicting the thermal conductivity of carbon aerogels derived from different organic precursors, and under different service conditions. No fitting parameters are involved in this model, and the only input data needed for the prediction procedure are microstructural characteristics of the carbon aerogels.

 Please wait while we load your content...
Please wait while we load your content...