A new hard phase and physical properties of Tc2C predicted from first principles
Abstract
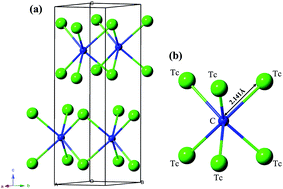
Using the first principles particle swarm optimization algorithm for crystal structural prediction, we have predicted a hexagonal P63/mmc structure of Tc2C. The new phase is mechanically and dynamically stable, as verified by its elastic constants and phonon dispersion. The formation enthalpy–pressure curves show that the predicted P63/mmc-Tc2C is more energetically favorable than the previously proposed Mo2C-, anti-MoS2-, Re2P-, and Fe2N-type structures in the considered pressure range. The calculated mechanical properties show that it is an ultra-incompressible and hard material. Meanwhile, the directional dependences of the Young's modulus, bulk modulus, and shear modulus for Tc2C are systematically investigated. The analyses of the density of states and electronic localization function reveal the presence of strong covalent bonding between Tc and C atoms, which is of crucial importance in forming a hard material.

 Please wait while we load your content...
Please wait while we load your content...