The origin of room temperature ferromagnetism mediated by Co–V_Zn complexes in the ZnO grain boundary

Abstract

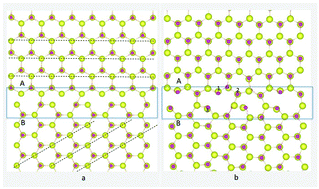
Ferromagnetism in polycrystalline ZnO doped with Co has been observed to be sustainable in recent experiments. We use first-principle calculations to show that Co impurities favorably substitute at the grain boundary (GB) rather than in the bulk. We reveal that room-temperature ferromagnetism (RTFM) at the Co-doped ZnO GB in the presence of Zn vacancies is due to ferromagnetic exchange coupling of a pair of closely associated Co atoms in the GB, with a ferromagnetic exchange coupling energy of ∼300 meV, which is in contrast to a previous study that suggested the O vacancy–Co complex induced ferromagnetism. Electronic structure analysis was used to predict the exchange coupling mechanism, showing that the hybridization of O p states with Co and Zn d states enhances the magnetic polarization originating from the GB. Our results indicate that RTFM originates from Co clusters at interfaces or in GBs.

---

I. Introduction

Dilute magnetic semiconductor (DMS) materials have both semiconducting and ferromagnetic characteristics that are favorable for magnetic moment applications, such as spintronic devices.¹ Early investigations focused on doping GaAs, but more recent experimental and theoretical studies are successfully achieving room temperature ferromagnetism (RTFM) by doping ZnO with transition metals (TMs), such as Co, Mn or Fe;^2–12 however, TM-doped ZnO is reported to also display paramagnetic behavior.¹³ The origin of RTFM in ZnO samples is proposed to be a result of the presence of TM dopants in combination with vacancies at locations of intrinsic structural defects, such as at grain boundaries (GBs).^3,11,14 Co-doped ZnO was recently reported to exhibit ferromagnetism emanating from Co clusters, indicating that these materials can be used as efficient spin filters.¹⁵ Subsequently, Co impurities in ZnO have been the subject of many experimental studies.^15–17 Co has been found to accumulate at the grain boundary of ZnO,⁹ and the accumulation of Co dopants at defective GBs has been found to stabilize RTFM of the ZnO samples.^9,11 For example, Ar annealing was shown to cause saturation magnetization in Co-doped ZnO films with grain boundary defects.³ The clustering of Co atoms alone has also been reported to induce ferromagnetism in ZnO,⁷ and the presence of excessive defect formations or phase separation has been shown to be a pre-requisite for achieving RTFM.^18–20 For example, formation of oxygen vacancy (V_O) near the GB is proposed to mediate ferromagnetism in Co-doped ZnO films.²¹ Therefore, the magnetic properties of Co-doped ZnO films are highly dependent on the experimental growth conditions: homogeneously Co-doped thin films have been reported to exhibit a spin-glass behavior and those with Co clusters have been recorded to display RTFM.²² Li et al. demonstrated that the high solubility of Co-doped ZnO resulted in RTFM at high doping concentrations.⁵ Several studies have shown that ZnO with GBs has higher Co solubility that leads to accumulation of Co atoms at the boundary, creating charge-carrier-mediated ferromagnetism.^9,15,23,24 Hence, the importance of GBs in promoting RTFM in ZnO is evident, as Co-doped ZnO is only found to be ferromagnetic if characterized by a sufficient GB density.¹¹ In a previous study, we successfully demonstrated that GBs promote the formation of point defects, and thus implicitly assist in mediating the ferromagnetism of ZnO.²⁵ However, the origin of ferromagnetism and mechanisms of exchange coupling in Co-doped ZnO GBs remains poorly understood.

To date, analytical simulations have not yet been carried out to investigate the inducing/mediating effects of the GB on the ferromagnetism of Co-doped ZnO, nor the ferromagnetic stability of the Co-doped ZnO GB and the mechanism of exchange coupling is not well understood. Here, we explore the origin of magnetism in TM-doped ZnO toward an understanding of these materials that will be applicable to the development of efficient spintronic devices. More specifically, we investigate the ferromagnetic mechanism of Co-doped ZnO GB in presence of intrinsic point defects, such as V_O and Zn vacancy (V_Zn). We focus on the structural, magnetic and electronic properties of the GB and on the possibility that Co atoms segregate in bulk-like and GB regions.

II. Computational methodology

The spin-polarized total energy calculations were carried out within the plane-wave-based density functional theory (DFT) method, as implemented in the Vienna Ab initio Simulation Package (VASP) code.^26,27 Projected augmented wave (PAW) based pseudopotentials were used with the exchange and correlations described using the Perdew–Burke–Ernzerhof (PBE) functional.²⁸ An energy cut-off of 400 eV was used to expand the plane waves included in the basis set. Due to the strong electronic correlations of d-state electrons, standard DFT cannot accurately describe the electronic structure of ZnO. To overcome this limitation, generalized gradient approximation (GGA)+U method was used with the following Hubbard parameters: U_Zn = 7, J_Zn = 1, U_Co = 3 and J_Co = 0.2, as implemented by Duradev'sapproach²⁹ in VASP.

Previous studies have reported Hubbard parameters U for Zn and Co in the 3–15 and U = 2–3 range, respectively, which ensures that the proper choice of U_eff (U–J) would yield values that are comparable with the experimental results.^30,31 Our current choice of U and the exchange parameter J values was guided by previous first-principles calculations for Co-doped ZnO, wherein these values accurately reproduced magnetic and electronic properties.³² The value of U for Zn is larger than that for Co because Zn has a deeper, more localized semi-core d¹⁰ shell.^33,34 We validated our choice of U and J by calculating the bulk–lattice parameter and comparing the results with the values obtained experimentally: the calculated bulk–lattice parameters, a₀ = b₀ = 3.32 Å and c₀ = 5.219 Å, were in reasonable agreement with the experimental findings (a₀ = b₀ = 3.286 Å; c₀ = 5.241 Å).³⁵ We used these optimized parameters for the GB supercell, such that a = 7 × a₀, b = √3 × 3 × b₀ and c = c₀, ensuring negligible interaction between the periodically repeated GB images. The Brillouin zone was sampled using a 1 × 1 × 6 Monkhorst–Pack k-point mesh. The ZnO supercell was optimized with energy and force tolerances of 0.001 eV and 0.001 eV Å⁻¹, respectively.

III. Results and discussion

We investigated the origin of magnetic polarization of ZnO that results when Co accumulates in the ZnO GB and the interaction between these Co dopants and other point defects. In polycrystalline materials, GBs have very different properties from the bulk. Since the co-ordination number of atoms in the GB differs from that of those in the bulk, over- or under-coordination of atoms and dangling bonds may appear in the GB, which can facilitate native defect formations and dopant segregations. As a result, diversity in atomic planes and angles within GBs cause them to have different structural, magnetic and electronic properties compared to the bulk. The properties of each GB depend on their unique orientation within the planes and the translation state of the two adjacent grains.^36,37 Previous experimental studies have evidenced that GBs formed at high or low angles have different characteristics.³⁸ Moreover, tilt angles in ZnO GBs can range from 0° to 60° due to the symmetry. However, for small angles (0° to 30°), the structural units comprising the GB will be straight, whereas the angle will be larger (30° to 60°) with zig-zag-ring patterns.³⁹ Atomic ring patterns are a common feature of both low- and high-angle GBs, causing them to have an amorphous shape with atoms possessing dangling bonds. Thus, any theoretical representation of a typical GB should include atomic ring patterns. For this reason, we focus on a GB generated in the wurtzite [0001] direction. The supercell consists of two grains, denoted as A and B in Fig. 1. The GB is created by rotating the ZnO crystal lattice of the lower part (B crystal in Fig. 1) by 45° in the a–b plane, which ensures that the boundary between the perfect part (A) and the rotated part (B) of the crystal will be amorphous, mimicking the experimentally observed GB.³⁹ This structure will give rise to periodically repeating atomic rings comprising 8- and 10-atom members. The supercell used to create the GB comprises 296 atoms (Zn₁₄₈O₁₄₈) because this structural set reduces the number of atomic sites entering the calculation to a necessary minimum. Hence, choice of tilt angle is determined by the inherent symmetry of the wurtzite crystal structure.

Fig. 1 The structure of a ZnO GB (a) before and (b) after optimization. The three Co doping locations are shown in Fig. 2(b). The yellow and pink spheres indicate Zn and O atoms, respectively. A and B denote the two single crystals of ZnO used to create the GB. The rectangle indicates the amorphous shape of the GB. The atomic ring patterns formed after relaxation can be observed in (b). Dashed lines are given to guide the eye.

The initial structure of a ZnO GB presented in Fig. 1(a) shows that the optimized supercell is well bonded at the GB (Fig. 1(b)) with no inter-granular structures. The structural units that form the GB are 8- and 10-membered atomic rings, compared to the six-fold coordinated open channel in the bulk ZnO. The Zn and O atoms in the atomic rings of the GBs are 4- and 3-fold coordinated in contrast to the bulk ZnO characterized by only 4-fold coordination. This ring pattern repeats, evidencing the periodic nature of the atomic arrangements in the GB. After optimization, the Zn–O bond lengths changed by about ∼0.05 Å in the 8- and 10-membered rings compared to those measured in the bulk. Thus, arrangement of these periodic units along the GB effectively minimizes the strain within. We introduced Co atoms to the Zn sites at the GB, such that one Co atom constituted a doping concentration of 0.33%. The location of Co dopants substituted at Zn sites is depicted in Fig. 1(b). The formation energy (E^f) of Co atoms is calculated using the following expression:

E^f = E(ZnO : Co) − E(ZnO) + nμ(Zn) − mμ(Co), (1)

where the first and second terms in the equation respectively indicate the total energy of GB containing a Co atom and pure GB with no added defects. The letters n and m denote the number of Zn atoms removed and Co atoms added to the supercell, respectively. The total energy of metallic Zn and Co is assumed to be equal to their chemical potentials as both atoms was considered to be divalent (no additional charge), which are represented by μ.

We considered three different locations for Co atoms, representing three different bonding arrangements in the GB (Fig. 1(b)); the corresponding E^f is shown in Table 1. We observed the greatest stability of Co impurities in the ZnO GB (lower E^f) located in position (3) (see Fig. 1(b)) because of the reduced coordination numbers at this neck site, which facilitates the easy breaking of bonds. However, no significant differences between the formation energies of all three positions, indicating that Co atoms are relatively stable due to the comparable bonding arrangements of cationic sites in the GB, irrespective of spatial location. We also introduced Co into the bulk-like region and obtained a higher formation energy, signifying that Co favorably accumulates at the GB. This finding confirms that the miscibility of Co dopants is higher in the GB of ZnO.⁹ Therefore, the presence of Co dopants in the GB is analogous to the occurrence of Co atoms clustering near the interfaces in ZnO.^12,15,19

Table 1 The formation energy (E^f; in eV) of Co with and without vacancies at GB and bulk-like regions. The E^f of V_O and V_Zn at the grain boundary without Co impurities is shown for comparison [from ref. 25]

Configuration	E^f (eV)
Co-1	−5.22
Co-2	−5.18
Co-3	−5.35
Co–VO	−1.01
Co–VZn	−2.58
VO	4.1 (ref. 25)
VZn	3.8 (ref. 25)
Co-in-bulk	−4.43

---

Table 2 shows that calculations of the formation energy as a function of separation distance (D) confirmed that Co atoms tend to aggregate in GB. The results shown in Table 2 reveal that the lowest formation energy value, E^f = −11 eV, is obtained for a pair of Co atoms with the smallest separation (D = 2.54 Å). As the distance between atoms increases (D > 2.54 Å), the formation energy increases slightly, suggesting a preference of Co atoms to remain in nearest-neighbor locations in the GB. The larger size of Co atoms compared to Zn atoms may induce local strain that attracts other Co atoms to nearby sites. A similar observation has been made for Pr-doped ZnO GBs.⁴⁰

Table 2 The formation energy (E^f; in eV) of Co atoms at various distances of separation (D; in Å) at the GB

D (Å)	E^f (eV)
2.54	−11.22
3.2	−10.97
3.31	−10.74
6.96	−10.69
10.14	−10.71

---

The magnetic moment of Co is mostly self-confined and no polarization is induced to nearby atoms as shown in Fig. 2(a). The iso-surfaces of the spin-polarized electron density (Δρ = ρ↑ − ρ↓) of the ZnO GB containing a Co atom are shown in Fig. 2(a). Note that while the Co atom is seen to magnetize the nearby atoms, the polarization is confined. Therefore, it is necessary to investigate the effect of the presence of point defects on inducing the ferromagnetism of Co-doped ZnO near the GB observed in previous studies.^9,11 In an earlier study, we showed that a V_Zn is more favorable than V_O in an undoped ZnO GB. Moreover, V_Zn preferably accumulated at the GB rather than in the bulk-like region. These findings imply that the presence of vacancies at the GB may facilitate the formation of vacancy–dopant complexes. Table 1 presents the V_O and V_Zn at GB and their respective formation energies with and without Co. These data allow us to investigate how point defects enhance magnetic properties.

Fig. 2 The spin density iso-surface plot (ρ = 1 × 10⁻³ e a.u.⁻³) for a ZnO GB in the presence of (a) a Co atom or (b) Co–V_Zn. The most stable configuration with the lowest formation energy for an atom of Co is presented. The pink, silver and green spheres indicate Zn, O and Co atoms, respectively, while yellow and blue indicate positive and negative iso-surfaces.

The introduction of V_O to the otherwise undoped ZnO GB failed to produce any spin-polarization in the system, while V_Zn at these GB induced strong magnetic moments in neighboring O atoms, extending to second and third neighbors; Zn atoms remained unpolarized. The under-coordinated O atoms created by the induction of V_Zn are easily polarized, and due to the peculiar atomic arrangements at the GB, the magnetic moments are distributed asymmetrically at the boundary. Hence, near V_Zn, O atoms have a local magnetic moment between 0.3 and 0.68 μ_B per atom.²⁵

Note that the formation energy of vacancies decreases in the presence of Co impurities at the GB (Table 1), indicating that the presence of vacancy–impurity complexes is preferred energetically and can lead to interesting magnetic and electronic properties.²⁵ The presence of V_Zn in the vicinity of Co atoms promotes sustainable magnetism at the GB, and the hybridization effects generated by the presence of vacancy–dopant Co complexes increases polarization. Fig. 2(b) shows that the presence of a V_Zn in the neighborhood increases the magnitude of spin-polarization in the GB, such that it also extends to its next-to-nearest neighbors as well. Thus, the presence of a cation vacancy–Co complex in the GB can induce magnetic polarization that can be further enhanced by the formation of metal clusters and the simultaneous occurrence of vacancies. In contrast to a previous work, we found that O vacancies do not contribute to ferromagnetism at the ZnO GB.²¹

The total density of state (TDOS) of the ZnO GB with a Co atom and the projected density of states (PDOSs) of Co, O and Zn are shown in Fig. 3–5. To explore the possible mechanisms contributing to magnetization, the density of states (DOSs) at the GB was calculated for three scenarios: a Co atom without point defects (Fig. 3), a Co atom in presence of an V_O (Fig. 4) and a Co atom in presence of a V_Zn (Fig. 5). The Co atoms that substituted Zn sites possessed a d⁷ valence configuration, and because of, tetrahedral crystal-field splitting, Co-3d states became separated, as shown in Fig. 3(b). As a result, unfilled minority states form in the conduction band (CB) to produce an effective magnetic moment of 3 μ_B per Co atom. Fig. 3 also shows that the DOSs at the Fermi level (E_F) is zero, indicating the absence of carriers that could mediate the exchange interactions. Since magnetic exchange primarily depends on the states at the valence band maximum (VBM), if the E_F remains at the VBM, this signifies that the hole density is insufficient to initiate magnetic exchange interactions.⁴¹ Therefore, isolated Co impurities at the GB can only induce weak magnetic polarization. In addition, Fig. 4(b) and (c) show that in presence of V_O, hybridization between O p and Co d bands occurs far from E_F. Therefore, the presence of V_O does not contribute to achieving RTFM as the E_F moves toward the CB minimum (CBM), while the minority Co 3d states shift further down, away from the CBM. When V_Zn is present in the GBs, hole carriers are available and E_F falls just below the VBM, increasing the DOS near the E_F as shown in Fig. 5. Consequently, the Co d states can effectively hybridize with the O p states and the Zn d states as shown in Fig. 5(b)–(d), respectively. Therefore, the minority-spin of O p and Co d states shift and overlap at E_F, leading to strong magnetic exchange. The majority of the Co d states are almost filled, and the minority states are half-filled. The minority Zn d states occur within the same energy interval, increasing the rate of hybridization with Co 3d and O p orbitals. The availability of empty minority levels of Co 3d at the CBM and the subsequent hybridization stabilize magnetic polarization at the GB. These findings suggest that magnetism originates from the combined effect of Co–V_Zn complexes in the GB of ZnO samples.^9,11

Fig. 3 (a) The TDOS of the ZnO GB with a Co atom, and the PDOSs of (b) Co, (c) O and (d) Zn.

Fig. 4 (a) The TDOS of a ZnO GB with a Co atom in the presence of V_O, and the corresponding PDOSs of (b) Co, (c) O and (d) Zn.

Fig. 5 (a) TDOS of a ZnO GB with a Co atom in the presence of V_Zn and the corresponding PDOSs of (b) Co, (c) O and (d) Zn.

Similar to previous works,^4,32,42 we used the standard DFT approach to examine the magnetic coupling between two Co atoms in different magnetic states. The exchange coupling parameter for the ferromagnetic (FM) and antiferromagnetic (AFM) configurations is defined as ΔE = E_FM − E_AFM for a pair of Co atoms, whereby a positive value of ΔE indicates preference for FM coupling and a negative value indicates a preference for AFM coupling. We found that nearest-neighbor Co atoms attain parallel magnetic moments: the sum of the local magnetic moments of the atoms corresponds to the total magnetic moment. Prominent positive magnetic moments can also be observed from the spin density iso-surface plots presented in Fig. 2(a) and (b). For a Co–Co distance of 2.54 Å, ΔE is measured at 236 meV, signifying strong ferromagnetic coupling at the GB in presence of closely separated Co atoms. Furthermore, the presence of V_Zn with Co atoms increases the value of ΔE to 300 meV, indicating that magnetic coupling can be sustained at room temperature, despite thermal fluctuations. (A minimum value of ΔE > 30 meV is necessary to establish ferromagnetic coupling at room temperature⁴³). Although the magnetic polarization does not extend to the entire ZnO matrix and is limited to the O sites that are in close proximity to dopant Co atoms, the higher value of magnetic exchange indicates the possibility of strong ferromagnetic coupling at the GB at room temperature. However, since the formation energy calculations show that clustering of Co atoms could occur at higher concentrations, the magnetic interactions emanating from the GB may be short-ranged.

IV. Conclusions

In summary, we have shown that the Co atoms prefer to accumulate at the grain boundaries rather than in the bulk-like region. Moreover, closely spaced Co atoms are characterized by a large ferromagnetic exchange coupling energy. We also demonstrated that native point defects are stable at the grain boundary in the presence of Co impurities and that V_Zn enhance magnetic polarization by inducing hole carriers. In presence of the Co–V_Zn complex, the p orbitals of O hybridize with the d orbitals of Zn and Co, increasing the magnetic polarization at the grain boundary; however, because the Co atoms prefer to aggregate at the GB, the magnetic polarization emanating from them is most likely short ranged.

Acknowledgements

The research reported in this publication was supported by funding from King Abdullah University of Science and Technology (KAUST).

References

1. T. Dietl and H. Ohno, Rev. Mod. Phys., 2014, 86, 187–251.
2. G. S. Chang, E. Z. Kurmaev, D. W. Boukhvalov, L. D. Finkelstein, S. Colis, T. M. Pedersen, A. Moewes and A. Dinia, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 195215.
3. H. S. Hsu, J. C. A. Huang, S. F. Chen and C. P. Liu, Appl. Phys. Lett., 2007, 90, 102506,  DOI:10.1063/1.2711763.
4. D. Karmakar, T. V. C. Rao, J. V. Yakhmi, A. Yaresko, V. N. Antonov, R. M. Kadam, S. K. Mandal, R. Adhikari, A. K. Das, T. K. Nath, N. Ganguli, I. Dasgupta and G. P. Das, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 184421.
5. L. Li, Y. Guo, X. Y. Cui, R. Zheng, K. Ohtani, C. Kong, A. V. Ceguerra, M. P. Moody, J. D. Ye, H. H. Tan, C. Jagadish, H. Liu, C. Stampfl, H. Ohno, S. P. Ringer and F. Matsukura, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 174430.
6. A. Ney, A. Kovács, V. Ney, S. Ye, K. Ollefs, T. Kammermeier, F. Wilhelm, A. Rogalev and R. E. Dunin-Borkowski, New J. Phys., 2011, 13, 103001.
7. J. H. Park, M. G. Kim, H. M. Jang, S. Ryu and Y. M. Kim, Appl. Phys. Lett., 2004, 84, 1338–1340.
8. H. Wei, T. Yao, Z. Pan, C. Mai, Z. Sun, Z. Wu, F. Hu, Y. Jiang and W. Yan, J. Appl. Phys., 2009, 105, 043903.
9. B. B. Straumal, A. A. Mazilkin, S. G. Protasova, A. A. Myatiev, P. B. Straumal and B. Baretzky, Acta Mater., 2008, 56, 6246–6256.
10. B. B. Straumal, A. A. Mazilkin, S. G. Protasova, A. A. Myatiev, P. B. Straumal, G. Schütz, P. A. van Aken, E. Goering and B. Baretzky, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205206.
11. B. B. Straumal, A. A. Mazilkin, S. G. Protasova, P. B. Straumal, A. A. Myatiev, G. Schütz, E. J. Goering, T. Tietze and B. Baretzky, Philos. Mag., 2012, 93, 1371–1383.
12. Z. Sun, W. Yan, G. Zhang, H. Oyanagi, Z. Wu, Q. Liu, W. Wu, T. Shi, Z. Pan, P. Xu and S. Wei, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 245208.
13. A. Barla, G. Schmerber, E. Beaurepaire, A. Dinia, H. Bieber, S. Colis, F. Scheurer, J. P. Kappler, P. Imperia, F. Nolting, F. Wilhelm, A. Rogalev, D. Müller and J. J. Grob, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125201.
14. M. N. Lin, H. S. Hsu, J. Y. Lai, M. C. Guo, C. Y. Lin, G. Y. Li, F. Y. Chen, J. J. Huang, S. F. Chen, C. P. Liu and J. C. A. Huang, Appl. Phys. Lett., 2011, 98, 212509,  DOI:10.1063/1.3593384.
15. M. Hamieh, N. Jedrecy, C. Hebert, D. Demaille and J. Perriere, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 155302.
16. M. Bibes, J. E. Villegas and A. Barthélémy, Adv. Phys., 2011, 60, 5–84.
17. O. Matthias, J. Phys. D: Appl. Phys., 2012, 45, 033001.
18. A. Ney, M. Opel, T. C. Kaspar, V. Ney, S. Ye, K. Ollefs, T. Kammermeier, S. Bauer, K.-W. Nielsen, S. T. B. Goennenwein, M. H. Engelhard, S. Zhou, K. Potzger, J. Simon, W. Mader, S. M. Heald, J. C. Cezar, F. Wilhelm, A. Rogalev, R. Gross and S. A. Chambers, New J. Phys., 2010, 12, 013020.
19. Y. Fukuma, H. Asada, J. Yamamoto, F. Odawara and T. Koyanagi, Appl. Phys. Lett., 2008, 93, 142510.
20. M. Venkatesan, P. Stamenov, L. S. Dorneles, R. D. Gunning, B. Bernoux and J. M. D. Coey, Appl. Phys. Lett., 2007, 90, 242508.
21. X. J. Liu, X. Y. Zhu, J. T. Luo, F. Zeng and F. Pan, J. Alloys Compd., 2009, 482, 224–228.
22. J. H. Kim, H. Kim, D. Kim, Y. E. Ihm and W. K. Choo, J. Appl. Phys., 2002, 92, 6066–6071.
23. K. R. Kittilstved, D. A. Schwartz, A. C. Tuan, S. M. Heald, S. A. Chambers and D. R. Gamelin, Phys. Rev. Lett., 2006, 97, 037203.
24. P. Sati, R. Hayn, R. Kuzian, S. Régnier, S. Schäfer, A. Stepanov, C. Morhain, C. Deparis, M. Laügt, M. Goiran and Z. Golacki, Phys. Rev. Lett., 2006, 96, 017203.
25. S. D. Assa Aravindh, U. Schwingenschloegl and I. S. Roqan, J. Chem. Phys., 2015, 143, 224703.
26. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
27. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
29. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
30. W. A. Adeagbo, G. Fischer, A. Ernst and W. Hergert, J. Phys.: Condens. Matter, 2010, 22, 436002.
31. P. Palacios, I. Aguilera and P. Wahnón, Thin Solid Films, 2010, 518, 4568–4571.
32. S. Ghosh, Q. Wang, G. P. Das and P. Jena, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 235215.
33. S. Lany, H. Raebiger and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 241201.
34. S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035215.
35. Ü. Özgür, Y. I. Alivov, C. Liu, A. Teke, M. A. Reshchikov, S. Doğan, V. Avrutin, S.-J. Cho and H. Morkoç, J. Appl. Phys., 2005, 98, 041301.
36. Y. Sato, T. Mizoguchi, F. Oba, M. Yodogawa, T. Yamamoto and Y. Ikuhara, J. Mater. Sci., 2005, 40, 3059–3066.
37. Y. Sato, T. Mizoguchi, F. Oba, Y. Ikuhara and T. Yamamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 064109.
38. H. Kaga, Y. Kinemuchi, H. Yilmaz, K. Watari, H. Nakano, H. Nakano, S. Tanaka, A. Makiya, Z. Kato and K. Uematsu, Acta Mater., 2007, 55, 4753–4757.
39. J.-Y. Roh, Y. Sato and Y. Ikuhara, J. Am. Ceram. Soc., 2014, 97, 617–621.
40. J.-Y. Roh, Y. Sato and Y. Ikuhara, J. Am. Ceram. Soc., 2015, 98, 1932–1936.
41. H. Peng, H. J. Xiang, S.-H. Wei, S.-S. Li, J.-B. Xia and J. Li, Phys. Rev. Lett., 2009, 102, 017201.
42. Q. Wang, Q. Sun, P. Jena and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115407.
43. P. Gopal and N. A. Spaldin, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 094418.

---