Detailed theoretical investigation on ESIPT process of pigment yellow 101
Abstract
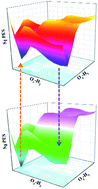
Based on density functional theory (DFT) and time-dependent density functional theory (TDDFT) methods, the detailed excited state intramolecular proton transfer (ESIPT) mechanism of 2,2′-dihydroxy-1,1′-naphthalazine (P.Y. 101) has been investigated theoretically. Unlike previous theoretical investigation of P.Y. 101, our calculated results not only reproduce the absorption and fluorescence spectra reported in the previous experiment, but also were completed with considering solvent effect. It further demonstrates that the TDDFT theory we adopted is very reasonable and effective. The calculations of main bond lengths and bond angles involving in the hydrogen bondings (O1–H2⋯N3 and O4–H5⋯N6) as well as the infrared vibrational spectra and as well as the calculated hydrogen bonding energies demonstrated the intramolecular hydrogen bond was strengthened in the S1 state. In addition, qualitative and quantitative intramolecular charge transfer based on the frontier molecular orbitals provided the possibility of the ESIPT reaction. The potential energy surfaces of ground state and the first excited state have been constructed to illustrate the ESIPT mechanism. Based on our calculations, the equilibrium ESIPT process exists in the S1 state. And after the radiative transition, reversed GSIPT can also occur in the S0 state.

 Please wait while we load your content...
Please wait while we load your content...