Facile fabrication of core/shell structured SiO₂/polypyrrole nanoparticles with surface modification and their electrorheology

Abstract

We synthesized conductive polypyrrole (PPy) coated silica core–shell structured nanoparticles, and investigated their electrorheological (ER) characteristics under electric fields applied when dispersed in silicone oil. Silica nanoparticle surfaces were initially modified using 3-(trimethoxysilyl)propyl methacrylate as a modifying agent to enhance the chemical affinity for more stable core–shell particle formation with PPy shells. Scanning electron microscopy and transmission electron microscopy images provided evidence of the structure and morphology of the fabricated particles. ER behavior of the obtained particles dispersed in an insulating silicone oil were observed via a controlled shear rate test using a rotational rheometer, while fibrillation of the ER fluid was observed using optical microscopy. The resulting responses show that the fluid composed of silica/PPy nanoparticles exhibits typical ER fluid behavior under an applied electric field. A CCJ model was used to explain the flow curves for overall shear rate range along with dielectric spectral measurements.

---

1. Introduction

Many intelligent and smart materials with diverse rheological and mechanical properties can be manipulated with external stimuli such as electric or magnetic fields. Such materials have various technological applications in dampening, drug delivery, microfluidics and robotics.^1–3 In particular, electrorheological (ER) fluids are important smart materials due to their phase changes between liquid-like and solid-like states using an applied external electric field.^4–9 ER fluids are in general composed of electro-responsive polarizable or semiconducting particles dispersed in an insulating oil. In the absence of an applied electric field, the dispersed electro-responsive ER particles are freely and randomly distributed, exhibiting Newtonian fluid-like behavior with relatively low particle concentrations. In contrast, the dispersed particles form fibril-like chain structures and the ER fluid demonstrates Bingham fluid-like characteristics with yield stress. As a result, their rheological properties such as shear viscosity, yield stress and dynamic moduli are being changed rapidly in this process^10–12 due to chain formation of the polarized particles having dipole moments generated by an electric field.¹³ ER fluids are similar to magnetorheological (MR) fluids which are controlled by a magnetic field, but applications of ER fluids are more limited than MR fluids mainly because of their lower yield stress than MR fluids (except in the case of giant ER fluids).^14,15 Thus, research on finding suitable ER materials for more robust applications remains an ongoing task.

Among suitable smart and intelligent ER materials, conducting polymers such as polyaniline,¹⁶ polypyrrole (PPy),¹⁷ polyphenylenediamine,¹⁸ polythiophene,¹⁹ and composites composed of polymer-inorganic particles including SiO₂, TiO₂, BaTiO₂ and graphene oxide have been widely investigated.^20–23 Related, core–shell structured composites combine the insulating effects of their core particles and the electrical properties of their conducting shells with optimal interfacial polarization and suitable conductivity. Therefore, electro-responsive particles with core–shell structures have enhanced ER effects, improved dispersibility, thermal stability, and rapid electro-response.^16,24,25 The core/shell designed particles have been introduced in a wide range of sections including rheology control²⁶ and biomedical application.²⁷ The core/shell structure is also deemed as an appropriate candidate for ER particles, especially for the polymer/polymer^28–30 and inorganic/polymer particles.^31,32

Using silica particles to synthesize conducting core/shell structures have advantages not found in polymeric core particles such as polystyrene spheres, such as synthetic simplicity.³³ Likewise, PPy is considered one of the most useful conductive polymers due to its excellent conductivity and fine environment stability, as well as its available electronic and photonic states.^34–36 However, it is difficult to encase single particles to effectively form core/shell structures with PPy without the use of a grafting agent. As such, improving the surface properties of the core is necessary. Previous research has sought to improve the surface properties of silica particles; for example, Hao et al.³⁷ used polyvinylpropylene to synthesize more stable core/shell particles by modifying the silica surface. Among the available modifying agents, 3-(trimethoxysilyl)propyl methacrylate (MPS) forms a chemical bond between core and shell. Therefore, using MPS yields more stable structures,³⁸ which are better suited for ER applications. It can be also noted that while silica/PPy nanocomposite particles in either core–shell type or bulk hybrid type have been seldom applied as for the ER materials compared to core–shell typed silica/polyaniline nanoparticles,^39–41 various mesoporous silica associated PPy nanocomposite particle based ER fluids have been mainly introduced.^42,43 Compared to previously reported irregular shapes of the PPy/silica composites, the core–shell structured particles could be considered as a model system for their ER study.

In this study, a facile and improved method was introduced to synthesize PPy-coated monodisperse SiO₂ core/shell structured particles. Silica nanoparticles were modified by MPS and a conducting PPy shell was then synthesized on the modified silica surface via oxidative polymerization with FeCl₃ as the oxidant. The ER properties of the resulting silica/PPy core/shell particles were then examined. The SiO₂/PPy ER particles had a lower particle density and a higher ER performance compared to pure SiO₂.⁴⁴ Owing to the PPy shell, the SiO₂/PPy particles respond to external electric field and exhibit similar ER behavior to pure PPy based ER fluid.^45,46

2. Experimental

2.1 Materials

Silica particles with a mean particle size of approximately 500 nm (Alfa Aesar) were used. Pyrrole (Sigma-Aldrich), 3-(trimethoxysilyl)propyl methacrylate (MPS) (Sigma-Aldrich), iron(III)chloride (FeCl₃, Sigma-Aldrich), and HCl (35%, DC Chemical Korea) were used as received without further purification. Ethanol and de-ionized (DI) water were used in all experimental procedures and washing.

2.2 Preparation of surface modified SiO₂ particles

Before the preparation process, 5 g of silica particles was dispersed in hydrochloric acid (1 M, 200 mL) and stirred for 24 h at 25 °C, then washed with deionized water and completely dried under vacuum for 12 h at 60 °C.⁴⁷ 1 g of the acid-treated silica was dispersed in 30 mL ethanol by sonication for 15 min. This solution and 20 mL of ethanol containing 4 mL MPS (modifying agent) were mixed by magnetic stirring for 24 h at room temperature, and then separated by centrifugation, washed with ethanol and water several times, and dried completely at 60 °C for 24 h under vacuum.

2.3 Synthesis of SiO₂/PPy core–shell nanoparticles

1 g of modified silica was dispersed in 75 mL ethanol 0.5 mL of pyrrole (as monomer) was added to this solution and sonicated for 30 min. The polymerization was initiated by adding 75 mL of an aqueous solution containing 4.5 g FeCl₃, and the reaction mixture was mixed for 12 h at room temperature by stirring to fabricate uniform SiO₂/PPy core/shell particles. It can be noted that when the reaction temperature increases, the conductivity of PPy is known to be decreased.⁴⁸ The resulting SiO₂/PPy composite particles were separated by centrifugation at 5000 rpm for 30 min and filtered with distilled water to remove residual monomer and oligomer. To be used as an ER material, the SiO₂/PPy particles were controlled by a dedoping process where 1 M NaOH was added to the particle suspension until the pH value reached 10. The conductivity of the particles decreased from 10⁻³ S cm⁻¹ to 10⁻⁸ S cm⁻¹. The dedoped particles were dried completely at 60 °C under vacuum condition for 24 h after being washed with DI water.

2.4 Preparation of ER fluid

The obtained SiO₂/PPy powder was sieved prior to use. For the ER fluid, 10 vol% of the fabricated particles was prepared by dispersing powder in silicone oil (dynamic viscosity = 100 cS), and agitating to obtain better dispersion.

2.5 Characterization

The morphologies and sizes of the synthesized particles were investigated by scanning electron microscopy (SEM, S-4300, Hitachi, Japan) and transmission electron microscopy (TEM, CM-220, Phillips, Holland). Infrared spectra of the products were measured using KBr pellets on a Fourier transform infrared spectrometer (FT-IR, Bruker VERTEX 80V) to determine the chemical structures present. Thermal properties of the samples were analyzed using thermal gravimetric analysis (TGA, TA instrument Q50, USA). All samples were placed in a pan and heated from 30 to 900 °C at a heating rate of 10 °C min⁻¹ under N₂. The density of the obtained particles was detected using a pycnometer (Accupyc 1330, Gas pycnometer, USA). After dedoping, the electric conductivity of the SiO₂/PPy particles in the disk-shaped pellet was tested using a 4-pin probe resistivity meter (LORESTA-GP). Fibrillation ER phenomena under an electric field were directly observed by optical microscopy (Olympus BX51, USA) using a direct-current (DC) high voltage generator. The ER behavior of the SiO₂/PPy particle-based ER fluid was investigated using a rotational rheometer (MCR 300, Anton Paar, Germany) equipped with a Couette-type geometry (CC17) and a high DC voltage generator. The dielectric properties of the ER suspension were measured by a LCR meter (Agilent HP 4284A) with a liquid cell.

3. Results and discussion

Scheme 1 outlines the entire preparation of the electro-responsive particles. The silane coupling agent MPS reacts with –OH groups of the silica surface, transforming the silica surface from hydrophilic to hydrophobic. Then, hydrophobic pyrrole monomer forms a more stable shell on the modified silica surface by hydrophobic adsorption.

Scheme 1 Schematic representation of the entire experimental mechanism for synthesize of SiO₂/PPy particles.

Fig. 1 presents SEM images of both pure silica particles used as the core and SiO₂/PPy core/shell particles synthesized using MPS. As shown in Fig. 1(a), silica particles have a smooth surface and good monodispersity with a mean diameter of 500 nm. After coating with a PPy shell (Fig. 1(b)), the SiO₂/PPy core/shell particles possess spherical shapes and remain monodisperse. The average size of SiO₂/PPy particles is approximately 680 nm, 180 nm larger than the unmodified silica particles, indicating that the thickness of the PPy shell is about 90 nm and that the PPy deposits onto the modified silica particles as a shell. The surface of the SiO₂/PPy particles is also coarser than that of the pure silica particles. Hence, this demonstrable difference in particle size and surface morphology indicates the successful synthesis of SiO₂/PPy core/shell particles.

Fig. 1 SEM images of pure SiO₂ (a), SiO₂/PPy core/shell particles (b).

The core/shell structure and shell morphology are more evident in TEM imaging, as shown in Fig. 2. After coating the SiO₂ core with PPy, Fig. 2(b) shows a coarse and dense PPy shell formed around the modified SiO₂ surface, with a mean thickness of approximately 90 nm (Fig. 2(c)). In addition, it can be also seen that the density of SiO₂/PPy core/shell particles becomes lower because of the lower density of PPy shell (ρ_Silica = 2.05 g cm⁻³, ρ_PPy = 1.66 g cm⁻³, ρ_Si/PPy = 1.98 g cm⁻³).

Fig. 2 TEM images of pure SiO₂ (a), core/shell structured particles of SiO₂/PPy (b), high-magnification image of SiO₂/PPy (c).

FT-IR spectra were collected to determine the functional groups of SiO₂, PPy, SiO₂/PPy particles, as shown in Fig. 3. The IR spectrum of the pure SiO₂ particles showed typical peaks, including absorption bands at 472 cm⁻¹ and 1107 cm⁻¹ corresponding to the Si–O–Si symmetric and asymmetric vibrations of SiO₂, respectively. Typical PPy peaks are present in the IR spectra of both pure PPy and SiO₂/PPy particles. The peaks at 1558 cm⁻¹ originate from the pyrrole ring essential vibration. In addition, the peaks at 1475 cm⁻¹ and 1188 cm⁻¹ are clearly present, which are attributed to the conjugated C–N stretching vibration and the =C–H in-plane vibration, respectively. The characteristic band of PPy at 1049 cm⁻¹ is covered by the SiO₂ peak at 1107 cm⁻¹.

Fig. 3 FT –IR spectra of pure SiO₂ ((a)-black), SiO₂/PPy core/shell particles ((b)-red), PPy ((c)-blue).

Fig. 4 shows TGA data of SiO₂ (black line), SiO₂-PPy particles (red line) and PPy (blue line) heated from 30 °C to 900 °C with a heating rate of 10 °C min⁻¹ (under N₂). The initial weigh loss at temperatures <100 °C was from the adsorbed moisture in the particles. In Fig. 4(a), there was minor SiO₂ weight loss because of its thermal stability. In Fig. 4(b) and (c), a clear decline in mass occurred at 200 °C, due to thermal degradation of the PPy chains. Although the weight loss occurs at a similar temperature, the SiO₂/PPy nanoparticles have a higher thermal stability than the pure PPy, showing lowered thermal decomposition according to the mild downtrend of the mass loss in its TGA curve. The residue percentages of SiO₂/PPy and PPy at 900 °C in N₂ were 76% and 46%, showing that PPy is carbonized to form graphitic structures and cannot be entirely decomposed under N₂.⁴⁹

Fig. 4 TGA curves of pure SiO₂ (a), SiO₂-PPy (b) and PPy (c).

ER materials must possess a suitable electrical conductivity in the range of 10⁻⁸ to 10⁻¹⁰ S cm⁻¹; the electric conductivity of our SiO₂/PPy core/shell particles was 2.3 × 10⁻⁸ S cm⁻¹, which is appropriate for use as an ER material. The SiO₂/PPy particle-based ER fluid was made by dispersing core/shell particles in 100 cS silicone oil. Changes in microstructure were shown by optical microscopy using a DC high voltage supply (E = 2 kV mm⁻¹) as given in Fig. 5, in which the SiO₂/PPy particle-based ER fluid was dropped into the gap between two electrodes for testing. Compared to the liquid-like behavior shown in Fig. 5(a) with no electric field, the SiO₂/PPy particles began to migrate and form fibril-like structures due to interfacial polarization within the SiO₂/PPy particles under an electric field (Fig. 5(b)). The fibril-like structures maintain their shape as long as the electric field is present.

Fig. 5 Optical microscopy images of SiO₂/PPy core/shell particle-based ER fluid without electric field (a) and with electric field (b) (2 kV mm⁻¹).

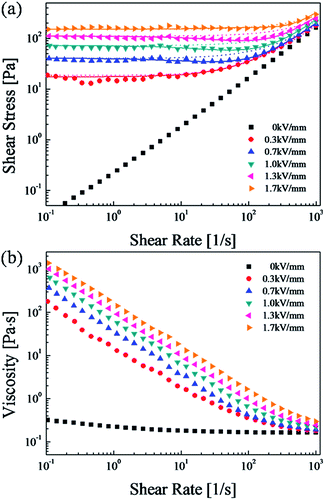
Moreover, ER characterizations were carried out using a rotational rheometer under conventional controlled shear rate (CSR) conditions, in which the shear rates were varied from 0.1 to 1000 s⁻¹ as a function of electric field from 0 to 1.7 kV mm⁻¹. With each shear rate sweep, we measured the measuring point's duration to 10 s during the initial step, and the final measurement step was set to 2 s in a log–log scale. When the electric field is zero, the ER fluid behaves like a Newtonian fluid, and the slope of shear stress to shear rate is nearly 1. When applying an electric field, the ER fluid shows non-Newtonian behavior with increased shear stress. When the intensity of the electric field strength is increased, the shear stress increases for the entire region of shear rate and in an elongated plateau area. These results can be explained by the resistance of the electrostatic force to the hydrodynamic force gradually increasing. As a common model for an ER fluid, the Bingham fluid model^50,51 is given in eqn (1).

This simple Bingham model has two parameters, the Newtonian viscosity η, and yield stress, τ_y, which represent a fit for the Bingham model over the entire shear rate region.

To better fit the ER fluid, especially in low shear rate regions, the Cho-Choi-Jhon (CCJ) model^52,53 with six parameters, is expressed as follows:

Here, η_∞ is the shear viscosity at an infinite shear rate and represents the shear viscosity in the absence of an electric field.

The t₂ and t₃ are time constants, the exponent α is associated with the reduction of shear stress in low shear rate areas, and the exponent β (0 < β ≤ 1, due to dτ/dγ ≥ 0) corresponds to high shear rate areas.⁵¹ The fitting for the flow curve of the SiO₂/PPy-based ER suspensions is shown in Fig. 6(a), and its physical meanings can be described with eqn (2). The first part in eqn (2) is suggested by the flow behavior in the low shear rate region, where the stress remains constant or decreases as a function of shear rate. The second part implies the increasing shear stress behavior in high shear rate areas, where the shear stress reaches a maximum at an extremely high shear rate. Accordingly, in low shear rate areas, the first part of eqn (2) is dominant. From the fitting curve in Fig. 6(a), a solid line can be accurately fitted with the stress curves over the whole shear rate area. Table 1 shows the optimal values for each parameter in eqn (1) and (2).

Fig. 6 Shear stress (a) and shear viscosity (b) curves of the SiO₂/PPy particle-based ER fluid (10 vol%) as a function of shear rate with increasing electric field strength (solid lines: CCJ model, dash line: Bingham model).

Table 1 Optimal values for parameters from Bingham and CCJ models estimated from the flow curves of SiO₂/PPy-based ER fluids (10 vol%)

Model	Para-meters	Electric field strength [kV mm^−1]
		0.3	0.7	1.0	1.3	1.7
Bingham	τy	17.6	36.4	64.2	101	151
	η	0.162	0.148	0.139	0.122	0.132
CCJ	τy	18.6	40.4	72.2	111	151
	t2	0.774	0.012	0.01	0.0072	0.003
	α	0.0035	0.663	0.73	0.78	1.614
	η∞	0.177	0.191	0.216	0.24	0.296
	t3	0.021	0.1237	0.081	0.112	0.247
	β	0.9923	0.8027	0.7629	0.723	0.697

---

As shown in Fig. 6(b), while a constant viscosity is observed in the absence of an electric field, we can observe shear thinning under a variety of electric field conditions. The shear thinning phenomenon (pseudoplastic behavior) implies a decrease in viscosity with increasing shear rates.⁵⁴

Dynamic oscillation tests are important methods to analyze the viscoelastic ability of ER fluids.⁵⁰ We conducted a strain amplitude sweep test at a fixed angular frequency of 6.28 rad s⁻¹ to measure the linear viscoelastic region (γ_LVE) before the dynamic oscillation testing, as shown in Fig. 7(a). The storage modulus (G′, elastic property) represents the deformation energy stored in the sample, while the loss modulus (G′′, viscous property) represents the deformation energy consumed by the sample are obtained as a function of amplitude strain in a range of 10⁻⁵ to 1.⁵¹ G′ is much higher than G′′, and both values eventually plateaued in what is referred to as the linear viscoelastic region (γ_LVE).⁵⁵ Because the elastic properties are superior to the viscous properties in this region (G′ > G′′), fibril-like structures are formed. When the strain surpasses a critical value (γ_LVE), both G′ and G′′ decrease drastically and G′ < G′′ due to the loss of structure in the ER fluid.

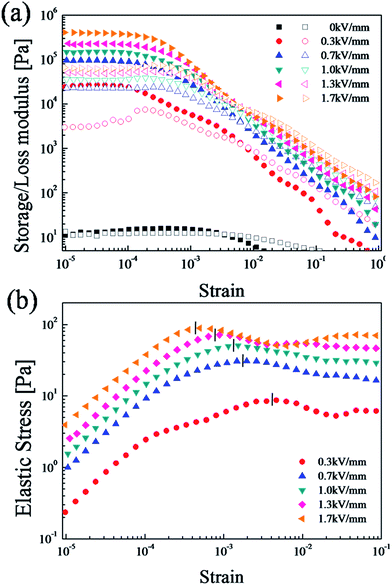Fig. 7 (a) Strain amplitude sweep (●closed symbols: G′, ○open symbols: G′′) and (b) elastic stress (τ' = G′γ) as a function of strain of the SiO₂/PPy-based ER fluid (10 vol%, 100 cS silicone oil).

When an electric field is applied, the ER fluid transitions from liquid-like to solid-like behavior.⁵⁵ This transition forms particle aggregates and then rigid fibril-like structures. To effectively show the progressive structural breakdown, we measure the magnitude of the elastic stress (τ′ = G'γ) within the range of the strain amplitude (γ).⁵⁶ As shown in Fig. 7(b), at low strain amplitudes (γ < 0.001), the elastic stress value increases linearly with increased strain in the linear viscoelastic domain. The solid-like structure of the SiO₂/PPy particle-based ER fluid begins to break down at the critical strain γ_c, which suggests the linearity limit of a dynamic modulus.⁵⁷

The dependence of the yield stress τ_y on electric field strength is shown in Fig. 8. The dynamic yield stress is obtained from the controlled shear rate (CSR) experiments through extrapolation of very low shear rate conditions (Fig. 6(a)) using the CCJ model and the elastic yield stress obtained from dynamic oscillation tests (Fig. 7(b)).

Fig. 8 Dynamic and elastic yield stress under different electric field strengths for the SiO₂/PPy-based ER fluid (10 vol%).

The correlation between the yield stress (dynamic and elastic) and electric field strength is expressed by a power-law equation as

τ_y ∝ E^α (3)

For both cases, the index α = 1.5 is the conduction model and another model is polarization model (α = 2.0).⁵³ We can be sure that the elastic yield stress measured from dynamic measurements is slightly lower than yield stress determined using steady-state measurement.^58,59 In conclusion, the yield stress of this ER fluid complies with a conduction model.

Changes in G′ and G′′ were measured over a wide angular frequency range with a strain of 0.004%, as shown in Fig. 9. The G′ values are higher than G′′ due to dominant elastic behaviors (compared to viscous behaviors) in the ER fluid. Both G′ and G′′ are stable over the entire frequency range. In addition, we can confirm that G′ and G′′ gradually increased with increasing electric field strength.

Fig. 9 Angular frequency sweep with a fixed strain amplitude of 4 × 10⁻⁵ for the 10 vol% SiO₂/PPy based ER fluid under different electric field strengths.

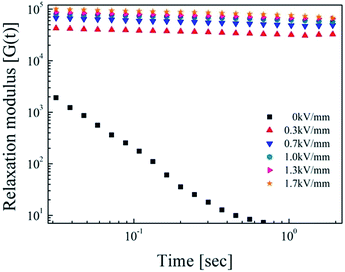
Stress relaxation behavior was observed to analyze the phase change from fluid-like to solid-like within the ER suspension. To predict the behavior of the SiO₂/PPy core/shell particle suspension, we calculated the relaxation modulus G(t) using the G′ and G′′ values from the frequency data in Fig. 9. To analyze several system, the Schwarzl equation⁶⁰ was used.^61,62

G(t) ≅ G′(ω) − 0.560G′′(ω/2) + 0.200G′′(ω) (4)

Fig. 10 shows the relaxation modulus of the SiO₂/PPy particles suspension, in which G(t) was calculated from eqn (4), showing linear behavior with increased electric fields as a function of time (log–log scale). These results demonstrate the strong interaction between SiO₂/PPy particles.

Fig. 10 Relaxation modulus of the ER fluid calculated from storage and loss modulus.

As shown in Fig. 11, to test the sensitivity and reliability of the SiO₂/PPy particle-based ER fluid, measurement conditions were set at a constant shear rate (γ = 1 s⁻¹) and square voltage pulse (20 s). Under each electric field, the shear stress increased immediately to higher levels when the electric field was applied, and decreased to zero when the electric field was removed. At each transition point, the change in shear stress of the SiO₂/PPy particle-based ER fluid was rapid without any notable hysteresis, indicating a reversible and fast transition of the SiO₂/PPy chain structure in the ER suspension based on electric field. On the other hand, some peculiar behavior of shear stress of the increase and then decrease in the next step requires, especially at the higher electric field strengths applied further investigation.

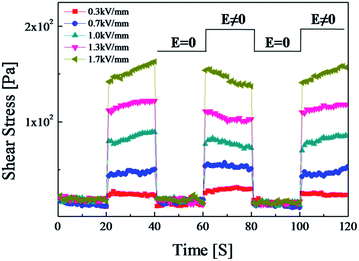Fig. 11 Shear stress of SiO₂/PPy-based ER fluids at a constant shear rate under electric fields and square voltage pulse.

To demonstrate the ER properties of the SiO₂/PPy particle-based ER fluid, the dielectric constant (ε′) and loss factor (ε′′) were obtained with a LCR meter. As shown in Fig. 12, ε′ and ε′′ are represented as functions of frequency, and a Cole–Cole plot for the SiO₂/PPy particles-based ER fluid was created using eqn (5):⁶³

where ε_∞ is the dielectric constant at a high-frequency limit and ε₀ is the dielectric constant when the frequency is 0.

Fig. 12 (a) Dielectric spectra and (b) Cole–Cole plot of the SiO₂/PPy core/shell particle-based ER fluid (10 vol%, 100 cS silicone oil).

The difference (Δε = ε₀ − ε_∞) of the dielectric strength represents the polarizability of the ER suspension, which is associated with the electrostatic interactions between the particles. When the electric field is applied, the rate of interfacial polarization is reflected by the relaxation time (λ = 1/2πf_max), where is f_max defined by maximum value of the dielectric loss in the ER suspension.^51,64 Distribution of the relaxation time for the entire frequency range is characterized by the exponent (1 – α), where α = 0–1. High stress enhancement is obtained when the relaxation time λ becomes smaller than the acceptable range and a larger difference between constants (Δε = ε₀ − ε_∞) was applied.

According to the experimental results fitted to eqn (5), the value of ε_∞ and ε₀ are 0.99 and 1.93, (α = 0.44), respectively, which implies fast response under an electric field. A short relaxation time (λ = 1.5 × 10⁻⁴ s⁻¹) is associated with rapid interfacial polarization, which means faster chain reformation when the chain is broken in a high shear flow region.⁶⁴

4. Conclusions

Monodisperse SiO₂/PPy core/shell particles were synthesized with silica-modified MPS. The morphology and size of the core/shell particles were measured by SEM and TEM. A SiO₂/PPy particle-based ER fluid showed typical ER fluid behavior in the oscillation and rotation tests under various electric fields. Finally, the obtained flow curve was analyzed by the Bingham and CCJ models, where the CCJ model provided a more accurate fit. The SiO₂/PPy-based fluid had a power-law dependence with a value of 1.5, which is a conduction model. In addition, the fluid displayed ER properties, showing that storage modulus, loss modulus, and relaxation modulus all increase with increasing electric field strength. It can be also noted that well controllable fabrication of core–shell structured monodisperse spherical SiO₂/PPy nano-sized particles is beneficial for not only their ER fluid but also various biomedical applications.⁶⁵

Acknowledgements

This work was supported by a research grant from National Research Foundation, Korea (NRF-2013R1A1A2057955).

Notes and references

1. J. Yin, X. Wang, R. Chang and X. Zhao, Soft Matter, 2012, 8, 294.
2. K. Shin, D. Kim, J. C. Cho, H. S. Lim, J. W. Kim and K. D. Suh, J. Colloid Interface Sci., 2012, 374, 18.
3. X. Q. Gong, L. M. Wang and W. J. Wen, Chem. Commun., 2009, 31, 4690.
4. M. Sedlacik, M. Mrlik, Z. Kozakova, V. Pavlinek and I. Kuritka, Colloid Polym. Sci., 2013, 291, 1105.
5. B. Wang, Y. Yin, C. Liu, S. Yu and K. Chen, Dalton Trans., 2013, 42, 10042.
6. Y. C. Cheng, J. J. Guo, X. H. Liu, A. H. Sun, G. J. Xu and P. Cui, J. Mater. Chem., 2011, 21, 5051.
7. J. Wu, T. Jin, F. Liu, J. Guo, Y. Cheng and G. Xu, RSC Adv., 2014, 4, 29622.
8. X. P. Zhao and J. B. Yin, Chem. Mater., 2002, 14, 2258.
9. X. R. Song, A. Q. Hu, N. Y. Tan, D. Ma and Y. B. Lin, Mater. Chem. Phys., 2011, 126, 369.
10. Y. D. Kim and I. C. Song, J. Mater. Sci., 2002, 37, 5051.
11. J. B. Yin, X. A. Xia, L. Q. Xiang and X. P. Zhao, Carbon, 2010, 48, 2958.
12. M. Parthasarathy and D. J. Klingenberg, Mater. Sci. Eng., R, 1996, 17, 57.
13. B. Horvath and I. Szalai, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 061403.
14. B. J. Park, F. F. Fang and H. J. Choi, Soft Matter, 2010, 6, 5246.
15. Y. G. Xu, X. L. Gong, S. H. Xuan, W. Zhang and Y. C. Fan, Soft Matter, 2011, 7, 5246.
16. V. Pavlinek, P. Saha, T. Kitano, J. Stejskal and O. Quadrat, Phys. A, 2005, 353, 21.
17. J. W. Kim, F. Liu and H. J. Choi, J. Ind. Eng. Chem., 2002, 8, 399.
18. J. Trlica, P. Saha, O. Quadrat and J. Stejskal, Phys. A, 2000, 283, 337.
19. O. Y. Gumus, O. Erol and H. I. Unal, Polym. Compos., 2011, 32, 756.
20. J. Yin, X. Xia, X. Wang and X. Zhao, Soft Matter, 2011, 7, 10978.
21. P. Feng, Q. Wan, X. Q. Fu, T. H. Wang and Y. Tian, Appl. Phys. Lett., 2005, 87, 033114.
22. S. Guzel, O. Erol and H. I. Unal, J. Appl. Polym. Sci., 2012, 124, 4935.
23. J. Y. Hong and J. Jang, Soft Matter, 2012, 8, 3348.
24. B. Wang and X. Zhao, Langmuir, 2005, 21, 6553.
25. J. K. Hwang, K. Shin, H. S. Lim, J. C. Cho, J. W. Kim and K. D. Suh, Macromol. Res., 2012, 20, 391.
26. E. van Ruymbeke, A. Pamvouxoglou, D. Vlassopoulos, G. Petekidis, G. Mountrichas and S. Pispas, Soft Matter, 2010, 6, 881.
27. S. Dai, P. Ravi and K. C. Tam, Soft Matter, 2009, 5, 2513.
28. M. Sedlacik, V. Pavlinek, M. Mrlik, Z. Morávková, M. Hajná, M. Trchová and J. Stejskal, Mater. Lett., 2013, 101, 90.
29. D. N. Kim, Y. Tian and H. J. Choi, RSC Adv., 2015, 5, 81546.
30. I. J. Moon and H. J. Choi, Materials, 2015, 8, 4932.
31. T. Plachy, M. Mrlik, Z. Kozakova, P. Suly, M. Sedlacik, V. Pavlinek and I. Kuritka, ACS Appl. Mater. Interfaces, 2015, 7, 3725.
32. B. Sim, H. S. Chae and H. J. Choi, eXPRESS Polym. Lett., 2015, 9, 736.
33. Y. Yang, Y. Chu, F. Yang and Y. Zhang, Mater. Chem. Phys., 2005, 92, 164.
34. E. M. Genies, A. Boyle, M. Lapkowski and C. Tsintavis, Synth. Met., 1990, 36, 139.
35. Y. Lu, A. Pich and H. Adler, Synth. Met., 2003, 37, 135.
36. W. Yin, J. Li and Y. Li, J. Appl. Polym. Sci., 2001, 80, 1368.
37. L. Hao, C. Zhu, C. Chen, P. Kang, Y. Hu, W. Fan and Z. Chen, Synth. Met., 2003, 139, 391.
38. F. Yang, Y. Chu, S. Ma, Y. Zhang and J. Liu, J. Colloid Interface Sci., 2006, 301, 470.
39. F. Miomandre, F. Chandezon, B. Lama, J. Besnardiere, M. Routier, A. Brosseau and P. Audebert, J. Nanopart. Res., 2011, 13, 879.
40. J. Y. Hong and J. Jang, Soft Matter, 2010, 6, 4669.
41. Y. D. Kim and G. G. Hong, Korean J. Chem. Eng., 2012, 29, 964.
42. Q. Cheng, Y. He, V. Pavlinek, A. Lengalova, C. Li and P. Saha, J. Mater. Sci., 2006, 41, 5047.
43. Q. Cheng, V. Pavlinek, C. Li, A. Lengalova, Y. He and P. Saha, Mater. Chem. Phys., 2006, 98, 504.
44. A. Kawai, K. Uchida, K. Kamiya, A. Gotoh and F. Ikazaki, Adv. Powder Technol., 1994, 5, 129.
45. S. Wu, F. Zeng and J. Shen, Polym. J., 1998, 30, 451.
46. D. H. Kim and Y. D. Kim, J. Ind. Eng. Chem., 2007, 13, 879.
47. X. J. Liang, S. Wang, S. J. Liu, X. Liu and S. X. Jiang, J. Sep. Sci., 2012, 35, 2003.
48. X. Chen, J. Devaux, J. P. Issi and D. Billaud, Polym. Eng. Sci., 1995, 35, 642.
49. M. Miah, Z. Iqbal and E. P. C. Lai, Anal. Methods, 2012, 4, 2866.
50. Q. Cheng, V. Pavlinek, Y. He, C. Li and P. Saha, Colloid Polym. Sci., 2009, 287, 435.
51. W. L. Zhang, Y. S. Seo and H. J. Choi, Macromol. Chem. Phys., 2013, 214, 1415.
52. F. F. Fang, B. M. Lee and H. J. Choi, Macromol. Res., 2010, 18, 99.
53. Y. Meheust, K. P. S. Parmar, B. Schjelderupsen and J. O. Fossum, J. Rheol., 2011, 55, 809.
54. Y. Zhao, S. Dong, A. M. Jamieson, X. Hsu, J. Lal, S. Nazarenko and S. J. Rowan, Macromolecules, 2005, 38, 5205.
55. B. D. Chin and H. H. Winter, Rheol. Acta, 2002, 41, 265.
56. M. Yang, L. E. Scriven and C. W. Macosko, J. Rheol., 1986, 30, 1015.
57. X. D. Pan and G. H. McKinley, Appl. Phys. Lett., 1997, 71, 333.
58. J. D. Vincente, F. Gonzalez-Caballero, G. Bossis and O. Volkova, J. Rheol., 2002, 46, 1295.
59. H. M. Laun, C. Gabriel and C. H. Kieburg, J. Intell. Mater. Syst. Struct., 2010, 21, 1479.
60. F. R. Schwarzl, Rheol. Acta, 1975, 14, 581.
61. W. L. Zhang, S. H. Piao and H. J. Choi, J. Colloid Interface Sci., 2013, 402, 100.
62. B. J. Park, T. H. Kim, H. J. Choi and J. H. Lee, J. Macromol. Sci., Part B: Phys., 2007, 46, 341.
63. H. J. Choi, C. H. Hong and M. Jhon, Int. J. Mod. Phys. B, 2007, 21, 4974.
64. B. M. Sim and H. J. Choi, RSC Adv., 2015, 5, 11905.
65. L. Zhou, G. Tan, K. Ouyang, Y. Liu and C. Ning, Part. Part. Syst. Charact., 2015, 32, 1068.

---