Structure and electrical properties of (0.965 − x)(K0.48Na0.52)NbO3–xBiGaO3–0.035(Bi0.5Na0.5)ZrO3 piezoelectric ceramics
Abstract
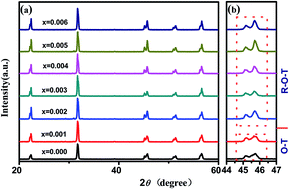
(0.965 − x)(K0.48Na0.52)NbO3–xBiGaO3–0.035(Bi0.5Na0.5)ZrO3 [(0.965 − x)KNN–xBG–BNZ] lead-free piezoelectric ceramics were prepared using normal sintering for improving the piezoelectric properties and temperature stability of KNN-based ceramics. The effects of the BiGaO3 (BG) content on their phase structure, microstructure, and piezoelectric properties were investigated. Orthorhombic–tetragonal phase coexistence has been found in the ceramics with the composition range of 0 ≤ x ≤ 0.001, and the coexistence of rhombohedral, orthorhombic and tetragonal phases at room temperature was obtained with 0.002 ≤ x ≤ 0.006. Then enhanced piezoelectric properties and a high Curie temperature (e.g., d33 = 312 pC N−1, kp ∼ 44%, and TC ∼ 341 °C) were observed. All the results show this system of potassium–sodium niobate-based ceramics demonstrates promising potential in practical applications.

 Please wait while we load your content...
Please wait while we load your content...