Constant rate thermal analysis of a dehydrogenation reaction
Abstract
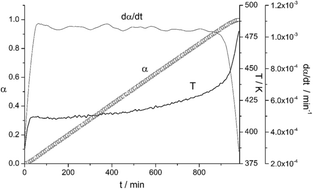
The Constant Rate Thermal Analysis (CRTA) procedure has been employed for the first time to study the kinetics of MgH2 dehydrogenation by thermogravimetry under high vacuum. CRTA implies controlling the temperature in such a way that the decomposition rate is maintained constant all over the process, employing the mass change as the experimental signal proportional to the reaction rate. The CRTA curves present a higher resolution power to discriminate the kinetic model obeyed by the reaction in comparison with conventional heating rate curves. The combined kinetic analysis has been applied to obtain the kinetic parameters, which show that MgH2 decomposition under high vacuum obeys first-order kinetics (F1). It has been proposed that the dehydrogenation of MgH2 under high vacuum takes place by instantaneous nucleation in the border line of the bidimensional crystallites followed by the growth of the nuclei.

 Please wait while we load your content...
Please wait while we load your content...