Computer simulation of self-assembly of cone-shaped nanoparticles†
Yali Wang and
Xuehao He*
Department of Chemistry, School of Science, Tianjin University, Tianjin 300350, China. E-mail: xhhe@tju.edu.cn
First published on 29th June 2016
Abstract
The self-assembly of cone-shaped particles into vesicle-like structures is an interesting yet poorly understood topic, of which its interpretation may assist in the exploration of beneficial applications of vesicles in drug and gene delivery. In the present work, two kinds of cone-like particles are modelled: one is the AB type with a Janus structure and the other is the BAB type with a sandwich structure that increases interaction specificity. Details of the assembled structures and kinetic mechanism of particle assembly are provided using Brownian dynamics simulations. Cluster growth follows the nucleation and growth mechanism in which each free particle is added to the growing seeds. The more specific interactions of the BAB-type particles reduce the growth rate compared to that of the AB-type ones. The cluster size is in good agreement with theoretical results, more dependent on the cone angle, and less dependent on the particle structure (i.e. AB type and BAB type), and the cluster geometries are co-determined by the cone angle, cone shape and particle structure, containing partial curved structures, malformed vesicles, perfect vesicles and closed large aggregates. Simulation results are anticipated to provide guidance for the design of non-spherical particles suitable for the assembly of nanostructures in materials science.
1. Introduction
Non-spherical particles with anisotropic shapes and interactions are expected to enable an enormous amount of materials with desirable structural and functional properties that are impossible for the assembled structures of spherical particles.1–7 The preparation of non-spherical particles in a controlled manner has emerged with a robust and flexible process,8–15 and their assembled structures include photonic and plastic crystals from dumbbells,16,17 colloidal fibres and colloidal crystals from Janus ellipsoids,18–20 super crystals from polyhedra,21,22 worm-like chains from key-lock and flattened particles,23,24 cubic crystals from cubic colloids,25 and micelle-like structures from amphiphilic wedge-shaped particles.26The assembled structures not only depend on the shape of the particles but also on the specificity of the inter-particle interactions. For Janus rods, the anisotropic surface properties can direct the formation of exotic structures such as colloidal ribbons and rings.27 In addition, the size of the patches, number of patches, shape of the patches, position of the patches, and patch–patch interactions are proposed as parameters to control the self-assembly of patchy particles.28 When particles are designed with both anisotropic shapes and interactions, the assembled structure can be significantly affected by these anisotropic traits.18,27 For cones with directional attractive interactions, the cone angle plays a key role in determining the packing structure.29,30 At large cone angles, cones form polyhedral structures, while at moderate and small cone angles, spherical clusters form. The orientation attraction and conical shape underlie their curved, closed structures. All formed clusters possess a definite cluster size which is mainly determined by the cone angle, and the cluster size increases with the increase of the cone angle.29–31 Although various assembled structures have been found in the past, the assembly mechanism through which particles interact to form an ordered cluster is not clear.
In order to systematically understand the self-assembly mechanism of non-spherical particles, computer simulation has been applied to explore the assembly process. Zhang et al.32 predicted that triangle plates with discrete, attractive sites assembled into two-dimensional sheets by applying Brownian dynamics (BD) simulations, and sheet formation occurs via a first-order transition as in equilibrium polymerization. The recognition of interaction sites may be used to control the overall structure of particle assemblies. Long et al.33 suggested that the formation of polyhedral aggregates from anisotropic patchy colloids proceeds by two distinct assembly pathways: monomeric addition and budding from a disordered liquid with BD simulations. The diffusion map approach is used to construct free energy landscapes of the assembly process, which may offer a powerful tool for the rational design of particle architecture. Rapaport demonstrated that trapezoidal particles assembled into 60-particle icosahedral capsids both in implicit and explicit solvent environments with molecular dynamics (MD) simulations,34,35 and this was found to follow the classical nucleation and growth mechanism.36–41 To our knowledge, simulation studies for cone particles are very rare besides ref. 29 and 30, where the Monte Carlo (MC) method was used to study the aggregation structure of cone particles.
The goal of this work is to seek the generic physical aspects of the role played by the cone angle and interaction specificity in the assembly process. A novel BD framework, developed in our prior work, is employed to simulate the self-assembly of cone-shaped particles. Critically, this framework has two advantages: (1) the specificity of the particle shape and inter-particle interaction is accurate because the target object is designed with an all-atomic model; and (2) the simulation computation does not depend on the number of atoms in the particle once the force field between two particles is achieved. Compared with conventional coarse-grained methods, this framework provides a fast and flexible way to explore the self-assembly of various particle shapes without approximation in the particle shape. In principle, this framework is valid for any shaped particle. Here, two kinds of cone-shaped particles are designed: one with a Janus structure and the other with a sandwich structure (Fig. 1a). The effects of the cone angle and particle structure (i.e. AB type and BAB type) on the kinetic pathway and assembled structures are discussed. The self-assemblies of these two kinds of cone-shaped particles proceed via a nucleation and growth mechanism, similar to capsid assembly. More specific interactions of BAB type particles decrease the assembled rate and increase the accessibility of a malformed structure.
2. Simulation model and method
Rigid cone-shaped particles are constructed with 11 layers of coarse-grained beads stacking from the top down, and the distances of two adjoining layers and two adjacent coarse-grained beads in the same layer are both set to 0.1 nm. Moreover, the distribution of beads in every layer is axisymmetric to provide an adequate approximation to the desired shape. The two-dimensional cone angle θ at the vertex controls the number of coarse-grained beads arranged within a cone (the unit of θ is degrees), and the height of a cone is fixed at 1.0 nm. As shown in Fig. 1a, the top five layers are composed of A beads and the remaining layers are B beads for the AB Janus structure; while for the BAB sandwich structure, A beads only comprise three layers in the middle part and B beads form the tapered and bottom regions (here, A and B beads are indicated by pink and cyan, respectively).Coarse-grained beads in two particles interact with each other through the Lennard-Jones potential, that is:
| U0 = 4εij[(σij/rij)12 − (σij/rij)6], | (1) |
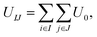 | (2) |
In this work, a cone-shaped particle is regarded as a rigid body and in every time step the particle updates its position and orientation, which results in a large computational cost when the number of coarse-grained beads in a cone is up to a hundred or a thousand. To reduce the computational cost for updating the positions and orientations, the pair-wise interaction potential between two cone-shaped particles can be expressed as a function of three orientation angles, UIJ(αI, αJ, βIJ) (these three orientation angles are shown in Fig. 1b). Thus, for a set of (αI, αJ, βIJ), the exact interaction potential can be mapped with a modified Lennard-Jones potential only considering the equilibrium conformation using a tabulated potential and interpolation technology, which remarkably improves the simulation efficiency and can well reflect the anisotropic shape and interaction. The form of this modified potential is:
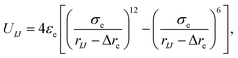 | (3) |
 | (4) |
After achieving the tabulated potential between two particles, Brownian dynamics (BD) simulation is carried out where the translational and rotational motions of rigid particles are evaluated through updating their positions and orientations with the following equation:
 | (5) |
BD simulations with an annealing method are carried out in a canonical ensemble containing 200 particles, and the simulation box is cubic with periodic boundary conditions to minimize edge effects (the box side is 12 nm). Annealing is initialized by generating randomly chosen positions and orientations of particles without particle–particle overlap. The cooling rate is 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps per K, which is affordably slow yet fast enough to obtain stable assembled structures. The positions and orientations of the particles, as well as inter-particle interactions, are collected at regular intervals of the annealing process for further analysis.
000 steps per K, which is affordably slow yet fast enough to obtain stable assembled structures. The positions and orientations of the particles, as well as inter-particle interactions, are collected at regular intervals of the annealing process for further analysis.
The potential energy surface (PES) between two particles is drawn to confirm the stable and metastable conformations between these two particles, and the minimum energy paths (MEPs) between these conformations on the PES are calculated with the improved string method43 to get the transition barrier, which is helpful to deepen our understanding of the assembly process and kinetic pathway. A total of 39 intermediate states are inserted into every MEP, and the positions and orientations of these intermediate states update until the calculation error is less than 10−6. The cluster size of the assembly, measuring the distances between centroids of particles, is calculated to discuss the effects of the cone angle and interaction specificity on assembly, and growth kinetics is monitored to identify the assembly mechanism.
Past research showed that the entropic effects of the shape of non-spherical particles are important.44–46 In this work, the directional entropic forces (DEFs)45,46 were analysed in terms of the free energy F, potential energy U and entropy S of the system. The free energy F is defined as F/kBT = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z where Z is the partition function, i.e., the statistical number of pair-wise configurations which depends on the orientation and distance of the pair-wise particle. The statistical number of pair-wise configurations Z = NrIJ/NrIJ=∞ and Nr is the number of pair-wise particle conformations at rIJ and αJ = 180 − αI. The entropy S is calculated according to the equation S = (U − F)/T where U/kBT is the pair-wise potential energy as a function of rIJ and it is computed following eqn (4). In this work, we calculate and compare the free energy (F), potential energy (U) and entropy (S) at β = 0, αI = 180 − αJ in several systems to address how DEFs affect the self-assembly of cone-shaped particles. The calculation employed 1000 particles in the system with a box length of 12 nm. The number density is five-fold of BD simulations. αJ is divided into 30 sections and rIJ = 6 nm is assumed to be the infinite distance rIJ = ∞.
Z where Z is the partition function, i.e., the statistical number of pair-wise configurations which depends on the orientation and distance of the pair-wise particle. The statistical number of pair-wise configurations Z = NrIJ/NrIJ=∞ and Nr is the number of pair-wise particle conformations at rIJ and αJ = 180 − αI. The entropy S is calculated according to the equation S = (U − F)/T where U/kBT is the pair-wise potential energy as a function of rIJ and it is computed following eqn (4). In this work, we calculate and compare the free energy (F), potential energy (U) and entropy (S) at β = 0, αI = 180 − αJ in several systems to address how DEFs affect the self-assembly of cone-shaped particles. The calculation employed 1000 particles in the system with a box length of 12 nm. The number density is five-fold of BD simulations. αJ is divided into 30 sections and rIJ = 6 nm is assumed to be the infinite distance rIJ = ∞.
3. Results and discussion
3.1. Entropic forces at moderate number density
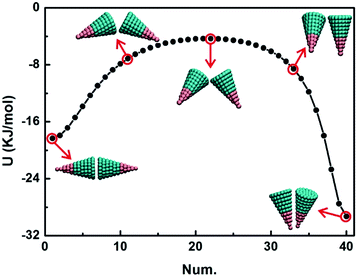
Fig. 2 shows U, S and F at T = 930 K in the plane βIJ = 0 considering a pair of particles changing from the bottom-to-bottom to vertex-to-vertex conformation. The minima in Fig. 2 are labelled with black points. The smallest entropy S and potential energy U appear at αJ = 96° and 0° for the cone angle θ = 15° and 60°, respectively, and they correspond to conformation 1, side-by-side for θ = 15° and bottom-to-bottom for θ = 60°. While at θ = 60°, there are four minima in the free energy diagram corresponding to conformations 1–4 displayed on the right of Fig. 2. Moreover, the free energy F of conformations 1–4 of the AB type is lower than that of the BAB type. It is shown that the DEF not only depends on the cone angle θ but also depends on the particle structure (i.e. AB type and BAB type). But the shape structure affects the DEF to a lesser extent than the cone angle θ does. Both the shape structure and cone angle θ influence the potential energy U, but the latter’s influence is even greater. Furthermore, the potential energy U affects the entropy S and free energy F. The entropy S at θ = 60° is much larger than that at θ = 15° for both the AB type and BAB type when rIJ < 4 nm, implying that particles tend to form regular conformations at θ = 60° (e.g. conformations 1–4 in Fig. 2) and particles are in a disordered state at θ = 15°. The entropic effect favours the desired ordered phase and disfavours the random tiling.44–46Actually, the entropic effect is a density-dependent quantity that often stems from the collective behaviour of the system.45,46 As the density increases, particles get closer to contact and are expected to exhibit greater alignment at a higher density. In Fig. S1,† the system contains 2000 particles of the AB type and the number density is ten-fold of BD simulations. With the number density increasing, entropic effects become more significant at θ = 60° than at θ = 15°, due to the difference of the potential energy U. The much larger potential energy U at θ = 60° of pair-wise particles favours particles stacking regularly. However, the increase of entropic effects is not obvious at θ = 15° and it is similar to that in Fig. 2. This is because the potential energy U is principally associated with the entropic effects and potential energy U is independent of the number density.
Entropic effects of particles at the cone angle θ = 15° are still very weak even though the number density is increased, so the effect of temperature on entropy S is considered. According to the BD annealing temperature range of the AB type at the cone angle θ = 15°, two temperatures (T = 80 K and T = 130 K) are selected in the high temperature zone where particles are mostly in a state of disorder, ensuring accuracy of sampling. At a lower temperature (Fig. S2†), the entropy S is significantly enhanced, especially at T = 80 K. At T = 80 K, several minima appear in the free energy diagram, like in Fig. 2 at θ = 60°, supporting the fact that temperature is another important factor associated with entropic effects because of the dependency of U/kBT on temperature. As the temperature decreases, particles begin to get closer and assemble, resulting in the significant enhancement of the DEF. However, the directional entropic force is weak compared with the van der Waals interaction used.
In general, the entropic effects on our self-assembled systems are dependent on the number density, cone angle θ, particle shape and temperature. And the influence of the cone angle θ on the entropic effects is much greater than the other three factors because the cone angle θ is the main factor that determines the potential energy U, and U greatly affects the entropy S and free energy F. So contributions of entropic effects to self-assembled processes can be omitted because the intrinsic van der Waals interactions between particles far exceed the entropic effects.
3.2. PESs and MEPs analysis
Due to the similarity of the PES architectures, all PESs are divided into three groups and only three typical PESs at θ = 15°, 30° and 45° are displayed (Fig. 3). The first group contains PESs at θ = 15°, 20° and 25°; the second group includes PESs at θ = 30°, 35° and 40°; and the third group comprises PESs at θ = 45° and 60°. Compared with AB-type particles, PESs between BAB-type particles are less sensitive to θ. PESs at θ = 30° and θ = 45° are classified into the first and second group, respectively (Fig. S3†). The red points on the PESs indicate saddle points, numbered in the order of the magnitude of potential energy, and the corresponding conformations of these saddle points are shown in the lower right corner in Fig. 3 and S3.† Saddle points on different PESs appear in a similar region, which means that the PES architecture and positions of the saddle points are mainly determined by the cone shape. Nevertheless, the potential energies of minimum energy points (i.e. conformation 1) depend on θ and the particle structure (i.e. AB type and BAB type). In the case of θ, the potential energies increase with the increase of θ; while in the case of particle structure (i.e. AB type and BAB type), the effects of the particle structure on the potential energies are in a manner dependent on θ: when θ is larger (e.g. θ = 45° and 60°), the effects can be ignored because for both the AB type and BAB type, the bottom of the particle is composed of B beads.The minimum potential energy on each PES corresponds to configuration 1, and it is a side-by-side conformation in Fig. 3a and b and a bottom-to-bottom conformation in Fig. 3c. As θ increases, the interactions of stable conformations become stronger and stronger, resulting in competition between the side-by-side and bottom-to-bottom packing, which will augment the formation of kinetic traps during assembly and will allow a smaller regulation degree within a conformation transition. A characteristic parameter f, defined as f = ΔEa/|Umin|, is introduced to the quantization regulation degree of the conformation transition. Here, ΔEa is the transition energy barrier and |Umin| is the absolute value of potential energy of conformation 1. The results for different transition processes are summarized in Tables 1 and S1.† The larger the value of f is, the lower the regulation degree of the conformation transition is. There are two cases: one is at θ ≤ 45° and the other is at θ > 45°. At θ ≤ 45°, the value of f increases with θ increasing, which implies that the competition between these conformations is becoming more and more intense and it further reduces the kinetic accessibility of the stable conformation due to kinetic traps. Here, metastable configuration 2 may be a kinetic trap because its potential energy is only less than that of conformation 1. Remarkably, the value of f2−1 at θ = 45° is the largest, so the conformation transition between these two conformations has a large energy barrier. While at θ > 45°, the value of f decreases with θ increasing, and at this θ range, the stable conformations are bottom-to-bottom packing, and the bottom-to-bottom packing is more stable than side-by-side packing, indicated by the smaller value of f2−1.
| The 1st group | The 2nd group | The 3rd group | ||||||
|---|---|---|---|---|---|---|---|---|
| a The unit of ΔEa and |Umin| is kJ mol−1, unless otherwise stated. | ||||||||
| θ | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 60 |
| |Umin| | 10.5 | 16.9 | 20.7 | 29.4 | 31.3 | 42.2 | 54.2 | 122 |
| ΔEa2−1 | 0.85 | 2.48 | 4.59 | 14.0 | 22.2 | 33.8 | 43.0 | 71.5 |
| ΔEa3−1 | 1.09 | 3.39 | 7.05 | 9.26 | 13.9 | 20.6 | 22.0 | 47.7 |
| ΔEa3−2 | 0.61 | 2.03 | 4.35 | 8.92 | 11.9 | 16.9 | 27.6 | 59.3 |
| f2−1 | 0.08 | 0.15 | 0.22 | 0.48 | 0.71 | 0.80 | 0.82 | 0.59 |
| f3−1 | 0.10 | 0.20 | 0.34 | 0.34 | 0.44 | 0.49 | 0.41 | 0.39 |
| f3−2 | 0.06 | 0.12 | 0.21 | 0.30 | 0.38 | 0.40 | 0.51 | 0.43 |
Examples of the intermediate states in the configuration transition process are shown in Fig. 4 at θ = 30° for the AB-type particle. A total of 39 intermediate states construct the MEP and only three intermediate configurations are displayed. First, the dihedral angle between these two particles decreases, leading to two particles close to each other; and then these two particles slowly adjust their orientations until their orientations satisfy the side-by-side conformation. These intermediate states make the transition process visualization more convenient for us to understand the details of the following assembly. Interactions between particles need to be sufficiently weak to enable the correction of errors during transition and meanwhile strong enough for the transition to proceed.47,48 In fact, the calculation of the transition energy barrier is different from that of the free energy landscape which can provide sufficient conditions for self-assembly.39,41,49 In this work, PESs and MEPs are considered as a different perspective to take the effects of particle shape and specific interactions into account. The interactions and conformation transitions between two contacting particles are the key aspects of particle assembly.
3.3. Particle assembly
The specific heat capacity CV is chosen as a first indicator to analyse the assembly process, and it is calculated according to the following equation:
 | (6) |
Results for CV as a function of annealing temperature are plotted in Fig. 5a. There is a clear maximum in each curve, indicating that the potential energy fluctuates remarkably in this narrow temperature interval. This narrow temperature interval resembles a two-phase coexistence region where disordered and ordered phases coexist. While crossing the maximum, the ordered phase gradually increases and the disordered phase gradually disappears. The annealing temperature corresponding to the maximum is defined as the aggregation temperature Tagg to discuss this abrupt change. Tagg increases monotonically with θ increasing (Fig. 5b). Furthermore, Tagg of the AB-type particle is smaller than that of the BAB-type particle at the same θ, which is mainly attributed to the particle structure (i.e. AB type and BAB type). The more complex sandwich structure results in smaller inter-particle interactions, besides the bottom-to-bottom interaction.
 | ||
| Fig. 5 (a) Specific heat capacity (CV) as a function of the annealing temperature (T). (b) Aggregation temperature Tagg (at CV = max) as function of the cone angle. | ||
At the lower temperature region, the CV curves reach a plateau stage, implying that the energy of the simulation system does not fluctuate obviously. The assembled structures at this temperature region are displayed in Fig. 6. The directional interactions between particles drive their assemblies and force them to generate stable structures with the maximum nearest neighbours to achieve the lowest energy. Meanwhile, the conical shape is expected to force the particles to form into a curved and close structure.29,30 Assembled structures contain partial structures (Fig. 6a and b) due to curvature constraints, complete vesicles (Fig. 6d–j) with a defined cluster size, a malformed vesicle (Fig. 6c) due to the orientation error of a small group of particles, and enclosed large aggregates (Fig. 6k–p) due to kinetic traps. The major determinants of the assembled structure are the particle shape and particle structure (i.e. AB type and BAB type). The effects of the cone shape could be explained by a critical packing parameter, and the critical packing parameter of the cone-shaped particle is exactly equal to 1/3, satisfying the critical formation condition for a spherical structure.31,50
 | ||
| Fig. 6 A gallery of assembled structures, containing partial structures (a, b), complete vesicles (d–j), a malformed vesicle (c), and enclosed large aggregates (k–p). | ||
At θ = 15°, the main determinant during assembly is particle shape, leading to a large curvature constraint, and partial structures still remain incomplete with 400 particles in simulations (Fig. S4†). At θ = 20°, BAB-type particles assemble a malformed vesicle (Fig. 6c), because the interactions of BAB-type particles are more specific due to the sandwich structure, and the more specific interactions increase the selectivity of the assembled structure. Meanwhile, AB-type particles form complete vesicles at θ = 20° (Fig. 6d). A complete vesicle is a spherical structure with side-by-side packing between particles (Fig. 6d–j). The enclosed large aggregates in Fig. 6k–p are the results of the minimum system energy with the maximum number of particle–particle contacts. When θ is larger, the potential energy between two particles increases obviously and the transition energy barrier between different configurations also increases significantly (Tables 1 and S1†), resulting in it being more difficult to regulate the conformation transition and to avoid kinetic traps. Above all, the final assembled structures are determined together by the cone angle, cone shape and particle structure (i.e. AB type and BAB type).
The assembled structures in Fig. 6 have a definite cluster size. The cluster size is in terms of the number of particles within a cluster, and the dependence of the cluster size on θ is illustrated in Fig. 7. The error bars represent the differences between numerical and theoretical results. The theoretical results are calculated according to the previous work,51 that is, Num. = [2π/3γ − π], where γ = arccos(cos(θ)/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(θ/2)). Theoretical results are certainly valid only when θ is no more than 60°. Fortunately, simulation results are in good agreement with MC simulation29,30 and geometric packing analysis.31 This agreement is first put forward on dynamics simulations and it demonstrates the correctness of simulation results directly. There is an exception: a malformed vesicle containing substantially more particles at θ = 20° for the BAB-type particle. Particles with imperfect orientations are trapped into a growing vesicle by subsequent particle additions, leading to the defective structure (inset in Fig. 7). This is very similar to the virus capsid of which cluster size is fully determined by the properties of capsomers.
cos2(θ/2)). Theoretical results are certainly valid only when θ is no more than 60°. Fortunately, simulation results are in good agreement with MC simulation29,30 and geometric packing analysis.31 This agreement is first put forward on dynamics simulations and it demonstrates the correctness of simulation results directly. There is an exception: a malformed vesicle containing substantially more particles at θ = 20° for the BAB-type particle. Particles with imperfect orientations are trapped into a growing vesicle by subsequent particle additions, leading to the defective structure (inset in Fig. 7). This is very similar to the virus capsid of which cluster size is fully determined by the properties of capsomers.
 | ||
| Fig. 7 Dependence of cluster size on the cone angle. The cluster size (y-axis) is in terms of the number of particles in a single vesicle-like structure. The inset is the misassembled vesicle geometry at θBAB = 20°. The indicated error bars represent the error between our simulation results and the theoretical analysis. The theoretical analysis was based on ref. 51, only considering the influence of the cone angle. | ||
However, vesicle geometries in this work are different to those in MC simulations (Fig. 8a). The main reason is the cone shape. In MC simulations, a cone is modelled with a spherical bottom and the precise structures share some polyhedral features (e.g. icosahedral structure).29,30 In this work, the cone-shaped particle has a flat bottom, and the final structure does not share the similar polyhedral traits. As time progresses, cones associate with the growing assembly and finally assemble into vesicles. For the AB-type particle, the inner walls of the vesicles are constructed by A beads, while for the BAB-type particle, B beads build the inner cores. The radial distribution function g(r) counting the number of neighbouring particle centroids in a full vesicle is shown in Fig. 8b. The particle centroid is positioned at a coarse-grained bead near the real physical mass centre. The whole g(r) is the inset in Fig. 8b, and the first peaks reflect the effects of neighbouring coarse-grained beads at about r = 0.1 nm with significantly large weights because the diameter of a coarse-grained bead is equal to 0.1 nm. So, the first peaks are omitted in Fig. 8b. The positions of the two peaks in Fig. 8b are approximately equal to rm and 1.8rm, respectively, and rm is the equilibrium distance which corresponds to the minimum energy configuration between two particles. At the θ range in Fig. 8a, the minimum energy configurations are side-by-side packing, and rm of the side-by-side conformations increases with θ increasing, which can explain the change of peak positions. Nevertheless, the effects of particle structures (i.e. AB type and BAB type) on the peak position can be negligible at this θ range, and the cluster size can only explain the difference between peak weights.
 | ||
| Fig. 8 (a) Examples of complete vesicle structures formed by self-assembly of AB-type and BAB-type particles. (b) Radial correlation function for these full vesicles. | ||
3.4. Visualization of cluster growth
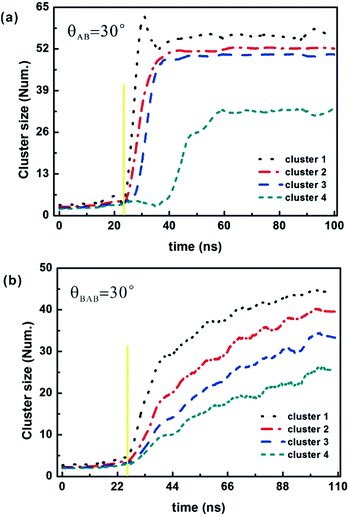
The image sequences in Fig. 9 show several stages in the vesicle growth process at θ = 30°. Starting from the initial condition of 200 particles randomly distributed throughout the simulation box (Fig. 9a and e), the initial population of free particles progressively generates larger and larger clusters (Fig. 9b and f) until all free particles are incorporated in the final several complete vesicles (Fig. 9c and g). The vesicles that have been created will gradually come closer (Fig. 9d and h), taking into account the lowest system energy state, but will never fuse because the cluster size is definite and it is determined by the cone angle and particle structure (i.e. AB type and BAB type). The self-assembly of vesicle-like structures depends on the lower-level interactions of a particle with its neighbours rather than on larger structural building blocks, implying that cluster formation is an energetically favourable assembly process, which is similar to that local rule-based theory of virus shell assembly.52,53 After a new particle is added, the resulting structure is optimized to minimize the energy by updating the position and orientation of each particle. In each time step, all of the particles move and rotate in accordance with the forces and torques calculated from the energy model. When the cooling rate is faster, particles will more easily be captured by a kinetic trap, and it will be difficult to form a stable structure, and instead of that, a misassembled cluster will be created. Thus, achieving a maximum number of on-pathway particles requires striking a balance between a moderate cooling rate and favourable energy.The time evolution process on the cluster size is given in Fig. 10. In all cases significant assemblies occur, and the rate of vesicle formation has a roughly sigmoidal shape, which is a general feature of an assembly reaction. At the beginning of the annealing simulation, there is a lag period where all particles are disorderly dispersed in the box at a higher temperature, and then particles diffuse and collide with each other with the cooling temperature dropping, which results in the generation of the growth seeds. Here, the initial seed size is evaluated and defined as the cluster size at the beginning of the growth stage where the cluster size begins to increase significantly (indicated by the yellow solid line in Fig. 10), and the initial seed size is about 4 particles. Once created, the seeds grow through a rapid growth period and gradually assemble into complete or partial vesicles. In the late stage of assembly, the growth becomes slow because free particles are depleted and each formed vesicle approaches its definite cluster size.
This growth process suffers a similar pathway to that of capsid assembly following a nucleation and growth mechanism. Initially, the formation rate is extremely gentle at the first stage where free particles generate the growth seeds. And then the growth rate becomes fast at the second growth stage where the addition of free particles into growing seeds makes a seed grow into a vesicle. When the free particles gradually disappear, the vesicle formation rate reaches the plateau. For the AB-type particle, there is a more rapid growth rate than that of the BAB-type one at the second stage because the more specific interactions between BAB particles lead to a decrease of assembly rates, which is attributed to its sandwich structure. In addition, the saturation of growth is also more obvious for the AB type, suggesting that the AB-type particle experiences a more favourable condition for assembly. The formation of an ordered cluster reduces the entropy of its constituent particles, and assembly must be driven by favourable interactions to overcome the entropic loss. The driving force for assembly is inter-particle interactions and is proportional to the number of particle–particle contacts. The cluster size of the AB-type particle is larger than that of the BAB-type one, while the inter-particle interactions of these two types are similar. So, AB-type particles undergo a faster growth.
A vesicle is the aggregation structure of side-by-side conformations and each particle in the vesicle maintains the orientation towards the centre of the vesicle, maximizing contact numbers towards the minimum system energy structure. Although growth by the merger of intermediate clusters is a rare event, it occasionally occurs. The sharp jump in Fig. 10a corresponds to a short-lived merger and it creates oversized misassembled structures. Vesicle formation not only depends on particle shape also on particle structure (i.e. AB type and BAB type). The present vesicle assembly mechanism is similar to that of the ring-like micelle structure from amphiphilic wedged particles in experiments.26 But compared with the 2-dimensional ring-like micelle, cone-shaped particles assemble into complex 3-dimensional vesicles, which may provide an alternative method to fabricate uniform vesicles, with a definite hollow cavity and hydrophobic (or hydrophilic) inner wall, as encapsulation vectors for drug and gene delivery.
4. Conclusions
By combining the Brownian dynamics framework with an anisotropic interaction model, the spontaneous formation of vesicle-like structures of 200 cone-like particles, starting from random configurations, is simulated. This enables us to discuss the details of the assembly mechanism which are rare in prior work. The kinetic mechanism of cluster assembly follows the nucleation and growth mechanism, similar to capsid assembly, in which a growth nucleus forms followed by free particles adding to the growing nucleus until the cluster is completed. Interestingly, cluster assembly of BAB-type particles proceeds with a slower growth rate than that of AB-type ones because BAB-type particles contain more complexity in inter-particle interaction and particle structure (i.e. BAB type), leading to the decrease of kinetic accessibility of a stable configuration. The final assembled structures are strongly dependent on the cone angle, particle structure (i.e. AB type and BAB type) and inter-particle interaction, including partial structures, misassembled vesicles, complete vesicles and large aggregates. When the cone angle is smaller (θ = 15°), the cone shape is the main determinant, resulting in a large curvature constraint of the partial structure formed. While at θ = 20°, the particle structure plays a key role in determining the final cluster geometries: a malformed vesicle for the BAB type with a sandwich structure and a complete vesicle for the AB type with a Janus structure. The more complex sandwich structure leads to more specific interactions between BAB-type particles, increasing the accessibility of kinetic trap formation. Although vesicle geometries are different with prior MC simulations, the cluster size is in good agreement with MC simulations and theoretical results.Unlike the free energy landscape for the whole system, the potential energy surface (PES) is chosen as a different perspective to analyse the interaction between only two contacting particles. The stable and metastable configurations of two interacting particles are listed, and the minimum energy path (MEP) between two configurations is calculated to evaluate the transition energy barrier. When the cone angle is ample, the stable configuration of two interacting particles is a bottom-to-bottom configuration, while when the cone angle is moderate, the stable configuration is a side-by-side configuration. As the cone angle increases, the transition energy barrier increases. But when the cone angle is large enough (i.e. θ > 45°), the transition barrier decreases with the increase of the cone angle. Furthermore, the intermediate configurations in the transition path make the transition process visualization more helpful to understand the details of the assembly.
In this work vesicle self-assembly proceeds at conditions that are not relevant to any specific system in experiments. Thus, comparisons with experimental data cannot be made quantitatively. However, the present work strongly suggests the kinetic pathway of self-assembly of cone-shaped particles, and this unified framework can be easily extended to explore self-assemblies of particles with any shape, providing fundamental insight into the assembly process. In future studies, the free energy landscape should be proposed by performing replica exchange molecular dynamics, integrating both the thermodynamic and kinetic aspects of assembly. By developing a more complicated interaction model with explicit solvents, more specific and realistic questions such as the salt effect of assembly in solution and protein assembly can be addressed. Ultimately, this Brownian dynamics simulation framework can explicitly reflect the role of interactions on the self-assembly of anisotropic particles and our goal is to seek the generic physical aspects underlying the assembly for nano/microstructures.
Acknowledgements
The project was supported by the National Natural Science Foundation of China (No. 21274107 and 21474075).References
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562 CrossRef PubMed.
- K. J. Lee, J. Yoon and J. Lahann, Curr. Opin. Colloid Interface Sci., 2011, 16, 195–202 CrossRef CAS.
- M. B. Ross, C. A. Mirkin and G. C. Schatz, J. Phys. Chem. C, 2016, 120, 816–830 CAS.
- S. Sacanna, D. J. Pine and G.-R. Yi, Soft Matter, 2013, 9, 8096–8106 RSC.
- R. Guo, J. Mao, X.-M. Xie and L.-T. Yan, Sci. Rep., 2014, 4, 7021 CrossRef PubMed.
- R. Guo, Z. Liu, X.-M. Xie and L.-T. Yan, J. Phys. Chem. Lett., 2013, 4, 1221–1226 CrossRef CAS PubMed.
- Z. Liu, R. Guo, G. Xu, Z. Huang and L.-T. Yan, Nano Lett., 2014, 14, 6910–6916 CrossRef CAS PubMed.
- Y. Wang, C. Zhang, C. Tang, J. Li, K. Shen, J. Liu, X. Qu, J. Li, Q. Wang and Z. Yang, Macromolecules, 2011, 44, 3787–3794 CrossRef CAS.
- S. H. Kim, A. D. Hollingsworth, S. Sacanna, S. J. Chang, G. Lee, D. J. Pine and G. R. Yi, J. Am. Chem. Soc., 2012, 134, 16115–16118 CrossRef CAS PubMed.
- S. Sacanna, W. T. M. Irvine, P. M. Chaikin and D. J. Pine, Soft Matter, 2011, 7, 1631–1634 RSC.
- Y. Wang, X. Zheng, G. R. Yi, S. Sacanna, D. J. Pine and M. Weck, J. Am. Chem. Soc., 2014, 136, 6866–6869 CrossRef CAS PubMed.
- M. Schuster, J. Lepschy, A. Biber, G. Engelhardt and P. R. Wallnöfer, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11901–11904 CrossRef PubMed.
- S. H. Kim, A. Abbaspourrad and D. A. Weitz, J. Am. Chem. Soc., 2011, 133, 5516–5524 CrossRef CAS PubMed.
- S. Q. Choi, S. G. Jang, A. J. Pascall, M. D. Dimitriou, T. Kang, C. J. Hawker and T. M. Squires, Adv. Mater., 2011, 23, 2348–2352 CrossRef CAS PubMed.
- Z. Cheng, F. Luo, Z. Zhang and Y.-q. Ma, Soft Matter, 2013, 9, 11392–11397 RSC.
- J. D. Forster, J.-G. Park, M. Mittal, H. Noh, C. F. Schreck, C. S. O’Hern, H. Cao, E. M. Furst and E. R. Dufresne, ACS Nano, 2011, 5, 6695–6700 CrossRef CAS PubMed.
- F. Chu, N. Heptner, Y. Lu, M. Siebenbuerger, P. Lindner, J. Dzubiella and M. Ballauff, Langmuir, 2015, 31, 5992–6000 CrossRef CAS PubMed.
- A. A. Shah, S. Benjamin, Z. Wenjia, S. C. Glotzer and M. J. Solomon, Nat. Mater., 2015, 14, 117–124 CrossRef CAS PubMed.
- D. Schneider, P. J. Beltramo, M. Mattarelli, P. Pfleiderer, J. Vermant, D. Crespy, M. Montagna, E. M. Furst and G. Fytas, Soft Matter, 2013, 9, 9129–9136 RSC.
- A. A. Shah, B. Schultz, K. L. Kohlstedt, S. C. Glotzer and M. J. Solomon, Langmuir, 2013, 29, 4688–4696 CrossRef CAS PubMed.
- J. Henzie, M. Grünwald, A. Widmer-Cooper, P. L. Geissler and P. Yang, Nat. Mater., 2012, 11, 131–137 CrossRef CAS PubMed.
- C. Lu and Z. Tang, Adv. Mater., 2016, 28, 1096–1108 CrossRef CAS PubMed.
- S. Sacanna, W. T. Irvine, P. M. Chaikin and D. J. Pine, Nature, 2010, 464, 575–578 CrossRef CAS PubMed.
- L. M. Ramirez, C. A. Michaelis, J. E. Rosado, E. K. Pabon, R. H. Colby and D. Velegol, Langmuir, 2013, 29, 10340–10345 CrossRef CAS PubMed.
- L. Rossi, S. Sacanna, W. T. M. Irvine, P. M. Chaikin, D. J. Pine and A. P. Philipse, Soft Matter, 2011, 7, 4139–4142 RSC.
- D. Dendukuri, T. A. Hatton and P. S. Doyle, Langmuir, 2007, 23, 4669–4674 CrossRef CAS PubMed.
- J. Yan, K. Chaudhary, B. S. Chul, J. A. Lewis and S. Granick, Nat. Commun., 2013, 4, 40–50 Search PubMed.
- Q. Chen, J. Yan, J. Zhang, S. C. Bae and S. Granick, Langmuir, 2012, 28, 13555–13561 CrossRef CAS PubMed.
- T. Chen, Z. Zhang and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 717–722 CrossRef CAS PubMed.
- T. Chen, Z. Zhang and S. C. Glotzer, Langmuir, 2007, 23, 6598–6605 CrossRef CAS PubMed.
- S. Tsonchev, G. C. Schatz and M. A. Ratner, Nano Lett., 2003, 3, 623–626 CrossRef CAS.
- Z. L. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407–1413 CrossRef CAS.
- A. W. Long and A. L. Ferguson, J. Phys. Chem. B, 2014, 118, 4228–4244 CrossRef CAS PubMed.
- D. C. Rapaport, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 051905 CrossRef CAS PubMed.
- D. C. Rapaport, Phys. Rev. E, 2012, 86, 051917 CrossRef CAS PubMed.
- O. M. Elrad and M. F. Hagan, Phys. Biol., 2010, 7, 045003 CrossRef PubMed.
- M. F. Hagan and D. Chandler, Biophys. J., 2006, 91, 42–54 CrossRef CAS PubMed.
- R. Zandi, P. van der Schoot, D. Reguera, W. Kegel and H. Reiss, Biophys. J., 2006, 90, 1939–1948 CrossRef CAS PubMed.
- H. D. Nguyen, V. S. Reddy and C. L. Brooks III, Nano Lett., 2007, 7, 338–344 CrossRef CAS PubMed.
- D. C. Rapaport, Phys. Biol., 2010, 7, 045001 CrossRef CAS PubMed.
- J. P. Mahalik and M. Muthukumar, J. Chem. Phys., 2012, 136, 135101 CrossRef CAS PubMed.
- J. Xu, Y. Wang and X. He, Soft Matter, 2015, 11, 7433–7439 RSC.
- E. Weinan, W. Ren and E. Vanden-Eijnden, J. Chem. Phys., 2007, 126, 164103 CrossRef PubMed.
- P. F. Damasceno, M. Engel and S. C. Glotzer, ACS Nano, 2012, 6, 609–614 CrossRef CAS PubMed.
- G. van Anders, D. Klotsa, N. K. Ahmed, M. Engel and S. C. Glotzer, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E4812–E4821 CrossRef CAS PubMed.
- E. S. Harper, R. L. Marson, J. A. Anderson, G. van Anders and S. C. Glotzer, Soft Matter, 2015, 11, 7250–7256 RSC.
- P. Ceres and A. Zlotnick, Biochemistry, 2002, 41, 11525–11531 CrossRef CAS PubMed.
- R. F. Bruinsma, W. M. Gelbart, D. Reguera, J. Rudnick and R. Zandi, Phys. Rev. Lett., 2003, 90, 248101 CrossRef PubMed.
- D. J. Wales, Philos. Trans. R. Soc., A, 2005, 363, 357–375 CrossRef CAS PubMed.
- J. N. Israelachvili, Intermolecular and surface forces: revised third edition, Academic press, 2011 Search PubMed.
- A. Trovato, T. X. Hoang, J. R. Banavar and A. Maritan, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 19187–19192 CrossRef CAS PubMed.
- B. Berger, P. W. Shor, L. Tucker-Kellogg and J. King, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 7732–7736 CrossRef CAS.
- R. Schwartz, P. W. Shor, P. E. Prevelige and B. Berger, Biophys. J., 1998, 75, 2626–2636 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: The influences of number density and temperature on the calculated potential energy U, entropy S and free energy F are shown. The potential energy surfaces and defined characteristic parameters, f and activation energies, ΔEa of BAB-type cone-shaped particles, and the size effect of AB-type cone-shaped particles are also included. See DOI: 10.1039/c6ra10146a |
| This journal is © The Royal Society of Chemistry 2016 |