Combining microfluidic devices with coarse capillaries to reduce the size of monodisperse microbubbles

Abstract

In this work we report a significant advance for the preparation of monodispersed microbubbles, which are increasingly used and have become a key constituent in many advanced technologies. A new device comprising of two T-junctions containing coarse capillaries and operating in series was assembled. Microbubble generation was facilitated by using bovine serum albumin solution and nitrogen as the liquid and the gas phase, respectively. The effect of operating parameters such as gas pressure and liquid flow rate on the size of the microbubbles generated were investigated for the two T-junction systems and the results were compared with a single T-junction process. The experimental results showed that microbubbles produced via the double T-junction setup were smaller at any given gas pressure for both liquid flow rates of 100 and 200 μm studied in this work. A predictive model is developed from the experimental data, and the number of T-junctions was incorporated into this scaling model. It was demonstrated that the diameter of the monodisperse microbubbles generated can be tailored using multiple T-junctions while the operating parameters such as gas pressure and liquid flow rates were kept constant. The stability of the microbubbles produced was also examined and indicated that microbubbles produced through the double T-junction were more stable.

---

Introduction

Microbubbles, widely defined as bubbles with diameters in the range 1–1000 μm, have numerous applications in scientific fields, such as in food and chemical industries,¹ oil and energy generation,² cosmetic and agricultural technologies.^3,4 In addition, microbubbles are in great demand in the biomedical field for use as contrast agents and thrombus destruction,⁵ drug carriers and gene delivery,⁶ and for bacterial scavenging and biosensing.⁷ Different applications can have various requirements on microbubble size and size distribution, therefore the precise control of these is an essential factor, for example key biomedical uses of microbubbles such as ultrasound imaging and drug delivery demand the generation of near-monodisperse microbubbles in the 2–8 μm diameter range which are stable over a longer duration. Several methods have been utilised to produce microbubbles, including sonication,⁸ ink-jet printing,⁹ coaxial electrohydrodynamic atomization¹⁰ and gyration.⁷ However, a major problem with all of these methods is the lack of total monodispersity of microbubbles produced.¹¹

In contrast to other microbubble making methods, microfluidic technology is one of the most promising tools to generate microbubbles due to its capability of consistently generating monodisperse microbubbles. However, the microbubble size formed is critically dependent on the size of capillaries used and therefore, for solutions with high viscosity, the production of fine microbubbles becomes difficult with this technique.¹² New attempts have been made to ease microbubble production in microfluidics, for instance, with multi-array microchips¹³ and the use of sudden deepened configuration in the micro-channel.¹⁴ Depending on the flow pattern and the output product characteristics, microfluidics are categorised into three main geometries: co-flowing,¹⁵ flow focusing¹⁶ and cross-flowing.¹⁷ T-Junction cross-flowing devices are one of the simplest and most reliable geometries for production of monodispersed microbubbles.¹⁸ A remarkable advantage of the T-junction device in addition to reusability and cost efficiency is the control over the flow rate and hence reproducibility of microbubble formation satisfying similar criteria.

Albumin is extensively used as a stabilizing shell for microbubbles.¹⁹ It is often heated to denature and cross-link in order to form a stable shell for microbubbles. Microbubbles produced with non-cross-linked albumin have a higher liquid–vapour pressure and as a result they are less stable than the cross-linked albumin-shell microbubbles. Achieving cross-linked albumin-shell microbubbles through microfluidics devices is difficult, resulting in very few dedicated investigations into production of stabilized albumin microbubbles,²⁰ thus extending the stability of these in other ways are in demand at present. The production of bovine serum albumin (BSA) microbubbles, as biocompatible and non-toxic templates for scaffolds, has been previously investigated.^21,22 The pore size of the scaffold plays an important role in cell binding, migration and ingrowth,²³ and microfluidic techniques can facilitate the formation of uniform microbubble templates for scaffolds having ordered and homogenous porous textures.

In this paper, a new microfluidic system is proposed as a possible route to produce monodispersed microbubbles where coarse (200 μm diameter) capillaries were used and two T-junctions were combined in series to investigate the effect of operating parameters on microbubble size. In order to demonstrate this advance, two capillary embedded T-junction devices were aligned in series with a simple geometry that provides two inlets for liquid flow as opposed to a single T-junction setup. For the purpose of hydrodynamic analysis and to investigate how the addition of the second T-junction affects the size, structure and stability of microbubbles, both liquid inlet channels were fed with the same BSA solution. Thus a comparative study on microbubble formation with the single T-junction setup was conducted and a scaling model that can predict the microbubble diameter was generated by incorporating the number of T-junctions in the model as one of the variables. Reduction of the microbubble size to <10 μm diameter and modifying the microbubble chemistry (by using different materials and surfactants) were not specific aims of this work, however it was demonstrated that by using a predictive model on how the proposed apparatus can be used to form microbubbles of <10 μm by combining several junctions.

Experimental

Materials

BSA (≥98% lyophilized powder, Sigma Aldrich, U.K), with a relative molar mass of 66 kDa was used to prepare the solution (continuous phase) that enables formation of the shell material of the microbubbles. Distilled water was used to prepare 15% w/w BSA solution, by dissolving BSA with magnetic stirrers in volumetric flasks until a homogeneous solution was formed. Nitrogen was chosen as the dispersed phase (gas) for all the experiments.

Solution characterisation

The solution was characterized to determine the density, surface tension and viscosity. Density was measured using a standard density bottle DIN ISO 3507-Gay-Lussac. A Kruss tensiometer (Model DSA100, Kruss GmbH, Hamburg, Germany) was used to measure the surface tension using the Wilhelmy's plate method. A Brookfield DV-11 Ultra programmable Rheometer (Brookfield Engineering Laboratory Inc., USA) was utilized to measure the solution viscosity. All the measurements, presented in Table 1, were conducted at ambient temperature (21 °C) and relative humidity of 45% after calibrating the equipment with distilled water.

Table 1 Properties of BSA solution used in this work

Solution	Density	Surface tension	Viscosity
15 wt% bovine serum albumin	1014.7 kg m^−3	50.4 mN m^−1	16.2 mPa s

---

Microbubble generation

A schematic of the double T-junction device used in this work is shown in Fig. 1. The initial T-junction was created by inserting two Teflon FEP (Fluorinated Ethylene Polypropylene) capillary tubing with inner diameter of 200 μm perpendicularly to each other in to a polydimethylsiloxane (PDMS) block as inlet channels for the gas and liquid flows. A third capillary of 200 μm diameter was inserted into the exit channel of the block and was aligned with the gas supply channel to create a 200 μm gap that resulted in a confluence junction of two phases. A second PDMS block was used to insert the exit channel of the first T-junction perpendicular to the second liquid inlet flow with the same diameter (200 μm) FEP capillary tubing. The exit channel was aligned with the exit capillary tube of the initial T-junction that was inserted as one of the inlets of the second T-junction. The gap between the two aligned capillaries were kept constant at 200 μm. The gas was supplied via a tube to one of the first T-junction's inlets. A regulator and a digital manometer were also connected to the tube and used for pressure control and measurement, respectively. The liquid was supplied at a same rate to both T-junction inlets via syringe pumps (Harvard Apparatus Ltd., Edenbridge UK). The capillaries were fixed and secured to the channels using connectors to avoid leakage of gas and liquid. Microbubbles were collected using glass slides from the outlet capillary of the second T-junction.

Fig. 1 Schematic of the (a) single and (b) double T-junction cross-flow microfluidic device setup and (c) single and double T-junction with different exit channel lengths of 110 and 200 mm.

For a solution with given viscosity and flow rate, monodisperse microbubble generation only takes place in a certain range of supplied gas pressures with the largest microbubble generated at the highest gas pressure and smallest microbubble at the lowest gas pressure.³ At gas pressures below this range, liquid pushes the gas upwards and liquid dripping occurs, while jetting occurs when the gas pressure is increased above this range and microbubbles with a large size distribution are produced. In this work, a range of gas pressures that produced monodisperse microbubbles for each flow rate and geometry were investigated.

In order to investigate the effect of inserting the second T-junction on microbubble formation, comparative experiments were conducted. Initially, monodispersed microbubbles were obtained from the single T-junction, and collected on microscope slides to measure the diameter. Later, a second T-junction was connected to the outlet channel of the first single T-junction and the same solution was used as the liquid phase for both liquid inlet channels. Microbubbles were collected at the exit channel of the second T-junction.

For both single and double T-junction geometries, microbubbles were obtained at two flow rates, 100 μl min⁻¹ and 200 μl min⁻¹. For the single T-junction geometry, the microbubbles were collected at every 5 kPa from 15 to 70 kPa and from 15 to 80 kPa at flow rate of 100 and 200 μl min⁻¹, respectively. For the double T-junction geometry at flow rates of 100 and 200 μl min⁻¹, the microbubbles were collected at every 5 kPa from 20 to 75 kPa and from 35 to 80 kPa, respectively. In order to determine the microbubble stability at different flow rates, gas pressures and geometries, the size of microbubbles collected at 20 to 65 kPa at flow rate of 100 μl min⁻¹; 35 to 80 kPa at flow rate of 200 μl min⁻¹, for both geometries, were monitored every 5 minutes until all the microbubbles disappeared or dried. All experiments were conducted at ambient temperature (21 °C) and relative humidity of 45%.

Microbubble characterization

Microbubbles collected from the outlet of the device on microscope slides were immediately observed under an optical microscope (Nikon Eclipse ME 600) fitted with a camera (JVC KY-F55B). Microbubbles were studied at 5×, 10× and 20× magnifications. For each sample, 100 microbubbles were chosen to measure the diameter and stability over a fixed collection area of 1.5 mm². A Phantom 7.3 high speed camera with a maximum resolution of 800 × 600 pixels at up to 4800 fps giving 1.2 seconds of recording time (Vision Research Ltd., UK) was also used to obtain real time video images of the microbubble formation process (see example in ESI†). The coefficient of variation (CV), defined as CV = o′/d_aν × 100%, where o′ is the standard deviation, and d_aν is for the mean diameter of microbubbles, was calculated by measuring the diameter of 100 microbubbles for each sample tested.

Results and discussion

Effect of the addition of the second T-junction on the formation of microbubbles

In this part of the work, high speed video images (see ESI†) were used to analyse how the addition of the second T-junction affects the flow and shape of microbubbles within the microchannels. At a constant liquid flow rate of 100 μl min⁻¹ for both liquid inlet channels, gas pressure was increased from 130 to 190 kPa. As shown in the micrographs in Fig. 2ai–ci, by increasing the gas pressure, microbubble size increased in the same manner as a single T-junction from 220 to 340 μm. The shape of microbubbles within the channels changed from nearly spherical to plug-like by increasing the gas pressure, which lead to a larger microbubble diameter after collection. Another factor that was observed through the high speed camera images is that by introducing the second T-junction, the distance between generated microbubbles was increased in all the cases after they passed through the second T-junction. For instance, the initial distance between two microbubbles prior to passing the second T-junction was L₁ = 600 μm at gas pressure of 130 kPa, which increased to L₂ = 810 μm. The same trend was detected for higher gas pressures (Fig. 2aii–cii). The introduction of an additional liquid flow via the second T-junction increases the velocity of bubbly flow in the exit channel of the second T-junction and hence the liquid phase pushes the adjacent microbubbles away from each other, that leads to increased distances between the microbubbles. This phenomenon can later assist with reduction in bubble coalescence within the microchannels prior to collection.

Fig. 2 Micrographs and high speed camera images of microbubbles produced in the double T-junction geometry at a constant flow rate of 100 μl min⁻¹ and gas pressures of (a) 130, (b) 160 and (c) 190 kPa. Microbubble diameter, L₁ and L₂ for each case (in μm) is (a) 220, 410, 620, (b) 280, 715, 995 and (c) 340, 945, 1080.

Effect of pressure, flow rate and geometry on microbubble diameter

Flow rates of 100 and 200 μl min⁻¹ were selected and applied to both the single and double T-junctions. Once the microbubbles were formed at the minimum gas pressure for a given flow rate, the gas pressure was systematically increased. The flow rate ratios as well as the microfluidic geometry determine the minimum gas pressure that enables microbubble production. In order to determine this minimum value, gas pressure was increased slowly until microbubbling was achieved. The minimum gas pressures that produced the smallest microbubbles using the single T-junction at flow rate of 100 and 200 μl min⁻¹ were 15 and 20 kPa, respectively. The value of the minimum gas pressure was increased to 20 and 35 kPa with flow rates of 100 and 200 μl min⁻¹, respectively using the double T-junction. Microbubble formation in a microfluidic device is governed by the pressure balance between continuous and dispersed phase at the junction.²⁴ For the case of liquid and gas, as the pressure becomes equal at the junction, the liquid column starts forcing the gas backwards. To generate microbubbles the gas pressure has to be increased so that it penetrates the liquid column and microbubble formation begins.²⁵ Consequently, at low liquid flow rates using the single T-junction, microbubbling occurs at relatively low gas pressures. On the contrary, at high liquid flow rates, high gas pressure is required to enable microbubble formation. However, the minimum gas pressure that enables microbubble production is always higher using the double T-junction than that of single T-junction even at the same liquid flow rate. This is most likely due to the fact that the additional liquid flow into the second junction causes the total flow rate of the liquid to increase; therefore the ratio of liquid to air flow is increased. Subsequently, in order to start microbubbling, higher gas pressure is required for the double T-junction.

As shown in Fig. 3, the largest microbubble was obtained from the single T-junction at the lower flow rate 100 μl min⁻¹ and highest gas pressure, whilst the smallest microbubble was obtained using the double T-junction with higher flow rate (200 μl min⁻¹) and lowest gas pressure. At a lower flow rate of 100 μl min⁻¹, the microbubbles generated using double T-junction had smaller dimensions than that formed by a single T-junction. Similarly, at the higher flow rate of 200 μl min⁻¹ (Fig. 3), the size of microbubbles obtained was smaller in the double T-junction. For a fixed flow rate and gas pressure, double T-junction geometry provides microbubbles with smaller diameters. According to the scaling law from Garstecki et al.,²⁶ the length of the immiscible slug, L, is proportional to the flow rate ratio in a T-junction: where d is the width of the channel, Q_l and Q_g are the liquid and gas flow rates, respectively, and α is a constant. By calculating the capillary numbers Ca = 0.002 and 0.003 (Ca < 0.01) of the liquid phase at both flow rates of 100 and 200 μl min⁻¹, respectively, the breakup mechanism of microbubble formation in this work is found to be in the squeezing regime. Therefore, microbubble diameter is dominated by the flow rate ratio .²⁷ The microbubble diameter is increased as the flow rate ratio increased. Therefore, the additional liquid phase in to the second T-junction resulted in a smaller flow rate ratio of gas to liquid. This process generated uniformly size microbubbles which are smaller than that generated from the single T-junction. As indicated in Fig. 3, microbubbles that were generated with higher flow rate were smaller than those with lower flow rate using the double T-junction device, which suggests that the size of these bubbles can be controlled by varying the rate of flow of the liquid and gas pressure at both T-junctions of the double T-junction setup.

Fig. 3 Graphs demonstrating the range of microbubble diameters obtained at various gas pressures for liquid flow rates of 100 and 200 μl min⁻¹ for both single and double T-junction geometries (D_b and P_g are the diameter of microbubble and gas pressure, respectively).

In order to provide a predictive model to better understand the effect of addition of second T-junction, the microbubble diameter scaled according to the channel diameter is plotted against 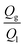(Fig. 4a). For the range of gas/liquid flow ratios studied in this work (i.e. the gas pressure range that microbubble formation is possible), a scaling model derived from the curve fit of plots presented in Fig. 4a can be represented as:

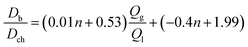where n (≥1) is the number of T-junctions, D_b and D_ch are, microbubble and channel diameter, respectively. The predictive data was plotted against the experimental results as demonstrated in Fig. 4b. The proximity of experimental points to the parity line shows that both the experimental and predictive data are in good agreement. For the given flow ratios used in this study at a channel diameter of 200 μm, the number of T-junctions required in order to achieve different microbubble size can be predicted from the model.

Fig. 4 (a) Plots of the dimensionless ratio between microbubbles and channel size at various gas to liquid flow ratios, (b) predicted scaling line fitted for experimental data (R² = 0.95).

The predictive scaling model was further used in order to demonstrate the number of T-junctions required for producing microbubbles of desired diameter. For this purpose, the range of gas/liquid flow ratios tested in this work as well as capillary diameter of 200 μm was incorporated in the model. The predicted microbubble diameters with the number of T-junctions were then plotted for . Fig. 5 illustrates these predictions and shows that with the 200 μm diameter coarse capillary used, at a given flow rate it is possible to generate monodisperse microbubbles with diameter approaching 10 μm, for example at this can be achieved with six T-junctions used in series. The capillary channel diameter (D_ch) has a significant influence on the predicted microbubble diameter, and at higher capillary diameters similar to the one used in this work (200 μm) more T-junctions may be required to be aligned to reduce microbubble diameter at a given flow rate. Conversely, using fine channel diameters < 200 μm aids to reduce the number of T-junctions required, however, as discussed earlier, this makes microbubble forming with viscous solutions more difficult and inconsistent.

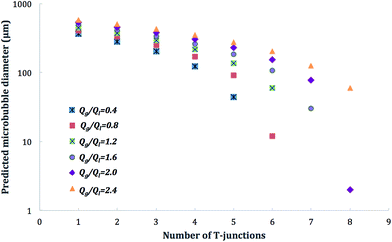Fig. 5 Relationship between diameter of monodisperse microbubbles generated and number of T-junctions used as a function of , channel diameter (D_ch) in eqn (1) was taken at 200 μm as used in our experiments.

Microbubble residence time within the channels and production rate

In this part of study, the microbubble residence time within the exit channel from formation to collection was measured using three different configurations shown in Fig. 1c. In order to verify the findings, microbubbles with different size and formation time were investigated by increasing the supplied gas pressure from 50 to 70 kPa at a constant flow rate of 100 μl min⁻¹. Microbubbles are formed at the orifice of the exit channel of the single T-junction and the first T-junction in case of double T-junction. Two different lengths were chosen for the single T-junction of 110 and 200 mm. From the measured data taken from high-speed camera images, plots of residence time are shown in Fig. 6. The residence time for shorter channel length was smaller (130 to 160 ms). The graph of residence time for the single T-junction with 200 mm exit channel length has shown the highest values of 270 to 310 ms. Microbubbles produced in the double T-junction had a smaller residence time than for the single T-junction with 200 mm exit channel length. However, the residence time for microbubbles within the double T-junction device was longer in comparison with the single T-junction of shorter exit channel (110 mm). While increasing the microbubble residence time within single T-junction channels can lead to lower production rates, the addition of second T-junction (i.e. increasing the exit channel length by introducing a second source of liquid flow) resulted in the reduction of microbubble size.

Fig. 6 Graphs representing residence time of microbubbles from formation to collection within the microchannels at different lengths of 110 and 200 mm for constant liquid flow rate of 100 μl min⁻¹.

The microbubble production rates of the systems used in this study are given in Table 2. This data shows that for a fixed value, the addition of a second T-junction was very effective in increasing production rates. Usually, microfluidic devices give lower microbubble production rates compared with jetting techniques such as co-axial electrohydrodynamic atomisation.^28,29 However, in the electrohydrodynamic jetting method the size distribution of the microbubbles generated is much wider and it is experimentally impossible to produce monodisperse microbubbles similar to the present work. Multi-array lithographic microfluidic devices can be effective in increasing microbubble production rates and the size of microbubbles generated.¹³ On the other hand, lithographic technology is expensive compared to the proposed device combing T-junction in series that also offers both increased production rates and reduction of microbubble size. The production rates reported in this work are lower than the values for T-junction microbubble production rates given in the review literature,²⁹ however these also depend on capillary diameter and microbubble size and flow rate.

Table 2 The effect of gas–liquid flow rate ratio and number of T-junctions used on measured microbubble production rate at a constant liquid flow rate of 100 μl min⁻¹. The percentage increase in microbubble production due to second T-junction is also given

Qg/Ql	Single T-junction production rate (microbubble per min)	Double T-junction production rate (microbubble per min)	% increase
1.4	1.697 × 10^4	2.787 × 10^4	64
1.6	1.971 × 10^4	2.790 × 10^4	42
1.7	2.039 × 10^4	2.923 × 10^4	43
1.9	2.112 × 10^4	3.001 × 10^4	43
2.0	2.242 × 10^4	3.75 × 10^4	40

---

Stability study of microbubbles generated with different geometries

The mean diameter of microbubbles generated at different gas pressures for a given flow rate and geometry was measured as a function of time. For each sample, 100 microbubbles were randomly selected and measured every 3 to 5 min until all the microbubbles disappeared or their BSA shell dried. As demonstrated in the micrographs in Fig. 7, the least stable microbubbles were produced from the single T-junction with flow rate of 100 μl min⁻¹ at 65 kPa and with flow rate of 200 μl min⁻¹ at 80 kPa with mean diameter of 484 ± 8.9 μm and 447 ± 6.5 μm, respectively. On the other hand, microbubbles produced with liquid flow rate of 200 μl min⁻¹ for both liquid phases at 35 kPa using double T-junction were found to be the most stable, with an average diameter of 272 ± 5.2 μm, being stable up to 40 minutes after collection.

Fig. 7 Micrographs showing the lifetime of microbubbles for both single and double T-junctions at both flow rates studied (100 and 200 μl min⁻¹) and various gas pressures.

Microbubbles shrink with time due to gas dissolution to the surroundings, and those produced with smaller size were found to be more stable. This behaviour could be explained by the fact that microbubbles made of a solution with given viscosity have a constant surface tension which is responsible for cohesive forces among liquid molecules. For microbubbles with larger size, their gas–liquid interface is loosely packed and therefore gas dissolution is more likely to take place.²⁰ Consequently, smaller microbubble whose gas–liquid interface is more densely packed were stable for a longer period.

The effect of liquid flow rate on microbubble stability was studied by comparative experiments. As shown in Fig. 8, microbubbles that were generated at higher liquid flow rates were found to be more stable than those generated at lower flow rates in both geometries. This is most likely to be due to the fact that microbubbles produced with higher liquid flow rate at the same gas pressure are smaller. According to Epstien and Plesset,³⁰ the rate of dissolution of gas and as a result the rate of change of microbubble size depends on factors such as surface tension, and rate of gas diffusion into the liquid shell. Laplace pressure is inversely proportional to microbubble diameter, however, BSA microbubbles act differently to surfactant coated microbubbles, as well as the packing and order of the bubbles vary and as a result Ostwald ripening seems to occur more in the larger microbubble diameter samples. Since the stability of microbubbles exposed to atmospheric conditions is dominated by their radius, smaller microbubbles have lower gas exchange rate with surroundings, hence they are more stable. On the other hand, the stability of the same size microbubbles generated at different flow rates and consequently different gas pressures were also studied. Microbubbles which were obtained from single T-junction with flow rate of 100 μl min⁻¹ at gas pressure of 20 and 50 kPa have mean diameter of 315 ± 3.9 and 405 ± 5.5 μm, respectively. Microbubbles with mean diameter of 321 ± 4.0 and 407 ± 6.3 μm were obtained with higher liquid flow rate of 200 μl min⁻¹ at higher gas pressures of 35 and 65 kPa, respectively. It was observed that both these microbubbles with similar diameter of 315 and 321 μm (1.9% variation) lasted for 20 minutes after collection, and microbubbles with diameter of 405 and 407 μm (0.49% variation) were stable for 15 minutes. This behaviour of microbubble stability is consistent with previous findings.³¹ Thus, we can assume that, the stability of microbubbles with same diameter generated via single T-junction is not significantly influenced by either flow rate or gas pressure.

Fig. 8 Graphs showing the reduction of microbubble diameter with time (after collection) for microbubbles produced in (a*) single T-junction, (a**) double T-junction at 100 μl min⁻¹ and (b*) single T-junction, (b**) double T-junction at 200 μl min⁻¹.

More importantly, the influence of the microfluidic production geometry on microbubble stability was significant. As illustrated in Fig. 7 and 8, for a given flow rate and gas pressure, microbubbles generated from double T-junction were relatively more stable than that generated from the single T-junction. For instance, microbubbles generated from single T-junction lasted for 10 minutes, however, the microbubbles obtained from the double T-junction at 200 μl min⁻¹ and 80 kPa lasted for 20 min. Also, microbubbles produced from the double T-junction have a steadier size decrease rate, whereas this is more rapid for microbubbles collected from the single T-junction. This could be attributed to size difference between microbubbles made form single and double T-junctions. As mentioned before, the addition of the second T-junction reduced the microbubble diameter, hence delivering improvement in the stability. Interestingly, for the same size microbubbles which were made from both single and double T-junctions at the same liquid flow rate, it was experimentally observed that the stability of the microbubbles generated from the double T-junction is higher. For instance, at liquid flow rate of 100 μl min⁻¹, microbubbles generated using the single T-junction at 20 kPa and double T-junction at 20 kPa have approximately similar size of 315 ± 3.9 and 308 ± 6.6 μm, respectively, and lasted for 20 and 25 min accordingly. Similarly, at higher flow rate, microbubbles (305 ± 6.2 μm) obtained from the double T-junction lasted up to 30 minutes after collection, while microbubbles (300 ± 3.8 μm) produced with the single T-junction were stable for only 20 minutes. This could be attributed to stabilization by the additional liquid phase provided at the second T-junction of double T-junction. In order to conclude from observations of stability of microbubbles, those microbubbles with approximately similar diameter were more stable owing to the additional BSA coating through the liquid phase on the second T-junction. From the findings in this study, it can be envisaged that it is advantageous to use multiple coating materials for the shell of microbubbles via multiple junctions to produce even more stable microbubbles. This is the focus of our present work.

Conclusions

In this work, a new double T-junction device was tested to investigate the potential for producing microbubbles. It was shown that the size and production of microbubbles could be manipulated by introduction of a second junction into the commonly used single T-junction device. A comparison study was conducted to produce BSA microbubbles both with a single T-junction and then a double T-junction. The microbubbles produced via the double T-junction were different in size and stability for a given flow rate and gas pressure. It was shown that for the highest liquid flow rate (200 μl min⁻¹) at the lowest gas pressure (35 kPa), microbubbles generated were smaller (272 ± 5.2 μm) in the double T-junction. This can be described by the diffusion of gas into the liquid phase due to a longer residence time inside the microchannels, compared to a single T-junction system. While the diffusion of gas takes place, the velocity of the mixed flow is increased by the additional liquid flow rate through the second T-junction and therefore the production rate is not compromised by keeping the microbubbles in microchannels by increasing the length of the single T-junction exit channel length. From the experimental data, for the range of the ratio of the gas/liquid flows studied, a scaling predictive model was obtained where the normalized microbubble diameter can be estimated for a given number of T-junctions connected. The experimental results and the predictive data were plotted and the proximity of the experimental data to the parity line proved that the predictive model is in agreement with the experimental data. A key feature from this predictive model is to investigate whether it is possible to reduce the microbubble size progressively by connecting more T-junctions to the current setup to enable production of microbubbles with diameters < 10 μm (such as would be required for intravenous administration in biomedical applications). It is shown from the predictive model that achieving this with the same coarse channel diameter of 200 μm is viable by increasing the number of T-junctions. Furthermore, it is shown that the stability of microbubbles was improved by inserting the second T-junction.

Acknowledgements

The authors wish to thank University College London for part financial support of this work, in particular for the first author.

References

1. G. M. Campbell and E. Mougeot, Trends Food Sci. Technol., 1999, 10, 283–296.
2. D. Mikhailov, J. Appl. Mech. Tech. Phys., 2012, 53, 366–378.
3. M. Parhizkar, M. Edirisinghe and E. Stride, Microfluid. Nanofluid., 2013, 14, 797–808.
4. H. Ikeura, F. Kobayashi and M. Tamaki, J. Food Eng., 2011, 103, 345–349.
5. J. H. Xu, S. W. Li, J. Tan, Y. J. Wang and G. S. Luo, AIChE J., 2006, 52, 3005–3010.
6. E. C. Unger, T. O. Matsunaga, T. McCreery, P. Schumann, R. Sweitzer and R. Quigley, Eur. J. Radiol., 2002, 42, 160–168.
7. S. Mahalingam, Z. Xu and M. Edirisinghe, Langmuir, 2015, 31, 9771–9780.
8. Q. Xu, M. Nakajima, S. Ichikawa, N. Nakamura and T. Shiina, Innovative Food Sci. Emerging Technol., 2008, 9, 489–494.
9. M. Kukizaki and M. Goto, Colloids Surf., A, 2007, 296, 174–181.
10. U. Farook, E. Stride and M. J. Edirisinghe, J. R. Soc., Interface, 2009, 6, 271–277.
11. H. Peng, Z. Xu, S. Chen, Z. Zhang, B. Li and L. Ge, Colloids Surf., A, 2015, 468, 271–279.
12. A. Gunther and K. F. Jensen, Lab Chip, 2006, 6, 1487–1503.
13. M. R. Kendall, D. Bardin, R. Shih, P. A. Dayton and A. P. Lee, Bubble Sci., Eng., Technol., 2012, 4, 12–20.
14. S. A. Peyman, R. H. Abou-Saleh, J. R. McLaughlan, N. Ingram, B. R. G. Johnson, K. Critchley, S. Freear, J. A. Evans, A. F. Markham, P. L. Coletta and S. D. Evans, Lab Chip, 2012, 12, 4544–4552.
15. R. Xiong, M. Bai and J. N. Chung, J. Micromech. Microeng., 2007, 17, 1002–1011.
16. T. T. Fu, Y. G. Ma, D. Funfschilling and H. Z. Li, Chem. Eng. Sci., 2009, 64, 2392–2400.
17. Y. Zhang and L. Wang, Nanoscale Microscale Thermophys. Eng., 2009, 13, 228–242.
18. T. Thorsen, R. W. Roberts, F. H. Arnold and S. R. Quake, Phys. Rev. Lett., 2001, 86, 4163–4166.
19. S. Sirsi and M. Borden, Bubble Sci., Eng., Technol., 2009, 1, 3–17.
20. J. L. Chen, A. H. Dhanaliwala, A. J. Dixon, A. L. Klibanov and J. A. Hossack, Ultrasound Med. Biol., 2014, 40, 400–409.
21. M. Parhizkar, P. Sofokleous, E. Stride and M. Edirisinghe, Biofabrication, 2014, 6, 045010.
22. A. Nair, J. Yang and L. Tang, Engineering in Medicine and Biology Workshop, 2007 IEEE Dallas, 2007, vol. 9903115, pp. 31–34.
23. S.-M. Lien, L.-Y. Ko and T.-J. Huang, Acta Biomater., 2009, 5, 670–679.
24. E. Castro-Hernandez, W. van Hoeve, D. Lohse and J. M. Gordillo, Lab Chip, 2011, 11, 2023–2029.
25. M. Parhizkar, E. Stride and M. Edirisinghe, Lab Chip, 2014, 14, 2437–2446.
26. P. Garstecki, M. J. Fuerstman, H. A. Stone and G. M. Whitesides, Lab Chip, 2006, 6, 437–446.
27. G. F. Christopher, N. N. Noharuddin, J. A. Taylor and S. L. Anna, Phys. Rev. E, 2008, 78(3), 036317.
28. S. Mahalingam, M. Meinders and M. Edirisinghe, Langmuir, 2014, 30, 6694–6703.
29. E. Stride and M. Edirisinghe, Soft Matter, 2008, 4, 2350–2359.
30. C. E. P. Epstein and M. S. Plesset, J. Chem. Phys., 1950, 18, 1505–1509.
31. G. Mohamedi, M. Azmin, I. Pastoriza-Santos, V. Huang, J. Perez-Juste, L. M. Liz-Marzan, M. Edirisinghe and E. Stride, Langmuir, 2012, 28, 13808–13815.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra09802a

---