Tuning the phase transition temperature, electrical and optical properties of VO₂ by oxygen nonstoichiometry: insights from first-principles calculations

Abstract

Vanadium dioxide (VO₂) is one of the most promising thermochromic materials with a reversible metal–insulator transition (MIT) from a high-temperature rutile phase to a low-temperature monoclinic phase, although a high MIT temperature (T_c) of 340 K for bulk VO₂ restricts its wide application. Our first-principles calculations show that the oxygen nonstoichiometry plays an important role in tuning the MIT behavior of VO₂. The O-vacancy in bulk VO₂ gives rise to an increase in electron concentration, which induces a decrease in T_c. On the other hand, O-vacancy and O-adsorption on VO₂(R) (1 1 0) and VO₂(M) (0 1 1) surfaces could alter their work functions and in turn regulate T_c. In addition, the formation and adsorption energies of O-adsorption on the two types of surfaces are negative, indicating that VO₂ surfaces are prone to oxidation in ambient air. The present results contribute to both tuning phase transition behaviors experimentally and reducing hindrances for the advanced applications of VO₂-based materials.

---

1. Introduction

Vanadium dioxide (VO₂), the most well-known one among vanadium oxides, has attracted widespread attention in recent years due to its reversible metal–insulator transition (MIT) at ∼340 K, accompanying a sharp change in electrical resistance spanning 5 orders of magnitude and optical change in the infrared region from a relative transparent state to a more reflective state.^1–3 Exploiting this unique feature, VO₂ becomes scientifically fascinating and technologically promising for various applications, such as optoelectronic devices, sensors, Mott transistors, memristors and thermochromic smart windows.^4–8

Although most of the practical applications of VO₂-based materials are based on its ultrafast MIT, the high phase transition temperature restricts the utilization of VO₂. Many efforts have been made to tune the metal–insulator phase transition behavior of VO₂, including doping,⁹ external strain,¹⁰ electric field,¹¹ surface and interface engineering,^12,13 and nonstoichiometry effect.^14–27 Among these measures, to control oxygen nonstoichiometry of VO₂ is one of the most effective routes. On the experimental side, through reactive magnetron sputtering, the resistivity ratios between the insulator and metallic phases for VO₂ with the voided boundaries and oxygen vacancies are limited to 10³ orders.¹⁵ Using the electrolyte gating with ionic liquids method, the electric field-induced creation of oxygen vacancies with the concentration between 0 and 50% suppresses the metal–insulator transition in VO₂ films and stabilizes the metal phase to temperature below 5 K.¹⁶ Recently, Chen et al.¹⁷ found that electrolyte gating with ionic liquids on VO₂ is effective to modulate the MIT behavior, which is due to the existence of oxygen-vacancy diffusion channel. Through controlling the oxygen partial pressure, the distinctive changes in the metal–insulator transition and transport behaviors were also observed.^16,18 In fact, it was firstly reported in ref. 20 and 21 that the introduction of O-vacancy into VO₂ reduces its T_c and even alters its electrical and optical properties. Later, Chen et al.^22,23 proposed that it is the left electrons upon the formation of oxygen vacancies in VO₂, corresponding to the donor doping, that cause the reduction of the phase transition temperature of VO₂.²⁸ Moreover, the high sensitivity of the MIT behavior of VO₂ to O-vacancy concentration has been observed via various experimental measurements such as optical pump-terahertz probe spectroscopy, positron annihilation spectroscopy or oxide-molecular beam epitaxial method.^24–26

On the theoretical side, only a few studies of oxygen-nonstoichiometry on the transition phase behavior of VO₂ could be located. Using the Tran–Blaha modified Becke–Johnson (TBmBJ) generalized gradient approximation (GGA) functional, it was found that O-vacancy in VO₂(M) has the higher thermodynamic stability than other defects such as V-vacancy and O-interstitial and exhibits ferromagnetism at room temperature.²⁹ Within the generalized gradient approximation of Perdew–Burke–Ernzerhof, Mellan et al. investigated the redox behavior of the VO₂(1 1 0) surface as a function of temperature and oxygen partial pressure, and found that the destabilization of VO₂(R) surface should be attributed to the redox reaction occurring both at ambient conditions and at the more reducing conditions.³⁰ The above experimental and theoretical investigations suggest that oxygen nonstoichiometry in VO₂ has great impact on its phase transition behavior and phase transition temperature.

It is worth mentioning that the degrees of MIT-induced variations in work function and resistivity of VO₂ are affected by oxygen nonstoichiometry^31,32 and even the reduced VO₂ nanobeams further induce the work function to a lower value with respect to the pure VO₂.³³ For instance, using Kelvin force microscopy (KFM) measurement, it is found that the work function of the VO₂ surface increases from 5.15 to 5.30 eV with the increase of temperature from 300 to 368 K.³² Therefore, it is of vital importance to reveal the underlying mechanism on the effects of oxygen nonstoichiometry to the phase transition behavior for realizing the rational tuning of the T_c. In the present work, using the first-principles calculations, we study the influence of oxygen nonstoichiometry on the phase transition behavior of VO₂ including phase transition temperature, electrical and optical properties, and work function, which will contribute to the general understanding of its intrinsic MIT properties and provide a theoretical reference for further experimental research.

The remainder of this paper is organized as follows. The computational details are outlined in Section 2. Section 3 details the computational models and energetics, while Section 4 discusses the influence of oxygen nonstoichiometry on the phase transition behavior of VO₂ from both bulk and surface aspects. The most significant conclusions from this study are summarized in Section 5.

2. Computational details

The calculations were conducted with the Vienna ab initio simulation package (VASP) based on a plane wave density functional code.^34,35 The projector augmented wave (PAW) pseudopotentials and the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional were used in the calculations.^36,37 To account for strong on-site Coulomb repulsion among the V 3d electrons, the Hubbard parameter U was added to the PBE functional by referring to the rotationally invariant approach of Dudarev et al.,³⁸ in which only the difference (U_eff = U − J) between the Coulomb repulsion U and screened exchange J parameters must be specified. Despite the fact that choice of the U is often adjusted to match existing experimental quantities, the Dudarev DFT + U method has been shown to accurately describe the electronic structure and strong correlation of VO₂.³⁹ As discussed in Pickett et al.,⁴⁰ optimal values for U_eff in GGA + U formalism are around 4.0 eV. For instance, Zhang et al.⁴¹ successfully described the effect of W doping on the T_c of VO₂. Our first-principles calculations showed that hydrogen is an efficient dopant which can stabilize the metallic VO₂ phase at ambient temperature⁴² and the T_c of VO₂ can be regulated by constructing Ag/VO₂ double film.¹³ As discussed in ref. 13 and 39–43, U_eff was chosen to be 3.4 eV in the present calculations.

Valence electron configurations for the elemental constituents are as follows: V-3d³4s², O-2s²2p⁴. The cutoff energy for the plane-wave basis is 530 eV, and Brillouin zones are sampled using 3 × 3 × 3 and 2 × 2 × 1 Monkhorst–Pack grids for bulk VO₂ and VO₂ surfaces, respectively. This set of parameters assures that the total energies converge to 1 × 10⁻⁵ eV per unit cell. Lattice constants and internal coordinates are fully optimized until Hellmann–Feynman forces become less than 0.01 eV Å⁻¹. For calculation of the electronic density of states (DOS), we use a 5 × 5 × 5 k-point mesh and the linear tetrahedron method with Blöchl corrections for bulk VO₂.

In general, the optical properties of the material are reflected by its transmissivity (T), the reflectivity (R) and the absorptivity (A), and their relationship can be expressed as

T + R + A = 1. (1)

Besides, the absorption coefficient (α(ω)) and reflectivity spectra (R(ω)) can be derived from ε₁(ω) and ε₂(ω), which are calculated via:

ε(ω) = ε₁(ω) + iε₂(ω), (2)

where the real part (ε₁(ω)) of the dielectric function can be obtained from the imaginary part with the famous Kramers–Kronig relationship. The imaginary part (ε₂(ω)) of the dielectric function can be regarded as detailing of the real transitions between the occupied and unoccupied electronic states.⁴⁴

3. Computational models and energetics

Based on the monoclinic and rutile VO₂ crystal structures as shown in Fig. 1, the basic calculations are performed in the supercells with 2 × 2 × 4 and 2 × 2 × 8 primitive unit cells containing 192 atoms for two phases, labeled as VO₂(M) and VO₂(R), respectively. In order to reveal the effect of the O-vacancy concentration on the phase transition between VO₂(M) and VO₂(R), the cases of one and two O-vacancies are simulated by removing one and two oxygen atoms from each phase, labeled as VO_1.984 and VO_1.969, respectively.

Fig. 1 Schematic drawings of the crystal structures of (a) monoclinic and (b) rutile VO₂. The V, O1 and O2 atoms are represented by gray, red and blue spheres, respectively.

Although the various low-index rutile (1 1 0), (1 0 0), (0 0 1), (1 0 1) and (1 1 1) surfaces were observed by high-resolution TEM,⁴⁵ the rutile (1 1 0) and monoclinic (0 1 1) surfaces are the energetically favorable with the lower surface energies (calculated values: 0.29 and 0.37 J m⁻²) compared with other surfaces.^19,30 Therefore, we focus on the rutile (1 1 0) and monoclinic (0 1 1) surfaces to analyze the influence of oxygen nonstoichiometry on the phase transition behavior of VO₂. Also, it is worth mentioning that the low-energy electron-diffraction shows the rutile VO₂(1 1 0) surface has diffraction patterns consistent with those expected from termination of the bulk,⁴⁵ i.e., no surface reconstruction was observed on the rutile VO₂(1 1 0) surface. As shown in Fig. 2(a) and (c), VO₂(R) (1 1 0) and VO₂(M) (0 1 1) surfaces are modeled by symmetric slabs with the p(4 × 2) and p(2 × 2) unit cells, respectively. The x[0 0 1] and y[1 1̄ 0] dimensions in VO₂(R) (1 1 0) surface are 11.408 and 12.875 Å, respectively. While, the x[0 1 1̄] and y[1̄ 0 0] dimensions in VO₂(M) (0 1 1) surface are 11.486 and 14.002 Å, respectively. These are based on the optimized bulk lattice parameters for two phases. Our test calculations with various supercell sizes indicate that a p(4 × 2) supercell for VO₂(R) (1 1 0) surface and a p(2 × 2) supercell for VO₂(M) (0 1 1) ensure a formation energy of oxygen vacancy (oxygen adsorption) convergence within 0.04558 eV per f.u. (0.03251 eV per f.u.) and 0.04638 eV per f.u. (or 0.04346 eV per f.u.), respectively. Fig. 2(a) and (c) show that the slabs for VO₂(R) (1 1 0) and VO₂(M) (0 1 1) surfaces have 12.22 Å and 12.36 Å thickness, respectively. A vacuum layer of 18 Å is introduced to separate the slabs along the z direction. The vacuum layer guarantees that no unphysical interactions between the slab and its periodic images perpendicular to the surface influence the calculations. The bottom 5 atomic layers are fixed to simulate a bulk environment (see regions enclosed by dashed lines in Fig. 2(a) and (c)) and remaining layers are allowed to relax.

Fig. 2 (a) VO₂(R) (1 1 0) with O-vacancy at different atom layers, (b) an oblique view of the possible sites for O-adsorption above the VO₂(R) (1 1 0) surface, (c) VO₂(M) (0 1 1) with O-vacancy at different atom layers, and (d) an oblique view of the possible sites for O-adsorption above the VO₂(M) (0 1 1) surface. The V and O atoms are represented by gray and red spheres, respectively.

To explore the various possible adsorption models of oxygen on the VO₂(R) (1 1 0) and VO₂(M) (0 1 1) surface, oxygen atom is placed at the various initial sites relative to surface O or V atoms as shown in Fig. 2(b) and (d). Four adsorption sites are considered: V_5c (O at the top of 5-fold coordinated V atom); V_6c (O at the top of 6-fold coordinated V atom); O_br (O at the top of 2-fold coordinated O atom); O_3c (O at the top of 3-fold coordinated O atom). To determine the formation of O-vacancy with different locations at the two surfaces, one oxygen atom in the first, second, and third O-atomic layer is removed, which are denoted as V_Obr, V_O3c, and V_O4c, respectively, as shown in Fig. 2(a) and (c).

The adsorption energy, E_ads, of oxygen on the surfaces is calculated via

where N is the number of adsorbed O atoms, E_O/VO2 and E_VO2 are the total energies with and without O adsorbed surfaces, respectively. E_O is the energy of an isolated oxygen atom. If the adsorption energy is negative, it means that O adsorption on the surface is energetically favorable.

To compare the relative stability among various configurations with O-vacancy and O-adsorption, the formation energy (E_f) is calculated via

where E_perfect and E_defect are the total energies of the VO₂ supercells with and without O-vacancy or O-adsorption. E(O₂) is the total energy of molecular oxygen. x is the number of oxygen atoms added into or removed from VO₂. ±: − denotes that oxygen atom is added into VO₂; + represents that oxygen atom is removed from VO₂.

4. Results and discussion

4.1 Bulk VO₂

4.1.1 Atomic and electronic structures of bulk VO₂ with and without O-vacancy. As shown in Fig. 1(a), there are two different oxygen sites (O1 and O2) in monoclinic VO₂,⁴⁶ which are labeled by red and green spheres, respectively. In order to determine O-vacancy position, the formation energies of O-vacancy at the two different oxygen sites (O1 and O2) in VO₂(M) are calculated. By using eqn (2), the vacancy formation energies for O1 and O2 site are 3.605 and 3.883 eV, respectively, showing that the O1 site is energetically favorable over the O2 site by about 0.278 eV in the bulk VO₂(M). The calculated O1-vacancy formation energy (3.605 eV) is very close to the value of 3.4 eV, which is reported by Appavoo et al.¹⁹ using the same PBE + U formulation with the U value of 4.0 eV and the J value of 0.68 eV. Simultaneously, the formation energy of O-vacancy obtained by Mellan et al.³⁰ is about 3.53 eV after correction using the GGA approximation. Our calculated bind energy and bond length of O₂ molecule are 6.67 eV and 1.233 Å, respectively, compared with the 7.43 eV and 1.21 Å in ref. 47. The overestimation of the bind energy of O₂ is a common feature in the DFT calculations. Accordingly, we only consider the O-vacancy on the O1 site in the following calculations.

Table 1 summarizes the lattice parameters and band gaps of bulk VO₂(R) and VO₂(M). It can been seen that the calculated lattice parameters are in good agreement with the experimental values^48,49 within 3% error. Our calculated band gap of pure VO₂(M) (0.69 eV) is well consistent with the experimental ones of 0.6–0.7 eV (ref. 48 and 49) and the other calculation ones of 0.7–0.78 eV.^50,51 Also, the lattice parameters of VO₂ with O vacancy are slightly larger than those of perfect VO₂. Even as the oxygen vacancy concentration increases, the calculated a, c-axis lattice parameters of VO_2−x(M) (x = 0.016, 0.031) also becomes slightly larger, which is attributed to the internal compressive strains in the VO₂ with O-vacancy.^19,52 Fig. 3 shows the local distortion around O-vacancy (V_O). As compared with pure VO₂, the three V atoms around O-vacancy move outward, with the increase of V–V and V–V_O distances ranging from 0.264 to 0.77 Å in VO_1.984(M), and from 0.214 to 0.502 Å in VO_1.984(R) (see Table 2), indicating that the oxygen vacancy induces a strong local distortion. As shown in Table 2, the short (2.519 Å) and long (3.143 Å) V–V chains arrange alternately in pure VO₂(M) along a axis. Nevertheless, the short and long V–V chain lengths in VO_1.984(M) range from 2.515 to 2.553 Å and from 2.781 to 3.294 Å, respectively. In VO₂(R), the V–V chains (2.788 Å) arrange linearly along c axis; however, in VO_1.984(R), the V–V chains are 2.501 to 2.549 Å and 2.842 to 3.354 Å, respectively, characterizing as a dimerization feature like that in VO₂(M) phase, which decreases the formation energy of VO₂(R) and stabilizes the VO₂(R).⁴² Note that V1–V2 for monoclinic VO₂ and V2–V3 for rutile one in Table 2 also belong to the V–V chains.

Table 1 The lattice parameters (a, b, c, α, β, γ) and volumes (V) of unit cells, band gaps (E_g) and calculated enthalpies (E) of VO₂(R) and VO₂(M) with and without O-vacancy

	a (Å)	b (Å)	c (Å)	α (°)	β (°)	γ (°)	Eg (eV)	V (Å^3)	E (eV per f.u.)	Ref.
R-phase
VO2	4.552	4.552	2.852	90	90	90	0	59.10	—	Exp.^48
VO2	4.652	4.652	2.789	90	90	90	0	60.34	−21.950	This calc.
VO1.984	4.647	4.674	2.816	89.89	89.98	90.13	0	60.83	−21.842	This calc.
VO1.969	4.653	4.653	2.825	89.99	90.15	90.07	0	61.17	−21.717	This calc.
M-phase
VO2	4.517	5.743	5.375	90	122.6	90	0.60	117.466	—	Exp.^49
VO2	4.638	5.626	5.453	89.99	121.72	90.01	0.69	121.016	−22.027	This calc.
VO1.984	4.645	5.626	5.458	89.57	121.61	90.06	0.51	121.453	−21.893	This calc.
VO1.969	4.658	5.638	5.471	90.10	121.53	89.93	0.50	122.458	−21.749	This calc.

---

Fig. 3 The local distortion around O-vacancy (V_O) for (a) VO_1.984(M) and (b) VO_1.984(R) after the structural optimization. The V and O atoms are represented by gray and red spheres, respectively; the blue dotted line ball denotes O-vacancy (V_O).

Table 2 The distances (d₁) between the V–V atoms and V–V_O around the O-vacancy (V_O), and the V–V chain lengths (d_V–V) in VO₂ and VO_1.984

	VO2(R)	VO2(M)	VO1.984(R)	VO1.984(M)
d1 (Å)
V1–VO	1.937	1.846	2.151	2.250
V2–VO	1.917	1.898	2.203	2.306
V3–VO	1.917	1.994	2.190	2.258
V1–V3	3.520	3.661	3.979	4.212
V1–V2	3.520	2.524	3.963	3.294
V2–V3	2.852	3.532	3.354	4.122
dV–V (Å)
Cal.	2.788	2.519	2.501–2.549	2.515–2.553
	—	3.143	2.842–3.354	2.781–3.294
Exp.^53	2.852	2.524	—	—
	—	3.257	—	—

---

On the other hand, it has been reported that due to a distorted VO₆ octahedron surrounding each V atom in VO₂, the V 3d states are split into the lower t_2g (d_xy, d_yz, d_xz) and higher e_g (d_z², d_x²−y²) levels.^54,55 Further, given that the linear orbit clouds extend along the c-axis and the behavior of d_z² orbital determines the electronic states of rutile phase VO₂,^55,56 we pay more attention to the V d_z² orbital. As shown in Fig. 4(a), compared with the pure VO₂(R), the occupied states of d_z² and d_xy in VO_1.984(R) shift down to −1.3 and −1.2 eV, respectively, and the unoccupied states of d_z² rise up to 1.22 eV, while, the states of d_yz, d_xz, d_z² and d_x²−y² are almost not altered. That is to say, after the introduction of O-vacancy in VO₂(R), the V–V bonding states descend and the anti-bonding states ascend, which will lower the energy of VO₂(R). However, in the case of VO₂(M) in Fig. 4(b), only the slight difference occurs between the occupied state distributions of d orbital in VO_1.984(M) and VO₂(M). Therefore, the energy difference between VO_2−x(R) and VO_2−x(M) (x = 0.016, 0.031) is reduced due to the introduction of O-vacancy. Namely, the creation of O vacancies in VO₂ is conducive to the transition from the metal phase to insulator phase.

Fig. 4 Comparison of the partial density of states of V-3d orbital between VO₂ and VO_1.984. (a) R-phase, and (b) M-phase. The zero point of the energy axis corresponds to the Fermi level E_F in (a) and the valence band maximum E_VBM in (b), respectively.

Fig. 5(a) is adopted from ref. 20 about the band schemes of pure VO₂(M). Note that the lower d_∥ band is completely filled whereas the π* band is empty, and E_g is associated with their band gaps between the lower d_∥ and π* band. Upon the formation of O vacancies in VO₂(M) as shown in Fig. 5(b), the left electrons are located at the empty π* band, and then form the localized bands, which will lower the energy barrier and thus trigger the decrease of metal–insulator transition temperature.^26,57–60 In addition, on the basis of the crystal field theory,⁵⁶ the dimerization of the V atoms are paired along the c axis, which makes the V upper d_∥ orbital and π* band partially occupied, and the V upper d_∥ orbital overlapped by the π* band as the Fermi level (E_F) moves into the conduction band, and thus induce the reduced band gap. Our calculated band gap of VO_1.984(M) (0.51 eV) is lower than that of pure VO₂(M) (0.69 eV), which is in good agreement with the values (0.46 eV vs. 0.60 eV) of VO₂(M) with and without oxygen vacancy from the photoluminescence spectra measurement²² and other experimental results.^25,58 VO₂(M) with oxygen vacancy exhibits the stronger near-infrared light adsorption due to the localized nature of defect states,⁴⁶ similarly to the cases of O_vac-Bi₂MoO₆ ⁶¹ and C-doped TiO₂.⁶² The same results also can be got from the density of states (DOSs) of VO₂(M) and VO_1.984(M) as shown in Fig. 6. For pure VO₂(M) in Fig. 6(a), the conduction-band minimum is mainly contributed by the O-2p and V-3d states hybridization, while the valence-band maximum is mainly ascribed to the V-3d states mixed with a small O-2p hybridization. The Fermi level (E_F) is pinned at the top of the valence band, behaving as an intrinsic characteristic. However, for VO_1.984(M) as shown in Fig. 6(b), the valence and conduction bands are both shifted toward the lower energy side, and the Fermi level (E_F) is located at the conduction band, presenting as n-type characteristic.

Fig. 5 Outline of the band scheme of VO₂ without and with O-vacancy. (a) VO₂(M), (b) VO_1.984(M), (c) VO₂(R), and (d) VO_1.984(R).

Fig. 6 The density of states (DOSs) of (a) VO₂(M) and (b) VO_1.984(M).

The band schemes of VO₂(R) and VO_1.984(R) in Fig. 5(c) and (d) show that the π* band overlaps the d_∥ band at different level and the d_∥ band is occupied partially by electrons. Different from the cases of VO₂(M) and VO_1.984(M), the Fermi levels of VO₂(R) and VO_1.984(R) are transferred to the conduction band and thus their band gaps disappear.

4.1.2 O-vacancy induced reduction in T_c for bulk VO₂. According to eqn (2) in ref. 42, the calculated phase transition temperatures of VO_1.984 and VO_1.969 are 226 K and 142 K (as shown in Fig. 7), respectively, which are much lower than the phase transition temperature (340 K) of pure VO₂. This suggests that the creation of the oxygen-deficiency-related defects in VO₂ belonging to donor doping could enhance the electron concentration, which will modify its metal–insulator transition behavior.^28,53 In addition, calculated results show that the T_c of VO₂ sharply decreases as the O-vacancy concentration increases from 0 to 3.1%, corresponding to the oxygen pressures ranging from 20 to 5 mTorr, which is in good agreement with other reports.^26,57–59 Experimentally, under vacuum conditions, Zhang et al. found O-vacancy in VO₂ nanobeam stabilizes the rutile phase suppressing the MIT as low as 103 K.⁵⁷ It has also been reported that increasing the O-vacancy concentration in VO₂ by controlling the oxygen partial pressure could lead to the decrease of the phase transition temperature.^{21,57–59,63}

Fig. 7 The dependence of transition temperature reduction (ΔT_c) in VO₂ on the oxygen vacancy (V_O) concentration with the corresponding oxygen partial pressure labeled as the upper horizontal axis.

4.1.3 Optical properties of VO₂ and VO_1.984. Because VO₂ is optically anisotropic, the optical properties including dielectric function, and adsorption and reflectivity coefficient, corresponding to the electric field parallel to (notated as E_∥ chain) and perpendicular to (notated as E_⊥ chain) the V–V chains, are considered. For convenience, the electric field parallel to the V–V chains (E_∥ chain) is taken as the representative one in the following discussion.

Fig. 8(a) and (b) show the calculated and experimental imaginary parts of the dielectric function of VO₂ near the infrared region, respectively. Obviously, for both phase of pure VO₂, the imaginary part of dielectric function increases drastically near the infrared region. More interesting is that the imaginary part of the dielectric function of VO₂ with O-vacancy has the same trend from the low temperature monoclinic phase to the high temperature rutile phase, in agreement with the experimental results of VO_1.963 at 10 mTorr as shown in Fig. 8(b) from ref. 58. It is seen from the imaginary functions of pure VO₂(M) in the inset of Fig. 8(a) that the main peaks occur in 1.47, 2.14, 4.84 and 6.75 eV, which are close to the experimental results pointed out its dielectric peaks between 0.25 and 5 eV.⁶⁴ The reasons of optical phenomenon of pure VO₂(M) are essentially stemmed from the transition between the relevant electronic states, in which the electrons at the occupied states (marked with A1) can be excited to the higher unoccupied states (marked with A2, A3, A4, and A5) in pure VO₂(M) (see Fig. 6(a)). However, for VO_1.984(M), as shown in Fig. 8(a), there exists a steep dielectric peak at lower energy region about 0.06 eV, which mainly derives from the transition from the occupied V-3d orbits near the Fermi level to the higher unoccupied orbits (as shown in Fig. 6(b) marked with B1, B2).

Fig. 8 (a) The calculated imaginary ε₂ parts of the complex dielectric functions of VO₂ and VO_1.984, (b) the experimental imaginary ε₂ parts of the complex dielectric functions for VO₂ at 10 mTorr (adapted with permission from ref. 58, Copyright 2015 Royal Society of Chemistry), (c) the absorption coefficients of VO₂ and VO_1.984. α(ω) is given in 10⁵ cm⁻¹, (d) the transmittance spectra of VO_1.963 at 10 mTorr. (experimental measured: adapted with permission from ref. 58, Copyright 2015 Royal Society of Chemistry), (e) the reflectivity spectra of VO₂ and VO_1.984, and (f) the reflectance spectra of VO₂(M) films deposited at different oxygen flow ratios (adapted with permission from ref. 65, Copyright 2014 Published by Elsevier B.V.).

Fig. 8(c) shows the absorption coefficient of VO₂ and VO_1.984. It can be found that for the case with or without O-vacancy, VO₂(R) shows the stronger absorption than VO₂(M) near the infrared region. Being comparable with the pure rutile (or monoclinic) phase, VO_1.984 exhibits a peak at 0.35 eV (or 0.23 eV) with an absorption coefficient of about 1.68 × 10⁴ cm⁻¹ (or 1.9 × 10⁴ cm⁻¹). These results also have been derived from the PDOS in Fig. 6(b), in which the existence of strong inner-band and inner-band absorption will induce the low transmittance.

The calculated and experimental⁶⁵ reflectivity spectra of VO₂ are shown in Fig. 8(e) and (f). It is clearly seen that the calculated values of VO_1.984(M) (0.771) and VO_1.984(R) (0.784) are higher than those of the pure VO₂ (0.368 and 0.620), which agrees well with the experiment results. This suggests that the introduction of O-vacancy in VO₂ can improve the reflectivity near the infrared region. Overall, the pure VO₂(M) shows very weak absorptivity and reflectivity near the infrared region whereas the relative strong ones are true for the pure VO₂(R). These aspects vividly indicate that the infrared light may easily penetrate the VO₂(M), but be significantly blocked by the VO₂(R). A similar conclusion was drawn by Zhang et al. who investigated the transmittance of VO₂ by using the HSE06 exchange–correlation functional.⁴¹ It is worth emphasizing that although VO_1.984(R) presents a larger reflectivity in the infrared range than VO₂(R), VO_1.984(M) exhibits large reflectivity in the light with energy less than 0.43 eV. In other words, the introduction of O-vacancy in VO₂ lowers its transmissivity in the infrared range as shown in Fig. 8(d), which in turn leads to the declination of the desired optical switching to some extent.

4.2 VO₂ surface

4.2.1 Formation energies. Tables 3 and 4 list the formation energies and geometry structural parameters of VO₂(R) (1 1 0) and VO₂(M) (0 1 1) surfaces with O-adsorption and O-vacancy. For the VO₂(R) (1 1 0) surface with O-vacancy, the thicknesses of the outermost surface bilayer for V_Obr, V_O3c and V_O4c configurations are 1.080, 0.729 and 0.577 Å, respectively. As compared with clean VO₂(R) (1 1 0) surface, O-vacancy located at the first O atomic layer induces the first atom-layer to move outward by 0.042 Å, whereas the opposite is true for the cases of O-vacancy at the second and third O atomic layers. Furthermore, the formation energies for V_Obr, V_O3c, and V_O4c configurations are 3.195, 2.787 and 2.405 eV, respectively, implying that O-vacancy prefers to locate in the inner O-atomic layer. The possible reason is that the longer distance between neighboring interatoms causes the weaker Coulomb repulsion. The same trend and relationship are true for the VO₂(M) (0 1 1) surface with O-vacancy. By the way, as compared the formation energy of bulk VO₂(M) with O-vacancy and VO₂(M) (0 1 1) with O-vacancy, i.e., V_O4c (3.605 eV vs. 2.568 eV), it exhibits O-vacancy in the surface layer is more stable than in the bulk, which is in agreement with the other calculation results (2.9 eV vs. 1.3 eV) of VO₂(M) bulk and surface using DFT + U approach.¹⁹ Actually, recently we found that the deposited V₂O₅/metal/V₂O₅ multilayer via radio frequency magnetron sputtering, undergoes a B to M phase transition depending on the quantity of the metal layers, and at a certain metal layer thickness after annealing, the film becomes VO₂(M) with oxygen vacancies by analyzing the V-2p and O-1s photoelectron spectra.⁶⁶ Here, it is worth pointing out that by modulating the oxygen partial pressure during deposition, oxygen vacancies can be introduced into the VO₂ films.^{16,17,57–60}

Table 3 Adsorption energies (E_ads) and formation energies (E_f), geometry structural parameters, and the surface dipole moment μ on the VO₂(R) (1 1 0) surface^a

	Eads (eV)	Ef (eV)	dO–O (Å)	dV–O (Å)	dad (Å)	d12 (Å)	μ (D)
a dO–O is the distance between the O adatom and its nearest neighboring O atom. dad is the distance from the O adatom to the O atom in the first layer. d12 is the thickness of the surface bilayer. The surface dipole moment μ (D) of one and two O atoms adsorption at different adsorption sites on the VO2(R) (1 1 0).
Clean	—	—	—	1.807–2.034	—	1.038	—
Obr	−1.373	2.014	1.313	—	1.313	1.300	0.982
V5c	−5.585	−2.198	—	1.606	1.606	1.241	0.998
V6c	−5.270	−1.883	—	1.607	1.607	0.659	1.029
O3c	−3.668	−0.281	1.472	—	1.281	1.101	0.156
C1	−5.276	−3.784	3.078	1.601–1.602	1.600	1.261	0.725
C2	−4.457	−2.148	1.396	1.850–1.859	1.720	1.195	0.320
C3	−4.315	−1.862	1.384	1.934–1.896	1.871	1.113	0.444
C4	−4.285	−1.802	1.272	1.765–2.017	1.755	1.214	0.437
VObr	—	3.195	—	—	—	1.080	—
VO3c	—	2.787	—	—	—	0.729	—
VO4c	—	2.405	—	—	—	0.577	—

---

Table 4 Adsorption energies (E_ads) and formation energies (E_f), geometry structural parameters, and the surface dipole moment μ on the VO₂(M) (0 1 1) surface^a

	Eads (eV)	Ef (eV)	dO–O (Å)	dV–O (Å)	dad (Å)	d12 (Å)	μ (D)
a dO–O is the distance between the O adatom and its nearest neighboring O atom. dad is the distance from the O adatom to the O atom in the first layer. d12 is the thickness of the surface bilayer. The surface dipole moment μ (D) of one and two O atoms adsorption at different adsorption sites on the VO2(M) (0 1 1).
Clean	—	—	—	1.712–2.225	—	1.010	—
Obr	−1.824	1.563	1.308	—	1.301	1.302	0.156
V5c	−5.279	−1.892	—	1.604	1.604	1.266	0.998
V6c	−2.065	1.322	—	1.872	1.458	1.342	0.374
O3c	−2.372	1.013	1.471	2.104–2.0444	1.276	1.197	0.203
C1	−4.925	−3.083	2.988	1.736–2.214	1.603–1.606	1.240	0.990
C2	−3.957	−1.146	1.398	1.706–2.231	1.718	1.215	0.445
C3	−4.031	−1.294	1.383	1.704–2.230	1.880	1.212	0.741
C4	−3.750	−0.733	1.264	1.845–2.216	1.730	1.257	0.593
VObr	—	3.596	—	—	—	1.198	—
VO3c	—	3.027	—	—	—	0.730	—
VO4c	—	2.568	—	—	—	0.506	—

---

For O-adsorption on the VO₂(R) (1 1 0) surface, the formation energy of the most stable configuration with one O-adsorption (V_5c: −2.198 eV) is higher than that of the more energetically favorable configuration about two O-adsorption (C₁: −3.784 eV), meaning that VO₂ is prone to oxidation at the ambient condition. This will be in detail discussed in Section 4.2.2. Note that the similar results can be obtained from the O-adsorption on the VO₂(M) (0 1 1) surface, which was also proved by Mellan et al.³⁰ who reported that the rutile (1 1 0) surface corresponds to the monoclinic (0 1 1) surface.

4.2.2 Adsorption energies. Compared with their respective clean surfaces after and before relaxation, the top O atoms layers of the VO₂(R) (1 1 0) and VO₂(M) (0 1 1) surface move inward by 0.243, and 0.278 Å, respectively. In the case of one oxygen atom adsorption, it is seen from Tables 3 and 4 that the adsorption energies (VO₂(R) (1 1 0): −5.585 eV and VO₂(M) (0 1 1): −5.279 eV) of O at the V_5c site are both the lowest among all the adsorption sites, indicating that O adsorption at V_5c is more favorable than others adsorption sites and the adsorption is an exothermic chemical process. For VO₂(R) (1 1 0) and VO₂(M) (0 1 1) surface, the distances between the adsorbed O and V atom of V_5c configurations are 1.606 and 1.604 Å, respectively. In addition, the thicknesses of surface bilayer of V_5c configurations (1.241 Å vs. 1.266 Å) both increase slightly being compared with their respective clean surfaces.

Starting from one O atom adsorption at V_5c, we examine four configurations involving two oxygen atoms adsorption on VO₂(R) (1 1 0) and VO₂(M) (0 1 1), which are labeled as C₁, C₂, C₃ and C₄, respectively. Their relaxed structures and adsorption energies are summarized in Fig. 9. For the VO₂(R) (1 1 0) and VO₂(M) (0 1 1) surfaces with two O atoms adsorption, the adsorption energy sequences follows C₁ < C₂ < C₃ < C₄ and C₁ < C₃ < C₂ < C₄, respectively. Note that the difference between C₂ and C₃ is slightly smaller for two surfaces (0.142 and 0.074 eV) and thus the adsorption behaviors of two O-atoms on the VO₂(M) (0 1 1) and the VO₂(R) (1 1 0) surfaces are similar to each other. The configuration C₁ with two O atoms adsorption at the V_5c is considered to be energetically more favorable, which can be explained from the relatively strong interaction between O adatoms and the surface atoms. The configuration C₁ exhibits the shorter V–O bond lengths (VO₂(R) (1 1 0): 1.601 and 1.602 Å; VO₂(M) (0 1 1): 1.603 and 1.606 Å), which agree well with the value of 1.61 Å using PBE method³⁰ and the values reported elsewhere for surface vanadyl species (1.55–1.70 Å).⁶⁷ As shown in Fig. 9, the O–O bond lengths (VO₂(R) (1 1 0): 1.272 Å; VO₂(M) (0 1 1): 1.264 Å) in C₁ are consistent with that of the typical O–O double bond (1.21 Å), whereas the calculated V–O bond lengths in the outermost layer (VO₂(R) (1 1 0): 1.755 Å; VO₂(M) (0 1 1): 1.730 Å) are both shorter than the V–O distance in the bulk (1.954 Å). Given the above characteristics about oxygen adsorption on the surfaces, there is another matter which we need to pay attention to in the actual application: VO₂ exposed to ambient condition is prone to oxidation, which will degrade its thermochromic properties. Experimentally, using atomic layer deposition (ALD) method, Wang et al. deposited an ultrathin Al₂O₃ film with 15 nm to protect the underlying VO₂ from degradation.⁶⁸

Fig. 9 Relaxed configuration about two oxygen atoms adsorption on the two types of surfaces. (a) VO₂(R) (1 1 0) surface and (b) VO₂(M) (0 1 1) surface. O and V atoms are represented by red and gray spheres, respectively.

4.2.3 Work functions and surface dipole moments. Experimentally, it has been reported that regulating the electron carrier concentration may result in the decrease of phase transition temperature.^{13,28,39,41,42} In addition, the oxygen compositional variation in VO₂ also can tune the structural and electronic phase transitions, and even modify its the work function.^32,33 Inspired by these results, the work functions of VO₂ surface with O-vacancy and O-adsorption are calculated. The work function of a surface is the minimum energy required to remove an electron from the surface, and is given by⁶⁹

Φ = x − E_F, (7)

where x is the average potential of the surface in the vacuum region, and E_F is the corresponding Fermi energy level. Note that the calculated work functions of clean VO₂(R) (1 1 0) and VO₂(M) (0 1 1) are 5.093 eV, and 5.433 eV, respectively. Fig. 10 compares the work functions of each surface with the O-vacancy and O-adsorption. It is found that the creation of O-vacancy favors lowering the average work functions of each surface reduce by 0.53% and 0.19% compared with their respective clean surfaces. Such decrease in the work function can be explained from (i) the reduction in V oxidation state caused by the electron transfer upon the oxygen vacancy and (ii) formation of electric dipoles at the surface. The reduction work function in turn leads to a lower T_c, in good agreement with the experimental results.^32,33,57

Fig. 10 Comparison of the work functions between O-vacancy and O-adsorption on the two types of surfaces. (a) VO₂(R) (1 1 0) and (b) VO₂(M) (0 1 1) surface.

However, it can be seen from Fig. 10 that the average work functions of each surface with the O-adsorption on VO₂(R) (1 1 0) and VO₂(M) (0 1 1) surfaces are increased by 0.20% and 0.9% for one or two oxygen adsorption higher than that of the corresponding clean surface, respectively. Consequently, as compared with the clean surface, the surface with O adsorption should exhibit the higher phase transition temperature. This can be explained from the smaller electronegativity of surface-V atom (1.63) as compared with O adatom (3.44) and the tendency that a number of electrons from V atoms on the surface layers transfer to the O adatoms.

By referring to ref. 70, the variation of the work function caused by the O vacancy (or O adsorption) is also related to the surface dipole moment via

μ = AΔΦ/(12πθ), (8)

where μ is the surface dipole moment, A is the area of the VO₂(R) (1 1 0) or VO₂(M) (0 1 1) surface, θ is the oxygen coverage, and ΔΦ is the work function difference between oxygen nonstoichiometric and clean surfaces. The absolute value of μ is the strength of the surface dipole moments. The positive μ denotes the direction from the surface to O atom, and vice versa. Table 4 lists the calculated surface dipole moments of each surface with the O-adsorption. It is seen that the surface dipole moment of VO₂(R) (1 1 0) with one O adsorption at the favorable site (V_5c) (0.998 D) is stronger than that of the most suitable configuration with two O atoms adsorption (0.725 D), demonstrating that the surface dipole moments become weaker with the O coverage increase. The same trend is true for VO₂(M) (0 1 1) surface with the O adsorption. Upon the O atoms adsorption on the VO₂ surface, due to the electron transfer from V atom, a positive direction dipole moment emerges at the interface, which results in the increase of work function and a rise in phase transition temperature.³²

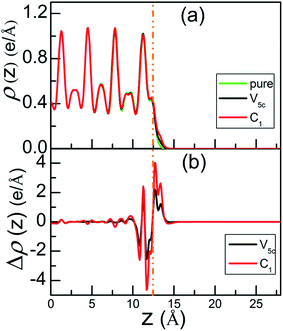
Fig. 11 shows the plane-averaged electronic charge density and electron density difference along the z axis. The charge redistribution caused by oxygen adsorption can be calculated by

Δρ = ρ_tot − ρ_clean − ρ_O, (9)

where ρ_tot, ρ_clean, and ρ_O are the charge densities of the adsorption configurations, clean surface and the O atoms at the adsorbed position, respectively. As shown in Fig. 11(a), the charge density is bulk-like in the slab middle for clean surface, V_5c and C₁, and the total charge transfer occurs from the V-atomic layer to the surface O-adatoms. Furthermore, the charge density difference in Fig. 11(b) indicates upon the O atom adsorption on the VO₂(R) (1 1 0), there is the electron transfer from the surface to the oxygen. Note that the more electron transfer occurs for two oxygen atoms adsorption. That can be explained in this way: oxygen atoms, being as an electronegative adsorbate, induce an electron transfer from the underlying V atomic-layer to adsorbated-O atom, which forms a positive surface dipole. This result is self-consistent with our above results about the calculated surface moment dipole. By the way, it is expected that the same results are true for the VO₂(M) (0 1 1) surface. Therefore, it can be concluded that nonstoichiometry in VO₂ can tailor the work function, and further regulate its T_c.

Fig. 11 (a) Average electron charge density and (b) charge density changes, Δρ of clean surface, V_5c and C₁ along the z axis. Δρ is given in 10⁻³. The vertical dash dot lines indicate the positions of V atoms in the surfaces.

Based on the above results and discussion, it is found that oxygen nonstoichiometry in VO₂ can modify its phase transition behavior, which agree well with the experimental results.^{16–22,32,33,57} However, in the ambient air, VO₂ is prone to oxidation,^19,30,68 which exhibits the lower adsorption energy, indicating a strong interaction between O and the surface V-atoms. Therefore, for VO₂, in actual use, the oxygen pressure should be controlled and a VO₂ film should avoid being exposed to ambient air.

5. Concluding remarks

The influence of O-vacancy and O-adsorption on the phase transition behavior of VO₂ has been investigated using first-principles calculations. The existence of O-vacancy in the bulk VO₂ increases the electron carrier concentration and reduces the phase transition temperature (T_c) to 226 K and 142 K for VO_1.984 and VO_1.969, respectively, in which the variation of T_c is related with the changes in atomic and electronic structures of VO₂. In contrast, the infrared light transmittance of VO₂ is lowered by the introduction of O-vacancy, hindering its application in the optical switching, which is consistent with the experimental observations.

For O-vacancy and O-adsorption on the VO₂ surfaces, the energetically favorable O-vacancy locates in the inner layer, whereas the adsorbated-oxygen atom is found to be most favorable at V_5c site. Furthermore, the negative formation and adsorption energies after O-adsorption mean that VO₂ surfaces can be easily oxidized. The work function of the presence of O-vacancy in the surface is lower than that of O-adsorption on the same surface, which has a great impact on the phase transition behavior of VO₂. These findings pave favorable explanations about the MIT behavior of O-vacancy and O-adsorption of VO₂ for specific applications such as ultrafast electronic switches and electron-optical devices.

Acknowledgements

The authors gratefully acknowledge the intense and helpful discussions with Prof. Wenqing Zhang. This work is supported by the National Natural Science Foundation of China (No. 51372228, 51325203 and 51402182), the Ministry of Science and Technology of China (No. 2014AA032802), the Shanghai Municipal Science and Technology Commission (No. 13521102100 and 15XD1501700), Shanghai Institute of Materials Genome from the Shanghai Municipal Science and Technology Commission (No. 14DZ2261200), Shanghai Pujiang Program (No. 14PJ1403900) and the high performance computing platform of Shanghai University.

References

1. F. J. Morin, Phys. Rev. Lett., 1959, 3, 34–36.
2. E. Strelcov, Y. Lilach and A. Kolmakov, Nano Lett., 2009, 9, 2322–2326.
3. M. M. Qazilbash, Z. Q. Li, V. Podzorov, M. Brehm, F. Keilmann, B. G. Chae, H. T. Kim and D. N. Basov, Appl. Phys. Lett., 2008, 92, 241906.
4. Q. Yu, W. Li, J. Liang, Z. Duan, Z. Hu, J. Liu, H. Chen and J. Chu, J. Phys. D: Appl. Phys., 2013, 46, 055310.
5. B. J. Kim, Y. W. Lee, B. G. Chae, S. J. Yun, S. Y. Oh, H. T. Kim and Y. S. Lim, Appl. Phys. Lett., 2007, 90, 023515.
6. S. Hormoz and S. Ramanathan, Solid-State Electron., 2010, 54, 654–659.
7. H. Coy, R. Cavrera, N. Sepulveda and F. E. Fernandez, J. Appl. Phys., 2010, 108, 1113115.
8. T. C. Koethe, Z. Hu, M. W. Haverkort, L. C. Schussler, F. Venturini, N. B. Brookes, O. Tjernberg, W. Reichelt, H. H. Hsieh, H. J. Lin, C. T. Chen and L. H. Tjeng, Phys. Rev. Lett., 2006, 97, 116402.
9. C. Tang, P. Georgopoulos, M. E. Fine, J. B. Cohen, M. Nygren, G. S. Knapp and A. Aldred, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 1000.
10. J. Cao, E. Ertekin, V. Srinivasan, W. Fan, S. Huang, H. Zheng, J. W. L. Yim, D. R. Khanal, D. F. Ogletree, J. C. Grossmanan and J. Wu, Nat. Nanotechnol., 2009, 4, 732–737.
11. Y. Gu, J. Cao, J. Wu and L. Q. Chen, J. Appl. Phys., 2010, 108, 083517.
12. M. Hada, D. F. Zhang, A. Casandruc, R. J. D. Miller, Y. Hontani, J. Matsuo, R. E. Marvel and R. F. Haglund Jr, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 134101.
13. L. Chen, X. Wang, S. Shi, Y. Cui, H. Luo and Y. Gao, Appl. Surf. Sci., 2016, 367, 507–517.
14. R. Chen, L. Miao, C. Liu, J. Zhou, H. Cheng, T. Asaka, Y. Iwamoto and S. Tanemura, Sci. Rep., 2015, 5, 14087.
15. E. Kusano and J. A. Theil, J. Vac. Sci. Technol., 1989, A7, 1314.
16. J. Jeong, N. Aetukuri, T. Graf, T. D. Schladt, M. G. Samant and S. S. P. Parkin, Science., 2013, 339, 1402–1405.
17. S. Chen, X. Wang, L. Fan, G. Liao, Y. Chen, W. Chu, L. Song, J. Jiang and C. Zou, Adv. Funct. Mater., 2016, 26, 3532–3541.
18. S. Kittiwatanakul, J. Laverock, J. D. Newby, K. E. Smith, S. A. Wolf and J. Lu, J. Appl. Phys., 2013, 114, 053703.
19. K. Appavoo, D. Y. Lei, Y. Sonnfraud, B. Wang, S. T. Pantelides, S. A. Maier and R. F. Haglund Jr, Nano Lett., 2012, 12, 780–786.
20. J. B. Goodenough, J. Solid State Chem., 1971, 3, 490–500.
21. J. F. Marucco, B. Poumellec and F. Lagnel, J. Mater. Sci. Lett., 1986, 5, 99–100.
22. C. Chen and Z. Fan, Appl. Phys. Lett., 2009, 95, 262106.
23. C. Chen, Y. Zhao, X. Pan, V. Kuryatkov, A. Bernussi, M. Holtz and Z. Fan, J. Appl. Phys., 2011, 110, 023707.
24. H. W. Liu, L. M. Wong, S. J. Wang, S. H. Tang and X. H. Zhang, Appl. Phys. Lett., 2013, 103, 151908.
25. S. Fan, L. Fan, Q. Li, J. Liu and B. Ye, Appl. Surf. Sci., 2014, 321, 464–468.
26. L. Fan, S. Chen, Y. Wu, F. Chen, W. Chu, X. Chen, C. Zou and Z. Wu, Appl. Phys. Lett., 2013, 103, 131914.
27. W. BrÜckner, U. Gerlach, H. P. BrÜckner, W. Moldenhauer and H. Oppermann, Phys. Status Solidi A, 1977, 42, 295–303.
28. X. Yuan, W. Zhang and P. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 035119.
29. D. Guo, C. Hu, Q. Yang, H. Hua, W. Liu and C. Kong, Mater. Res. Bull., 2014, 53, 102–106.
30. T. A. Mellan and R. G. Crespo, J. Chem. Phys., 2012, 137, 154706.
31. Y. Wang and Z. Zhang, Phys. E, 2009, 41, 548–551.
32. C. Ko, Z. Yang and S. Ramanathan, ACS Appl. Mater. Interfaces, 2011, 3, 3396–3401.
33. W. K. Hong, J. B. Park, J. Yoon, B. J. Kim, J. I. Sohn, Y. B. Lee, T. S. Bae, S. J. Chang, Y. S. Huh, B. Son, E. A. Stach, T. Lee and M. E. Welland, Nano Lett., 2013, 13, 1822–1828.
34. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
35. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
37. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
38. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
39. J. Wei, H. Ji, W. H. Guo, A. H. Nevidomskyy and D. Natelson, Nat. Nanotechnol., 2012, 7, 357.
40. W. E. Pickett, S. C. Erwin and E. C. Ethridge, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 1201.
41. J. Zhang, H. He, Y. Xie and B. Pan, J. Chem. Phys., 2013, 138, 114705.
42. Y. Cui, S. Shi, L. Chen, H. Luo and Y. Gao, Phys. Chem. Chem. Phys., 2015, 17, 20998.
43. S. Biermann, A. Poteryaev, A. I. Lichtenstein and A. Georges, Phys. Rev. Lett., 2005, 94, 026404.
44. S. Z. Karazhanov, P. Ravindran, A. Kjekshus, H. Fjellvag and B. G. Svensson, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 155104.
45. E. Goering, M. Schramme, O. Muller, R. Barth, H. Paulin, M. Klemm, M. L. Denboer and S. Horn, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 4225.
46. L. Dai, S. Chen, J. Liu, Y. Gao, J. Zhou, Z. Chen, C. Cao, H. Luo and M. Kanehira, Phys. Chem. Chem. Phys., 2013, 15, 11723.
47. J. Behler, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115421.
48. G. Andersson, Acta Chem. Scand., 1956, 10, 623–628.
49. K. D. Rogers, Powder Diffr., 1993, 8, 240–244.
50. J. Wan, Q. Ren, N. Wu and Y. Gao, J. Alloys Compd., 2016, 662, 621–627.
51. A. Liebsch, H. Ishida and G. Bihlmayer, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 085109.
52. H. Kim, N. Charipar, M. Osofsky, S. B. Qadri and A. Piqué, Appl. Phys. Lett., 2014, 104, 081913.
53. A. Zylbersztejn and N. F. Mott, Phys. Rev. B: Condens. Matter Mater. Phys., 1975, 11, 4383.
54. V. Evert, Ann. Phys., 2002, 11, 650–702.
55. C. Wu, F. Feng, J. Feng, J. Dai, L. Peng, J. Zhao, J. Yang, C. Si, Z. Wu and Y. Xie, J. Am. Chem. Soc., 2011, 133, 13798–13801.
56. C. Wu, F. Feng and Y. Xie, Chem. Soc. Rev., 2013, 42, 5157.
57. S. Zhang, I. S. Kim and L. J. Lauhon, Nano Lett., 2011, 11, 1443–1447.
58. P. Zhang, K. Jiang, Q. Deng, Q. You, J. Zhang, J. Wu, Z. Hu and J. Chu, J. Mater. Chem. C, 2015, 3, 5033–5040.
59. C. H. Griffith and H. K. Eastwood, J. Appl. Phys., 1974, 45, 2201–2206.
60. M. Nazari, C. Chen, A. A. Bernussi, Z. Fan and M. Holtz, Appl. Phys. Lett., 2011, 99, 071902.
61. T. Jing, Y. Dai, W. Wei, X. Ma and B. Huang, Phys. Chem. Chem. Phys., 2014, 16, 18596.
62. J. Lu, Y. Dai, M. Guo, L. Yu, K. Lai and B. Huang, Appl. Phys. Lett., 2012, 100, 102114.
63. N. Kimizuka, M. Saeki and M. Nakahir, Mater. Res. Bull., 1970, 5, 403–408.
64. H. W. Verleur, A. S. Barker Jr and C. N. Berglund, Phys. Rev., 1968, 172, 788–797.
65. M. Jiang, X. Cao, S. Bao, H. Zhou and P. Jin, Thin Solid Films, 2014, 562, 314–318.
66. H. Liu, D. Wan, A. Ishaq, L. Chen, B. Guo, S. Shi, H. Luo and Y. Gao, ACS Appl. Mater. Interfaces, 2016, 8, 7884–7890.
67. M. Iwamoto, H. Furukawa, K. Matsukami, T. Takenaka and S. Kagawa, J. Am. Chem. Soc., 1983, 105, 3719.
68. X. Wang, Y. Cao, C. Yang, L. Yan and Y. Li, J. Vac. Sci. Technol., A, 2016, A34, 01A106.
69. A. L. Rosa and J. Neugebauer, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 205346.
70. W. X. Li, C. Stampfl and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 075407.

---