Studies on the magnetoelastic and magnetocaloric properties of Yb1−xMgxMnO3 using neutron diffraction and magnetization measurements
Bhumireddi Sattibabu*a,
A. K. Bhatnagar*ab,
K. Vinodc,
S. Rayaprold,
Awadhesh Manic,
V. Sirugurid and
D. Dasa
aSchool of Engineering Sciences and Technology, University of Hyderabad, Hyderabad 500046, India. E-mail: bsb.satti@gmail.com; anilb42@gmail.com
bSchool of Physics, University of Hyderabad, Hyderabad 500046, India
cIndira Gandhi Centre for Atomic Research, Kalpakkam-603102, India
dUGC-DAE Consortium for Scientific Research, Mumbai Centre, BARC Campus, Mumbai-400085, India
First published on 11th May 2016
Abstract
We report the magnetic ordering and magnetoelastic coupling of polycrystalline hexagonal Yb1−xMgxMnO3 (x = 0.00 and 0.05) compounds by using neutron diffraction measurements. The magnetocaloric properties of these Yb1−xMgxMnO3 compounds are also studied using magnetization measurements. The temperature dependence of the lattice parameters (a and c/a ratio) and unit cell volume V show anomalous behavior near TN1 ∼ 85 K (the Mn ordering temperature) due to the magnetoelastic effect. Also all the Mn–O bond distances display considerable variation at TN1. Isothermal magnetization curves measured near the Yb long range ordering temperatures indicate a field induced magnetic transition with applied field. The isothermal magnetic entropy change (−ΔSM) is calculated from the magnetization curves measured for different temperatures. Values of maximum entropy change (−ΔSmaxM), the adiabatic temperature change (ΔTad) and the relative cooling power (RCP) for these compounds are found to be 3.02 ± 0.37 J mol−1 K−1, 8.6 ± 0.95 K and 41 ± 9 J mol−1 for x = 0.00, and 2.63 ± 0.36 J mol−1 K−1, 9.06 ± 0.96 K and 40.0 ± 10 J mol−1 for x = 0.05, respectively, for ΔH = 100 kOe. Rescaling of the −ΔSM vs. T curves for various fields fit into a single curve, implying the second-order phase transition.
1. Introduction
The hexagonal rare-earth manganites, RMnO3 (R = Ho, Er, Tm, Yb, Lu, Y etc.) show magnetoelectric coupling effects in which both ferroelectricity and magnetic ordering can exist simultaneously in the ordered phase. Such materials, called multiferroics, have potential for a variety of applications since the magnetic ordering can be controlled by an electric field and vice versa.1,2 Besides the magnetoelectric coupling, there are reports on these materials3–5 showing coupling between magnetic and lattice degrees of freedom giving rise to interesting magnetoelastic effects.Hexagonal YbMnO3 consists of layers of corner-sharing MnO5 trigonal bipyramids separating layers of Yb3+ ions. In the MnO5 trigonal bipyramids, each manganese ion is surrounded by three in-plane and two apical oxygen ions. A net electric polarization arises in YbMnO3 due to buckling of the layered MnO5 polyhedra accompanied by displacements of the Yb ions resulting in ferroelectric behavior with ferroelectric transition at 990 K.6 YbMnO3 has a complex magnetic phase diagram below the Neel temperature (∼85 K), the magnetic structure of YbMnO3 can be described as frustrated antiferromagnetic on a triangular lattice in the ab-plane.7 The Mn3+ moments get aligned in the ab-plane to produce antiferromagnetic order at the Néel temperature (TN1 = 85 K) while the Yb moments at the 4b crystallographic site order due to the Mn molecular field.8 Further, Yb3+ moments at the 2a crystallographic site show long range ordering through Yb–Yb interactions below TN2 ∼ 3.5 K.8,9 It is reported, a magnetic field applied along the c-axis below TN2 ∼ 3.5 K induces magnetic transition at a critical field of H||c ∼ 35 kOe (ref. 9) due to the spin-flip/reorientation of the Yb(2a) moments.8
The interesting behavior of YbMnO3 motivated us to study the magnetic structure and spin lattice coupling of YbMnO3 and Yb0.95Mg0.05MnO3 compounds using neutron diffraction. The later compound was studied to study changes due to Mg substitution. In our previous studies,7,10 we reported room temperature neutron-diffraction (ND) results of these samples presenting structural parameters like cell volume, bond lengths and angles at room temperature (300 K). Our previous studies based on temperature depended magnetization and heat capacity7,10 show Yb3+ ordering at around 3.5 K, and antiferromagnetic Mn3+ ordering around 85 K. Here, in the present work, we extend the neutron-diffraction (ND) studies to lower temperatures, presenting the temperature dependence of various structural parameters near the magnetic transition/ordering temperatures. In the earlier reports10,11 the magnetocaloric properties were studied using heat capacity measurements. In the present work we also present results on the isothermal magnetization measurements carried out around the Yb3+ ordering temperature and evaluate magnetocaloric properties from the isothermal magnetization data. The magnetocaloric properties evaluated from the isothermal magnetization data in the present work is complementary to the magnetocaloric properties evaluated from the heat capacity measurements in.10,11
2. Experimental details
Polycrystalline samples of Yb1−xMgxMnO3 (x = 0.0 and 0.05) were synthesized by a conventional solid-state reaction method from stoichiometric mixtures of Yb2O3, MgO, and MnCO3 powders. The experimental details of sintering, measurement of X-ray diffraction (XRD) patterns, magnetic and thermal properties are given in our previous papers.7,10 In addition, the neutron-diffraction (ND) measurements were carried out on powder samples with a wavelength of 1.48 Å using a multi-position sensitive detector based focusing crystal diffractometer PD-3 set up by the UGC-DAE Consortium for Scientific Research at the National Facility for Neutron Beam Research NFNBR, Dhruva reactor, Mumbai, India.12 Neutron diffraction (ND) patterns were recorded at different temperatures between 2.5 K and 300 K. The magnetization measurements were performed using a Cryogenic Inc. (UK) make vibrating sample magnetometer operating at 20.4 Hz. Magnetization isotherms were measured at different temperatures in fields up to 100 kOe near the low temperature ordering transition.3. Results and discussions
3.1. Neutron diffraction
Neutron diffraction (ND) measurements on polycrystalline Yb1−xMgxMnO3 (x = 0.00 and 0.05) were performed at different temperatures near the Mn ordering temperature with incident neutron wavelength λ = 1.48 Å. Room temperature ND results on these compounds reported earlier7 showed subtle structural changes in cell volume, bond lengths and angles and polyhedral distortions. The nuclear structure peaks can be described by a single phase with space group P63cm at all temperatures. The temperature variation of the ND patterns is shown in Fig. 1a. The figure shows that the intensity of (102) as well as (101) Bragg positions increases below TN1 ∼ 85 K and the intensity of (100) increases below TN2 ∼ 3.5 K, where the nuclear reflections are forbidden by the P63cm symmetry. The temperature variations of the integrated intensities of Bragg peaks (100), (101), and (102) are shown in Fig. 1b. It is observed that large changes occur in the integrated intensities of these Bragg peaks around antiferromagnetic transition TN1 ∼ 85 K and ferromagnetic transition TN2 ∼ 3.5 K which correspond to the long range magnetic ordering of Mn and Yb ions, respectively. It is further observed that the intensity at the onset/start of corresponding Bragg peaks intensity slightly shift to higher temperature for x = 0.05 sample. The (100) and (101) Bragg peaks differ from each other with temperature dependences. The (101) peak intensity rises abruptly below 85 K while the (100) peak intensity remains rather weak down to about 10 K then suddenly increases below 10 K. The observed temperature dependences suggest that the (101) and (100) peak intensities are controlled by the Mn and Yb orderings, respectively, while the (102) Bragg peak probably has contributions from both orderings.8 The observed temperature dependences of the (101) peak in YbMnO3 is similar to that of the (100) peak in YMnO3,13,14 whereas the Mn order does not induce a strong (101) magnetic peak in YMnO3 which suggests that the Mn order is affected by the nature of the R ion.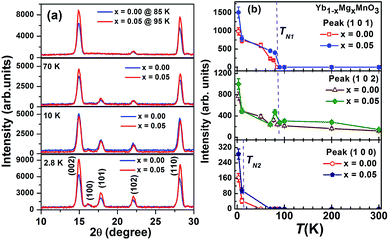 | ||
| Fig. 1 (a) Neutron diffraction patterns (b) integrated intensities of the (100), (101), and (102) reflections between 2.8 K and 100 K of Yb1−xMgxMnO3 (x = 0.0 and 0.05). | ||
Fig. 2 shows Rietveld refinement of temperature dependent ND data for selected temperatures (2.5 K, 10 K and 70 K) which confirm the hexagonal structure of Yb1−xMgxMnO3 with space group P63cm. To analyze these results, one need to remember that six different irreducible representations are possible with k = 0 according to magnetic group theories.13 Only four unidimensional irreducible representations seem to be particularly favorable among all the hexagonal manganites known to date. For example, the magnetic peaks of YMnO3 can be explained by either Γ1 or Γ3 representation while those of ErMnO3 are compatible with Γ2 or Γ4 representation. Fabreges et al.8 reported that the best fit of the YbMnO3 data was obtained assuming Γ4 representation for Mn ordering, and the ordered moment at 1.5 K was found to be 3.25 μB. For the Γ1 and Γ4 representations, the magnetic moment of Mn at the (x, 0, 0) position is aligned perpendicular to the crystallographic a and b axes. Furthermore, the Γ1 representation has an antiferromagnetic coupling between the moments at z = 0 and z = 1/2 planes whereas for the Γ4 representation the inter-plane coupling is ferromagnetic. On the other hand, for the Γ2 and Γ3 representations, the in-plane magnetic moment of Mn is aligned parallel to the crystallographic a and b axes. For the Γ2 representation the inter-plane moments are coupled antiferromagnetically, while for the Γ3 representation the inter-plane moments are coupled ferromagnetically along the c axis.14 For the magnetic refinement of the present ND data, the structure described by the basis vectors of the irreducible representations Γ6 for Yb3+ (at Wyckoff site 2a), Γ2 for Yb3+ at 4b site and Γ2 representation for Mn at 6c site were used.8
 | ||
| Fig. 2 Rietveld refinement of temperature dependent ND data of Yb1−xMgxMnO3 (x = 0.00 and 0.05) at 2.5 K, 10 K and 70 K. | ||
From the Rietveld refinement of temperature dependent ND data, the structural and magnetic properties of the samples were extracted and selected data are shown in Fig. 3–5. Fig. 3a–c show the temperature dependence of the lattice parameters a, c/a, and the unit cell volume V of Yb1−xMgxMnO3. In general, the lattice parameter a and unit cell volume V decrease and c/a increases with decreasing temperature except near the magnetic transition temperatures (TN1 ≈ 85 K, TN2 ≈ 3.5 K for x = 0.00 and TN1 ≈ 89 K, TN2 ≈ 3.5 K for x = 0.05). Close to the magnetic transition temperatures all the lattice parameters (a, c/a, and V) show anomalous variation4,5,15 as a sudden change in value/slope from the background. This anomaly in lattice parameters near the magnetic transition temperatures implies strong spin-lattice coupling and consequently a magnetoelastic coupling.4,16,17 The magnetoelastic effect is clearly visible in the temperature variation of the unit cell volume V data as shown in Fig. 3d. This figure shows the temperature dependence of experimentally measured cell volume (red square symbol + line) and the calculated unit cell volume (blue solid line) in the absence of the magnetic transition for the Yb0.95Mg0.05MnO3 sample. The temperature dependence of the cell volume in the absence of magnetic transition is obtained using the Debey–Gruneisen approximation.18 The measured unit cell volume V in the paramagnetic state (T > TN1) is fitted to the Debey–Gruneisen equation and using the fit parameters (from the high temperature region fitting) the cell volume for the low temperature (T < TN1) nonmagnetic phase is calculated and is shown (blue line in the figure) in Fig. 3d. By subtracting the calculated volume for the nonmagnetic phase from the measured data, we determined the volume strain ΔV which is plotted in the inset of Fig. 3d. The maximum volume magnetostriction (ΔV/V) near the magnetic transition temperature (TN1) is found to be ∼0.09% for the Yb0.95Mg0.05MnO3.
Variation of different Mn–O bond lengths for both YbMnO3 and Yb0.95Mg0.05Mn03 are shown in Fig. 4a–c as a function of temperature. The Mn–O4 and Mn–O3 bond distances show significant variation at TN1. The Mn–O4 bond length shows decrease below TN1 while the Mn–O3 bond length shows increase below TN1. The Mn–O1 and Mn–O2 bond lengths do not show significant changes with temperature. The difference between Mn–O3 and Mn–O4 bond lengths (ΔL), which reflects the change of the average Mn position along the x direction from its neutral position, varies with temperature as shown in Fig. 4d. Fig. 4e, f and g show the variation of Mn x position, O3 z position and O4 z position in the unit cell as a function of temperature for both YbMnO3 and Yb0.95Mg0.05Mn03. The figures clearly show the systematic variations in the atomic positions as the sample cools through TN1. In Fig. 4h–j temperature dependence of the polyhedral distortion (Δ), the tilting angle and the buckling angle are shown for the samples showing clear signatures at the magnetic transition temperatures. These results of variation of temperature dependence of different structural parameters near the magnetic transition temperature clearly indicate strong magnetoelastic coupling in the YbMnO3 system.
Fig. 5a shows the magnetic structure of YbMnO3 from the Rietveld refinement. Fig. 5b shows the temperature dependence of the ordered Mn and Yb magnetic moments extracted from the neutron diffraction data refinement. Below TN1, for both compounds, ordered Mn moment increases with decrease in temperature. The value of the saturated moment is 3.55 μB for both the samples which is smaller than 4 μB for Mn3+. In Fig. 5b symbols show the data points and the solid lines show the fit to the data using a self-consistent mean-field calculation described in ref. 8. Following ref. 8, we used the expression  to fit the observed moment versus T for both the samples. Here B2(x) is the Brillouin function for S = 2 and λ0 is the molecular field constant representing Mn–Mn exchange.8 Best fit to the experimental data points are obtained with msat = 3.55 μB and λ0 = 20 for undoped YbMnO3 and with msat = 3.55 μB and λ0 = 26 for Mg doped YbMnO3. These results suggests that with Mg doping at the Yb site, the geometrical frustration for the antiferromagnetic interaction for the triangular lattice of Mn3+ ions is reduced and the exchange interaction is strengthened. Compared with the undoped YbMnO3, higher value of TN1 (89 K for x = 0.05 and 85 K for x = 0.00), reduced unit cell volume (shown in Fig. 3c) and reduced frustration parameter7,10 (2.045 for x = 0.05 and 2.576 for x = 0.00) for the Mg doped sample support this fact. The Yb moment values at 2.8 K are found to be mYb(4b) = 1.404 μB, mYb(2a) = 1.4697 μB for x = 0.00 and mYb(4b) = 1.307 μB, mYb(2a) = 1.387 μB for x = 0.05.
to fit the observed moment versus T for both the samples. Here B2(x) is the Brillouin function for S = 2 and λ0 is the molecular field constant representing Mn–Mn exchange.8 Best fit to the experimental data points are obtained with msat = 3.55 μB and λ0 = 20 for undoped YbMnO3 and with msat = 3.55 μB and λ0 = 26 for Mg doped YbMnO3. These results suggests that with Mg doping at the Yb site, the geometrical frustration for the antiferromagnetic interaction for the triangular lattice of Mn3+ ions is reduced and the exchange interaction is strengthened. Compared with the undoped YbMnO3, higher value of TN1 (89 K for x = 0.05 and 85 K for x = 0.00), reduced unit cell volume (shown in Fig. 3c) and reduced frustration parameter7,10 (2.045 for x = 0.05 and 2.576 for x = 0.00) for the Mg doped sample support this fact. The Yb moment values at 2.8 K are found to be mYb(4b) = 1.404 μB, mYb(2a) = 1.4697 μB for x = 0.00 and mYb(4b) = 1.307 μB, mYb(2a) = 1.387 μB for x = 0.05.
3.2. Magnetocaloric effect
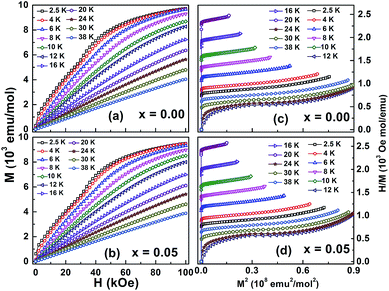
We recently reported magnetization results of Yb1−xMgxMnO3 (x = 0.00 and x = 0.05) which show ferromagnetic ordering in Yb3+ sub-lattice at low temperature around 3 K, and antiferromagnetic ordering of Mn3+ around 85 K.7 In Fig. 6a and b show magnetization isotherms, M(H), for Yb1−xMgxMnO3 (x = 0.00 and x = 0.05) taken over a certain temperature range close to their low temperature transition TN2 at which the Yb ordering takes place. The magnetic field was varied from 0 to 100 kOe. Some representative plots of field variation of M in the temperature range 2–40 K are shown in Fig. 6a and b. From these plots, one can clearly differentiate the nature of H dependence of M below TN2 from that above TN2. Below TN2, M increases slowly with H in the low field region and suddenly the slope changes at a critical field Hc and then increases slowly with further increase of H. This change of slope in M vs. H suggests a field induced magnetic transition.To understand the magnetic phase transition, we have transformed M(H) data into Arrott plots, H/M versus M2 as shown in Fig. 6c and d.19 A positive or negative slope of the Arrot plots (H/M versus M2) indicates a second order or first order transition, respectively.20 Data of both samples show positive slopes in the complete M2 ranges indicating that the system exhibits a second-order phase transition.
From the isothermal magnetization curves at different temperatures magnetic-entropy change ΔSM can be obtained from Maxwell's thermodynamic relationship:21
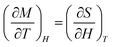 | (1) |
The magnetic-entropy change ΔSM due to the variation of the applied magnetic field from 0 to H is given by
 | (2) |
The value of ΔSM is determined using eqn (2.3b) and the error/uncertainity in ΔSM is calculated using eqn (2.4b) of ref. 22. Calculation details of the same are explained in ref. 23. Using the given manufacturer data and following ref. 22, errors of 0.5%, 0.1% and 0.25% were considered for uncertainties in magnetization, magnetic field and temperature values to calculate the error in ΔSM. The relative error in ΔSM is 10–20% for ΔH = 100 kOe and T around 10 K.
Values of −ΔSM for different ΔH as a function of temperature determined under an applied magnetic field up to 100 kOe are presented in Fig. 7a and b. The −ΔSM is positive in the entire temperature range for both samples. The curves present a characteristic shape with a broad maximum in the vicinity of the FM transition of the Yb moments. The magnitude of the peak increases with increasing value of ΔH for each composition and the position of the maximum shifts from 3 to 9 K when the magnetic field change increases from 1 to 100 kOe. The values of the peak −ΔSmaxM of Yb1−xMgxMnO3 are 3.02 ± 0.37 J mol−1 K−1 for x = 0.00, and 2.63 ± 0.36 J mol−1 K−1 for x = 0.05 with ΔH = 100 kOe. The magnitude of maximum −ΔSM(−ΔSmaxM) increases with increasing magnetic field.24
The adiabatic temperature rise ΔTad is determined from the magnetization and the heat capacity measurements as functions of temperature and magnetic field. The specific heat data (CP) of Yb1−xMgxMnO3 (x = 0.00 and 0.05) as a function of temperature is already published in ref. 10.
The total entropy S(0, T) under zero magnetic field can be calculated from the heat capacity data from the relation,
 | (3) |
ΔTad is the isentropic difference between S(0, T) and S(H, T). S(H, T) is obtained by subtracting the corresponding ΔSmag(H, T) (calculated from the magnetization data above) from S(0, T).24,25 The temperature dependence of ΔTad is plotted in Fig. 7c and d for different fields. The peak of the curve corresponds to ΔTad ∼ 8.6 ± 0.95 K for x = 0.00 and ∼9.06 ± 0.96 K for x = 0.05 for a field change of 100 kOe.
The MCE values (magnitudes of |−ΔSM| and ΔTad) determined from magnetization measurements are slightly higher compared to that determined from the heat capacity measurements.10 This may be due to the difference in measurement conditions;26 magnetization measurements are done under isothermal conditions while heat capacity measurements are done under adiabatic or semi/quasi adiabatic conditions. Also the temperature steps (ΔT) used for magnetization and heat capacity measurements are different. For comparison, we list the magnetocaloric data in Table 1 of various magnetic materials that could be used as magnetic refrigerants.
| Composition/material | TPeak (K) | ΔH (kOe) | ΔSmaxM (J mol−1 K−1) | ΔTad (K) | RCP (J mol−1) | Ref. |
|---|---|---|---|---|---|---|
| YbMnO3 | ∼7 | 100 | 3.02 ± 0.37 | 8.6 ± 0.95 | 41 ± 9 | Present |
| Yb0.95Mg0.05MnO3 | ∼7 | 100 | 2.63 ± 0.36 | 9.06 ± 0.96 | 40.0 ± 10 | Present |
| Yb0.7Ho0.3MnO3 | ∼9 | 100 | 3.75 ± 0.78 | 90 ± 27 | 32 | |
| Yb0.8Sc0.2MnO3 | ∼9 | 100 | 1.87 ± 0.31 | 30.1 ± 8 | 23 | |
| YbMnO3 (single crystal) | ∼9 | 80 | ∼2.3 | ∼15 | ∼26 | 27 |
| HoMnO3 (single crystal) | ∼12 | 80 | ∼5.2 | ∼12.5 | ∼144 | 27 |
| DyMnO3 (single crystal) | ∼12 | 80 | ∼5.5 | ∼11.5 | ∼155 | 27 |
| HoMnO3 (single crystal) | ∼9.5 | 70 | ∼3.5 | ∼6.5 | ∼86 | 24 |
| EuTiO3 | ∼10 | 70 | 12.1 | 21 | ∼124 | 31 |
| ErMn2Si2 | ∼6.5 | 50 | 8.4 | 12.9 | 122 | 33 |
| TmZn | ∼10 | 70 | 6.96 | 11.2 | 98.9 | 34 |
| TmAgAl | ∼10 | 70 | 4.3 | 96 | 35 | |
| TmZnAl | ∼10 | 70 | 3.1 | 76 | 35 | |
| Dy2Cu2O5 | ∼10 | 70 | 6.4 | 145 | 36 | |
| Ho2Cu2O5 | ∼14 | 70 | 6.7 | 137 | 36 | |
| ErNiBC | 5 | 50 | 6.2 | 8.6 | 78 | 37 |
| GdCr2Si2 | 8 | 50 | 4.5 | 67 | 38 | |
| Er4NiCd | 17 | 50 | 15.4 | 500 | 39 |
In addition to the values of ΔSM and ΔTad the relative cooling power RCP is also evaluated to determine the cooling efficiency of these material. RCP is a measure of the quantity of heat transferred by the magnetic refrigerant between hot and cold sinks and is defined as
| RCP = |ΔSmaxM| × |δTFWHM| | (4) |
The RCP values of Yb1−xMgxMnO3 are 30 ± 6 J mol−1, and 29.0 ± 6 J mol−1 with ΔH = 80 kOe for x = 0.0 and 0.05 respectively. These values are higher than single crystal YbMnO3 (RCP = 26 J mol−1 with ΔH = 80 kOe).27 The RCP values increase with increasing field for both compounds. For different class of materials, the magnetocaloric data are extensively reviewed by V. Franco et al.28 and Zhong Wei et al.29 for near room temperature range magneto caloric materials and by Ling-Wei Li30 for low temperature range magneto caloric materials. For comparison, we list the magnetocaloric data of present samples in Table 1 together with similar materials which have the potential as magnetic refrigerants for temperatures below 20 K. The MCE parameters |ΔSmaxM|, RCP and ΔTad values of the present Yb1−xMgxMnO3 samples are slightly lower compared to several of the intermetallic compounds reported by Ling-Wei Li30 and are significantly lower compared to the EuTiO3.31
Compared to YbMnO3, the substitution of nonmagnetic Mg ion at the Yb site causes slight reduction of magnetization and hence slight reduction in the values of magnetic entropy change (ΔSmaxM) and RCP. Results of our earlier studies with doping of nonmagnetic Sc and magnetic Ho ions at the Yb site together with the results of present study are compiled in Table 2. Table 2 presents |ΔSmaxM| and RCP values at 100 kOe together with the effective moment (calculated: μeff = ((1 − x)μ2Yb3+ + μ2Mn3+)1/2 for Mg and Sc doping and μeff = ((1 − x)μ2Yb3+ + xμ2Ho3+ + μ2Mn3+)1/2 for Ho doping) and the value of maximum magnetization M (at 2.5 K, 100 kOe) for YbMnO3 doped with different types (magnetic and non magnetic) of dopants. There is a clear trend between the |ΔSmaxM|, RCP values and the effective moment/maximum magnetization (M) for different series of samples. The |ΔSmaxM|, RCP values are higher for samples having high effective moment (high M).
| Sample | μeff (μB) | M at 2.5 K, 100 kOe (μB/(f.u.)) | |ΔSmaxM| at 100 kOe (J mol−1 K−1) | RCP at 100 kOe (J mol−1) |
|---|---|---|---|---|
| Yb0.70Ho0.30MnO3 (ref. 32) | 8.49 | 3.738 | 3.75 ± 0.78 | 90 ± 27 |
| YbMnO3 | 6.68 | 1.74 | 3.02 ± 0.37 | 41 ± 9 |
| Yb0.95Mg0.05MnO3 | 6.6 | 1.698 | 2.63 ± 0.36 | 40 ± 10 |
| Yb0.80Sc0.20MnO3 (ref. 23) | 6.36 | 1.274 | 1.87 ± 0.31 | 30.1 ± 8 |
The magnetic materials with a second order transition generally obey the relation  , where h is the reduced field just around TC
, where h is the reduced field just around TC  , k is a constant, Ms(0) is the saturation magnetization at low T and S(0, 0) is a reference parameter.40 Fig. 8a shows the linear dependence of −ΔSmaxM versus h2/3 which implies the second order transition for Yb1−xMgxMnO3 (x = 0.0 and 0.05).
, k is a constant, Ms(0) is the saturation magnetization at low T and S(0, 0) is a reference parameter.40 Fig. 8a shows the linear dependence of −ΔSmaxM versus h2/3 which implies the second order transition for Yb1−xMgxMnO3 (x = 0.0 and 0.05).
 | ||
| Fig. 8 (a) Temperature dependence of magnetic entropy change −ΔSmaxM vs. h2/3. Symbols correspond to data points and the solid lines are linear fit to it. (b) The universal curve behavior of the normalized entropy change curves as a function of the rescaled temperature for different magnetic field for Yb1−xMgxMnO3 (x = 0.0 and 0.05). Symbols correspond to data points and the solid line is the curve representing eqn (6). | ||
For a second order transition, the phenomenological universal curve, suggested by Franco and Conde,41 converges ΔSM versus temperature data on a single universal curve if (−ΔSM/ΔSmaxM) versus a rescaled temperature (θ) is plotted where θ is defined in eqn (5) below,
 | (5a) |
 | (5b) |
 | (6) |
4. Conclusions
We reported in this work detailed investigations of the magnetic, magnetoelastic and magnetocaloric properties of Yb1−xMgxMnO3 (x = 0.00 and 0.05) using neutron diffraction and magnetization measurements. The lattice parameter a and unit cell volume V decrease continuously with decreasing temperature but close to the Neel temperature TN1 ≈ 85 K, the Yb ordering temperature TN2 ≈ 3.5 K for x = 0.00 and TN1 ≈ 89 K, TN2 ≈ 3.5 K for x = 0.05 show a magnetoelastic or magnetostriction anomaly. Anomalous variations near the magnetic transition temperatures are observed in the temperature dependence of other structural parameters such as bond lengths, atomic positions etc. From the magnetization measurements, magnetocaloric parameters have been derived. The RCP values of Yb1−xMgxMnO3 are found to be 41 ± 9 J mol−1, and 40.0 ± 10 J mol−1 with ΔH = 100 kOe for x = 0.00 and 0.05, respectively. ΔSmaxM versus h2/3 shows that these compounds exhibit a second order transition. The universal curve for the normalized entropy change vs. the rescaled temperature for the Yb1−xMgxMnO3 constructed.Acknowledgements
This work has been supported by UGC-DAE Consortium for Scientific Research, Mumbai Centre, India in the form of a collaborative research scheme (CRS) through project number CRS-M-199. BSB acknowledges UGC-DAE CSR, Mumbai Centre for project fellowship. AKB is thankful to the National Academy of Sciences, India for their support to this work through Senior Scientist Platinum Jubilee Fellowship Scheme.References
- M. Fiebig, J. Phys. D: Appl. Phys., 2005, 38, R123 CrossRef CAS.
- S. W. Cheong and M. Mostovoy, Nat. Mater., 2007, 6, 13 CrossRef CAS PubMed.
- S. Lee, A. Pirogov, M. Kang, K.-H. Jang, M. Yonemura, T. Kamiyama, S.-W. Cheong, F. Gozzo, N. Shin, H. Kimura, Y. Noda and J.-G. Park, Nature, 2008, 451, 805 CrossRef CAS PubMed.
- S. Lee, A. Pirogov, J. H. Han, J.-G. Park, A. Hoshikawa and T. Kamiyama, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 180413 CrossRef.
- A. K. Singh, S. Patnaik, S. D. Kaushik and V. Siruguri, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 184406 CrossRef.
- T. Lonkai, D. G. Tomuta, U. Amann, J. Ihringer, R. W. A. Hendrikx, D. M. Többens and J. A. Mydosh, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 134108 CrossRef.
- B. Sattibabu, A. K. Bhatnagar, S. Rayaprol, D. Mohan, D. Das, M. Sundararaman and V. Siruguri, Phys. B, 2014, 448, 210 CrossRef CAS.
- X. Fabreges, I. Mirebeau, P. Bonville, S. Petit, G. Lebras-Jasmin, A. Forget, G. Andre and S. Pailhes, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 214422 CrossRef.
- H. Sugie, N. Iwata and K. Kohn, J. Phys. Soc. Jpn., 2002, 71, 1558 CrossRef CAS.
- B. Sattibabu, A. K. Bhatnagar, S. S. Samatham, D. Singh, S. Rayaprol, D. Das, V. Siruguri and V. Ganesan, J. Alloys Compd., 2015, 644, 830 CrossRef CAS.
- B. Sattibabu and A. K. Bhatnagar, Mater. Lett., 2015, 158, 395–398 CrossRef CAS.
- A. V. Pimpale, B. A. Dasannacharya, V. Siruguri, P. D. Babu and P. S. Goyal, Nucl. Instrum. Methods Phys. Res., Sect. A, 2002, 481, 615 CrossRef CAS.
- A. Munoz, J. A. Alonso, M. J. Martinez-Lope, M. T. Casais, J. L. Martinez and M. T. Fernandez-Diaz, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 9498 CrossRef CAS.
- M. Chandra Sekhar, S. Lee, G. Choi, C. Lee and J.-G. Park, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 014402 CrossRef.
- T. Chatterji, B. Ouladdiaf, P. F. Henry and D. Bhattacharya, J. Phys.: Condens. Matter, 2012, 24, 336003 CrossRef PubMed.
- S. Rayaprol, V. Siruguri, A. Hoser, C. Ritter and E. V. Sampathkumaran, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 134417 CrossRef.
- T. Chatterji, T. C. Hansen, S. A. J. Kimber and D. Bhattacharya, Solid State Commun., 2014, 180, 46–51 CrossRef CAS.
- T. Chatterji, G. N. Iles, B. Ouladdiaf and T. C. Hansen, J. Phys.: Condens. Matter, 2010, 22, 316001 CrossRef PubMed.
- A. Arrott and J. Noakes, Phys. Rev. Lett., 1967, 19, 786 CrossRef CAS.
- B. K. Banerjee, Phys. Lett., 1964, 12, 16 CrossRef.
- A. H. Morrish, The Physical Principles of Magnetism, Wiley, New York, 1965, ch. 3 Search PubMed.
- V. V. Pecharsky and K. A. Gschneidner, J. Appl. Phys., 1999, 86, 565 CrossRef CAS.
- B. Sattibabu, A. K. Bhatnagar, K. Vinod, A. Mani and D. Das, RSC Adv., 2015, 5, 86697 RSC.
- A. Midya, P. Mandal, S. Das, S. Banerjee, L. S. Sharath Chandra, V. Ganesan and S. Roy Barman, Appl. Phys. Lett., 2010, 96, 142514 CrossRef.
- V. K. Pecharsky and K. A. Gschneidner Jr, Phys. Rev. Lett., 1997, 78, 4494 CrossRef CAS.
- M. Foldeaki, W. Schnelle, E. Gmelin, P. Bernard, B. Koszegi, A. Giguere, R. Chahine and T. K. Bose, J. Appl. Phys., 1997, 82, 309 CrossRef CAS.
- A. Midya, S. N. Das, P. Mandal, S. Pandya and V. Ganesan, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 235127 CrossRef.
- V. Franco, J. S. Blazquez, B. Ingale and A. Conde, Annu. Rev. Mater. Res., 2012, 42, 305–342 CrossRef CAS.
- W. Zhong, C. K. Au and Y. W. Du, Chin. Phys. B, 2013, 22, 057501 CrossRef.
- L.-W. Li, Chin. Phys. B, 2016, 25, 037502 CrossRef.
- A. Midya, P. Mandal, K. Rubi, R. Chen, J.-S. Wang, R. Mahendiran, G. Lorusso and M. Evangelisti, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 93, 094422 CrossRef.
- B. Sattibabu, A. K. Bhatnagar, K. Vinod, A. Mani and D. Das, Appl. Phys. Lett., 2015, 107, 262904 CrossRef.
- L. Li, K. Nishimura, W. D. Hutchison, Z. Qian, D. Huo and T. Namiki, Appl. Phys. Lett., 2012, 100, 152403 CrossRef.
- L. Li, Y. Yuan, Y. Zhang, T. Namiki, K. Nishimura, R. Pottgen and S. Zhou, Appl. Phys. Lett., 2015, 107, 132401 CrossRef.
- Y. Zhang, L. Hou, Z. Ren, X. Li and G. Wilde, J. Alloys Compd., 2016, 656, 635–639 CrossRef CAS.
- L. Li, J. Wang, K. Su, D. Huo and Y. Qi, J. Alloys Compd., 2016, 658, 500–504 CrossRef CAS.
- Y. K. Zhang and G. Wilde, Phys. B, 2015, 472, 56 CrossRef CAS.
- L. W. Li, G. Hu, I. Umehara, D. Huo, W. D. Hutchison, T. Namiki and K. Nishimura, J. Alloys Compd., 2013, 575, 1 CrossRef CAS.
- W. Hermes, U. C. Rodewald and R. Pöttgen, J. Appl. Phys., 2010, 108, 113919 CrossRef.
- H. Oesterreicher and F. T. Parker, J. Appl. Phys., 1984, 55, 4334 CrossRef CAS.
- V. Franco and A. Conde, Int. J. Refrig., 2010, 33, 465 CrossRef CAS.
- Q. Y. Dong, H. W. Zhang, J. R. Sun, B. G. Shen and V. Franco, J. Appl. Phys., 2008, 103, 116101 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |