Insulator-quantum Hall transition in monolayer epitaxial graphene

Abstract

We report on magneto-transport measurements on low-density, large-area monolayer epitaxial graphene devices grown on SiC. We observe temperature (T)-independent crossing points in the longitudinal resistivity ρ_xx, which are signatures of the insulator-quantum Hall (I-QH) transition, in all three devices. Upon converting the raw data into longitudinal and Hall conductivities σ_xx and σ_xy, in the most disordered device, we observed a T-driven flow diagram approximated by the semi-circle law as well as the T-independent point in σ_xy near e²/h. We discuss our experimental results in the context of the evolution of the zero-energy Landau level at low magnetic fields B. We also compare the observed strongly insulating behaviour with metallic behaviour and the absence of the I-QH transition in graphene on SiO₂ prepared by mechanical exfoliation.

---

1. Introduction

When a strong magnetic field B is applied perpendicular to the plane of monolayer graphene,^1–3 Landau quantization results in a series of Landau levels whose energies are given by⁴where N, ħ, e, v_F are an integer, reduced Planck constant, electronic charge and Fermi velocity, respectively. According to eqn (1), the energy of the N = 0 Landau level (LL) is always zero and thus is independent of B. Such a zeroth LL, which is shared equally by electrons and holes with a degeneracy of four, is unique in graphene and has no counterparts in any semiconductor-based two-dimensional (2D) systems. It is worth mentioning that graphene on SiO₂ can form electron hole puddles⁵ due to the interactions between graphene and its substrate. Such an effect can greatly modify the electronic properties of graphene. Therefore the B-independent zero-energy LL (eqn (1)) should be considered as the theoretical limit of non-interacting, ideal graphene system.

Although in most cases, transport in graphene on SiO₂ prepared by mechanical exfoliation shows metallic behavior or a very weak T dependence,^1,2 insulating behavior in the sense that the resistivity decreases with increasing T can appear in suspended graphene on SiO₂,⁶ and in graphene on hexagonal boron nitride (h-BN) when sublattice symmetry is broken.⁷ It is also known that h-BN can substantially increase the mobility of graphene device and the induced sublattice symmetry breaking allows the observation of Zeeman spin degeneracy lifting of the LLs in the presence of a magnetic field.^8,9 Interestingly, recent experiments show very low conductivity near the charge neutrality point for monolayer graphene on boron nitride with a suspended top gate⁷ and for monolayer epitaxial graphene (EG) with a point-like constriction caused by bilayer patches.¹⁰ Such important results on monolayer graphene suggest further studies are required and may be related to the possible splitting of the zeroth LL¹¹ at low B. Moreover, insulating behavior and a temperature-independent point in the measured resistivity are observed in a disordered monolayer EG device.¹² Here, we address the two aforementioned fundamental issues: the fate of the zero-energy LL at low fields and the insulating behavior in disordered graphene. In the most disordered EG device, we observe a well-defined T-independent point in the measured Hall conductivity σ_xy and the appearance of a semicircle relation in the T-driven flow diagram.¹³ Such results are in sharp contrast to the theoretical understanding of the zero-energy LL which is believed to be B-independent. Moreover, our data provide a thorough understanding of the low-field insulator-quantum Hall (I-QH) transition in disordered EG as well as the metallic-like behavior in graphene on SiO₂.

2. Experimental section

Our EG devices were fabricated utilizing a clean lithography process¹⁴ that leaves the surface free of resist residues. After the fabrication process, doping occurs due to or initiated by chemical etching of the protective layer and exposure to air. We have engineered the carrier density as low as n ≈ 10¹⁵ m⁻². Here, the exposed Si atoms in the SiC(0001) lattice form partial covalent bonds to carbon atoms in the lower graphene layer (buffer layer), and only the top layer is conducting. Si–C covalent bonds and defects such as interfacial dangling bonds affect the electrical environment of the graphene sheet and graphene-substrate coupling may break its sublattice symmetry.¹⁵ Low carrier density is known to reduce the screening of Coulomb potential fluctuations, and therefore enhances the SiC substrate effect on the conducting graphene sheet.

Large-area EG devices are suitable for studies of QH transitions and insulating behavior since the long-range effects of increasing disorder may be hidden by local or size-dependent phenomena for small samples.¹⁶ Moreover, in EG grown on SiC,^17,18 E_F can be pinned to the localized states¹⁹ such that the ν = 2 QH plateau extends from a low field (∼1 T) to exceptionally high values (30 T),²⁰ making EG an ideal system for studying an isolated low-field QH transition, although no such high-field transition has been reported. A possible reason for this is the reservoir model responsible for the long ν = 2 QH plateau¹⁹ so that one does not observe the high-field insulating state. Measurements on large-area (0.6 mm × 0.1 mm) devices were made in a perpendicular magnetic field up to 9 T in a variable-temperature cryostat using standard low-frequency lock-in techniques.

3. Results and discussion

Fig. 1a–c show the atomic force microscope (AFM) images taken on the three samples (EG1, EG2 and EG3) which were studied in this work. Although both samples were grown at the same temperature of 1900 °C, the surface roughness of EG1 appears to be lower than that of EG2. As will be shown later, although the surface roughness of EG3 is slightly lower than that of EG2, the resistivity of EG3 device is higher than that of EG2 (and that of EG1). One possible reason is that the growth temperature of EG3 (1800 °C) is lower than those of EG1 and EG2, rendering EG3 the most disordered among the three devices which will be described later.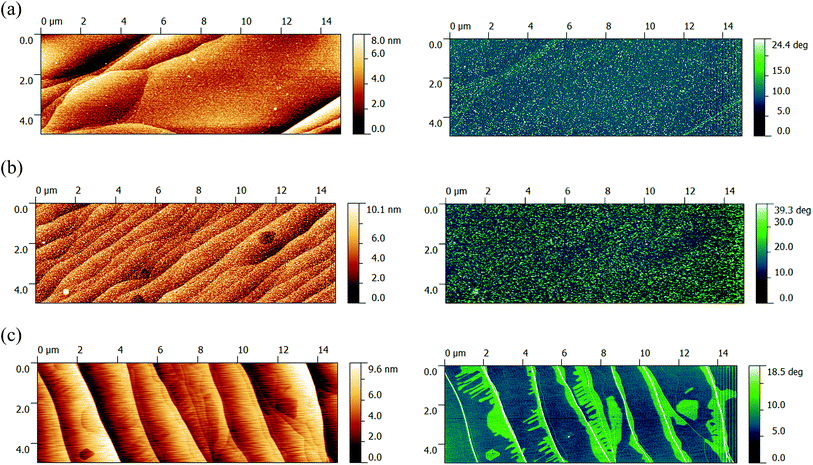

Fig. 1 AFM images taken on (a) EG1, (b) EG2, and (c) EG3. Left: surface and right: phase measurements.

The longitudinal and Hall resistivities (ρ_xx and ρ_xy) for EG1, EG2, and EG3 at various T are plotted in Fig. 2a–c. The low-T resistivity of EG1 is nearly two times lower than that of EG2. However, the mobility of EG1 is lower than that of EG2. Therefore it is not possible to tell whether the level of disorder in EG1 or in EG2 is higher. Nevertheless, since both the mobility and zero-field conductivity of EG3 is the lowest among the three devices, we believe that EG3 is the most disordered sample. We can immediately see the T-independent points in ρ_xx at crossing fields B_c in all three samples. For B < B_c, the device behaves as an insulator in the sense that ρ_xx decreases with increasing T.²¹ For B > B_c, the device shows QH-like behavior and ρ_xx increases with increasing T.^21–24 Our results show characteristics of the insulator to ν = 2 QH transition observed in disordered 2D systems.^20–22 Like other disordered 2D systems, localization and interaction effects are observed in our devices (see ESI†).

Fig. 2 ρ_xx and ρ_xy at different temperatures T for (a) EG1, (b) EG2, and (c) EG3. The vertical arrows indicate the temperature increase: T = 2.52 K, 3.50 K, 4.25 K, 5.50 K, 7.00 K, 8.50 K, and 10.0 K for EG1; T = 2.60 K, 3.54 K, 4.55 K, 5.56 K, and 7.00 K for EG2; T = 4.45 K, 7 K, 10 K, 15 K, and 25 K for EG3.

To further study the observed I-QH transition,¹² we plot σ_xx and σ_xy for EG1, EG2 and EG3 in Fig. 3a–c. Interestingly, a clear T-independent crossing point in σ_xy develops near e²/h for EG2 and EG3. In the scaling theory of the QH effect, values of σ_xy that are half multiples of e²/h (per spin) behave as unstable points under renormalization.²¹ Therefore the observed crossing point near e²/h suggests a delocalization/localization process occurs when the zeroth LL passes upwards through E_F when B is decreased.²²

Fig. 3 The directly converted conductivities, σ_xx and σ_xy, at different T for (a) EG1, (b) EG2, and (c) EG3. The vertical arrows indicate the temperature increase. The temperature points are the same as those given in the caption of Fig. 2 for each sample.

A T-driven flow diagram in the (σ_xy, σ_xx) plane can be used to study the physics of localization processes in 2D systems.^25,26 A field-induced transition involves a transition between two fixed points in this diagram, with a sudden increase and a similar decrease in σ_xx once the LL is emptied or filled. It has been experimentally verified that this transition traces out a semicircle²⁵ in the (σ_xy, σ_xx) plane and for systems with a single conduction channel the semicircle represents a critical boundary for the QH state. The semicircle is centered at (0, e²/h) and follows (σ_xx)² + (σ_xy − e²/h)² = (e²/h)², where the transition to the ν = 2 QH state occurs.

Fig. 4a and b show that samples EG1 and EG2 develop robust ν = 2 QH characteristics to the right of the semicircle (σ_xy > e²/h) at fields B ≈ 1 T, and approach the limiting point of the QH state at (2e²/h, 0). Conductivity data is given in Fig. 4 for all three EG samples with arrows showing T-driven flow superimposed at a series of fixed B. For a given sample, results at constant magnetic field strength that follow a vertical T-driven flow line corresponds to a critical field denoted by B_c^σ identified as a crossing point of constant conductivity σ_xy. Similar curved arrows show how flow divides along the critical boundary of the QH state, shown by a dotted semicircle, starting at an unstable point indicated by a black dot. EG1 avoids the critical boundary with high conductivity (σ_xx ≈ 4e²/h) at low fields, and the vertical flow line occurs at σ_xy < e²/h. Vertical T-driven flow arrows in Fig. 4b and c show that the crossing magnetic field B_c^σ occurs close to σ_xy = e²/h for both EG2 and EG3, while the magnitude of σ_xx decreases from σ_xx ≈ 2e²/h to σ_xx ≈ e²/h. Thus, we can characterize the T-driven flow for increasing disorder strength in our samples by vertical flow along σ_xy = e²/h, the line that points toward the center of the ν = 2 QH semicircle. Elsewhere the flow diverges from verticality especially near the semi-circle boundary, as clearly seen for sample EG3, where flow lines become nearly tangent to the semicircle.

Fig. 4 Conductivity σ_xx plotted against σ_xy for (a) EG1, (b) EG2 and (c) EG3. The dotted curves denote the theoretical prediction of semicircle σ_xx–σ_xy relation for the 0–2 transition. Each group of triangle markers connected by dashed lines denotes the data for the same magnetic field. The arrows indicate the flow line to the low temperature extreme at fixed magnetic fields. The black ones correspond to the flow at the observed crossing point B_c^σ in σ_xy.

Based on the floating up picture,^27,28 Kivelson, Lee, and Zhang have proposed the global phase diagram (GPD) which describes possible phase transitions in a 2D system.²⁹ When the spin degeneracy is considered, for a strongly disordered 2D system in which the spin-splitting is not well-resolved, the only I-QH transition is the 0–2 transition, where the numbers 0 and 2 correspond to the insulating phase and the ν = 2 QH state. This 0–2 transition and the 2–0 transition, from the QH state to the insulating regime, are equivalent within the GPD framework.²⁹ The establishment of the semicircle relation for the 0–2 transition requires that the lowest extended band continuously floats up above E_F with smaller B.^{22,23,27–29} Experimental evidence for the floating-up of the extended states in GaAs has been claimed.³⁰ On the other hand, at low magnetic fields, extended states can float up and then merge in a Si 2D system.³¹ It was pointed out that chaotic potentials and possible oscillation of the boundary between the metallic and insulating phases³² can make the observation of the pronounced floating-up of the extended states not realizable.³³

The semicircle-like flow lines obtained on EG3 appears to be in line with the levitation of the zeroth LL in disordered graphene, linking the observed insulating behavior in EG3 at low fields to the zeroth Landau band floating up above.³⁰ However, without the ability to tune the carrier density to trace the crossing point in σ_xy in our case, we cannot confirm the floating-up of the extended states at low B. The semicircle law does not provide a good explanation for the transition in the cleaner devices EG1 and EG2. The possible origin is that their weak disorder prohibits the observation of the levitating Landau band. Moreover we found that the slope of σ_xy at B_c^σ scales with temperature following T^−κ with κ = 0.21 and 0.36 for EG2 and EG3, respectively (see Fig. S7 in the ESI†). At such low-field transitions, the Zeeman splitting plays a minor role, preserving the spin degeneracy. Therefore the increase in κ can be attributed to the breaking of sublattice symmetry in the presence of potential fluctuations, which may split the zeroth Landau band.³⁴ With the strongest disorder in EG3, the semicircle relation between σ_xy and σ_xx becomes apparent, linking out results with possibly B-dependent zeroth Landau band due to disorder.

For EG3, the T-independent crossing point in ρ_xx occurs at the filling factor ν_c = nh/(eB_c) of 0.6, which is in agreement with the recently reported value for the high-field levitation of the zeroth Landau band.³⁵ However for EG1 and EG2, it corresponds to ν_c = 16 and ν_c = 7, respectively, which is much higher than that for EG3. These values deviate from the prediction of plateau-to-plateau transition between the ν = 6 and ν = 2 QH state, suggesting that the transition in weakly disordered EG1 and EG2 does not result from the N = 1 Landau band passing through the Fermi energy with magnetic field. In addition, at zero magnetic field, we have estimated the width Γ ≈ ħ/τ of Landau level broadening due to disorder. The results are 23 meV, 24 meV, 76 meV for EG1, EG2, and EG3, respectively. However the Fermi energy lies at E_F = 49 meV, 35 meV, and 28 meV for EG1, EG2, and EG3. Interestingly, for EG3, E_F is smaller than the estimated Γ. This finding infers a narrowing of the zeroth Landau band, which is robust against some sorts of disorder³⁶ such that we can still observe the ν = 2 quantum Hall character in highly disordered EG3. It is worthwhile noting that the finite size effect and the charge transfer from the buffer layer/SiC interface (which partially determines the carrier density in a QH state) to the graphene sheet²⁰ would modify the transitions. Moreover, since we have observed logarithmic temperature dependent Hall slope in all the devices due to interaction effects (see Fig. S4a in the ESI†), electron–electron interactions which are not considered within the global phase diagram may be regarded as perturbation/modification to the original floating-up picture.

It was shown that graphene-substrate-induced sublattice symmetry breaking coupled with charge disorder in epitaxial graphene layer can substantially modify the transport properties of graphene.³⁷ We note that in graphene on h-BN, strongly insulating behavior solely due to graphene-substrate related sublattice symmetry breaking is observed.⁶ Interestingly, such an insulating phase makes a direct transition to the ν = 0 state at an extremely low field (B ∼ 0.1 T) without an intermediate transition to the ν = 2 QH state,⁵ in sharp contrast to our experiments. In our case, the mobility of EG3 is 20 times lower than that of the graphene on h-BN. The stronger disorder and the fact that our device is not exactly at the Dirac point should inhibit the formation of the ν = 0 state as supported by no sign of the ν = 0 plateau in σ_xy. Therefore although insulating behavior can be observed in both graphene on h-BN and disordered EG, we observe a transition from the insulating phase to the ν = 2 QH state as well as the semi-circle-like T-driven flow diagram, in line with floating up of the N = 0 electron LL due to stronger disorder compared with that of Amet et al.⁷ Our results, together with the pioneering work of Amet et al. suggest that sublattice symmetry breaking plays an important role in the observed insulating behavior in graphene subject to the environment effect. The strength of disorder, however, determines the allowable transition between the insulating state and the ν = 2 QH state or the ν = 0 state.

The unique B-dependent carrier density in epitaxial graphene grown on SiC, which can be ascribed to the reservoir model, has a pronounced effect on the QH transition. We would like to point out that though such an effect is believed to be responsible for the extremely long ν = 2 quantum Hall plateau, it should not significantly affect the low-field I-QH transition observed in our devices. The reason for this is that a good crossing point requires fixed carrier density in the system as previously observed in conventional semiconductor-based systems in which the carrier density is B-independent.^21–23 Moreover, in all the theoretical studies on the I-QH transition, the carrier density is assumed to be constant, independent of both temperature and magnetic field.^27–29 Therefore the reservoir model describing charge transfer between epitaxial graphene and the SiC substrate as a function of B (ref. 16) should not play an important role in the observed low-field I-QH transition in the work of Pallecchi et al.¹² as well as in our devices.

4. Conclusions

In conclusion, we have reported magneto-transport measurements on low-density monolayer EG with various amount of disorder. T-independent crossing points are observed in all three samples. We have found that the observed T-independent point in ρ_xx survives after subtraction of the electron–electron interaction corrections (see ESI†), demonstrating that such crossing points are related to magnetic-field-induced delocalization/localization transitions. T-independent points in σ_xy can emerge, corresponding to the unstable points under renormalization in the scaling theory of the QH effect. Our results therefore suggest that σ_xy, rather than ρ_xx, is the more important physical quantity in the study of quantum Hall transitions. Most importantly, in the most disordered device, we have observed T-driven flow lines approximated by the semi-circle law. Such results are in line with the fact that the zeroth LL is levitated for B < B_c and can explain the insulating behavior in our EG. In the future, we plan to work on a gated EG device in order to tune the effective disorder and carrier density within the same sample so that the evolution of the crossing point in σ_xy as well as T-driven flow diagram can be used to probe the fate of the zero-energy LL in graphene-based systems.

Acknowledgements

This work was funded by the Ministry of Science and Technology (MOST), Taiwan. C. T. L. was supported by the MOST, Taiwan (grant numbers MOST 103-2918-I-002-028, MOST 103-2622-E-002 -031, MOST 104-2622-8-002 -003 and MOST 102-2119-M-002 -016 -MY3).

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
2. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200.
3. Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201–204.
4. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162.
5. J. Martin, N. Akerman, G. Ulbricht, T. Lohmann, J. H. Smet, K. von Klitzing and A. Yacoby, Nat. Phys., 2008, 4, 144–148.
6. K. I. Bolotin, K. J. Sikes, J. Hone, H. L. Stormer and P. Kim, Phys. Rev. Lett., 2008, 101, 096802.
7. F. Amet, J. R. Williams, K. Watanabe, T. Taniguchi and D. Goldhaber-Gordon, Phys. Rev. Lett., 2013, 110, 216601.
8. K. I. Bolotin, F. Ghahari, M. D. Shulman, H. L. Stormer and P. Kim, Nature, 2009, 462, 196–199.
9. C. R. Dean, A. F. Young, P. Cadden-Zimansky, L. Wang, H. Ren, K. Watanabe, T. Taniguchi, P. Kim, J. Hone and K. L. Shepard, Nat. Phys., 2011, 7, 693–696.
10. C. Chua, M. Connolly, A. Lartsev, T. Yager, S. Lara-Avila, S. Kubatkin, S. Kopylov, V. Fal’ko, R. Yakimova, R. Pearce, T. J. B. M. Janssen, A. Tzalenchuk and C. G. Smith, Nano Lett., 2014, 14, 3369–3373.
11. A. J. M. Giesbers, L. A. Ponomarenko, K. S. Novoselov, A. K. Geim, M. I. Katsnelson, J. C. Maan and U. Zeitler, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 201403.
12. E. Pallecchi, M. Ridene, D. Kazazis, F. Lafont, F. Schopfer, W. Poirier, M. O. Goerbig, D. Mailly and A. Ouerghi, Sci. Rep., 2013, 3, 1791.
13. M. Hilke, D. Shahar, S. H. Song, D. C. Tsui, Y. H. Xie and M. Shayegan, Europhys. Lett., 1999, 46, 775–779.
14. Y. Yang, L.-I. Huang, Y. Fukuyama, F.-H. Liu, M. A. Real, P. Barbara, C.-T. Liang, D. B. Newell and R. E. Elmquist, Small, 2015, 11, 90–95.
15. S. Y. Zhou, G. H. Gweon, A. V. Fedorov, P. N. First, W. A. de Heer, D. H. Lee, F. Guinea, A. H. Castro Neto and A. Lanzara, Nat. Mater., 2007, 6, 770–775.
16. T. Nakajima, T. Ueda and S. Komiyama, J. Phys. Soc. Jpn., 2007, 76, 094703.
17. C. Berger, Z. Song, T. Li, X. Li, A. Y. Ogbazghi, R. Feng, Z. Dai, A. N. Marchenkov, E. H. Conrad, P. N. First and W. A. de Heer, J. Phys. Chem. B, 2004, 108, 19912–19916.
18. C. Riedl, C. Coletti and U. Starke, J. Phys. D: Appl. Phys., 2010, 43, 374009.
19. T. J. B. M. Janssen, A. Tzalenchuk, R. Yakimova, S. Kubatkin, S. Lara-Avila, S. Kopylov and V. I. Fal’ko, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 233402.
20. J. A. Alexander-Webber, A. M. R. Baker, T. J. B. M. Janssen, A. Tzalenchuk, S. Lara-Avila, S. Kubatkin, R. Yakimova, B. A. Piot, D. K. Maude and R. J. Nicholas, Phys. Rev. Lett., 2013, 111, 096601.
21. S. H. Song, D. Shahar, D. C. Tsui, Y. H. Xie and D. Monroe, Phys. Rev. Lett., 1997, 78, 2200–2203.
22. H. W. Jiang, C. E. Johnson, K. L. Wang and S. T. Hannahs, Phys. Rev. Lett., 1993, 71, 1439–1442.
23. R. J. F. Hughes, J. T. Nicholls, J. E. F. Frost, E. H. Linfield, M. Pepper, C. J. B. Ford, D. A. Ritchie, G. A. C. Jones, E. Kogan and M. Kaveh, J. Phys.: Condens. Matter, 1994, 6, 4763.
24. T. Wang, K. P. Clark, G. F. Spencer, A. M. Mack and W. P. Kirk, Phys. Rev. Lett., 1994, 72, 709–712.
25. H. P. Wei, D. C. Tsui and A. M. M. Pruisken, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 1488–1491.
26. C. P. Burgess and B. P. Dolan, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 113406.
27. D. E. Khemelinskii, Pis'ma Zh. Eksp. Teor. Fiz., 1983, 38, 454 (JETP Lett., 1983, 38, 552).
28. R. B. Laughlin, Phys. Rev. Lett., 1984, 52, 2304.
29. S. Kivelson, D.-H. Lee and S.-C. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 2223–2238.
30. I. Glozman, C. E. Johnson and H. W. Jiang, Phys. Rev. Lett., 1995, 74, 594–597.
31. A. A. Shashkin, G. V. Kravchenko and V. T. Dolgopolov, JETP Lett., 1993, 58, 220–224 (Pis'ma Zh. Eksp. Teor. Fiz., 1993, 58, 215–219).
32. G. M. Gusev, U. Gennser, X. Kleber, D. K. Maude, J. C. Portal, D. I. Lubyshev, P. Basmaji, M. D. P. A. Silva, J. C. Rossi and Y. V. Nastaushev, Solid State Commun., 1996, 100, 269–273.
33. V. T. Dolgopolov, Phys.-Usp., 2014, 57, 105–127.
34. F. Ortmann and S. Roche, Phys. Rev. Lett., 2013, 110, 086602.
35. L. Zhang, Y. Zhang, M. Khodas, T. Valla and I. A. Zaliznyak, Phys. Rev. Lett., 2010, 105, 046804.
36. A. J. M. Giesbers, U. Zeitler, M. I. Katsnelson, L. A. Ponomarenko, T. M. Mohiuddin and J. C. Maan, Phys. Rev. Lett., 2007, 99, 206803.
37. X. Peng and R. Ahuja, Nano Lett., 2008, 8, 4464–4468.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra07859a

---