Theoretical and thermogravimetric study on the thermo-oxidative decomposition of Quinolin-65 as an asphaltene model molecule

Abstract

In this study, the thermal oxidation of an asphaltene model molecule, Quinolin-65, was investigated using the density functional theory (DFT) and the second-order Møller–Plesset (MP2) perturbation theory. The reactions studied involved thermal decompositions as well as the interactions between the model molecule and singlet atomic (O¹D) and molecular (O₂¹Δ) oxygen. The theoretical study was performed under conditions similar to those of the uncatalyzed thermal oxidation of asphaltenes. A new reaction pathway for the loss of the olefin chain in Quinolin-65 via a 1,3-hydrogen shift mechanism was revealed. Thermogravimetric analysis of Quinolin-65 was also performed and the reaction products were probed by a mass spectrometer. Both the theoretical study and the thermogravimetric analysis concluded that the thermo-oxidative decomposition of Quinolin-65 is a complex multi-step reaction process, which involves different reaction pathways. The thermodynamic parameters obtained in this study showed that the reaction process should start with the loss of the olefin chain in the Quinolin-65 molecule, followed by the oxidation of the aromatic chain, to produce mainly, H₂O, CO₂, and SO₂.

---

1. Introduction

Because of the recent fluctuation in global oil prices, both the revenues earned and expected from heavy oil industries have dropped. Accompanied by the impact of pollution, as well as water and energy consumptions of the recovery of oil sands, the current situation represents another challenge for the world's third-largest and Canada's largest oil reserve.¹ The heavy nature of Alberta's oil, resulting from its high viscosity, low H/C ratio and high sulphur and nitrogen content, requires researching new technologies to improve its recovery and quality. Actually, the production of both conventional and unconventional crude oil can be affected by several sources of damage under subsurface and surface conditions that can affect oil production. Heavy compounds in crude oil, such as asphaltenes, are a source of damage in light, medium and heavy oils.^2,3 These asphaltenes are considered to be the heaviest, most aromatic and most surface-active fraction of crude oil.⁴ Because of their complex chemical structures, amphiphilic behaviour, and polarizability, asphaltenes exhibit a self-associating feature that promotes aggregation and subsequently increases the viscosity of crude oil.⁴ To overcome the asphaltenes process challenges, the Nassar group at the University of Calgary has recently introduced metal-based nanoparticle technology to enhance upgrading and recovery of crude oil. The new technique involves adsorptive removal of asphaltenes from the crude oil matrix followed by catalytic upgrading of the adsorbed asphaltenes using different types of supported and unsupported metal oxide nanoparticles to upgrade the adsorbed asphaltenes into valuable commodity chemicals.^5–10 The catalytic upgrading involves thermal oxidation/gasification of asphaltenes at moderate temperatures.^11–13 Using the new technology, nanoparticles or functionalized nanoparticles have proven to alter the thermo-oxidative decomposition of asphaltenes, and lower the activation energies of the reaction.^6,8,14–16 Our results showed that asphaltene adsorption and post-adsorption catalytic decomposition is strongly dependent on the type of asphaltenes, its origin, type of solvent and the chemical structure and surface chemistry of the nanoparticles.^16,17 However, because of the complexity of asphaltenes, the understanding of their properties, in particular the structural factors ruling their self-association and subsequent adsorption and cracking tendencies are difficult. Hence, proper model molecule with well-defined structure that can mimic the properties of real asphaltenes would help to improve this understanding.

For instance, Song and Parish have employed theoretical methods to study the pyrolysis mechanisms of thiophene and methylthiophene, as asphaltene model molecules.¹⁸ The reaction mechanism involved C–C, C–S, and C–H bond ruptures, in addition to H-migration. The major products were found to be ethane, thioketene, propyne, CS, and CO. Similarly, Song considered the recombination reaction between 2-thienylmethyl and HO₂ radical to play an important role in asphaltenes decomposition.¹⁹ Using high-level theoretical calculations, Song's study concluded that the most favorable pathway in the reaction mechanism was the insertion of carbonyl group leading to the formation of H₂O. Simple nitrogen-containing structures such as quinoline and isoquinoline have also been used as asphaltene model molecules in many experimental and theoretical studies.^20–22 Full reaction mechanisms were drawn for quinoline that showed the important role of indene as an intermediate. Similar to the thiophene studies, H-migration has also played a significant role in the reaction mechanism.

Nevertheless, simple molecules cannot completely simulate or mimic the complex nature of asphaltenes. Hence, in this study, a heavy model molecule, like Quinolin-65 (Q65), has been proposed to better mimic asphaltenes and understand their chemical properties.²³ Q65 is not only more representative heavy molecule, but also its structure is composed of polyaromatic cores containing heteroatoms such as S, N, and O with attached aliphatic chains. These features are commonly reported in a typical asphaltenes structure.² Actually, Q65 was proven to resemble asphaltenes in their chemical and physical properties and adsorption behaviour on solid surfaces^10,23,24 as well as thermal cracking.²⁴

Herein, we are practically interested in the thermo-oxidative decomposition of asphaltenes using Q65 as a model molecule. Oxidation of hydrocarbons had gained an intense interest for long time.^25–28 Although the ground state of molecular oxygen has a spin multiplicity of three, designated as triplet oxygen (O₂³Σ⁺_g), singlet oxygen (O₂¹Δ_g) has gained special interest due to its high reactivity.^29,30 Oxygen addition to organic molecules such as ethane,²⁸ ethanol,³¹ 1,3-butadiene,³² benzene,^25,32 and toluene,²⁶ have been extensively studied using high-level theoretical methods. Widely speaking, addition of singlet molecular oxygen was shown to proceed by both stepwise and concerted mechanisms. While the former involves the formation of a diradical intermediate, the latter proceeds to form a peroxide moiety (benzene oxide). Generally, the addition of triplet oxygen to hydrocarbons and aromatic rings is highly endergonic, such as in the cases of ethane²⁸ and benzene.³² However, addition of the more reactive singlet oxygen is usually exergonic.^25,29,30 The study of Chen et al. on the reaction dynamics of singlet oxygen (O¹D) with benzene shapes a milestone in this field.²⁵ Using laser photolysis, TOF-MS, and theoretical methods, the authors proposed a full mechanism for the O(¹D) reactions with benzene to produce, mainly, CO, C₅H₅, and H species.

Accordingly, we explored in this study the interaction of Q65 with singlet atomic (O¹D) and molecular (O₂¹Δ_g) oxygen. The study aimed to construct a thermo-oxidative reaction mechanism of Q65. For which, we employed the density functional theory (DFT) and second-order Møller–Plesset perturbation theory (MP2) to examine different possible reaction pathways for Q65 thermal oxidation and decomposition. In addition to the theoretical study, thermo-oxidative behavior of virgin Q65 was investigated by using a thermogravimetric analyzer coupled with an online mass spectrometer. The main products formed upon the thermo-oxidative decomposition of Q65 were CO₂, H₂O and SO₂ gases. Therefore, these experimental and theoretical investigations provide a comprehensive reaction mechanism, which provides both full understanding of the reactions involved, as well as vital kinetic parameters such activation energies, rate constants, and pre-exponential factors. In addition, theoretical calculations could predict the transition state structures, which cannot be observed directly during experiments. Hence, a general reaction mechanism for the non catalyzed Q65 thermal oxidation can be drawn.

2. Experimental section

2.1 Materials

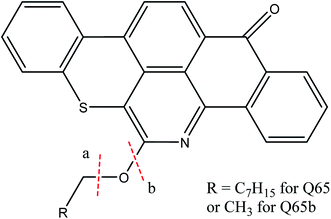
A model asphaltene molecule, Quinolin-65 (Q65) (C₃₀H₂₇NO₂S, MW = 467.62 g mol⁻¹, λ_max = 565, 80 wt% dye content) purchased from Sigma-Aldrich, Ontario was considered in this study. Scheme 1 shows the chemical structure of Q65, as drawn with ChemDraw V14.^19,33 As seen, this model molecule contains molecular characteristics present in asphaltene fractions reported for Athabasca crude oil,²³ like alkyl chains, aromatic moieties and heteroatoms such as sulfur, nitrogen and oxygen. This model molecule represents an asphaltene of the continental type due to the presence of one significant large aromatic area plus side chains per molecule.^23,24

Scheme 1 Q65 molecular structure drawn with ChemDraw V14.³³ The resemblance with an asphaltene molecule can be seen by the archipielago aromatic region, the alkyl chain and the presence of heteroatoms like sulfur, nitrogen and oxygen.

2.2 Thermogravimetric analysis

Thermogravimetric analysis (TGA) was carried out using a simultaneous thermogravimetric analysis/differential scanning calorimetry (TGA/DSC) analyzer (SDT Q600, TA Instruments, Inc., New Castle, DE). In a typical experiment, approximately 5 mg of dried solid Q65 (50 °C, under vacuum) oxidized at three heating rates of 5, 10, and 20 °C min⁻¹, in separate experiments. The airflow was kept at 100 cm³ min⁻¹ during the experiments. The experiments were performed under ambient pressure. Evolved gas analysis (EGA) was also carried out by an online mass spectrometer (MS) (Pfeiffer Vacuum GSD 301 O2, Omnistar, Deutschland) attached to the TGA/DSC system. For EGA experiments, a sample mass of 11 mg, airflow of 30 cm³ min⁻¹ and a heating rate of 10 °C min⁻¹ was used. The TGA instrument was calibrated for mass and heat changes using sapphire as a reference for heat calibration and zinc as a reference for temperature calibration.

3. Theoretical calculations

For the theoretical calculations involved in this study, the universal hybrid density functional (B3LYP) was used.^34,35 All minimum-energy structures of reactants and products, intermediates and transition states were located and optimized at B3LYP/6-31+g(d) level of theory. We chose to use a single diffuse function (+) and a (d) polarization to the heavy atoms in order to accommodate the heavy calculations of the complex Q65 structure. All species involved in this study were minima in their singlet state, unless stated otherwise. Transition states were located by exploring the potential energy surface (PES) along the expected reaction coordinate, followed by a transition state optimization for the highest point at the PES. All transition states were confirmed to have one imaginary frequency along the reaction coordinate as per the criteria. Intrinsic reaction coordinate (IRC) was used to confirm that each TS certainly connects the two desired minima. Final single point energies were calculated at MP2/6-311g(d,p) level of theory.³⁶ Therefore, the full notation for the calculation method used in this work is referred herein by MP2/6-311g(d,p)//B3LYP/6-31+g(d). For open-shell species such as atomic oxygen and free radicals, the unrestricted version was specified by using the prefix u, i.e., uB3LYP or uMP2. Zero-point energies (ZPE) were computed at the B3LYP/6-31+g(d) level of theory and were scaled by a factor of 0.9806 as suggested by Scott and Radom.³⁷

Enthalpies at 0 K (H₀) were obtained by adding the single-point energy to the scaled ZPE. Enthalpies and Gibbs free energies at 298 K (H₂₉₈ and G₂₉₈) were obtained by adding a value of x to the enthalpies or Gibbs free energies at 0 K (H₀, or G₀), which is equivalent to the energies after the scaled ZPE corrections. x was calculated by subtracting the unscaled ZPE from the thermal correction to enthalpy (H_corr.) or thermal correction to Gibbs free energy (G_corr.). For calculating the thermodynamic values at different temperatures, the same calculation method mentioned above was used by utilizing different corrections (H_corr. and G_corr.) obtained at a given temperature. All calculations in this work were performed using the Gaussian 09 program.³⁸

The enthalpies of activation (ΔH^‡) and Gibbs free energies of activation (ΔG^‡) were determined by computing the difference between the H^‡ or G^‡ for the reactant and those of the transition state. The values were scaled as described above prior to obtaining the difference. The entropies of activation (ΔS^‡) was calculated using eqn (1)

The reaction enthalpies (ΔH), Gibbs free energies (ΔG), and entropies (ΔS) were determined similarly using H, G, and S of the reactants and products.

4. Results and discussion

4.1 Theoretical study

4.1.1 Thermal decomposition of Q65. As a preliminary step for Q65 thermal decomposition, we considered the homolytic bond cleavages of the aliphatic chain as depicted in Scheme 2. In route (a), an aliphatic C–O bond cleavage leads to the formation of n-octyl radical and an aromatic oxyl radical. In route (b), instead, an aromatic C–O bond cleavage leads to the formation of octyloxy and aromatic radicals. Typically, homolytic cleavages proceed with no energy barrier, i.e., no transition state.^39–41 Hence, at MP2/6-311g(d,p)//B3LYP/6-31+g(d) level of theory, we have not been able to locate any transition states for the bond rupture reactions shown in Scheme 2. This also has been confirmed by exploring the potential energy surface (PES) for both reaction routes, (a) and (b). This was done by scanning the C–O bond and following the rise in energy up to a distance of 4.0 Å; no saddle points were located along the PES.

Scheme 2 Aliphatic and aromatic bond ruptures in Q65 and Q65b.

Using our calculation method at 0 K, the aliphatic (route a) and the aromatic (route b) bond ruptures in Q65 were endothermic by 192.4 and 234.6 kcal mol⁻¹, respectively. In order to simplify the highly demanding calculations of Q65, we shortened the aliphatic chain down into two carbon atoms. This new structure is referred hereinafter by Q65b. Calculations on Q65b provided close values of 190.8 and 233.4 kcal mol⁻¹ for routes (a) and (b), respectively. Using these values, and the thermal and the Gibbs free energies corrections from the Gaussian program, we calculated the Gibbs free energy at room temperature (ΔG₂₉₈) for the two reactions, (a) and (b), to be 178.2 and 222.1 kcal mol⁻¹, respectively. The energy level diagram for these reactions is shown in Fig. 1.

Fig. 1 Energy level diagrams for the homolytic bond cleavages reactions, 1,3-H shift mechanism, and H abstraction by singlet oxygen of Q65b. Energy values represent the relative Gibbs free energies in kcal mol⁻¹ at 298 K (ZPE corrections included).

In addition to the loss of the olefinic chain by homolytic cleavages, we also considered the 1,3-hydrogen migration from the ethyl group to the O atom in Q65b, as illustrated in Scheme 3. The H-shift results in the formation of ethylene and the aromatic alcohol (I). A similar migration in the parent Q65 molecule will lead to the formation of 1-octene and (I). Using our calculation method, a transition state (TS1) was located for this mechanism. The transition state was confirmed by using the intrinsic reaction coordinate (IRC) as explained earlier. An optimized structure for TS1 and product (I) are shown in Fig. 2. The strong imaginary frequency of 672.4i cm⁻¹ in TS1 corresponds to H migration from C to O as expected. Also, Fig. 1 shows the Gibbs free energy of activation (ΔG^‡₂₉₈) for the 1,3-H shift mechanism to be 70.8 kcal mol⁻¹. This barrier is the lowest among all reaction routes calculated in this study. This suggests that the thermal decomposition of Q65b to form an olefin and (I) is the most favorable among all other routes. This is also supported by the low value of free Gibbs energy of reaction (ΔG₂₉₈) of 6.3 kcal mol⁻¹, as seen in Fig. 1. Later, the thermochemical parameters of this mechanism are correlated to those obtained from the experimental thermogravimetric analysis of Q65, in order to show the importance of this reaction pathway.

Scheme 3 Decomposition of Q65b via 1,3-H-shift mechanism.

Fig. 2 Optimized structure for (a) the transition state involved in the 1,3-H shift mechanism (TS1), and (b) the alcohol (I) produced from the 1,3-H shift mechanism in Q65. Grey atoms represent carbon, blue atoms represent nitrogen, white atoms represent hydrogen, yellow atoms represent sulfur and red atoms represent oxygen.

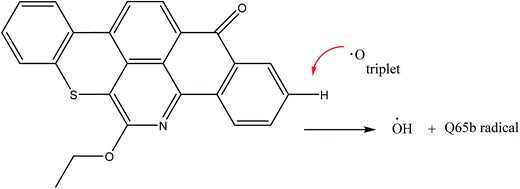
The next reaction pathway we considered in the Q65b thermal decomposition is the abstraction of aromatic hydrogen by an oxygen atom. We have explored this type of abstraction on both singlet and triplet energy surfaces. Under the level of theory used in this work, we have only located the transition state of abstraction at the triplet surface. The abstraction has resulted in the formation of a hydroxyl radical and a Q65b free radical stabilized by the large aromatic system, as illustrated in Scheme 4. The barrier height between Q65b + triplet O and the triplet transition state, TS2(t), was found to be 151.4 kcal mol⁻¹, as seen in Fig. 1. The figure also shows a ΔG₂₉₈ of 134.1 kcal mol⁻¹. Clearly, these values are much higher than those of the 1,3-H shift mechanism, due to the triplet nature of the transition state and the products of the reaction. In addition, one need to keep in mind that the bond dissociation energy of the triplet ground state of the O₂(³Σ⁺_g) molecule needed to form two triplet O(³P) atoms is estimated to be 119 kcal mol⁻¹.²⁹ This suggests that H abstraction by a triplet O is highly unfavorable in the course of Q65b thermal decomposition. This agrees with previous studies on the abstraction reaction of hydrogen by O(³P) in benzene, where the reaction does not play an important role at room temperature.^27,42

Scheme 4 Abstraction of aromatic hydrogen by oxygen atom.

4.1.2 Singlet oxygen (O¹D) attacks on Q65b. As mentioned in the introduction section, singlet oxygen (O¹D) attacks on aromatic systems are usually exothermic and proceed with no transition state. Here, the singlet oxygen was chosen in our calculations because of the fact that the considered aromatic model molecule (i.e., Q65) has a ground state spin multiplicity of singlet. Prior to studying the addition reactions of singlet oxygen (O¹D) to Q65b, we explored the molecular orbitals of the aromatic molecule. This allows us to construct the reaction mechanism based on the principles of the molecular orbital theory. Fig. 3 shows a representation of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of Q65b, generated by the Gaussian program at B3LYP/6-31+g(d) level of theory. Based on the MO's, we expect the attack of the electron-rich O(¹D) atom to be most favorable on the LUMO of Q65b, which is centered on the N=C bond, as seen from Fig. 3.

Fig. 3 A representation of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of Q65b at B3LYP/6-31+g(d) level of theory. Grey atoms represent carbon, blue atoms represent nitrogen, white atoms represent hydrogen, yellow atoms represent sulfur and red atoms represent oxygen.

Scheme 5 summarizes the results of our explorations for the O(¹D) additions on different sites of Q65b, at MP2/6-311g(d,p)//B3LYP/6-31+g(d) level of theory. The negative values shown in the scheme represent ΔG₂₉₈ for each addition reaction. Interestingly, we found the most favorable site of addition to take place on C2, which represent the LUMO of Q65b, in perfect agreement with our previous speculation. Also, we were unable to locate any transition state for the additions shown in Scheme 5, in concert with previous studies on benzene.²⁵ Hence, we propose that any addition of O(¹D) to Q65b to be barrierless, and highly exothermic.

Scheme 5 Addition of O(¹D) on different sites of Q65b.

Fig. 4 shows optimized structures for the different addition products of O(¹D) on Q65b at different sites as discussed above. The addition of singlet oxygen on the LUMO of Q65b, i.e., on the C2 atom, has led to the formation of an aromatic oxide product (II), similar to benzene oxide. Analogue oxides were produced from the attacks on C3 and C5, named IV and V, respectively. In their study on O(¹D) reactions with benzene, Chen et al. computed ΔH for the formation of benzene oxide to be −106.8 kcal mol⁻¹. This value is less exothermic than the ΔH values for the addition of O(¹D) to Q65b obtained in this work. This suggests that the addition of singlet oxygen to the large aromatic system of Q65b produces relatively stabilized products, and therefore, larger negative values of ΔH.

Fig. 4 Optimized structure for the addition products resulting of O(¹D) attack on (a) C1, (b) C2, (c) C3, (d) C5, and (e) N atoms in Q65b; obtained MP2/6-311g(d,p)//B3LYP/6-31+g(d) level of theory. Grey atoms represent carbon, blue atoms represent nitrogen, white atoms represent hydrogen, yellow atoms represent sulfur and red atoms represent oxygen.

The O(¹D) attack on the C1 atom of Q65b has caused a ring opening to form (III), as depicted in Fig. 4a. This attack, which happens to be on the LUMO+1 of the Q65b molecule, has led to the formation of a stable “ketonic” terminal, and also freed the sulfur atom forming a phenyl sulfur terminal. Under the level of theory used in this work, we located a transition state, named TS3, that connects II with III. An optimized structure for TS3 is shown in Fig. 5. The imaginary frequency of this transition state corresponds to swinging of the newly attached O atom between the ketonic and the oxide forms. In addition, the small magnitude of the imaginary frequency (69.3i cm⁻¹) corresponds to a small energy barrier of 28.7 kcal mol⁻¹. From the intermediate (III), a homolytic C–C bond cleavage can lead to the formation of two other intermediates, VII, and VIII, as shown in Scheme 6. Under the level of theory used in this work, we were unable to locate any transition state that connects III with the intermediates VII and VIII. Nevertheless, the phenyl sulfur intermediate (VIII) can either undergo further thermal decompositions or react with the readily available oxygen atoms to form SO₂ gas. An energy level diagram for this reaction mechanism is shown in Fig. 6. Experimental evidence for the production of SO₂ will be provided later.

Fig. 5 Optimized structure for the transition state (TS3) connecting products II and III. Grey atoms represent carbon, blue atoms represent nitrogen, white atoms represent hydrogen, yellow atoms represent sulfur and red atoms represent oxygen.

Scheme 6 Decomposition mechanism for the attack of O(¹D) on the LUMO of Q65b.

Fig. 6 Energy level diagrams for the series of reactions followed the attack of O(¹D) on the LUMO of Q65b, energy values represent the relative Gibbs free energies in kcal mol⁻¹ at 298 K (ZPE corrections included).

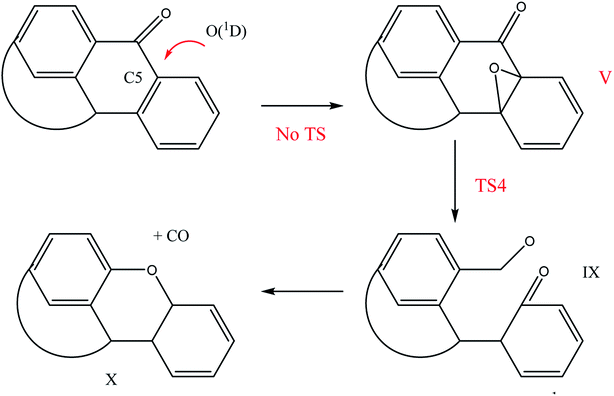
Another interesting route for Q65b oxidation is the one evolving from the attack of O(¹D) on C5, which led to the formation of the oxide V, as explained earlier in Scheme 5. In a similar fashion to the ring opening caused by TS3, we have located a transition state, TS4, shown in Fig. 7, that transformed the oxide intermediate (V) into the intermediate (IX), which can easily decompose into carbon monoxide and intermediate X through a ring closure.⁴³ This mechanism is illustrated in Scheme 7. The importance of this reaction path lies in the possible formation of CO₂ gas out of IX, via further oxidation with molecular oxygen.⁴³

Fig. 7 Optimized structure for the transition state (TS4) connecting the intermediates V and IX. Grey atoms represent carbon, blue atoms represent nitrogen, white atoms represent hydrogen, yellow atoms represent sulfur and red atoms represent oxygen.

Scheme 7 Decomposition mechanism for the attack of O(¹D) on C5 of Q65b.

In addition to the reactions of Q65 with atomic oxygen, we also explored its reactions with molecular oxygen in its singlet state (O₂¹Δ). In contrast to the barrier-less reactions with O(¹D), we found that reactions with O₂(¹Δ) proceed through a transition state, which implies the need for an activation barrier. Fig. 8a shows an optimized geometry for the transition state (TS5) involved in the addition of O₂(¹Δ) to the carbon atoms C1 and C3 in Q65b. The imaginary frequency of TS5 (216.5i cm⁻¹) shows a synchronized bond stretching between the O₂ molecule and the two carbon atoms in order to form an aromatic peroxide (XI). The peroxide, shown in Fig. 8b, resembles the one obtained from the reaction of O₂(¹Δ) with benzene. Under the level of theory used in this work, the activation barrier (ΔG^‡₂₉₈) was determined to be only 0.9 kcal mol⁻¹, and the reaction energy was determined to be slightly exergonic, i.e., ΔG₂₉₈ = −9.9 kcal mol⁻¹. In their study on singlet oxygen reactions with benzene, Bobrowski et al.³² determined the addition of O₂(¹Δ) to benzene to form benzene peroxide moiety to be remarkably endergonic. This was attributed to the high strain in the bicyclic compound formed and the loss of aromaticity. With a large aromatic system like Q65b, these two effects can be largely released, which accounts for the high stability of the peroxide (XI) and the exothermicity of the reaction.

Fig. 8 Optimized structure for (a) the transition state (TS5), and (b) the addition product resulted from the addition of molecular oxygen O₂(¹Δ) to Q65b; obtained MP2/6-311g(d,p)//B3LYP/6-31+g(d) level of theory. Grey atoms represent carbon, blue atoms represent nitrogen, white atoms represent hydrogen, yellow atoms represent sulfur and red atoms represent oxygen.

So far, we discussed the reactions of atomic and molecular oxygen with the asphaltene model molecule, Q65b, at 0 K and room temperature. In order to gain more insights into the reactions at higher temperatures, and to better compare the outcomes of this theoretical study with those from the experimental investigation of Q65, we computed the thermochemical parameters for the main reactions of Q65b with O(¹D) and O₂(¹Δ) at temperatures ranging from 298 to 873 K at 100 K intervals. Fig. 9 shows the reaction Gibbs free energies (ΔG) for some of the main reaction routes of Q65b. Generally, changing the reaction temperature from room temperature to 800 K has little effect on ΔG. Nevertheless, one noticeable reaction route is the 1,3-H shift mechanism, where ΔG switches to exergonic at around 473 K (200 °C). In addition, the figure shows a slight increase in the endergonicity of the reactions involving addition of either O(¹D) or O₂(¹Δ) to Q65b as temperature rises. This can be explained by the changes in the translational entropy, which affects the TΔS term in eqn (1).

Fig. 9 Reaction Gibbs free energies (ΔG) for some reactions of Q65b with singlet oxygen as a function of temperature.

Similar to the calculations on the reaction Gibbs free energies (ΔG), we computed the Gibbs free energies of activation (ΔG^‡) for the main reaction routes of Q65b. Fig. 10 shows changes of ΔG^‡ for five main reactions described in this work. In the course of this analysis, we considered ΔG of the barrier-less aliphatic rupture reaction to be equal to the activation barrier, in accordance with the principles of the variational transition state theory.^39,40 As seen in Fig. 10, the values of ΔG^‡ for the aliphatic rupture and the 1,3-H shift (TS1) reaction routes are decreasing with temperature, and increasing for other reaction routes. This can be explained by the tight nature of the transition state, such as in the case of the 1,3-H shift mechanism, or the loose nature of it, such as in the case of TS3 and TS5.

Fig. 10 Activation Gibbs free energies (ΔG^‡) for some reactions of Q65b with singlet oxygen as a function of temperature.

Based on the above findings, Q65 thermal oxidation in the gas phase, in the absence of any catalyst, should start with highly endothermic reactions; such as attacks of triplet oxygen on the aromatic part of Q65, or those responsible for producing singlet oxygen from its ground state triplet, or hemolytic bond ruptures that lead to the loss of the aliphatic “olefin” chain. Once these primary endothermic initiating steps are completed, exothermic attacks of singlet O and O₂ should follow, accompanied by a series of propagation reactions with low activation barriers (e.g., TS3 and TS4).

4.2 Thermogravimetric study

4.2.1 TGA/DSC and evolution profiles. Fig. 11 shows the TGA/DSC thermo-oxidative profiles for Q65 in air. As evident from the mass loss profile, the mass loss occurs in two temperature regions. First, a low temperature oxidation (LTO) region between 250 and 400 °C and the second, a high temperature oxidation (HTO) between 450 and 650 °C. Heat profile shows little heat loss below 400 °C. The main exothermic peak depicting high temperature oxidation of Q65 takes place beyond 550 °C. The fact that the mass loss of Q65 was not observed at temperatures below 250 °C supports our previous argument that the initiating steps for Q65 thermal oxidation are highly endothermic, especially, in the absence of any catalyst.

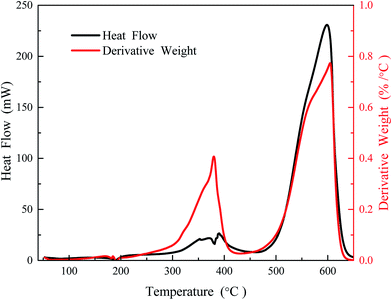Fig. 11 TG-DTA curve for Q65 heat flow and rate of mass loss as a function of temperature, air flow is 30 cm³ min⁻¹ and heating rate 10 °C min⁻¹.

Fig. 12 shows the evolution profiles of CO₂, H₂O and SO₂ as a function of the temperature during the thermo-oxidative process of Q65. Evolved gas analysis by MS showed very small peak for CO₂ below 400 °C suggesting very little oxidation. Interestingly, the MS data in the high temperature oxidation region showed not only H₂O and CO₂ peaks, but also a small peak for SO₂. The formation of SO₂ supports our theoretical mechanism as previously explained in Section 4.1.2. The fact that insignificant CO₂ and H₂O form below 400 °C suggests that formation is preceded by primary decomposition reactions, such as those corresponding to the loss of the olefin chain, and O and O₂ addition, as proposed in our theoretical assessment earlier. It should be noted here that the mass spectrometric analysis of gases produced during the reaction did not show any formation of octene nor methanol. This could be due to the low mass content present in the sample, which was due to the crucible size (50 to 60 μL). Thus, the concentration of octene or methanol remained very dilute and too low to be detected.

Fig. 12 Evolution of the production of CO₂, H₂O and SO₂ during Q65 oxidation at air flow of 30 cm³ min⁻¹ and heating rate of 10 °C min⁻¹.

4.2.2 Thermo-oxidative decomposition kinetics. For a linear heating rate, the non-isothermal overall rate of reaction for a condensed phase can be described by the differential form as follows:⁴⁴where α denotes the reaction conversion ranging between 0 and 1.0, β = dT/dt heating rate, A_α (s⁻¹) pre-exponential factor, E_α (kcal mol⁻¹) effective activation energy, R (cal mol⁻¹ K⁻¹) the ideal gas constant, T absolute reaction temperature and f(α) is the reaction mechanism function dependent on the particular reaction model. α can be calculated from thermogravimetric analysis as follows:where, m₀, m_t and m_f are the initial sample mass, the sample mass at a given time and the final mass of the sample, respectively. The kinetic parameters in eqn (2) can be estimated by a number of methods.⁴⁴ Here we followed the corrected isoconversional equation of Ozawa–Flynn–Wall (OFW) to estimate the effective activation energies (E_α) needed for the oxidation of Q65.⁴⁵ Using the Doyle approximation,^46,47 the OFW equation is expressed as follows:

Hence, the effective activation energy is obtained from the slope of the best-fit line of the plot of log(β) against 1/T. The error in the estimation of E_α due to the Doyle's approximation is corrected using a correction factor as follows

E_corrected = E_α/F(x_m) (5)

where , and

Fig. 13 shows plots of α as a function of temperature and at three different heating rates. As anticipated, the rate of mass loss changes with the heating rate. At a fixed temperature, α is different for different heating rates with an exception (between 400 and 450 °C). These results are consistent with our description of the TGA/DSC thermo-oxidative and evolution gas profiles in Section 4.2.1. This clearly indicates that Q65 thermal oxidation passes through multi-steps.¹⁶

Fig. 13 Percent conversion of Q65 during oxidation in air at flow of 100 cm³ min⁻¹ and heating rates of 5, 10 and 20 °C min⁻¹, respectively.

Recall that during our theoretical assessment the loss of the olefin chain by 1,3-H shift mechanism is both thermodynamically and kinetically favorable overall other reaction pathways, including the formation of singlet oxygen itself. Therefore, we propose that the loss of the olefin chain is responsible of producing the first peak on the thermoanalytical curve. This step resembles the first stage in Fig. 10, where α is between 0 and 0.28. This is supported by the fact that the olefin chain is almost 28% by weight of the whole Q65 molecule. The next stage, where α is between 0.35 and 1, depicts the oxidation of the aromatic rings, as already mentioned in the theoretical and the gas analysis sections. In the region where α is between 0.3 and 0.35, due to the overlapping of the conversion profiles, the OFW isoconversional method cannot be applied here because the method is used only for estimation of the data sets with well-separated steps. Therefore, activation energy was calculated separately from α = 0.1 to 0.3 and from 0.35 to 0.9, to avoid the overlapping limitations.⁴⁸ This overlapping, in the region of α between 0.3 and 0.35, is attributed to the fact that the total reaction effect is the same and independent of the heating rate within this region.⁴⁸ This suggests the consecutive reaction sequence and the oxidation of aromatic ring (Step 2, resembled by the second peak in the TGA profile) must be always after the oxidation of olefin chain (Step 1, resembled by the first peak in the TGA profile). Hence, Step 1 will be the rate-limiting step for the reaction.

Fig. 14 shows the estimated effective activation energy as a function of conversion. It is obvious that a constant value of effective activation energy, at various values of α, is an indication of a single-step reaction, while a change of activation energy with an increase in α is an indication of a complex reaction mechanism.¹⁶ Clearly, the E_α profile in the figure shows a multi-step reaction mechanism (high temperature oxidation region), as different effective activation energies are obtained at various stages of the oxidation process.^44,48 Here, E_α exhibited two distinct trends of variation. For low α region, E_α appears almost constant showing a single step reaction mechanism confirming cracking of olefin chain. During the region α = 0.35 to 0.9, oxidative cracking of aromatic as well as formed char/coke is occurring with gradual decrease in E_α, an indication that the presence of oxygen at high temperature alters the reaction mechanism and facilitates its rate.⁴⁹ Again, this is consistent with our description of the TGA/DSC thermo-oxidative decomposition and evolution gas profiles in Section 4.2.1, where two major peaks appear. It is also interesting to notice the correlation between our theoretical determination for the different values of activation energies, as seen in Fig. 10, and the effective E_α values obtained from the experimental study, as seen in Fig. 14. Clearly, the differences in E_α values obtained by both approaches support the multi-step reaction mechanism. Worth noting here that the E_α values obtained from the thermogravimetric analysis and our theoretical treatment are quite different. The E_α values obtained from the experimental part were in the range of 24–33 kcal mol⁻¹, while those obtained from the theoretical assessment ranged between 0 and 180 kcal mol⁻¹. This difference can be explained by the fact that not all reactions from our theoretical study can be part of the Q65 thermo-oxidative decomposition, i.e., the olefin loss by homolytic cleavage. Further treatment of the E_α values will be discussed later in this article.

Fig. 14 Calculated activation energies for Q65 studied by thermogravimetry in air. Experimental conditions: heating rates, 5, 10 and 20 °C min⁻¹; air flow, 100 cm³ min⁻¹.

4.2.3 Determination of the most probable mechanism function, pre-exponential factor and reaction order. The general equation of Šesták and Berggren⁵⁰ was employed here to determine the reaction mechanism and calculate the reaction order and pre-exponential factor from the previously determined effective activation energies, Section 4.2.2. Hence, here we combined the isoconversional method of OFW with model fitting. Accordingly, upon considering different reaction model as proposed by Šesták and Berggren,⁵⁰ and plotting ln(g(α)) against ln(β) following eqn (2), and using a linear regression of the least squares method, the most probable reaction mechanism is determined. If the considered reaction mechanism complies with the specified g(α) function, then the linear correlation coefficient of the best-fit-line (R²) should be close to 1.0 and the slope close to −1.0.¹⁰ Here, we limited our calculations to two maximum specified temperatures, namely: Tp₁ (for Step 1) and Tp₂ (for Step 2). These two temperatures, corresponding to the highest mass loss rate at heating rate 5 °C min⁻¹, were chosen for the calculation of most probable mechanism functions following the procedure of previous work.^16,51,52 For this, α was obtained at Tp₁ and Tp₂ for all three heating rates (i.e., 5, 10 and 20 °C min⁻¹). The results are shown in Table 1. As expected, two different reaction mechanisms are occurring. At Tp₁, it can be stated that the mechanism function is of one and a half order; while it was a three-quarters order mechanism at Tp₂. This result is consistent with our description of the thermo-oxidative decomposition and gas evolution described in Section 4.2.2, where two consecutive reactions were assumed. This also supports our findings in the theoretical assessment in Section 4.1.2.

Table 1 Most probable mechanism functions, slopes, and the linear regression coefficients

	T (°C)	α at 5 °C	Function	g(α)	f(α)	R^2	Slope
Tp1	333	0.2	One and a half order	(1 − α)^−1/2 − 1	2(1 − α)^3/2	0.98	−1.53
Tp2	517	0.75	Three-quarters order	1 − (1 − α)^1/4	4(1 − α)^3/4	0.99	−0.72

---

After calculating the effective activation energies and the most probable mechanism function, the pre-exponential factor (A_α) is estimated from the intercept of the best-fit-line of the plots of ln(g(α)) against ln(β). The obtained pre-exponential factors are shown in Fig. 15. As seen, to some extent, the A_α trend had followed that of that activation energy, especially in the high temperature oxidation zone. This can be explained by the fact that the pre-exponential factor reflects the nature of the transition state. In other words, a loose transition state will convey a higher A_α value. Because of the different types of transition states involved in the Q65 thermal oxidation, the changes in A_α values can be rationalized.

Fig. 15 Dependencies of pre-exponential factor A_α on α for oxidation reaction of Q65.

4.2.4 Estimation of thermodynamic transition state parameters. After finding the kinetic triplets (i.e., reaction mechanism function, effective activation energy and pre-exponential factor), the oxidation of Q65 now can be explained on the basis of thermodynamic parameters of the transition state functions, namely changes in Gibbs free energy of activation (ΔG^‡), enthalpy of activation (ΔH^‡), and entropy of activation (ΔS^‡). These thermodynamics parameters were estimated at the T_p's that correspond to highest mass loss derivative peaks at a heating rate 5 °C min⁻¹ using eqn (1), (7) and (8):^16,53

ΔH^‡ = E^‡_p − RT_p (7)

where E^‡_p is the activation energy and A_p is the pre-exponential factor estimated at T_p, e is the Neper number (=2.7183), κ is the transmission coefficient (≈1.0), k_B is the Boltzmann's constant (=1.3806 × 10⁻²³ J K⁻¹), h is the Planck's constant (=6.6261 × 10⁻³⁴ J s), and R is the universal ideal gas constant (=8.314 J mol⁻¹ K⁻¹). The estimated values of the thermodynamic parameters are listed in the first two columns of Table 2. In addition, results for the main reactions studied in our theoretical assessment are presented for comparison as well.

Table 2 Values of ΔS^‡, ΔH^‡, and ΔG^‡ for thermo-oxidative reaction of Q65 at T_p = 333 °C and 517 °C

	Exp. (Tp1)^a	Exp. (Tp2)^b	Theo. aliphatic rupture	Theo. 1,3-H shift^c	Theo. TS3^c	Theo. O(^1D) addition^c^,^d	Theo. O2(^1Δ) addition^c^,^e
a Tp1 = 333 °C.b Tp2 = 517 °C.c Theoretical values were obtained at 300 °C.d Attack on C2.e Attack of O2 at C1–C3 of Q65b.
ΔS^‡ (cal mol^−1 K^−1)	−27.9	−32.5	26.4	4.6	−0.4	−27.4	−43.1
ΔH^‡ (kcal mol^−1)	23.7	24.6	192.0	73.3	28.6	—	—
ΔG^‡ (kcal mol^−1)	40.6	50.3	165.6	68.7	28.8	—	—

---

The negative values of ΔS^‡ obtained experimentally can be explained by the fact that the entropy of the activated complex, i.e. transition state, is lower than that of the reactants. From the theoretical values for ΔS^‡ presented in Table 2, we can see that the addition reactions of atomic and molecular oxygen to Q65 can explain the sign and the magnitude of ΔS^‡. In addition, it is clear that the ΔH^‡ and ΔG^‡ values obtained experimentally are more close to those of the 1,3-H shift mechanism, suggested in our theoretical assessment. This again supports our finding on this mechanism, and its important role during the Q65 thermo-oxidative decomposition. Finally, the increase in ΔH^‡ and ΔG^‡ values between the two stages, Tp₁ and Tp₂, is unexpected. However, we showed during our thermal analysis for the different reactions of Q65 that some of these reactions might involve an increase in the thermodynamic values, as shown earlier in Fig. 9 and 10.

5. Conclusions

The thermo-oxidative decomposition of the asphaltene model molecule, Quinolin-65 (Q65), was theoretically investigated at MP2/6-311g(d,p)//B3LYP/6-31+g(d) level of theory and validated by thermogravimetric analysis. In addition, some thermal decomposition pathways were explored. The theoretical assessment revealed that the loss of the olefin chain in the Q65 molecule can proceed via a 1,3-hydrogen shift mechanism, which was found to be both thermodynamically and kinetically favorable. In addition, the primary attacks of atomic and molecular oxygen in their singlet states that are responsible for the thermal oxidation of Q65 were investigated. It was found that addition of O(¹D) to Q65 is highly exothermic and barrier-less, i.e., proceed with no transition state. The most exothermic attack was found to be on the LUMO of the Q65 molecule, in good agreement with the principles of the molecular orbital theory. For the O₂(¹Δ), however, the attack was less exothermic than that of O(¹D) and passes through a transition state. From the primary attacks of O(¹D), individual reaction pathways ways were drawn for the formation of SO₂ and CO. A thermal analysis for the thermodynamic data was finally done for the main reactions of Q65 with oxygen in order to better understand the temperature dependence of the reactions, and to correlate them later with experimental data. In addition to the theoretical investigation, thermogravimetric experiments on Q65 were performed and the reaction products were probed by an online mass spectrometer. There was good agreement between the reaction mechanism proposed by our theoretical study and the one drawn from the experimental part. It was clear from both, the theoretical and the experimental investigations, that Q65 thermo-oxidative decomposition is a complex multi-step reaction process, which involves different reaction routes. It was proposed that the thermal oxidation of Q65 starts with the loss of the olefin chain, followed by atomic or molecular oxygen attacks on the aromatic part of the Q65 molecule, which then ruled the next steps of the complex reaction mechanism. The nature of activated complexes, i.e., transition states, formed have led to thermo-oxidative decomposition different trends in the activation energy observed during the actual experiments on Q65.

The significance of this work lies in the fact that the thermodynamic parameters obtained, ΔG in particular, are highly endogenic, including those involved in the formation of singlet oxygen. In addition, and because of the complexity and size of the Q65 molecule, its oxidation reaction mechanism suggests slow and tough reaction pathways, which strongly suggests the need for a catalyst. Therefore, the outcomes of this study will be used to shape the framework for future studies that aim to understand Q65 reactions on nanoparticle surfaces as catalysts, in order to allow better optimization and control of the catalytic recovery and upgrading of asphaltenes.

Acknowledgements

The authors are grateful to the Natural Sciences and Engineering Research Council of Canada (NSERC), the Department of Chemical and Petroleum Engineering at the Schulich School of Engineering at the University of Calgary and Western Canada Research Grid. The authors are also thankful to Dr Arvi Rauk for his valuable input and feedback.

References

1. Impiantistica Italiana Settembre, Alberta's Oil Sands: Challenges and Opportunities, 2013.
2. J. J. Adams, Energy Fuels, 2014, 28, 2831–2856.
3. S. Betancur, J. C. Carmona, N. N. Nassar, C. A. Franco and F. B. Cortés, Ind. Eng. Chem. Res., 2016, 55, 6122–6132.
4. K. Akbarzadeh, H. Alboudwarej, W. Y. Svrcek and H. W. Yarranton, Fluid Phase Equilib., 2005, 232, 159–170.
5. C. A. Franco, F. B. Cortés and N. N. Nassar, J. Colloid Interface Sci., 2014, 425, 168–177.
6. C. A. Franco, T. Montoya, N. N. Nassar, P. Pereira-Almao and F. B. Cortés, Energy Fuels, 2013, 27, 7336–7347.
7. R. Hashemi, N. N. Nassar and P. Pereira Almao, Appl. Energy, 2014, 133, 374–387.
8. N. N. Nassar, A. Hassan, G. Luna and P. Pereira-Almao, Catal. Today, 2013, 207, 127–132.
9. N. N. Nassar, A. Hassan and P. Pereira-Almao, Energy Fuels, 2011, 25, 1017–1023.
10. N. N. Nassar, A. Hassan and G. Vitale, Appl. Catal., A, 2014, 484, 161–171.
11. A. Hassan, L. Carbognani-Arambarri, N. N. Nassar, G. Vitale, F. Lopez-Linares and P. Pereira-Almao, Appl. Catal., A, 2015, 507, 149–161.
12. N. N. Nassar, C. A. Franco, T. Montoya, F. B. Cortés and A. Hassan, Fuel, 2015, 156, 110–120.
13. N. N. Nassar, A. Hassan and P. Pereira-Almao, Energy Fuels, 2011, 25, 1566–1570.
14. N. N. Nassar, A. Hassan and P. Pereira-Almao, Colloids Surf., A, 2011, 384, 145–149.
15. N. N. Nassar, A. Hassan, L. Carbognani, F. Lopez-Linares and P. Pereira-Almao, Fuel, 2012, 95, 257–262.
16. N. N. Nassar, A. Hassan and G. Vitale, Appl. Catal., A, 2014, 484, 161–171.
17. N. N. Nassar, A. Hassan and P. Pereira-Almao, Energy Fuels, 2011, 25, 3961–3965.
18. X. L. Song and C. A. Parish, J. Phys. Chem. A, 2011, 115, 2882–2891.
19. X. L. Song and C. A. Parish, J. Phys. Chem. A, 2011, 115, 14546–14557.
20. L. Ling, R. Zhang, B. Wang and K. Xie, Chin. J. Chem. Eng., 2009, 17, 805–813.
21. A. Laskin and A. Lifshitz, J. Phys. Chem. A, 1998, 102, 928–946.
22. F.-J. Tian, J.-L. Yu, L. J. McKenzie, J.-I. Hayashi and C.-Z. Li, Energy Fuels, 2006, 20, 159–163.
23. F. López-Linares, L. Carbognani, M. F. González, C. Sosa-Stull, M. Figueras and P. Pereira-Almao, Energy Fuels, 2006, 20, 2748–2750.
24. A. Devard, R. Pujro, G. de la Puente and U. Sedran, Energy Fuels, 2012, 26, 5015–5019.
25. H.-F. Chen, C.-W. Liang, J. J. Lin, Y.-P. Lee, J. F. Ogilvie, Z. F. Xu and M. C. Lin, J. Chem. Phys., 2008, 129, 174303.
26. G. da Silva, C.-C. Chen and J. W. Bozzelli, J. Phys. Chem. A, 2007, 111, 8663–8676.
27. T. L. Nguyen, J. Peeters and L. Vereecken, J. Phys. Chem. A, 2007, 111, 3836–3849.
28. A. S. Sharipov and A. M. Starik, J. Phys. Chem. A, 2012, 116, 8444–8454.
29. C. Schweitzer and R. Schmidt, Chem. Rev., 2003, 103, 1685–1758.
30. J. Pittner, P. Čársky and I. Hubač, Int. J. Quantum Chem., 2002, 90, 1031–1037.
31. A. Liwo, D. Dyl, D. Jeziorek, M. Nowacka, T. Ossowski and W. Woźnicki, J. Comput. Chem., 1997, 18, 1668–1681.
32. M. Bobrowski, A. Liwo, S. Ołdziej, D. Jeziorek and T. Ossowski, J. Am. Chem. Soc., 2000, 122, 8112–8119.
33. Chemdraw V14 Structural Drawing Software, Cambridgesoft Corporation, a Subsidiary of Perkinelmer, Inc, 2014.
34. A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160.
35. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
36. J. S. Binkley and J. A. Pople, Int. J. Quantum Chem., 1975, 9, 229–236.
37. A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513.
38. G. W. T. M. J. Frisch, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision B.01, Gaussian, Inc., Wallingford, CT, 2004; Journal, 2009.
39. D. G. Truhlar and B. C. Garrett, Acc. Chem. Res., 1980, 13, 440–448.
40. Y. Ge, M. S. Gordon, F. Battaglia and R. O. Fox, J. Phys. Chem. A, 2010, 114, 2384–2392.
41. I. Badran, A. Rauk and Y. J. Shi, J. Phys. Chem. A, 2012, 116, 11806–11816.
42. C. Saggese, A. Frassoldati, A. Cuoci, T. Faravelli and E. Ranzi, Combust. Flame, 2013, 160, 1168–1190.
43. H. Togo, Advanced free radical reactions for organic synthesis, Elsevier, Amsterdam Boston, 1st edn, 2004.
44. S. Vyazovkin, A. K. Burnham, J. M. Criado, L. A. Pérez-Maqueda, C. Popescu and N. Sbirrazzuoli, Thermochim. Acta, 2011, 520, 1–19.
45. T. Ozawa, Bull. Chem. Soc. Jpn., 1965, 38, 1881–1886.
46. C. D. Doyle, J. Appl. Polym. Sci., 1961, 5, 285–292.
47. C. D. Doyle, Nature, 1965, 207, 290–291.
48. E. Moukhina, J. Therm. Anal. Calorim., 2012, 109, 1203–1214.
49. K. Chenoweth, A. C. van Duin and W. A. Goddard, J. Phys. Chem. A, 2008, 112, 1040–1053.
50. J. Šesták and G. Berggren, Thermochim. Acta, 1971, 3, 1–12.
51. L. Vlaev, N. Nedelchev, K. Gyurova and M. Zagorcheva, J. Anal. Appl. Pyrolysis, 2008, 81, 253–262.
52. A. El-Qanni, N. N. Nassar, G. Vitale and A. Hassan, J. Colloid Interface Sci., 2016, 461, 396–408.
53. P. Atkins and J. Paula, Atkin's Physical Chemistry, Oxford University Press, Oxford, 8th edn, 2006.

---