A novel transmission model for plasmon-induced transparency in plasmonic waveguide system with a single resonator
Hui Yangab,
Guanhai Li*ab,
Xiaofang Suab,
Wenchao Zhaoab,
Zengyue Zhaoab,
Xiaoshuang Chen*ab and
Wei Luab
aNational Laboratory for Infrared Physics, Shanghai Institute of Technical Physics, Chinese Academy of Sciences, 500 Yu Tian Road, Shanghai, 200083, P. R. China. E-mail: ghli0120@mail.sitp.ac.cn; xschen@mail.sitp.ac.cn
bUniversity of Chinese Academy of Science, No. 19 A Yuquan Road, Beijing 100049, P. R. China
First published on 12th May 2016
Abstract
We investigate the electromagnetically induced transparency (EIT)-like effect in a single rectangle resonator modulated MIM bus waveguide system. A modified transmission model with two branches is proposed to characterize the physics of the two orthogonal electromagnetic modes formed in the resonator. Close agreement between the analytical results and the finite-difference time-domain (FDTD) simulations verifies the validity of the proposed transmission model. In addition, two different three-level systems mimicking the atomic EIT effect are utilized to further clarify the underlying physics of the plasmon-induced transparency (PIT) effect. It is found that better EIT-like shapes and larger values of group index can be achieved in the horizontal excited system (HES) than in the vertical excited system (VES). The results may deepen the understanding of the EIT-like effect and provide a helpful guideline for the control of light in highly integrated optical circuits.
1. Introduction
Electromagnetically induced transparency (EIT), a narrow optical transmission window with extreme dispersion, results from the quantum interference between the two pathways for excitation to higher atomic levels.1–3 By virtue of strong dispersion and slow-light effect within the transparency window, EIT promises potential applications in the fields of slow-light effects,4,5 optical data storage6 and integrated photonic devices.7,8 However, the rigorous experimental conditions needed to implement the EIT effect hinder its practical application, which leads to ongoing research on mimicking EIT in classical systems. Similar to the EIT effect in atomic systems, plasmon-induced transparency (PIT) can provide an analogue for EIT, and recent studies have shown that PIT is observed in many classical configurations, such as coupled dielectric resonators,9,10 split-ring resonators11,12 and phase-coupled PIT.13,14 Among various plasmonic structures used to realize PIT, metal–insulator–metal (MIM) plasmonic waveguides, which support modes in deep wavelength scale and possess an acceptable surface plasmon polariton (SPP) propagation length, have attracted considerable attention, and many plasmonic waveguide systems have been theoretically predicted and experimentally illustrated in recent reports.8,11,14–29In order to further investigate the underlying physics of PIT in plasmonic waveguide systems, a variety of sufficiently accurate approximate theoretical methods have been established, such as LC circuit mode,11 coupled mode theory (CMT)14,29,30 and transmission-line theory.22–25 However, the LC circuit model cannot give a precise analytical expression while the CMT requires complicated extraction of physical parameters from the numerical simulations. The transmission-line theory, which can give a precise analytical expression and calculate the transmission characteristics without the need to extract physical parameters from the numerical simulations, has been proved to be accurate enough in modelling plasmonic structure.22,24,25
In this work, we analytically and numerically investigate the EIT-like phenomenon in a single rectangle resonator modulated MIM bus waveguide system. Firstly, a modified transmission model is proposed to simplify the structure, which allows us to establish an equivalent network and calculate the optical transmission spectra. Then, to verify the accuracy of our model, the results are compared with simulation results obtained from the finite-difference time-domain (FDTD) method. The origin of the two orthogonal electromagnetic modes supported in the resonator is clarified in detail. Moreover, two different three-level models analogous to the atomic EIT effect are proposed to explain the underlying physics of the PIT effect.
2. Structure and analytical model
Fig. 1(a) is a schematic illustration of the proposed plasmonic two-dimensional structure which is composed of an MIM waveguide and a side-coupled rectangle resonator. The selected metal and insulator are silver and air, respectively. The frequency-dependent permittivity of the silver is approximated by the Drude model, which defines ε(ω) = 1 − ωp2/(ω2 + iωγp), with the plasma frequency ωp = 1.38 × 1016 Hz and the absorption coefficient γp = 2.73 × 1013 Hz. These parameters are obtained by fitting the experimental results.31 The width w for the bus waveguide is 100 nm. The silver gap between the bus waveguide and the rectangle resonator is G = 20 nm. And these values are set to be constant throughout this paper. The length and width of the rectangle cavity are a and b, respectively. When transverse magnetic (TM)-polarized light is introduced along the x-axis, SPP waves are excited in the waveguide and propagate along the metal–insulator interfaces.As shown in Fig. 1(a), the bus waveguide is treated as an infinite transmission line with characteristic impedance ZMIM. Unlike the previous studies, the rectangle resonator is creatively treated as two coupled finite transmission lines, which respectively correspond to the two orthogonal electromagnetic modes excited in the single resonator. The transmission line along the x-axis (TL1) possesses propagation constant β(b) and characteristic impedance ZSx, which is terminated with a load ZLx. The other transmission line, along the y-axis (TL2), possesses propagation constant β(a) and characteristic impedance ZSy, which is terminated with a load ZLy. Based on the transmission-line theory,22–25,32 the characteristic impedance of the infinite transmission line has the form
 | (1) |
 | (2) |
Note that, unlike the plasmonic waveguide structures with stub resonators,22,24 there is a silver gap between the bus waveguide and the rectangle resonator. The silver gap will play a significant role in modulating the transmission characteristics of the structure, which is confirmed in.34 To solve this problem, an attenuation coefficient r is introduced to approximately describe the effect of the silver gap while the SPP passes the silver gap. According to the definition of penetration depth,35 the attenuation coefficient r can be expressed as
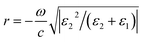 | (3) |
Hence, the total attenuation can be expressed as
 | (4) |
 | (5) |
 | (6) |
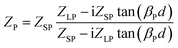 | (7) |
According to the transfer matrix method,32,33 the transmittance efficiency of the proposed system can be derived as
 | (8) |
3. Simulation results and discussion
Fig. 2(a) shows the transmission spectra of the proposed structure with b = 160 nm, 220 nm, 230 nm and 240 nm, and with a = 200 nm. The solid curves are calculated by the FDTD method and the circles lines are the theoretical results calculated by transmission-line theory. It is obvious that the theoretical results show close agreement with the FDTD simulations and the transmission spectra exhibit typical EIT-like shapes. The discrepancy between the two lines results from the approximate calculations owing to the introduction of the silver gap in our structure. Moreover, the transparency window grows in strength and becomes more prominent as b increases from 160 nm to 240 nm. To further investigate the spectral features, the evolution of the transmission spectrum versus resonator width b is depicted in Fig. 2(b). A splitting of the transmission dip is observed and the transparency window becomes obvious as the increment of b, which shows good agreement with Fig. 2(a). Close agreement between the theoretical results and FDTD simulations verifies the validity of our improved transmission model.The z-component magnetic field distributions in the plasmonic system are illustrated in Fig. 2(c)–(f). For our plasmonic system, the resonance modes are denoted by TMmn, where m and n denote the node numbers of standing waves along the x-axis and y-axis, respectively, in the rectangle resonator. In the following, we aim to demonstrate the underlying physical mechanism of the PIT effect and the formation of two orthogonal EM modes. Fig. 2(c) corresponds to the resonant wavelength λ = 585 nm for b = 160 nm. It is found that only the TM10 resonance mode exists in the resonator, leading to the dipole-like resonant dip. Fig. 2(d)–(f) show z-component magnetic field, for the case b = 230 nm, at wavelengths λ = 570 nm, 595.5 nm and 617.6 nm, respectively. It is obvious that two resonance modes TM10 and TM01 are excited, which correspond to the two finite transmission lines (TL1 and TL2) in our proposed transmission model. The two modes separately dominate the resonances in the MIM system at λ = 570 nm and 617.6 nm while at the PIT peak position λ = 595.5 nm the two orthogonal modes suffer severe competition. The destructive interference results in the PIT phenomenon and the magnetic field distribution in Fig. 2(e) verifies the hybridized state – about 45 degree rotational distribution with respect to the individual mode. Fig. 2(g) shows the resonant wavelengths and full width at half maximum (FWHM) of the transparent window in Fig. 2(a). Combining Fig. 2(a) and (g), we observe that the TM01 mode presents a red shift with the increase in b, whereas the TM10 mode exhibits a blue shift. We attribute this property to the change of shunt capacitance and shunt inductance brought in by the width variation. Fig. 2(h) shows the phase shift corresponding to the cases in Fig. 2(a). As shown in Fig. 2(h), a π-phase shift arises at the transparency window, which leads to the transparent response.19,20 Therefore, the EIT-like spectral characteristics achieved by regulating the width of the rectangle resonator may play a significant role in the dynamic control of light in nanostructures.
To demonstrate the impact of the resonator length on the PIT effect, in Fig. 3(a) we plot the transmission spectra of the plasmonic waveguide structure with b = 200 nm, and with different lengths a = 140 nm, 205 nm, 215 nm, 220 nm, respectively. The solid curves are calculated by the FDTD method and the circles are the theoretical results calculated by the transmission-line theory. It is apparent that the two lines show close agreement and both of them exhibit the typical EIT-like shapes with the increase of a. The field distributions (Hz) of SPPs in the plasmonic system for the case a = 215 nm, at wavelengths λ = 546.7 nm, 568.6 nm, 578.5 nm, are depicted in Fig. 3(b)–(d). Unlike the modes formed in Fig. 2(d)–(f), the TM10 mode is no longer the dominant mode like dipole resonance but it is excited at longer wavelength 578.5 nm. On the contrary, TM01 is the fundamental mode. According to the modified TL theory, the mode distribution difference is due to the competition of TL1 and TL2 since the shunt inductance and capacitance are frequency-dependent. Hence, the EIT-like effect results from destructive interference between TM01 and TM10 modes and the peak occurs at the wavelength where the hybridized state is formed. The resonant wavelengths of the two modes and the FWHM of transparent window versus a are plotted in Fig. 3(e). Different from when we changed the width b, we can observe that the TM10 mode presents a red shift with the increase of a, while the TM01 mode shows a blue shift in Fig. 3(e).
In order to further clarify the physics of PIT and show the similarity of the atomic EIT system with the proposed PIT model, two different three-level systems analogous to the atomic EIT effect are proposed in Fig. 4. We define them as the horizontal excited system (HES) and the vertical excited system (VES), respectively. For both systems, |0〉 is the ground state and |1〉, |1′〉, |2〉 and |2′〉 are the excited states. For the HES shown in Fig. 4(a), |0〉–|1〉 represents the horizontal TM10 mode directly excited in the rectangle resonator and |0〉–|2〉 is the TM01 mode excited in the rectangle resonator. However, for the VES shown in Fig. 4(b), |0〉–|1′〉 represents the vertical TM01 mode directly excited in the rectangle resonator and |0〉–|2′〉 is the TM10 mode excited in the rectangle resonator. The coupling coefficient ki (i = 1, 2) between the excited states is analogous to the coupling between the TM10 and TM01 modes. Consequently, there are two possible pathways: |0〉–|1〉 and |0〉–|1〉–|2〉–|1〉 (|0〉–|1′〉 and |0〉–|1′〉–|2′〉–|1′〉). The two competitive pathways interfere destructively, resulting in the typical PIT effect. From the above-mentioned definitions of the two systems, it is easy to see that the model investigated in Fig. 2 is classified as the HES and the model investigated in Fig. 3 is classified as the VES. Comparing Fig. 2(a) with Fig. 3(a), we find that better EIT-like shapes can be achieved in the HES than in the VES.
 | ||
| Fig. 4 Three-level systems analogous to the atomic EIT effect. (a) The horizontal excited system (HES). (b) The vertical excited system (VES). | ||
In addition, the slow-light effect is one of the most important applications for the EIT effect in atom systems. Here, our plasmonic system also supports the slow-light effect and the group index can be calculated by the formula14,24,29
 | (9) |
4. Conclusion
In summary, we have analytically and numerically investigated the EIT-like phenomenon in a single rectangle resonator modulated MIM bus waveguide system. A modified transmission model is proposed to characterize the modulation property of the resonator. Close agreement between the FDTD simulations and the theoretical fitting verifies the validity of the improved transmission model and reveals that the EIT-like effect results from the destructive interference between the two orthogonal modes. Moreover, two different three-level systems analogous to the atomic EIT effect are utilized to demonstrate the underlying physics of the PIT effect. It is found that the HES possesses better EIT-like shapes and larger values of group index than the VES, whereas the variation of the FWHM in the VES is more sensitive than that in the HES. Owing to the advantages of compact structure and easy fabrication, the single resonator modulated plasmonic structure holds potential in optical switching, optical filter and slow-light devices in highly integrated optical circuits.Acknowledgements
The authors acknowledge the support provided by the State Key Program for Basic Research of China (2013CB632705, 2011CB922004), the National Natural Science Foundation of China (10990104, 11334008, and 61290301), the Fund of Shanghai Science and Technology Foundation (13JC1408800, 16ZR1445300) and Shanghai Sailing Program (16YF1413200).References
- K. J. Boller, A. Imamolu and S. E. Harris, Phys. Rev. Lett., 1991, 66, 2593 CrossRef CAS PubMed.
- Y. Zhang, K. Hayasaka and K. Hasai, Phys. Rev. A, 2005, 71, 062341 CrossRef.
- S. Harris and L. Hau, Phys. Rev. Lett., 1999, 82, 4611 CrossRef CAS.
- K. Totsuka, N. Kobayashi and M. Tomita, Phys. Rev. Lett., 2007, 98, 213904 CrossRef PubMed.
- Y. Huang, C. Min and G. Veronis, Appl. Phys. Lett., 2011, 99, 143117 CrossRef.
- R. W. Boyd and D. J. Gauthier, Nature, 2006, 441, 701–702 CrossRef CAS PubMed.
- Z. H. Han and S. I. Bozhevolnyi, Opt. Express, 2011, 19, 3251–3257 CrossRef CAS PubMed.
- Z. R. Zhang, L. W. Zhang, H. Q. Li and H. Chen, Appl. Phys. Lett., 2014, 104, 231114 CrossRef.
- H. Lu, X. M. Liu, D. Mao, Y. K. Gong and G. X. Wang, Opt. Lett., 2011, 36, 3233–3235 Search PubMed.
- Y. F. Xiao, X. B. Zou, W. Jiang, Y. L. Chen and G. C. Guo, Phys. Rev. A, 2007, 75, 063833 CrossRef.
- Y. H. Guo, L. S. Yan and W. Pan, Opt. Express, 2012, 20, 24348–24354 CrossRef PubMed.
- I. Zand, M. S. Abrishamian and P. Berini, Opt. Express, 2013, 21, 79–86 CrossRef PubMed.
- R. D. Kekatpure, E. S. Barnard, W. Cai and M. L. Brongersma, Phys. Rev. Lett., 2010, 104, 243902 CrossRef PubMed.
- H. Lu, X. Liu and D. Mao, Phys. Rev. A, 2012, 85, 053803 CrossRef.
- J. J. Chen, Z. Li, S. Yue, J. H. Xiao and Q. H. Gong, Nano Lett., 2012, 12, 2494–2498 CrossRef CAS PubMed.
- L. Chen, C. M. Gao, J. M. Xu, X. F. Zang, B. Cai and Y. M. Zhu, Opt. Lett., 2013, 38, 1379–1381 CrossRef PubMed.
- Z. H. Han, C. E. Garcia-Ortiz, I. P. Radko and S. I. Bozhevolnyi, Opt. Lett., 2013, 38, 875–877 CrossRef CAS PubMed.
- Y. Zhu, X. Y. Hu, H. Yang and Q. H. Gong, Sci. Rep., 2014, 4, 3752 Search PubMed.
- K. H. Wen, L. S. Yan, W. Pan, B. Luo, Z. Guo, Y. H. Guo and X. G. Luo, J. Lightwave Technol., 2014, 32, 1701–1707 CrossRef.
- Q. Z. Huang, Z. Shu, G. Song, J. G. Chen, J. S. Xia and J. Z. Yu, Opt. Express, 2014, 22, 3219–3227 CrossRef PubMed.
- R. Hokari, Y. Kanamori and K. Hane, Opt. Express, 2014, 22, 3526–3537 CrossRef PubMed.
- P. Asanka, D. R. Ivan, P. Malin, T. H. Haroldo and P. A. Govind, Opt. Express, 2010, 18, 6191–6204 CrossRef PubMed.
- Y. J. Zhu, T. Wang, X. Han and B. Y. Wang, J. Appl. Phys., 2015, 117, 133108 CrossRef.
- J. C. Wang, L. Sun, Z. D. Hu, X. Y. Liang and C. Liu, Appl. Phys. Lett., 2014, 4, 123006 Search PubMed.
- M. Rezaei, S. Jalay, M. Miri, A. Khavasi, A. P. Fard, K. Mehrany and B. Rashidian, IEEE J. Sel. Top. Quantum Electron., 2012, 18, 1692–1699 CrossRef CAS.
- M. Miyata, J. Hirohata, Y. Nagasaki and J. Takahara, Opt. Express, 2014, 22, 11399–11406 CrossRef PubMed.
- Y. Zhu, X. Y. Hu, H. Yang and Q. H. Gong, Appl. Phys. Lett., 2014, 104, 211108 CrossRef.
- Z. H. He, H. J. Li, S. P. Zhan, G. T. Cao and B. X. Li, Opt. Lett., 2014, 39, 5543–5546 CrossRef PubMed.
- G. T. Cao, H. J. Li, S. P. Zhan, Z. H. He, Z. B. Guo, X. K. Xu and H. Yang, Opt. Lett., 2014, 39, 216–219 CrossRef PubMed.
- Q. Li, T. Wang, Y. K. Su, M. Yan and M. Qiu, Opt. Express, 2010, 18, 8367–8382 CrossRef CAS PubMed.
- E. D. Palik, Handbook of Optical Constants of Solids, Academic press, 1998 Search PubMed.
- D. M. Pozar, Microwave Engineering, Wiley, New York, 2nd edn, 1998 Search PubMed.
- M. A. Parker, Physics of Optoelectronics, CRC Press, 2005 Search PubMed.
- Q. Zhang, X. G. Huang, X. S. Lin, T. Jin and X. P. Jin, Opt. Express, 2009, 17, 7549–7555 CrossRef CAS.
- W. L. Barnes, J. Opt. A: Pure Appl. Opt., 2006, 8, S87–S93 CrossRef.
| This journal is © The Royal Society of Chemistry 2016 |




