Corrosion of aluminium alloy 1100 in post-LOCA solutions of a nuclear reactor
S. Guoa,
J. J. Leavittb,
X. Zhoua,
E. Lahtia and
J. Zhang*a
aDepartment of Mechanical and Aerospace Engineering, The Ohio State University, Columbus, OH 43210, USA. E-mail: Zhang.3558@osu.edu
bAlion Science and Technology, Albuquerque, NM 87110, USA
First published on 28th April 2016
Abstract
The corrosion and release of aluminum alloy 1100 in characteristic solutions in the containment sump of a nuclear reactor after a loss-of-coolant accident has been studied by an integral approach of electrochemical characterization and solution analysis by inductively coupled plasma (ICP) techniques. Various temperatures and pHs for a reactor in post-LOCA conditions are investigated to identify the effects of the temperature and solution composition on the corrosion. It was found that the oxygen reduction dominants the cathodic reaction below 55 °C, while water reduction becomes more pronounced at a higher temperature. The adsorption of boron on aluminum was identified by electrochemical impedance spectroscopy (EIS) and X-ray photoelectron spectroscopy (XPS). The boron adsorption decreased the thickness of the passive film by increasing the aluminum hydroxide solubilities, resulting in a very thin (<1.5 nm) passive film in the high boron concentrated post-LOCA solutions. The aluminium corrosion rate and passive film resistance obey an Arrhenius-type correlation with temperature in post-LOCA solutions. The slopes of the logarithmic release rate of aluminium in post-LOCA solutions against the pH and the reciprocal temperature are found to keep constant in solutions with a pH between pH 4–12, and a temperature range of 25 to 130 °C.
Introduction
Due to its mechanical properties and corrosion resistance, aluminium and its alloys have a wide range of applications, such as aerospace, metal/air batteries, and nuclear power systems. Aluminium corrosion has been recently noticed as a serious issue that can impact the emergency core cooling system (ECCS) of a pressurized water reactor.1–4 During a loss-of-coolant accident (LOCA), the hot, pressurized cooling water is ejected from a broken pipe of the primary cooling system and rushes into the concrete containment building.5 The ECCS is used to recirculate the cooling water collected in the containment back to the primary cooling system and spray system to continuously cool down the reactor core during the shutdown of the reactor after a LOCA.6 However, the metals in the containment can be corroded by the hot cooling water which contains up to 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 mg L−1 of boric acid.7 The aluminium content in the containment could be as high as 90% in some reactors, and studies have found that the aluminium is the most corrodible metal in the post-LOCA solutions.8,9 The resulting corrosion products, along with other debris generated by the LOCA, could clog the sump strainer and the recirculation pump, thus causing a failure of the ECCS. Experimental results have reported that the rapid increase of head loss through the filter screen due to the dissolution of aluminium and subsequent precipitation of aluminium oxyhydroxide/hydroxide.10,11
000 mg L−1 of boric acid.7 The aluminium content in the containment could be as high as 90% in some reactors, and studies have found that the aluminium is the most corrodible metal in the post-LOCA solutions.8,9 The resulting corrosion products, along with other debris generated by the LOCA, could clog the sump strainer and the recirculation pump, thus causing a failure of the ECCS. Experimental results have reported that the rapid increase of head loss through the filter screen due to the dissolution of aluminium and subsequent precipitation of aluminium oxyhydroxide/hydroxide.10,11
The kinetics of aluminium corrosion/release in post-LOCA solutions at various temperatures and solution pHs are of great interest because the temperature changes during the shutdown of the reactor and the post-LOCA water chemistry is controlled by different buffer agents at various pH in nuclear plants to minimize volatilization of radioactive iodine. Several groups have studied aluminium corrosion in post-LOCA solutions in the pH range from 7 to 11 at various temperatures using multiple test facilities.9,12–15 The results showed that the corrosion rate of aluminium in the post-LOCA borated solution is 1–2 orders of magnitude higher than in a solution with the same pH without boron. The strong dependences on temperature and pH were also observed. The Westinghouse Owners Group provided the nuclear industry with aluminium release equations that is dependent on the parameters of solution pH and temperature.9 The equations for corrosion and release rates of aluminium alloy 6061 were also given by Edwards et al. recently according to the experimental results in the pH 7–11 range at 40, 60, 90 and 130 °C.14
While improvements in the characterization of aluminium corrosion and release had been made, most of the aforementioned experiments were carried out under poorly characterized hydrodynamic conditions. For example, the experiments were conducted in reaction vessels that placed on a rock platform, or a flask with a magnetic stirring bar at the bottom to ‘simulate’ a flowing water in post-LOCA conditions. The fluid flow is unclear and the mass transfer rate is unable to be characterized. There are some results that are not consistent with each other. For example, Bahn et al.16 reported that the corrosion rate of aluminium alloy 1100 in their flow loop is approximately two times higher than the Westinghouse's results of the same alloy at same temperature and pH, indicating the importance of hydrodynamic conditions. Furthermore, it is impossible to gain the fundamental corrosion mechanism in such special solution based on the weight loss and ICP measurements from available data.
The rotating cylinder has been widely used to study electrochemical corrosion behaviour under flowing conditions.17 The corrosion of aluminium was found to depend on many factors including the solution's pH, temperature, and flow velocity, as well as the presence of specific anions, the native oxide film characteristics, and the aerating conditions.18–29 Soltis18 found that the corrosion and pitting potentials of aluminium decrease with the increase of temperature in chloride-containing solutions. However, higher corrosion potentials were found at higher temperature in NaCl solutions with dissolved, SO42−, S2O32− or HSO4− (ref. 19) and in deaerated synthetic sea water.20 Various temperature dependences, including non-Arrhenius dependence and no temperature dependence, on aluminium corrosion have been observed.12 This is attributed to the multiple oxide films that may form on the aluminium surface. These oxides includes amorphous Al(OH)3, boehmite (γ-AlOOH), gibbsite (α-Al(OH)3) and bayerite (β-Al(OH)3)30,31 and their solubilities are different, depending on the solution chemistry. For pH effects, it is believed that the corrosion rate of aluminium is at its minimum value in the neutral solution due to the formation of a stable passive oxide film.21,22 In an alkaline solution, the increased pH increases the corrosion rate of aluminium because high pH favours the formation of Al(OH)4−,23,24,32 thus increasing the solubility of the oxide films. However, the high concentration of boron in post-LOCA solutions might significantly influence the aluminium hydroxide solubility.33,34 Therefore, the temperature and pH dependence of aluminium corrosion in post-LOCA solutions still needs to be investigated.
The electrochemical corrosion behaviours of aluminium alloys in specific borate buffer solution have also been studied.35,36 However, there is little study on the electrochemical behaviour of aluminium in the post-LOCA solution with such high boron concentration. In this paper, the corrosion and release rates of aluminium alloy 1100 in various simulated post-LOCA solutions at various temperatures were investigated using electrochemical measurements and inductively coupled plasma techniques.
Experimental
The rotating cylinder working electrodes for the electrochemical measurements were made of aluminium alloy 1100 with a chemical composition (wt%) Si 0.14%, Fe 0.43%, Mn 0.01%, Mg 0.02%, Cr 0.01%, Zn 0.01%, Ti 0.01%, V 0.01%, and Al balance. The washer shape specimens, able to be mounted onto the rotating cylinder electrode (RCE) shaft, have an outer diameter of 15 mm and height of 6.4 mm. The exposed area of the washer specimen is 3.016 cm2. The specimens were ground up to 600 grit silicon carbide paper, rinsed with deionized water, and degreased in acetone. Since the presence of native oxide layer on aluminium could influence the corrosion and release rates in post-LOCA conditions, the specimen was exposed to atmospheric air for two weeks at 21 °C with relative humidity of 50% to form a native oxide film before the test.Test solutions, simulating a reactor containment building pool water under various break scenarios after a LOCA, were made from analytical grade boric acid, sodium tetraborate, sodium hydroxide, and deionized water (18.2 MΩ cm in resistivity). Sodium tetraborate is selected in this work because it is found to have a lower potential for precipitate formation in post-LOCA conditions than other buffer agents such as trisodium phosphate. The compositions of the test solutions and the pHs of the test solutions are listed in Table 1.
| Concentration (mg L−1) | H3BO4 | Na2B4O7 | NaOH |
|---|---|---|---|
| pH 7.2 solution | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 603 603 |
2857 | 0 |
| pH 7.5 solution | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 506 506 |
3268 | 0 |
| pH 8.2 solution | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 506 506 |
3268 | 1020 |
A typical three-electrode glass cell was used where a graphite rod was used as the counter electrode, an Ag/AgCl (4 M KCl) probe was used as the reference electrode, and an aluminium specimen was used as the rotating working electrode. The rotation speed of the working electrode was controlled through the Pine Research Instrumentation modulated speed rotator. The glass cell was filled with 1 L of a test solution. The temperature of the test solution was controlled within ±1 °C by using a thermocouple and hot plate with a built-in temperature control unit. The test solution was exposed to the atmosphere via a condenser, which can prevent the evaporation of water. All the experiments reported in this paper, if not specified, were conducted in a flowing condition with a rotating speed of 193 RPM of the RCE corrosion specimen to simulate a flow velocity of 0.15 m s−1 in the containment sump.
A Gamry Interface 1000 potentiostat with the Gamry Framework software was used for various electrochemical measurements. EIS measurements were carried out at the open circuit potential (OCP) over a frequency range from 100 kHz to 10 mHz. A sinusoidal voltage with a 10 mV amplitude was applied as the disturbance signal. The EIS was measured at 2 h, 8 h, 14 h, 20 h, 26 h, 32 h, 38 h, 44 h and 48 h. Finally, the potentiodynamic polarization curves were conducted by sweeping the potential at a rate of 0.5 mV s−1.
Before the potentiodynamic scan at 48 h, about 30 mL of the solution sample was collected from the drain port at the bottom of the glass cell. The solution sample was acidified using 0.3 mL Suprapure™ 65% nitric acid to avoid the precipitation of aluminium due to the cooling during sampling process. Then, the concentration of aluminium ions in the acidified solution was measured by ICP-OES.
Results and discussion
Identification of the cathodic reaction
Considering there is very scarce data on the electrochemical properties of the post-LOCA solution, dynamic polarization was conducted to identify the cathodic reactions in such solutions. The polarization curves in the range of potentials below the corrosion potential were measured to characterize the cathodic reactions occurring on the aluminium surface. Fig. 1 shows the polarization curves at different temperatures in pH 7.2 borate buffer solution. | ||
| Fig. 1 Cathodic polarization curves of aluminium after 48 h of immersion in simulated pH 7.2 solution at a velocity of 0.15 m s−1. | ||
It is acknowledged that,28,37 the cathodic reactions in an aerated neutral or alkaline solution can be the water reduction and/or oxygen reduction reactions:
| 2H2O + 2e− → H2 + 2OH− | (1) |
| O2 + 2H2O + 4e− → 4OH− | (2) |
The rate of oxygen reduction reaction could be limited by the mass transport of the dissolved oxygen from the bulk solution to the metal surface.38 The current density corresponding to the limiting mass transport rate is related to the mass transfer coefficient:
| Ilim = zFCkm | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 484.6 C mol−1; C is the concentration of O2 in the solution, mol cm−3; and km is the mass transfer coefficient of O2, cm s−1.
484.6 C mol−1; C is the concentration of O2 in the solution, mol cm−3; and km is the mass transfer coefficient of O2, cm s−1.
The mass transfer coefficient km can be calculated from a rotating cylinder correlation:39
| km = 0.0791ρ0.344μ−0.344d−0.3D0.644v0.7 | (4) |
The concentration of dissolved O2 in the solution is determined by the Henry's law constant and O2 partial pressure. The calculated O2 limiting current densities according to eqn (3) and (4) are 0.22 mA cm−2 at 25 °C, 0.20 mA cm−2 at 55 °C and 0.10 mA cm−2 at 85 °C, respectively. It can be seen from Fig. 1 that the measured limiting current density at 25 and 55 °C matches the calculated value, indicating that oxygen reduction is the main cathodic reaction around the corrosion potential at 25 and 55 °C. But the water reduction becomes more pronounced at higher temperatures, since the measured cathodic current densities at 85 °C are significantly higher than the calculated O2 limiting current densities. Therefore, the water reduction is the predominant cathodic reaction at high temperature in simulated post-LOCA solution.
Identification of the passivation layer
The polarization curves scanning from the potential slightly more negative than OCP to the anodic direction were also conducted to identify the anodic reaction as well as the corrosion potential. As shown in Fig. 2, anodic passivation phenomenon was observed in the polarization curves in all test solutions and temperatures after 48 hours of corrosion. As the pH increased at a certain temperature, the anodic passive current density increased and the corrosion potential slightly moved to more negative values. It is also noted that the increase of temperature significantly increased the passive current density and decreased the corrosion potential. | ||
| Fig. 2 Polarization curves of aluminium after 48 h of immersion at a velocity of 0.15 m s−1 (a) 25 °C, (b) 55 °C, (c) 85 °C. | ||
The anodic passivation current increases with the pH from 7.2 to 8.2 for a given temperature, which indicates the passivation properties of Al corrosion in such special solution depends on solution pH. EIS measurement which has been successfully used to characterize the property of the passive oxide film on aluminium alloys,27,35,36,40–44 was conducted. The impedance spectra of 1100 Al alloy after 48 h of immersion in test solutions are presented as Nyquist and Bode plots in Fig. 3–5.
At 25 °C (Fig. 3), two time constants were identified: a capacitive semicircle at high frequencies (HF), and an inductive loop at low frequencies (LF). The capacitive semicircle at HF is due to the relaxation process in the passive film formed on aluminium surface and its dielectric properties. Namely, the passive film can be considered to be a parallel circuit of a resistor due to the ionic conduction in the film, and a capacitor due to its dielectric properties. The diameter of this semicircle decreases with the increasing pH, indicating a decrease of passive film resistance with the increasing pH. This finding corresponds with the increase in anodic passive density with the increasing pH in Fig. 2. The inductive behaviour is observed at LF which corresponds to Gudic's EIS results of aluminium alloys in borate buffer solution.35,43 The inductive loop at LF may be related to the coverage of adsorbed species at the passive film.42,43 Studies have found that Al(OH)3 adsorbed a great quantities of boron, and the experimental evidence and various mechanisms are reviewed in ref. 33. It was found that the boron is bonded predominantly to the surface hydroxide ligands as an anion, i.e., anion exchange with hydroxyl ions.45 Increase of pH will cause the surface becoming more negative charged and less attractive to anion or anion exchange reactions, resulting in less boron adsorbed on aluminium hydroxide. This interprets the decrease of the inductive loop with increasing pH, so the inductive loop at LF might be attributed to the adsorption of boron.
 | ||
| Fig. 3 EIS results for aluminium at 48 h of immersion in borate buffer solutions at 25 °C and a velocity of 0.15 m s−1: (a) Nyquist plot, (b) Bode plot. | ||
Similarly, the capacitive loop at HF and an inductive loop were also observed at 55 °C and 85 °C, as shown in Fig. 4 and 5. The shrunken inductive loop at 85 °C indicates less boron adsorbed on the passive film which corresponds to the finding that decreasing temperature favours the boron adsorption.46 This can be proved by the XPS analysis of the passive film formed on aluminium specimens from tests without the polarization measurement, as shown in Fig. 6. It is seen that B 1s at a binding energy of 192–193 eV was detected in the passive film formed in various pH solution at 25 °C, while almost no B 1s peak was observed in the film formed at 85 °C.
 | ||
| Fig. 4 EIS results for aluminium at 48 h of immersion in borate buffer solutions at 55 °C and a velocity of 0.15 m s−1: (a) Nyquist plot, (b) Bode plot. | ||
 | ||
| Fig. 5 EIS results for aluminium at 48 h of immersion in borate buffer solutions at 85 °C and a velocity of 0.15 m s−1: (a) Nyquist plot, (b) Bode plot. | ||
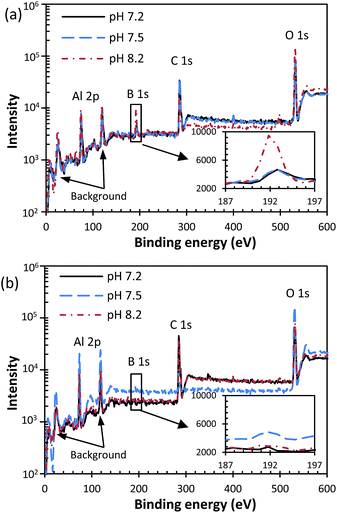 | ||
| Fig. 6 XPS survey spectra of the passive film formed in various pH post-LOCA solutions at (a) 25 °C, (b) 85 °C. | ||
It is also noted from Fig. 4 and 5 that a second capacity semicircle is present at the lower frequencies after the inductive loop. The second capacity semicircle can be assigned to metal dissolution47 since the current density of anodic dissolution is significantly increased at higher temperature (Fig. 2) which can influence the coverage of boron on surface. De Wit et al.42 suggested that the competition between adsorption of anion from the electrolyte (such as boron) and the adsorption of oxygen ions which is the intermediate product of water reduction, could cause an additional capacity semicircle after the inductive loop. This interpretation might also be acceptable, since the water reduction becomes more pronounced at elevated temperature (Fig. 1). Nevertheless, it was also claimed that the impedance response on the passive film at very low frequencies may be non-stationary.41 Therefore, the attention will be focused on the analysis of the passive film properties from the first capacity time constant at HF.
The impedance spectra have been fitted with the equivalent circuit (EC) shown in Fig. 3–5, where Rs is the solution resistance, Qf is the constant phase element (CPE) representing the capacitance of the passive film, Rf is the resistance of passive film, RL is the inductive resistance and L is the inductance. Here, a capacitance C1 with a parallel resistance R1 was added in the equivalent circuit to obtain an accurate fit due to the presence of the extra time constant at LF.
The CPE impedance, ZCPE, is described by expression:
| ZCPE = 1/(Y0jω)n | (5) |
The exponent n in eqn (5) may vary between 0 and 1. Y0 is defined as pure capacity for n = 1.
The data obtained with the proposed equivalent circuits showed a good agreement with the experimental EIS results as shown in Fig. 3–5. The values of all elements used to fit the experimental data as well as the goodness of fit are listed in Table 2. It can be seen that the oxide film resistance Rf decreased with the increase in temperature and pH. The decrease of L and RL with temperature and pH correspond the less adsorption of boron at higher temperature and higher pH. The plot of film resistance in the logarithmic scale against the temperature, T, and the 1000/T is given in Fig. 7(a). It can be clearly seen that the oxide film resistance, Rf, decreased exponentially with the increase in temperature by an order of magnitude per 30 °C. Fig. 7(b) shows that the increase of pH is linear with the decrease of the film resistance in logarithmic scale, which indicates that the film resistance decreases linearly with the increases of OH− concentration in solution.
| Test # | Rs (Ω cm2) | Y0 (μF cm−2 sn−1) | n | Rf (Ω cm2) | L (H cm−2) | RL (Ω cm2) | C1 (mF cm−2) | R1 (Ω cm2) | Goodness of fit |
|---|---|---|---|---|---|---|---|---|---|
| pH 7.2, 25 °C | 270.5 | 8.3 | 0.96 | 7861.7 | 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 040 040 |
— | — | 1.4 × 10−3 |
| pH 7.5, 25 °C | 227.0 | 8.7 | 0.96 | 5630.9 | 54![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 070 070 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 310 310 |
— | — | 3.6 × 10−3 |
| pH 8.2, 25 °C | 109.6 | 9.5 | 0.96 | 4034.3 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 250 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 730 |
— | — | 6.0 × 10−4 |
| pH 7.2, 55 °C | 176.8 | 12.2 | 0.93 | 693.2 | 245.9 | 1254.0 | 20.4 | 627.2 | 8.8 × 10−4 |
| pH 7.5, 55 °C | 135.8 | 11.2 | 0.96 | 534.3 | 212.1 | 1039.0 | 14.1 | 1876.0 | 8.3 × 10−4 |
| pH 8.2, 55 °C | 71.2 | 15.1 | 0.97 | 345.3 | 110.8 | 790.1 | 14.4 | 1181.0 | 1.0 × 10−3 |
| pH 7.2, 85 °C | 105.3 | 32.1 | 0.94 | 79.0 | 53.49 | 446.7 | 21.2 | 84.7 | 1.3 × 10−3 |
| pH 7.5, 85 °C | 90.9 | 41.5 | 0.91 | 73.7 | 51.65 | 481.1 | 21.8 | 81.5 | 1.5 × 10−3 |
| pH 8.2, 85 °C | 50.6 | 71.5 | 0.90 | 28.9 | 10.0 | 141.3 | 27.1 | 25.1 | 2.5 × 10−4 |
 | ||
| Fig. 7 Dependence of resistance of the passive film on (a) temperature and (b) pH for aluminium in simulated borate buffer solutions. | ||
The thickness of the passive oxide film, d, is inversely proportional to the value of the oxide film capacitance:
| d = εε0/Cf | (6) |
The effective capacity Cf for CPE can be calculated according to48
| Cf = Y0(2πfm)n−1 | (7) |
The dielectric constant, ε, of the aluminium oxide layer shows limited value between 8 and 15 in various aqueous solutions.37,40,44,49 Taking ε = 10, the thickness of the passive film at different temperature and pH can be calculated as shown in Fig. 8. It is seen that, the thickness of the passive film decreases with the increase of pH, which can be attributed to the increasing solubility of oxide films with pH. The passive film also become thinner with the increase of temperature, because the passive zone in the Pourbaix diagram becomes narrower and shifts to lower pH at elevated temperature.50
 | ||
| Fig. 8 The thickness of the passive films at various temperatures and pHs. Film thickness determined from the effective capacity of the passive film. | ||
It is important to note that the thickness of the passive film is less than 1.5 nm in the simulated borated buffer solutions with a pH 7.2–8.2. The thickness of the film formed in the NaOH solution without boron at pH 12 is about 1.5 nm.37 This indicates the passive film is expected to be much thicker than 1.5 nm in the boron free solution at pH 7.2 than that in the simulated borated solution since the neutral pH favours the formation of aluminium hydroxide. So the 1–2 orders of magnitude higher aluminium corrosion rate in simulated post-LOCA solution than boron free solution at same pH should be due to the boron effect on the thinning of oxide film. It has been revealed that the formation of aluminium borate complexes significantly increases the solubility of gibbsite and boehmite34 by the adsorption of boron on aluminium hydroxide which precludes the crystallization of aluminium hydroxide.45 So the decrease of film thickness in boron concentrated solution can be attributed to the increase of solubility limit in simulated post-LOCA solution, leading to a higher aluminium corrosion rate.
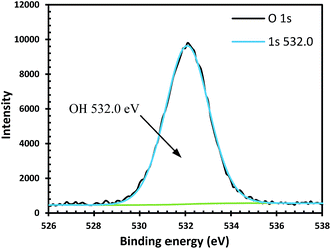
The non-Arrhenius dependence and no temperature dependence on aluminium corrosion can be observed,12 because different type of aluminium hydroxides such as amorphous Al(OH)3, gibbsite (α-Al(OH)3), bayerite (β-Al(OH)3) and boehmite (γ-AlOOH) may form on aluminium surface. The phase transition of these aluminium hydroxides is dependent on solution pH, temperature and aging. Kloprogge et al.51 found that the XPS spectrum for O 1s can be used to distinguish between Al(OH)3 and boehmite (γ-AlOOH) by identifying the O 1s peaks for oxygen and hydroxyl groups. Only hydroxyl group at a binding energy of 531.8 ± 0.2 eV was observed from our O 1s high resolution spectra at different pHs and temperatures which indicates the passive film is composed of gibbsite and/or bayerite. The O 1s high resolution spectrum of sample from 25 °C and pH 7.2 solution test is given in Fig. 9 as an example. Our Al 2p high resolution spectra showed a single Al 2p peak in the range from 73.9 to 74.7 eV at various conditions. But it is difficult to identify the phase composition from the Al 2p spectra, since the chemical shifts in the Al 2p binding energies among the aluminium oxides, hydroxides and oxohydroxides are very small (in the order of 0.2 to 0.5 eV).51
The evolution of the resistance of the passive film with time is given in Fig. 10. The film resistance are displayed in logarithmic scale. The film resistance was obtained by fitting the in situ measured EIS data at various time intervals during the test using the equivalent circuits shown in Fig. 3–5. At 25 °C, the film resistance first decreased at the beginning due to the dissolution of the native oxide layer. Then the film resistance gradually increased with time. The initial decrease of film resistance was not observed at 55 °C and 85 °C, which might be due to the rapid dissolution of native oxide layer at higher temperature. It should be mentioned that the rapid dissolution of native oxide layer at beginning may cause a high release rate of aluminium in post-LOCA event in which a temperature around 130 °C is expected at the first hour, and then cause a rapid increase of head loss at the beginning of post-LOCA. The film resistance also increased with time at higher temperature, indicating the instantaneous corrosion rate gradually decreasing with time.
 | ||
| Fig. 10 Evolution of oxide film resistance with time. Film resistance obtained from the fitting results of EIS data. | ||
Discussion on the effects of pH and temperature on corrosion rate and comparisons
The corrosion rates and the release rate of aluminium at various temperatures and pHs are shown in Fig. 11. The corrosion rate of aluminium was calculated from the corrosion current density in Fig. 2, which was obtained by extrapolating the anodic polarization curve in the passivation region to the corrosion potential. The release rate of aluminium into solution could be obtained by aluminium concentration in the solution that measured by ICP-OES. It is seen that the corrosion rate of aluminium at temperatures ranging from 25 to 85 °C display Arrhenius-type correlations at all investigated pH, which corresponds with the exponential decrease of film resistance with increasing temperature in Fig. 7(a). It is also noticed that the logarithmic corrosion rate increases linearly with the increase of solution pH, as shown in Fig. 11(b). The release rate of aluminium, which is of more relevance to strainer clogging than corrosion rate, is slightly lower than the corrosion rate due to the formation of the thin oxide film (<1.5 nm) on aluminium surface. | ||
| Fig. 11 Dependence of corrosion and release rates on the (a) temperature and the (b) solution pH at a velocity of 0.15 m s−1. | ||
Electrochemical studies have not been conducted previously for aluminium corrosion in post-LOCA solutions, therefore, it is impossible to compare the present electrochemical data such as the corrosion potential with previous study for post-LOCA solution. However, release rates in the similar solution have been reported.9,14 Westinghouse has provided an aluminium release equation as a function of temperature and post-LOCA solution pH by empirically fitting the experimental results:9
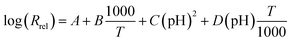 | (8) |
Edwards et al.14 also conducted a systematic study of the effect of pH and temperature on aluminium corrosion in post-LOCA solution, and developed a model to describe the experimental data as a function of temperature, pH and time duration.
 | (9) |
The predictions of the aluminium release rate using above models are compared with the experimental results in this work, as shown in Fig. 12. The models developed by Westinghouse and Edwards et al. were labelled as ‘model 1’ and ‘model 2’ in Fig. 12. It is seen that the predicted release rates by both models in logarithmic scale show a linear relation with the solution pH and reciprocal temperature. And the slopes of the curves at various temperatures and pHs are consistent with the experimental results in this work.
 | ||
| Fig. 12 Dependence of aluminium release rate on (a) temperature and (b) pH. Exp: experimental data in this work; model 1: WCAP's model predictions; model 2: Edwards' model predictions. | ||
It should be mentioned that the Westinghouse's model is based on the 90 minutes experimental results in the pH 4, 8, 12 solutions with a boron concentration of 4.4 g L−1 at the temperature of 88 and 130 °C, while Edwards et al.'s model is based on the long term (6–21 days) experiments in the solution with 2.8 g L−1 of boron in pH 7–11 range at the temperature ranging from 40 to 130 °C. The boron concentration of test solutions in this work is 2.8 g L−1. It can be seen that, the experiments were conducted at different boron concentrations in a wide range of temperature, pH and time duration, but the results from these studies show very similar dependence of release rate on temperature and pH. This finding is important for model development and its application in aluminium release predication in the post-LOCA conditions using sodium tetraborate as the buffer agent.
It is also noticed that Westinghouse's results are about 5–10 times lower than the results from this work and Edwards et al.'s work. In fact, Westinghouse's experimental solutions have a boron concentration of 4.4 g L−1, which is higher than the concentration of 2.8 g L−1 B in the solution used in Edwards' work and this work. Therefore, it is expected that the aluminium exposed in Westinghouse's experimental solutions should have a higher release rate due to the ‘boron effect’ on increasing aluminium corrosion. But Westinghouse's results actually shows a lower corrosion rate, which has also been found by Bahn16 and might be attributed to the fluid flow effect. Westinghouse's experiments were conducted in the reaction vessels placed on a rocking platform, which might be a quasistatic condition. The solutions of Edwards et al.'s experiments were stirred at a slow speed using a magnetic bar in the flask. The cylinder specimens were rotated in a speed of 193 RPM in this work. It is very likely that the deviations of the release rates from these studies are caused by the hydrodynamic conditions.
Fig. 13 shows the potentiodynamic polarization curves measured from aluminium alloy 1100 specimens at various rotation speeds after 48 hours of immersion in pH 7.2 simulated post-LOCA solution. The 1200 RPM and 4000 RPM represent a flow velocity of 0.94 m s−1 and 3.14 m s−1, respectively. It can be seen that the anodic current density increases with the increasing in rotation speeds, which means a higher aluminium dissolution rate at higher flow velocity. It has been reported that the increase of corrosion rate due to increasing flow velocity is attributed to the a fast supply of OH− to the film/solution interface and a rapid removal of Al(OH)4− away from the interface which could result in a faster dissolution of the formed oxide film on aluminium surface.32,37 Therefore, use of published experimental data for reactor plant design should be treated with caution, which means the mass-transfer rate of species across the diffusion boundary layer should be compared at various flow velocities in different flow system.
 | ||
| Fig. 13 Polarization curves of aluminium alloy 1100 after 48 hours of immersion in pH 7.2 simulated solution at various rotation speeds at 55 °C. | ||
Conclusions
Corrosion of aluminium alloy 1100 in simulated post-LOCA solutions have been studied by polarization, electrochemical impedance, XPS and ICP techniques for different temperatures and pHs. Based on the study, it is concluded:(1) The corrosion of aluminium alloy 1100 is limited by the anodic passive current density; the oxygen reduction is the predominant cathodic reaction below 55 °C, and the water reduction becomes more pronounced at higher temperature;
(2) The adsorption of boron on aluminium hydroxide decreased the thickness of the passive film by increasing the aluminium hydroxide solubility, resulting in a very thin (<1.5 nm) passive film in the high boron concentrated post-LOCA solutions;
(3) The resistance of the passive film decreases with the increase of temperature and pH, which means the passive film become less protective with the increasing temperature and pH;
(4) The corrosion rate and release rate were found to obey an Arrhenius-type correlation with temperature, and depend logarithmically on the pH due to the chemical attack of OH−;
(5) The release rate is slightly lower than the corrosion rate due to the formation of very thin oxide film in boron concentrated solutions;
(6) The slopes of the logarithmic release rate of aluminium in post-LOCA solutions against the pH and reciprocal temperature are found to be similar in pH 4–12 range at the temperature ranging from 25 to 130 °C.
Acknowledgements
The study was funded by Entergy LLC.References
- D. Chen, K. J. Howe, J. Dallman, B. C. Letellier, M. Klasky, J. Leavitt and B. Jain, Nucl. Eng. Des., 2007, 237, 2126 CrossRef CAS.
- C. B. Bahn, Nucl. Eng. Technol., 2013, 45, 295 CrossRef CAS.
- R. Sandrine, L. Cantrel, A. Yves, M. Jean-Marie, L. Marek, G. Dagmar, V. Yvan and S. Bela, Chem. Eng. Res. Des., 2008, 86, 633 CrossRef.
- R. Choromokos, P. Mast and J.-H. Park, ECS Trans., 2010, 28, 37 CAS.
- E. A. Lahti and J. Zhang, International Electronic Journal of Nuclear Safety and Simulation, 2014, 5, 92 Search PubMed.
- K. J. Howe, L. Mitchell, S.-J. Kim, E. D. Blandford and E. J. Kee, Nucl. Eng. Des., 2015, 292, 296 CrossRef CAS.
- D. Chen, K. J. Howe, J. Dallman and B. C. Letellier, Corrosion Sci., 2008, 50, 1046 CrossRef CAS.
- J. C. Griess and A. L. Bacarella, Design Considerations of Reactor Containment Spray Systems-Part III, The Corrosion of Materials in Spray Solutions, Oak Ridge Natioanl Laboratory, Oak Ridge, Tennessee, 1969 Search PubMed.
- A. E. Lane, T. S. Andreychek, W. A. Byers, R. J. Jacko, E. J. Lahoda and R. D. Reid, Evaluation of Post-Accident Chemical Effects in Containment Sump Fluids to Support GSI-191, WCAP-16530-NP-A, Westinghouse Electric Company LLC, Pittsburgh, PA, 2008 Search PubMed.
- J. W. Park, B. G. Park and C. H. Kim, Nucl. Eng. Des., 2009, 239, 3161 CrossRef CAS.
- S. J. Kim, K. J. Howe, J. J. Leavitt, K. Hammond, L. Mitchell, E. Kee and E. D. Blandford, Nucl. Eng. Des., 2015, 282, 71 CrossRef CAS.
- J. Piippo, T. Laitinen and P. Sirkia, Corrosion Behaviour of Zinc and Aluminum in Simulated Nuclear Accident Environments, STUK-YTO-TR 123, Finnish Centre for Radiation and Nuclear Safety, Helsinki, Finland, 1997 Search PubMed.
- D. Chen, K. J. Howe, J. Dallman and B. C. Letellier, Corrosion Sci., 2008, 50, 1046 CrossRef CAS.
- M. Edwards, J. Semmler, D. Guzonas, H. Q. Chen, A. Toor and S. Hoendermis, Nucl. Eng. Des., 2015, 288, 163 CrossRef CAS.
- R. D. Reid, K. R. Crytzer and A. E. Lane, Evaluation of Additional Inputs to the WCAP-16530-NP Chemical Model, Westinghouse Electric Company LLC, Pittsburgh, PA, 2007 Search PubMed.
- C. B. Bahn, K. E. Kasza, W. J. Shack, K. Natesan and P. Klein, Nucl. Eng. Des., 2011, 241, 1926 CrossRef CAS.
- B. Poulson, Corrosion Sci., 1983, 23, 391 CrossRef CAS.
- J. Soltis, N. J. Laycock and D. Krouse, Corrosion Sci., 2011, 53, 7 CrossRef CAS.
- K.-H. Na and S.-I. Pyun, J. Solid State Electrochem., 2005, 9, 639 CrossRef CAS.
- B. A. Bonewitz, Corrosion, 1973, 29, 215 CrossRef.
- K. Ishii, R. Ozaki, K. Kaneko, H. Fukushima and M. Masuda, Corrosion Sci., 2007, 49, 2581 CrossRef CAS.
- B. Zaid, D. Saidi, A. Benzaid and S. Hadji, Corrosion Sci., 2008, 50, 1841 CrossRef CAS.
- V. Vujicic and B. Lovrecek, Surf. Tech., 1985, 25, 49 CrossRef CAS.
- S.-M. Moon, S.-I. Pyun and J. Solid, J. Solid State Electrochem., 1999, 3, 104 CrossRef CAS.
- M. R. Tabrizi, S. B. Lyon, G. E. Thompson and J. M. Ferguson, Corrosion Sci., 1991, 32, 733 CrossRef CAS.
- L. Tomcsanyi, K. Varga, I. Bartik, G. Horanyi and E. Maleczki, Electrochim. Acta, 1989, 34, 855 CrossRef CAS.
- S.-I. Pyun, S.-M. Moon, S.-H. Ahn and S.-S. Kim, Corrosion Sci., 1999, 41, 653 CrossRef CAS.
- W. A. Badawy, F. M. Al-Kharafi and A. S. El-Azab, Corrosion Sci., 1999, 41, 709 CrossRef CAS.
- I. Boukerche, S. Djerad, L. Benmansour, L. Tifouti and K. Saleh, Corrosion Sci., 2014, 78, 343 CrossRef CAS.
- C. Vargel, Corrosion of Aluminum, Elsevier, New York, 2004 Search PubMed.
- A. C. Vermeulen, J. W. Geus, R. J. Stol and P. L. Debruyn, J. Colloid Interface Sci., 1975, 51, 449 CrossRef CAS.
- S.-M. Moon and S.-I. Pyun, Electrochim. Acta, 1999, 44, 2445 CrossRef CAS.
- J. Zhang, M. Klasky and B. C. Letellier, J. Nucl. Mater., 2009, 384, 175 CrossRef CAS.
- B. Tagirov, J. Schott, J. C. Harrichoury and J. Escalier, Geochim. Cosmochim. Acta, 2004, 68, 1333 CrossRef CAS.
- S. Gudic, J. Radosevic and M. Kliskic, Electrochim. Acta, 2002, 47, 3009 CrossRef CAS.
- S. Krakowiak, K. Darowicki and K. Jurak, CorrosionAnti-Corrosion Methods Mater., 2012, 59, 285 CrossRef CAS.
- S.-I. Pyun and S.-M. Moon, J. Solid State Electrochem., 2000, 4, 267 CrossRef CAS.
- S.-M. Moon and S.-I. Pyun, Corrosion, 1998, 54, 546 CrossRef CAS.
- M. Eisenberg, C. W. Tobias and C. R. Wilke, J. Electrochem. Soc., 1954, 101, 306 CrossRef CAS.
- J. Bessone, C. Mayer, K. Juttner and W. J. Lorenz, Electrochim. Acta, 1983, 28, 171 CrossRef CAS.
- J. Ryl, J. Wysocka, M. Jarzynka, A. Zielinski, J. Orlikowski and K. Darowicki, Corrosion Sci., 2014, 87, 150 CrossRef CAS.
- J. H. W. de Wit and H. J. W. Lenderink, Electrochim. Acta, 1996, 41, 1111 CrossRef CAS.
- S. Gudic, J. Radosevic, A. Visekruna and M. Kliskic, Electrochim. Acta, 2004, 49, 773 CrossRef CAS.
- J. V. Petrocelli, J. Electrochem. Soc., 1959, 106, 566 CrossRef CAS.
- G. A. Beyrouty, G. E. Vanscoyoc and J. R. Feldkamp, Soil Sci. Soc. Am. J., 1984, 48, 284 CrossRef.
- C. Su and D. L. Sparks, Soil Sci. Soc. Am. J., 1995, 59, 395 CrossRef.
- M. A. Amin, S. S. Abd EI-Rehim, E. E. F. El-Sherbini, O. A. Hazzazi and M. N. Abbas, Corrosion Sci., 2009, 51, 658 CrossRef CAS.
- C. H. Hsu and F. Mansfeld, Corrosion, 2001, 57, 747 CrossRef CAS.
- J. Hrrzig, K. Juttner, W. J. Lorenz and W. Paatsch, Corrosion Sci., 1984, 24, 945 CrossRef.
- P. A. Brook, Corrosion Sci., 1972, 12, 297 CrossRef CAS.
- J. T. Kloprogge, L. V. Duong, B. J. Wood and R. L. Frost, J. Colloid Interface Sci., 2006, 296, 572 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |