Porous Ni–Cr–Fe alloys as cathode materials for the hydrogen evolution reaction
Yifeng Xiaoa,
Yan Liua,
Zhi Tanga,
Liang Wu*a,
Yi Zengbc,
Yanfei Xua and
Yuehui Heb
aSchool of Mechanical Engineering, Xiangtan University, Xiangtan 411105, China. E-mail: csuwuliang0830@aliyun.com
bState Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China
cMaterials Science Centre, School of Materials, University of Manchester, Grosvenor Street, Manchester M13 9PL, UK
First published on 12th May 2016
Abstract
The objective of this work was to investigate the electrocatalytic efficiency and stability of porous Ni–Cr–Fe cathode materials, obtained by reactive synthesis of Ni, Cr and Fe elemental powders, using cyclic voltammetry, cathodic polarization and impedance spectroscopy techniques. The kinetic parameters have been determined from an electrochemical steady-state polarization technique in 6 M KOH solution. The Tafel slope of the best-performing porous Ni–Cr–Fe cathode materials is −130 mV dec−1, and the exchange current density is 7 × 10−4 A cm−2 at elevated temperature. Moreover, the porous Ni–Cr–Fe cathode materials possess high stability during a prolonged electrolysis process. The results suggest that the significant catalytic and stability performances of the materials are from the high real surface area and good intrinsic catalytic effect.
1. Introduction
With the rapid consumption of fossil fuels, the development of sustainable and renewable energy sources is a worldwide concern.1,2 Hydrogen is considered to be the main medium for energy storage in the future, since the energy can be stored in the form of chemical energy and transform into electrical energy in fuel cells. One of the most commonly used technologies for hydrogen production is alkaline electrolysis.3,4 However, the modern industrial cathode materials for the hydrogen evolution reaction (HER) are ferrous and nickels, which have high hydrogen evolution overpotentials of 380 and 480 mV respectively, leading to great consumption of electrical energy.5 Thus, substantial investigations on the HER are focusing on the development of cathode materials to increase the electrocatalytic activity and reduce hydrogen evolution overpotentials.6In principle, cathode materials with low overpotential towards the HER should possess two characteristics, which are a high surface area and good intrinsic catalytic activity.7–10 Porous materials as cathode materials for water electrolysis with large surface areas have usually been obtained through leaching active elements (such as Al, Zn, Cu, etc.) out of the precursor, among which porous RANEY® Ni is a typical representative.11 It exhibits good electrocatalytic activity for the HER and sufficient corrosion resistance in alkaline solution. However, the instability of RANEY® Ni limits its practical application due to the dissolution of active elements during the working process. In addition, the alloying of two or more metals from the two branches of the “volcano” curve has long appeared as the most straightforward way to improve the intrinsic catalytic activity of the materials.12 Nickel alloys have been considered as one of the most important cathode materials for the HER because of their low cost, high corrosion resistance and low overpotential. Many coatings of nickel alloys on bulk materials have been researched, such as Ni–Mo,13 Ni–Sn,14 Ni–S,15 Ni–Co,16 Ni–Mo–Cu,17 Ni–Co–Sn18 and Ni–Mo–Zn,19 by electrodeposition,16 thermal preparation20 or addition in situ.4 Despite a large amount of data having been collected in this field, it should be emphasized that for technological applications, besides the electrocatalytic activity, the stability of cathode materials in strong alkaline solutions at elevated temperature is even more crucial. During the process of the HER, hydrogen can enter the pores of the coatings and peel off the coatings from the bulk materials.21 Such behavior has been reported for Ni–Mo coatings electrodeposited onto mild steel substrates, where it was found by the analysis of a cross-section of the electrodeposited Ni–Mo coatings22 after a long time of hydrogen evolution in 1 M NaOH at 25 °C. So it is important to produce new kinds of porous alloys which combine both a high surface area and good intrinsic catalytic activity, and also have excellent stability in the process of the HER.
In our previous work, some porous materials with high surface area and excellent stability in strong alkaline solution were fabricated by elemental powder reactive synthesis methods.23,24 In the Engel–Brewer theory, strong bonding is considered to be achieved by filling the vacant d-orbitals of the early transition metals with the electrons donated from non-bonding orbitals of the late transition metals, which results in the formation of stable alloys which have high intrinsic catalytic activity for the HER.25,26 In this research, porous Ni–Cr–Fe alloys have been fabricated by elemental powder reactive synthesis methods. The porous structures can largely increase the surface area and the combination of 3d8 of Ni, 3d6 of Fe and 3d5 of Cr can elevate the intrinsic catalytic activity of the cathode materials. We will firstly offer the results of the investigation of the porous Ni–Cr–Fe cathode materials fabricated by a powder metallurgy method, which reveals high electrocatalytic activity and stability under working conditions simulated for the industrial application of the HER (in concentrated KOH solutions at elevated temperatures). Results are presented to show the Tafel slopes, exchange current densities, apparent energies of activation and stability performance of the cathode materials.
2. Experimental
Pure commercial powders of Ni (3–5 μm), Cr (3–5 μm) and Fe (3–5 μm) were mixed in the ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by weight. The powders were ball-milled for 10 h using a mixer, and pressed into compact specimens with dimensions of 5 mm × 45 mm × 1 mm under a pressure of 100 MPa. The specimens were then sintered in a vacuum furnace under 1 × 10−3 Pa at temperatures of 850 °C for a duration of 1 h. Porous Ni–Cr–Fe materials with powder compositions of 5
1 by weight. The powders were ball-milled for 10 h using a mixer, and pressed into compact specimens with dimensions of 5 mm × 45 mm × 1 mm under a pressure of 100 MPa. The specimens were then sintered in a vacuum furnace under 1 × 10−3 Pa at temperatures of 850 °C for a duration of 1 h. Porous Ni–Cr–Fe materials with powder compositions of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 6
2, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 6
1 and 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
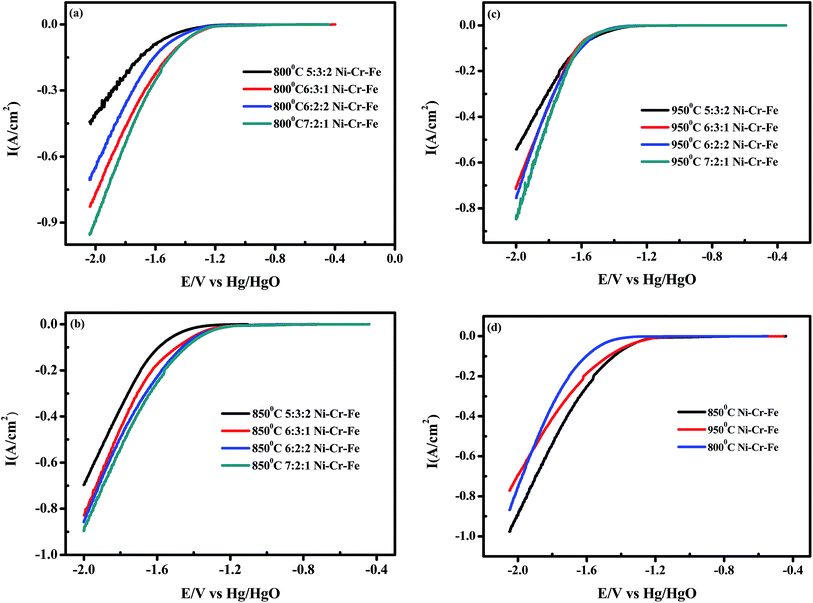
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 by weight and sintering temperatures of 800 °C, 850 °C and 950 °C were also prepared for comparing the HER activities. Without special version, all the figures and tables illustrate the performances of porous Ni–Cr–Fe alloys with the composition of 7 : 2 : 1 and under the sintering temperature of 850 °C.
2 by weight and sintering temperatures of 800 °C, 850 °C and 950 °C were also prepared for comparing the HER activities. Without special version, all the figures and tables illustrate the performances of porous Ni–Cr–Fe alloys with the composition of 7 : 2 : 1 and under the sintering temperature of 850 °C.
X-ray diffraction (XRD) (Rigaku D/max-2500, graphite monochromator, Cu Kα) and field-emission scanning electron microscopy (SEM) (NOVA NANOSEM 230) were employed to identify the phase composition, crystalline structures and surface morphology of the materials. The open porosities were measured by the Archimedes method in water.
All the electrochemical tests were carried out using a CS350 electrochemical workstation in a standard three-electrode electrochemical cell in 6 M KOH solution. Pt foil and Hg/HgO/OH− electrodes were used as the counter and reference electrodes, respectively. The latter was connected to the working electrode via a Luggin capillary positioned close to the working electrode. The electrocatalytic activity of the Ni–Cr–Fe species for the HER was studied by the following kinetic parameters: the Tafel slope (b), the exchange current density (j0), the overpotential needed for a fixed current density and the apparent energy of activation (Ea). Cathodic polarization curves were recorded by sweeping the electrode potential from −0.2 V to −2.0 V vs. Hg/HgO, at the scan rate of 1 mV s−1. During the measurements, the current interrupt technique was applied for iR compensation. The cyclic voltammograms were recorded at a scan rate of 0.050 V s−1 within the evaluated range of temperatures. Before each measurement, the electrode was held at −1.200 V vs. Hg/HgO for 0.5 h to reduce the oxide film on the electrode film on the electrode surface. Then, the working electrode was held at its open circuit potential until equilibrium was reached. Due to the fact that during the first 5 potential cycles stability was reached in the voltammograms, the presented results correspond to the evaluation performed after 5 potential scans. AC impedance spectra were recorded in the frequency range from 10 kHz to 10 mHz, using a 10 mV ac amplitude, at constant overpotentials ranging from 10 mV to 70 mV. The temperature of the solution in the electrochemical cell varied between 298 and 358 K. In the case of the anodic treatment (oxygen evolution), polarization diagrams were recorded immediately after the anodic treatment. Cathodic polarization at −1.5 V was applied for 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s to test the aging effect. For each experiment, a freshly prepared cathode and solution were used. All solutions were made from analytical grade chemicals and deionized water.
000 s to test the aging effect. For each experiment, a freshly prepared cathode and solution were used. All solutions were made from analytical grade chemicals and deionized water.
3. Results and discussion
3.1. Characterization of porous Ni–Cr–Fe cathode materials
Fig. 1 shows a typical XRD pattern of a prepared porous Ni–Cr–Fe alloy. The pattern indicates that the prepared porous material has a very similar crystal stucture to that of Ni owing to the high solubility of Cr and Fe atoms in the Ni matrix. The diffraction peaks are (111), (200) and (220). Compared with Ni, the (111) peak of the Ni–Cr–Fe alloy shows an obvious shift to the left (lower angle) due to the solid solution of Cr and Fe in the Ni. | ||
| Fig. 1 (a) XRD pattern of the porous Ni–Cr–Fe cathode material and porous Ni; (b) the negative shift of the (111) peak of the porous Ni–Cr–Fe cathode material relative to that of the porous Ni. | ||
Scanning electron micrographs of the porous Ni–Cr–Fe cathode material and porous Ni are shown in Fig. 2. The porous microstructure indicates that the fabricated porous Ni–Cr–Fe has a higher open porosity than porous Ni. It is widely accepted that one of the methods for the activity enhancement of cathode materials is the increase of the surface area.
The pore structure parameters of the freshly prepared porous Ni–Cr–Fe cathode material are shown in Table 1. Obviously, the porous Ni–Cr–Fe cathode material has a larger porosity and mean pore size than the porous Ni.
| Electrode | Sintering temperature (°C) | Mean pore size (μm) | Porosity (%) |
|---|---|---|---|
| Ni–Cr–Fe | 850 | 3.1 | 39.2 |
| Ni | 850 | 1.2 | 18.0 |
3.2. Electrocatalytic activity of the porous Ni–Cr–Fe cathode materials
Cyclic voltammetry (CV) was employed to determine the double layer capacity of the porous Ni–Cr–Fe cathode material, and a typical CV recorded at different scan rates is displayed in Fig. 3(a). The variation of the average double layer current densities, jdl,ave = (jc + ja)/2, as a function of potential sweep rate can be described as follows:| jdl,ave = Cd1(dE/dt), | (1) |
| Electrocatalysts | b (mV dec−1) | j0 (A cm−2) | Cdl (μF cm−2) | Rf | j0/Rf (A cm−2) | Onset potential (V vs. Hg/HgO) | I−1.4 V (A cm−2) |
|---|---|---|---|---|---|---|---|
| Porous Ni–Cr–Fe | −195.58 | 2.4 × 10−4 | 157![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 260 |
786.3 | 3.0628 × 10−7 | −1.0 | −0.175 |
| Porous Ni | −527.25 | 4.1 × 10−5 | 609.8 | 30.49 | 1.38 × 10−7 | −1.6 | −0.08 |
The linear sweep cathodic polarizations of the different kinds of porous Ni–Cr–Fe cathode materials for the HER in 6 M KOH at 298 K are illustrated in Fig. 4. Porous Ni–Cr–Fe materials with the composition of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sintered at different temperatures all showed excellent activity for the HER, and porous Ni–Cr–Fe with the composition of 7
1 sintered at different temperatures all showed excellent activity for the HER, and porous Ni–Cr–Fe with the composition of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sintered under a temperature of 850 °C displayed the best activity for the HER.
1 sintered under a temperature of 850 °C displayed the best activity for the HER.
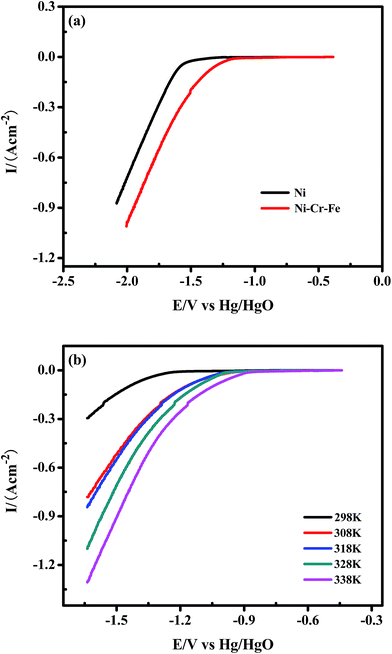
The linear sweep cathodic polarization of the porous Ni–Cr–Fe cathode materials for the HER in 6 M KOH is illustrated in Fig. 5(a). The kinetic parameters for the HER (j0 and b) for the investigated systems are derived from the Tafel equation:
η = a + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j, j,
| (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j0, where R is the gas constant (8.314 kJ mol−1 K−1), β is the symmetry factor, n is the number of electrons exchanged and F is the Faraday constant (96
j0, where R is the gas constant (8.314 kJ mol−1 K−1), β is the symmetry factor, n is the number of electrons exchanged and F is the Faraday constant (96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1). The Tafel slope (b), exchange current density (j0) and onset potential are shown in Table 2, where the apparent activity of the porous Ni–Cr–Fe cathode material is 5 times as high as that of porous Ni, while the intrinsic catalytic activity is just two-fold that of porous Ni; this indicates that the dopants of Ni, Cr and Fe, not only increase the real surface area of porous Ni–Cr–Fe materials, but also improve the catalytic properties of materials towards HER.
485 C mol−1). The Tafel slope (b), exchange current density (j0) and onset potential are shown in Table 2, where the apparent activity of the porous Ni–Cr–Fe cathode material is 5 times as high as that of porous Ni, while the intrinsic catalytic activity is just two-fold that of porous Ni; this indicates that the dopants of Ni, Cr and Fe, not only increase the real surface area of porous Ni–Cr–Fe materials, but also improve the catalytic properties of materials towards HER.
Another important aspect has been found by comparing the polarization behavior of porous Ni–Cr–Fe and porous Ni, as shown in Fig. 5(a). At the fixed current density value of 0.1 A cm−2, there is a significant decrease in the HER overvoltage of about 50 mV. This finding is very important since these operating conditions are close to the operating conditions of the commercial alkaline electrolyzers.
The determination of the reaction mechanism of the HER and the process of the rate determining step (RDS) can be accomplished using Tafel analysis. Generally, the overall reaction in alkaline solution proceeds via a three-step reaction mechanism:
| M + H2O + e− ↔ MHads + OH−, Volmer reaction; | (3) |
| MHads + H2O + e− ↔ H2 + M + OH−, Heyrovsky reaction; | (4) |
| MHads + MHads ↔ H2 + M, Tafel reaction. | (5) |
The HER starts with a proton discharge electrosorption step, the Volmer reaction, followed by an electronic desorption step, the Heyrovsky reaction and/or a catalytic recombination step, the Tafel reaction. Thus, the overall reaction proceeds via two possible reaction pathways, Volmer–Heyrovsky and Volmer–Tafel. For each step (3)–(5) being the RDS, the Tafel slopes have values of −120 mV dec−1, −240 mV dec−1 and −30 mV dec−1, respectively.
Fig. 5(b) presents polarization curves obtained for the porous Ni–Cr–Fe alloy at temperatures ranging from 298 to 338 K. As shown in Fig. 5(b), the polarization curves exhibit the expected behavior. With increasing operation temperature, there is an evident increase of the exchange current density and a slight decrease of the equilibrium potential. The Tafel slopes (b) and exchange current densities (j0) at different temperatures are shown in Table 3. Tafel slopes, b, for the HER for all investigated systems range from −190 mV dec−1 to −130 mV dec−1. These values indicate that the charge transfer (Volmer) reaction is the rate determining step for the HER.
| T (K) | b (mV dec−1) | j0 (A cm−2) |
|---|---|---|
| 308 | −195.6 | 2.4 × 10−4 |
| 318 | −186.1 | 3.0 × 10−4 |
| 328 | −171.6 | 3.6 × 10−4 |
| 338 | −159.2 | 5.0 × 10−4 |
| 348 | −146.8 | 6.0 × 10−4 |
| 358 | −135.6 | 7.0 × 10−4 |
The electrocatalytic activity of the porous Ni–Cr–Fe cathode material was also analyzed through the effect of temperature on the rates of chemical reactions. For a single rate-limited thermally activated process, Arrhenius plots show a straight line, from which the apparent activation energy can be determined. The apparent energy of activation for the porous Ni–Cr–Fe cathode material has been calculated from the slope of the Arrhenius plot presented in Fig. 6.
Arrhenius plots display a semi-logarithmic dependence of exchange current density plotted against inverse temperature. The Arrhenius equation is given in the following form:29
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) j0 = log j0 = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A − Ea/2.303RT, A − Ea/2.303RT,
| (6) |
Fig. 6 reveals that the activation energy obtained from the Arrhenius plot for the porous Ni–Cr–Fe cathode material is ∼21 kJ mol−1. Through comparing the apparent activation energy from this work with literature data, 40 kJ mol−1 for nickel electrodes,30 it is inferred that the porous Ni–Cr–Fe cathode material exhibits a significant catalytic performance. The decrease in the apparent free energy of activation is caused by the electrocatalytic synergistic effect of the Ni, Cr and Fe elements on the material.
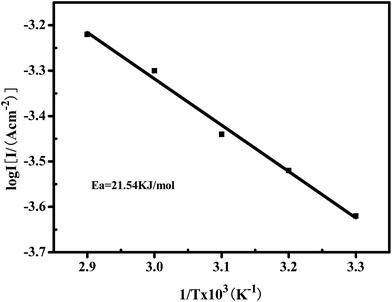 | ||
| Fig. 6 An Arrhenius plot displaying the semi-logarithmic dependence of exchange current density on inverse temperature for the porous Ni–Cr–Fe cathode material in a 6 M KOH electrolyte. | ||
Fig. 7 corresponds to the cyclic voltammograms of the porous Ni–Cr–Fe and porous Ni materials at 338 K. The reduction peaks are associated with the hydrogen evolution, including R1 and R2, and the oxidation peaks, O1 and O2, correspond to the hydrogen desorption reaction on the porous materials. As shown in Fig. 7, the intensity of the hydrogen desorption peak for the porous materials is directly in proportion to the hydrogen evolution reaction. The intensity of the O peak of the porous materials decreases with the weakening of the hydrogen reduction (R). Compared with the R1 of the porous Ni, the R2 of the porous Ni–Cr–Fe alloy shows a much higher intensity at the respective overpotentials, which is in accordance with the results of the polarization measurement.
 | ||
| Fig. 7 Cyclic voltammograms of the porous Ni–Cr–Fe cathode material and porous Ni material in the scan range −2.0 V to 0.5 V at 338 K. | ||
In alkaline and neutral solution, Ni alloys behave like an electropositive metal because the anodic process is the oxidation of nickel to a slightly soluble hydroxide or oxide:31–33
| Ni + 2OH− = α-Ni(OH)2 + 2e−, | (7) |
| Ni + 2H2O = NiO + 2H+ + 2e−; | (8) |
| Ni(OH)2 + OH− = NiOOH + H2O + e−. | (9) |
This electrochemical oxidation results in the expulsion of a proton from the Ni hydroxide layer to produce H2O in the strong alkaline solution.34–36
Compared with porous Ni, the increase in the anodic peak current of porous Ni–Cr–Fe renders the material with better properties. The broad region observed in the anodic scan indicates the capacity of charge, i.e. the quantity of hydrogen in the cathode materials; below this region, the current rapidly increases in the negative direction. It is necessary to mention that the anodic polarization current for the as-prepared cathode materials involves two typical steps, which are the hydrogen charge transfer reaction across the electrode–electrolyte interface and hydrogen diffusion in the surface. Thus, our investigation indicates that the HER activity of the porous Ni–Cr–Fe is higher than that of porous Ni.
The interfacial behavior of the electrode/electrolyte and the electrocatalytic activity of the porous Ni–Cr–Fe cathode material for the HER have been investigated with the help of the EIS technique. EIS measurements were carried out in the potential range corresponding to the linear part of the current–potential curves (Fig. 5) at different overpotentials. Representative Nyquist plots of the porous Ni–Cr–Fe and porous Ni cathode materials at different overpotentials are given in Fig. 8.
As shown in Fig. 8(a) and (b), two semi-circles can be detected on the Nyquist diagrams, which indicate the presence of two time constants. In order to fit the impedance spectra obtained on the porous Ni–Cr–Fe electrode, a two constant phase elements (CPE) serial model was applied, shown in Fig. 8(c). It consists of the solution resistance, Rs, in series with two parallel CPE-R elements (a 2-CPE model).37 According to this model, the high-frequency time constant, independent of the potential, is described by the Rp and CPEp connected in parallel. Rp is basically related to the mass transfer resistance of the adsorbed intermediate Hads, usually called the pseudo-resistance, and Cp is the pseudo-capacitance of the working electrode. The deviation from the ideal capacitance behavior corresponds to a frequency-dependent phase angle and the behavior can be represented by a so-called constant phase element, CPE.38 This capacitance dispersion of the electrodes depends strongly on the state of the electrode’s surface, e.g. its roughness or the electrode porosity. The potential-dependent time constant is related to the kinetics of the HER, Rct is the charge-transfer resistance and Cdl is the double layer capacitance.
The EIS spectra presented in Fig. 8 exhibit the expected behavior in that the total resistance decreases with increasing HER overvoltage, which indicates the increase of activity in the hydrogen evolution reaction. In addition, it is noticeable that the total resistance of the porous Ni is higher than that for the electrolyte of the porous Ni–Cr–Fe, which indicates that the porous Ni–Cr–Fe cathode material has a good hydrogen evolution activity.
The Nyquist plots presented in Fig. 9 were obtained by measuring the frequency response of the porous Ni–Cr–Fe cathode material at temperatures ranging from 298–338 K. The decrease in resistance with the elevated temperature indicates the increase in the activity of the hydrogen evolution reaction.
 | ||
| Fig. 9 Nyquist plots for the porous Ni–Cr–Fe cathode material with increasing cathodic overvoltage at temperatures ranging from 298 K to 338 K. | ||
3.3. Stability performance of the porous Ni–Cr–Fe cathode material
The cathodic current density evolution vs. time is shown in Fig. 10. The change of the current density at the beginning is normal in the electrolyte, possibly because of the reduction of the oxides on the electrode surface. The cathodic current density of the porous Ni–Cr–Fe fluctuated a little during the initial period of time, but could keep stable after 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s, which reveals a good stability of the electrocatalytic performance of the electrode. The porous Ni also showed good electrocatalytic stability, but performed with a much lower current density than the porous Ni–Cr–Fe. In addition, SEM images show that the surface morphology and the pore structure of the porous Ni–Cr–Fe alloy remained unchanged after polarization, as seen in Fig. 10.
000 s, which reveals a good stability of the electrocatalytic performance of the electrode. The porous Ni also showed good electrocatalytic stability, but performed with a much lower current density than the porous Ni–Cr–Fe. In addition, SEM images show that the surface morphology and the pore structure of the porous Ni–Cr–Fe alloy remained unchanged after polarization, as seen in Fig. 10.
 | ||
Fig. 10 The cathodic current densities of the porous Ni–Cr–Fe and porous Ni vs. time, with the morphology of the porous Ni–Cr–Fe before and after 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s in 6 M KOH. 000 s in 6 M KOH. | ||
In their industrial application, the reverse polarization of cathode materials happens when the power is shut down. In this case, the cathodes become anodically polarized, while anodes become cathodically polarized. Such a polarization can cause significant changes in the electrochemical behavior of the materials and they might lose their catalytic properties. In order to investigate the influence of such a polarization on the porous Ni–Cr–Fe cathode material, a sample was exposed to the polarization at a constant anodic potential in the region of oxygen evolution and its polarization characteristics were investigated.
When this electrode was exposed to an oxygen evolution potential at 0.5 V for 1000 s and the polarization curve was recorded immediately after oxygen evolution, the overpotential for the HER became higher than before. After additional oxygen evolution at 0.6 V for 1000 s, the polarization curve for the HER became worse. It is obvious from the results presented in Fig. 11 that the oxide layer formed during the anodic treatment was almost reduced during the hydrogen evolution and accordingly, the polarization curve for the HER became almost identical to one recorded before any anodic treatment at 298 K.
 | ||
| Fig. 11 The polarization curves for the porous Ni–Cr–Fe cathode material at 298 K before and after different anodic treatments: (1) after oxygen evolution at 0.5 V for 1000 s (I–t response shown in the inset of Fig. 10); (2) after oxygen evolution at 0.6 V for 1000 s (I–t response shown in the inset of Fig. 10); (3) after additional hydrogen evolution at I = −100 mA cm−2 for 1000 s; (4) no anodic treatment. | ||
Nyquist plots obtained in 6 M KOH solution at open circuit after 24 h, 48 h and 120 h are given in Fig. 12, to evaluate the corrosion behavior of the porous Ni–Cr–Fe cathode material. With the increasing time, the corrosion resistance of the material became better due to the growth of a surface protective layer of metal oxides and/or hydroxides during the longer immersion time. The layer effectively limited the transfer of corrosive ions to the metal surface through the pores.
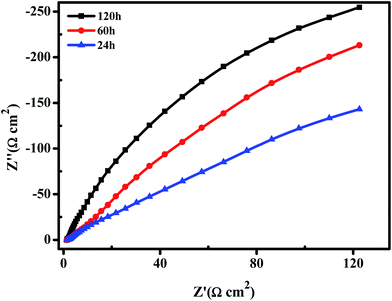 | ||
| Fig. 12 Representative Nyquist plots of the porous Ni–Cr–Fe cathode material at open circuit after 24 h, 60 h and 120 h of immersion. | ||
The open circuit potential (Eocp) of the porous Ni–Cr–Fe cathode material as a function of immersion time is given graphically in Fig. 13. Eocp of the porous material starts from a value of −0.52 V and shifts to a nobler direction in the initial period of electrolysis and then nearly remains the same. The data obtained suggest a passive film formation on the surface, and the following reaction may occur:39
| Mn+(m) or Mn+(ox) ↔ Mn+(aq), | (10) |
| Mn+(aq) + xOH− ↔ M(OH)x(n−x)(aq) (where = 1, 2, …, n + 1), | (11) |
| M(OH)n(aq) ↔ M(OH)n(ox) → MOn/2(ox) + n/2H2O, | (12) |
4. Conclusions
The electrocatalytic efficiency of a porous Ni–Cr–Fe cathode material obtained by reactive synthesis of Ni, Cr and Fe elemental powders in 6 M KOH has been investigated using cyclic voltammetry, cathodic polarization and impedance spectroscopy techniques. The Tafel slope of best-performing porous Ni–Cr–Fe alloy is −130 mV dec−1 at high temperature, implying that the rate determining step for the HER is the proton discharge electrosorption (Volmer reaction). The value for the exchange current density is 7 × 10−4 A cm−2 at elevated temperature. The apparent energy of activation obtained from an Arrhenius plot for the porous Ni–Cr–Fe cathode material has been calculated to be ∼21 kJ mol−1. The results suggest that the significant catalytic performance is not only from the increase of the real surface area of the cathode material, but also from the intrinsic catalytic effect.Moreover, the porous Ni–Cr–Fe cathode material possesses high stability during prolonged electrolysis and good corrosion resistance in 6 M KOH solution. Porous Ni–Cr–Fe alloys exhibit promising characteristics as cathode materials for the HER at an industrial scale.
Acknowledgements
The authors are grateful for the financial support from the NSF of China (51504213, 51401175, 51271158) and the Project of Hunan province (2015WK3021, 2015JJ3123).References
- M. S. Xiao, Y. Q. Miao, Y. P. Tian and Y. H. Yan, Electrochim. Acta, 2015, 165, 206–210 CrossRef CAS.
- R. M. A. Tehrani and S. A. Ghani, Electrochim. Acta, 2012, 70, 153–157 CrossRef CAS.
- V. M. Nikolic, S. L. Maslovara, G. S. Tasic, T. P. Brdaric, P. Z. Lausevic, B. B. Radak and M. P. Marceta Kaninski, Appl. Catal., B, 2015, 179, 88–94 CrossRef CAS.
- J. L. Tang, X. H. Zhao, Y. Zuo, P. F. Ju and Y. M. Tang, Electrochim. Acta, 2015, 174, 1041–1049 CrossRef CAS.
- Z. Q. Shan, Y. J. Liu, Z. Chen, G. Warrender and J. H. Tian, Int. J. Hydrogen Energy, 2008, 33, 28–33 CrossRef CAS.
- Z. Zheng, N. Li, C. Q. Wang, D. Y. Li, Y. M. Zhu and G. Wu, Int. J. Hydrogen Energy, 2012, 37, 13921–13932 CrossRef CAS.
- L. Yang, X. L. Wu, X. S. Zhu, C. Y. He, M. Meng, Z. X. Gan and P. K. Chu, Appl. Surf. Sci., 2015, 341, 149–156 CrossRef CAS.
- S. Muralikrishna, K. Manjunath, D. Samrat, V. Reddy, T. Ramakrishnappa and D. H. Nagaraju, RSC. Adv., 2015, 5, 89389–89396 RSC.
- J. B. Raoof, S. R. Hosseini, R. Ojani and S. Mandegarzad, Energy, 2015, 90, 1075–1081 CrossRef CAS.
- R. Ojani, R. Valiollahi and J. B. Raoof, Energy, 2014, 74, 871–876 CrossRef CAS.
- Y. P. Li, X. M. Huang, Q. Zhang, L. G. Chen, X. H. Zhang, T. J. Wang and L. L. Ma, Appl. Energy, 2015, 160, 990–998 CrossRef CAS.
- F. Safizadeh, E. Ghali and G. Houlachi, Int. J. Hydrogen Energy, 2015, 40, 256–274 CrossRef CAS.
- O. Aaboubi, Int. J. Hydrogen Energy, 2011, 36, 4702–4709 CrossRef CAS.
- Y. B. Zhu, X. H. Zhang, J. L. Song, W. Wang, F. F. Yue and Q. Ma, Appl. Catal., A, 2015, 500, 51–57 CrossRef CAS.
- Z. Zheng, N. Li, C. Q. Wang, D. Y. Li, F. Y. Meng, Y. M. Zhu, Q. Li and G. Wu, J. Power Sources, 2013, 230, 10–14 CrossRef CAS.
- F. J. Pérez-Alonso, C. Adán, S. Rojas, M. A. Peña and J. L. G. Fierro, Int. J. Hydrogen Energy, 2015, 40, 51–61 CrossRef.
- M. Xia, T. Lei, N. L. Lv and N. F. Li, Int. J. Hydrogen Energy, 2014, 39, 4794–4802 CrossRef CAS.
- J. Vijayakumar, S. Mohan, S. Anand Kumar, S. R. Suseendiran and S. Pavithra, Int. J. Hydrogen Energy, 2013, 38, 10208–10214 CrossRef CAS.
- X. Q. Wang, R. Su, H. Aslan, J. Kibsgaard, S. Wendt, L. H. Meng, M. D. Dong, Y. D. Huang and F. Besenbacher, Nano Energy, 2015, 12, 9–18 CrossRef CAS.
- E. Fachinotti, E. Guerrini, A. C. Tavares and S. Trasatti, J. Electroanal. Chem., 2007, 600, 103–112 CrossRef CAS.
- N. V. Krstajić, V. D. Jović, Lj. Gajić-Krstajić, B. M. Jović, A. L. Antozzi and G. N. Martelli, Int. J. Hydrogen Energy, 2008, 33, 3676–3687 CrossRef.
- V. D. Jović, B. M. Jović, G. R. Stafford, V. N. Krstajić and Z. Twardowski, in SURFIN, Chicago, 2002, pp. 76–84 Search PubMed.
- L. Wu, Y. Jiang, H. X. Dong, Y. H. He, N. P. Xu, J. Zou, B. Y. Huang and C. T. Liu, Intermetallics, 2011, 19, 1759–1765 CrossRef.
- L. Wu, Y. H. He, T. Lei, B. Nan, N. P. Xu, J. Zou, B. Y. Huang and C. T. Liu, Macromol. Chem. Phys., 2013, 141, 553–561 CAS.
- M. M. Jakšic, Int. J. Hydrogen Energy, 1987, 12, 727–752 CrossRef.
- M. M. Jakšic, Electrochim. Acta, 1984, 29, 1539–1550 CrossRef.
- N. V. Krstajić, V. D. Jović, L. j. Gajić-Krstajić, B. M. Jović, A. L. Antozzi and G. N. Martelli, Int. J. Hydrogen Energy, 2008, 33, 3676–3687 CrossRef.
- B. Cui, H. Lin, L. B. Li, X. Li, J. Yang and J. Tao, Adv. Funct. Mater., 2008, 18, 1440–1447 CrossRef CAS.
- D. M. F. Santos, B. Sljukic, C. A. C. Sequeira, D. Macciò, A. Saccone and J. L. Figueiredo, Energy, 2013, 50, 486–492 CrossRef CAS.
- H. X. Dong, T. Lei, Y. H. He, N. P. Xu, B. Y. Huang and C. T. Liu, Int. J. Hydrogen Energy, 2011, 36, 12112–12120 CrossRef CAS.
- A. Dmochowska and A. Czerwinski, J. Electroanal. Chem., 2001, 512, 16–26 CrossRef.
- S. L. Yau, F. R. F. Fan, T. P. Moffat and A. J. Bard, J. Phys. Chem., 1994, 98, 5493–5499 CrossRef CAS.
- L. D. Burke and T. A. M. Twomey, J. Electroanal. Chem., 1984, 162, 101–119 CrossRef CAS.
- B. Beden and A. Bewick, Electrochim. Acta, 1988, 33, 1965–1968 CrossRef.
- H. M. French, M. J. Henderson, A. R. Hillman and E. Vieil, J. Electroanal. Chem., 2001, 500, 192–207 CrossRef CAS.
- H. M. French, M. J. Henderson, A. R. Hillman and E. Vieil, Solid State Ionics, 2002, 150, 27–37 CrossRef CAS.
- P. Elumalai, H. N. Vasan, N. Munichandraiah and S. A. Shivashankar, J. Appl. Electrochem., 2002, 32, 1005–1010 CrossRef CAS.
- S. M. Miulovic, S. L. Maslovara, I. M. Perovic, V. M. Nikolic and M. P. Marceta Kaninski, Appl. Catal., A, 2013, 451, 220–226 CrossRef CAS.
- A. Y. Musa and J. C. Wren, Corros. Sci., 2016 DOI:10.1016/j.corsci.2016.03.015.
| This journal is © The Royal Society of Chemistry 2016 |