Carbon rings: a DFT study on geometry, aromaticity, intermolecular carbon–carbon interactions and stability

Abstract

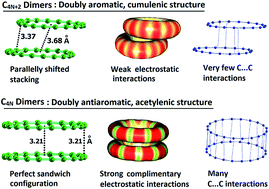
Non-covalent dimer formation and intermolecular bonding features of planar monocyclic carbon rings showing C_4N+2 and C_4N configurations have been studied using the meta-GGA DFT method, M06L/6-311+G(d) for N = 1–8. The C_4N+2 show cumulenic structures with equal bond lengths and C_4N form structures with clear bond length alternation. The doubly Hückel aromatic nature of C_4N+2 is revealed through two cyclic delocalized π-molecular orbitals and highly negative nucleus independent chemical shift (NICS) parameters while the doubly Hückel antiaromatic nature of C_4N is brought out through two localized π-molecular orbitals and highly positive NICS parameters. Further, the uniform electron distribution over the delocalized CC bonds in C_4N+2 and the alternate electron rich and electron deficient regions in C_4N are assessed on the basis of the critical features of the molecular electrostatic potential (MESP). The contrasting geometric, electronic and magnetic features of C_4N+2 compared to C_4N result in a drastic difference in their intermolecular bonding behaviour. The C_4N showed a much higher tendency than C_4N+2 for dimer formation as the former, in general show a 4N number of intermolecular C⋯C interactions due to complimentary electrostatic interactions between electron rich shorter CC bonds and electron deficient longer CC bonds. In C_4N dimers, a perfect sandwich configuration is preferred to maximize the attractive complementary electrostatic interactions while in C_4N+2 dimers a shifted-parallel stacked arrangement indicated the non-complementary character of interactions arising from smooth aromatic distribution of electrons. The comparative stability of the carbon rings and unsubstituted polyynes is quantified by measuring the homodesmotic reaction energy (E_hdr) with acetylene. The E_hdr indicated significant stabilization of C_4N+2 compared to C_4N. The energy required to open up a carbon ring to the linear form is computed as E_opening and this quantity is used to estimate the aromatic stabilization of C_4N+2 as well as the antiaromatic destabilization of C_4N systems.

---

Introduction

Laser vaporization of graphite results in the formation of carbon clusters.¹ Depending on the size of the cluster, several types of carbon clusters exist such as linear chains, rings, bowls, plates and cages.^2–6 Very small clusters such as C₂ and C₃ exist as linear chains. At larger sizes, they form rings. Carbon rings are stable in the size range of approximately C₆–C₃₀, which show slight variation with the theoretical methods used as well as the experimental conditions. At even higher sizes, these high energy sp hybridized clusters start converting into sp² hybridized forms such as plates and cages. These structures rearrange to form fullerenes, the mechanism of which has been studied extensively.^7–13 The ring structures are relatively stable non spheroidal forms. Among the ring structures, the monocyclic rings are relatively more stable compared to other configurations.¹⁴

The properties of planar monocyclic carbon rings have been extensively studied theoretically as well as experimentally.^{2,5,6,14–27} The properties of these rings vary with the number of carbon atoms, n depending on whether n is odd, n = 4N or n = 4N + 2 where N is an integer. The stabilization of this type of molecules in different structural types has been explained in terms of aromaticity, second order Jahn–Teller distortions and Peierls instability effects.²⁷ The structures reported by Torelli and Mitas for the molecules with 4N + 2 carbon atoms using quantum Monte Carlo methods include (i) rings with all bond lengths and bond angles equal (D_nh symmetry), (ii) rings with alternating bond angles (D_n2h symmetry) or (iii) rings with alternating bond lengths (D_n2h symmetry).²⁷ The concept of double aromaticity²⁸ was first coined by Schleyer et al. in 1979.²⁹ In the rings with 4N + 2 carbon atoms, the presence of two sets of conjugated π electron systems (in plane and out of plane) suggests double aromaticity. Theoretical studies have shown that, at smaller sizes, carbon rings with 4N + 2 carbon atoms show double aromaticity whereas those with 4N carbon atoms show double antiaromaticity.^30–32 The diatropic and paratropic ring currents in both the delocalized π electron systems of C_4N+2 and C_4N molecules respectively have been described well by Fowler et al.³³ using the maps of current density. At very large sizes, both types of rings are expected to show non aromatic behaviour.³⁰

The structure for a carbon ring C_n is predicted to be cumulenic with bond angle alternation if n = 4N + 2 (type (ii)) and acetylenic with bond length alternation if n = 4N (type (iii)) while both maintains a D_n2h symmetry.^{25–27,30,33,34}

Here, we focus mainly on the intermolecular interactions in planar monocyclic carbon rings. In a previous study, we have shown that inter-molecular C⋯C interactions between carbon atoms in similar chemical environments exist in several dipolar organic molecules.³⁵ These interactions result from complimentary electrostatic interaction of electron rich region of one molecule with electron deficient region of another. For instance, in the case of polyyne molecules, the electron rich formal triple bond of one molecule interacts with electron deficient formal single bond of another³⁶ (Scheme 1) and several such interactions along the polyyne chain lead to significant stabilization of the dimer, approximately 1.00 kcal mol⁻¹ for each C⋯C interactions. Natural bond orbital (NBO) analysis showed both the donor and acceptor character of the interacting carbon atoms (i.e., in a C₁⋯C₂ interaction, a charge transfer from C₁ to C₂ is also complimented by a similar charge transfer from C₂ to C₁, where C₁ and C₂ are chemically almost identical).³⁵

Scheme 1 (a) Polyyne dimers showing intermolecular C⋯C interactions (b) C₁₆ with acetylenic structure and (c) C₁₈ with cumulenic structure.

In polyynes, though the interacting carbon atoms belong to similar chemical environments, local differences in electron concentration result in the C⋯C interactions. The end substitutions, which affected the electron distribution throughout the length of the polyyne molecules, had a strong influence on the strength of the C⋯C interactions.³⁶ In the case of C_n rings, intermolecular interactions could not be varied by substitutions as such manipulations are not possible for them. The only option is to vary the electronic configuration of the ring structure. As illustrated in Scheme 1, the C_4N rings have similarity with polyyne molecules as they possess alternate electron rich and electron deficient regions which would lead to several intermolecular C⋯C interactions. On the other hand, in C_4N+2 molecules, all the CC bonds are identical due to aromatic π-electron delocalization and the chance of seeing several C⋯C interactions is less. For testing this hypothesis, dimers of C_n molecules are studied for n = 4N + 2 and n = 4N, where N is a natural number. First, we illustrate the doubly aromatic stabilization of C_4N+2 molecules and anti-aromatic nature of C_4N molecules using their geometric, molecular electrostatic potential (MESP) and magnetic features for C₆ to C₃₂ molecules and then study the intermolecular C⋯C interactions in them. A study of aromatic and antiaromatic character of planar carbon rings based on their MESP features and their intermolecular bonding behaviour have not been reported in the literature. Further, the stability of these C_n molecules is compared with polyynes using homodesmotic reactions to predict their existence. Finally, ring opening reaction leading to chain structures is examined to assess the aromatic stabilization or antiaromatic destabilization of the systems.

Computational methods

The C_n molecules with n = 4N + 2 and n = 4N are optimized for n varying from 6 to 32. Dimers of molecules up to C₂₈ are also optimized. All the molecules are optimized using the meta-GGA density functional M06L³⁷ with the basis set 6-311++g(d,p). This method is shown to be very good in the study of non-covalently interacting system in an extensive benchmark study³⁸ followed by several other studies^35,36,39,40 where the results given by this method are confirmed using many reliable DFT and ab initio methods. The geometries are confirmed to be minima by frequency calculation. All the calculations have been done using Gaussian09 ⁴¹ suit of programs. Interaction energy (E_int) of a dimer is calculated by subtracting twice the energy of an isolated monomer from the energy of the dimer. Basis set superposition energy (BSSE) is calculated using Boys and Bernardi method⁴² as implemented in Gaussian09. Maps of molecular electrostatic potential (MESP)⁴³ are used for illustrating the delocalized (in C_4N+2) and localized (in C_4N) nature of electrons. Also, the intermolecular interactions are explained using the MESP features of the dimers. MESP features have been used for understanding several phenomena in chemistry^44,45 including different types of intermolecular interactions.^{35,36,46–48} The most negative value of MESP in a molecule is denoted as V_min. The position and magnitude of V_min can used for understanding the position and strength of electron rich regions such as lone pairs of molecules as well as their interactions with nucleophiles.^49–52 Here, V_min values are taken as indicators of localization/delocalization nature of π electrons in the carbon rings. Quantum theory of atoms-in-molecule (QTAIM) analysis as implemented in AIMAll software package⁵³ is used for the study of intermolecular interactions. This analysis gives (3, −1) critical point, known as bond critical points (BCPs) between two bonded atoms. The value of electron density, ρ at a BCP is considered as a measure of the strength of that bonding interaction. Nucleus-independent chemical shift (NICS),^54–56 which is the absolute magnetic shielding of the induced ring currents at the centre of rings is used for studying the aromatic/antiaromatic behaviour of a molecule. Negative value for NICS indicates aromaticity and positive value indicates antiaromaticity. Since the chemical shift values calculated at the centre of a ring namely NICS(0) can be contaminated by shielding contributions from the core as well as σ electrons, we have also calculated NICS(1),⁵⁷ observed at 1 Å above the plane of the ring, where the effect of σ electrons is reduced and the π system is maximized.⁵⁸

Results and discussion

Geometry of the carbon rings

All C_4N+2 molecules show a cumulenic structure with all the bond lengths equal while all the C_4N molecules show a clear bond length alternation with alternate shorter (formal triple) and longer (formal single) bonds. The cumulenic structure of a C_4N+2 is indicative of a delocalized π-electron distribution and aromatic stabilization. The variation of average of all the CC bond lengths in C_4N+2 molecules with n varying from 6 to 30 is represented in Fig. 1. The largest CC bond length (1.33 Å) is observed in C₆, which is decreased to 1.29 Å in C₁₀ and is almost constant (around 1.28 Å) in all other molecules. The C_4N molecules show localized triple bonds, which is a characteristic feature of antiaromatic molecules.⁵⁴ In C₈ to C₃₂, the longer (single) bond lengths vary in the range 1.39 to 1.32 Å and the shorter (triple) bonds vary from 1.27 to 1.24 Å. The variation of the average of single and triple bond lengths of all the C_4N molecules with the value of n is also shown in Fig. 1. Both single and triple bond lengths first decrease and then become almost a constant.

Fig. 1 Average bond lengths of the planar carbon rings (C_n). C_4N+2 molecules show nearly equal lengths for all the C–C bonds indicating π-electron delocalization. The C_4N molecules show alternating long and short bonds.

The bond angles are found to depend only on the ring size and not on the aromatic or antiaromatic behaviour of the molecules. To some extent, all the C_n molecules show bond angle alternation. The difference between two adjacent bond angles decreases with increase in ring size and the bond angles reaches almost the same value in larger rings. For instance, the two bond angles observed in C₆ are 154° and 86° while in C₃₂, the bond angles show only a small variation between 168° and 170°. In every C_4N+2 and C_4N systems, two symmetrically unequal sets of carbon atoms can be identified referred to herein as C_α and C_β. The C_α atoms are characterized by larger CCC angles centred on them compared to C_β. As the system size increases, the symmetrical inequality to distinguish C_α and C_β decreases. This can be attributed to the tendency for bond angle equalization in C_4N+2 leading to the formation of chemically identical environment for individual atoms as well as CC bonds. Whereas in C_4N systems, bond angle equalization suggests the tendency of all the carbon atoms in the system to remain in identical chemical environment but the bond length alternation suggests the tendency to keep two kinds of bonds in the system.

Molecular electrostatic potential (MESP)

The MESP mapped on to 0.01 au electron density surface and MESP isosurface of −0.00075 au are shown in Fig. 2 for the C_4N+2 molecules. The V_min values of all the C_n systems are given in Table 1. The MESP map of C₆ clearly shows that C_α atoms are electron deficient compared to the C_β atoms. The MESP topography of C₆ reveals a MESP minimum (V_min) value −12.14 kcal mol⁻¹ for the C_β atoms, which has the highest magnitude for V_min among all the C_n molecules studied. This indicates some amount of divalent carbene type character to these atoms due to underutilization of its electrons for π-conjugation. The inter-atomic distance between C_α carbon atoms is 1.809 Å which suggests weak interactions between them. The electron deficient nature of these carbon atoms could be attributed to the utilization of their electrons for such interactions. In C₁₀, the electron rich C_β shows V_min value of −3.53 kcal mol⁻¹, which is 8.63 kcal mol⁻¹ less negative than C₆, indicating increased delocalization of the π-electrons. In C₁₄, the bond angle alternation at C_α and C_β atoms is very small (about 10°) compared to C₆ (about 68°) and C₁₀ (about 38°) indicating a near perfect π-electron delocalization characteristic of aromatic systems. Unlike C₆ and C₁₀, the MESP isosurface map of C₁₄ does not show significant electron localization in the molecular plane whereas negative-valued MESP appears above and below the ring plane. Such a feature identified as typical of a π-electron cloud is well-known in the case of benzene. Also, the lowest magnitude for V_min among all the molecules is shown by C₁₄, indicating highly delocalized nature of π electrons. Beyond C₁₄, all higher members of C_4N+2 series show the π-electron cloud. However, unlike C₁₄, the larger rings show the influence of the π-electron in the interior central regions.

Fig. 2 MESP mapped on to 0.01 au electron density isosurface (left) and MESP isosurface (pink-coloured) at −0.00075 au of C_4N+2 molecules. Colour coding from blue to red indicates MESP values in the range −0.03 to 0.05 au.

Table 1 Values of the most negative electrostatic potential (V_min) of C_4N+2 and C_4N rings in kcal mol⁻¹

C4N+2	Vmin	C4N	Vmin
C6	−12.14	C8	−11.81
C10	−3.53	C12	−5.11
C14	−0.54	C16	−2.35
C18	−1.29	C20	−1.16
C22	−1.39	C24	−1.24
C26	−1.30	C28	−1.22
C30	−1.17	C32	−1.27

---

In the case of C_4N series, MESP features of C₈ and C₁₂ show electron rich character of C_β compared to C_α (Fig. 3). The V_min values of C₈ and C₁₂ are −11.81 and −5.11 kcal mol⁻¹, respectively. In the case of C₁₆ and other higher systems, the MESP isosurface is localized on the shorter CC bonds. The red-coloured regions in the MESP surface maps indicate electron deficient longer CC bonds. As the ring size increases, the colour contrasts indicating electron rich and electron deficient region decreases. Such an effect is more evident in C_4N+2 systems than C_4N indicating more delocalized distribution of electrons in the former than the latter. The MESP map also suggests that C_4N+2 rings possess a cumulenic carbyne structure while C_4N rings possess acetylenic carbyne structure. The acetylenic character of the latter can be correlated to the cylindrical distribution of π-electrons characterized by the MESP isosurface shaped like a ‘ring’ around the shorter CC bonds as seen in C₂₀–C₃₂.

Fig. 3 MESP mapped on to 0.01 au electron density isosurface (left) and MESP isosurface (pink-coloured) at −0.00075 au of C_4N molecules. Colour coding from blue to red indicates MESP values in the range −0.03 to 0.05 au.

Nucleus-independent chemical shift (NICS)

The NICS(0) and NICS(1) values of C_4N+2 and C_4N rings are listed in Table 2. The negative NICS values of C_4N+2 clearly illustrate their aromatic behaviour. The high values of NICS in these rings support double aromaticity, viz. one due to the conjugation of the π-electron that lie in the σ-plane and the other due to the conjugation of π-electrons orthogonal to this plane. To illustrate this point, the two delocalized π-molecular orbitals of a representative C_4N+2 system C₁₈ is shown in Fig. 4. The C_4N rings show positive NICS(0) and NICS(1), showing their anti-aromatic character. The high positive values of NICS may indicate the possibility of double antiaromatic character arising from 4N π-electrons in the σ-plane and 4N π-electrons in the plane perpendicular to the σ-plane. The localized nature of the two π-molecular orbitals of C₁₆ given in Fig. 4 supports the double antiaromatic nature of C_4N systems.

Table 2 NICS values in ppm of the C_4N+2 and C_4N rings

C4N+2	NICS(0)	NICS(1)	C4N	NICS(0)	NICS(1)
C6	−22.64	−9.30	C8	44.21	36.39
C10	−30.89	−22.82	C12	54.69	45.42
C14	−40.53	−34.10	C16	50.31	44.10
C18	−42.30	−37.94	C20	43.47	39.83
C22	−42.54	−39.52	C24	37.49	35.25
C26	−42.73	−40.51	C28	32.14	30.71
C30	−42.87	−41.18	C32	28.26	27.29

---

Fig. 4 The delocalized π-molecular orbitals of a C_4N+2 system C₁₈ (top) and the localized π-molecular orbitals of a C_4N system C₁₆ (bottom).

The magnitude of NICS(0) in C_4N+2 increases with the ring size from C₆–C₁₈ and then remains almost constant up to C₃₀. NICS(1) also follows almost similar trends. Although this data may suggest enhancement in aromaticity of a C_4N+2 ring with increase in its size up to C₁₈ and not much variation afterwards, a confirmation of this feature is difficult as NICS is ring size dependent. Therefore, we compare the NICS(0) value of C₆ (−22.64) with that of benzene (−9.7 (ref. 54)), which indeed proposes double aromatic character to the former. In the case of C_4N systems, both the NICS values are higher for C₁₂ than for C₈ and a steady decrease with further increase in size. Although this may indicate increasing stabilization of larger rings, the size dependency of NICS has to be accounted to get the true effect. Hence, we compare the NICS(0) of C₈ (44.21) with that of similar sized ring system cyclooctatetraene NICS(0) (30.1 (ref. 54)) and proposes that the former has significant double antiaromatic character.

Study of intermolecular interactions: formation of dimers

The nature of intermolecular interactions of the C_4N+2 and C_4N molecules are compared by studying their dimers. Fig. 5 displays the optimized geometries of the dimers of C_n containing 6 to 28 carbon atoms. In C_4N+2 dimers, the monomers show a shifted-parallel stacked orientation whereas in C_4N dimers, the monomers are seen in a perfect stacking arrangement. The C_4N dimer structure can be described as a sandwich type configuration wherein the shorter CC bonds orient on top of the longer CC bonds. The centre-to-centre distances and the nearest C⋯C distances in the dimers are also given in Fig. 5. These distances are almost constant in C_4N+2 dimers. The centre-to-centre distances show a slight decrease of 0.57 Å with increase in ring size from C₈ (2.77 Å) to C₂₈ (3.34 Å) in the case of C_4N dimers. The nearest C⋯C distances also possess similar values in them. The QTAIM plots of dimers of C_4N+2 and C_4N molecules are given in Fig. 6 and it clearly shows that in C_4N dimers, the monomers are connected together by a larger number of C⋯C interactions compared to C_4N+2 dimers. The interactions shown by dotted lines in Fig. 5 represent bond paths and are characterized by a bond critical point at the midpoint region. Except for C₈, the number of C⋯C interactions in a C_4N dimer is equal to the number of carbon atoms in a monomer.

Fig. 5 Optimized geometry of (a) C_4N+2 dimers and (b) C_4N dimers. The centre-to-centre distances and the nearest C⋯C distances in the dimers are given in Å.

Fig. 6 QTAIM plots of (a) C_4N+2 dimers and (b) C_4N dimers. Dotted lines indicate bond paths for the C⋯C interactions.

The MESP map of C_n dimers given in Fig. 7 can explain the difference in intermolecular bonding behaviour in C_4N and C_4N+2 rings. As shown previously, the monomers of C_4N rings are clearly partitioned into electron rich and electron deficient regions. When these molecules form dimers, the electron rich regions on one monomer faces the electron deficient regions of the other to obtain maximum complimentary electrostatic interactions, which leads to large number of intermolecular C⋯C interactions. In C_4N+2 rings, partitioning of the monomers into electron rich and electron deficient regions is not clearly demarcated due to double aromaticity and leads to fewer number of C⋯C interactions, lower interaction energy and lower tendency towards dimer formation ​ compared to C_4N systems.

Fig. 7 MESP mapped on to 0.01 au isosurface of dimers of (a) C_4N+2 and (b) C_4N. Colour coding from blue to red indicates MESP values in the range −0.03 to 0.05 au.

The interaction energies (E_int) and average electron density at intermolecular bond critical points (ρ_ave) of each of the C_n dimers are given in Table 3. In C_4N+2 dimers, the magnitude of E_int shows a steady increase from C₆ (−2.23 kcal mol⁻¹) to C₂₆ (−11.77 kcal mol⁻¹). The ρ_ave values are almost similar in all the C_4N+2 dimers (a small variation between 0.0049 and 0.0057 au) indicating similar strength of intermolecular C⋯C interactions in all of them. On the other hand, in C_4N dimers, the largest magnitude for E_int is shown by dimers of the smallest rings, viz. C₈ (−23.31 kcal mol⁻¹) and C₁₂ (−21.80 kcal mol⁻¹). The magnitude of E_int decreases up to C₂₀ and then shows a steady increase for C₂₄ and C₂₈. This trend of E_int values is the result of a balance between the number of C⋯C interactions and the strength of individual C⋯C interactions. The ρ_ave values show that C₈ (ρ_ave = 0.0179 au) and C₁₂ (ρ_ave = 0.0113 au) dimers possess the strongest C⋯C interactions as they show the highest amount of charge separation in terms of MESP features. The value of ρ_ave gradually decreases from 0.0179 au in C₈ to 0.0056 au in C₂₈ as the ring size increases. The ρ_ave value of C₂₄, 0.0058 au is close to that of C₂₈ and suggests that with further increase in ring size, the ρ_ave value may not undergo substantial changes. Since the number of C⋯C interactions is equal to 4N in C_4N dimers, an increase in the ring size beyond C₂₈ is bound to increase the total interaction energy. The presence of a large number of intermolecular C⋯C interactions in C_4N molecules also supports our previous studies^35,36 that a clear demarcation of electron rich and electron deficient regions in molecules can result in intermolecular complimentary electrostatic interactions between even chemically similar atoms.

Table 3 Interaction energy (E_int) and average of electron density (ρ_ave) at intermolecular BCPs corresponding to C⋯C interactions of C_4N+2 and C_4N dimers

C4N+2	Eint (kcal mol^−1)	ρave (au)	C4N	Eint (kcal mol^−1)	ρave (au)
C6	−2.23	0.0053	C8	−23.31	0.0179
C10	−5.20	0.0049	C12	−21.80	0.0113
C14	−6.92	0.0057	C16	−15.83	0.0092
C18	−8.32	0.0055	C20	−15.39	0.0061
C22	−9.98	0.0049	C24	−16.88	0.0058
C26	−11.77	0.0049	C28	−18.27	0.0056

---

Though the presence of a BCP may not always indicate a bonding situation,^59,60 analysis of molecular orbitals (MOs) suggests strong orbital overlap between the two monomers in C_4N dimers. Occupied MOs corresponding to the C⋯C interactions in C₁₆ are given in Fig. 8 as a typical example for the C_4N systems. On the other hand, C_4N+2 systems show very few such MOs corresponding to C⋯C interactions. For e.g., C₁₈ shows only one such MO (ESI†).

Fig. 8 Occupied MOs corresponding to the inter-molecular C⋯C interactions in C₁₆ plotted at 0.02 au isosurface.

Band gap of C_n systems

The HOMO–LUMO gap of C_n systems are given in Fig. 9. This gap in C_4N+2 shows a steady decrease with increase in ring size suggesting increased degree of delocalization in the larger systems, except in the case of C₆. In C₆, the three inner lying carbons mutually interact at the CC distance 1.809 Å. These additional bonding interactions changes the nature of the HOMO and LUMO states compared to the other systems. The HOMO–LUMO gap value decreases from 4.31 eV in C₁₀ to 1.44 eV in C₃₀. Though small, a decrease in band gap is observed in C_4N rings, on going from C₈ (1.36 eV) to C₃₂ (0.84 eV).

Fig. 9 Band gap of C_4N+2 and C_4N molecules.

Homodesmotic reactions leading to polyynes

The stability of the cyclic C_n molecules has been assessed on the basis of energy of hypothetical homodesmotic reactions. In these reactions, a C_n ring reacts with acetylene to form a polyyne (Fig. 10). The hybridization state of all the atoms, number of CC bonds and number of CH bonds are conserved in the reaction. However, the aromatic/antiaromatic character of the ring and the associated strain effects are not conserved in the product side of the reaction. Therefore the energy of the reaction gives a direct estimate of the total stabilizing/destabilizing effect of the molecule from aromatic/antiaromatic character and strain in the ring structures.

Fig. 10 Hypothetical homodesmotic reaction between C₁₈ and acetylene to form linear C₂₀H₂ (10yne).

Table 4 gives the energy of the homodesmotic reactions (E_hdr) for C_4N+2 and C_4N rings. All the reactions are exothermic suggesting that the ring systems are less stable than the linear configurations. For smaller rings, the reaction is expected to be more exothermic due to larger strain effects. The energy released in the reaction (E_hdr) could be used as a measure of the stability of the ring structure with respect to the stability of the linear structure. If ring strain is the only effect contributing to the relative stability of these cyclic molecules, one would expect the highest exothermicity in the smallest ring, C₆. However, from the Table 4, it is clear that the reaction of C₈ is more exothermic by 16.5 kcal mol⁻¹ compared to that of C₆. Similarly, the reactions of the C_4N systems, viz. C₁₂, C₁₆ and C₂₀ with acetylene are more than 20 kcal mol⁻¹ exothermic compared to those of the smaller sized C_4N+2 systems, viz. C₁₀, C₁₄ and C₁₈ respectively. In fact, E_hdr of C₁₀ is comparable to that of C₁₆. The C_4N appears to be far more unstable than C_4N+2 as the former is doubly antiaromatic while the latter is doubly aromatic. For both the sets, the magnitude of E_hdr decreases as the ring size increases, which can be attributed to decrease in ring strain with increase in ring size. Except in the case of the smallest rings (i.e., C₆ and C₈), the difference in E_hdr between each set of C_4N+2 and the next higher C_4N are lowered compared to the preceding set. For instance, the difference in E_hdr between C₁₀ and C₁₂ is 28.39 kcal mole⁻¹, between C₁₄ and C₁₆ is 25.99 kcal mol⁻¹ and between C₃₀ and C₃₂ is 9.88 kcal mol⁻¹. This observation supports the assumption that at sufficiently large size of the ring, both kinds of molecules may show non aromatic character. The difference in the value of E_hdr between C₆ and C₈ is very small compared to that between C₁₀ and C₁₂, which can be attributed to the instability caused by high ring strain in C₆. The results show that these ring systems are thermodynamically less stable compared to polyyne molecules.

Table 4 Energy of formation of polyynes from C_n rings and acetylene (E_hdr, in kcal mol⁻¹)

Reactants	Product	Ehdr	Reactants	Product	Ehdr
C6 + C2H2	4yne	−130.01	C8 + C2H2	5yne	−146.54
C10 + C2H2	6yne	−77.52	C12 + C2H2	7yne	−105.91
C14 + C2H2	8yne	−55.35	C16 + C2H2	9yne	−81.34
C18 + C2H2	10yne	−41.74	C20 + C2H2	11yne	−62.33
C22 + C2H2	12yne	−33.27	C24 + C2H2	13yne	−49.35
C26 + C2H2	14yne	−27.55	C28 + C2H2	15yne	−40.14
C30 + C2H2	16yne	−23.53	C32 + C2H2	17yne	−33.41

---

Opening up of carbon rings to linear carbon chains

A C_n carbon ring is isomeric to a linear C_n carbon chain. The former with n C–C bonds is expected to be more stable compared to the latter with n − 1 C–C bonds. The ring structure experiences destabilizing ring strain effect. Aromaticity is another factor that controls the stability. Therefore, the energy of a reaction (E_opening) that addresses the opening up of the ring structure of a C_4N or C_4N+2 system to the corresponding chain structure (Fig. 11) is very useful to compare their stability.

Fig. 11 Opening of cyclic C18 to linear C18.

In the case of C_4N+2 rings, the extra stabilization due to aromaticity will be lost while in C_4N, the destabilizing antiaromaticity will disappear due to ring opening. Therefore, opening up of a C_4N+2 ring will be thermodynamically more difficult compared to that of a C_4N ring. In both the cases, the ring strain effect will work in favour of the forward direction of the reaction. E_opening of both C_4N and C_4N+2 rings are given in Table 5. This data suggests that as the ring size increases, the stability of the ring increases which is graphically illustrated in Fig. 12. In the case of C₆, the ring opening is endothermic by 22.8 kcal mol⁻¹ while the value of E_opening of C₈ is only 0.8 kcal mol⁻¹. Similarly all the smaller rings, viz. C₁₀, C₁₄, C₁₈, C₂₂, C₂₆ and C₃₀ with C_4N+2 character give higher endothermic reactions than the larger rings with C_4N configuration, viz. C₁₂, C₁₆, C₂₀, C₂₄, C₂₈ and C₃₂, respectively. In fact, if C_4N behave similar to C_4N+2, the expected E_opening would be significantly higher (the data labelled using white squares in Fig. 12) than the actual values. Similarly, if C_4N+2 behave like C_4N, the expected E_opening would be much lower (the data labelled using the white circles). The ‘aromatic’ and ‘antiaromatic’ curves plotted in Fig. 12 are useful to derive a ‘non aromatic’ curve which is assumed to pass through the mid region of these two curves. This assumption is helpful to make a rough estimate about aromatic stabilization of a C_4N+2 ring or the antiaromatic destabilization of C_4N ring. The data in Fig. 12 suggest that C₆, C₁₀, C₁₄, C₁₈, C₂₂, C₂₆, and C₃₀ are stabilized by 21.9, 23.3, 18.1, 14.5, 11.0, 8.1 and 6.7 kcal mol⁻¹ due to aromaticity while C₈, C₁₂, C₁₆, C₂₀, C₂₄, C₂₈ and C₃₂ are destabilized by 22.7, 21.1, 17.0, 12.7, 9.7, 7.3 and 5.6 kcal mol⁻¹ due to antiaromaticity. This data further indicate that as the ring size increases (one exception is C₁₀), stabilization/destabilization due to aromaticity/antiaromaticity decreases and the energetics of the system may favour a non aromatic state at sufficiently large size. However, the NICS values support this conclusion only for C_4N systems. For C_4N+2 systems, these values indicate highly aromatic character even at larger sizes.

Table 5 The energy required for ring opening (E_opening) in kcal mol⁻¹ of C_4N and C_4N+2 rings

C4N+2	Eopening	C4N	Eopening
C6	22.84	C8	00.79
C10	66.38	C12	35.56
C14	84.34	C16	57.08
C18	95.66	C20	74.27
C22	102.72	C24	86.17
C26	107.62	C28	94.75
C30	111.09	C32	101.05

---

Fig. 12 The variation in E_opening with number of carbon atoms in aromatic and antiaromatic C_n rings.

Conclusions

C_n rings (from n = 6–32) with even number of carbon atoms have been studied for their aromatic and dimer formation features using the DFT method M06L. The geometric, electrostatic, magnetic and energetic features indicated strong aromatic stabilization in C_4N+2 rings and strong antiaromatic character in C_4N rings. The C_4N+2 systems showed cumulenic structures with all the bond lengths being equal while the C_4N rings possessed acetylenic structures with clear bond length alternation. The MESP features clearly indicated delocalization of π-electrons and aromaticity in C_4N+2 rings while electron localization around the shorter CC bond (formal triple bond) in C_4N rings as visualized from MESP proposed their antiaromaticity. The NICS analysis showed high negative values in C_4N+2 and high positive values in C_4N. The magnitude of these values was much higher than similar sized aromatic hydrocarbons and indicated double aromatic/antiaromatic features of the corresponding C_n rings. With increase in the ring size, the magnitude of NICS in a C_4N+2 ring increased while those of C_4N ring decreased, both indicating stabilization, which is attributed mainly to the decrease in ring strain effects. Hypothetical homodesmotic reactions and ring opening reactions have been used to quantify the higher stability of C_4N+2 rings over C_4N rings. The C_n rings are thermodynamically less stable compared to the corresponding polyyne systems which is accounted by the ring strain effect in the former. As the ring size increases, the destabilizing strain effect decreases and the stability of a C_n ring approaches close to that of a polyyne. In fact, the aromatic C_4N+2 systems such as C₁₄, C₁₈, C₂₂, C₂₆ and C₃₀ possessing a smooth MESP distribution should be targeted for synthesis.

The difference in geometric features has a clear effect in the dimer formation behaviour of C_4N+2 and C_4N rings. The dimer of C_4N+2 always showed significantly lower magnitude of E_int compared to the dimer of a C_4N ring. C_4N+2 with equal bond lengths and a well delocalized system of π electrons have very low tendency to form dimers compared to C_4N. The number and strength of intermolecular C⋯C interactions are also very less in C_4N+2 dimers due to the lack of intermolecular complimentary electrostatic interactions. On the other hand, the very high magnitude of E_int observed for C_4N could be correlated to the large number (equal to the number of carbon atoms in the monomer, except for C₈) of inter-molecular C⋯C interactions as seen in the QTAIM analysis. These interactions, resulting from complimentary electrostatic interactions between electron rich formal triple bond regions of one monomer with the relatively electron deficient region of the second give rise to perfect stacking sandwich type arrangement of the monomers in a C_4N dimer. The fact that the C_4N dimers possess large number of C⋯C interactions supports our previous studies^35,36 that separation of electron rich and electron deficient regions in a molecule can result in the formation of intermolecular C⋯C bonding interaction between atoms in similar chemical environments.

Acknowledgements

This research is supported by the Council of Scientific and Industrial Research (CSIR), Govt. of India, through a project CSC0129. K. R. is thankful to CSIR, India, for providing a senior research fellowship.

References

1. J. Hunter, J. Fye and M. F. Jarrold, Science, 1993, 260, 784–786.
2. R. O. Jones, J. Chem. Phys., 1999, 110, 5189–5200.
3. S. Tongay, S. Dag, E. Durgun, R. T. Senger and S. Ciraci, J. Phys.: Condens. Matter, 2005, 17, 3823–3836.
4. A. Van Orden and R. J. Saykally, Chem. Rev., 1998, 98, 2313–2358.
5. J. Hutter, H. P. Luethi and F. Diederich, J. Am. Chem. Soc., 1994, 116, 750–756.
6. G. von Helden, M. T. Hsu, N. Gotts and M. T. Bowers, J. Phys. Chem., 1993, 97, 8182–8192.
7. S. Irle, G. Zheng, Z. Wang and K. Morokuma, J. Phys. Chem. B, 2006, 110, 14531–14545.
8. W.-H. Lin, C.-C. Tu and S.-L. Lee, Int. J. Quantum Chem., 2005, 103, 355–368.
9. K. M. Rama, Y.-T. Lin and S.-L. Lee, Int. J. Quantum Chem., 2001, 84, 642–648.
10. J. M. Hunter, J. L. Fye, E. J. Roskamp and M. F. Jarrold, J. Phys. Chem., 1994, 98, 1810–1818.
11. H. Schwarz, Angew. Chem., Int. Ed., 1993, 32, 1412–1415.
12. N. S. Goroff, Acc. Chem. Res., 1996, 29, 77–83.
13. G. von Helden, M. T. Hsu, P. R. Kemper and M. T. Bowers, J. Chem. Phys., 1991, 95, 3835–3837.
14. R. O. Jones and G. Seifert, Phys. Rev. Lett., 1997, 79, 443–446.
15. J. M. Hunter, J. L. Fye and M. F. Jarrold, J. Chem. Phys., 1993, 99, 1785–1795.
16. T. Giesen, A. Van Orden, H. Hwang, R. Fellers, R. Provencal and R. Saykally, Science, 1994, 265, 756–759.
17. S. Tongay, R. T. Senger, S. Dag and S. Ciraci, Phys. Rev. Lett., 2004, 93, 136404.
18. F. A. Fernandéz-Lima, C. R. Ponciano, E. F. da Silveira and M. A. C. Nascimento, Chem. Phys. Lett., 2007, 445, 147–151.
19. K. Raghavachari and J. S. Binkley, J. Chem. Phys., 1987, 87, 2191–2197.
20. K. B. Shelimov, J. M. Hunter and M. F. Jarrold, Int. J. Mass Spectrom. Ion Processes, 1994, 138, 17–31.
21. G. von Helden, N. G. Gotts, P. Maitre and M. T. Bowers, Chem. Phys. Lett., 1994, 227, 601–608.
22. N. G. Gotts, G. von Helden and M. T. Bowers, Int. J. Mass Spectrom. Ion Processes, 1995, 149–150, 217–229.
23. V. A. Schweigert, A. L. Alexandrov, Y. N. Morokov and V. M. Bedanov, Chem. Phys. Lett., 1995, 238, 110–115.
24. T. Wakabayashi, M. Kohno, Y. Achiba, H. Shiromaru, T. Momose, T. Shida, K. Naemura and Y. Tobe, J. Chem. Phys., 1997, 107, 4783–4787.
25. E. J. Bylaska, J. H. Weare and R. Kawai, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, R7488–R7491.
26. M. Saito and Y. Okamoto, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 8939–8942.
27. T. Torelli and L. Mitas, Phys. Rev. Lett., 2000, 85, 1702–1705.
28. V. I. Minkin, M. N. Glukhovtsev and B. I. A. Simkin, Aromaticity and antiaromaticity: electronic and structural aspects, J. Wiley & Sons, 1994.
29. J. Chandrasekhar, E. D. Jemmis and P. von Ragué Schleyer, Tetrahedron Lett., 1979, 20, 3707–3710.
30. E. J. Bylaska, R. Kawai and J. H. Weare, J. Chem. Phys., 2000, 113, 6096–6106.
31. S.-h. Xu, M.-y. Zhang, Y.-y. Zhao, B.-g. Chen, J. Zhang and C.-C. Sun, Chem. Phys. Lett., 2006, 421, 444–447.
32. M. D. Wodrich, C. Corminboeuf, S. S. Park and P. v. R. Schleyer, Chem.–Eur. J., 2007, 13, 4582–4593.
33. P. W. Fowler, N. Mizoguchi, D. E. Bean and R. W. A. Havenith, Chem.–Eur. J., 2009, 15, 6964–6972.
34. S. Sen, P. Seal and S. Chakrabarti, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 245401.
35. K. Remya and C. H. Suresh, Phys. Chem. Chem. Phys., 2015, 17, 18380–18392.
36. K. Remya and C. H. Suresh, Phys. Chem. Chem. Phys., 2015, 17, 27035–27044.
37. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
38. K. Remya and C. H. Suresh, J. Comput. Chem., 2013, 34, 1341–1353.
39. N. Mohan and C. H. Suresh, Int. J. Quantum Chem., 2014, 114, 885–894.
40. K. Remya and C. H. Suresh, J. Comput. Chem., 2014, 35, 910–922.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. FoxGaussian 09, Revision C.01, Gaussian, Inc.: Wallingford CT, 2010.
42. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
43. S. R. Gadre and R. N. Shirsat, Electrostatics of Atoms and Molecules, Universities Press, Hyderabad, India, 2000.
44. J. S. Murray, K. Paulsen and P. Politzer, Proc.–Indian Acad. Sci., Chem. Sci., 1994, 106, 267–275.
45. P. Sjoberg and P. Politzer, J. Phys. Chem., 1990, 94, 3959–3961.
46. T. Clark, M. Hennemann, J. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296.
47. J. Murray, P. Lane and P. Politzer, J. Mol. Model., 2009, 15, 723–729.
48. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189.
49. J. Tomasi, B. Mennucci and R. Cammi, A Tool for Interpretation and Prediction. From Molecular Structure to Solvation Effects, in Molecular Electrostatic Potentials: Concepts and Applications, Elsevier, Amsterdam, 1996.
50. S. R. Gadre, P. Bhadane, S. S. Pundlik and S. S. Pingale, Molecular Electrostatic Potentials: Concepts and Applications, in Molecular Electrostatic Potentials: Concepts and Applications, Elsevier, Amsterdam, 1996.
51. S. R. Gadre and S. S. Pundlik, J. Phys. Chem. B, 1997, 101, 3298–3303.
52. A. Kumar, S. R. Gadre, N. Mohan and C. H. Suresh, J. Phys. Chem. A, 2014, 118, 526–532.
53. T. A. KeithAIMAll (Version 14.04.17); TK Gristmill Software, Overland Park KS, USA, 2014.
54. P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318.
55. J. Poater, M. Duran, M. Solà and B. Silvi, Chem. Rev., 2005, 105, 3911–3947.
56. F. Feixas, E. Matito, J. Poater and M. Sola, Chem. Soc. Rev., 2015, 44, 6434–6451.
57. P. v. R. Schleyer, H. Jiao, N. J. R. v. E. Hommes, V. G. Malkin and O. L. Malkina, J. Am. Chem. Soc., 1997, 119, 12669–12670.
58. C. Foroutan-Nejad, S. Shahbazian and P. Rashidi-Ranjbar, Phys. Chem. Chem. Phys., 2010, 12, 12630–12637.
59. J. Poater, M. Solà and F. M. Bickelhaupt, Chem.–Eur. J., 2006, 12, 2889–2895.
60. J. Poater, M. Solà and F. M. Bickelhaupt, Chem.–Eur. J., 2006, 12, 2902–2905.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra06833b

---