Self-assembled π-conjugated organic nanoplates: from hexagonal to triangular motifs†
Abstract
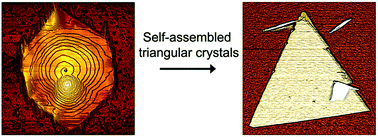
Organic semiconducting materials in confined geometries present interesting properties connected to change or the coexistence of molecular organizations, depending on their characteristic scales. In this work the preparation and structural characterization of self-assembled π-conjugated organic nanoplates of 2,7-diperfluorohexyl-[1]benzothieno[3,2,b]benzothiophene are studied. These nanostructures were prepared by spin coating, implementing a fast precipitation method. We observed an evolution of the nanostructures from hexagonal towards triangular nanoplates, possibly driven by enhanced solvent/molecule interactions, and accompanied by the formation of a new polymorph.

 Please wait while we load your content...
Please wait while we load your content...