Synthesis of hierarchical cobalt dendrites based on nanoflake self-assembly and their microwave absorption properties†
Xiaolei Wang*ab,
Guimei Shia,
Fa-Nian Shi*a,
Ge Xua,
Yuanyang Qia,
Da Lib,
Zhidong Zhangb,
Yajing Zhangc and
Hongpeng Youd
aSchool of Science, Shenyang University of Technology, 110870 Shenyang, PR China. E-mail: xlwang@alum.imr.ac.cn; fshi96@foxmail.com
bShenyang National Laboratory for Materials Science, Institute of Metal Research, and International Centre for Materials Physics, Chinese Academy of Sciences, Shenyang 110016, PR China
cCollege of Chemical Engineering, Shenyang University of Chemical Technology, Shenyang 110142, PR China
dState Key Laboratory of Rare Earth Resource Utilization, Changchun Institute of Applied Chemistry, Chinese Academy of Sciences, Changchun 130022, PR China
First published on 19th April 2016
Abstract
Three dimensional (3D) cobalt dendritic architectures composed of nanoflakes have been successfully fabricated by a facile hydrothermal self-assembly route. This method includes the preparation of cobalt dendritic architectures in a solution of cobalt chloride (CoCl2·6H2O) and sodium hydroxide (NaOH) at 110 °C for 24 h using pyromellitic acid (C10H6O8) as the complex agent and sodium hypophosphite (NaH2PO2·H2O) as the reducing agent. The crystal structure, morphology, and microwave absorption properties of the as-prepared samples were characterized by X-ray diffraction (XRD), X-ray photoelectron spectra (XPS), scanning electron microscopy (SEM), and a network analyzer. The results show that reaction parameters, such as the molar ratio of C10H6O8 to CoCl2·6H2O, and concentration of NaOH, play a crucial effect on the morphology of the products. A plausible mechanism for the formation of hierarchical cobalt dendrites based on the Ostwald ripening process is proposed. The Co dendrite–paraffin composite containing 65 wt% of Co dendrites shows excellent microwave absorption properties. The optimal reflection loss (RL) of −30.2 dB is obtained at 12.5 GHz and RL below −10 dB covers the frequency range of 10.5–14.5 GHz with a thickness of 1.5 mm. The maximum RL values can reach −35.6 dB at 5.6 GHz with a thickness of 3 mm and the effective bandwidth (RL < −10 dB) is up to 11.8 GHz, in the frequency range of 2.7–14.5 GHz by adjusting the thickness of 1.5–5 mm. The excellent microwave absorption properties can be attributed to multiple dielectric relaxation and magnetic resonances, which contribute to proper impendence matching and a microwave attenuation constant. These results show that the 3D cobalt dendritic architecture is a great candidate for microwave absorption applications.
1. Introduction
In recent years, with the rapid development of communication tools and electronic devices in commercial, industrial, and military applications at high frequency, serious electromagnetic interference problems have been apparent issues in both military and civil applications.1–3 Thus, great efforts have been devoted towards exploring electromagnetic (EM) wave absorption materials.4–7 Such as dielectric loss-based carbon nanochains,8 SiC nanowires,9 BaTiO3 nanotubes,10 flower CuS architectures,11 and magnetic loss-based Ni nanowires,12 Fe dendrites,13 and dielectric/magnetic loss-based carbon nanotubes/Fe nanocomposites,14 Ni/polyaniline,15 FeCo/C/BaTiO3 nanocomposites,16 graphene@Fe3O4@SiO2@NiO nanosheet architectures.17Among the candidates of EM wave absorbents, ferromagnetic metal particles have attracted great interest due to its higher complex permittivity than ferrites.18 However, ferromagnetic metallic materials have high electric conductivity, which makes the effective permeability in high frequency attenuate drastically because of the skin effect.19 In order to avoid eddy current induced by EM wave in higher frequency, many efforts have been paid for the development of ferromagnetic metallic absorbents with the microstructures characterization such as a size less than the skin depth, a large specific surface area, and more dangling chemical bonds. For examples, one-dimension Ni chains prepared by Zhao and co-workers20 exhibited the maximum reflection loss of −19.9 dB at 17.2 GHz with a thickness of 0.8 mm and the absorption bandwidth below −10 dB was up to 4.3 GHz in the high frequency range of 13.7–18.0 GHz by adjusting the thickness of 0.8–1.0 mm. Zhen and co-workers21 prepared two-dimension hexagonal Fe microflakes, and the maximum reflection loss reached −15.3 dB at 14 GHz with a thickness of 1.1 mm, while the absorption bandwidth with reflection loss lower than −10 dB was about 4.4 GHz (12.2–16 GHz). Porous coin-like iron prepared by Ji groups22 had the maximum reflection loss of −53.2 dB at 16 GHz and the effective frequency bandwidth with reflection loss lower than −10 dB was up to 6.3 GHz (11.7–18 GHz) at a thickness of 1.4 mm. Sun and co-workers23 synthesized hierarchical Fe dendrites and the maximum reflection loss was −22.5 dB at 5.8 GHz with a thickness of 1.5 mm. He and co-workers24 prepared hollow porous Co spheres showing efficient EM wave absorption characteristics (reflection loss lower than −20 dB) in the ranges of 11.3–18.0 GHz over absorber thicknesses of 1.4–2.0 mm. All of the above investigations show that the enhanced EM wave absorption properties of ferromagnetic metallic nanomaterials combining lightweight and wide absorption bandwidth can be achieved by accurate constructing their size and preferable microstructures.
Rational design and fabrication of hierarchical architectures self-assembled by inorganic building blocks generally bring collective physical and chemical properties, which is deeply depended on their dimensions, spacing, and high-ordering microstructures, and the investigation of crystal growth kinetics can supply a crucial insight to control the creation of inorganic building blocks and their ordered self-assemblies and optimize their optical, electrical, magnetic, catalytic, and other related properties.25–30 A dendrite is a kind of hierarchical structures that has a main stem from which many side branches grow out and a hierarchical architecture with primary, secondary, tertiary, and even higher-order branches, and this unique microstructure with large specific surface areas can be beneficial for enhancing the EM wave absorption.18,23 A variety of wet chemical methods have been exploited to fabricate hierarchical architectures based on different driving mechanisms including surface tension, capillary effects, electromagnetic forces, and hydrophobic interactions.31–34 As an effective strategy, hydrothermal route has aroused more attentions because it is simple and inexpensive for large-scale preparation.35 However, as the chemical reaction occurring in this high-temperature and high-pressure system is quite complicated and uncontrollable, it is still a big challenge to develop simple, efficient and reliable synthetic methods for hierarchically self-assembled architectures with designed chemical components and controlled morphologies.
In the present work, we reported the synthesis of three-dimensional (3D) hierarchical Co dendrites with a main stem and several secondary branches composed of pentagonal-like building blocks by a simple, efficient, and morphologically controllable hydrothermal self-assembly route. Compared with other Co microwave absorption nanomaterials, the advantages of Co dendrites are as follows: (1) hierarchical architectures with pentagonal-like building blocks oriented self-assembly layer by layer possess abundant of grain boundary, which can induce the stronger intrinsic electric dipole polarization and grain boundary polarization (2) Co dendrites possess abundant of secondary branches and a large numbers of interface polarization between Co dendrites and paraffin can be formed. (3) Co dendrites conductive networks can be easily formed because the plenty of branches can extend to three-dimensional space supplying the channels for electron transport. (4) Sheet-like building blocks, which can exceed the Snoek's limit due to the high shape anisotropy, would induce good microwave absorption properties.36 A possible growth mechanism for the 3D hierarchical Co dendrites was proposed based on experimental analysis. The maximum RL values can reach −35.6 dB at 5.6 GHz with a thickness of 3 mm and the effective bandwidth (RL < −10 dB) is up to 11.8 GHz, in the frequency range of 2.7–14.5 GHz by adjusting the thickness of 1.5–5 mm. Moreover, the optimal microwave absorption properties is −30.2 dB at 12.5 GHz covering 10.5–14.5 GHz frequency range (RL < −10 dB) with a thickness of 1.5 mm. These results indicated that 3D hierarchical Co dendrites had the features of light weight, thin thickness, strong absorption, and broad bandwidth, which meet the current requirement of EM wave absorbents.
2. Experimental details
2.1 Preparation of hierarchical Co dendrites
All reagents in analytic grade were purchased from commercial company and used as received without any further purification. In a typical process, 1 mmol of CoCl2·6H2O, 2 mmol of C10H6O8, and 12 mmol NaOH were first dissolved in distilled water (35 mL), and the solution was constantly stirred for 40 min at room temperature. After addition of 24 mmol of NaH2PO2·H2O, the solution was constantly stirred for another 40 min and then was transferred into Teflon-lined stainless steel autoclave of 50 mL capacity. The autoclave was sealed and maintained at 110 °C for 24 h and then cooled down to room temperature naturally. The resulting products were collected by magnetic separation and sequentially washed with distilled water and ethanol for several times and finally dried in a vacuum oven at room temperature over night.2.2 Characterizations
The phases of the products were identified by using powder X-ray diffraction (XRD) on a D/Max 2200 diffractometer at a voltage of 40 kV with Cu Kα radiation (λ = 0.15406 nm). The surface compositions were investigated by X-ray photoelectron spectroscopy (XPS, ESCALAB-250). The morphology and size were investigated by scanning electron microscopy (SEM) with a JEOL-6490 scanning electron microscope operated at an acceleration voltage of 20 kV. HRTEM images were observed on a JEOL 2100F with an emission voltage of 200 kV. The hierarchical Co powders/paraffin composite samples were prepared by uniformly mixing the hierarchical Co dendrites in a paraffin matrix, and then pressing the mixture into a cylindrical-shaped compact with an outer diameter of 7.00 mm and inner diameter of 3.04 mm. The complex permittivity and permeability of the composites were measured between 1 and 18 GHz on a vector network analyzer (Agilent E5071C) and the reflection loss (RL) at different frequencies and thickness was calculated using the measured εr and μr according to the transmission line theory.3. Results and discussion
The typical XRD pattern of the hierarchical cobalt dendrites is shown in Fig. 1(a). All of the diffraction peaks of the products can be well indexed to a pure hexagonal close-packed (hcp) phase Co and are consistent with the standard card JCPDS no. 05-0727 (space group P63/mmc; a = 2.503 Å; c = 4.060 Å). No additional peaks for other phase can be found and the intense diffraction peaks confirm the well crystallization of the products. The average crystallite size of the products can be estimated from the Scherrer equation, d = kλ/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where d is the average diameter of crystal grain, k is a particle shape factor and taken as 0.9 for spherical nanoparticles, λ is the wavelength of Cu Kα radiation, θ is the corresponding Bragg angle, and β is the angular half-width of the diffraction peak at 2θ. The average grain size is estimated to be 19 nm. Fig. 1(b) shows the binding energy of Co 2p3/2 electron in the products for different etching time. The photoelectron peak at 781.2 eV belongs to the Co 2p3/2 in CoO, indicating the surface oxidation of Co products. When the etching time is 30 s, the location of photoelectron peak is shifted into low binding energy, which can be attributed to the decrease of CoO contents in the products. The sharp photoelectron peak at 778.3 eV for the etching time of 60 s is clearly observed and belongs to the Co 2p3/2 in Co. From XRD and XPS analysis, it demonstrates that the slight surface oxidation of Co dendrites occurs with trace amount of CoO.
θ, where d is the average diameter of crystal grain, k is a particle shape factor and taken as 0.9 for spherical nanoparticles, λ is the wavelength of Cu Kα radiation, θ is the corresponding Bragg angle, and β is the angular half-width of the diffraction peak at 2θ. The average grain size is estimated to be 19 nm. Fig. 1(b) shows the binding energy of Co 2p3/2 electron in the products for different etching time. The photoelectron peak at 781.2 eV belongs to the Co 2p3/2 in CoO, indicating the surface oxidation of Co products. When the etching time is 30 s, the location of photoelectron peak is shifted into low binding energy, which can be attributed to the decrease of CoO contents in the products. The sharp photoelectron peak at 778.3 eV for the etching time of 60 s is clearly observed and belongs to the Co 2p3/2 in Co. From XRD and XPS analysis, it demonstrates that the slight surface oxidation of Co dendrites occurs with trace amount of CoO.
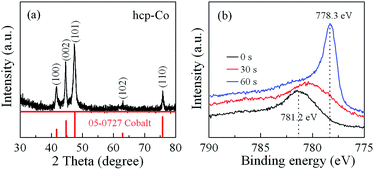 | ||
| Fig. 1 (a) XRD pattern and of Co products; (b) XPS spectra of Co products for Co 2p3/2 at the surface for different etching time. | ||
The morphology of the hierarchical cobalt dendritic architecture is characterized by SEM, as shown in Fig. 2. Fig. 2(a) shows the low-magnification SEM image of products. It is obvious that the hierarchical cobalt dendrites have high uniformity of 3–6 μm in length. Fig. 2(b) and (c) displays the high-magnification SEM image of the as-prepared products. Each cobalt dendrite is composed of three parts: a main stem, bulky secondary branches, and many pentagonal-like building blocks. The secondary branches, with length of 2–4 μm and width of ca. 1 μm, are closely attached to the main stem and separated from each other at the tip. Moreover, the pentagonal-like building blocks with the average particle size of ca. 300 nm have tightly connected with each other and induce bulky secondary branches. Furthermore, the clear atomic lattice fringe could be observed from the HRTEM image (inset in Fig. 2(a)) and the interlayer distance is calculated to be ca. 0.202 and 0.244 nm, which well agree with the (002) interplanar spacing of Co and (111) plane of CoO, respectively, and are consistence with the analysis of XRD and XPS spectrum. In short, the morphologies and sizes of the products obtained from Fig. 2 confirm that our samples belong to a 3D hierarchical Co architecture.
 | ||
| Fig. 2 (a) Low-magnification and (b) and (c) high-magnification SEM images of the hierarchical cobalt dendritic architecture. Inset image in (a): HRTEM pattern of Co dendrites. | ||
To verify the effect of different reaction conditions on the formation and morphology of products, a series of controllable experiments were carried out with other reaction parameters unchanged. Fig. 3 demonstrate the effect of molar ratio of C10H6O8 to CoCl2·6H2O (represented by H4ma/Co2+ ratio) in the solution on the morphology of the resulting Co products. In the absence of C10H6O8 (i.e., H4ma/Co2+ = 0), the products are mainly comprised of an irregular aggregation of spherical particles with some polyhedrons (Fig. 3(a)). When the H4ma/Co2+ ratio is increased to 0.5 and 1, hierarchical Co dendritic structures are gradually formed, as shown in Fig. 3(b) and (c). Well-defined hierarchical Co dendrites can be prepared at an optimal H4ma/Co2+ ratio of 2 shown in Fig. 2. Further increasing the H4ma/Co2+ ratio, for example, to 2.5, not only spherical aggregates but also the hierarchical architectures with sword-like leaves can be observed. The results reveal that the morphology of the resulting Co products are controlled by changing the ration of H4ma/Co2+. As one of important ligands, C10H6O8, which is capable of coordinating with Co2+, Ni2+, and Cd2+ ions to form the corresponding complex, has been reported previously.37,38 In the solution, the complex Co(C10H2O8)2− is firstly produced in an excess amount of C10H6O8, and then the redox reaction occurs during the hydrothermal reaction process, which can be expressed as follows:
| Co(C10H2O8)2− + H2PO2− + OH− = Co + C10H4O82− + HPO32− | (1) |
 | ||
| Fig. 3 SEM images of cobalt products prepared at different molar ratios of C10H6O8 to CoCl2·6H2O (represented by H4ma/Co2+ ratio): (a) 0, (b) 0.5, (c) 1, and (d) 2.5. | ||
The overall growth mechanism of the resulting Co products can be described into two stages based on the eqn (1): the initial nucleation process and subsequent growth of the nuclei. In the absence of C10H6O8, the concentration of free Co2+ ions in the solution of CoCl2·6H2O and NaOH is so high enough to accelerate the reduction and formation of almost all of Co nuclei at initial stage and almost no Co solutes are available for subsequent nuclei growth. Thus, the nuclei aggregates become spheres and even some polyhedrons (Fig. 3(a)) driven by the magnetic dipole–dipole interaction and the minimization of interfacial energy according to Gibbs–Thomson law.39 With the proper increase of usage of C10H6O8, the concentration of free Co2+ ions is decreased so that the fewer nuclei are produced at the initial stage and on the other hand, the concentration of NaOH is reduced to some extent because of the dissolution of C10H6O8, which further decrease the quantity of Co nuclei due to the depression of reaction rate in terms of eqn (1). Accordingly, the concentration of Co solutes available for the subsequent nuclei growth stage is relatively high, resulting in a high growth rate. This growth mechanism is kinetically favorable for growing hierarchical dendritic architectures (Fig. 3(b) and (c), and 2) according to the well-known diffusion-limited aggregation (DLA) model.40 However, further increasing the amount of C10H6O8 results in more lowering the quantity and growth rate of Co nuclei, the spherical aggregates and hierarchical architectures with large sword-like leaves can be observed (Fig. 3(d)). It has been demonstrated that the complex reagent plays at least two roles in the formation of inorganic building and assemblies.41 First, the complex reagent can coordinate with metallic ions to form complex, inducing a lower concentration of metallic ions and thus a lower nucleation rate. In other words, the growth rate of the products can be controlled by adjusting the concentration of the complex reagent. Second, for the sequent growth process, the selectively preferential capping or stabilization of some crystal faces by a complex reagent give rise to the kinetic control of the growth of different crystal faces and the further efficient domination of the morphology of the final products.42–44 The images of Fig. 2 and 3 indicate that in both aspects the complex reagent of C10H6O8 has a crucial role on the formation of hierarchical Co dendrites.
General, the reaction temperature plays an important role in determining the morphology of the products. We systematically investigated this system with different reaction temperatures of 100–160 °C and the morphology of the Co samples are shown in Fig. 4. From the observation of Fig. 4(a)–(d), although having a slight difference the dendritic morphology can be obtained when reaction temperature is 100–130 °C. Further increasing reaction temperature to 160 °C, the irregular aggregates by small particles can be obtained (Fig. 4(e) and (f)). These results indicate that the proper reaction temperature is crucial for the formation of hierarchical Co dendrites and higher reaction temperature faster reaction rate can be induced resulting formation of irregular aggregates.
Fig. 5 shows the morphology transformation of the products prepared at different concentration of NaOH. When the concentration of NaOH is decreased from 1.5 to 0.8 M, the products are mainly composed of irregular aggregates, as shown in Fig. 5(a) and (b). Further decreasing the concentration of NaOH to 0.6 M, the big sheet aggregates can be observed shown in Fig. 5(c) and (d). When the concentration of NaOH is decreased 0.4 M, hierarchical cobalt dendritic architecture can be produced (Fig. 2). It should be mentioned that magnetic cobalt powders can not be harvested when the concentration of NaOH is lower than 0.3 M, indicating redox reaction unhappen according to eqn (1). These results indicate that higher concentration of NaOH faster reaction rate occurs and the concentration of NaOH has the similar roles as the reaction temperature in controlling the morphology of the Co samples.
 | ||
| Fig. 5 SEM images of cobalt products prepared at different concentration of NaOH: (a) 1.5 M, (b) 0.8 M, (c) and (d) 0.6 M. | ||
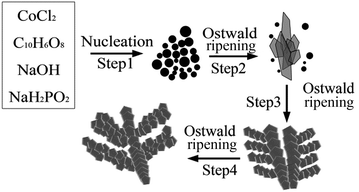
To further investigate the growth mechanism of the hierarchical Co dendrites, the products were collected at different reaction time of 5–24 h under the hydrothermal reaction process. When the reaction time is 5 h, the products are composed of spherical aggregates and the sword-like aggregates with attached sheet-like particles shown in Fig. 6(a). When the reaction time is extended to 12 h, the hierarchical dendritic architectures are gradually formed (Fig. 6(b)). The reaction is completely finished at 24 h, and the hierarchical Co dendrites composed of pentagonal-like leaves are obtained as shown in Fig. 2. On the basis of the above mentioned experimental results, the formation mechanism of hierarchical Co dendrites could be attributed to the Ostwald ripening process, which involve in the dissolution of smaller particles, diffusion and re-deposition of dissolved species on to the surface of bigger particles in a sufficient ripening time.45 Fig. 7 shows the schematic illustration of whole morphology evolution process of hierarchical Co dendrites, which may include four consecutive steps in an Ostwald ripening process. At the initial stage of the reaction system, numerous Co nuclei with different sizes are first reduced from the complex (Step 1). The larger particles further grow into flake-like particles at the expense of the smaller particles due to the higher activity and solubility of the smaller particles in terms of Ostwald ripening process and further self-assemble into sword-like aggregates combination with the collective effect of selective absorption of C10H6O8 onto the some crystal faces of the particles, diffusion-limited growth route, and magnetic dipolar interaction (Step 2). With further increasing reaction time, the freshly reduced Co crystals are spontaneously self-assembled onto the surface of sword-like aggregates and form the main stem and secondary branches through the similar growth process as mentioned in Step 2 (Step 3). Finally, the well-defined hierarchical Co dendrites with pentagonal-like building blocks can be obtained (Step 4). Moreover, it should be mentioned that the samples prepared with other morphology controllable reagent such as PVP, CTAB can not possess the dendritic microstructures in our experiments. Zhang et al.31 prepared the hierarchical Co dendrites with leave-like building blocks by the assistance of Na2C4H4O6·H2O. In the present work, hierarchical Co dendrites based on pentagonal-like building blocks in the presence of C10H6O8 maybe attributed to the strong coordination ability due to four carboxylic groups and planar structure of benzene ring. On basis of the above results and discussions, it demonstrates that self-assembly growth process for the formation of Co dendrites in solution-reduction route is the synergic effects of proper H4ma/Co2+ ratio, reaction temperature, concentration of NaOH and reaction time, among which the H4ma/Co2+ ratio are more essential to control the nucleation velocity and growth dynamics process for the formation of Co dendrites due to the role of H4ma as the complex and capping reagent.
 | ||
| Fig. 6 SEM images of cobalt products prepared at 110 °C under different reaction time: (a) 5 h and (b) 12 h. | ||
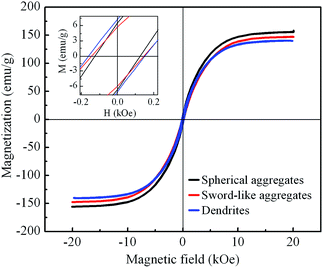
The magnetic hysteresis loops at room temperature of Co samples with different morphologies are shown in Fig. 8. The saturation magnetization of the samples are 155 emu g−1. 146 emu g−1, and 140 emu g−1 for spherical aggregates, sword-like aggregates and dendrites, respectively, which are smaller than Co bulk materials of 168 emu g−1 as a result of size effect, surface antiferromagnetic oxidation and surface spin disorder in the products.31 The coercivity force of the samples are 124, 145, and 160 Oe for spherical aggregates, sword-like aggregates and dendrites, respectively, which are larger compared with Co bulk materials of 10 Oe. Compared with spherical and sword-like aggregates, Co dendrites possess relative large concercivity. It is generally known that the coercivity is proportional to the magnetic anisotropy including magnetocrystalline anisotropy, surface anisotropy and shape anisotropy.46 The enhancement of coercivity for Co dendrites may result from the size effect, shape anisotropy and hierarchical nanostructures.
To reveal the microwave absorption properties of the as-prepared samples, the reflection loss (RL) values of Co dendrites–paraffin composites were simulated in terms of the relative complex permittivity and permeability at a given frequency and thickness of the absorbents according to the transmission-line theory, which can be described as the following equations.47
RL = 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log|(Zin − Z0)/(Zin + Z0)| log|(Zin − Z0)/(Zin + Z0)|
| (2) |
Zin = Z0(μr/εr)1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) tanh[j(2πfd/c)(μrεr)1/2] tanh[j(2πfd/c)(μrεr)1/2]
| (3) |
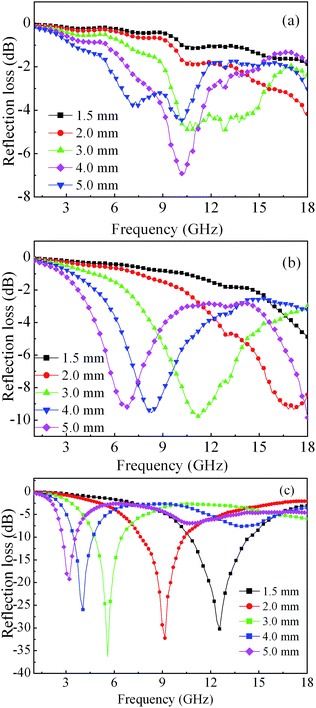 | ||
| Fig. 9 Microwave reflection losses of Co/paraffin composites with different Co morphologies: (a) spherical aggregates; (b) sword-like aggregates; (c) dendrites. | ||
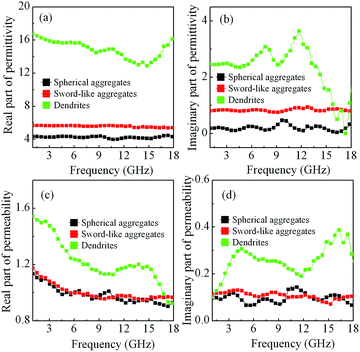
To investigate the possible microwave absorption mechanism of the Co samples, the electromagnetic parameters, i.e., the relative complex permittivity (εr = ε′ − jε′′) and the relative complex permeability (μr = μ′ − jμ′′) of Co/paraffin composites were measured at room temperature. The real part (ε′ and μ′) and imaginary part (ε′′ and μ′′) symbolize the storage and loss capability for EM wave based on dielectric and magnetic properties, respectively. Fig. 10 shows the frequency dependence of the electromagnetic parameters of the Co/paraffin composites with different Co morphologies. As shown in Fig. 10(a) and (b), Co dendrites exhibit larger ε′ and ε′′ values compared with the two other samples, and spherical aggregates have the smallest values. For spherical and sword-like aggregates, both ε′ and ε′′ are almost constants with a slight fluctuation along with frequency increasing. For Co dendrites, the ε′ firstly decreases from 16.8 to 12.7 in 1.0–14.5 GHz and then increases to 16.5 at 18.0 GHz; the ε′′ has a significant dielectric relaxation feature and exhibits obvious double resonance peaks around 7.8 and 11.7 GHz (Fig. 10(b)). The polarization ability of a material generally arises from the following probable mechanism, such as ionic, electric, or atomic orientation polarization, dipole polarization and interfacial polarization. The three samples with different permittivity in microwave frequency should mainly originate from the dipole polarization and interfacial polarization. For the Co dendrites, hierarchical architectures with pentagonal-like building blocks oriented growth layer by layer possess abundant of grain boundary, which can induce the stronger intrinsic electric dipole polarization and grain boundary polarization.46 Moreover, Co dendrites possess abundant of secondary branches and a large numbers of interface can be formed among the Co/CoO and CoO/paraffin enhancing the interfacial polarization. Additionally, according to the free electron theory,48 ε′′ ≈ 1/2πε0ρf, where ρ is the resistivity. Higher ε′′ means higher conductivity. It is rational that conductive Co dendrites networks can be easily formed due to the plenty of branches can extend to three-dimensional space supplying the channels for electron transport compared with the two other samples. Thus, the ohmic loss caused by the drain current for the Co dendrites can be enhanced. Furthermore, both ε′ and ε′′ values of Co dendrites/paraffin improve with the Co loading increasing, which can be attributed to interfacial polarization obviously improved with mass fraction increase except for electric dipole polarization (Fig. S2(a) and (b)†).
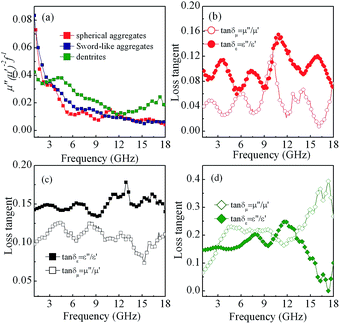
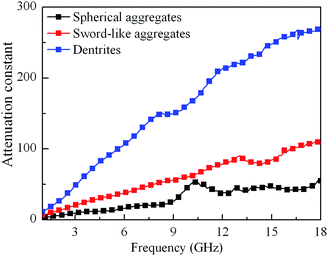
As shown in Fig. 10(c), the μ′ decreases with frequency increasing for the three kinds of Co samples. The Co dendrites exhibit largest μ′′ value and more obvious multiresonance peaks (Fig. 10(d)). With the loadings of Co dendrites increasing, the similar tendency of variation of μ′ and μ′′ with frequency can be seen and obvious multiresonance peaks are also observed (Fig. S2(c) and (d)†). The μ′ and μ′′ values of composites with 72 wt% loading of Co is slight lower than that of composites with 65 wt% of Co, which maybe attributed to the relatively higher conductivity.49,50 It is well-known that the magnetic loss generally arises from the magnetic hysteresis, domain wall displacement, eddy current loss, natural resonance, and exchange resonance mode.51 The magnetic hysteresis takes place only in a high magnetic field originating from irreversible magnetization and the domain wall displacement often occurs in the frequency range of 1–100 MHz. If the magnetic loss mainly arises from the eddy current loss, the value of μ′′(μ′)−2f−1 could be equal to a constant value of 2πμ0d2σ (d is the thickness of absorber, σ is the electrical conductivity, μ0 is the permeability of vacuum) and be independence of frequency.52 As shown in Fig. 11(a), the values of μ′′(μ′)−2f−1 of all of composites alternate gradually with increasing frequency in the whole range of 1–18 GHz. Similar results have been observed from the Co dendrites/paraffin composites with the increase of Co loadings (Fig. S3(a)†). Thus, the magnetic loss in our samples is mainly caused by natural resonance and exchange resonance mode due to a consequence of small size effect, surface anisotropy and spin wave excitations.52–54 Compared to the bulk Co (several tens of megahertz), the present higher resonance frequency of Co dendrites is attributed to large surface anisotropy field, which is mainly due to hierarchical dendrites with bulky secondary branches self assembled by pentagonal-like Co sheet, surface/defect affected by the size effect etc.55–57 In other words, Co dendrites show a relatively high value for the effective anisotropy energy and the resonance frequency shifts to a higher frequency, which will be significant for application as EM wave absorption materials in the microwave range. It is general that the natural resonance occurs at a low frequency and the exchange resonance occurs at a high frequency, indicating strong magnetic loss.51,58
As we know, the excellent microwave absorption properties of absorbents should simultaneously satisfy impedance matching and attenuation capability. The impedance matching requires the complex permittivity to be equal or close to the complex permeability, which can induce the incidence of EM wave into interior of absorbents, and the attenuation constant can demonstrate the EM wave absorption ability of absorbents, which can be written according to transmission line theory as following:49
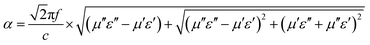 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δε = ε′′/ε′) and magnetic loss tangent (tan
δε = ε′′/ε′) and magnetic loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δμ = μ′′/μ′) of the Co/paraffin composites are shown in Fig. 11(b)–(d). For spherical and sword-like aggregates, although the difference between tan
δμ = μ′′/μ′) of the Co/paraffin composites are shown in Fig. 11(b)–(d). For spherical and sword-like aggregates, although the difference between tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δε and tan
δε and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δμ is slight inducing the good impedance matching, both values of tan
δμ is slight inducing the good impedance matching, both values of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δε and tan
δε and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δμ are so low that the attenuation ability is weak (Fig. 11(b) and (c) and 12). For Co dendrites, more favorable impedance matching with a comparable value between tan
δμ are so low that the attenuation ability is weak (Fig. 11(b) and (c) and 12). For Co dendrites, more favorable impedance matching with a comparable value between tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δε and tan
δε and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δμ combination with strong attenuation constant due to the strong dielectric relaxation and multiple magnetic resonances (Fig. 11(d) and 12), contribute to the excellent microwave absorption properties. For the samples with 55 wt% of Co dendrites loadings, the relative smaller values of tan
δμ combination with strong attenuation constant due to the strong dielectric relaxation and multiple magnetic resonances (Fig. 11(d) and 12), contribute to the excellent microwave absorption properties. For the samples with 55 wt% of Co dendrites loadings, the relative smaller values of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δε and tan
δε and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δμ induce weak attenuation ability (Fig. S3(b) and S4†), resulting in the week microwave absorption. For the samples with 72 wt% content of Co dendrites, the higher tan
δμ induce weak attenuation ability (Fig. S3(b) and S4†), resulting in the week microwave absorption. For the samples with 72 wt% content of Co dendrites, the higher tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δε enlarges the difference (higher than 0.2) between tan
δε enlarges the difference (higher than 0.2) between tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δε and tan
δε and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δμ in the whole measured frequency range, which lead to impedance mismatch and result in reflection of the much more incident EM wave from the surface of the absorbents although its attenuation constant is higher than that of others (Fig. S3(d) and S4†). Thus, the samples with 72 wt% content of Co have relatively poor microwave absorption properties compared with samples with 65 wt% content of Co can be attributed to the impedance mismatching due to the increase of tan
δμ in the whole measured frequency range, which lead to impedance mismatch and result in reflection of the much more incident EM wave from the surface of the absorbents although its attenuation constant is higher than that of others (Fig. S3(d) and S4†). Thus, the samples with 72 wt% content of Co have relatively poor microwave absorption properties compared with samples with 65 wt% content of Co can be attributed to the impedance mismatching due to the increase of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δε.
δε.
4. Conclusions
In summary, cobalt dendritic architectures based on self-assembly of nanoflakes have been fabricated by a facile hydrothermal method. The effect of the reaction conditions including concentration of reactants, reaction temperatures and times, on the morphology of Co samples was systematically investigated. The results show that the molar ratio of C10H6O8 to CoCl2·6H2O in the present system plays a crucial role in the formation of Co dendritic hierarchical architectures, while the other reaction parameters, such as reaction temperature, concentration of NaOH, and reaction time, have the close relationship with the final morphology of the Co samples. The growth mechanism for the Co dendritic architectures has been proposed based on time-dependent experiments. The microwave absorption properties of the Co powders/paraffin composites were measured in the frequency range of 1–18 GHz. Co dendrites with 65 wt% loadings exhibit excellent microwave absorption than that of spherical and sword-like aggregates based on more favorable impedance matching with a comparable value between tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δε and tan
δε and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δμ combination with strong attenuation constant due to the strong dielectric relaxation and multiple magnetic resonances. The optimal reflection loss (RL) is −30.2 dB at 12.5 GHz covering 10.5–14.5 GHz frequency range (RL < −10 dB) with a thickness of 1.5 mm and the effective bandwidth (RL < −10 dB) is up to 11.8 GHz in the frequency range of 2.7–14.5 GHz by adjusting the thickness of 1.5–5 mm. This efficient and morphologically controllable self-assembly method can be extended to prepare complex 3D micro/nanoarchitectures of other materials.
δμ combination with strong attenuation constant due to the strong dielectric relaxation and multiple magnetic resonances. The optimal reflection loss (RL) is −30.2 dB at 12.5 GHz covering 10.5–14.5 GHz frequency range (RL < −10 dB) with a thickness of 1.5 mm and the effective bandwidth (RL < −10 dB) is up to 11.8 GHz in the frequency range of 2.7–14.5 GHz by adjusting the thickness of 1.5–5 mm. This efficient and morphologically controllable self-assembly method can be extended to prepare complex 3D micro/nanoarchitectures of other materials.
Acknowledgements
This work has been supported by Doctoral Science Foundation of Shenyang University of Technology (2012), Science Research Foundation of Education Department of Liaoning Province (L2015396) and the National Natural Science Foundation of China (51331006, 51301114, 51171185, and 21571132).Notes and references
- H. Wang, Y. Y. Dai, D. Y. Geng, S. Ma, D. Li, J. An, J. He, W. Liu and Z. D. Zhang, Nanoscale, 2015, 7, 17312 RSC.
- Z. Wang, H. Bi, P. Wang, M. Wang, Z. Liu, L. Shen and X. Liu, Phys. Chem. Chem. Phys., 2015, 17, 3796 RSC.
- X. L. Shi, M. S. Cao, J. Yuan and X. Y. Fang, Appl. Phys. Lett., 2009, 95, 163108 CrossRef.
- P. Zhan, C. Liang, X. Gong, R. Gao, J. Liu, M. Wang and R. Che, Nanoscale, 2013, 5, 8022 RSC.
- H. Wang, N. Ma, Z. Yan, L. Deng, J. He, Y. Hou, Y. Jiang and G. Yu, Nanoscale, 2015, 7, 7189 RSC.
- Q. Liu, D. Zhang and T. Fan, Appl. Phys. Lett., 2008, 93, 013110 CrossRef.
- Y. Ren, C. Zhu, S. Zhang, C. Li, Y. Chen, P. Gao, P. Yang and Q. Ouyang, Nanoscale, 2013, 5, 12296 RSC.
- X. Qi, J. Xu, W. Zhong and Y. Du, RSC Adv., 2015, 5, 16010 RSC.
- H. Zhang, Y. Xu, J. Zhou, J. Jiao, Y. Chen, H. Wang, C. Liu, Z. Jiang and Z. Wang, J. Mater. Chem. C, 2015, 3, 4416 RSC.
- Y. F. Zhu, L. Zhang, T. Natsuki, Y. Q. Fu and Q. Q. Ni, ACS Appl. Mater. Interfaces, 2012, 4, 2101 CAS.
- B. Zhao, G. Shao, B. Fan, W. Zhao, Y. Xie and R. Zhang, J. Mater. Chem. A, 2015, 3, 10345 CAS.
- B. Gao, L. Qiao, J. Wang, Q. Liu, F. Li, J. Feng and D. Xue, J. Phys. D: Appl. Phys., 2008, 41, 235005 CrossRef.
- Z. X. Yu, Z. P. Yao, N. Zhang, Z. J. Wang, C. X. Li, X. J. Han, X. H. Wu and Z. H. Jiang, J. Mater. Chem. A, 2013, 1, 4571 CAS.
- R. Che, L. M. Peng, X. Duan, Q. Chen and X. Liang, Adv. Mater., 2004, 16, 401 CrossRef CAS.
- X. L. Dong, X. F. Zhang, H. Huang and F. Zuo, Appl. Phys. Lett., 2008, 92, 013127 CrossRef.
- J. Jiang, D. Li, D. Geng, J. An, J. He, W. Liu and Z. Zhang, Nanoscale, 2014, 6, 3967 RSC.
- L. Wang, Y. Huang, X. Sun, H. Huang, P. Liu, M. Zong and Y. Wang, Nanoscale, 2014, 6, 3157 RSC.
- T. Liu, P. H. Zhou, J. L. Xie and L. J. Deng, Appl. Phys. Lett., 2011, 110, 033918 Search PubMed.
- X. F. Zhang, X. L. Dong, H. Huang, Y. Y. Liu, W. N. Wang, X. G. Zhu, B. Lv, J. P. Lei and C. G. Lee, Appl. Phys. Lett., 2006, 89, 053115 CrossRef.
- B. Zhao, B. B. Fan, G. Shao, B. B. Wang, X. X. Pian, W. Li and R. Zhang, Appl. Surf. Sci., 2014, 307, 293 CrossRef CAS.
- L. S. Fu, J. T. Jiang, C. Y. Xu and L. Zhen, CrystEngComm, 2012, 14, 6827 RSC.
- H. Lv, X. Liang, Y. Cheng, G. Ji, D. Tang, B. Zhang, H. Zhang and Y. Du, RSC Adv., 2015, 5, 25936 RSC.
- G. Sun, B. Dong, M. Cao, B. Wei and C. Hu, Chem. Mater., 2011, 23, 1587 CrossRef CAS.
- C. Z. He, S. Qiu, X. Z. Wang, J. R. Liu, L. Q. Luan, W. Liu, M. Itoh and K. Machida, J. Mater. Chem., 2012, 22, 22160 RSC.
- Y. J. Zhang, Y. Zhang, Z. H. Wang, D. Li, T. Cui, W. Liu and Z. D. Zhang, Eur. J. Inorg. Chem., 2008, 2008, 2733 CrossRef.
- L. S. Zhong, J. S. Hu, H. P. Liang, A. M. Cao, W. G. Song and L. J. Wan, Adv. Mater., 2006, 18, 2426 CrossRef CAS.
- Y. Qiu, W. Chen, S. Yang, B. Zhang, X. X. Zhang, Y. C. Zhong and K. S. Wong, Cryst. Growth Des., 2010, 10, 177 CAS.
- X. Wang, T. Cui, F. Cui, Y. Zhang, D. Li and Z. Zhang, Chem. Commun., 2011, 47, 6329 RSC.
- Q. Hao, J. Wang and C. Xu, J. Mater. Chem. A, 2014, 2, 87 CAS.
- J. Ge, Q. Zhang, T. Zhang and Y. Yin, Angew. Chem., 2008, 120, 9056 CrossRef.
- Y. Zhang, S. W. Or and Z. Zhang, RSC Adv., 2011, 1, 1287 RSC.
- S. L. Tripp, S. V. Pusztay, A. E. Ribbe and A. Wei, J. Am. Chem. Soc., 2002, 124, 7914 CrossRef CAS PubMed.
- X. W. Teng and H. Yang, Nano Lett., 2005, 5, 885 CrossRef CAS PubMed.
- H. Q. Yan, R. R. He, J. Johnson, M. Law, R. J. Saykally and P. D. Yang, J. Am. Chem. Soc., 2003, 125, 4728 CrossRef CAS PubMed.
- H. L. Niu, Q. W. Chen, Y. S. Jia, H. F. Zhu and M. Ning, Nanotechnology, 2004, 15, 1054 CrossRef CAS.
- Y. Yang, C. Xu, Y. Xia, T. Wang and F. Li, J. Alloys Compd., 2010, 493, 549 CrossRef CAS.
- F. Jaber, F. Charbonnier and R. Faure, J. Chem. Crystallogr., 1997, 27, 397 CrossRef CAS.
- S. Vairam, T. Premkumar and S. Govindarajan, J. Therm. Anal. Calorim., 2010, 101, 979 CrossRef CAS.
- J. W. Mullin, Crystallization, Butterworth-Heinemann, Oxford, UK, 3rd edn, 1997 Search PubMed.
- T. C. Halsey, B. Duplantier and K. Honda, Phys. Rev. Lett., 1997, 78, 1719 CrossRef CAS.
- L. P. Zhu, H. M. Xiao, W. D. Zhang, Y. Yang and S. Y. Fu, Cryst. Growth Des., 2008, 8, 1113 CAS.
- R. Xu, T. Xie, Y. Zhao and Y. Li, Cryst. Growth Des., 2007, 7, 1904 CAS.
- X. W. Wei, G. X. Zhu, Y. J. Liu, Y. H. Ni, Y. Song and Z. Xu, Chem. Mater., 2008, 20, 6248 CrossRef CAS.
- T. He, D. Chen, X. Jiao and Y. Wang, Adv. Mater., 2006, 18, 1078 CrossRef CAS.
- A. R. Roosen and W. C. Carter, Phys. A, 1998, 261, 232 CrossRef CAS.
- Z. Wang, H. Bi, M. Wang, P. Wang and X. Liu, Mater. Chem. Phys., 2015, 159, 173 CrossRef CAS.
- G. Wan, L. Yu, X. Peng, G. Wang, X. Huang, H. Zhao and Y. Qin, RSC Adv., 2015, 5, 77443 RSC.
- S. Ramo, J. R. Whinnery and T. V. Duzer, Fields and Waves in Communication Electronics, Wiley, New York, 1984, p. 181 Search PubMed.
- G. Wang, X. Peng, L. Yu, G. Wang, S. Lin and Y. Qin, J. Mater. Chem. A, 2015, 3, 2734 CAS.
- J. Wang, H. Wang, J. Jiang, W. Gong, D. Li, Q. Zhang, X. Zhao, S. Ma and Z. Zhang, Cryst. Growth Des., 2012, 12, 3499 CAS.
- B. Zhao, G. Shao, B. Fan, W. Zhao, Y. Xie and R. Zhang, Phys. Chem. Chem. Phys., 2015, 17, 8802 RSC.
- J. Zou, Z. Wang, M. Yan and H. Bi, J. Phys. D: Appl. Phys., 2014, 47, 275001 CrossRef.
- C. Kittel, Phys. Rev., 1948, 73, 155 CrossRef CAS.
- A. Aharoni, J. Appl. Phys., 1991, 69, 7762 CrossRef.
- D. A. Dimitrov and G. M. Wysin, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 11947 CrossRef CAS.
- V. P. Shilov, J. C. Bacri, F. Gazeau, F. Gendron, R. Perzynski and Y. L. Raikher, J. Appl. Phys., 1999, 85, 6642 CrossRef CAS.
- F. Bødker, S. Mørup and S. Linderoth, Phys. Rev. Lett., 1994, 72, 282 CrossRef PubMed.
- P. Toneguzzo, G. Viau, O. Acher, F. Fiévet-Vincent and F. Fiévet, Adv. Mater., 1998, 10, 1032 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Microwave reflection losses (Fig. S1), electromagnetic parameters (Fig. S2), loss tangent (Fig. S3) and attenuation constant (Fig. S4) of Co dendrites/paraffin composites with different loadings of Co. See DOI: 10.1039/c6ra06112e |
| This journal is © The Royal Society of Chemistry 2016 |