Molecular-level insight into the interactions of DNA with phospholipid bilayers: barriers and triggers

Abstract

Interactions of nuclear acids with cell membranes are at the heart of numerous biomedical and nanotechnological applications of DNA and DNA-based nanodevices. Despite enormous recent development in DNA nanotechnology, very little is known about DNA–membrane interactions at a molecular level. Here we employ biased atomic-scale computer simulations to calculate for the first time the free energy profile for partitioning a DNA molecule into a phospholipid bilayer, a system that is routinely used to mimic the properties of cell membranes. Our findings clearly show that a zwitterionic lipid bilayer represents a repulsive barrier for DNA: the potential of the mean force profile does not develop any local minima upon moving DNA from water into the lipid/water interface. This energetic barrier can be overcome e.g. via adsorption of divalent calcium ions on the surface of a lipid bilayer, which makes the lipid bilayer effectively cationic. Indeed, our biased molecular dynamics simulations confirm that the corresponding free energy profile for partitioning DNA into a lipid bilayer with adsorbed Ca ions is characterized by a deep minimum. Therefore, the bilayer-bound calcium ions can serve as a trigger of the electrostatic attraction between DNA and zwitterionic phospholipids. In addition, we performed a series of unbiased computer simulations for lipid bilayers with absorbed calcium ions and showed that the initial DNA binding is driven by an overall positive charge of the bilayer, while DNA is stabilized on the bilayer surface by Ca ions that laterally diffuse towards DNA to form tight bridges between phosphate groups of DNA and lipids. Overall, our computational findings contribute to a long-standing problem of interactions of charged nano-objects (such as DNA and DNA-base nanostructures) with cell membranes.

---

Introduction

Besides its biological function, DNA represents an important class of macromolecules with unique properties. In particular, DNA nanotechnology has attracted enormous attention in recent years due to the fact that DNA molecules, being highly specific in their hydrogen bonding, can serve as versatile building blocks for constricting programmable nanomaterials.¹ Recent technological advances allow one to create 2D and 3D DNA-based molecular objects of almost arbitrary shapes.^2,3 A great advantage of such nanoscale objects is that they are essentially biocompatible and therefore can be used safely in natural biological systems. One of the well-known examples includes synthetic membrane channels made from DNA nanostructures.⁴ Furthermore, DNA was successfully used to induce fusion of phospholipid vesicles^5,6 and to modify adhesion properties of the cell membrane surface.⁷

Interaction of DNA-based nanostructures with biological systems inevitably leads to interactions of DNA with the surface of cells – or more specifically – with the lipid bilayer matrix of cell membranes.⁸ This also highlights the importance of DNA–lipid interactions for our understanding of the impact of nanomaterials on living matter. In principle, such interactions should be characterized by considerable energetic barriers due to the nature of both DNA and lipid molecules. Indeed, the interior of a phospholipid bilayer is essentially hydrophobic, while DNA is a highly charged (anionic) object. Correspondingly, it comes as no surprise that DNA does not adsorb on the membrane surface composed of zwitterionic (neutral) lipids as demonstrated earlier by several experimental studies.^9,10

To overcome the barrier in DNA–lipid interactions one can think of two different scenarios. First approach is related to chemical modification of DNA to make it compatible with the hydrophobic core of lipid membranes. To this end, DNA was conjugated with several molecules such as cholesterol,¹¹ porphyrin,¹² lipids,^6,13etc. The hydrophobicity of the molecules covalently linked to DNA and DNA-based nano-objects promotes attachment of DNA to lipid membranes.

Second approach is to invoke the electrostatic attraction between the lipid bilayer surface and DNA. Such an attraction is easily achieved in liposome-based delivery vectors through mixing zwitterionic (neutral) lipid species with synthetic cationic lipids.^14,15 However, this is not applicable to cell membranes as they mostly constitute of zwitterionic lipids (along with some amount of anionic ones). In this case the surface of a neutral lipid bilayer can be made positively charged through adding divalent cations (calcium or magnesium) to the system, thereby promoting electrostatic interactions of the membrane with anionic DNA molecules.^9,10,16,17

Despite the importance of DNA–lipid interactions the precise molecular mechanism behind such interactions still remains obscure due to current limitations of experimental methods. Such a situation normally calls for computer modeling along with realistic models of high (atomistic) resolution. However, on a computational side, only a very limited number of related studies has been published. Bandyopadhyay et al. employed atomistic molecular dynamics (MD) simulations to study a complex of DNA with a mixed zwitterionic/cationic lipid bilayer.¹⁸ Tarek et al. studied lipid bilayer systems with DNA/RNA but a primary focus was on electroporation phenomena.^19,20 In addition to the above atomistic simulations, coarse-grained models were also used to explore the interactions of DNA with cationic^21,22 and zwitterionic²¹ lipid bilayers at the cost of fine atomic details and dipolar nature of water. Very recently we reported a preliminary insight into the lipid–DNA interactions through unbiased atomistic MD simulations.²³

In this paper we employ biased atomic-scale molecular dynamics simulations to explore for a first time the energetic barriers between DNA and phospholipid bilayers. We calculated the potential of mean force that corresponds to the energetic costs of moving DNA from the water phase towards the bilayer interior. Two distinct situations were considered: (i) a zwitterionic (neutral) lipid bilayer and (ii) a bilayer with pre-adsorbed Ca ions, i.e. an effectively cationic lipid bilayer. For the lipid–DNA system with pre-adsorbed calcium we additionally performed unbiased simulations to study the kinetics of DNA adsorption as well as the factors responsible for the stability of the resulting DNA–bilayer complex. Overall, our findings clearly demonstrate that a zwitterionic lipid bilayer represents an energetic barrier for DNA molecules; this barrier can be overcome through adsorption of divalent cations to the bilayer surface.

Methods

We have performed biased atomic-scale molecular dynamics simulations of two DNA–lipid systems; one of the systems was calcium-free, while another had a lipid bilayer with Ca ions adsorbed on its surface. Both systems consisted of a bilayer of 128 palmitoyl-oleoyl-phosphatidylcholine (POPC) lipids and a Dickerson's DNA dodecamer^24,25 and were solvated in ∼10 000 water molecules along with 22 DNA conterions (Na ions).

Atomistic force-fields AMBER Lipid14 (ref. 26) and AMBER parmbsc0 (ref. 27) were used for POPC lipid molecules and DNA, respectively. Water was represented by the TIP3P model.²⁸ Standard AMBER parameters were used for monovalent and divalent ions. Simulations were performed at T = 303 K and P = 1 bar with the use of the velocity-rescaling thermostat²⁹ and the anisotropic Berendsen barostat³⁰ to control temperature and pressure, respectively. The time step was 2 fs. For the long-range electrostatic interactions the particle-mesh Ewald (PME) method was used.³¹ The Gromacs 4.5.6 package was used for all simulations.³²

Umbrella sampling³³ was employed to calculate the potential of mean force (PMF) for partitioning a DNA molecule into a POPC lipid bilayer. Prior actual biased simulations a calcium-free lipid bilayer was pre-equilibrated for 250 ns (system 1 in Table 1). The final structure of the bilayer was used then to perform 400 ns equilibration of a bilayer system with Ca ions (system 3 in Table 1). The lipid/calcium ratio in the system was 6.4.

Table 1 Simulated DNA–lipid bilayer systems

#	System	Lipid/Ca ratio	Time (ns)
a Systems marked by A and B differ by the initial distance between DNA and the bilayer surface (0.5 and 1.0 nm for systems A and B, respectively).
1	POPC128	—	250
2	DNA-POPC128-PMF	—	35 × 100
3	POPC128-Ca02	6.4	400
4	DNA-POPC128-Ca02-PMF	6.4	35 × 100
5	POPC288	—	200
6	POPC288-Ca01	13.1	400
7	POPC288-Ca02	6.4	400
8	DNA-POPC-Ca01-A^a	13.1	1000
9	DNA-POPC-Ca01-B^a	13.1	1000
10	DNA-POPC-Ca02-A^a	6.4	600
11	DNA-POPC-Ca02-B^a	6.4	1200

---

A DNA molecule was placed parallel to the bilayer surface. The pull code supplied with the Gromacs suite³² was used to obtain starting configurations for subsequent umbrella sampling calculations. A DNA molecule was pulled along the reaction coordinate (the distance between centers of mass of DNA and a lipid bilayer in the direction perpendicular to the bilayer surface) with a velocity of 0.05 nm ns⁻¹ and a force constant of 1000 kJ mol⁻¹ nm⁻². From this steered MD trajectory we extracted 35 windows for the umbrella sampling; the spacing between windows was 0.1 nm (from 1.4 to 4.8 nm along the reaction coordinate). Each window was then equilibrated for 20 ns, followed by a 80 ns production run (the force constant was set to 3000 kJ mol⁻¹ nm⁻²). The potential of mean force was calculated with the use of the weighted histogram analysis method (WHAM)³⁴ as it is implemented in the Gromacs suite.³⁵ The overall simulation time of the biased MD simulations amounted to 7 microseconds.

For DNA–lipid systems with Ca ions the umbrella sampling calculations were complemented by unbiased molecular dynamics simulations. These simulations were performed for larger systems as compared to those considered in biased simulations. Each system consisted of a bilayer of 288 POPC lipids, a double Dickerson's DNA dodecamer (24 bp), 46 DNA counterions (Na ions) and water molecules (from ∼15 000 to 24 000 H₂O). In the same fashion as for smaller systems, the larger bilayers were first properly equilibrated: a Ca-free bilayer was simulated for 200 ns, while bilayers with CaCl₂ salt (we considered two different lipid/calcium ratios 6.4 and 13.1) were run for 400 ns each (systems 5–7 in Table 1). For unbiased simulations a DNA molecule was placed parallel to the bilayer, the initial distances between DNA and the bilayer surface being either 0.5 or 1.0 nm (the systems marked by A or B, respectively, see Table 1). Most simulation conditions stayed unchanged as compared to smaller systems, see above. Simulation times of the four DNA–bilayer systems with calcium ions (two lipid/calcium ratios by two initial DNA–bilayer distances) ranged from 600 to 1200 ns, amounting to 3.8 microseconds of overall simulated time.

Results and discussion

DNA–lipid bilayer: a barrier

Previously we reported the results of unbiased MD simulations for DNA–phospholipid bilayer systems.²³ In particular, it was shown that DNA did not interact with a lipid bilayer in a series of independent unbiased simulations on a time scale of 100 ns. Although this computational finding is in line with experimental observations,^9,10 unbiased MD simulations cannot serve as an solid proof of the absence of attractive interactions between DNA and a lipid bilayer. For instance, a recent computational study clearly demonstrated that anionic gold nanoparticles were able to attach to the surface of a zwitterionic phospholipid membrane through the interactions between negatively charged groups of a nanoparticle and positively charged choline groups of PC lipids.³⁶ As a DNA molecule is also anionic, hypothetically it can interact favorably with choline lipid groups as well.

To eliminate (or to confirm) such a scenario, here we employ biased MD simulations to explore the profile of the energetic barrier between DNA and a lipid bilayer. In Fig. 1 (Top) we present the corresponding potential of mean force evaluated through the umbrella sampling calculations. The reaction coordinate z is the distance between centers of mass of DNA and a lipid bilayer. When a highly charged object such as DNA approaches the hydrophobic core of a bilayer, one would expect an abrupt increase in the free energy. This is indeed the case as is evident from Fig. 1: the energetic cost for DNA to be located in the membrane as deep as the position of phosphate groups amounts to ∼130 kJ mol⁻¹. A non-trivial part of the free energy profile is on the right-hand side from the average position of lipids' phosphate groups. It is clearly seen that there is a gradual growth of the energetic barrier between DNA and a lipid bilayer when DNA approaches the lipid/water interface from aqueous solution. The absence of any local minima in the PMF profile implies that attractive DNA–lipid interactions are indeed absent. Note that in our simulations the overall charge of DNA stays unchanged upon embedding DNA into the bilayer. Strictly speaking, the protonation state of DNA could change in line with recent findings reported for amino acids.³⁷ Such DNA protonation should decrease the height of an energetic barrier in the hydrophobic core of a lipid bilayer.³⁸ However, a smaller DNA charge also weakens possible attractive interactions between DNA and lipid head groups, so that the shape of the PMF curve (Fig. 1 (Top)) will hold.

Fig. 1 (Top) Free energy profile (PMF) for transferring a DNA molecule from salt-free aqueous solution to the lipid/water interface. A dashed line indicates the average position of lipid phosphate groups. Statistical errors were estimated with the use of bootstrapping analysis.³⁵ (Bottom) Component-wise density profiles for a phospholipid bilayer. Shown are the densities of POPC lipids (orange), water (blue) and lipid phosphate groups (green). The center of the bilayer is at z = 0 nm.

Thus, our PMF calculations demonstrate that DNA molecules do not interact favorably with zwitterionic lipid bilayers. In other words, a zwitterionic phospholipid bilayer represents an energetic barrier for DNA molecules.

Lipid–calcium system

As mentioned in the Introduction, one of the means to trigger attractive DNA–lipid interactions is to add divalent cations to the bilayer system. In this section we explore the impact of calcium ions on the properties of a zwitterionic PC lipid bilayer. To this end, we consider POPC lipid bilayers in aqueous solution with two different lipid/calcium ratios: 13.1 and 6.4 (systems 6 and 7, see Table 1). Note that system 3 differs from system 7 only by the size of a bilayer (128 vs. 288 lipids); all findings for system 7 also hold for system 3.

Fig. 2 (Top) visualizes the process of adsorption of calcium ions on the bilayer surface through time evolution of the overall number of contacts between Ca ions and lipid phosphate groups of a lipid monolayer. The number of contacts was calculated in line with our previous studies.^23,39 As one can see, equilibration is achieved at ∼200 ns for both lipid/calcium ratios, so that the numbers of contacts of Ca ions with lipid phosphate groups reach their equilibrium values. The adsorption of calcium ions changes the structural properties of the lipid/water interface. As a Ca ion is able to bind to phosphate groups of several lipid molecules, one can observe formation of different types of ion–lipid aggregates. In Fig. 2 (Bottom) we show the number of the Ca–lipid aggregates of different types as a function of time. The majority of the Ca–lipid aggregates constitutes complexes of a Ca ion and 3 lipids, although aggregates “Ca-4 lipids” also contribute and one can witness a dynamic re-distribution of lipids among aggregates of different types. The average number of PC lipids per calcium ion equals 3.2 ± 0.2 (the averaging was performed over last 100 ns of MD simulations of system 6 and over both its monolayers).

Fig. 2 (Top) The number of contacts between Ca ions and lipid phosphate groups as a function of time. Shown are results for a lipid monolayer of systems 6 (black) and 7 (red). (Bottom) The number of different Ca–lipid aggregates as a function of time. Shown are the aggregates composed of a Ca ion and one (black), two (red), three (green), and four (blue) phosphate groups of lipid molecules (a monolayer of system 6).

Calcium ions that bind to the membrane with formation of tight lipid aggregates induce a decrease in the area for per lipid. The area per lipid equals 0.63 ± 0.01 nm² and 0.62 ± 0.01 nm² for systems 6 and 7, respectively, while a Ca-free lipid bilayer has the area per lipid of 0.65 ± 0.01 nm² (system 5). Furthermore, we observed a considerable re-orientation of lipid head group dipoles towards the water phase due to calcium adsorption. For a Ca-free lipid bilayer the average angle between the lipid PN vector and the outward membrane normal equals 69.3 ± 1.4 degrees. Adding Ca ions decreases the angle to 62.8 ± 1.5 and 58.6 ± 1.6 degrees for systems 6 and 7, respectively. We note that the above characteristics were averaged over last 100 ns of MD trajectories. All the Ca-induced changes in the structure of a POPC bilayer agree well with an earlier computational study.⁴⁰

It is essential that all calcium ions were bound to the lipid/water interface at the end of 400 ns simulations, so that there were no free Ca ions in aqueous solution. Overall, we had 22 and 45 calcium ions adsorbed for systems 6 and 7, respectively. This implies that the POPC bilayers have now a net positive charge of +44e and +90e (systems 6 and 7, respectively). Thus, adding calcium ions to a zwitterionic lipid bilayer makes it positively charged. As we proceed to show in next section, this positive charge will trigger adsorption of DNA to the bilayer surface.

DNA–lipid bilayer: Ca ions as a trigger

To explore the impact of Ca ions on the interactions between DNA and a zwitterionic lipid bilayer, we repeated the umbrella sampling calculations (see Fig. 1) for a bilayer with pre-adsorbed Ca ions (final configuration of system 3 in Table 1). Similar to a larger system 7, in this case all Ca ions adsorbed to the bilayer surface during unbiased 400 ns simulations, amounting to an overall positive bilayer charge of +40e (20 Ca ions adsorbed).

In Fig. 3 (Top) we present the potential of mean force for a DNA molecule that approaches the surface of a lipid bilayer with adsorbed Ca ions from the water phase. Comparison of Fig. 1 (Top) and 3 (Top) provides us with an important conclusion: Ca ions adsorbed on the bilayer surface give rise to the appearance of the minimum in the free energy profile. This minimum is a signature of the electrostatic attraction between DNA and a lipid bilayer. The minimum is located at z = 3 nm, i.e. approximately 1 nm apart from the average positions of lipid phosphate groups and adsorbed Ca ions, see Fig. 3 (we recall that z denotes the distance between the center of masses of DNA and a lipid bilayer). In turn, the diameter of DNA in the canonical B-form is 2 nm. Therefore, based on Fig. 3, the most energetically favorable position of DNA at the lipid/water interface is such that negatively charged phosphate groups of DNA are in contact with Ca ions adsorbed on the bilayer surface. Furthermore, it turns out that the adsorbed Ca ions reduce the energetic cost for permeating DNA to the average location of lipid phosphate groups to ∼45 kJ mol⁻¹, see Fig. 3 (compare to 130 kJ mol⁻¹ for a calcium-free system).

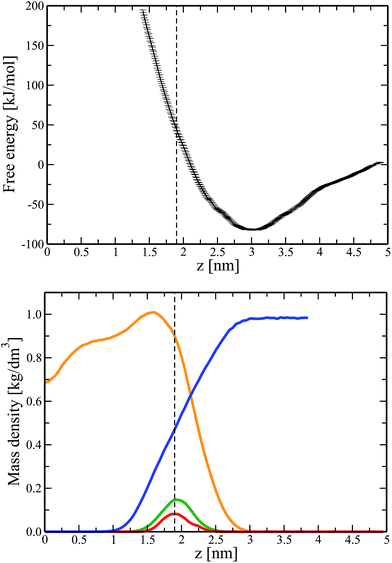Fig. 3 (Top) Free energy profile (PMF) for transferring a DNA molecule from aqueous solution to the surface of a lipid bilayer with adsorbed Ca ions (system 4). A dashed line indicates the average position of lipid phosphate groups. Statistical errors were estimated with the use of bootstrapping analysis.³⁵ (Bottom) Component-wise density profiles for a lipid bilayer system. Shown are the densities of POPC lipids (orange), water (blue), lipid phosphate groups (green), and adsorbed calcium ions (red). For clarity's sake the density profile for Ca ions was scaled by a factor of 5.

The depth of the observed energy minimum, amounting to ∼80 kJ mol⁻¹, is relatively large, see Fig. 3 (Top). This is due to a large number of Ca ions adsorbed at the membrane surface (one calcium ion per approximately 6.4 lipids). Such a number of ions exceeds considerably the physiological level⁴¹ and is chosen to accelerate calculations and to make the observed effects more pronounced. Furthermore, for some nanotechnological applications the concentration of salt ions can deviate significantly from the biologically relevant one. Apparently, decreasing the number of Ca ions in the systems should decrease the depth of the potential well and correspondingly weaken the electrostatic attraction between DNA and a lipid bilayer. In view of this, Fig. 3 (Top) should be considered mainly as a basis for qualitative conclusions. Thus, Ca ions adsorbed on the surface of a zwitterionic (neutral) phospholipid bilayer trigger attractive interactions between DNA and the bilayer. With this fundamental result at hand, we now can employ unbiased MD simulations to follow the kinetics of formation of a DNA–lipid complex and to study the stability of the resulting supramolecular complex.

Overall, we performed unbiased simulations of four DNA–bilayer systems with two different content of Ca ions and with two different initial distances between the nuclear acid and the bilayer surface (systems 8–11, see Table 1). In all cases we observed a very fast adsorption of a DNA molecule on the surface of a bilayer. In Fig. 4 we show an initial 100 ns domain for time evolution of the distance between centers of mass of DNA and a lipid bilayer along the bilayer normal for all systems considered. It is seen that adsorption of DNA occurs within just 20 ns. Therefore, in line with the PMF profile presented in Fig. 3 (Top), one can witness strong electrostatic attraction between DNA and a lipid bilayer with adsorbed Ca ions. To characterize further the kinetics of DNA adsorption we estimated the number of contacts between DNA and lipid molecules as a function of time. In general, one can think of two different types of DNA–lipid contacts: (i) contacts between choline lipid groups and DNA's phosphate groups, Npc–Pdna, and (ii) calcium-mediated bridges between phosphate groups of lipids and DNA, Ppc–Ca–Pdna.^16,23 As an illustration, in Fig. 5 (Top) we show the number of both types of contacts as a function of time for system 9. Upon electrostatically driven DNA adsorption, phosphate groups of DNA meet choline lipid groups first because the choline groups of PC lipids are located closer to the water phase as compared to lipid phosphate groups. Therefore, we witness a steep increase in the number of Npc–Pdna contacts in the very beginning of simulations.

Fig. 4 Time evolution of the distance between centers of mass of DNA and a lipid bilayer along the direction perpendicular to the bilayer surface. Shown are results for systems 8–11, see Table 1.

Fig. 5 (Top) The number of different DNA–lipid contacts as a function of time (system 9). Shown are the contacts of lipid choline groups with DNA phosphate groups (black) and the Ca-mediated bridges between lipid and DNA phosphate groups (red). The number of contacts are calculated in line with ref. 23. (Bottom) The number of Ca ions involved in Ppc–Ca–Pdna bridges as a function of time.

As far as the Ppc–Ca–Pdna contacts are concerned, they can be formed only when DNA embeds deeper into the bilayer and – at the same time – if a Ca ion, being bound to a lipid head group, is localized in close vicinity of a DNA's phosphate group. As can be seen in Fig. 5, this is not the case for first 120 ns of simulations of system 9. The Ca-mediated bridges appear on a later stage due to lateral diffusion of Ca ions towards an adsorbed DNA molecule. As can be seen in Fig. 5 (Bottom), one has a gradual increase of Ca ions involved in the Ppc–Ca–Pdna bridges with time when more and more ions approach the DNA molecule adsorbed on the bilayer surface. Because this multi-step process is diffusion-limited, formation of Ppc–Ca–Pdna contacts is a relatively slow process and can take 800–1000 ns, see Fig. 5.

In Fig. 6 we further illustrate formation of Ppc–Ca–Pdna bridges due to lateral diffusion of calcium ions (system 9). A series of snapshots clearly demonstrates that Ca ions that are initially far from DNA can diffuse eventually to DNA and to form stable calcium-mediated bridges between phosphate groups of DNA and lipid molecules. We note that upon bridge formation a Ca ion can get inserted underneath a DNA molecule, so that this ion becomes invisible for the top view on a DNA–lipid system, see Fig. 6.

Fig. 6 Lateral diffusion of several Ca ions (yellow, red, green and magenta spheres) on the lipid surface (gray) towards DNA (blue) to form Ppc–Ca–Pdna bridges (top view for system 9): (a) 72 ns, (b) 126 ns, (c) 350 ns and (d) 900 ns.

One of the possible implications of the formation of tight Ppc–Ca–Pdna bridges is that DNA can immobilize some of lipids upon adsorption on the bilayer surface. To verify this hypothesis we evaluated the lateral diffusion coefficient of lipid molecules.

The lateral diffusion coefficient was calculated in line with ref. 39 and 42. In practice, we split last 100 ns of a MD trajectory into 10 pieces. For each piece we calculated the mean-square displacement (MSD) of a lipid; the diffusion coefficient was then evaluated from the slope of the MSD. To improve accuracy, the diffusion coefficient was calculated separately for every piece of the trajectory, providing thereby an estimation for the error margin.

For a pure POPC lipid bilayer (system 5) the lateral diffusion coefficient was found to be 6.8 ± 0.6 × 10⁻⁸ cm² s⁻¹. The experimental value⁴³ for the diffusion coefficient of a POPC bilayer at T = 300 K is 7.8 × 10⁻⁸ cm² s⁻¹. When Ca ions are added to a POPC bilayer system (system 6) the lateral diffusion coefficient drops to 5.5 ± 0.7 × 10⁻⁸ cm² s⁻¹ in line with findings of an earlier computational study.⁴⁰ This is because some of the lipids are now involved in Ca–lipid aggregates and cannot diffuse freely. Finally, for a bilayer–DNA system we first define the lipid molecules that are located beneath DNA by projecting a DNA molecule on the bilayer surface. Given that the lateral displacement of lipids on a time scale of 100 ns is relatively small (no more than ∼0.5 nm), we limit our diffusion coefficient calculations to these selected lipids only. The corresponding value of the lateral diffusion coefficient amounts to 3.8 ± 1 × 10⁻⁸ cm² s⁻¹. Thus, adsorption of DNA on the bilayer surface almost halves the lateral diffusion coefficient of lipids, leading therefore to a considerable immobilization of lipids.

Conclusions

Interactions of DNA with cell membranes and – more specifically – with the phospholipid bilayer matrix lie at the heart of biomedical and nanotechnological applications of DNA and DNA-based nano-structures. Despite enormous recent developments in the field of DNA nanotechnology, very little is known about the lipid–DNA interactions at a molecular level. In this paper we employ biased molecular dynamics simulations to get an atomic-scale insight into such interactions. To this end, we calculated for a first time the free energy profile for partitioning a DNA molecule into a phosphatidylcholine lipid bilayer. Our findings clearly demonstrate that there are no local minima in the energetic profile upon moving DNA from water into the lipid/water interface, so that a zwitterionic lipid bilayer represents a repulsive barrier for DNA. In particular, this eliminates a noticeable contribution of the electrostatic attraction between oppositely charged choline lipid groups and phosphate groups of DNA into DNA–lipid bilayer interactions.

As one of the possible approaches to overcome the DNA–lipid barrier is to use divalent cations to promote the electrostatic attraction between the lipid bilayer surface and DNA, we repeated our biased computer simulations also for a lipid bilayer with adsorbed calcium ions. We show that in this case the free energy profile is characterized by a deep minimum, so that bilayer-bound calcium ions indeed can serve as a trigger of the electrostatic attraction between DNA and lipids. The position of the minimum (which also defines the most probable location of DNA within lipid/water interface) corresponds to a DNA molecule those phosphate groups are in contact with adsorbed Ca ions and – via the ions – with lipid phosphate groups. Additional unbiased simulations of DNA and lipid bilayers with adsorbed Ca ions show interesting features of the kinetics of the DNA adsorption and the equilibrium structure of resulting DNA–lipid complexes. In particular, while the initial binding of DNA is driven by an overall positive charge of the bilayer, the DNA molecule on the bilayer is stabilized by Ca ions that diffuse along with lipids towards DNA and form tight bridges between phosphate groups of DNA and lipids. We also demonstrate that DNA adsorbed on the bilayer surface drastically decreases the mobility of nearby lipid molecules. Overall, our computational results contribute to a long-standing problem of interactions of charged nano-objects (including DNA and DNA-based nanodevices) with cell membranes.

Acknowledgements

The authors wish to acknowledge the use of the Lomonosov supercomputer at the Moscow State University and the computer cluster of the Institute of Macromolecular Compounds RAS. This work was partly supported by the Presidium of the Russian Academy of Sciences through the grant program “Molecular and Cellular Biology”, by the Russian Foundation of Basic Research through Grants 14-03-01073 and 16-33-00167, and by the Saint-Petersburg State University through the grant program “The Event 6” 11.42.1370.2015.

Notes and references

1. M. R. Jones, N. C. Seeman and C. A. Mirkin, Science, 2015, 347, 1260901.
2. Y. Suzuki, M. Endo and H. Sugiyama, ACS Nano, 2015, 9, 3418–3420.
3. S. Kocabey, S. Kempter, J. List, Y. Xing, W. Bae, D. Schiffels, W. M. Shih, F. C. Simmel and T. Liedl, ACS Nano, 2015, 9, 3530–3539.
4. M. Langecker, V. Arnaut, T. G. Martin, J. List, S. Renner, M. Mayer, H. Dietz and F. C. Simmel, Science, 2012, 338, 932–936.
5. G. Stengel, R. Zahn and F. Hook, J. Am. Chem. Soc., 2007, 129, 9584–9585.
6. Y. H. M. Chan, B. van Lengerich and S. G. Boxer, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 979–984.
7. N. S. Selden, M. E. Todhunter, N. Y. Jee, J. S. Liu, K. E. Broaders and Z. Gartner, J. Am. Chem. Soc., 2012, 134, 765–768.
8. M. Langecker, V. Arnaut, J. List and F. C. Simmel, Acc. Chem. Res., 2014, 47, 1807–1815.
9. S. Gromelski and G. Brezesinski, Langmuir, 2006, 22, 6293–6301.
10. V. G. Budker, A. A. Godovikov, L. P. Naumova and I. A. Slepneva, Nucleic Acids Res., 1980, 8, 2499–2516.
11. I. Pfeiffer and F. Hook, J. Am. Chem. Soc., 2004, 126, 10224–10225.
12. K. Börjesson, J. Wiberg, A. H. El-Sagheer, T. Ljungdahl, J. Mårtensson, T. Brown, B. Nordén and B. Albinsson, ACS Nano, 2010, 4, 5037–5046.
13. C. Yoshina-Ishii, G. P. Miller, M. L. Kraft, E. T. Kool and S. G. Boxer, J. Am. Chem. Soc., 2005, 127, 1356–1357.
14. J. O. Rädler, I. Koltover, T. Salditt and C. R. Safinya, Science, 1997, 275, 810–814.
15. B. Pitard, O. Aguerre, M. Airiau, A. M. Lachages, T. Boukhnikachvili, G. Byk, C. Dubertret, C. Herviou, D. Scherman, J. F. Mayaux and J. Crouzet, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 14412–14417.
16. J. J. McManus, J. O. Rädler and K. A. Dawson, J. Phys. Chem. B, 2003, 107, 9869–9875.
17. M. L. Ainalem, N. Kristen, K. J. Edler, F. Hook, E. Sparr and T. Nylander, Langmuir, 2010, 26, 4965–4976.
18. S. Bandyopadhyay, M. Tarek and M. L. Klein, J. Phys. Chem. B, 1999, 103, 10075–10080.
19. M. Tarek, Biophys. J., 2005, 88, 4045–4053.
20. M. Breton, L. Delemotte, A. Silve, L. M. Mir and M. Tarek, J. Am. Chem. Soc., 2012, 134, 13938–13941.
21. S. Khalid, P. J. Bond, J. Holyoake, R. W. Hawtin and M. S. P. Sansom, J. R. Soc., Interface, 2008, 5, 241–250.
22. J. Corsi, R. W. Hawtin, O. Ces, G. S. Attard and S. Khalid, Langmuir, 2010, 26, 12119–12125.
23. A. Yu. Antipina and A. A. Gurtovenko, J. Phys. Chem. B, 2015, 119, 6638–6645.
24. H. R. Drew and R. E. Dickerson, J. Mol. Biol., 1981, 151, 535–556.
25. R. E. Dickerson and H. L. Ng, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 6986–6988.
26. C. J. Dickson, B. D. Madej, A. A. Skjevik, R. M. Betz, K. Teigen, I. R. Gould and R. C. Walker, J. Chem. Theory Comput., 2014, 10, 865–879.
27. A. Perez, I. Marchan, D. Svozil, J. Sponer, T. E. Cheatham, C. A. Laughton and M. Orozco, Biophys. J., 2007, 92, 3817–3829.
28. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935.
29. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
30. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
31. U. Essman, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8592.
32. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447.
33. G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199.
34. S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011–1021.
35. J. S. Hub, B. L. de Groot and D. van der Spoel, J. Chem. Theory Comput., 2010, 6, 3713–3720.
36. E. Heikkila, H. Martinez-Seara, A. A. Gurtovenko, I. Vattulainen and J. Akola, Biochim. Biophys. Acta, Biomembr., 2014, 1838, 2852–2860.
37. V. H. Teixeira, D. Vila-Vicosa, P. B. P. S. Reis and M. Machuqueiro, J. Chem. Theory Comput., 2016, 12, 930–934.
38. A. Arcella, G. Portella, R. Collepardo-Guevara, D. Chakraborty, D. J. Wales and M. Orozco, J. Phys. Chem. B, 2014, 118, 8540–8548.
39. A. A. Gurtovenko and I. Vattulainen, J. Phys. Chem. B, 2008, 112, 1953–1962.
40. R. A. Bockmann and H. Grubmuller, Angew. Chem., Int. Ed., 2004, 43, 1021–1024.
41. D. Vila-Vicosa, V. H. Teixeira, H. A. F. Santos, A. M. Baptista and M. Machuqueiro, J. Chem. Theory Comput., 2014, 10, 5483–5492.
42. A. A. Gurtovenko, J. Chem. Phys., 2005, 122, 244902.
43. R. A. Bockmann, A. Hac, T. Heimburg and H. Grubmuller, Biophys. J., 2003, 85, 1647–1655.

---