Oscillatory regimes of capillary imbibition of viscoelastic fluids through concentric annulus

Abstract

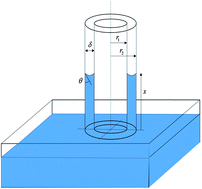
In this study, we analyze the capillary filling dynamics of a viscoelastic fluid through a concentric annulus, which has far reaching consequences in practical applications and offers a distinct disparity in the dynamical characteristics as compared to the classical cylindrical capillary based paradigm. Such non-trivial characteristics are primarily attributed to a complex and intricate interplay between the intrinsic fluid rheology and the annular flow geometry, as is effectively manifested through distinctive features of the underlying oscillatory dynamics. We also estimate a criterion for the onset of oscillations, as a function of the Bond number. Our results predict remarkably attenuated oscillatory behavior and a higher capillary rise due to the presence of an annular geometry, as compared to a cylindrical one. We further relate the primary peak overshoot response with the Bond number that enables us to draw further physical insights into the oscillatory regime dynamics.

---

1. Introduction

Flow actuation and transport phenomena due to capillary action find their use in various fields of science and engineering, namely droplet dynamics,^1–8 groundwater movement, heat pipes, lab-on-a-chip micro-devices, micro-total analysis systems, candle wicks, marker pens, to name a few.^1,9–12 Capillary action is the phenomenon in which fluid motion is driven by surface tension effects through narrow confinements.^1,12 Analysis of capillary dynamics, thus, demands a comprehensive understanding of the basic physical concepts arising within it, in an effort to optimize various flow conditions and increase the volume throughput.

A careful observation of the reported studies on capillary filling^{1–8,13–15} indicates that those are primarily concerned with the transport of fluids through circular or rectangular channel geometries. However, besides studies related to the capillary filling in simple geometries, certain other channel geometries find emerging importance in capillary filling studies due to the interesting consequences of shape-induced alterations in the surface tension and viscous effects. In practice, the use of different geometries in capillary filling dynamics may be exploited to harvest and study a non-trivial interplay of the different forces affecting the capillary front motion, and may find relevance in the fields of transport phenomena in concrete structures, porous materials with complex pore structures, heat pipes^16–18 and other industrial applications. In oil and gas industry, the pumping of drill mud through concentric annular space (space between the drill pipe and the wellbore) over long distances is necessary.^19,20 In industries dealing with slurries like processed foodstuff, sewage and industrial waste, and in those handling molten plastic undergoing extrusion processes, flow of non-Newtonian fluid through annular space is essentially encountered.^19,21 Furthermore, studies regarding capillary action of complex fluids find ever-increasing importance in various interdisciplinary fields, like blood flow through micro-capillaries or flow of polymers through porous media,^1,11 flow of polymer solution, lubricants and other biofluids.^22,23 Many of these fluids are non-linear in their constitutive behavior and have viscoelastic characteristics.^19,24–28 Capillary filling dynamics of viscoelastic fluids through concentric annulus, however, has not been investigated previously,^13,29 to the best of our knowledge.

Here we analyze the capillary front evolution of a viscoelastic fluid, particularly following the Phan-Thien and Tanner (PTT) constitutive model,³⁰ through a concentric annulus. We employ the reduced order model^3,4 for the study of the capillary filling dynamics, which is found to be fairly accurate in estimating the capillary front evolution within the conduit.^29,31,32 In particular, we focus on the oscillatory regime that the capillary front encounters, before the front settles at the equilibrium Jurin height.^14,33 In the literature, researchers have observed the tendency of oscillation before attaining an equilibrium Jurin height for capillary filling of viscoelastic fluids through simple cylindrical geometries.¹⁴ Here, we report the distinctive features in such oscillatory behavior of the capillary front, as an intrinsic consequence of the annular geometry. Furthermore, we attempt to address the criterion for the onset of oscillatory dynamics for the present scenario and link it with the corresponding dimensionless numbers in the linear rheological regime.

2. Mathematical modeling

We consider a viscoelastic liquid rising through a narrow annular capillary formed by the gap between two concentric cylinders, under the action of surface tension forces, as shown in Fig. 1. The concentric cylinder has an inner radius of r₁ and outer radius r₂, with capillary gap δ = r₂ − r₁. The origin of the cylindrical coordinate system is present at the plane of capillary entry and the center of the concentric cylinders. We appeal to the reduced order description^3,4,13,14,34 and attempt to build the governing equation of the meniscus height development, the equilibrium height, and the oscillatory characteristics. For the present analysis, we denote the density of the fluid by ρ, viscosity by μ, the equilibrium contact angle at the fluid–solid–gas interface by θ, and the surface tension at the fluid–gas interface by σ.

Fig. 1 A schematic representation of capillary penetration through concentric cylindrical geometry. The angle θ represents the contact angle during the capillary motion.

In order to capture the transients of the capillary height rise, one must account for all the forces; namely the inertial, viscous, surface tension and gravitation forces. Applying the above mentioned force balance, the governing equation to model the capillary filling dynamics is given as,^13,14

where x denotes the axial coordinate in the direction of capillary rise and r is the radial coordinate. Descriptions of the surface tension and gravity forces in eqn (1) are trivial. However, more comprehensive considerations are demanded for evaluating the viscous drag force, which we outline first.

2.1. Viscous force evaluation following the Phan-Thien and Tanner (PTT) model

Diverse constitutive models describing viscoelastic fluid rheology^35,36 range from linear Maxwell's model to the non-linear Oldroyd B model.^37,38 In this present work, we consider one of the most commonly studied viscoelastic models, known as Phan-Thien and Tanner (PTT) constitutive model,³⁰ which describes the behavior of wide variety of fluids including complex biofluids such blood.^24,25,27 In this section, first we model the viscous forces that the PTT fluid experiences under the capillary action. Towards this, we appeal to the relation describing linear PTT constitutive behavior that is given by³⁰where τ and D denotes the deviatoric stress and deformation rate tensor, respectively; λ denotes the relaxation time, μ stands for the viscosity coefficient and τ^∇ is the Gordon–Schowalter derivative, while ε signifies the elongation behavior of the fluid and u is the velocity vector field.

For the estimation of viscous forces in the scope of the reduced order formalism,^4,13,14 we first proceed to calculate the average flow velocity for a fully developed laminar flow of PTT fluid within a concentric annular channel of radius ratio κ = r₁/r₂, and successively formulate the resulting viscous forces. This average velocity further represents the rate of advancement of the capillary front in the form U = dx/dt.⁴ The non-vanishing components of the stress tensor of PTT rheology from eqn (2) are then given by

where [small gamma, Greek, dot above] = du/dr is the shear rate. Dividing eqn (4) by the square of eqn (3) gives the form

For a steady pressure-driven flow, P = −dp/dx, within an annular channel of micro-scale dimensions, the shear stress distribution is given by the form³⁹

where r_* denotes the position between r₁ and r₂ signifying the plane of vanishing shear stress. A specific challenge in studying the capillary rise through any confinement is finding the location of the zero-shear plane. The plane of zero-shear (r_*) cannot be explicitly assumed beforehand in the solution process for an annular geometry, unlike what has been previously done for geometries involving circular or rectangular cross-section. The non-dimensional shear stress using eqn (6) is then represented aswhere ⁴⁰ is used to define the characteristic velocity scale, U defines the average velocity of the capillary fluid and y ≡ r/δ with y_* ≡ r_*/δ defining the non-dimensional positional parameters. Similarly, eqn (5) has the dimensionless form as;

T_xx = 2De_cT_rx² (8)

where De_c = λU/δ denotes the Deborah number, which is the ratio of the relaxation time-scale of the fluid to the characteristic time-scale of the flow system.

The velocity gradient may now be directly deduced from eqn (3), having the form

The shear rate may be described in a non-dimensional form by taking Γ ≡ [small gamma, Greek, dot above]/(U/δ)

Γ = T_rx(1 + εDe_cT_xx) (10)

Substituting eqn (7) and (8) into eqn (10), we obtain the following equation for dv/dy as

The form obtained above is integrated employing the no-slip boundary condition at the inner wall u(y = κ/1 − κ) = 0, giving an expression for ν (where v = u/U) as

The no-slip boundary condition at the outer boundary of the annulus u(y = 1/1 − κ) = 0 is imposed on this expression for ν, resulting in the following equation which is cubic in m_* (where m_* = y_*²)

here G is defined as a dimensionless number G = U_c/U which physically signifies as the non-dimensional pressure gradient. The average velocity across the cross-section of the concentric annulus is determined using , where the velocity u is obtained from relation of ν from eqn (12). The following equation is obtained after integration:⁴⁰

I₁G − 32εDe_c²y_*²I₂G³ − 1/y_*²(8(1 − κ)/(1 + κ)) = 0 (14)

where and

The two unknowns y_* and G can now found using an iterative solution of the eqn (13) and (14). Once we have the knowledge of G, the total viscous force per unit length acting on both cylindrical walls is determined using eqn (6) in terms of U and G, to get

2.2. Equation of motion

In an effort to complete the description of the equation of motion of the capillary front, following eqn (1), the surface tension force and the gravity force also need to be prescribed. The surface tension force is given by F_surf = 2π(r₂ + r₁)σ cos(θ) and the hindering force of gravity is given in the form F_grav = ρπg(r₂² − r₁²)x. Thus, the resulting dimensionless governing equation, using the dimensionless parameters x̄ = x/δ, t̄ = t/t₀, as obtained from the viscous, surface tension, gravitational and inertial force balance (as shown in eqn (1)) reads

The simplification to non-dimensional form is performed using the terms x̄ = x/δ and where the reference time scale is given by , with the dimensionless parameters appearing in the governing equation are and .

Eqn (16) is a non-linear governing equation that describes the forward motion of the capillary front, wherein the value of G has to be updated in every time step calculation. A subtle observation from eqn (16) reveals that the motion is independent of radius ratio κ except through the value of G. However, a striking characteristics to note that the magnitude of G itself is independent of κ,⁴⁰ and therefore, the height rise of the capillary front becomes effectively κ-independent. An elaboration and further discussion on this will be made in the Results and discussion section.

2.3. Criterion of oscillation

One of the important but subtle features of the above equation is that it predicts an oscillatory nature of the capillary front near the Jurin height, which can be tracked by a linearized approximation of the governing equation about the Jurin height. Previously, numerous studies were performed where scaling analysis were employed to delineate the condition of oscillation.^13,14 At large times in capillary filling, the capillary front either gradually reaches to the equilibrium Jurin height and stops or undergoes a damped oscillatory motion about the mean Jurin height before cessation of motion. The prediction on the criteria of oscillation has previously been captured theoretically by employing the relevant non-dimensional parameters;¹³ and these criteria also been experimentally verified.⁴¹ Here a quantitative approach is followed to obtain a close approximation of the oscillatory regime and predict a dimensionless criterion for the onset of oscillation as the capillary front approaches the Jurin height (the non-linearity of the constitutive model leads to the approximation in onset of oscillatory criteria evaluation). Towards this, we first obtain the equilibrium Jurin height from eqn (16) which can be determined by setting the inertial and viscous terms to zero. The required dimensionless form of the Jurin height is given by

Now, we recast eqn (16) with the substitution x̄ = J̄ − x⌢, which transforms the origin of the measurement at the Jurin height. This facilitates the linearization of the governing equation about the Jurin height wherein we neglect all the nonlinear terms involving and as each of these terms are ≪1 near the equilibrium height. Finally, a rescaling of the governing equation by X = x⌢/J̄, in order to magnify the variations about the Jurin height is done, and the resulting equation reads

where and . Eqn (18) is the governing form of a damped oscillatory motion with a natural frequency . Here we use eqn (18) to find the criteria for oscillation. The onset of oscillation will occur if the system is under-damped whereas over-damped system, signifying dominant viscous effects compared to gravitational effects, will ensure that no oscillatory motion occurs.¹³

Resorting to a solution of type , we find the roots of the equation of type (18) are . Here we note that the criterion for the onset of oscillations is achieved when A² − 4ω² < 0. With the aforementioned analysis of the capillary motion, the criterion of onset of oscillation derivation leads to the form

An equivalent non-dimensional form for the above criteria reads¹⁴

wherein the right hand side of eqn (20) will be denoted as , or the critical Bond number. In the above equations, the value of G is either obtained during the simulation, when fluid reaches close to Jurin height, or by solving eqn (13) and (14) simultaneously, using the scaled Deborah number which is

It must here be noted that the Deborah number De_c needs to be dynamically estimated during the simulation run, while the scaled Deborah number De is the dimensionless input parameter representing the extent of viscoelasticity that the fluid exhibits. If G is calculated using the scaled value (eqn (21)), there would not be any need to obtain it dynamically from the simulation. Accuracy of the will significantly depend on how G is estimated, and will be further explored in the subsequent section.

The effects of rheology are estimated through the parameter G, which in turn is a function of λ (or De). From qualitative considerations, it may be inferred that for a particular radius difference (δ), an increase in the value of De causes the viscous damping to get attenuated, therefore, leading to oscillations. The influence of radius ratio has a complicated and intricate influence on the resulting criteria; however, qualitatively it can be inferred that for a given outer radius an increase in the radius ratio κ, reduces the capillary front oscillation.

3. Results and discussions

As discussed earlier, various factors may contribute to the oscillatory nature of the capillary front before it finally settles to the equilibrium Jurin height. In the present section, we focus on the oscillatory regimes of the capillary filling dynamics, and discuss the effects of various parameters that lead to capillary oscillation. Further, we make an analytical argument on the accuracy of the onset of oscillation criteria in terms of linearity of the governing equations.

Fig. 2 depicts the capillary front advancement for a viscoelastic fluid as a function of the dimensionless time for different Deborah numbers (De). An increase in De leads to elasticity dominated behavior of the fluid, thereby, enhancing the oscillatory characteristic of the capillary front. An increase in De increases the relaxation time λ as compared to the system time scale, and in turn decreases the shear stress (or viscous effects) monotonically. Therefore, an increase in De results in higher oscillation amplitude and a larger settling time, as can be observed in the above figure. For fluids belonging to the viscoelastic regime, such trends have also been reported in previous studies.^14,42 Inset of Fig. 2 describes the variation of the rate of capillary front advancement with dimensionless time for corresponding De values. It is apparent that the initial stages of filling, the capillary front velocities are high owing to the surface tension dominated transport. With time, as the front reaches the equilibrium Jurin height, the rate of capillary front advancement reduces and settles to zero. However, the settling characteristics become increasingly oscillatory as the De number is increased. In fact, higher De gives a higher oscillation velocity, and consequently, larger oscillation amplitude is observed.

Fig. 2 Non-dimensional capillary penetration distance x̄ as a function of non-dimensional time t̄ for viscoelastic fluids, corresponding to different scaled Deborah numbers. Other parameters in the figure include Ca = 0.002, Bo = 0.02, ε = 0.25 and κ = 0.5. Inset of the figure shows the variation of the capillary filling velocity as a function of time, for different Deborah number.

Fig. 3 depicts the progress of the capillary front with dimensionless time for various combinations of radius ratio κ and the capillary number. The corresponding dimensionless governing equation that is solved for the present case, re-normalized with x̃ = x/r₂ and t̃ = t/t̃₀, is given as wherein the dimensionless parameters have the form ; ; and the modified time scale is chosen as . In the previous δ − t₀ non-dimensionalization procedure, even changing the value of radius ratio κ, the effective gap may be kept constant, and hence, the effect of change in κ cannot be explicitly depicted (as seen from eqn (16)). However, with the present r₂ − t̃₀ non-dimensionalization procedure, the dependence on radius ratio can be clearly shown. A direct observation from the present derived equation with r₂ − t̃₀ normalization shows that for a given outer radius r₂, the liming case of κ → 0 explicitly provides the governing equation for capillary filling through a cylindrical channel. It is observed in Fig. 3 that for a given outer radius, increasing the radius ratio κ (or decreasing the effective gap between the concentric capillaries) increases the Jurin height. At the limiting case for κ → 0 signifying a cylindrical geometry, the equilibrium height is minimum for a given outer radius. Although the Jurin height is independent of the Capillary number, as discussed earlier, the onset of oscillation depends both on the Capillary number and the effective gap (r₂ − r₁). Thus, for a lower Capillary number and higher gap (low κ), oscillations of the capillary front set in. It can be concluded from this figure that for a given outer radius, a pure cylindrical channel will induce higher oscillations to the capillary front than an annular channel.

Fig. 3 Dimensionless capillary penetration length x̃ = x/r₂ as a function of non-dimensional time for different κ and . Here the capillary filling length is non-dimensionalized using outer radius r₂. The other parameters for the present figure include , , ε = 1. The tilde sign is to demarcate the different type of dimensionalization from that shown above, the rationale of which will be elaborated in the corresponding discussion. The solid and dashed lines that converge at large times are drawn for same capillary number.

The effect of Capillary number and Bond number has also intriguing influence on the characteristics of the capillary filling dynamics. However, since the influences of these parameters have fairly been well documented in the literature,^13,14,34,43 for the sake of brevity, we have not included them in the present work. Nevertheless, few significant remarks at this stage must be reported. It is observed that at larger Deborah number, an increase in Ca induces higher oscillation amplitudes, attributable to further decrease in the viscous damping. However, for the systems not exhibiting oscillations (large Ca filling regime),an increase in De reduces viscous effects, thereby decreasing the settling time if the capillary number is greater than the critical capillary number (signifying no oscillations) for a particular Bond number. One further interesting aspect to note is that the oscillatory nature is revealed at higher Bond number regimes. This is consistent with an inference previously drawn (as shown in eqn (20)) that there is a critical Bond number above which the capillary front experiences an oscillatory motion before finally reaching the equilibrium Jurin height. With these observations, we proceed to demonstrate the effect of fluid rheology on the oscillation criteria and peak overshoot of the capillary front.

3.1. Rheological influence on peak overshoot

Fig. 4a represents the evolution of x̄_max/J̄ as a function of Bo/ for viscoelastic fluids, corresponding to different Deborah numbers. For the evaluation of the critical Bond number criterion (or ) for the above figure, we have used the values of G as obtained dynamically from simulations using eqn (20). The rationale of choosing the updated value of G will be clear while elaborating the figure inset. It is noteworthy that the expression of is obtained after linearization of the pertinent differential equation, and therefore, value of should always fail to take into account the non-linear viscoelastic nature.¹⁴ It can be seen that as the Deborah number increases, the prediction from the above equation becomes erroneous suggesting that the non-linear viscoelastic nature enhances with an increase in the Deborah number (while De = 0 represents the Newtonian fluid case). It must, however, be noted that for low Deborah number (De < 1), the formulation can effectively capture the Bond number criteria. This can be seen clearly since the ratio of x̄_max/J̄ remains unity suggesting no oscillations till the point the ratio Bo/ remains unity. Nevertheless, to visualize how the start of oscillations or changes with De, we need to look at inset of Fig. 4a, where circular marker describes the actual critical Bond number (or Bo*), square marker gives criteria using the updated velocity from simulation (to obtain De used by the coupled equations), and criteria represented by rhombus shaped markers can be found without simulation. The Bo* is obtained from the simulations by noting the Bond number at which the oscillation just initiates. Both the criteria obtained in the mathematical modeling section closely follow the trend shown by the actual critical Bo (Bo*). However, the Bond number criteria associated with the updated simulated velocity (eqn (20)) gives a fundamentally more consistent prediction with Bo* for low De values. This is the primary reason to employ the updated value of G for Fig. 4a. The deviation of estimation of Bond number criteria prediction using the scaled velocity from Bo* is attributed to the high non-linearity in the viscoelastic fluid rheology.

Fig. 4 Variation of x̄_max/J̄ as a function of Bo/ for (a) different Deborah numbers; (b) different capillary numbers with De = 0.05. Extensibility parameter ε and radius ratio κ are fixed at 0.25 and 0.5 for all cases, respectively. Inset of (a) represents Bo criteria obtained using different calculation methodologies mentioned in mathematical formulation section.

Fig. 4b represents the evolution of x̄_max/J̄ as a function of Bo/ for viscoelastic fluids for different Capillary numbers, with a fixed Deborah number at 0.05. A small De effectively signifies the case when the fluid tends toward Newtonian rheology. It is interesting to note that for such low De, the different lines practically converge together exhibiting a capillary number independence regime. To explore the reason, why the ratio is independent of the Capillary number for the limiting linear (Newtonian) regime (De < 1), we attempt to explore the analytical framework starting from a general form of a second order differential equation governing oscillatory motion:

where T₁ and T₂ are arbitrary, constant coefficients. The ratio of the initial peak overshoot to the equilibrium height (similar to x̄_max/J̄), for a differential equation of the form in eqn (22) is represented by M given by:⁴⁴where is the damping factor in eqn (22),⁴⁴ and results in the form

The criteria for onset of oscillations, as was mentioned before, read T₁² < 4T₂.The above differential form is similar to the one that we obtain pertinent to the present work, after linearizing the governing equation, which gives the form as shown in (18).

Proceeding exactly in a similar manner for a Newtonian fluid that is rising through an annular channel due to surface tension effects, the values of the constants shall be and The corresponding dimensional values would be and .

Comparing the form of eqn (18) and (22), it can be said that T₁ and T₂ of eqn (22) can be written in the form of T₁ = Caf₁ and T₂ = Bo²f₂, where f₁ = 8G and f₂ = 1/cos(θ) are functions of radius ratio (κ) and the contact angle (θ), respectively. Substituting these values into the form we get,

The dimensionless criterion for oscillation for the Newtonian counterpart, obtained in a similar manner as shown for viscoelastic fluid, is . Now, the criterion for oscillation for Newtonian fluids may be cast as ( is the critical Bond number above which oscillations may occur), which, when substituted in eqn (25) gives

From eqn (26), it is apparent that M = x̄_max/J̄ is only a function of and a plot with x̄_max/J̄ against , thus, becomes independent of the Capillary number, radius ratio (κ) and contact angle (θ) for Newtonian fluid rheology (which is simulated as De → 0). Such a trend can only be expected if the equations have a fairly linear nature; however, for highly non-linear governing equations, as in the case for PTT rheology, a deviation from this a trend has been observed.

3.2. Experimental perspective

Although the literature lacks thorough experimental investigations of viscoelastic flows through capillary annulus, there are comprehensive experimental studies for the capillary rise of Newtonian fluids through cylindrical channels.^41,45–47 No parallel study, however, has been performed where these studies are theoretically verified as a limiting case of capillary dynamics for a viscoelastic fluid. Towards this, we attempt to validate our theoretical model in the limiting case with De → 0 (signifying Newtonian rheology) and κ → 0 (signifying single cylindrical capillary) with experimental studies performed previously.

Fig. 5 depicts the progression of the capillary front (in m) as a function of time (in seconds) for different values of the relaxation time (or, equivalently, De number). In the figure t₀ represents the system time scale that is chosen as . A relaxation time, for example, λ = 5t₀ signifies an equivalent dimensionless De = 5. From the figure it is apparent that in the limit of De → 0, as the viscoelastic nature reduces (as λ vanishes), the theory simulates the case of capillary rise of Newtonian fluid through a cylindrical channel. For De = 0 and κ = 0, our theoretical lumped parameter model makes a close prediction of the experimental data obtained from ref. 45. However, with an increase in the relaxation time, and thereby the De, a higher oscillation of the capillary front is observed which is characteristic to any viscoelastic fluid. In the figure inset, we further attempt to simulate the case of another experimental study (ref. 46) in the limit De = 0 and κ = 0. We find a close prediction for the same where the oscillation peaks are grossly captured by the lumped-order model. Therefore, a close approximation of capillary front dynamics is obtained for Newtonian fluids employing the present theoretical analysis and such an analysis may be extended to predict capillary rise dynamics involving viscoelastic flows.

Fig. 5 The capillary front progression x with time t for different values of relaxation time λ (t₀ represents the system time scale). The lines represent the results from the theoretical analysis and the circular markers represent the experimental data for Newtonian rheology obtained from ref. 45. Experimental conditions: density, capillary radius, contact angle, surface tension, and viscosity are 710 kg m⁻³, 0.5 mm, 0, 16.7 mN m⁻¹ and 0.6 mPa s. Inset shows the capillary front position with time based on theoretical analysis (solid line; plotted for Newtonian rheology) and experimental data (circular markers) obtained from ref. 46. Experimental conditions: density, capillary radius, contact angle, surface tension, and viscosity are 710 kg m⁻³, 0.68 mm, 0, 16.6 mN m⁻¹ and 0.3 mPa s.

4. Conclusions

In the present study, we have investigated the capillary filling dynamics of a viscoelastic fluid rising through a concentric annular channel. Reduced order formalism has been employed to derive the differential form of the governing equations and various forces associated with the flow for a fluid modeled using the PTT-constitutive relation. It must be noted that the Lucas–Washburn formulation has been rigorously applied in numerous theoretical studies in order to predict the capillary front dynamics in the scope of lumped-order parameter analysis.^13,14,23,34 The same is also used for the present problem, following an approach that has been grossly successful to closely predict the results of numerous experimental^{34,41,48–50} and molecular dynamic studies.⁵¹ An approximate analytically-based and numerically-based criterion for the onset of oscillation for such fluids has been derived. It is observed that the capillary front encounters an oscillatory regime for particular cases before settling to the equilibrium Jurin height. It has been shown that as the radius ratio decreases, there is a greater tendency for the capillary front to encounter an oscillatory regime before flow cessation. In sharp contrast to the case of capillary filling of viscoelastic fluid through a cylindrical capillary, for annular geometry, we report attenuation in the oscillatory tendency, with a greater Jurin height attainment for an annular channel having the same outer radius. This is attributed to the interplay between the complex constitutive behavior and the annular nature of the geometry. Furthermore, oscillatory regime for Newtonian fluids has previously been predicted from linearity analysis,^{13,14,22,33,41} although no such parallel analysis for concentric annular capillary rise of viscoelastic fluids has been reported. Since the oscillatory nature of any viscoelastic fluid is enhanced due to its extensibility property, a closer look at the oscillatory regime in the presence of such non-linearity is essentially demanded.¹⁴ In the present study, therefore, we additionally address the oscillation criteria of the capillary front about the Jurin height and demarcate the oscillatory nature established for a concentric annular channel from that in a cylindrical channel. The approximate criterion is compared with the actual criterion obtained through simulations. Besides the oscillatory criterion, we appeal to the non-linearity of the flow behavior and re-focus on the added insights in the oscillatory dynamics due to the viscoelastic nature. We demonstrate that in the oscillatory regime of the capillary filling, the ratio of the peak overshoot of the capillary front to its Jurin height is independent of the Capillary number of the flow when the fluid rheology tends towards Newtonian constitutive nature as a limiting case. However, such a Capillary-number independent situation disappears as non-linear effects, due to the viscoelastic nature of the fluid, become dominant in the physical paradigm. These results may have significant implications in designing of annular flow geometries for capillary filling with complex fluids that are inherently nonlinear in their constitutive nature.

Nomenclature

δ	Capillary gap
r1	Inner radius
r2	Outer radius
θ	Equilibrium contact angle
x	Axial coordinate in direction of capillary rise
x̄	Non-dimensional axial coordinate with respect to δ
	Non-dimensional axial coordinate with respect to δ variation with respect to time
x̃	Non-dimensional axial coordinate with respect to r2
J	Jurin height
J̄	Non-dimensional Jurin height with respect to δ
r	Radial coordinate
t	Dimensional time
t0	Reference time-scale
t̄	Non-dimensional time with respect to
t̃	Non-dimensional time with respect to
τ	Deviatoric stress
D	Deformation rate tensor
λ	Relaxation time
μ	Viscosity coefficient
τ^∇	Gordon–Schowalter derivative
ε	Elongation behavior
κ	Radius ratio
[small gamma, Greek, dot above]	Shear rate
r*	Radial distance of cylindrical surface of zero-shear
Trx	Non-dimensional shear stress
Uc	Characteristic velocity scale
U	Average velocity of capillary fluid
y and y*	Non-dimensional radial coordinates
m*	Equals to y*^2
Dec	Deborah number
De	Scaled Deborah number
Bo	Bond number
	Critical Bond number
Bo*	Actual critical Bond number
Ca	Capillary number
	Critical Capillary number
G	Non-dimensional pressure gradient

Acknowledgements

The corresponding author gratefully acknowledges the financial support provided by the Indian Institute of Technology Kharagpur, India [Sanction Letter no.: IIT/SRIC/ATDC/CEM/2013-14/118, dated 19.12.2013]. All the authors acknowledge the help and references provided Dr Uddipta Ghosh, a researcher in the same group of authors.

References

1. S. Chakraborty, Lab Chip, 2005, 5, 421–430.
2. N. Fries and M. Dreyer, J. Colloid Interface Sci., 2008, 320, 259–263.
3. R. Lucas, Kolloid-Z., 1918, 23, 15–22.
4. E. W. Washburn, Phys. Rev., 1921, 17, 273–283.
5. D. Quéré, Europhys. Lett., 1997, 39, 533–538.
6. N. Desai, U. Ghosh and S. Chakraborty, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 063017.
7. A. Hamraoui and T. Nylander, J. Colloid Interface Sci., 2002, 250, 415–421.
8. F. Chauvet, S. Geoffroy, A. Hamoumi, M. Prat and P. Joseph, Soft Matter, 2012, 8, 10738–10749.
9. T. M. Squires and S. R. Quake, Rev. Mod. Phys., 2005, 77, 977–1026.
10. K. D. Altria, Capillary Electrophoresis Guidebook: Principles, Operation, and Applications, Springer Science & Business Media, 1996.
11. L. A. Richards, Physics, 1931, 1, 318.
12. P. M. Ajayan and S. lijima, Nature, 1993, 361, 333–334.
13. S. Das and S. K. Mitra, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 063005.
14. A. Bandopadhyay, U. Ghosh and S. Chakraborty, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 053024.
15. R. Chebbi, J. Colloid Interface Sci., 2011, 361, 639–642.
16. H. T. Nguyen and B. R. Sørensen, Adv. Mater. Res., 2013, 652–654, 1201–1208.
17. S. Chibbaro, E. Costa, D. I. Dimitrov, F. Diotallevi, A. Milchev, D. Palmieri, G. Pontrelli and S. Succi, Langmuir, 2009, 25, 12653–12660.
18. H. Smirnov, in Transport Phenomena in Capillary-Porous Structures and Heat Pipes, CRC Press, 2009, pp. 17–40.
19. M. Escudier, P. Oliveira, F. Pinho and S. Smith, Exp. Fluids, 2002, 33, 101–111.
20. Y.-J. Kim, S.-M. Han and N.-S. Woo, Korea Aust. Rheol. J., 2013, 25, 77–85.
21. C. C. Wilson, Computational Rheology for Pipeline and Annular Flow, Gulf Professional Publishing, 2001.
22. S. G. Hatzikiriakos, J. Rheol., 1992, 36, 845.
23. S. Chakraborty, Anal. Chim. Acta, 2007, 605, 175–184.
24. F. T. Akyildiz, Int. J. Eng. Sci., 2002, 40, 859–872.
25. G. B. Thurston, Biophys. J., 1972, 12, 1205–1217.
26. T. Hayat, S. Noreen and A. A. Hendi, Journal of Biorheology, 2011, 25, 8–17.
27. P. C. Sousa, F. T. Pinho, M. S. N. Oliveira and M. A. Alves, Biomicrofluidics, 2011, 5, 014108.
28. J. S. Field, M. V. Swain and N. Phan-Thien, J. Non-Newtonian Fluid Mech., 1996, 65, 177–194.
29. R. M. Digilov, Langmuir, 2008, 24, 13663–13667.
30. N. P. Thien and R. I. Tanner, J. Non-Newtonian Fluid Mech., 1977, 2, 353–365.
31. G. Martic, F. Gentner, D. Seveno, D. Coulon, J. De Coninck and T. D. Blake, Langmuir, 2002, 18, 7971–7976.
32. P. Joos, P. Van Remoortere and M. Bracke, J. Colloid Interface Sci., 1990, 136, 189–197.
33. O. Shardt, P. R. Waghmare, J. J. Derksen and S. K. Mitra, RSC Adv., 2014, 4, 14781–14785.
34. J. Dhar, U. Ghosh and S. Chakraborty, Soft Matter, 2015, 11, 6957–6967.
35. K. G. Kornev and A. V. Neimark, J. Colloid Interface Sci., 2003, 262, 253–262.
36. G. R. Cokelet, Annu. Rev. Physiol., 1980, 42, 311–322.
37. J. C. Maxwell, Philos. Trans. R. Soc. London, 1867, 157, 49–88.
38. J. G. Oldroyd, Proc. R. Soc. London, Ser. A, 1950, 200, 523–541.
39. A. Fredrickson and R. B. Bird, Ind. Eng. Chem., 1958, 50, 347–352.
40. F. T. Pinho and P. J. Oliveira, J. Non-Newtonian Fluid Mech., 2000, 93, 325–337.
41. R. Masoodi, E. Languri and A. Ostadhossein, J. Colloid Interface Sci., 2013, 389, 268–272.
42. P. P. Bhat, O. A. Basaran and M. Pasquali, J. Non-Newtonian Fluid Mech., 2008, 150, 211–225.
43. S. Das, P. R. Waghmare and S. K. Mitra, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 067301.
44. K. Ogata, Modern Control Engineering, Prentice Hall, 5th edn, 1970.
45. B. V. Zhmud, F. Tiberg and K. Hallstensson, J. Colloid Interface Sci., 2000, 228, 263–269.
46. D. Quéré, É. Raphaël and J.-Y. Ollitrault, Langmuir, 1999, 15, 3679–3682.
47. A. Hamraoui and T. Nylander, J. Colloid Interface Sci., 2002, 250, 415–421.
48. N. R. Tas, J. Haneveld, H. V. Jansen, M. Elwenspoek and A. van den Berg, Appl. Phys. Lett., 2004, 85, 3274.
49. J. Haneveld, N. R. Tas, N. Brunets, H. V. Jansen and M. Elwenspoek, J. Appl. Phys., 2008, 104, 014309.
50. J. M. Oh, T. Faez, S. de Beer and F. Mugele, Microfluid. Nanofluid., 2010, 9, 123–129.
51. D. I. Dimitrov, A. Milchev and K. Binder, Phys. Rev. Lett., 2007, 99, 054501.

---