Open Access Article
Open Access ArticleSurface free energy tuning of supported mixed lipid layers†
Dubravko
Risović
*ab,
Abra
Penezić
c,
Vida
Čadež
c,
Suzana
Šegota
c and
Blaženka
Gašparović
c
aMolecular Physics Laboratory, Ruđer Bošković Institute, POB 180, HR-10002 Zagreb, Croatia. E-mail: drisovic@irb.hr
bCentre of Excellence for Advanced Materials and Sensing Devices, Ruđer Bošković Institute, Croatia
cDivision for Marine and Environmental Research, Ruđer Bošković Institute, POB 180, HR-10002 Zagreb, Croatia
First published on 26th May 2016
Abstract
Supported lipid layers are commonly used as model systems for biological membranes with high potential for diverse (bio)technological applications including the development of novel sensors. The aim of this study was to investigate the influence of mixing ratio and subphase used in the monolayer assembly on the surface free energy (SFE) of supported palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and oleic acid triglyceride (triolein) (TO) mixed lipid monolayers on a mica substrate. The supported layers were formed by Langmuir–Blodgett transfer of mixed monolayers assembled on a subphase of ultra-pure water and electrolyte (0.55 M NaCl, pH 8.1). AFM and fractal/lacunarity analysis were used to elucidate their relevant topographical features while the SFE and its polar and dispersive component were determined using contact angle measurements. The results showed that the monolayers formed on an electrolyte subphase are more stable than those on a water subphase, while their homogeneity and topographical features depend on the mixing ratio. The SFE of a mixed layer depends on the mixing ratio and the subphase type used in the self-assembly of the Langmuir monolayer, but is also influenced by the saturation/unsaturation of the hydrophobic tail chain. Thus, changing the subphase and the POPC/TO mixing ratio allows for change of the supported layer's wetting properties from hydrophilic to strongly hydrophobic. The results of this study should contribute to better understanding of the SFE of supported mixed lipid films and allow the tailoring of surfaces with targeted properties.
1. Introduction
Supported lipid layers formed by the transfer of Langmuir monolayers from a liquid subphase onto a solid surface are commonly used as model systems for biological membranes. Such systems are increasingly attracting attention and recently have been the subject of intense studies due to their potential (bio)technological applications.1–5 In particular, the supported lipid mono- and bilayers are often used as sensing element hosts in the development of various novel sensors.6–10 The energetic and wetting properties of lipid films deposited on a solid support can be characterized by the determination of the surface free energy (SFE). The SFE significantly influences the physicochemical processes occurring at the interface, and its magnitude arises from the kind and strength of the involved intermolecular interactions. In particular, it influences interfacial adhesion processes, film functionalization and also the diffusive transport in microfluidic sensors.11–14 Hence, the performance of a sensor relying on functionalized or membrane based lipid films depends on the film's SFE. On the other hand, aside from the lipid type, the SFE of a supported mixed lipid layer is influenced by several other parameters, of which the mixing ratio, type of a subphase used in the self-assembly of a Langmuir layer and wetting properties (hydrophobicity/hydrophilicity) of the supporting substrate play a significant role. Understanding the influence of these parameters on SFE could provide the means allowing for tuning of surface free energy of a supported layer in a systematic manner.13 This, in turn, should contribute to the ability of designing supported layers with novel or desired properties. Although recently considerable efforts were put into investigation of SFE of mixed lipid layers,11,15–17 insofar as we know there was no investigation into the influence of the subphase used in the assembly of Langmuir layer on the SFE of the transferred mixed lipid layer.In this context, our aim was to investigate the influence of mixing ratio on SFE of supported mixed lipid films, assembled on different liquid subphases and subsequently transferred to a hydrophilic substrate. To that purpose we have used pure and mixed monolayers assembled from a major membrane forming phospholipid 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) and oleic acid triglyceride–triolein (TO) in different mixing ratios. The layers were assembled on water and on NaCl-electrolyte subphase and subsequently transferred to a mica support as a representative hydrophilic substrate. These particular selections were motivated by potential usefulness of such systems in sensor development. Recent investigations revealed that supported mixed POPC–TO lipid layers provide advantageous sensor platform due to its sensitive and selective response to polycyclic hydrocarbons in water solution.7,9
Characterization of mixed phospholipid monolayers and the involved interactions at the liquid subphase/air interface was accomplished through analysis of the surface pressure–area per molecule (π–A) isotherms. The isotherms provided information on the mean molecular area occupied by one molecule in the monolayer, the film compression modulus, miscibility and the excess Gibbs energy of mixing. The AFM and fractal/lacunarity analysis were used to elucidate relevant topographical features of the transferred monolayers of analogous composition, on a mica substrate. Corresponding wettability characteristics were investigated by measurements of the contact angles of standard liquids. This allowed calculation of film surface free energy according to the theoretical approach developed by Owen–Wendt–Rabel–Kaelble (OWRK).18–20 In this way it was possible to correlate the properties and composition of a monolayer at the air/subphase interface with SFE of the solid-supported monolayer.
2. Experimental and theoretical methods and materials
2.1 Materials
Phospholipid 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC – 99%) and oleic acid triglyceride–triolein (TO) were purchased from (Sigma–Aldrich) and used without further purification. Ultra-pure water from the Milli-Q Plus system (resistivity 18.2 MΩ cm) (Direct – Q, Millipore system, Billerica, Massachusetts) was used both as a subphase for the Langmuir monolayers and as a probe liquid in the contact angle measurements. The electrolyte used as a second subphase was 0.55 mol L−1 NaCl, buffered to pH 8.1 with NaHCO3 (Sigma–Aldrich), thus mimicking seawater. The electrolyte was prepared with ultra-pure water and NaCl calcined at 450 °C for 4 hours and purified with activated charcoal in order to remove residual traces of organic matter. Chloroform (HPLC grade from Sigma-Aldrich) used for lipid dissolution was employed as received. Probe liquids used in contact angle measurements (beside ultra-pure water) were formamide (98%), diiodomethane (99%), and ethylene glycol (0% H2O), all by Sigma-Aldrich and used without further purification. Freshly cleaved mica plates grades V-5 (40 mm × 10 mm × 0.3 mm) from SPI Supplies (USA) were used as a solid support.2.2 Monolayer preparation and determination of π–A isotherms
The spreading solutions were prepared by dissolving pure lipid or a lipid mixture with selected molar fractions in chloroform with concentration of 1 mg mL−1. An aliquot of a solution was spread onto the surface of ultra-pure water or electrolyte using a microsyringe (Hamilton, USA). After the spreading and before the initiation of the compression the solution was left for 10 min allowing for the solvent to evaporate. The compression was initiated with a barrier speed of 50 cm2 min−1. Surface pressure–area (π–A) measurements were carried out using a NIMA Langmuir Blodgett Deposition Trough model 1212D1 (Nima Technology Ltd, Coventry, UK) placed on an anti-vibration table. Surface pressure was measured at room temperature (21 ± 2 °C) with the accuracy of ±0.1 mN m−1 using a Wilhelmy plate as the pressure sensor. Each measurement was repeated at least three times to ensure reliability and validity of results.2.3 Thermodynamic analysis
The thermodynamic characteristics of the mixed monolayer systems were examined in more detail through the following analysis. For a binary system, the Gibbs free energy of mixing, ΔGmix, can be expressed as| ΔGmix = ΔGid + ΔGex, | (1) |
| ΔGid = −TΔSid |
ΔGid (J mol−1) = RT(X1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X1 + X2 ln X1 + X2 ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) X2) X2) | (2) |
The excess energy of mixing ΔGex represents the deviation of free energy of a mixed system from that of an ideal mixed one. Based on the definition, ΔGex is the contribution of mutual interactions between molecules on the free energy of mixing. The ΔGex at a specific surface pressure π can be calculated from the π–A isotherm data through the following equation:21
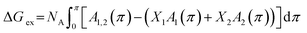 | (3) |
2.4 Transfer of a monolayer onto solid substrate
The investigated monolayers were transferred onto the hydrophilic mica plates using Langmuir–Blodgett technology, a well-established method for preparation of supported mono- and bilayers.24 The deposition of monolayers on a mica substrate was conducted by drawing a mica plate vertically from the subphase in the Langmuir–Blodgett trough at the rate of 2 mm min−1 through the monolayer spread at the air–water or air–electrolyte interface. For a selected lipids' mixing ratio the transfer was made at a pressure slightly below the corresponding envelope pressure, πe (for the explanation see 4.1). The surface pressure of the lipid monolayer, the rate of deposition, and the temperature were kept constant. The average transfer ratio was 0.92 ± 0.1. After the transfer the supported lipid layers were put into an exicator for about 20 h at room temperature to dry out. Assuming that the molecular organization within the monolayers at the air/subphase interface does not change when deposited onto the solid support,25 the samples were further used for the determination of the surface free energy of transferred layers.2.5 Estimation of surface free energy
The assessment of the surface free energy, i.e. surface tension of a solid, can, in principle, be achieved considering its wetting properties i.e. by use of the value of the equilibrium contact angle of a liquid drop placed on the surface. In the case of wetting systems relationship between the interfacial tensions at a point on three-phase (air–liquid–solid) contact line is given by the Young equation:γs = γsl + γl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (4) |
Even if the contact angle θ and γl are known, γsl is still unknown, and therefore eqn (4) cannot yet be solved for the surface tension of the solid γs. The information regarding γsl must be independently provided, for example, by a correlation between γsl, γs, and γl. There are several types of correlations that have been employed and discussed in the literature.26,27 In this work we have used the correlation proposed by Owens, Wendt, Rabel and Kaelble (OWRK) considering the surface tension to consist of nonpolar (dispersion) and polar contributions.18–20
In the OWRK method considering a liquid drop on a solid surface the surface tension γ of each phase is split up into polar (P) and disperse (D) fraction (subscripts l and s denote liquid and solid, respectively):
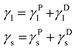 | (5) |
With this assumption, the equation for the surface tension (Good's equation28) becomes
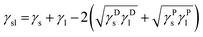 | (6) |
Combining and transposing eqn (4) and (6) gives:
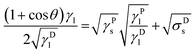 | (7) |
This equation due to its form of a general linear regression line, y = ax + b, enables us to determine the components of the total surface free energy. Namely, if we use two or more liquids with known polar and disperse components of the surface tension, measure the corresponding contact angles and plot the results as y vs. x i.e.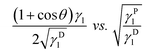 , then the polar component γPs is obtained from the square of the slope of the regression line and the disperse component γDs from the square of the ordinate of the intercept. The total surface free energy is the sum of these two components. In addition, it is important to realize that, while the dispersion part of this equation (square-root dependence) is derived from an approximate theory for dispersion interactions, the functional form of the terms related to the polar components has not yet been substantiated by theory.27
, then the polar component γPs is obtained from the square of the slope of the regression line and the disperse component γDs from the square of the ordinate of the intercept. The total surface free energy is the sum of these two components. In addition, it is important to realize that, while the dispersion part of this equation (square-root dependence) is derived from an approximate theory for dispersion interactions, the functional form of the terms related to the polar components has not yet been substantiated by theory.27
In order to elucidate the surface free energy components of a solid, experiments need to be done using the same solid surface with various liquids.29,30 Moreover, it turns out that the choice of the set of liquids must be done very carefully; otherwise mathematical problems in solving the set of equations may lead to major errors.31 It has been shown that optimal results are obtained using combination of apolar and polar liquids. In concordance with these considerations the set of probe liquids used in the contact angle measurements included ultra-pure water, formamide, ethylene glycol and diiodomethane, spanning the range from a highly polar to an apolar liquid, respectively. The surface free energy is calculated following OWRK method from a series of contact angle measurements using selected liquids with known surface tensions and corresponding polar and dispersive components.
2.6 Contact angle measurements
“Static” contact angle measurements and corresponding calculations of SFE were accomplished using KRÜSS Drop shape analysis system DSA 100. The drop size (∼2 mm in diameter) was selected to be sufficiently large relative to the scale of possible heterogeneity.26,32–34 The indications seem to suggest a relative drop size of at least 103 should be employed.34 Thus, it seems realistic to have a drop of a few millimeters in diameter on a surface whose roughness is of the order of magnitude of a few micrometers. On each sample the contact angle measurements were repeated three times applying all four liquids.2.7 AFM measurements
The surface structure and topography of the supported monolayers including roughness profiles were determined by using a Multimode AFM with a Nanoscope IIIa controller (Bruker, Billerica, USA) with a vertical engagement 125 μm scanner (JV). Tapping mode imaging was performed under ambient conditions in air, by using silicon tips (RTESP, Bruker, nom. freq. 320 kHz, nom. spring constant of 42 N m−1) and at a scan resolution of 512 samples per line. The linear scanning rate was optimized between 1.0 and 2.0 Hz at a scan angle of 0°. Images were processed and analyzed by means of the offline AFM NanoScope software, version 5.12r5 and NanoScope Analysis 1.7. Roughness Analysis software option was used to performed roughness analyses on 2 × 2, 5 × 5 and 10 × 10 μm2 imaged surface areas for each surface. The results are presented as values of Ra – the average surface roughness parameter defined as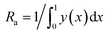 .
.
2.8 Fractal and lacunarity analysis
Fractal analysis of images is potentially powerful tool for extraction of topographic/structural features of considered surfaces. In particular it has been shown that adsorbed lipid layers are fractal structures35 whose fractal dimension is related to the dominant mechanism responsible for their growth.36 Furthermore, fractal dimension provides insight into the lattice structure and in plane molecular organization of Langmuir monolayer of amphiphilic material.37 Thus, in this context, we have conducted fractal analysis of gray-scale and binarized (black and white) AFM images of supported lipid layers. For purpose of this study only the values of fractal dimension D inferred from a gray scale AFM images using the box-counting algorithm38 are presented. The fractal analysis using box counting or cube counting methods implies use of boxes/cubes whose dimensions cover the range from one pixel up to 512 pixels (dimension of an AFM image) hence, 1 pixel corresponds to about 4 nm. Thus, enabling fine resolution in analysis of monolayer surface. However, as fractal dimension does not provide a complete characterization of a sample texture we have also conducted the lacunarity analysis aiming at obtaining the information on monolayer gappiness. Prior to lacunarity estimation gray scale AFM images were binarized (i.e. to each pixel the value of 1 or 0 was assigned depending on weather its gray scale intensity is above or below the median value, respectively). For lacunarity estimation of binary AFM images, the gliding-box algorithm39 was used. According to this algorithm a box of size r slides over an image. The gliding box of a specific size r, (length of a square box) is first placed at the top left corner of an image in which each and every pixel has an assigned value of either 1 or 0. Then the box “mass” M (the number of pixels occupied with 1's), is computed. The gliding box is systematically moved through the binary image one pixel at a time and the box mass value is determined for each of the overlapping boxes. The number of gliding-box with dimension r and mass M is defined as n(M, r). The probability distribution Q(M, r) is obtained by dividing n(M, r) by the total number of boxes. Lacunarity at scale r is defined as the mean-square deviation of the variation of mass distribution probability Q(M, r) divided by its square mean: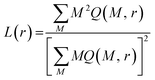 | (8) |
3. Results and discussion
3.1 Miscibility
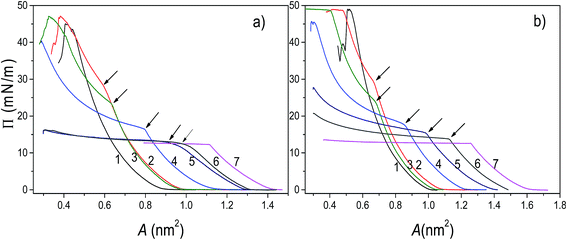
The analysis of π–A isotherms was conducted in order to provide insight into miscibility of components of the mixed systems. In general, when two components are miscible, the value of collapse pressure of a mixed monolayer depends on molar fraction of its components, and is lying between the collapse pressures of pure components. If the components are immiscible, two collapse pressures at constant values corresponding to the pure components are observed.40The π–A isotherms of POPC, TO, and mixed POPC/TO monolayers measured on subphases of water and electrolyte are shown in Fig. 1. The most noticeable difference between isotherms of pure POPC and TO and those of mixed layers is the appearance of a point where there is an abrupt change in the isotherm's slope, which occurs below the POPC collapse pressure (∼48 mN m−1) and after TO collapse pressure (∼12.5 mN m−1).
However, as evident from the corresponding compressibility curves (shown in Fig. S1 and S2 in the ESI†), it does not reflect a typical liquid expanded/liquid condensed (LE/LC) phase transition. It is rather an evidence of TO beginning to be expelled from the monolayer and deposited on top of the monolayer not as a new regular monolayer but rather as irregular inhomogeneous TO patches. Thus, forming a new bulk (three-dimensional) phase regardless of the starting composition of the mixed layer.
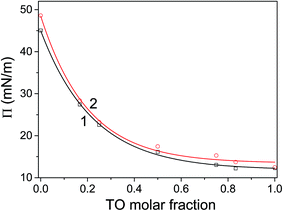
The corresponding pressure in the isotherm is called the envelope pressure or envelope point, πe.41 The envelope point occurs at a pressure higher than the collapse pressure of TO and corresponds to the initial formation of a new bulk phase. The pressures corresponding to envelope points of mixed layers on water and electrolyte subphase inferred from analysis of corresponding isotherms are shown in Fig. 2. The value of πe decreases with increase of the TO content in a mixed layer. Compression of the layer beyond the envelope point results in more TO molecules being expelled from the surface and incorporated into the new phase. Finally, with further increase of the pressure, an abrupt second change in the isotherm's slope occurs indicating the final collapse of the monolayer which is confirmed by the analysis of the corresponding compressibility curve provided in the ESI (Fig. S1 and S2†). Such behaviour has been also observed in other mixed systems.41,42
The mechanism of TO expulsion from the monolayer is the same, hence the curves in Fig. 2 have the similar shape. In contrast to POPC, TO with increase of the pressure cannot reach the condensed phase (as seen from the corresponding isotherms in Fig. 1) regardless of the subphase (water or electrolyte). Hence, in a mixed layer it remains as a “soft” component that at a certain pressure starts to be squeezed out. As the share of TO in the monolayer increases this expulsion occurs at even lower pressures. However, since the layers on electrolyte are more stable higher pressures are needed to induce the change of the monolayer structure. Hence, the curve 2 in Fig. 2, corresponding to an electrolyte phase, although similar in shape is shifted toward higher pressures. Here it's worth noting that due to the properties of TO isotherm the excess Gibbs energy of mixing, reflecting the stability of the layer, depicted in Fig. 3 could be calculated only up to pressure of approximately 12.5 mN m−1.
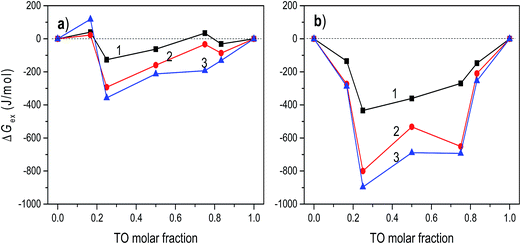 | ||
| Fig. 3 The excess Gibbs energy of mixing of POPC/TO assemble on the water (a) and on 0.55 M NaCl (b) subphases at surface pressures 5, 10 and 12.5 mN m−1 (curves 1–3, respectively). | ||
At the pressure lower than that of an envelope point the components in the monolayer mix well, while at higher pressures the components are separated. During the compression, domains may form as a result of stronger interactions between the molecules of the same kind. Depending on composition of the mixed monolayer, the environment consisting of single-component domains embedded in the environment of other single-component domains may change. This could provide the explanation for the observed stoichiometry-dependent shift of the envelope points in the mixed POPC/TO monolayers. The insight into stability of a layer and involved intermolecular interactions can be obtained by considering the excess Gibbs energy of mixing (see 3.2).
For all mixing ratios πe and collapse pressures occur at higher pressures for a monolayer assembled on electrolyte then on water subphase. This observation is compliant with the results of thermodynamic analysis (presented below in 3.2.) showing that monolayers assembled on the electrolyte subphase are more stable than those assembled on pure water. The difference in πe between layers on water and electrolyte is not constant. It varies depending on the lipid mixing ratio and follows the corresponding differences in excess Gibbs energy of mixing (cf.Fig. 3), reflecting the difference in the relative stability between layers assembled on different subphases.
3.2 Thermodynamic analysis
Generally, thermodynamic analysis on the basis of the excess Gibbs energy of mixing allows quantitative interpretation of intermolecular interactions and determination of thermodynamic stability of mixed monolayers. The negative values of ΔGex indicate that stronger attractive interactions exist between molecules in the mixed monolayer in comparison to the interactions in one-component monolayers. Thus, the negative sign of ΔGex is considered as a criterion of monolayer's stability, while a positive value can suggest a phase separation.43,44The excess Gibbs energies of mixed POPC/TO monolayers formed on water and on the electrolyte subphase at various surface pressures are shown in Fig. 3. For layers assembled on the water subphase for the pressures bellow ∼5 mN m−1 the ΔGex oscillates around zero for all values of TO molar fraction, indicating that the strength of molecular interactions in the mixed monolayer is the same as in the one-component monolayers. The increase of surface pressure in the loose packing density regimes (LE and LE/LC), i.e. in the pressure range below the TO collapse pressure (∼12.5 mN m−1), causes the ΔGex values to become more negative.
This is explained by the increase in the magnitude of the intermolecular attractive van der Waals forces that occurs with the decreased intermolecular separation accompanying the increase of surface pressure. The corresponding interaction energies evaluated from excess Gibbs energy (not presented here) show the increase of interaction energy with increase of the pressure, justifying this explanation. Thus, for this pressure range, POPC and TO mix and interact weakly, forming relatively stable monolayers. The most stable mixed monolayer is obtained for TO molar fraction 0.25. This composition corresponds to the complex stoichiometry of POPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TO = 3
TO = 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Positive values of ΔGex, occurring at higher pressures (π > 12.5 mN m−1) for most of the TO molar fractions (except for the TO molar fraction 0.25), suggest that due to stronger interactions between identical molecules the domains of POPC and TO are formed, resulting in phase separation in the monolayer.40 For pressures higher than ∼15 mN m−1 ΔGex is positive irrespectively of the TO molar fraction.
1. Positive values of ΔGex, occurring at higher pressures (π > 12.5 mN m−1) for most of the TO molar fractions (except for the TO molar fraction 0.25), suggest that due to stronger interactions between identical molecules the domains of POPC and TO are formed, resulting in phase separation in the monolayer.40 For pressures higher than ∼15 mN m−1 ΔGex is positive irrespectively of the TO molar fraction.
The calculated values of ΔGex for the layers assembled on 0.55 M NaCl subphase are depicted in Fig. 3b. Comparison of these values with the values of ΔGex obtained for mixed monolayers at water subphase reveals significantly higher thermodynamic stability of layers formed on the electrolyte subphase (i.e. the corresponding values of ΔGex are several times lower), even at low pressures, implying existence of much stronger attractive interactions between molecules in the layer. This indicates that the presence of ions in the electrolyte subphase changed the molecular interactions in the mixed monolayers, making them much more stable. In particular, although the net charge on the POPC head group is zero, the polar head group contains both positive and negative sites that can potentially interact with charged molecules or dipoles. In the NaCl subphase Na+ and Cl− ions interact with these charges resulting in decrease of repulsion and consequently in net increase of the attractive forces. For the POPC molecules, the most favourable location for the Na+ ions is near the phosphatidyl oxygen atoms and for Cl− ions near choline group.45 Furthermore, at surface pressures greater than 15 mN m−1, two orientations of the POPC head groups are present: one nearly parallel to the monolayer interface and another one pointing toward the water. The conformational variations around the bonds connecting the phosphorus atom to the adjacent oxygens are held to be responsible for these two orientations of the headgroup.46 Thus, presence of Na+ ions influences this orientation by “straightening” the headgroup towards the bulk water and reducing area per molecule. The change of headgroup orientation and decrease of repulsion should contribute to increase in lipid packing, decrease in area-per molecule (cf.Fig. 1), and increase in acyl chain order parameters. Such effects were also observed in other similar systems.45 All together these effects result in apparent increase of attractive interactions and observed increased stability of the layer assembled on the NaCl subphase.
Two minimums in ΔGexvs. mixing ratio (molar fraction) occur at TO molar fractions of 0.25 and 0.75. Again, the most stable layer is obtained for TO molar fraction of 0.25. This relative difference in stability of monolayers assembled on different subphases is in turn reflected in difference in corresponding πe which is greatest at TO molar fraction 0.75 (cf.Fig. 2). Here, in regard to hydration parameters of TO/POPC mixtures it is interesting and worth noting that activity coefficient for water when plotted against TO mol fraction has dips at 0.25 and 0.75 mol fraction TO and that at TO 0.75 all hydration parameters for mixture POPC–TO increase.47 However, deeper analysis of impacts and intricate interplay between hydration, electrostatics, and dispersion forces resulting in changes in interaction energies in a mixed monolayer is out of scope of this investigation.
3.3 Analysis of layers' topography
AFM measurements and fractal analysis were used to get an insight into supported layers' topographies and provide additional information in support of the SFE measurements. However, the detailed topography analysis (the subject of work in progress) is out of scope of this article. Hence, here we briefly present only the results pertinent to the matter at hand. More details of topography analysis including the corresponding AFM images are included in the ESI.†All AFM images showed uniform substrate coverage with relatively homogenous and compact monolayer. However, analysis of corresponding roughness profiles show increase of roughness with increase of TO fraction in the monolayer. This is especially noticeable in layers assembled on NaCl subphase. The observed differences in respect to layers assembled on water subphase are compliant with recent findings48 revealing the influence of electrostatic interactions of sodium and chloride ions positioned around lipid polar heads on the compactness of the layer.
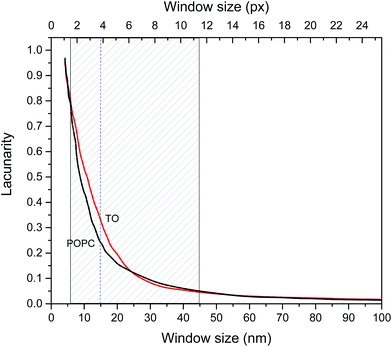
The fractal dimensions of mica supported pure TO and POPC layers derived from AFM images are 2.5 ± 0.05 and 2.6 ± 0.05 respectively and these could be considered as fractal dimensions of “reference”/pure layers. Fractal dimensions of mixed monolayers assembled on both subphases are in range 2.5 ± 0.05(TO) to 2.6 ± 0.05 (POPC) increasing with increase of POPC fraction. Although the difference in D between POPC and TO layer is small it indicates somewhat more compact POPC layer. However, fractal dimension does not provide a complete characterization of a sample texture. Namely, different fractal sets may share the same fractal dimension values but have different appearances or textures due to differences in lacunarity.49,50 Lacunarity measures the deviation of a geometric structure from translational invariance, or gappiness of geometric structure.51 Lacunarity represents the distribution of gap sizes: low lacunarity geometric objects are homogeneous because all gap sizes are the same, whereas high lacunarity objects are heterogeneous.49 It is worth noting that objects that are homogeneous at a small scale can be heterogeneous at a larger scale. Hence, lacunarity analysis can provide significant insight into layer topography. The results of lacunarity analysis of pure POPC and TO layers are depicted in Fig. 4.
The difference in lacunarity (Fig. 4) at a particular scale is the difference of the values at that scale, these values should be compared and not the area under the curves. Comparison of the areas under the curves could indicate differences in an “integral lacunarity” i.e. lacunarity over all considered scales. Although this difference could be small the differences at particular scale can be significant indicating differences in homogeneity on that scale, i.e. some structure at low magnification (large scale) may look less heterogeneous than at high magnification (small scale). In our case at scale 15 nm the difference in lacunarity is about 40%. Significant differences in lacunarity between TO and POPC layers can be observed in the size range 5–45 nm. In this range TO layer is significantly more heterogeneous than the POPC layer. At larger scales (>45 nm) both layers exhibit low lacunarity corresponding to relatively homogenous structure. The highest difference in lacunarity appears at 15 nm scale thus coinciding with the subordering periodicity in TO layer of 16 nm inferred from AFM analysis (cf. Fig. S3 in the ESI†).
3.4 Surface free energy
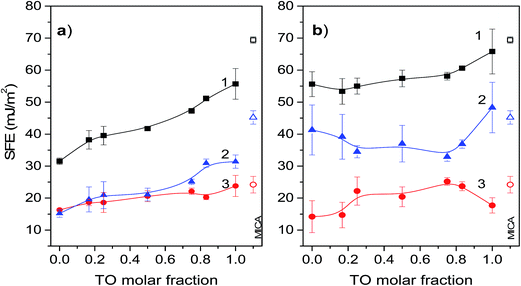
SFE derives from the unsatisfied bonding potential of molecules at a surface. These molecules try to reduce the free energy by interacting with molecules in an adjacent phase. Hence, surface phenomena are driven primarily by a tendency to reduce the surface free energy. Thus, generally, adhesion and wetting are better on hydrophilic solid surfaces with high SFE than on low energy hydrophobic surfaces. In this context mica is known to be strongly hydrophilic with total SFE about 69 mJ m−2, and a high value of the polar part of the surface energy.52 This property favours strong interactions of mica surface with polar molecules to form a compact monolayer. Thus, generally, it could be expected that the Langmuir–Blodget transfer of the POPC monolayer onto mica surface would considerably decrease surface free energy. This firstly, due to the interaction between hydrophilic mica surface and polar heads of the POPC molecules causing their apolar hydrocarbon chains to orient outwards, and secondly, due to a relatively high degree of POPC condensation in the Langmuir layer. Namely, the degree of condensation in the Langmuir layer is reflected in the SFE values of the transferred/supported layer since the SFE of a more condensed monolayer with denser packing of hydrocarbon chains is lower.17 On the other hand, deposition of a pure TO layer on mica should decrease its SFE only slightly. This occurs due to differences between POPC and TO in polarity (TO is apolar) and molecular structure influencing the degree of condensation in the corresponding Langmuir layer. Namely, in the glycerol backbone POPC molecule has two fatty acid chains one of which is saturated and another is unsaturated, while the TO molecule has three unsaturated fatty acid chains preventing dense packing in the Langmuir layer. Hence, the SFE of a mica supported mixed POPC/TO layer should decrease considerably with increase of POPC molar fraction.The results of SFE measurements of pure and mixed monolayers depicted in Fig. 5 support these general conclusions: total SFEs are lower than that of pure mica, pure POPC layer has lower total SFE than TO layer and for a mixed layer total SFE depends on mixing ratio and increases with increase of TO molar fraction. However, the subphase used for monolayer assembly significantly influences contributions of polar and dispersive component to the total SFE as well as their change with the mixing ratio. Thus, between the two subphases, the change in mixing ratio results in considerably different dynamic of total SFE and its components.
Total SFE of a mixed layer assembled on a water subphase and its components are depicted in Fig. 5a. As expected the total SFE is significantly lower than the SFE of mica and increases with increase of TO molar fraction. For mixtures with TO molar fractions <0.75, the contributions to SFE coming from the polar and disperse components are nearly equal and gradually increase with increase of TO fraction. The significant contribution of dispersive component to the total SFE reflects the hydrophobic nature of such film. Low values of total SFE for the POPC rich monolayers also reflect higher degree of condensation in these monolayers in comparison to the TO rich monolayers, which is enabled by combination of one saturated and one unsaturated fatty acid in the glycerol backbone of POPC. For mixed monolayers with TO molar fractions >0.75 the contributions to the SFE coming from the polar component are about 30–40% higher than those coming from the disperse component. The increase of the polar component in this mixing ratio range is attributed to the dipolar interactions between mica and TO ester groups. The disperse part of SFE of pure TO layer is about 24 mJ m−2, which is in agreement with theoretical values obtained from continuum theory and Hamaker constant.53 This corresponds to the situation of TO molecules adopting a conformation with the glycerol residue at the mica surface and the three oleic acid residues directed toward the bulk and the layer of water molecules next to the mica surface that form hydrogen bonds with the ester groups of the triglyceride.53
Surface free energy of mica supported mixed layers assembled on the NaCl electrolyte subphase are shown in Fig. 5b. In comparison to the layers assembled on a water subphase, for all TO molar fractions these layers are characterized with much lower variations and a significantly higher total SFE due to the high contributions coming from the polar component. While the corresponding contributions of the disperse components are nearly equal for both subphases, the corresponding contributions to SFE coming from the polar component in a layer assembled on an electrolyte subphase are almost two times higher. This is explained with a less compact molecular packing in the Langmuir layer due to penetration of electrolyte ions into the polar head-group region,54,55 thus influencing the bonding potential of the layer. The influence of the electrolyte ions on monolayer structure and ordering discussed in paragraph 3.3 is also apparent from the corresponding π–A isotherms. By comparison it is evident that the values of area-per-molecule in monolayers on the electrolyte subphase are higher than those in monolayers on the water subphase. This occurs due the presence of ions promoting the solvation of polar head groups of phospholipid, making their effective size greater.56 The greater polar head groups in turn require a greater area per molecule resulting in less dense packing. Such monolayers when transferred to a mica substrate will have higher SFE. Furthermore, in regard to this, it is worth noting that the layers assembled on NaCl have higher fractal dimension than that of a layer assembled on pure water. Now, as the relative permittivity (dielectric constant κ) of a fractal structure is not constant but rather depends on its fractal dimension57 (increase in D results in decrease of κ), the fractaly induced change in κ favours electrostatic interactions over dispersive in layers assembled on NaCl subphase, thus increasing the polar contributions to SFE. More details on influence of fractal dimension on the dielectric constant is provided in the ESI.† Finally, in this context, somewhat unexpectedly high SFE of pure TO layer assembled on the NaCl subphase could be possibly attributed to relatively less compact packing of TO molecules as mentioned before and indicated by relatively high lacunarity of pure TO layer. This relatively lose packing leaves (at molecular level) exposed mica surface, thus enabling access of probing liquids to the free mica surface. This in turn contributes to rise of measured SFE towards the value of mica's SFE. This is also supported by appearance of “valleys” in the roughness profile of the corresponding AFM scanned area of pure TO layer (cf. Fig. S3d in the ESI†). The bottom of these “valleys” probably represent free mica surface. The dimensions and separation of the “valleys” are smaller for pure TO layer assembled on the water subphase than on the NaCl subphase (Fig. S3a†), indicating relatively smaller accessible free mica surface within the layer. Hence, the corresponding SFE of a layer assembled on water subphase is significantly lower than that of mica.
4. Conclusions
Supported lipid layers formed by transfer of a Langmuir monolayer from a liquid subphase onto a solid surface are commonly used as model systems for biological membranes with high potential for (bio)technological applications including development of various novel sensors incorporating membrane based films. Conclusions drawn from the results of this study including pure and mixed POPC/TO monolayers assembled on water and on NaCl subphase and transferred to a hydrophilic (mica) substrate are summarized as follows.Analysis of recorded isotherms indicates that the POPC/TO form a partially immiscible system on both subphases. At surface pressures below the envelope point, the two components are miscible, while at pressures above the envelope point TO be expelled from the layer. Calculated excess free energies of mixing indicate that the mixed POPC/TO layers assembled on the NaCl subphase are more stable than those assembled on a water subphase. Regardless of the subphase used for the assembly the most stable layers are obtained for POPC molar fraction 0.75. SFE of the supported mixed layers depends primarily on the mixing ratio and the type of a subphase used in the self-assembly of Langmuir layer, and is significantly influenced by the chain saturation/unsaturation in the considered lipid. The SFE of a supported mixed lipid monolayer assembled on water subphase can be tuned in a range of 31–58 mJ m−2 by changing the TO molar fraction. Thus, allowing for change of supported layer's wetting properties from hydrophobic to hydrophilic. The SFE of mixed layers assembled on the NaCl subphase are characterized with high polar component, almost two-times higher than the disperse part. The variation in SFE due to change in mixing ratio is lesser than for the layers assembled at water subphase allowing for tuning of SFE in range 53–72 mJ m−2. Between the two subphases used in the assembly the SFE of the investigated mixed layers on mica can be tuned in a range of 31–72 mJ m−2 by changing the POPC/TO mixing ratio. Considering that different bio-functionalized surfaces (such as with antibody, albumin, bacteria, cells, and phospholipids) were reported to have the surface free energies in the range of 35–75 mJ m−2 (ref. 26, 58–61) one may conclude that the attained SFE tuning range could allow significant modification of interfacial interactions and surface properties of supported mixed POPC/TO lipid layers.
Results of this study should contribute to better understanding of the SFE tuning of supported mixed lipid films. Also, through the identification of influential parameters that allow for tailoring of the surface properties, they should help in design of a more efficient lipid host layers for various applications including superhydrophobic low surface energy materials.62
Acknowledgements
This work was supported by the North Atlantic Treaty Organization (NATO) Science for Peace (SfP) Award Reference SfP 983147, and by the Croatian Ministry of Science, Education and Sports, Grant No. 098-0982915-2899 “Organizational processes and optical interactions in condensed molecular systems”.References
- E. Castellana and P. Cremer, Surf. Sci. Rep., 2006, 61, 429–444 CrossRef CAS.
- J. A. Jackman, W. Joshua and C. Nam-Joon, Materials, 2012, 5, 2637–2657 CrossRef CAS.
- J. Sołoducho and J. Cabaj, J. Anal. Bioanal. Tech., 2013, S7, 005 Search PubMed.
- D. A. Cadenhead, Monomolecular Films as Biomembrane Models, in Structure and Properties of Cell Membranes, ed. G. Benga, CRC Press, Boca Raton, FL, 1985, vol. 3, ch. 2, pp. 21–62 Search PubMed.
- Y. H. Chan and S. G. Boxer, Curr. Opin. Chem. Biol., 2007, 11, 581–587 CrossRef CAS PubMed.
- C. H. Nielsen, Anal. Bioanal. Chem., 2009, 395, 697–718 CrossRef CAS PubMed.
- A. Penezić, B. Gašparović, D. Stipaničev and A. Nelson, Environ. Chem., 2014, 11, 173–180 CrossRef.
- M. Bally, K. Bailey, K. i. Sugihara, D. Grieshaber, J. Vörös and B. Städler, Small, 2010, 6, 2481–2497 CrossRef CAS PubMed.
- Z. Coldrick, A. Penezić, B. Gašparović, P. Steenson, J. Merrifield and A. Nelson, J. App. Electrochem., 2011, 41, 939–949 CrossRef CAS.
- S. Mohamadi, D. J. Tate, A. Vakurov and A. Nelson, Anal. Chim. Acta, 2014, 813, 83–89 CrossRef CAS PubMed.
- M. Gołabek and L. Hołysz, Appl. Surf. Sci., 2010, 256, 5463–5469 CrossRef.
- J. Comelles, M. Estevez, E. Martinez and J. Samitier, Nanomed. Nanotech. Biol. Med., 2010, 6, 44–51 CrossRef CAS PubMed.
- R. Chepyala and S. Panda, Appl. Surf. Sci., 2013, 271, 77–85 CrossRef CAS.
- B. Zhao, J. Moore and D. Beebe, Science, 2001, 291, 1023–1026 CrossRef CAS PubMed.
- E. Chibowski and M. Jurak, Colloids Surf., A, 2011, 383, 56–60 CrossRef CAS.
- M. Golabek, M. Jurak, L. Holysz and E. Chibowski, Colloids Surf., A, 2011, 383, 56–60 CrossRef.
- M. Jurak and E. Chibowski, Colloids Surf., B, 2010, 75, 165–174 CrossRef CAS PubMed.
- D. K. Owens and R. C. Wendt, J. Appl. Polym. Sci., 1969, 13, 1741–1747 CrossRef CAS.
- D. H. Kaelble, J. Adhes., 1970, 2, 66–81 CrossRef CAS.
- W. Rabel, Farbe und Lack, 1971, vol. 77, pp. 997–1005 Search PubMed.
- G. Barnes and I. Gentle, Interactions in Monolayers, in Interfacial Science: An Introduction, Oxford University Press, New York, 2nd edn, 2011, ch. 5.7, pp. 134–137 Search PubMed.
- P. Joos and R. A. Demel, Biochim. Biophys. Acta, 1969, 183, 447–457 CrossRef CAS.
- C. Mestres, M. A. Alsina, M. Espina, L. Rodrìguez and F. Reig, Langmuir, 1992, 8, 1388–1391 CrossRef CAS.
- A. P. Girard-Egrot and L. J. Blum, Langmuir–Blodgett Technique for Synthesis of Biomimetic Lipid Membranes, in Nanobiotechnology of Biomimetic Membranes, ed. D. Martin, Springer, Heidelberg, 2007, ch. 2, pp. 23–62 Search PubMed.
- J. Günster and R. Souda, Langmuir, 2006, 22, 6939–6943 CrossRef PubMed.
- D. Cwikel, Q. Zhao, C. Liu, X. Su and A. Marmur, Langmuir, 2010, 26, 15289–15294 CrossRef CAS PubMed.
- A. J. Marmur and D. Valal, Langmuir, 2010, 26, 5568–5575 CrossRef CAS PubMed.
- R. J. Good and L. A. Girifalco, J. Phys. Chem., 1960, 64, 561–565 CrossRef CAS.
- R. J. Good, and C. J. van Oss, The Modern Theory of Contact Angles and the Hydrogen Bond Components of Surface Energies, in Modern Approaches to Wettability, ed. M. E. Schrader and G. I. Loeb, Plenum Press, New York and London, 1992, ch. 1, pp. 1–27 Search PubMed.
- C. Della Volpe and S. J. Siboni, Colloid Interface Sci., 1997, 195, 121–136 CrossRef CAS.
- S. Shalel-Levanon and A. J. Marmur, Colloid Interface Sci., 2003, 262, 489–499 CrossRef CAS.
- S. Brandon, N. Haimovich, E. Yeger and A. J. Marmur, J. Colloid Interface Sci., 2003, 263, 237–243 CrossRef CAS PubMed.
- G. Wolansky and A. J. Marmur, Colloids Surf., A, 1999, 156, 381–388 CrossRef CAS.
- A. J. Marmur and E. Bittoun, Langmuir, 2009, 25, 1277–1281 CrossRef CAS PubMed.
- D. Risović, B. Gašparović and B. Ćosović, Langmuir, 2001, 17, 1088–1095 CrossRef.
- D. Risović, B. Gašparović and B. Ćosović, Colloids Surf., A, 2003, 223, 145–156 CrossRef.
- D. Risović, S. Frka and Z. Kozarac, J. Colloid Interface Sci., 2012, 373, 116–121 CrossRef PubMed.
- R. Voss, Fractals in nature: From characterization to simulation, in The Science of Fractal Images, ed. H. O. Peitgen and D. Saupe, Springer Verlag, New York, 1988, ch. 1, pp. 21–70 Search PubMed.
- C. Allain and M. Cloitre, Phys. Rev. A, 1991, 44, 3552–3558 CrossRef.
- P. Dynarowicz-Łatka and K. Kita, Adv. Colloid Interface Sci., 1999, 79, 1–17 CrossRef.
- M. A. Mitsche, L. Wang and D. M. Small, J. Phys. Chem. B, 2010, 114, 3276–3284 CrossRef CAS PubMed.
- A. Więcek, P. Dynarowicz-Łatka, N. Vila-Romeu, M. Nieto-Suarez and M. Flasiński, Colloids Surf., A, 2008, 321, 201–205 CrossRef.
- M. A. Alsina, C. Mestres, J. M. Garcia Antón, M. Espina, I. Haro and F. Reig, Langmuir, 1991, 7, 975–977 CrossRef CAS.
- M. Y. Levy, S. Benita and A. Baszkin, Colloids Surf., 1991, 59, 225–241 CrossRef CAS.
- A. Dickey and R. Faller, Biophys. J., 2008, 95(6), 2636–2646 CrossRef CAS PubMed.
- L. Huynh, N. Perrot, V. Beswick, V. Rosilio, P. A. Curmi, A. Sanson and N. Jamin, Langmuir, 2014, 30(2), 564–573 CrossRef CAS PubMed.
- J. M. Smaby and H. L. Brockman, J. Biol. Chem., 1987, 262, 8206–8312 CAS.
- S. Šegota, D. Vojta, G. Pletikapić and G. Baranović, Chem. Phys. Lipids, 2015, 86, 17–29 CrossRef PubMed.
- P. Dong, Int. J. Geogr. Inf. Sci., 2000, 6, 20–26 Search PubMed.
- R. Voss, Random fractals: characterization and measurements, in Scaling Phenomena in Disordered Systems, ed. R. Pynn and A. Skyeltorp, Plenum Press, New York, 1986, ch. 1, pp. 1–11 Search PubMed.
- Y. Gefen, Y. Meir, B. B. Mandelbrot and A. Aharony, Phys. Rev. Lett., 1983, 50, 145–148 CrossRef.
- E. Chibowski and K. Terpilowski, Comparison of Apparent Surface Free Energy of Some Solids Determined by Different Approaches, in Contact Angle, Wettability and Adhesion, ed. K. L. Mittal, CRC Press, Boca Raton, FL, 2009, vol. 6, Part 4, pp. 283–301 Search PubMed.
- P. M. Claesson, A. Dedinaite, B. Bergenståhl, B. Campbell and H. Christenson, Langmuir, 1997, 13, 1682–1688 CrossRef CAS.
- K. Toko and K. Yamafuji, Chem. Phys. Lipids, 1980, 26, 79–99 CrossRef CAS PubMed.
- P. Garidel and A. Blume, Chem. Phys. Lipids, 2005, 138, 50–59 CrossRef CAS PubMed.
- K. Gong, S. S. Feng, M. L. Go and P. H. Soew, Colloids Surf., A, 2002, 207, 113–125 CrossRef CAS.
- D. Risović, B. Gašparović and B. Ćosović, J. Phys. Chem. B, 2002, 106, 9810–9814 CrossRef.
- B. Li and B. E. Logan, Colloids Surf., B, 2004, 36, 81–90 CrossRef CAS PubMed.
- N. Hallab, K. Bundy, K. O'Connor, R. L. Moses and J. J. Jacobs, Tissue Eng., 2001, 71, 55–71 CrossRef PubMed.
- E. Chibowski, L. Holysz, G. A. M. Kip, A. V. Silfhout and H. J. Busscher, J. Colloid Interface Sci., 1989, 32, 54–61 CrossRef.
- H. Tavana and A. W. Neumann, Adv. Colloid Interface Sci., 2007, 132, 1–32 CrossRef CAS PubMed.
- S. Alexander, J. Eastoe, A. M. Lord, F. Guittard and A. R. Barron, ACS Appl. Mater. Interfaces, 2016, 8(1), 660–666 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The compressibility moduli Cs−1 of pure and mixed POPC/TO layers assembled on water and electrolyte subphases. AFM images of supported lipid layers. Dielectric constant of fractal structures. See DOI: 10.1039/c6ra04926e |
| This journal is © The Royal Society of Chemistry 2016 |