Atmospheric chemistry of ethers, esters, and alcohols on the lifetimes, temperature dependence, and kinetic isotope effect: an example of CF3CX2CX2CX2OX with OX reactions (X = H, D)†
Feng-Yang Bai,
Xu Wang,
Yan-Qiu Sun,
Rong-Shun Wang and
Xiu-Mei Pan*
Institute of Functional Material Chemistry, Faculty of Chemistry, Northeast Normal University, Changchun, 130024, People's Republic of China. E-mail: panxm460@nenu.edu.cn; Fax: +86-431-85099511; Tel: +86-431-85099963
First published on 5th April 2016
Abstract
The dual-level direct dynamics method is employed to investigate the hydrogen abstraction reaction of CF3CH2CH2CH2OH (CF3CD2CD2CD2OD) with OH (OD) radicals. Four possible reaction channels caused by different positions of hydrogen atom attack are found. All the stationary points are studied with the ab initio and density functional theories. Single points computation is further refined by CCSD(T) and QCISD(T) methods combined with the 6-311++G(d,p) basis set in the minimum energy paths (MEP). Rate constants for each reaction channel, obtained by canonical variational transition state (CVT) coupled with the small curvatures tunneling (SCT) correction, are found to coincide with the available data in experiments. Calculations show that the variational effect was small in 200–2000 K, while the tunneling effect is large for every reaction channel in low-temperature regions. It is shown that the H-abstraction from the –CH2O– group is the primary channel. Standard enthalpies of formation for the species are computed, and the kinetic isotope effects for reactions CF3CH2CH2CH2OH/CF3CD2CD2CD2OD + OH and CF3CH2CH2CH2OH + OH/OD are discussed to provide valuable information for subsequent research. In addition, atmospheric lifetimes of a series of related ethers, esters, and alcohols are estimated. The Arrhenius expression for the title reaction k(T) = 3.43 × 10−21T3.22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(741.70/T) cm3 per molecule per s is also provided.
exp(741.70/T) cm3 per molecule per s is also provided.
1 Introduction
Rising concern about the potential impact of various industrial chlorofluorocarbons (CFCs) on the Earth's climate has stimulated further search for chemicals that satisfy various industrial needs while having little impact on either stratospheric ozone or climate. Hydrofluorocarbons (HFCs) and hydrofluorochlorocarbons (HCFCs) have found extensive use in replacing CFCs in the past few decades.1 In general, extensive efforts have been made to search for suitable replacements as a result of HFCs and HCFCs having rather long lifetimes and large greenhouse effect potentials.2 Recently, partially fluorinated alcohols (FAs) have been suggested as substitutes for HFCs,3 and the fluorinated ethers (FEs) and FAs are new classes of compounds currently under consideration for use as CFC replacements.4,5 The FAs are expected to have not the ability to destroy the ozone layer and large reactivity. Because of containing hydrogen atoms, thus, these FAs can be removal by means of reactions with OH radical in the atmosphere.6 Hence OH reaction rate constants for such compounds were required to determine their atmospheric lifetimes and possible effects on the Earth's radiation budget. Also, fate of the oxidation products from such reactions were also important in determining environmental acceptability, information on the initial rate of reaction was a necessary first step.CF3CH2CH2CH2OH is a primary FAs, which seems to be suitable alternative to HFCs.7 Kinetic content of the reaction of CF3CH2CH2CH2OH with OH radical is crucial to determine the tropospheric lifetimes of CF3CH2CH2CH2OH and its impact on the environment. In 2010, Albaladejo et al.8 have performed a kinetic study of CF3CH2CH2CH2OH reaction with hydroxyl radical at 298 K. Subsequently, to further investigate temperature effect of reaction of CF3CH2CH2CH2OH + OH, they have also reported rate constants of the above reaction between 263 to 358 K in experiment.7 Hence, theoretical studies on the accurate extrapolation of rate constants in higher temperatures for the title reaction are very necessary. Because no experimental information was available on the branching ratios of the products, it is desirable to give a further understanding of the reaction mechanisms and the dynamics. For the reaction of CF3CH2CH2CH2OH with OH radical, there are four classes of reaction channels as follows:
| CF3CH2CH2CH2OH + OH → CF3CH2CH2CH2O + H2O | (R1) |
| → CF3CH2CH2CHOH + H2O | (R2) |
| → CF3CH2CHCH2OH + H2O | (R3a and R3b) |
| → CF3CHCH2CH2OH + H2O | (R4) |
No other theoretical or experimental work has reported for above reactions. The mechanisms of reactions of ethers, esters, and alcohols with various free radicals have been comprehensively studied and continue to need paying considerable attention in experiment7–13 and theory.14–31 A number of experimental or theoretical investigations were also performed the rate coefficients of the ethers, esters, and alcohols with OH radicals or Cl atoms. However, it is unclear that the lifetime of some ethers, esters, and alcohols in theory or experiment. As is well known, the substituted ethers, esters, or alcohols by fluorine or chlorine will increase the environmental damage and pollution of the atmosphere compared to the un-substituted species. How to explain this issue? The atmospheric lifetimes of these species have a great significance to the understanding of their environmental behaviors and potential impact on human health, which they need to be more accurately estimated. The studies about the atmospheric lifetimes of ethers, esters, and alcohols are discussed detailed in following section. In addition to the atmospheric lifetimes of ethers, esters, and alcohols, we have summarized the recent theoretical researches about the ethers, esters, and alcohols with OH and Cl radicals about the rate constant, calculation methods. For all three systems, the optimized geometries, calculated frequencies are obtained from the density functional theory (DFT) or ab initio method. The rates are computed by using the (improved) canonical variational transition state theory with the small curvatures tunneling correction or canonical transition state theory (CTST). As is known that, the CVT/SCT rate constant is more accurate than the TST rate constant. The CVT/SCT methods not only can investigate the reaction path properties but also analysis the contribution of variational and tunneling effects. Furthermore, the tunneling effects are thought to be significant for H-abstraction reactions with many primary radicals. The canonical transition state theory, based on the assumption that trajectory will not return, is bound to overestimate the rate constant. On basis of the theoretical results, we can also deduce that optimized parameters from B3LYP, MPWB1K, M06-2X, BH&HLYP, BMK, and MP2 can be used to compute the rate constants. For the ethers, if the carbon chain is same, the fluorine or chlorine substitution can decrease the reactivity of C–H bond and the F-substitution results in a greater decrease than Cl-substitution in reactivity trend due to the larger electronegativity. For the rate constant with OH radical as an example, kCH3OCH3 > kCH3OCHCl2 > kCH3OCF3, kCH3OCH2CH3 > kCH3OCH2CF3 > kCH3OCHFCF3, kCHF2OCH2CF3 > kCHF2OCHClCF3 > kCHF2OCHFCF3, kCH3OCH2CF2CF3 > kCH3OCF2CF2CF3, k(CF3)2CHOCH2F > k(CF3)2CHOCH3.30–39 Comparing the rate constant of OH with CH3OCH3 and CH3OCH2CH3, we can find that the kCH3OCH2CH3 > kCH3OCH3, which suggest that the rate constant can increase with the carbon chain. Similar conclusions can be also found about the esters and alcohols. For the ethers reactions with Cl atom, esters, and alcohols, the above conclusion is also applicable. We also find that the rate constant of most ethers reaction with hydroxyl radical is larger than that with chlorine atom. However, the esters and alcohols reaction with hydroxyl radical is smaller than that with atomic chlorine. This may be owing to the difference of activation energy.
In this work, the variational transition state theory (VTST) with interpolated single-point energies (ISPE) are adopted to compute rate coefficient product branching ratios. Using the existing rate constants of ethers, esters, and alcohols reaction with OH and Cl radicals in the literatures, the atmospheric lifetime is estimated in this paper. And the literatures, only used for calculating the lifetimes, are presented in the ESI.† The discussion between the experimental and computational results is also listed. The kinetic isotope effects (KIEs) have been verified non-ignorable in studying the nature of some reactions about kinetics in experiment and theory.40,41 Investigations of KIEs can help elucidate origins of particular deviations from natural abundance and provide detailed insight into dependent isotope reaction mechanisms. The KIEs are likely to be important in the kinetic investigations of the title reaction. As a result, theoretical studies on the KIEs for CF3CH2CH2CH2OH + OH/OD and CF3CH2CH2CH2OH/CF3CD2CD2CD2OD + OH reactions are desirable for laying direction for experiment.
2 Methodology and calculations details
Electronic structure calculations are performed with Gaussian 09 program package.42 MP2 (ref. 43) level combined with 6-311G(d,p) basis set is adopted to optimize and calculate the equilibrium geometries and frequencies of the reactants, products, complexes, and transition states. The MP2 method has been proven to be an accurate computational model for predicting electronic structure and energies in many articles.44,45 In addition, M06-2X/6-311G(d,p)46 method is also applied to optimize the parameters and calculate the frequencies. Intrinsic reaction coordinate (IRC)47,48 calculations are done to ensure that the transition states connect to the correct reactants and products at MP2/6-311G(d,p) level. Moreover, single points energies of reactants, products, complexes, and transition states at the MP2/6-311G(d,p) geometries are refined computed by using CCSD(T)49 and QCISD(T)50 methods coupled with 6-311++G(d,p). The T1 values of all species in our system are below 0.045, showing that multireference character in CCSD(T) wave function is not an issue.26By POLYRATE-Version 9.7 program,51 rate constants are received within 200–2000 K using the canonical variational transition state theory (CVT)52–54 with the small-curvature tunneling (SCT) correction.55,56 The relevant expressions are given as [eqn (1) and (2)]:
kCVTs(T) = min![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kGT(T, s) kGT(T, s)
| (1) |
 | (2) |
In these equations, s is the location of the generalized transition state on the IRC; σ is the symmetry factor; β equals (kBT)−1 where kB is Boltzmann's constant; h is Planck's constant; and QGT and QR are partition functions for the generalized transition state and reactants, respectively. In the calculation of the electronic partition functions, the two electronic states of the OH radicals, with a 140 cm−1 splitting in the 2Π ground state, are included. The total rate constant k is calculated from the sum of the individual rate constants. The severe spin contamination can bring about errors in the barrier height.57 The doublet range from 0.754 to 0.779 before annihilation, and after annihilation, the 〈s2〉 is 0.750. This suggests that the wave function is not severely contaminated.
3 Results and discussion
3.1 Stationary points and reaction mechanisms
The structural parameters of stationary points performed at the MP2/6-311G(d,p) and M06-2X/6-311G(d,p) levels are presented in Fig. 1, together with the limited experimental data.28 We can get that the computed values are in accord with the experimental geometries parameters of OH and H2O (given in the square bracket). Fig. 1 demonstrates that the breaking O–H bond in TS1 is 1.079 Å, which is 12.5% longer than the equilibrium O–H bond in CF3CH2CH2CH2OH, and the breaking C–H bonds are 6.3%, 9.8%, 8.9%, and 9.6% in TS2, TS3a, TS3b, and TS4 than the equilibrium C–H bonds length in CF3CH2CH2CH2OH. The forming O–H bonds are elongated by 28.2%, 46.6%, 35.5%, 37.9%, and 35.1% in TS1, TS2, TS3a, TS3b, and TS4 as compared to the O–H equilibrium bond length of H2O, respectively. The elongation of the breaking bond is smaller than that of the forming bond, indicating that the transition states are reactant-like and the reactions R1–R4 may proceed via early transition states. Consequently, all the transition states can be considered as early barriers. Similar results can be found at the M06-2X/6-311G(d,p) level.The harmonic vibrational frequencies are computed to confirm the stationary nature and to make zero-point energy (ZPE) corrections. The calculated frequencies at the MP2/6-311G(d,p) level are displayed in Table 1, along with the experimental data of OH and H2O.28 The five transition states are all confirmed by normal-mode analysis to have one and only one imaginary frequency, which corresponds to the stretching modes of coupling between breaking and forming bonds. The values of those imaginary frequencies are 2840i, 1241i, 1860i, 1720i, and 1826i cm−1 for TS1, TS2, TS3a, TS3b, and TS4, respectively. Above large absolute values of the imaginary frequencies indicate that the tunneling effect may be more important in the evaluating of the rate constants.
| Species | Frequencies | 〈s2〉 |
|---|---|---|
| a Experimental values in parenthesis are taken from ref. 28. | ||
| CF3CH2CH2CH2OH | 62, 78, 124, 149, 241, 283, 331, 371, 479, 547, 582, 665, 789, 863, 890, 1056, 1071, 1089, 1118, 1190, 1215, 1274, 1275, 1300, 1339, 1353, 1361, 1446, 1495, 1502, 1524, 1554, 3026, 3071, 3102, 3111, 3158, 3177, 3909 | 0.0 |
| CF3CH2CH2CH2O | 70, 76, 124, 149, 277, 326, 371, 383, 491, 547, 586, 665, 782, 863, 936, 1058, 1087, 1094, 1108, 1199, 1254, 1286, 1313, 1325, 1363, 1414, 1429, 1453, 1498, 1518, 3000, 3048, 3100, 3109, 3156, 3175 | 0.757 |
| CF3CH2CH2CHOH | 63, 76, 126, 135, 281, 336, 358, 375, 479, 547, 582, 664, 673, 809, 864, 1018, 1063, 1098, 1143, 1186, 1228, 1261, 1280, 1302, 1353, 1356, 1439, 1490, 1501, 1512, 3049, 3111, 3132, 3159, 3176, 3910 | 0.760 |
| CF3CH2CHCH2OH | 40, 44, 94, 164, 225, 281, 333, 363, 429, 489, 544, 586, 662, 860, 892, 985, 1063, 1106, 1140, 1166, 1188, 1256, 1280, 1298, 1325, 1346, 1442, 1480, 1499, 1531, 2964, 3020, 3053, 3138, 3257, 3914 | 0.763 |
| CF3CHCH2CH2OH | 32, 46, 99, 163, 236, 273, 327, 333, 467, 481, 581, 601, 671, 808, 879, 1037, 1053, 1110, 1153, 1161, 1192, 1236, 1275, 1293, 1329, 1351, 1469, 1494, 1497, 1553, 3035, 3046, 3086, 3148, 3257, 3911 | 0.762 |
| OH | 3855 (3775) | 0.754 |
| H2O | 1666 (1595), 3908 (3657), 4015 (3756) | 0.0 |
| TS1 | 2480i, 32, 67, 82, 93, 149, 152, 240, 293, 313, 371, 425, 510, 547, 584, 666, 784, 863, 868, 894, 1070, 1073, 1082, 1104, 1198, 1213, 1269, 1289, 1304, 1330, 1341, 1362, 1431, 1458, 1500, 1522, 1550, 1586, 3056, 3104, 3112, 3113, 3161, 3179, 3868 | 0.779 |
| TS2 | 1241i, 35, 55, 82, 110, 131, 152, 203, 288, 333, 346, 374, 480, 548, 583, 666, 706, 820, 864, 879, 1046, 1060, 1092, 1115, 1171, 1192, 1261, 1270, 1274, 1304, 1337, 1355, 1364, 1445, 1481, 1507, 1522, 1567, 3066, 3100, 3113, 3158, 3182, 3833, 3900 | 0.773 |
| TS3a | 1860i, 35, 70, 108, 152, 156, 177, 270, 295, 338, 369, 462, 471, 545, 560, 642, 675, 789, 865, 926, 998, 1051, 1087, 1093, 1143, 1197, 1199, 1270, 1283, 1305, 1330, 1350, 1358, 1442, 1478, 1493, 1540, 1569, 3039, 3093, 3094, 3152, 3165, 3793, 3904 | 0.779 |
| TS3b | 1720i, 43, 80, 98, 124, 138, 169, 187, 270, 294, 332, 372, 481, 545, 581, 650, 666, 777, 860, 911, 1006, 1061, 1091, 1102, 1135, 1194, 1202, 1268, 1290, 1301, 1338, 1347, 1393, 1404, 1448, 1491, 1498, 1540, 3016, 3079, 3099, 3151, 3169, 3852, 3915, | 0.778 |
| TS4 | 1826i, 57, 62, 77, 87, 117, 169, 210, 240, 282, 333, 357, 460, 548, 567, 631, 669, 804, 834, 894, 927, 1056, 1082, 1113, 1139, 1186, 1220, 1252, 1276, 1308, 1320, 1337, 1354, 1419, 1479, 1497, 1511, 1555, 3034, 3086, 3094, 3154, 3168 | 0.778 |
| ER1 | 19, 50, 75, 96, 125, 151, 209, 282, 306, 331, 371, 478, 502, 547, 583, 666, 683, 792, 864, 891, 1054, 1073, 1081, 1110, 1191, 1215, 1270, 1281, 1302, 1343, 1353, 1369, 1446, 1489, 1502, 1528, 1551, 3048, 3101, 3103, 3115, 3161, 3183, 3706, 3897 | 0.754 |
| ER2 | 30, 58, 78, 100, 108, 123, 174, 236, 253, 284, 332, 357, 378, 480, 548, 582, 665, 784, 857, 890, 1058, 1062, 1091, 1117, 1196, 1208, 1267, 1278, 1301, 1340, 1349, 1364, 1445, 1495, 1506, 1518, 1555, 3030, 3085, 3108, 3116, 3164, 3183, 3836, 3911 | 0.754 |
| ER3 | 17, 49, 63, 88, 112, 127, 152, 204, 239, 282, 329, 351, 376, 479, 550, 582, 664, 792, 864, 894, 1055, 1079, 1090, 1184, 1164, 1216, 1270, 1276, 1305, 1339, 1355, 1369, 1448, 1496, 1507, 1525, 1555, 3028, 3074, 3104, 3112, 3162, 3181, 3842, 3909 | 0.755 |
| EP1 | 13, 50, 72, 80, 107, 126, 149, 173, 245, 288, 343, 371, 488, 495, 547, 585, 615, 665, 793, 863, 964, 1049, 1091, 1094, 1106, 1201, 1253, 1311, 1326, 1363, 1414, 1423, 1456, 1498, 1518, 1686, 3008, 3063, 3101, 3157, 3175, 3857, 3983 | 0.758 |
| EP2 | 26, 40, 61, 96, 124, 133, 153, 171, 216, 285, 337, 375, 387, 431, 481, 549, 584, 666, 688, 816, 864, 1023, 1062, 1100, 1147, 1194, 1228, 1259, 1281, 1304, 1354, 1365, 1443, 1489, 1507, 1517, 1674, 6053, 3114, 3130, 3167, 3187, 3838, 3902, 3967 | 0.760 |
| EP3 | 34, 35, 78, 89, 144, 196, 200, 245, 286, 316, 372, 392, 411, 424, 542, 554, 563, 666, 706, 848, 898, 938, 1015, 1086, 1164, 1164, 1178, 1205, 1259, 1296, 1303, 1334, 1449, 1488, 1499, 1537, 1704, 3057, 3079, 3119, 3174, 3251, 3787, 3871, 3963 | 0.763 |
| EP4 | 18, 35, 67, 86, 102, 116, 184, 211, 235, 240, 268, 311, 332, 338, 474, 489, 579, 609, 660, 806, 868, 1021, 1047, 1103, 1146, 1164, 1184, 1229, 1271, 1298, 1335, 1348, 1475, 1487, 1506, 1562, 1684, 3040, 3062, 3129, 3166, 3260, 3900, 3913, 3996 | 0.762 |
The diagrammatic potential energy diagram of the title reaction with ZPE corrections, received at the CCSD(T)/6-311++G(d,p)//MP2/6-311G(d,p) level, is plotted in Fig. 2. At the CCSD(T)/6-311++G(d,p)//MP2/6-311G(d,p) level, the reactant complexes (ER1, ER2, ER3) and product complexes (EP1, EP2, EP3, EP4) lie at the entrances and exits of H-abstraction pathways, respectively. For R1, R2, and R3a, these reactions are found to take place by pre-reaction complex (ER1) with 3.81 kcal mol−1 binding energy. The OH can attack and abstract H of –OH group reaction R1, one of the H of –CH2O– group reaction R2, or the H of beta carbon reaction R3a. Then, starting from the complex ER1, the transition states (TS1, TS2, and TS3a) are occurred with 8.26, 3.86, and 6.19 kcal mol−1 barriers height, respectively. The geometries and pattern of attack of OH radical ER1 (OH⋯O(H)CH2CH2CH2CF3) is similar to the pre-complex (OH⋯O(H)CH2CH3) of reaction C2H5OH with OH radical24 and COM0 (OH⋯O(H)CH2CH2CH2CH3) of reaction of n-butanol by OH radical,17 which indicates the ER1 is credible. After crossing these transition states, the product complexes EP1, EP2, and EP3 are respectively formed with energies of 2.21, 2.29, and 5.20 kcal mol−1 below the products.
 | ||
| Fig. 2 Schematic potential energy surface for the reaction of CF3CH2CH2CH2OH + OH. Relative energies (in kcal mol−1) are calculated at the CCSD(T)/6-311++G(d,p)//MP2/6-311G(d,p) + ZPE level. | ||
For reactions R3b and R4, the reactant compounds ER2 and ER3 are come into being with energies −1.72 and −2.06 kcal mol−1 relative to the reactants. Afterwards, the reactions form EP3 and EP4 in the exit routes by means of TS3b and TS4, respectively, which are about 3.35 and 3.75 kcal mol−1 in energy. The hydrogen-bond attraction interaction between the H atom of –OH and the O atom of CF3CH2CH2CH2OH in TS3a, the H atom of –OH and the F atom of –CF3 group in TS3b because of fluorine and oxygen atom have high electronegativities. Both of TS3a and TS3b can proceed via EP3 to form CF3CH2CHCH2OH (P3) and H2O. By comparing the barrier height of the reaction channels R1–R4 each other, we deduce that R2 is the main contribution channel. Similar results can be shown that the barrier height of OH reaction with CF3CH2OH, CF3CF2CH2OH, and CF3CH2CH2OH to abstract the H atom of –CH2O– is lower than other site.18–20 Some investigations on Cl atom reaction with FAs have also found that the H atom of –CH2O– group is the easiest to be abstracted, such as Cl atom with CH3−nFnCH2OH by Wang et al.22 and with CF3CF2CH2OH by Yu23 and Garzón58 et al. For reaction of CF3CH2CH2CH2OH with Cl atom, only one experimental research performed at 298 K was reported the rate coefficient by Albaladejo et al.8 There is no evidence to suggest the most favorable channel in theoretical and experimental analysis. Here, we predict that Cl atom will also attack the –CH2O– group primarily by the comparison with similar reactions. An in-deep study about the reaction of CF3CH2CH2CH2OH + Cl and its comparisons with similar reactions will proceed in the future. With respect to reaction trends of some FAs with OH radical, a detailed discussion is shown in the following section of comparison with similar reactions.
3.2 Thermodynamics data prediction
The relative energy (Er) of species for R1–R4 with ZPE corrections and T1 diagnostic values at CCSD(T)/6-311++G(d,p) level is organized in Table 2. Reaction enthalpies (ΔHθr,298), reaction Gibbs free energies (ΔGθr,298) for R1–R4, and bonds dissociation energy (Dθ298) of C–H in molecule CF3CH2CH2CH2OH are displayed in Table 3. As listed in Tables 2 and 3, the results acquired by CCSD(T) and QCISD(T) ways show good mutual accord. Note that the following mentioned data is obtained at the CCSD(T)/6-311++G(d,p)//MP2/6-311G(d,p) level. It is easy to see that all of the individual reactions are exothermic From Table 3. The results of ΔGθr,298 indicate that all hydrogen abstraction reactions of CF3CH2CH2CH2OH by OH radical are spontaneous. Comparing the values of ΔHθr,298 each other of all reactions, it can be seen that heats of exothermic R1 and R2 are the fewest and most, respectively. The value of ΔGθr,298 of reaction R2 is lowest, −21.44 kcal mol−1, which shows that the spontaneous tendency is the largest of all the reactions. The value of Dθ298 (99.20 kcal mol−1) of reaction CF3CH2CH2CH2OH → CF3CH2CH2CHOH + H is lower than that of other reactions, and the Dθ298 value of reaction CF3CH2CH2CH2OH → CF3CH2CH2CH2O + H (108.64 kcal mol−1) is higher than other reactions. These indicate that owing to the H atom of –CH2O– is easiest to be dissociated, thus, is easy to be abstracted, and the H atom of –OH is hardest to be dissociated, thus, is difficult to be abstracted. Wang et al. have calculated the Dθ298 value of C–H bond of CH3–xFxCH2OH (x = 0–3),18,22 CF3CF2CH2OH,19 similar conclusion is obtained in their paper. Comparing the Dθ298 values of reaction CF3CH2CH2CH2OH → CF3CH2CHCH2OH + H and reaction CF3CH2CH2CH2OH → CF3CHCH2CH2OH + H, we can deduce that the R3 and R4 will be competitive with each other. The above conclusion further supports the cases occurred in the barrier heights for reactions R1–R4 and will be proved again in the section of rate constant computations.| Species | ZPEa | T1b | Era | Erb | Erc |
|---|---|---|---|---|---|
| a Obtained at the MP2/6-311G(d,p) level.b Obtained at CCSD(T)/6-311++G(d,p)//MP2/6-311G(d,p) level.c Obtained at QCISD(T)/6-311++G(d,p)//MP2/6-311G(d,p) level. | |||||
| R + OH | 0.125401 | 0.012, 0.010 | 0.00 | 0.00 | 0.00 |
| ER1 | 0.128756 | 0.012 | −6.09 | −3.81 | −3.75 |
| TS1 | 0.123540 | 0.021 | 6.40 | 4.45 | 4.20 |
| EP1 | 0.126637 | 0.014 | −14.08 | −14.68 | −14.80 |
| P1 + H2O | 0.122724 | 0.014, 0.010 | −9.70 | −12.47 | −12.56 |
| TS2 | 0.123914 | 0.018 | 2.34 | 0.05 | −0.25 |
| EP2 | 0.127140 | 0.014 | −26.50 | −22.94 | −23.10 |
| P2 + H2O | 0.124719 | 0.014, 0.010 | −21.97 | −20.65 | −20.79 |
| TS3a | 0.123836 | 0.016 | 3.26 | 2.38 | 2.16 |
| ER2 | 0.127403 | 0.013 | −3.55 | −1.73 | −1.75 |
| TS3b | 0122996 | 0.016 | 4.84 | 3.35 | 3.13 |
| EP3 | 0.127929 | 0.013 | −23.26 | −20.15 | −20.26 |
| P3 + H2O | 0.123171 | 0.013, 0.010 | −15.25 | −14.95 | −15.00 |
| ER3 | 0.127163 | 0.012 | −3.43 | −2.06 | −2.07 |
| TS4 | 0.122411 | 0.016 | 5.53 | 3.75 | 3.53 |
| EP4 | 0.126156 | 0.013 | −19.05 | −16.75 | −16.88 |
| P4 + H2O | 0.123683 | 0.013, 0.010 | −14.39 | −13.98 | −14.08 |
| MP2 | CCSD(T)//MP2 | QCISD(T)//MP2 | |
|---|---|---|---|
| ΔHθr,298 | |||
| CF3CH2CH2CH2OH + OH → CF3CH2CH2CH2O + H2O | −9.53 | −12.52 | −12.62 |
| CF3CH2CH2CH2OH + OH → CF3CH2CH2CHOH + H2O | −21.72 | −20.41 | −20.54 |
| CF3CH2CH2CH2OH + OH → CF3CH2CHCH2OH + H2O | −14.72 | −14.42 | −14.48 |
| CF3CH2CH2CH2OH + OH → CF3CHCH2CH2OH + H2O | −13.86 | −13.46 | −13.56 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| ΔGθr,298 | |||
| CF3CH2CH2CH2OH + OH → CF3CH2CH2CH2O + H2O | −10.38 | −13.00 | −13.10 |
| CF3CH2CH2CH2OH + OH → CF3CH2CH2CHOH + H2O | −22.75 | −21.44 | −21.57 |
| CF3CH2CH2CH2OH + OH → CF3CH2CHCH2OH + H2O | −16.78 | −16.48 | −16.54 |
| CF3CH2CH2CH2OH + OH → CF3CHCH2CH2OH + H2O | −16.02 | −15.62 | −15.72 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Dθ298 | |||
| CF3CH2CH2CH2OH → CF3CH2CH2CH2O + H | 111.47 | 108.64 | 108.60 |
| CF3CH2CH2CH2OH → CF3CH2CH2CHOH + H | 98.48 | 99.20 | 99.12 |
| CF3CH2CH2CH2OH → CF3CH2CHCH2OH + H | 106.17 | 105.88 | 105.87 |
| CF3CH2CH2CH2OH → CF3CHCH2CH2OH + H | 106.71 | 106.52 | 106.48 |
The enthalpy of formation (ΔHθf,298) are predicted by means of isodesmic reaction, in which the electron pairs and types of bond are conserved in both sides of the reaction. Herein, the ΔHθf,298 of the reactant CF3CH2CH2CH2OH and product radicals CF3CH2CH2CH2O CF3CH2CH2CHOH, CF3CH2CHCH2OH, and CF3CHCH2CH2OH are predicted as follows:
| CF3CH2CH2CH2OH + CH3 + CH3 + CH3 → CH2OH + CH3CF3 + CH2CH3 + CH2CH3 | (R5a) |
| CF3CH2CH2CH2OH + CH3 + CH3 + CH4 → CH3OH + CH3CF3 + CH2CH3 + CH2CH3 | (R5b) |
| CF3CH2CH2CH2OH + CH3 + CH4 + CH4 → CH3OH + CH3CF3 + CH2CH3 + CH3CH3 | (R5c) |
| CF3CH2CH2CH2O + CH3 + CH3 + CH4 → CH2OH + CH3CF3 + CH2CH3 + CH2CH3 | (R6a) |
| CF3CH2CH2CH2O + CH3 + CH4 + CH4 → CH3OH + CH3CF3 + CH2CH3 + CH2CH3 | (R6b) |
| CF3CH2CH2CH2O + CH4 + CH4 + CH4 → CH3OH + CH3CF3 + CH2CH3 + CH3CH3 | (R6c) |
| CF3CH2CH2CHOH + CH3 + CH3 + CH4 → CH2OH + CH3CF3 + CH2CH3 + CH2CH3 | (R7a) |
| CF3CH2CH2CHOH + CH3 + CH4 + CH4 → CH3OH + CH3CF3 + CH2CH3 + CH2CH3 | (R7b) |
| CF3CH2CH2CHOH + CH4 + CH4 + CH4 → CH3OH + CH3CF3 + CH2CH3 + CH3CH3 | (R7c) |
| CF3CH2CHCH2OH + CH3 + CH3 + CH4 → CH2OH + CH3CF3 + CH2CH3 + CH2CH3 | (R8a) |
| CF3CH2CHCH2OH + CH3 + CH4 + CH4 → CH3OH + CH3CF3 + CH2CH3 + CH2CH3 | (R8b) |
| CF3CH2CHCH2OH + CH4 + CH4 + CH4 → CH3OH + CH3CF3 + CH2CH3 + CH3CH3 | (R8c) |
| CF3CHCH2CH2OH + CH3 + CH3 + CH4 → CH2OH + CH3CF3 + CH2CH3 + CH2CH3 | (R9a) |
| CF3CHCH2CH2OH + CH3 + CH4 + CH4 → CH3OH + CH3CF3 + CH2CH3 + CH2CH3 | (R9b) |
| CF3CHCH2CH2OH + CH4 + CH4 + CH4 → CH3OH + CH3CF3 + CH2CH3 + CH3CH3 | (R9c) |
The ΔHθf,298 in experiment for the other species involved in above reactions are (in units of kcal mol−1): CH3, 34.82; CH4, −17.8; CH2OH, −2.2; CH3OH, −48.1; CH2CH3, 28.40; CH3CH3, −20.04; CH3CF3, −178.94.18,26 The ΔHθf,298 of the CF3CH2CH2CH2OH, CF3CH2CH2CH2O, CF3CH2CH2CHOH, CF3CH2CHCH2OH, and CF3CHCH2CH2OH are calculated at MP2/6-311G(d,p), CCSD(T) and QCISD(T)/6-311++G(d,p)//MP2/6-311G(d,p) levels. As shown in Table 4, the values of ΔHθf,298 for the species obtained at the CCSD(T) and QCISD(T) levels are very close with the greatest difference of 0.13 kcal mol−1. On basis of the computational results, the values of ΔHθf,298 for CF3CH2CH2CH2OH, CF3CH2CH2CH2O, CF3CH2CH2CHOH, CF3CH2CHCH2OH, and CF3CHCH2CH2OH are recommended to be (−225.48 ± 0.70), (−173.46 ± 0.73), (−181.36 ± 0.75), (−175.33 ± 0.71), and (−174.40 ± 0.73) kcal mol−1, respectively. These above mentioned results are unavailable in the literature and may be useful for further researching thermodynamics and kinetics of reactions related to these species.
| Species | Isodesmic reaction | MP2 | CCSD(T)//MP2 | QCISD(T)//MP2 | |||
|---|---|---|---|---|---|---|---|
| ΔHθf,298 | Average | ΔHθf,298 | Average | ΔHθf,298 | Average | ||
| CF3CH2CH2CH2OH | R5a | −225.45 | −226.73 | −225.26 | −225.40 | −225.18 | −225.39 |
| R5b | −228.21 | −226.17 | −226.17 | ||||
| R5c | −226.52 | −224.78 | −224.81 | ||||
| R6a | −171.18 | −173.21 | −173.18 | ||||
| CF3CH2CH2CH2O | R6b | −172.94 | −171.79 | −174.11 | −173.35 | −174.18 | −173.39 |
| R6c | −171.25 | −172.73 | −172.81 | ||||
| R7a | −182.61 | −181.09 | −181.11 | ||||
| CF3CH2CH2CHOH | R7b | −184.38 | −183.22 | −182.00 | −181.23 | −182.10 | −181.32 |
| R7c | −182.68 | −180.61 | −180.74 | ||||
| R8a | −175.61 | −175.10 | −175.04 | ||||
| CF3CH2CHCH2OH | R8b | −177.38 | −176.22 | −176.00 | −175.24 | −176.04 | −175.25 |
| R8c | −175.68 | −174.62 | −174.68 | ||||
| R9a | −174.75 | −174.15 | −174.13 | ||||
| CF3CHCH2CH2OH | R9b | −176.52 | −175.37 | −175.05 | −174.29 | −175.12 | −174.34 |
| R9c | −174.83 | −173.67 | −173.76 | ||||
3.3 Reaction channel content
A dual-level direct kinetics calculation is adopted to compute the dynamic content at the CCSD(T)/6-311++G(d,p)//MP2/6-311G(d,p) level. Fig. 3a and b depict the classical potential energy curve (VMEP), ground-state vibrational adiabatic energy curve (VGa), and zero-point energy curve (ZPE) as functions of s (amu)1/2 bohr for the reactions R2 and R3a. From Fig. 3a, it is seen that the plots of the VGa and VMEP are similar, and zenith of VGa and VMEP are same at 0.17 (amu)1/2 bohr, indicating that the negligible variational effect can be found for the channel R2. Wang and Li have theoretically studied the reactions of some FAs with OH radical or Cl atom, similar results can be found about potential energy curves in their papers.18,19,22 Fig. 3b shows that the maximum of VGa is located as s = −0.34 (amu)1/2 bohr in the reactant side for R3a. However, the maximum value of VMEP is located as the saddle point (s = 0). The variational effect may be worthy of consideration in evaluating the rate constant.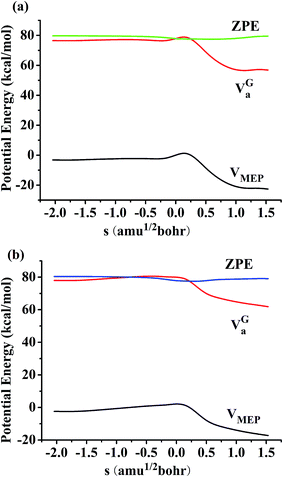 | ||
| Fig. 3 Classical potential energy curve (VMEP), ground-state vibrational adiabatic energy curve (VGa), and zero-point energy curve (ZPE) as functions of s (amu)1/2 bohr at the CCSD(T)/6-311++G(d,p)//MP2/6-311G(d,p) level (a) for the reaction channel R2 and (b) for the R3a. | ||
Fig. 4a and b exhibit that the variations of the vibrational frequencies along with the MEPs for R2 and R3a, respectively. In the negative of s = −2.0 (amu)1/2 bohr, the frequencies are connected with those of the pre-complexes, and at about s = 1.5 (amu)1/2 bohr, the frequencies amount to those of the product complexes. In the process of the reaction, the frequency of mode 1 which is referred to as the “reactive mode” shows an evident drop along with the reaction. This is the characteristic of these reactions which transfer H atoms. Fig. 4b suggests that in the vicinity of the TS, there are 44 frequencies and deep minimum in frequency occurs from 0 to 0.34 (amu)1/2 bohr.
 | ||
| Fig. 4 Changes of generalized normal-mode vibrational frequencies as functions of s (amu)1/2 bohr at the CCSD(T)/6-311++G(d,p)//MP2/6-311G(d,p) level for reaction R1 via TS2 (a) and R2 via TS3a (b). | ||
3.4 Rate-constant computations and branching ratios
Seen from Fig. 2, the mechanism of the CF3CH2CH2CH2OH + OH can be represented as:| R1 + R2 ↔ R1⋯R2 step 1 |
| R1⋯R2 → P1 + P2 step 2 |
The first reversible step leads to the formation of reactant complex, and the second irreversible step yields the corresponding products. k1 is the forward rate constant while k−1 is the reverse rate constant in the first step. k2 is equivalent to the second step. According to the steady-state analysis, the total rate constant can be displayed by [eqn (3)]
 | (3) |
As first discussed in the paper of Singleton and Cvetanović,59 k−1 is much larger than k2, thus k could be rewritten as [eqn (4)]
 | (4) |
Using basic statistical thermodynamic theory, the equilibrium constant (Keq) between the two reactants and the reactant complex can be denoted as [eqn (5)]. Under high-pressure conditions, the k2 calculated by classical TST method and corresponding rate constant k can be expressed as [eqn (6) and (7)]
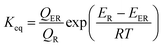 | (5) |
 | (6) |
 | (7) |
In the above equations, the QER, QTS, and QR are the partition functions of the reactant complex, transition state, and the reactants, respectively. The κ is the tunneling factor; kB is Boltzmann constant and h is Planck constant. In fact, previous articles for similar mechanisms60–64 always assumed reactant complex undergoes collisional stabilization in a high-pressure limit. Option “well” can be used for the dynamic calculations in the Polyrate program, so both above steps are considered in the theoretical discussion.
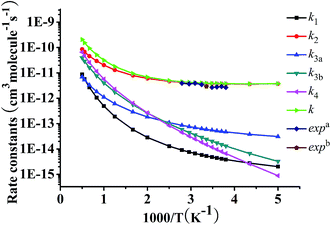
The rate constants of TST, CVT, CVT/SCT for the primary channel R2 and secondary reaction pathway R3a are illustrated in Fig. 5a and b, respectively. The k1, k2, k3a, k3b, k4 and k (k= k1 + k2 + k3a + k3b + k4) are listed in Table 5 and depicted in Fig. 6 (CVT/SCT rate constants). For reaction R2, Fig. 5a shows that the CVT and TST are overlap each other over the whole temperature range, illustrating that the effect from variational effects may be negligible. Nevertheless, difference between the CVT and CVT/SCT is distinct in 200–800 K and coincide with each other with the temperature increasing, demonstrating that the tunneling effects are momentous at low temperatures and can be ignored when temperatures are above 800 K. The characteristics of the current reactions can be also discovered in other similar systems, as investigated by Wang et al.18,19,21,22 and other authors.23,25–31 Moreover, Fig. 5b depicts that the ratios of CVT and TST are 0.75–0.77 in temperature limits from 200 to 2000 K, showing that the we should attach importance to the variational effects in calculations of rate coefficient of R3a. The tunneling effects come under observation to be important for reaction R3a in the temperature of 200–1000 K, while with the temperature increasing, the tunneling effect can be neglectful. For example, the ratios between the CVT/SCT and CVT are 10.92, 3.33, 1.12, and 1.03 at 200, 298, 1000, and 2000 K, respectively. From Table 5, it is pleasing to observe that our rate constants in 200–2000 K are in line with the coefficients in experimental temperatures (263–358 K). So for example, computed values of 3.93 × 10−12, 4.01 × 10−12 and experimental values of 2.62 × 10−12, 3.14 × 10−12 cm3 per molecule per s at 298 and 308 K, respectively. In order to display the calculated and experimental data in point and range style more intuitively, we also depict the CVT/SCT rate constants of k1, k2, k3a, k3b, and k4 and the total rate constant k in Fig. 6. As is shown in Fig. 6, positive temperature effect dependence effect can be observed from 230 to 2000 K for the main reaction channel R2. Reaction channels R1, R3a, R3b, and R4 all have positive temperature effect in the whole temperature range.
 | ||
| Fig. 5 Computed TST, CVT, and CVT/SCT rate constants versus 103/T between 200 and 2000 K (a) for reaction channel R2, (b) for the R3a. | ||
| T (K) | k1 | k2 | k3a | k3b | k4 | k |
|---|---|---|---|---|---|---|
| a Obtained from ref. 7.b Obtained from ref. 8. | ||||||
| 200 | 2.02 × 10−15 (Y) | 3.73 × 10−12 (Y) | 3.09 × 10−14 (Y) | 3.25 × 10−15 (Y) | 8.86 × 10−16 (Y) | 3.77 × 10−12 (Y) |
| 230 | 2.78 × 10−15 (Y) | 3.64 × 10−12 (Y) | 3.78 × 10−14 (Y) | 6.62 × 10−15 (Y) | 2.58 × 10−15 (Y) | 3.69 × 10−12 (Y) |
| 263 | 3.84 × 10−15 (Y) | 3.69 × 10−12 (Y) | 4.72 × 10−14 (Y) | 1.31 × 10−14 (Y) | 6.61 × 10−15 (Y) | 3.76 × 10−12 (Y) |
| (2.41 ± 0.25) × 10−12 a | ||||||
| 270 | 4.11 × 10−15 (Y) | 3.71 × 10−12 (Y) | 4.95 × 10−14 (Y) | 1.49 × 10−14 (Y) | 7.89 × 10−15 (Y) | 3.79 × 10−12 (Y) |
| (2.63 ± 0.27) × 10−12 a | ||||||
| 278 | 4.43 × 10−15 (Y) | 3.74 × 10−12 (Y) | 5.22 × 10−14 (Y) | 1.72 × 10−14 (Y) | 9.57 × 10−15 (Y) | 3.82 × 10−12 (Y) |
| (2.48 ± 0.30) × 10−12 a | ||||||
| 287 | 4.81 × 10−15 (Y) | 3.78 × 10−12 (Y) | 5.53 × 10−14 (Y) | 2.02 × 10−14 (Y) | 1.18 × 10−14 (Y) | 3.87 × 10−12 (Y) |
| (2.42 ± 0.26) × 10−12 a | ||||||
| 298 | 5.33 × 10−15 (Y) | 3.83 × 10−12 (Y) | 5.94 × 10−14 (Y) | 2.43 × 10−14 (Y) | 1.49 × 10−14 (Y) | 3.93 × 10−12 (Y) |
| (2.62 ± 0.32) × 10−12 b | ||||||
| 308 | 5.83 × 10−15 (Y) | 3.89 × 10−12 (Y) | 6.33 × 10−14 (Y) | 2.85 × 10−14 (Y) | 1.84 × 10−14 (Y) | 4.01 × 10−12 (Y) |
| (3.14 ± 0.32) × 10−12 a | ||||||
| 323 | 6.67 × 10−15 (Y) | 3.99 × 10−12 (Y) | 6.96 × 10−14 (Y) | 3.59 × 10−14 (Y) | 2.46 × 10−14 (Y) | 4.13 × 10−12 (Y) |
| (3.53 ± 0.37) × 10−12 a | ||||||
| 338 | 7.61 × 10−15 (Y) | 4.10 × 10−12 (Y) | 7.63 × 10−14 (Y) | 4.46 × 10−14 (Y) | 3.22 × 10−14 (Y) | 4.26 × 10−12 (Y) |
| (3.34 ± 0.34) × 10−12 a | ||||||
| 358 | 9.05 × 10−15 (Y) | 4.27 × 10−12 (Y) | 8.61 × 10−14 (Y) | 5.85 × 10−14 (Y) | 4.51 × 10−14 (Y) | 4.47 × 10−12 (Y) |
| (3.54 ± 0.37) × 10−12 a | ||||||
| 400 | 1.29 × 10−14 (Y) | 4.69 × 10−12 (Y) | 1.10 × 10−13 (Y) | 9.75 × 10−14 (Y) | 8.38 × 10−14 (Y) | 4.99 × 10−12 (Y) |
| 500 | 2.86 × 10−14 (Y) | 6.06 × 10−12 (Y) | 1.84 × 10−13 (Y) | 2.61 × 10−13 (N) | 2.67 × 10−13 (Y) | 6.80 × 10−12 (Y) |
| 600 | 5.82 × 10−14 (Y) | 7.89 × 10−12 (Y) | 2.89 × 10−13 (Y) | 5.60 × 10−13 (N) | 6.42 × 10−13 (Y) | 9.44 × 10−12 (Y) |
| 800 | 1.91 × 10−13 (Y) | 1.30 × 10−11 (Y) | 6.11 × 10−13 (Y) | 1.75 × 10−12 (N) | 2.29 × 10−12 (N) | 1.78 × 10−11 (Y) |
| 1000 | 4.91 × 10−13 (Y) | 2.03 × 10−11 (N) | 1.11 × 10−13 (Y) | 4.02 × 10−12 (N) | 5.71 × 10−12 (N) | 3.16 × 10−11 (N) |
| 1200 | 1.06 × 10−12 (Y) | 2.95 × 10−11 (N) | 1.82 × 10−13 (N) | 7.67 × 10−12 (N) | 1.15 × 10−11 (N) | 5.16 × 10−11 (N) |
| 1500 | 2.69 × 10−12 (Y) | 4.58 × 10−11 (N) | 3.31 × 10−13 (N) | 1.62 × 10−11 (N) | 2.56 × 10−11 (N) | 9.36 × 10−11 (N) |
| 1800 | 5.69 × 10−12 (N) | 6.79 × 10−11 (N) | 5.33 × 10−13 (N) | 2.88 × 10−11 (N) | 4.70 × 10−11 (N) | 1.55 × 10−10 (N) |
| 2000 | 8.70 × 10−12 (N) | 8.57 × 10−11 (N) | 6.95 × 10−13 (N) | 3.95 × 10−11 (N) | 6.57 × 10−11 (N) | 2.07 × 10−10 (N) |
Fig. 7 shows branching ratios of each pathways. It can be found that channel R2 plays a fundamental role within 200–2000 K. However, the contribution of channel R1 is fewest in the whole temperature range. Competitive channels R3 contributes more than R4 to the total reaction coefficient when the temperature is below 800 K, but with the temperature increasing, channel R4 should be considered. When the temperature is above 800 K, contributions of the reaction pathways are in this order, k2 > k4 > k3 > k1. Thus, for the multi-channel reaction, the dominant channel is the H-abstraction from the –CH2O– group leading to the product CF3CH2CH2CHOH.
 | ||
| Fig. 7 Computed branching ratios versus 103/T between 200 and 2000 K for the reaction of CF3CH2CH2CH2OH + OH. | ||
3.5 Kinetic isotope effects (KIEs)
KIEs for the systems CF3CH2CH2CH2OH + OD (R′) and CF3CD2CD2CD2OD + OH (R*) have been investigated over the whole temperature scope of 200–2000 K, in which the KIEs are defined as the specific values of the between kH and kD. The calculated KIEs for reactions R1′ (R1*), R2′ (R2*), R3a′ (R3a*), R3b′ (R3b*), and R4′ (R4*) are displayed in the Fig. 8a and b, respectively. It can be seen that the KIEs of the total rate coefficients k/k′ and k/k* are normal, that is, larger than 1 (kH/kD > 1) at the whole temperature range. In general, the KIEs of the k/k′ and k/k* mostly increase with the decreasing of temperature. For the main pathway R2, the KIEs of k2/k′2 and k2/k*2 also get a similar circumstance with the total reaction rate constant. For reaction channel R3a, the KIEs for R3a′ are within 0.40–0.70, suggesting that a noticeable inverse (kH/kD < 1) exists. The KIEs for R3a* are within 1.1–1.2 (around 1.0), indicating that the KIE is of less importance for this channel. The KIEs for R4′ are within 0.86–1.00, 1.00–1.24 at the temperature range of 200–287 K and 287–2000 K, respectively. This implies a noticeable inverse can be found in the 200–287 K for R4′ and a slight normal KIE between 287 and 2000 K. Similar results exist in the 200–500 K for R4*. Comparing the KIEs of R′ with R*, we find that the results of KIEs result from the CF3CH2CH2CH2OH + OD (R′) and CF3CD2CD2CD2OD + OH (R*) are different and the KIEs of main pathway R2* is larger than R2′. For example, the KIEs are 2.06 at 298 K, 1.95 at 500 K, 1.73 at 1000 K, and 1.45 at 2000 K for R*, and 1.27 at 298 K, 1.11 at 500 K, 1.05 at 1000 K, and 1.04 at 2000 K for R′. Taking a comparison between the reactions R1′–R4′, it is seen that the R3a′ affected by the KIE is significant. However, we find that the KIE for R1* is 6.99, 6.10, 4.02, and 3.07 at 298, 500, 1000, and 2000 K, respectively, which suggests that the KIE of R1* is the most important of for reactions R1*–R4*. Above isotope effects have also been found in many reactions.39–41,65,66 Although there can be not provide a comparison between corresponding experiment and theory, our results can add unprecedented information for using in further experimental study.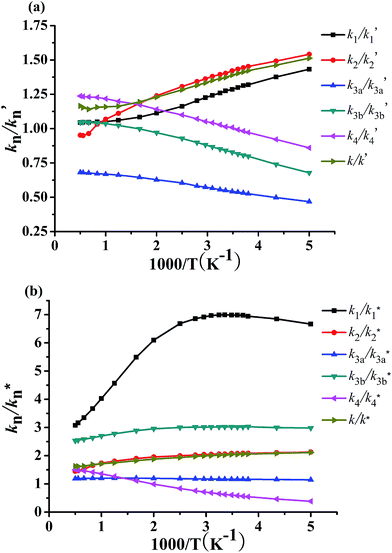 | ||
| Fig. 8 Plot of the calculated ratios k1/k′1 (k1/k*1), k2/k′2 (k2/k*2), k3a/k′3a (k3a/k*3a), k3b/k′3b (k3b/k*3b), and k4/k′4 (k4/k*4) versus 103/T in the temperature range of 200–2000 K. | ||
3.6 Comparison with similar reactions
It is desirable to make a comparison between the title reaction and the similar alcohols (OH radical with the CH3CH2CH2CH2OH, CH3CH2CH2OH, CF3CF2CH2OH, CF3CH2CH2OH, CF3CH2OH, CH3CH2OH, CF3OH, and CH3OH) in dynamics.14–16,18–20,24 The comparisons will give some worthy similarities and differences. Comparing the overall rate constants of OH + CF3(CH2)mOH (m = 0−3) each other, we can find the following relationship at 298 K: kCF3CH2CH2CH2OH > kCF3CH2CH2OH > kCF3CH2OH > kCF3OH. This trend could be attributed to the electron donating group effect. The rate constants will increase with the increasing of carbon chain when CF3(CH2)mOH reaction with electron withdrawing group, like OH radical. To compare the overall reaction constants of OH with CH3(CH2)mOH (m = 0–3),15–17,24 similar conclusion can be found, in which should be as: kCH3CH2CH2CH2OH > kCH3CH2CH2OH > kCH3CH2OH > kCH3OH. It should be noted that for the reactions of OH with R(CH2)nOH (R = –CF3 or –CH3; n = 1–3), the attack takes place at the –CH2O– group for the most part, which was discussed in the preceding part of the text. In fact, the fluorine substitution can decrease the reactivity, it is a matter of concern that OH radical reaction with a series of alcohols about rate coefficient at 298 K are in the sequence: kCF3CH2CH2OH > kCF3CF2CH2OH, kCH3CH2CH2OH > kCF3CH2CH2OH, kCH3CH2OH > kCF3CH2OH, kCH3OH > kCF3OH.3.7 Atmospheric lifetime of ethers, esters, and alcohols
The atmospheric lifetime can be estimated by the expression can be shown as [eqn (8)–(10)]:
 | (8) |
 | (9) |
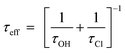 | (10) |
Using the average atmospheric OH and Cl concentrations67 of 1 × 106 and 1 × 104 molecule per cm3, the atmospheric lifetime is estimated based on the existing data to add atmospheric content of the ethers, esters, and alcohols. Using the total rate constant 3.82 × 10−12 cm3 per molecule per s at 278 K and the OH concentrations of 1.0 × 106 molecule per cm3, the computed atmospheric lifetime of CF3CH2CH2CH2OH is being of 3.03 days, which coincides with the values of 3.70 days and 4.5 days in experiment.7,8 The lifetime of CF3CH2CH2CH2OH is relatively short, suggesting its inconsiderable impact to the global warming of Earth. In addition, theoretical researches about the ethers, esters, and alcohols with OH radicals and Cl atoms about the rate constant, calculation methods, and lifetimes are summarized in Tables S1a–S1c.† For the ethers, esters, and alcohols, because of the atmospheric lifetime is going conversely with the rate constant when the concentration of OH and Cl radicals is set to be constant. For example, the atmospheric lifetime of CF3OCH2CF3 is 0.521 years, which is smaller than that of CF3OCHFCF3 (24.38 years). For typical esters and alcohols, the atmospheric lifetimes are in this order, τCF3COOCH3>τCF2HCOOCH3, τCF3CH2OH>τCH3CH2OH. Therefore, the fluorine or chlorine substitution can increase lifetime of ethers, esters, and alcohols, that is, more and more fluorine or chlorine substitution can add its contribution to the global warming of Earth and ability to destroy the ozone layer. In terms of atmospheric lifetimes, the disadvantage of fluorine or chlorine substitution can be explained thoroughly.
Due to experimental data is lacking in higher temperatures, the fitted three-parameter on basis of the calculated rate constants within 200–2000 K give expressions as follows (in units of cm3 per molecule per s):
k1(T) = 3.27 × 10−24T3.79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(–483.24/T) exp(–483.24/T) |
k2(T) = 3.43 × 10−19T2.50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(579.78/T) exp(579.78/T) |
k3a(T) = 1.53 × 10−20T2.62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(8.69/T) exp(8.69/T) |
k3b(T) = 1.60 × 10−18T2.33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1333.72/T) exp(−1333.72/T) |
k4(T) = 3.90 × 10−18T2.30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−1689.15/T) exp(−1689.15/T) |
k(T) = 3.43 × 10−21T3.22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(741.70/T). exp(741.70/T). |
4 Conclusions
In this article, reaction of CF3CH2CH2CHOH with OH radical is investigated in kinetics by the dual-level direct method. The PES information is obtained at the CCSD(T) and QCISD(T)/6-311++G(d,p)//MP2/6-311G(d,p) levels. By means of the group-balanced isodesmic reaction R5a–R9c, the standard enthalpy of formation obtained by combining the results at the CCSD(T) and QCISD(T) levels based on the MP2 geometries are: (−225.48 ± 0.70) kcal mol−1 for CF3CH2CH2CH2OH, (−173.46 ± 0.73) kcal mol−1 for CF3CH2CH2CH2O, (−181.36 ± 0.75) kcal mol−1 for CF3CH2CH2CHOH, (−175.33 ± 0.71) kcal mol−1 for CF3CH2CHCH2OH, and (−174.40 ± 0.73) kcal mol−1 for CF3CHCH2CH2OH.The rate constants of all the reactions are calculated by CVT incorporating SCT correction. The agreement between theoretical and experiment result is very excellent. For the dominant channel R2, the variational effect is almost not existing or negligible in the temperature range of 200–2000 K. The KIEs for the main channel and total reaction are normal and decrease with the temperature increasing. Atmospheric lifetimes of a series of relevant ethers, esters, and alcohols are estimated. The estimated atmospheric life time of CF3CH2CH2CH2OH is expected to be around 3.03 days. The relatively short atmospheric lifetime of CF3CH2CH2CH2OH make its negligible contribution towards ozone depletion. The three-parameter Arrhenius expression for the title reaction is k(T) = 3.43 × 10−21T3.22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(741.70/T) cm3 per molecule per s. We hope the present theoretical studies are helpful for further understanding the title reaction.
exp(741.70/T) cm3 per molecule per s. We hope the present theoretical studies are helpful for further understanding the title reaction.
Acknowledgements
The authors thank Professor Donald G. Truhlar for providing the Polyrate, Version 9.7 program. We are grateful to financial support from National Natural Science Foundation of China (No. 21377021).Notes and references
- T. J. Wallington, W. F. Schneider, D. R. Worsnop, O. J. Nielsen, J. Sehested, W. J. Debruyn and J. A. Shorter, Environ. Sci. Technol., 1994, 28, 320–326 CrossRef PubMed.
- T. Kelly, V. Bossoutrot, I. Magneron, K. Wirtz, J. Treacy, A. Mellouki, H. Sidebottom and G. Le Bras, J. Phys. Chem. A, 2005, 109, 347–355 CrossRef CAS PubMed.
- Environmental Protection Agency, EPA, http://www.epa.gov.
- M. D. Hurley, T. J. Wallington, M. P. Sulbaek Andersen, D. A. Ellis, J. W. Martin and S. A. Mabury, J. Phys. Chem. A, 2004, 108, 1973–1979 CrossRef CAS.
- E. Moreno, A. Aranda, Y. Díaz-de-Mera, A. Notario, D. Rodríguez and I. Bravo, Atmos. Environ., 2012, 60, 76–81 CrossRef CAS.
- D. R. Salahub and C. Sandorfy, Chem. Phys. Lett., 1971, 8, 71–74 CrossRef CAS.
- M. Antinolo, E. Jimenez and J. Albaladejo, Environ. Sci. Technol., 2011, 45, 4323–4330 CrossRef CAS PubMed.
- E. Jimenez, M. Antinolo, B. Ballesteros, E. Martinez and J. Albaladejo, ChemPhysChem, 2010, 11, 4079–4087 CrossRef CAS PubMed.
- Y. Diaz-de-Mera, A. Aranda, I. Bravo, D. Rodriguez, A. Rodriguez and E. Moreno, Environ. Sci. Pollut. Res., 2008, 15, 584–591 CrossRef CAS PubMed.
- M. Antinolo, S. Gonzalez, B. Ballesteros, J. Albaladejo and E. Jimenez, J. Phys. Chem. A, 2012, 116, 6041–6050 CrossRef CAS PubMed.
- Y. N. Indulkar, S. SenGupta, S. B. Waghmode, A. Kumar, S. Dhanya and P. D. Naik, Atmos. Environ., 2011, 45, 6973–6979 CrossRef CAS.
- I. Bravo, Y. Diaz-de-Mera, A. Aranda, K. Smith, K. P. Shine and G. Marston, Phys. Chem. Chem. Phys., 2010, 12, 5115–5125 RSC.
- M. D. Hurley, J. A. Misner, J. C. Ball, T. J. Wallington, D. A. Ellis, J. W. Martin, S. A. Mabury and M. P. Sulbaek Andersen, J. Phys. Chem. A, 2005, 109, 9816–9826 CrossRef CAS PubMed.
- K. Brudnik, J. T. Jodkowski, E. Ratajczak, R. Venkatraman, A. Nowek and R. H. Sullivan, Chem. Phys. Lett., 2001, 345, 435–444 CrossRef CAS.
- A. Galano, J. R. l. Alvarez-Idaboy, G. Bravo-Perez and M. E. Ruiz-Santoyo, Phys. Chem. Chem. Phys., 2002, 4, 4648–4662 RSC.
- P. Seal, G. Oyedepo and D. G. Truhlar, J. Phys. Chem. A, 2013, 117, 275–282 CrossRef CAS PubMed.
- J. Moc and J. M. Simmie, J. Phys. Chem. A, 2010, 114, 5558–5564 CrossRef CAS PubMed.
- Y. Wang, J. Y. Liu, Z. S. Li, L. Wang and C. C. Sun, J. Comput. Chem., 2007, 28, 802–810 CrossRef CAS PubMed.
- Y. Wang, J. Y. Liu, Z. S. Li, L. Wang, J. Y. Wu and C. C. Sun, J. Phys. Chem. A, 2006, 110, 5853–5859 CrossRef CAS PubMed.
- T. Y. Jin, C. G. Ci, Y. Wu and J. Y. Liu, Comput. Theor. Chem., 2013, 1007, 63–75 CrossRef CAS.
- Y. Wang, J. Y. Liu and Z. S. Li, Chem. Phys., 2007, 335, 28–36 CrossRef CAS.
- Y. Wang, J. Y. Liu and Z. S. Li, J. Comput. Chem., 2007, 28, 2517–2530 CrossRef CAS PubMed.
- A. Y. Yu and H. X. Zhang, J. Mol. Model., 2013, 19, 4503–4510 CrossRef CAS PubMed.
- S. Xu and M. C. Lin, Proc. Combust. Inst., 2007, 31, 159–166 CrossRef.
- F. Y. Bai, Y. Q. Sun, X. Wang, Z. M. Jia, R. S. Wang and X. M. Pan, J. Mol. Model., 2014, 20, 2419 CrossRef PubMed.
- F. Y. Bai, X. L. Zhu, Z. M. Jia, X. Wang, Y. Q. Sun, R. S. Wang and X. M. Pan, ChemPhysChem, 2015, 16, 1768–1776 CrossRef CAS PubMed.
- G. C. Song, X. J. Jia, Y. Gao, J. Luo, Y. B. Yu, R. S. Wang and X. M. Pan, J. Phys. Chem. A, 2010, 114, 9057–9068 CrossRef CAS PubMed.
- X. J. Jia, Y. J. Liu, J. Y. Sun, H. Sun, Z. M. Su, X. M. Pan and R. S. Wan, J. Phys. Chem. A, 2010, 114, 417–424 CrossRef CAS PubMed.
- F. Y. Bai, G. Sun, X. Wang, Y. Q. Sun, R. S. Wang and X. M. Pan, J. Phys. Chem. A, 2015, 119, 1256–1266 CrossRef CAS PubMed.
- H. Sun, H. W. Gong, X. M. Pan, L. Z. Hao, C. C. Sun, R. S. Wang and X. R. Huang, J. Phys. Chem. A, 2009, 113, 5951–5957 CrossRef CAS PubMed.
- J. Y. Wu, J. Y. Liu, Z. S. Li and C. C. Sun, J. Chem. Phys., 2003, 118, 10986–10995 CrossRef CAS.
- B. K. Mishra, M. Lily, R. C. Deka and A. K. Chandra, J. Mol. Graphics Modell., 2014, 50, 90–99 CrossRef CAS PubMed.
- B. K. Mishra, M. Lily, A. K. Chandra and R. C. Deka, J. Phys. Org. Chem., 2014, 27, 811–817 CrossRef CAS.
- D. Bhattacharjee, B. K. Mishra and R. C. Deka, J. Mol. Model., 2015, 21, 1–8 CrossRef CAS PubMed.
- B. K. Mishra, M. Lily, A. K. Chakrabartty, D. Bhattacharjee, R. C. Deka and A. K. Chandra, New J. Chem., 2014, 38, 2813–2822 RSC.
- K. Jogeshwari Devi and A. K. Chandra, Chem. Phys. Lett., 2011, 502, 23–28 CrossRef CAS.
- B. K. Mishra, A. K. Chakrabartty and R. C. Deka, Mol. Phys., 2014, 112, 1512–1519 CrossRef CAS.
- L. Yang, J. Y. Liu, L. Wang, H. Q. He, Y. Wang and Z. S. Li, J. Comput. Chem., 2008, 29, 550–561 CrossRef CAS PubMed.
- L. Yang, J. Y. Liu, S. Q. Wan and Z. S. Li, J. Comput. Chem., 2009, 30, 565–580 CrossRef CAS PubMed.
- L. Yang, J. Y. Liu and Z. S. Li, J. Chem. Theory Comput., 2008, 4, 1073–1082 CrossRef CAS PubMed.
- V. I. Jaramillo and M. A. Smith, J. Phys. Chem. A, 2001, 105, 5854–5859 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, P. W. M. Gill, B. G. Johnson, M. A. Robb, J. R. Cheeseman, T. A. Keith, G. A. Petersson and J. A. Pople, et al., Gaussian 09, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef.
- H. Zhang, L. Yang, J. Y. Liu and Z. S. Li, J. Comput. Chem., 2012, 33, 203–210 CrossRef CAS PubMed.
- X. J. Jia, Y. J. Liu, J. Y. Sun, H. Sun, F. Wang, Z. M. Su, X. M. Pan and R. S. Wang, J. Comput. Chem., 2010, 31, 2263–2272 CAS.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- C. Gonzalez and H. B. Schlegel, J. Chem. Phys., 1989, 90, 2154–2161 CrossRef CAS.
- C. Gonzalez and H. B. Schlegel, J. Phys. Chem., 1990, 94, 5523–5527 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975 CrossRef CAS.
- J. C. Corchado, Y. Y. Chuang, P. L. Fast, W. P. Hu, Y. P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. Fernandez-Ramos and B. A. Ellingson, et al., POLYRATE, version 9.7, University of Minnesota, Minneapolis, MN, 2007 Search PubMed.
- B. C. Garrett and D. G. Truhlar, J. Chem. Phys., 1979, 70, 1593–1598 CrossRef CAS.
- B. C. Garrett and D. G. Truhlar, J. Am. Chem. Soc., 1979, 101, 4534–4548 CrossRef CAS.
- B. C. Garrett, D. G. Truhlar, R. S. Grev and A. W. Magnuson, J. Phys. Chem., 1980, 84, 1730–1748 CrossRef CAS.
- D. H. Lu, T. N. Truong, V. S. Melissas, G. C. Lynch, Y. P. Liu, B. C. Garrett, R. Steckler, A. D. Isaacson, S. N. Rai, G. C. Hancock, J. G. Lauderdale, T. Joseph and D. G. Truhlar, Comput. Phys. Commun., 1992, 71, 235–262 CrossRef CAS.
- Y. P. Liu, G. C. Lynch, T. N. Truong, D. H. Lu, D. G. Truhlar and B. C. Garrett, J. Am. Chem. Soc., 1993, 115, 2408–2415 CrossRef CAS.
- H. B. Schlegel and C. Sosa, Chem. Phys. Lett., 1988, 145, 329–333 CrossRef CAS.
- A. Garzón, M. Antiñolo, M. Moral, A. Notario, E. Jiménez, M. Fernández-Gómez and J. Albaladejo, Mol. Phys., 2013, 111, 753–763 CrossRef.
- D. L. Singleton and R. J. Cvetanović, J. Am. Chem. Soc., 1976, 98, 6812–6819 CrossRef CAS.
- V. H. Uc, J. R. Alvarez-Idaboy, A. Galano, I. Garcia-Cruz and A. Vivier-Bunge, J. Phys. Chem. A, 2006, 110, 10155–10162 CrossRef CAS PubMed.
- J. R. Alvarez-Idaboy, L. Reyes and N. Mora-Diez, Org. Biomol. Chem., 2007, 5, 3682–3689 CAS.
- J. R. Alvarez-Idaboy, N. Mora-Diez and A. Vivier-Bunge, J. Am. Chem. Soc., 2000, 122, 3715–3720 CrossRef CAS.
- J. R. Alvarez-Idaboy, N. Mora-Diez, R. J. Boyd and A. Vivier-Bunge, J. Am. Chem. Soc., 2001, 123, 2018–2024 CrossRef CAS PubMed.
- A. Cruz-Torres and A. Galano, J. Phys. Chem. A, 2007, 111, 1523–1529 CrossRef CAS PubMed.
- M. T. Baeza-Romero, D. R. Glowacki, M. A. Blitz, D. E. Heard, M. J. Pilling, A. R. Rickard and P. W. Seakins, Phys. Chem. Chem. Phys., 2007, 9, 4114–4128 RSC.
- L. Wang, Y. Zhao, J. Wen and J. Zhang, Theor. Chem. Acc., 2013, 132, 1–14 CrossRef CAS.
- O. W. Wingenter, M. K. Kubo, N. J. Blake, T. W. Smith Jr, D. R. Blake and F. S. Rowland, J. Geophys. Res., 1996, 101, 4331–4340 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra04902h |
| This journal is © The Royal Society of Chemistry 2016 |