Preparation of rutile TiO2 by hydrolysis of TiOCl2 solution: experiment and theory
Abstract
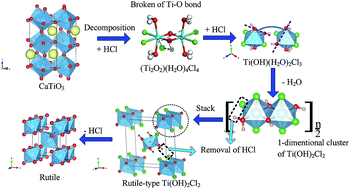
Titanium slag with a perovskite phase (CaTiO3) is difficult to use in traditional titanium dioxide production. Herein, we demonstrate that HCl can decompose CaTiO3 with a high acidolysis ratio of >97 wt% to obtain a TiOCl2 solution. With subsequent hydrolysis and calcination, rutile TiO2 was synthesised in one step without crystalline-structure transformation. As hydrolysis of the TiOCl2 solution to prepare metatitanic acid (H2TiO3) is an essential step in the process, a simulated pure TiOCl2 solution (prepared from TiCl4 and H2O) was confirmed to have the same structure in water as HCl-treated CaTiO3 slag by Raman spectroscopy. The TiOCl2 solution was also concluded to have the Ti compound cluster of (Ti2O2)(H2O)4Cl4, based on DFT calculations from the Raman data and the curve fit for the hydrolysis ratio. By elucidating the relationship between the H2TiO3 particle size and the concentration of Ti4+ and HCl, we identified the nuclear energy as -19.46 kJ mol−1. Moreover, a complete scheme for the production of rutile TiO2, induced by TiOCl2 solution hydrolysis, was proposed. Periodic structures show the feasibility of the following transformation occurring through a simple structural rearrangement: (Ti2O2)(H2O)4Cl4 (in solution)–Ti(OH)(H2O)2Cl3 (with addition of HCl)–Ti(OH)2Cl2 (1-dimentional growth and removal of HCl)–rutile-type Ti(OH)2Cl2 (stack)–rutile TiO2 (with removal of HCl).

 Please wait while we load your content...
Please wait while we load your content...