Relaxation and magnetocaloric effect in the Mn12 molecular nanomagnet incorporated into mesoporous silica: a comparative study
Maria Bałanda*a,
Robert Pełkaa,
Magdalena Fittaa,
Łukasz Laskowskib and
Magdalena Laskowskab
aH. Niewodniczański Institute of Nuclear Physics, Polish Academy of Sciences, ul. Radzikowskiego 152, 31-342 Krakow, Poland. E-mail: Maria.Balanda@ifj.edu.pl
bInstitute of Intelligent Computational Systems, Częstochowa University of Technology, Al. Armii Krajowej 36, 42-200 Częstochowa, Poland
First published on 13th May 2016
Abstract
This paper presents the synthesis and investigation of the magnetic properties of mesoporous silica SBA-15 functionalized with Mn12 ([Mn12O12(CH3COO)16(H2O)4]·2CH3COOH·4H2O) high-spin molecular clusters. The SBA-Mn12 sample has been examined by means of X-ray diffraction, infrared spectroscopy, nitrogen sorption and TEM techniques. AC and DC magnetic measurements, including measurements of the magnetocaloric effect (MCE) were carried out both for SBA-Mn12 and for polycrystalline Mn12. An increase in the activation energy and in the distribution of relaxation times was observed for SBA-Mn12 as compared to those of Mn12. Differences in the MCE were also revealed. The maximum magnetic entropy change at the field change of 50 kOe for SBA-Mn12 is equal to 13.8 J K−1 mol−1 at T = 2.8 K, which is significantly less than 25.3 J K−1 mol−1 observed for Mn12 at 3.2 K. The altered relaxation and the magnetocaloric effect point to a successful incorporation of Mn12 molecules into the silica channels.
1 Introduction
One of the possible applications of magnetic molecular clusters is using them for magnetic refrigeration in the low and ultra-low temperature range. Due to the high spin values S shown by some molecules, the total molar magnetic entropy Smax = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(2S + 1) (R is the gas constant) is large and the isothermal entropy change ΔS on the change of the applied magnetic field should be substantial. Values of ΔS or of ΔTad, which are the related adiabatic change of temperature, are the two measures of the magnetocaloric effect (MCE). The ideal molecular refrigerant requires large spin, negligible magnetic anisotropy, dominant ferromagnetic exchange and a large magnetic density.1 Very large values of ΔS and ΔTad have been reported for molecular discrete Gd clusters, such as the ferromagnetic Gd3+ dimer,2 the high nuclearity Gd42Co10 cluster3 or the 24-Gd capsule-like cluster.4 The advances in the design of magnetic molecules for use as cryogenic magnetic coolants have been recently reviewed.5,6
ln(2S + 1) (R is the gas constant) is large and the isothermal entropy change ΔS on the change of the applied magnetic field should be substantial. Values of ΔS or of ΔTad, which are the related adiabatic change of temperature, are the two measures of the magnetocaloric effect (MCE). The ideal molecular refrigerant requires large spin, negligible magnetic anisotropy, dominant ferromagnetic exchange and a large magnetic density.1 Very large values of ΔS and ΔTad have been reported for molecular discrete Gd clusters, such as the ferromagnetic Gd3+ dimer,2 the high nuclearity Gd42Co10 cluster3 or the 24-Gd capsule-like cluster.4 The advances in the design of magnetic molecules for use as cryogenic magnetic coolants have been recently reviewed.5,6
It is known that magnetic anisotropy of high-spin molecules (if present) leads to the strong increase of the relaxation time and the irreversible behavior below the blocking temperature Tb. While for T > Tb molecular nanomagnets behave like superparamagnets, at T < Tb they show magnetic hysteresis resulting from the slow response of the collection of isolated molecules. Increase of magnetic anisotropy of an isolated cluster would shift the MCE maximum to higher temperatures and result in a lower peak value.1 Another interesting feature of MCE in molecular clusters around Tb is the dependence on the sweeping rate of the field. The peak of entropy variation ΔS shifts to higher temperature with an increased sweeping rate of the field, as determined for the representative molecular clusters Mn12 (ref. 7) and Fe8.8
Application of molecular clusters in any device needs organization of the species on a determined surface or in a particular matrix. It is important that the molecular complexes would be distributed efficiently, homogenously and without disturbing their structure nor magnetic properties. Mesoporous silica is a stable and chemically inert material, suitable for incorporation of ions or molecules inside the pores of nanometer size. It was found that magnetic properties of molecular clusters of the Mn12 SMM (Single Molecule Magnet) family inserted into hexagonal SBA-15 (ref. 9 and 10) or MCM-41 (ref. 11) – silicas stayed globally unmodified. Successful incorporation of high-spin [CuII6Gd] clusters inside the channels of the –COOH-functionalized SBA-15 silica was also reported.12 In order to check the efficiency of the synthesis and to characterize the material obtained, methods such as X-ray diffraction, TEM, N2 physisorption, UV-vis and IR spectroscopies are commonly used. Additionally, the micro-Raman technique combined with numerical simulations of characteristic frequencies as well as quantitative magnetic measurements is used.13
The present work is devoted to the magnetic relaxation and the magnetocaloric effect of the Mn12 molecules ([Mn12O12(CH3COO)16(H2O)4]·2CH3COOH·4H2O) immobilized in the SBA-15 mesoporous silica (hereafter called SBA-Mn12). The assumed molar concentration of the Mn12 units in the silica matrix was 20%, which means one O–Si–propyl–COOMn12 group per 4 SiO2 groups. The distribution of the relaxation times and the activation energy for a spin reversal Ea were found from phase-sensitive AC susceptibility measurements. Due to the magnetic hysteresis and remanence of Mn12, the ΔS magnetic entropy change which characterizes MCE could not be determined from the magnetization curves M(H) on increasing field. Instead, it was determined from the isothermal demagnetization curves. In order to compare magnetic behaviour of the Mn12 immobilized inside the silica channels with the performance of the free molecules, besides the SBA-Mn12 sample, the polycrystalline Mn12 was also investigated. The additional aim of the work was learning whether the relaxation times and the MCE could give the evidence that Mn12 clusters are linked inside the silica channels, and not stay unbound outside the walls.
2 Experimental
2.1 Synthesis
The samples of mesoporous silica functionalized with Mn12 have been synthesized adopting the three stage procedure, namely: (a) preparation of SBA-15 containing cyanopropyl groups (SBA-CN),9 (b) hydrolysis into SBA-15 containing carboxylic acid groups (SBA-COOH) and (c) functionalization of COOH groups with Mn12 molecules in order to obtain SBA-COO-Mn12.10 In order to get the 20% molar concentration of the Mn12 units in silica, an adequate number of SBA-COOH groups in the material was obtained. The similar procedure was successfully applied to obtain SBA-15 functionalized by nickel-phosphonic units.14 The process is shown schematically in Fig. 1.Details of the sample preparation are as follows:
(a) SBA-15 mesoporous silica with cyano groups (SBA-CN) was prepared according the co-condensation method.15 First step was preparing the solution of surfactant: 8.0 grams of EO20PO70EO20 (P123) was dissolved in 320 mL of aqueous solution of HCl (pH = 1.5). To this solution was added a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of mixture of tetraethylorthosilicate (TEOS) and cyanopropyltriethoxysilan ((4-butyronitrile) triethoxysilane – BNTES), respectively. This mixture was vigorously stirred at room temperature. Next, a small amount of NaF was added in order to induce hydrolysis and polycondensation; the material was immediately heated to 60 °C in a hot oil bath and then stirred at 60 °C for 48 hours. The resulting template was filtered and washed by ethanol and acetone. The surfactant was removed by hot ethanol extraction in a Soxhlet apparatus.
1 molar ratio of mixture of tetraethylorthosilicate (TEOS) and cyanopropyltriethoxysilan ((4-butyronitrile) triethoxysilane – BNTES), respectively. This mixture was vigorously stirred at room temperature. Next, a small amount of NaF was added in order to induce hydrolysis and polycondensation; the material was immediately heated to 60 °C in a hot oil bath and then stirred at 60 °C for 48 hours. The resulting template was filtered and washed by ethanol and acetone. The surfactant was removed by hot ethanol extraction in a Soxhlet apparatus.
(b) To avoid unwanted side reactions, the obtained powder has been silylised by treating of the mesoporous powder by Me3SiCl in toluene. Next, SBA-15 mesoporous silica is hydrolyzed into SBA-15 containing carboxylic acid groups (SBA-COOH). The procedure was as follows: 2.00 grams of SBA-CN was suspended in 25 mL of 50% sulfuric acid (H2SO4). The suspension was stirred for 5 hours under reflux at a temperature of 150 °C. Subsequently, the solid was recovered by filtration, washed with water (the powder obtained on the filtering funnel was stirred 5 times in an Erlenmeyer flask with water and filtrated). After washing, the pH was checked in order to obtain a roughly neutral product (pH from 5 to 7). Next, powder was washed once with acetone and dried under vacuum at room temperature.
(c) SBA-COO-Mn12 (SBA-Mn12 for short) was obtained as follows: Mn12-ac (Mn12 in short) crystals were synthesized according to the procedure used originally for Mn8Fe4 [Mn8Fe4O12(CH3COO)16(H2O)4]·2CH3COOH·4H2O,16 (Mn8Fe4), which is isostructural to Mn12: 8.0 g of Mn(CH3CO2)2·4H2O was added to 80 mL of a 60% acetic acid water solution. The mixture was stirred and then 2.0 g of finely ground KMnO4 was slowly added in small amounts. The stirring period and the stirring frequency had an influence on the crystals size. In order to obtain the relatively large crystals, KMnO4 was added over the course of about 1.5 minutes to the solution under vigorously stirring (800 rpm). The final solution was removed from the stir plate and left undisturbed for 3 days, during which the long black rectangular rods of about 1.0 × 1.0 × 7.0 mm3 crystallized. The crystals were filtered, washed with acetone, then bottled and stored in a refrigerator. Mn12 molecules are difficult to solve. The most appropriate solvent is acetonitrile, but Mn12 dissolved in CH3CN can easily decompose when the solution is exposed in air. For this reason, the next step has been carried out under protective argon atmosphere. The appropriate amount of Mn12 nanocrystals and powder of SBA-COOH were mixed and powdered in a mortar. The mixture was put into an Erlenmeyer flask and 200 mL of acetonitrile was added. The resulting suspension was stirred at room temperature. The solid SBA-COO-Mn12 was quantitatively recovered by filtration and washed with acetonitrile (5 times) to remove the excess of Mn12 crystals. It is worth noting that after filtration only clear CH3CN was received.
2.2 Characterization and measurements
The SBA-Mn12 material was characterized by a number of physical techniques. The Fourier transform infrared (FT-IR) absorption spectra at room temperature were recorded by means of EXCALIBUR FTS-3000 spectrometer within the wavenumber range of 400–4000 cm−1 using the sample mixed with KBr. Transmission electron microscope (TEM) FEI Tecnai G2 20 X-TWIN was used to obtain the microstructure image of the sample. Nitrogen sorption isotherms were measured at 77 K using a Micromeritics ASAP 2020 analyzer. XRD patterns were obtained by means of X'PERT PRO Panalytical diffractometer operated at 40 kV and 30 mA, in a standard Bragg–Brentano geometry with CuKα radiation of wavelength 1.541 Å and fixed slits. Magnetic AC and DC measurements were carried out with a Quantum Design MPMS magnetometer. Measurements were performed also for the silica matrix containing carboxylic acid groups (SBA-COOH). Powder samples were packed in a piece of thin paper and placed in plastic straws. Such addenda was the same for the samples under study. DC susceptibility, χ, in the field of 500 Oe was measured in the temperature range of 2–300 K in the field cooling (FC) mode. Magnetization curves M(H) at T = 2 K were measured in the ±50 kOe field range. Magnetocaloric effect was determined from the isothermal demagnetization curves, measured under decreasing field from 5 T to 0 T at small temperature intervals in the range from 2 to 20 K. Samples of mass ca. 15 mg were used.3 Results
3.1 Infrared spectroscopy and structural characterization
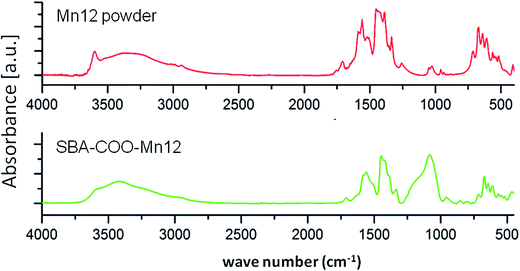
The FT-IR spectrum of the SBA-Mn12 sample, shown in Fig. 2 together with that of Mn12 powder, attests to the successful preparation of our hybrid sample. The low frequency bands in the 500–750 cm−1 range are assigned to stretching of the Mn–O bonds, while those around 1500 cm−1 correspond to the free O–C–O stretching vibrations.17 The wide absorbance maximum centered at 1080 cm−1 comes from Si–O–Si stretching bands.18Fig. 3 shows the XRD pattern of SBA-Mn12. The inset presents the result for 2θ up to 20° in the log scale. The main intensive reflection at 2θ = 0.7° is related to an ordered pore arrangement and can be indexed as (100) diffraction from the SBA-15 structure of the hexagonal symmetry. The corresponding d spacing is 12.6 nm. The (110) and (200) reflections which should be expected at 2θ = 1.21° and 1.40° are only faintly disclosed. The weak intensity visible in the inset for 2θ > 5° and coming from the Mn12 powder, amounts to less than 10−4 of the main intensity. Therefore, the absence of Mn12 Bragg reflections points to the efficient and homogenous incorporation of Mn12 into the silica matrix.
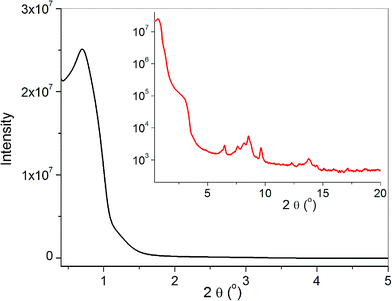 | ||
| Fig. 3 The low angle X-ray diffraction pattern of SBA-Mn12 – linear scale. Inset: the wide-angle pattern – log scale. | ||
The TEM image displayed in Fig. 4 shows the morphology and the pore structure in two perpendicular directions for SBA-15 containing Mn12 units. The pores are composed in an ordered hexagonal arrangement, therefore the obtained material retains the mesopore uniformity of the original SBA-15 silica structure.
 | ||
| Fig. 4 TEM images of SBA-Mn12: direction of pores is perpendicular (a) and parallel (b) to the view plane. The scale bar is (a) 50 nm and (b) 100 nm respectively. | ||
The nitrogen adsorption–desorption test has been performed to supplement the structural research described above. As presented in Fig. 5, the sample shows the typical IV type hysteresis, which is characteristic for a mesoporous material with the homogenous pore size. The specific surface area in the sample calculated using the Brunauer–Emmett–Teller (BET) method19 is 686 m2 g−1. The average pore size, w, determined according to the Barrett–Joyner–Halenda (BJH) model20 is 4.8 nm (see Fig. 5 inset). The total volume of the pores based on the maximum nitrogen vapour adsorption at p/p0 = 0.98 is equal to 0.87 cm3 g−1 (92%).
 | ||
| Fig. 5 The nitrogen sorption/desorption isotherm of SBA-Mn12. Inset: the pore size distribution calculated from the adsorption curve. | ||
3.2 Magnetic behaviour – static and dynamic features
Fig. 6 shows hysteresis loops at T = 2 K for the SBA-Mn12 and Mn12 powder samples under study. Like for Mn12, magnetization values of SBA-Mn12 are given in Nβ (number of Bohr magnetons, due to one mol of Mn12). The shape of the loops is different: a superparamagnetic like for Mn12 and more conventional for Mn12 incorporated into silica. Larger coercive force for the latter may point to the increased anisotropy which hampers reorientation of the magnetic moments of the clusters. Magnetization of saturation Msat, determined from extrapolation M vs. 1/H for 1/H approaching zero, is 20 Nβ for Mn12 and 17 Nβ for SBA-Mn12. As the diamagnetic contribution of the silica to magnetization is negligible (less than 0.1%), the shortage of magnetization in the latter may be explained with the incomplete efficiency of the synthesis. Thermomagnetic remanence (TRM) is 14 Nβ for Mn12 and 6.0 Nβ for SBA-Mn12.Static magnetic susceptibility χ, defined as a ratio of magnetization, M, to magnetic field, H, measured at H = 500 Oe as a function of temperature for SBA-Mn12 is shown in Fig. 7a together with the susceptibility of SBA-15 containing carboxylic acid groups (SBA-COOH). Susceptibility of the SBA-COOH matrix is very weak and originates from the residual paramagnetic impurities in the material and from the diamagnetic silica. The susceptibility of the silica matrix could not be described with the Curie–Weiss law. Instead, the modified formula, given by
| χ = χ0 + C/(T − θC–W) + A × T | (1) |
 | ||
| Fig. 7 (a) Temperature dependence of the DC magnetic susceptibility of SBA-Mn12 (blue points) as compared to that of SBA-15 containing carboxylic acid groups (SBA-COOH) (open squares). Inset: fit of the SBA-COOH data with the modified Curie–Weiss law (see eqn (1)). (b) Temperature dependence of DC magnetic susceptibility expressed for one mol of Mn12 incorporated to SBA-Mn12; red line is a fit of the modified Curie–Weiss law (see eqn (1)). Inset: product of the susceptibility (corrected for the contribution of silica) and temperature. | ||
In spite of the fact that susceptibility of the SBA-COOH matrix is much weaker than that of SBA-Mn12 (the factor of ∼5 × 10−3 at T = 2 K), it influences the temperature behaviour of the latter. The Curie–Weiss law modified with the A × T term (eqn (1)) was more suitable to fit the experimental data than the usual Curie–Weiss law. The following results of the fit were obtained: the temperature independent contribution χ0 = (−2.0 × 10−4 ± 7 × 10−6) cm3 Oe−1 g−1, the Curie constant C = (0.0249 ± 0.0002) cm3 Oe−1 g−1 K, the Weiss paramagnetic temperature relevant to the possible interaction between magnetic centres θC–W = (−2.32 ± 0.04) K and the temperature-dependence coefficient A = (5.20 ± 0.25) × 10−6 cm3 Oe−1 g−1 K−1. Taking that the mass of Mn12 is 84% of the sample mass, one receives the susceptibility expressed for one mol of Mn12 incorporated to SBA-Mn12 (Fig. 7b) and the adequate fit parameters: χ0 = (−0.345 ± 0.012) cm3 Oe−1 mol−1, C = (42.8 ± 0.4) cm3 Oe−1 mol−1 K, θC–W = (−2.32 ± 0.04) K and A = (0.00120 ± 0.00006) cm3 Oe−1 mol−1 K−1. The C value is in agreement with Msat determined above. It is also close to the low temperature plateau of the χmolT product given in Fig. 7b inset, where χmol(T) is the susceptibility corrected for silica contribution, i.e. with χ0 and A × T subtracted. Negative θC–W is responsible for the sudden drop of χmolT at the lowest temperatures and reveals some antiferromagnetic coupling between the moments of Mn12 centres which may come from the dipolar origin. The flat χmolT maximum at 180 K, in Fig. 7b inset, is similar to the one observed in ref. 6 and reflects a complicated ordering of the higher energy spin states of the Mn12 cluster.
Temperature dependence of the real part of the AC susceptibility, χ′, for SBA-Mn12 measured at frequencies from 1 Hz up to 1500 Hz is presented in Fig. 8a together with DC susceptibility from the previous picture. As expected, the χ′ peaks, as well as χ′′ peaks (not shown), move to a higher temperature when the frequency increases, thus showing the superparamagnetic character. The temperature dependence of the relaxation time τ obtained from the frequency shift of the χ′′ maxima is described by the Arrhenius law τ = τ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ea/kBT), where the activation energy for spin reversal Ea for SBA-Mn12 is (70.0 ± 0.8) K and the pre-exponential factor τ0 is (6.3 ± 1.0) × 10−8 s (see Fig. 8b). The appropriate values for the Mn12 sample is (68.1 ± 0.8) K and τ0 is (9.6 ± 1.1) × 10−8 s. The AC singularity visible in Fig. 8a in the (2–3) K temperature range coincides with the low-temperature relaxation in the Mn12 cluster isomer of Ea = (38.0 ± 0.4) K and τ0 = (5.6 ± 1.1) × 10−9 s.
exp(Ea/kBT), where the activation energy for spin reversal Ea for SBA-Mn12 is (70.0 ± 0.8) K and the pre-exponential factor τ0 is (6.3 ± 1.0) × 10−8 s (see Fig. 8b). The appropriate values for the Mn12 sample is (68.1 ± 0.8) K and τ0 is (9.6 ± 1.1) × 10−8 s. The AC singularity visible in Fig. 8a in the (2–3) K temperature range coincides with the low-temperature relaxation in the Mn12 cluster isomer of Ea = (38.0 ± 0.4) K and τ0 = (5.6 ± 1.1) × 10−9 s.
The χ′′ vs. χ′ Cole–Cole plots for both samples at T = 5 K displayed in Fig. 9 deviate from semicircles and form arcs of size (1 − α)π with α parameter representing the distribution of relaxation times. There is a significant difference in the distribution for both compared samples: at T = 5 K, α is equal to 0.24 for SBA-Mn12, while it is 0.11 for Mn12. Therefore, attachment of the Mn12 molecules to the silica pores by means of the carboxylic acid groups resulted in the increase in the activation energy and in the wider distribution of the relaxation times.
 | ||
| Fig. 9 The Cole–Cole plots for Mn12 and SBA-Mn12 samples at T = 5 K, showing a different distribution of the relaxation times. | ||
3.3 Magnetocaloric effect
The isothermal ΔS magnetic entropy change which characterizes MCE, may be determined from heat capacity or magnetic measurements. In the second case, ΔS is calculated from the magnetization isotherms using the integrated Maxwell relation:
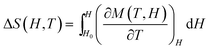 | (2) |
Eqn (2) is valid only for the systems in the thermodynamic equilibrium,24 therefore for Mn12 and SBA-Mn12, showing the magnetic hysteresis and remanence at T < Tb, ΔS could not be determined from the magnetization curves M(H) on field increasing. Instead, it was determined from the isothermal demagnetization curves which are reversible. The demagnetization curves were measured under decreasing field from 50 kOe to zero at small temperature intervals in the range from 2 to 20 K. Fig. 10 shows the data for SBA-Mn12 together with the temperature dependence of TRM displayed in the inset. As expected, the TRM goes to zero at T = Tb.
 | ||
| Fig. 10 Isothermal demagnetization curves measured at temperatures from 2 K to 20 K. Inset: temperature dependence of the remanent magnetization. | ||
Fig. 11 shows the temperature dependence of the isothermal entropy change |ΔS| determined using eqn (2) for SBA-Mn12 at the magnetic field decrease from 10 kOe, 20 kOe, 30 kOe, 40 kOe and 50 kOe to zero. |ΔS| shows a narrow maximum below Tb and then slowly decreases or levels off, as seen for the field 50 kOe. For SBA-Mn12, |ΔS|max = 13.8 J mol−1 K−1 at T = 2.8 K. It is seen that the MCE in molecular clusters close to the blocking temperature has different character than in the long-range ordered molecular magnets close to the phase transition.25 As reported by Torres et al.,7,8 the MCE in slowly relaxing molecules is time-dependent and the position, width and height of |ΔS| depends on the sweeping rate of the applied magnetic field. The narrow peak presented in Fig. 11 is the consequence of the small sweeping rate (3 × 10−4 Hz) applied in our experiment.
 | ||
| Fig. 11 Magnetic entropy change determined from demagnetization curves given in Fig. 10 for different magnetic field change (shown). | ||
Fig. 12 shows the MCE for both samples obtained with the same measuring scenario. The effect in Mn12 is much stronger and the peak maximum shifts towards higher temperature with the field. In the field of 10 kOe, the peak |ΔSmax| = 21.2 J mol−1 K−1 is positioned at 3.0 K, while for 50 kOe |ΔSmax| = 23.6 J mol−1 K−1 at 3.2 K. At T > Tb the data for both samples are similar. There is however a significant difference at the lowest temperatures: ΔS for Mn12 shows the change of sign and some dependence on the field, while this is not the case for SBA-Mn12. According to von Ranke,26 the inverse effect at T < 2.2 K may be related to the antiferromagnetic coupling of the dipolar origin operating between the Mn12 molecules. In Table 1 we compare the relaxation data and the MCE details for Mn12 and for SBA-Mn12 obtained in the present study.
 | ||
| Fig. 12 Changes of magnetic entropy at different field changes (shown) for SBA-Mn12 and for Mn12 samples. Values of Tpeak are given for ΔH = 5 kOe. | ||
| Mn12 | SBA-Mn12 | |
|---|---|---|
| Ea [K] | 68.1 | 70.0 |
| τ0 [s] | 9.6 × 10−8 | 9.6 × 10−8 |
| α | 0.11 | 0.24 |
| Tmax [K] | 3.2 | 2.8 |
| |ΔSmax| [J K−1 mol−1] | 25.3 | 13.8 |
| |S|l [J K−1 mol−1] | 5.9 | 4.8 |
| MTRM [Nβ] | 14.0 | 6.0 |
4 Summary and conclusions
The mesoporous silica SBA-15 of the average pore size equal to 4.8 nm has been functionalized with the Mn12 ([Mn12O12(CH3COO)16(H2O)4]·2CH3COOH·4H2O) high-spin clusters linked to the silica channel walls by means of the COOH groups. The assumed concentration of the Mn12 units in the silica matrix was 20%. The SBA-Mn12 sample was examined by means of X-ray diffraction, infrared spectroscopy, nitrogen sorption and TEM techniques. AC and DC magnetic measurements, as well as measurements of the magnetocaloric effect given by the ΔS magnetic entropy change, were carried out both for SBA-Mn12 and for the polycrystalline Mn12. The blocking temperature Tb = 3.4 K was the same for both samples. MCE was determined from the isothermal demagnetization curves.As a result of incorporation into silica, the relaxation of the Mn12 magnetic moments slightly slowed down. The activation energy increased from 68 K for free Mn12 molecules up to 70 K, while the distribution of the relaxation times increased twice. Differences in MCE were also revealed. Maximum magnetic entropy change at the field variation of 50 kOe for SBA-Mn12 was equal to 13.8 J K−1 mol−1 at T = 2.8 K, which is significantly less than 25.3 J K−1 mol−1 observed for Mn12 at 3.2 K. Narrow |ΔS| peaks discovered below Tb were due to the small sweeping rate of the applied field. Interestingly, the temperature of |ΔSmax| for SBA-Mn12 was not dependent on the field, while it increased with the field for the polycrystalline Mn12.
In our opinion the altered relaxation and significant differences in the magnetocaloric effect point to the successful and homogenous incorporation of Mn12 molecules into the silica channels. We believe that the present work will be the first step into obtaining well-defined technologically important layers functionalized with high-spin entities.
Acknowledgements
Financial support for this investigation has been provided by the National Center of Science (Grant-No. 2011/03/D/ST5/05996). Dr F. Birk is kindly acknowledged for revision of the manuscript.References
- M. Evangelisti and E. K. Brechin, Dalton Trans., 2010, 39, 4672 RSC.
- M. Evangelisti, O. Roubeau, E. Palacios, A. Camón, T. N. Hooper, E. K. Brechin and J. J. Alonso, Angew. Chem., Int. Ed., 2011, 50, 6606 CrossRef CAS PubMed.
- J. B. Peng, Q. C. Zhang, X. J. Kong, Y. Z. Zheng, Y. P. Ren, L. S. Long, R. B. Huang, L. S. Zheng and Z. Zheng, J. Am. Chem. Soc., 2012, 134, 3314 CrossRef CAS PubMed.
- L. X. Chang, G. Xiong, L. Wang, P. Cheng and B. Zhao, Chem. Commun., 2013, 49, 1055 RSC.
- R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 5143 CrossRef PubMed.
- J.-L. Liu, Y.-C. Chen, F.-S. Guo and M.-L. Tong, Coord. Chem. Rev., 2014, 281, 26 CrossRef CAS.
- F. Torres, X. Bohigas, J. M. Hernandez and J. Tejada, J. Phys.: Condens. Matter, 2003, 15, L119 CrossRef CAS.
- F. Torres, J. M. Hernandez, X. Bohigas and J. Tejada, Appl. Phys. Lett., 2000, 77, 3248 CrossRef CAS.
- T. Coradin, J. Larionova, A. A. Smith, G. Rogez, R. Clerac, Ch. Guerin, G. Blondin, R. E. P. Winpenny, C. Sanchez and T. Mallah, Adv. Mater., 2002, 14, 896 CrossRef CAS.
- S. Willemin, G. Arrachart, L. Lecren, J. Larionova, T. Coradin, R. Clerac, T. Mallah, C. Guerin and C. Sanchez, New J. Chem., 2003, 27, 1533 RSC.
- M. Clemente-Leon, E. Coronado, A. Forment-Aliaga, P. Amoroz, J. Ramirez-Castellanos and J. M. Gonzalez-Calbet, J. Mater. Chem., 2003, 13, 3089 RSC.
- I. Kornarakis, G. Sopasis, C. J. Milios and G. S. Armatas, RSC Adv., 2012, 2, 9809 RSC.
- Ł. Laskowski and M. Laskowska, J. Solid State Chem., 2014, 220, 221–226 CrossRef.
- Ł. Laskowski, M. Laskowska, M. Bałanda, M. Fitta, J. Kwiatkowska, K. Dziliński and A. Karczmarska, Microporous Mesoporous Mater., 2014, 200, 253 CrossRef.
- B. Folch, J. Larionova, Y. Guari, C. Guerin, A. Mehdi and C. Reye, J. Mater. Chem., 2004, 14, 2703 RSC.
- A. R. Schake, H. Tsai, R. J. Webb, K. Folting, G. Christou and D. N. Hendrickson, Inorg. Chem., 1994, 33, 6020 CrossRef CAS.
- P. Artus, C. Boskovic, J. Yoo, W. E. Streib, L. Brunel, D. N. Hendrickson and G. Christou, Inorg. Chem., 2001, 40, 4199 CrossRef CAS PubMed.
- M. Yu, J. Lin and J. Fang, Chem. Mater., 2005, 17, 1783 CrossRef CAS.
- S. Brunauer, L. S. Deming, W. E. Deming and E. Teller, J. Am. Chem. Soc., 1940, 62, 1723–1732 CrossRef CAS.
- E. P. Barrett, L. G. Joyner and P. H. Halenda, J. Am. Chem. Soc., 1951, 73, 373–380 CrossRef CAS.
- R. M. Candea, S. J. Hudgens, M. Kastner and J. C. Knights, Phys. Rev. B: Condens. Matter Mater. Phys., 1977, 16, 2657 CrossRef CAS.
- Z. Li, L. Chen, S. Meng, L. Guo, J. Huang, Y. Liu, W. Wang and X. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094429 CrossRef.
- V. Zeleňák, A. Zeleňáková and J. Kováč, Colloids Surf., A, 2010, 357, 97–104 CrossRef.
- C. M. Soukoulis, K. Levin and G. S. Grest, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 1495 CrossRef CAS.
- M. Fitta, R. Pełka, M. Gajewski, M. Mihalik, M. Zentkova, D. Pinkowicz, B. Sieklucka and M. Bałanda, J. Magn. Magn. Mater., 2015, 396, 1 CrossRef CAS.
- P. J. von Ranke, N. A. de Oliveira, B. P. Alho, E. J. R. Plaza, V. S. R. de Sousa, L. Caron and M. S. Reis, J. Phys.: Condens. Matter, 2009, 21, 056004 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2016 |