DOI:
10.1039/C6RA03119F
(Paper)
RSC Adv., 2016,
6, 36942-36953
Recycling of spodumene slag: preparation of green polymer composites
Received
2nd February 2016
, Accepted 30th March 2016
First published on 31st March 2016
Abstract
Nowadays, spodumene ores have become an important lithium resource. The generated slag, as a new member of the slag family, would cause the environmental burden to mount up. Therefore, the recycling of spodumene slag was studied in this work, with the objective of exploring the possibility of using spodumene slag as a common polymer filler. The microsized slag powder was firstly incorporated with polylactide (PLA) through solution mixing, followed by injection molding, and the obtained composites were then studied in terms of morphology, rheological and mechanical properties, as well as the creep and degradation behavior. The results reveal that the presence of slag powder enhances the system modulus evidently, while maintaining the normal strength level of PLA. Therefore, the slag powder can be used as a good inert filler in the polymeric material industry, with a desirable reduction in cost. Then, the slag powder was further refined into nanoparticles, and again mixed with PLA. The results show that the presence of these nanoparticles increases both the modulus and strength remarkably because of their good dispersion and distribution in the PLA matrix. As a result, these spodumene slag-derived nanoparticles can be used as a good reinforcement material or as an active filler in the polymer additive industry. Both the slag powder and slag-derived nanoparticles highly restrain the creep of the PLA chain, while promoting the degradation of PLA remarkably. Therefore, these particles can be used to tailor the final properties of PLA. In addition, a modified model was developed successfully to predict the mechanical strength of the as-obtained green composites. This work provides a new way to fabricate a novel green polymer composite with controllable performance by the recycling of spodumene slag.
1. Introduction
The increased demand for lithium for batteries, especially for electronic products and electric vehicles, has focused attention on the adequacy of known and anticipated lithium resources recently. As the most important source of electrolyte and anode materials, lithium carbonate is mainly obtained by mining, extracting and treating two main resources: spodumene ores and salt-lake brines.1 Currently, there are between 37.1 million tons (Mt) and 43.6 Mt of available lithium-rich resources. 62% of the available resources consist of brines and 38% of rock minerals.2 The supply today most commonly comes from the processing of brines, but ores are used increasingly. The future supply requirements could be met with another important lithium resource, seawater, although extraction from seawater is currently uneconomical.3
Spodumene is a lithium-rich ore contained in a special type of stone called pegmatite.2 In comparison with the salt-lake brines, spodumene ores are distributed more widely around the world. Although the production process for mined ore lithium costs about 50% more than that for the brine-water one,4 the former is much more convenient than the latter, and is independent of the climate. Accordingly, the production from spodumene ores becomes an increasingly important way of obtaining lithium. However, the production process for mined ore also makes the environmental burden mount up, as for the brine-water. The difference is that the latter leads to substantial water consumption and waste generation, while the former generates large amounts of solid waste, namely slag. This problem becomes more and more severe with an increasing production capacity for the extraction of spodumene ores.
Landfill deposition and incineration are the conventional solutions for disposing of or treating solid waste such as steel scrap, dust and sludge, and also including slag.5 However, these traditional approaches are not environment-friendly, and would increase disposal costs and may cause permanent damage to the flora and fauna. Therefore, much effort has been made in recent years to recycle these solid wastes.6–10 Some kinds of slag such as glass waste, fly ash and sewage sludge can be used to fabricate ceramic because their silicate components improve the flexural strength and the densification process of ceramic.6 Other kinds of slag with silica-rich and alumina-rich components, for instance, fly ash and blast furnace slag, can be utilized to boost the compressive strength of cement concrete.7 Additionally, for the slag derived from metallic minerals (iron slag, steel slag, alloy steel slag, ferroalloy slag, copper slag, etc.), the metals can be recovered by chemical processes.8
It is well known that silicates and aluminosilicates, as well as sulfates and carbonates, are important additives or fillers in the plastic and rubber industry fields.11 Since most kinds of slag are mainly composed of silicate and sulfates,12 they may have potential applications in the fabrication of polymeric materials and products as additives or fillers. However, merely very few reports13–15 could be found in the literature. Pati et al.13 reported that micro-sized Linz–Donawitz (LD) slag could possess fairly good filler characteristics as it improved the erosion resistance of epoxy resin. Cornacchia and coworkers found that incorporating electric-arc furnace (EAF) slag could raise the Young’s modulus and the tensile strength at yield of polypropylene (PP).14 A similar reinforcing effect has also been found in rubber materials filled with fly ash particles.15 The reported research results reveal that slag might be a good candidate to be used as a common filler or for reinforcement of polymer materials, which is indicative of an economically convenient new approach for the application of slag, especially for the new member of the slag family, spodumene slag. This is interesting and worthy of deep study.
Therefore, in this work, micro-sized spodumene slag powder was incorporated with a polymer through solution mixing, followed by injection molding. The rheology, mechanical and creep properties, as well as the degradation behavior of the as-obtained composites were studied in detail, aiming at exploring the possibility of recycling the spodumene slag as a common polymer filler. An aliphatic polyester, polylactide (PLA) with biodegradable characteristics, was chosen as the polymer matrix to prepare an environment-friendly polymer composite with spodumene slag. Then, the slag powder was further processed into silica nanoparticles, and again mixed with PLA, with the objective of obtaining a new kind of green nanocomposite based on the recycling of slag. Besides, a modified model was developed in this work to describe the mechanical performance of the as-obtained green composites, which can provide a common guide for the property prediction of filled polymer composites.
2. Experimental
2.1. Material preparation
The polylactide (PLA, trade name is 4060D) used in this work is a commercial product of NatureWorks Co. Ltd., USA with L/D ratios ranging from 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 30
1 to 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Its number average molecular weight (Mn) and density are about 87
1. Its number average molecular weight (Mn) and density are about 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 and 1.25 g cm−3, respectively. Spodumene slag, the residue after extraction of lithium minerals, was provided by Shandong Mingrui Chemical Engineering Co. Ltd., P. R. China. It is a kind of white powder with an average particle size of 31.2 μm with a standard deviation of 12.7, as shown in Fig. 1. The density of this kind of slag powder is about 1.95 g cm−3 (measured by drainage).
000 g mol−1 and 1.25 g cm−3, respectively. Spodumene slag, the residue after extraction of lithium minerals, was provided by Shandong Mingrui Chemical Engineering Co. Ltd., P. R. China. It is a kind of white powder with an average particle size of 31.2 μm with a standard deviation of 12.7, as shown in Fig. 1. The density of this kind of slag powder is about 1.95 g cm−3 (measured by drainage).
 |
| | Fig. 1 SEM image of the pristine slag powder with a scale bar of 100 μm. The inset graph is the TEM image with a scale bar of 5 μm. | |
Firstly, the pristine slag powder was dispersed in NaOH solution and stirred for 72 h, then, the suspension was filtered to remove undissolved substances. Secondly, the pH value of the as-obtained transparent solution was adjusted to 7 using hydrochloric acid, and the precipitate yielded was collected on a Büchner funnel, washed with distilled water to remove chloridion and further washed with absolute ethyl alcohol to remove the water. Finally, the as-obtained floccules were dispersed in a chloroform (CHCl3) solution of PLA, and stirred for 6 h at room temperature. The obtained homogeneous solution was then dried to form PLA nanocomposites (PLACs, where s denotes the weight percent (wt%) of filler). Three kinds of particle loading levels, 7 wt%, 10 wt% and 15 wt%, were studied in this work. Composites with 15 wt% pristine slag powder (PLAC′15) were also prepared by solution mixing for comparison of the properties. Sheet samples with a thickness of about 1 mm were prepared using compression molding at 180 °C and 10 MPa for the morphological and rheological measurements. The dog-bone shaped specimens (32 mm × 4 mm × 2 mm) used for the mechanical properties tests were prepared by injection molding using a Haake mini-jet (Thermo Scientific Co., USA), which was performed at a cylinder temperature of 180 °C and mold temperature of 25 °C with an injection pressure of 600 bar and holding pressure of 500 bar. For better comparison, the neat PLA sample was subjected to the same solution procedures as those of the composites before molding.
2.2. Element and component analyses
The elements and possible compositions of the slag and obtained silica powder were determined using an X-ray photoelectron spectroscope (XPS, Escalab250Xi, Thermo Scientific, USA) and an X-ray diffractometer (XRD, D8 ADVANCE, BRUKER AXS, Germany). The XPS tests were conducted with a spot size of 500 nm at a voltage of 1.486 kV using a monochromatic Al K Alpha source (FWHM < 0.6 eV, sensitivity > 5 M cps). The XRD measurements were performed with a Cu target and a rotating anode generator operated at 40 kV and 40 mA. The scanning rate was 6° min−1 from 5° to 80°. Three specimens were used for the XPS and XRD tests for each sample.
2.3. Morphology and structure characterization
A Tecnai 12 transmission electron microscope (TEM, Philips, Netherlands) and an S-4800 field-emission scanning electron microscope (SEM, Hitachi, Japan) were used to characterize the morphology and structure of the slag, the silica powder and the PLA composites. Microtomed sample sections with about a 100 nm thickness were used for TEM observation (120 kV accelerating voltage) to evaluate the dispersion of the particles in PLA (nanocomposite sample with 15 wt% filler). Frozen-fractured and tensile-broken specimens (nanocomposite and composite sample with 15 wt% filler) were used for SEM observation (15 kV accelerating voltage) to evaluate the particle distribution in PLA and the surface morphology. The fractured surface was coated with gold using an SPI sputter coater before observation. The number average particle diameter (dn) was determined according to the following relation by analyzing the SEM images using Nano Measure software:| |
 | (1) |
where ni is the number of particles with a diameter of di. The total particle number was about 50 in the analysis. The interactions between the PLA chain and filler particles were evaluated using a Fourier transform infra-red spectrometer (TENSOR27 FT-IR, Bruker Co., Germany). The FT-IR spectra were obtained by collating 64 scans and were collected at room temperature with the reflection mode. The resolution was within 2 cm−1. Three specimens were tested for each sample.
2.4. Thermal and mechanical measurements
Thermal events of the neat PLA and its composites were recorded using a differential scanning calorimeter (DSC, NETZSCH DSC-204F1, Germany). The sample, about 5 mg, was first heated from room temperature to 200 °C and held for 5 min to eliminate the previous thermal histories, then cooled to room temperature, and again heated to 200 °C, during which the thermal responses of heat flow were recorded. Three specimens were tested for each sample. All the experiments were performed under nitrogen with a heating/cooling rate of 10 °C min−1. The tensile properties of the PLA composites were determined using an Instron Mechanical Tester (Illinois Tool Works, USA) at a crosshead speed of 50 mm min−1 at room temperature using the dog-bone shaped specimens (ASTM D638). The strength and modulus values reported herein represent an average of the results for tests run on six specimens. Creep tests were conducted on a DMA Q800 analyzer (TA Instruments, USA) with a tensile mode at various temperature and stress levels. The applied stress levels of 0.5–3 MPa were used during the tensile tests, which is within the linear viscoelastic region of all the samples. The appropriate duration for the measurements was determined as 10 min for full creep development. The creep strain and compliance were recorded as a function of the time. The neat PLA, the nanocomposite with 15 wt% nanoparticles and the composite with 15 wt% pristine slag were used for the thermal and creep tests. Three rectangular specimens (30 mm × 5 mm × 1 mm) were tested for each sample.
2.5. Melt rheology measurements
Rheological tests were performed on a rheometer (Haake RS600, Thermo Scientific Co., USA) with a parallel plate geometry using 20 mm diameter plates. The sheet samples with a thickness of about 1.0 mm were heated until molten at 180 °C for 5 min to eliminate any residual thermal histories, and then were subjected to a small amplitude oscillatory shear (SAOS). A frequency sweep was applied on all samples at a common linear strain level, 1%, which was predetermined by the strain sweep. The samples of neat PLA, the composites with 15 wt% nanoparticles and the one with 15 wt% pristine slag powder, were used for tests. Three specimens were tested for each sample.
2.6. Degradation experiments
The degradation study of the PLA composites was performed according to the standard BS EN ISO 10993-13. Specimens were placed individually into 30 mL glass vials. The vials were filled with phosphate buffer solution (PBS) media (pH = 7.4 ± 0.2) and maintained at the degradation temperature (37.5 ± 0.2 °C). At various time points (0, 3, 5, 7, 10 and 15 days) the specimens were extracted and blot dried, followed by weighing. The samples were then placed back into vials with fresh PBS at each time point. The average mass loss values were obtained from at least three repeats. The percentage mass change was determined using the following equation:| |
 | (2) |
where m represents the measured mass at each time period and mi the initial mass. Three kinds of samples, including the neat PLA and the composites with 15 wt% nanoparticles and with 15 wt% pristine slag powder, were used for tests. The mass change values reported herein represent an average of the results for tests run on five specimens.
3. Results and discussion
3.1. Chemical composition and morphology of slag and nano-silica
The chemical and mineralogical composition of the raw slag can be determined using XPS and XRD measurements. The obtained results are shown in Fig. 2, which are similar to those observed for other kinds of slag.16,17 The Auger peaks from the constituent elements in the spodumene slag were easily identified and marked on the XPS spectra, and the possible mineralogical composition can be further evaluated according to the characteristic XRD peaks. The chemical composition and oxidation states in the slag are summarized in Table 1. It is seen that the slag mainly consists of silicon and aluminium oxides, as well as calcium sulfate, accompanied by small quantities of residual carbonates of the metals lithium and zinc. There are no heavy metal salts or oxides, or other hazardous substances in the slag, which means that the slag powder with an average particle size of 35 μm (Fig. 1) may be a good candidate for a filler for plastics or rubbers because oxides or salts of silicon and aluminium, as well as calcium, are the main components of the most commonly used inorganic fillers in the polymer industry.11
 |
| | Fig. 2 (a and b) Survey-scan XPS spectra and (c and d) XRD patterns for the pristine slag and obtained silica powder, respectively. | |
Table 1 Chemical compositions of the spodumene slag
| SiO2 |
Al2O3 |
CaSO4 |
Mg(OH)2 |
LiCO3 |
ZnCO3 |
| 38.3 wt% |
33.2 wt% |
19.5 wt% |
3.0 wt% |
3.9 wt% |
1.9 wt% |
After alkaline leaching and acid treatment, the remaining component in the slag is silica, which was determined using the XPS spectrum shown in Fig. 2b. Only an amorphous pattern could be detected using XRD (Fig. 2d), indicating that the remaining silica is in a glassy state,18 namely amorphous. The amorphous silica particles are on a nanometer scale, with an average size of about 40 nm, as can be seen in Fig. 3. It should be mentioned that the chemical composition of the remaining particles can be controlled by varying the final pH value of the system after acid treatment, changing from silicon oxide-dominated to aluminium salt-dominated. This can give the nanoparticles different degrees of crystallinity and more functionalities as a filler of polymer composites, or more possibility in other applications, which will be reported soon.
 |
| | Fig. 3 (a) SEM and (b) TEM images, and (c) the size distribution of the silica particles. The scale bars of (a) and (b) are 10 μm and 1 μm, respectively. The scale bars of the insets in (a) and (b) are 400 nm and 200 nm, respectively. | |
3.2. Distribution and dispersion of slag powder and nano-silica in PLA
Fig. 4 shows SEM images of the PLA composites with pristine slag powder and nano-silica particles. Clearly, the two kinds of particles show a large difference in their distribution in the PLA matrix. The slag powder is not that well distributed, showing poor interfacial adhesion with PLA (Fig. 4a), while the nano-silica particles are fully distributed throughout the PLA matrix, presenting a far higher volume filling ratio than the slag powder at identical weight loadings due to their nanoscale size. In addition, it is notable that most of the nano-silica particles are well embedded in the PLA matrix (inset in Fig. 4b), indicating good interfacial adhesion between the two phases.
 |
| | Fig. 4 SEM images of the frozen-fractured surface of the samples (a) PLAC′15 and (b) PLAC15 with scale bars of 50 μm and 40 μm, respectively. The scale bars of the insets in (a) and (b) are 5 μm and 2 μm, respectively. | |
The good affinity between the PLA chain and silica particles was further confirmed using FT-IR spectra, as shown in Fig. 5a. Compared with that of neat PLA, the location of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration peak of PLAC′15 sample is nearly unchanged. However, this peak shifts from 1747 cm−1 to 1751 cm−1, by about 4 cm−1, in the presence of silica particles. This upshift is believed to be due to the weakening of the polymer–polymer hydrogen bonding19 because the presence of silica particles leads to a lowering of chain mobility and to a disordering of the chain arrangement due to dipole–dipole coupling or hydrogen bonding between the surface hydroxyl groups of silica and the carboxyl groups in the polyester chain.20,21 A similar ‘red shift’ observation has also been reported for PLA composites with clay.22–24 This confirms good affinity between the PLA chain and silica particles.
O stretching vibration peak of PLAC′15 sample is nearly unchanged. However, this peak shifts from 1747 cm−1 to 1751 cm−1, by about 4 cm−1, in the presence of silica particles. This upshift is believed to be due to the weakening of the polymer–polymer hydrogen bonding19 because the presence of silica particles leads to a lowering of chain mobility and to a disordering of the chain arrangement due to dipole–dipole coupling or hydrogen bonding between the surface hydroxyl groups of silica and the carboxyl groups in the polyester chain.20,21 A similar ‘red shift’ observation has also been reported for PLA composites with clay.22–24 This confirms good affinity between the PLA chain and silica particles.
 |
| | Fig. 5 (a) FT-IR spectra and (b) DSC traces of the neat PLA and PLAC15, as well as PLAC′15, samples. | |
However, the interactions between the silica and the PLA chain do not highly restrain the movements of the chain segments, and as a result, the composites have very close values for the glass transition temperature (Tg) to that of the neat PLA within the experimental error range, as shown in Fig. 5b. A similar observation has also been reported for PLA composites with carbon nanotubes.25 Macosko et al.26 believed that there was possibly not a very strong confinement effect between the nano-filler and polymer chain segments in a composite system synthesized merely via physical blending processes such as solvent blending or melt compounding. On the contrary, chemical blending processes such as in situ polymerization commonly yield significant increases in the Tg of the polymer. Therefore, the relaxation of the PLA chain segments is not restricted in the PLAC15 sample, and the dipole–dipole interactions between the silica and PLA chain may have an influence on the movements of the chain structure on a different size scale, which will be discussed in the rheology and creep sections.
The different distributions of these two kinds of particles, slag powder and silica, have different influences on the linear viscoelasticity of the PLA matrix, as can be seen in Fig. 6. It is clear that PLAC15 shows the highest modulus among the three samples, and its low-frequency modulus increases by about 2 orders of magnitude relative to PLAC′15. This indicates that the nano-silica has a greater contribution to the elasticity of the composite system during dynamic shear flow compared with the slag powder, which is believed to be attributed to the differences in their volume filling ratios25 in the PLA composite systems. The Krieger equation27 is commonly used to evaluate the volume filling ratio of a filled polymer composite system:
| |
 | (3) |
where
ηr is the relative viscosity,
ϕm the maximum volume fraction, and the exponent
q is determined from the intrinsic viscosity [
η],
q = [
η]
ϕm. As the concentration of particles reaches the semi-concentrated region, a mesoscopic percolation network forms because of strong interactions among the particle themselves. In this case, the effective volume fraction (
ϕeff) is commonly used:
28| |
 | (4) |
where
ϕm is set to be 0.637 assuming random close packing and
q is fixed as 2.
29 The
ϕeff can then be calculated and the values are shown in
Fig. 6. Clearly, PLAC15 shows a far higher
ϕeff value than PLAC′15, which is consistent with the SEM observations (
Fig. 4). Besides, the
ϕeff value of 35.2% is far higher than the critical value of percolation (∼26 vol%), according to close packing theory,
30 and hence the PLAC15 sample shows typical percolated behavior, namely its storage modulus is higher than the loss modulus at lower frequencies (see arrow in
Fig. 6). In other words, with the current silica particle loadings, the shear flow of the PLA matrix is dominated by elastic deformation, instead of viscous flow. This is attributed to the formation of percolated particle networks,
31 as detected clearly using TEM and shown in
Fig. 7. Relative to the neat PLA, the sharp increase in viscosity or modulus for PLAC15 is mainly due to the lack of surface treatment of the silica particles.
 |
| | Fig. 6 The dynamic storage modulus (G′) and loss modulus (G′′) for the neat PLA, PLAC15 and PLAC′15 samples. | |
 |
| | Fig. 7 TEM image of the PLAC15 sample with a scale bar of 2 μm. The scale bar of the inset is 200 nm. | |
It is seen that the silica nanoparticles are mainly dispersed as flocs in the PLA matrix, rather than individual particles. Each floc is composed of tens of individual silica nanoparticles (see the inset in Fig. 7), forming a percolation network at the loading of 15 wt%. Accordingly, it can be concluded that the nanosilica is dispersed as flocculation structures with full distribution in the PLA matrix. With increase of the silica particle loading, the low-frequency modulus increases monotonously, as shown in Fig. 8. A similar trend has also been observed for clay-filled32–34 and carbon nanotube-filled35,36 PLA composite systems. This non-terminal response is attributed to restrained large scale polymer relaxations due to the presence of nanoparticles.31,37 The relaxation time (λ) for viscoelastic deformation of a polymer chain coil can be calculated as follows:35
| |
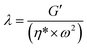 | (5) |
 |
| | Fig. 8 The dynamic storage modulus (G′) for the neat PLA and its composites with various silica loadings. | |
The calculated ratios of the relaxation time of composites to that of neat PLA, namely the relative relaxation time, λr, are summarized in Fig. 8. Clearly, the λr values increase gradually with the silica loading and, finally reach about 7 for the PLAC15 sample at a frequency of 0.01 Hz. Combining this with the DSC results (Fig. 5b), it can hence be concluded that the presence of nano-silica strongly retards local chain coil movements, rather than restraining the relaxation of the chain segments. This is reasonable because the scale of the polymer chain segments is far smaller than that of the nanoparticle flocs.25,37 Moreover, it is notable that even the PLAC7 sample shows a far higher relaxation time value than the neat PLA, which indicates that this sample may be already percolated.
3.3. Tensile properties and model predictions for the composites
Since the slag powder and silica particles have different dispersion and distribution states in the PLA matrix, they may have different roles in the mechanical performance of the composite systems. Fig. 9 shows the stress–strain behavior for the neat PLA and its composite samples, and the obtained values for the tensile strength and Young’s modulus are listed in Table 2. It is clear that the tensile strength and Young’s modulus increase monotonously with the increasing of the silica particle loading. For the loading of 15 wt%, the values of tensile strength and Young’s modulus for the composite (PLAC15) increase from 46 MPa to 57 MPa, by about 20%, and from 1.6 GPa to 2.2 GPa, by about 35%, respectively, relative to those of the neat PLA. This suggests that the nano-silica particles derived from industrial spodumene slag could be used as a good reinforcement material for polymer composites or as a good active filler in the polymer additive industry. Besides, as for the neat PLA sample, the tensile specimen of PLAC15 still presents good transparency, confirming a nanoscale dispersion of the silica particles and their good distribution in the PLA matrix, as can be seen in the inset of Fig. 9.
 |
| | Fig. 9 Stress–strain curves for the neat PLA and its composite samples. The inset is a picture of the specimens used for the tensile tests. | |
Table 2 Tensile strength and Young’s modulus of the neat PLA and its composites
| Samples |
PLA |
PLAC7 |
PLAC10 |
PLAC15 |
PLAC′15 |
| Tensile strength (MPa) |
47.81 ± 3.65 |
51.93 ± 5.34 |
52.61 ± 2.56 |
57.14 ± 2.06 |
46.93 ± 6.48 |
| Young’s modulus (GPa) |
1.63 ± 0.07 |
2.00 ± 0.05 |
2.14 ± 0.02 |
2.20 ± 0.01 |
2.21 ± 0.08 |
As for the composite with slag powder (PLAC′15), its tensile strength is far lower than that of the composite with nano-silica (PLAC15) at identical loading levels, and is at the same level as that of the neat PLA. This is in accordance with the SEM observations shown in Fig. 10. The broken surface of PLAC′15 is smooth, without an evident stress yield structure and shear zone, which is different from the morphology observed for PLAC15. This is caused by poor interfacial strength between the matrix phase and slag powder. However, it is notable that PLAC′15 has almost the same level of Young’s modulus as PLAC15, indicating an enhanced rigidness of the composite system. Clearly, the presence of slag powder increases the system modulus remarkably, but does not decrease the system strength. This suggests that the slag powder could also be used as a good inert filler for polymeric materials with a desirable reduction in cost. Therefore, both the raw slag powder and the yielded nanosilica particles are good candidates for a filler in the polymer product industry.
 |
| | Fig. 10 SEM images of the broken surface of the (a) PLAC15 and (b) PLAC′15 tensile samples with scale bars of 3 μm and 20 μm, respectively. | |
A mechanical model description can reveal more information on the property–structure relationships of the filled polymer composites. The Halpin–Tsai (H–T) equation38 is the most commonly used model to describe mechanical properties:
| |
 | (6) |
where
Em and
Ef are the modulus of the matrix and filler, respectively, and
Vf is the volume fraction of filler particles.
c is a constant shape factor related to the effective aspect ratio (
λeff) of the filler particles. Cox
39 further developed an orientation factor,
α, to account for the randomness of discontinuous filler particles:
| |
 | (7) |
If the filler length is greater than the thickness of the specimen, the filler is assumed to be randomly oriented in two dimensions, and an α value of 1/3 is used; while if the filler length is much smaller than the thickness of the specimen, the filler is assumed to be randomly oriented in three dimensions and an α value of 1/6 (ref. 39) or 1/5 (ref. 40) is used. It is seen that the Cox modified H–T model merely gave a linear-like description, and is not applicable to the nonlinear increasing trend of the composite modulus at higher particle loadings, as shown in Fig. 11a. This is attributed to particle aggregation and a resulting nonlinear change of the apparent interface area at a high concentration of filler particles.37,41
 |
| | Fig. 11 Model predictions for (a) all five experimental points and (b) the first four points of the Young’s modulus of the neat PLA and its nanocomposites. | |
Yeh and coworkers42 used an exponential shape factor ξ to replace the constant shape factor c in the case of high filler loading levels:
| |
ξ = 2λeff![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−aVf−b e−aVf−b
| (8) |
where
ξ is related to the effective aspect ratio (
λeff).
a and
b are constants, related to the degree of filler particle aggregation, which account for the nonlinear behavior of the H–T equation as the particle concentration reaches the semi-dilute region. The modified H–T equation is hence expressed as
| |
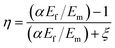 | (9) |
Clearly, the Yeh modified model gives a good description of the trend of alteration of the composite modulus with nano-silica loading. The obtained parameter values are summarized in Fig. 11a. Here, the average Ef value is assumed to be 70 GPa,43,44 and the density of silica particles is 1.55 ± 0.05 g cm−3 (measured by drainage). However, the effective aspect ratio (λeff) is a hydrodynamic physical quantity, which is determined not only by the effective length (L′) and effective diameter (d′) of the filler particle/aggregate, but also by the orientation degree of the particles and stress direction. This means that λeff is not the real aspect ratio of the filler, and its value is hard to obtain accurately. Thus, λeff is commonly used as an adjustable parameter when using a modified H–T model. For the fitting of the Yeh modified model, there are three adjustable parameters, λeff, a and b. The values of a and b are therefore not constant with changes in λeff. But this three-parameter model can give multiple results with good fitting. In other words, the physical significance of these two parameters, a and b, is not that clear. This possibly leads to failed prediction using this model, as shown in Fig. 11b. It is seen that the Yeh modified model can provide a good description of the former four data points, and the obtained λeff value almost equals that of case (2) in Fig. 11a. However, it cannot be used well to predict the fifth experimental point at 15 wt% (see indicated part in Fig. 11b).
In general, for a suspension system, the average floc size (R) and the mesh size (ζ) are nearly changeless in the semi-concentrated region.45,46 This is also applicable to a polymer composite system.37,47,48 As the filler particle loading reaches a high level, for instance, the percolation level, the space between each of the particles in the same one aggregate or floc, namely the mesh size (ζ), does not change any more. Therefore, all structural parameters related to the particle flocs can be integrated into one parameter, λeff, which is closely related to the real floc size and stress/orientation direction. In this case, the shape factor ξ is expressed as:
| |
ξ = 2λeff![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−λeffVf e−λeffVf
| (10) |
In this case, only one parameter is adjustable when using this modified H–T model. Clearly, it can provide a very satisfactory description of the composite modulus (Fig. 11a). Besides, a good prediction can also be achieved using this model. The fitted line for the former four points passes well through the fifth experimental point at 15 wt%, as can be seen in Fig. 11b, and the most important aspect is that the obtained λeff has almost the same value as that of case (4) in Fig. 11a. The value of about 20 is reasonable for the current silica filled system because most of the silica nanoparticles are dispersed as flocculation structures with a certain aspect ratio during composite preparation, as indicated in Fig. 7, but not as individual spherulitic particles with an isotropic structure. This therefore clarifies that the modified H–T model can be used to well describe and even to predict the modulus of the current composite system.
3.4. Creep behavior and model descriptions of the composites
The PLA matrix polymer used in this work is of the grade of film blowing, which is mainly used for packaging applications. The creep properties are therefore very important. Fig. 12 shows creep curves for the neat PLA and its composites at various stress levels. All the applied stresses are within the linear viscoelastic region, as indicated in Fig. 9. Clearly, the creep strain for all the samples increases with time and the applied stress level monotonously, showing typical viscoelastic–viscoplastic characteristics. A test duration of 10 min is enough for all the samples because strain development is already constant after this duration.25,49
 |
| | Fig. 12 Creep curves for the (a) PLAC15 and (b) PLAC′15 samples at various stress levels (20 °C). The inset shows creep curves for the neat PLA sample. | |
At the same stress level, the composites have a lower creep strain level relative to the neat PLA, as can be seen in Fig. 13. It should be mentioned that the PLA matrix is amorphous (see Fig. 5b), which means that all issues related to crystallization could be ignored. Therefore, it is reasonable to propose that the reduced creep strain level of the composite system is fully caused by the presence of particles, instead of alteration of the crystallization structure and degree of PLA matrix. As expected, the PLAC15 sample has lower strain levels than PLAC′15, indicating that the silica nanoparticles have a stronger suppression effect on the PLA creep than the microsized spodumene powder. This is because nanosilica has a much higher volume filling ratio than spodumene particles at identical loadings, as summarized in Fig. 6.
 |
| | Fig. 13 Theoretical predictions (lines) of the experimental creep data (symbols) of neat PLA and its composites (20 °C, 0.5 MPa) using (a) Findley power law model and (b) Burgers model. | |
A power law model developed by Findley50 was used for an overall evaluation of the creep of all the samples:
where
ε(
t) is the creep strain at time
t,
ε0 is the instantaneous initial strain,
n is the time exponent and
A is the amplitude of transient creep strain. It is clear that the Findley model can provide a good description of the creep behavior of the neat PLA and its composites, as shown in
Fig. 13a. The decrease of
A (
Table 3) is indicative of reduced creep levels of PLA in the presence of graphitic fillers,
25,51 confirming a barrier effect of both nanosilica and spodumene particles on the linear elastic deformation of PLA. The Burgers model
52 can be used to further explore this impeding effect caused by the presence of nanosilica and spodumene particles:
| |
 | (12) |
where the subscripts
E, Vl and Vp correspond to the elastic, viscoelastic and viscoplastic contributions.
EE and
EVl are elastic moduli,
ηVl and
ηVp are viscosities,
σ is the applied stress and
t is the creep time. Detailed explanations of these viscoelastic parameters and the fitting methods can be found elsewhere.
49,51 Clearly, the Burgers model predictions also agree well with the experimental creep data for the neat PLA and its composites, although not as well as those using the Findley model, as can be seen in
Fig. 13b. The obtained parameter values are listed in
Table 4.
Table 3 Structural parameters of the neat PLA and its composites
| Samples |
A |
n |
| PLA |
0.0447 ± 0.001 |
0.7582 ± 0.018 |
| PLAC′15 |
0.0216 ± 0.001 |
0.8345 ± 0.029 |
| PLAC15 |
0.0158 ± 0.001 |
0.5949 ± 0.034 |
Table 4 Average values of the viscoelastic parameters obtained from the Burgers model prediction of the neat PLA and its composites
| Samples |
EE (GPa) |
EVl (MPa) |
ηVl (MPa s) |
ηVp (MPa s) |
τ (s) |
| PLA |
1.63 |
12.66 |
1.08 |
25.02 |
0.08 |
| PLAC′15 |
2.20 |
16.91 |
0.52 |
34.28 |
0.03 |
| PLAC15 |
2.20 |
18.16 |
0.97 |
85.75 |
0.05 |
EE values can be predetermined according to tensile tests. The increased values in the presence of spodumene and silica particles are attributed to the reinforcing effect on the Maxwell spring unit of those particles. EVl, which is related to the stiffness of amorphous polymer chains, also increases with the addition of particles, indicating reinforcement of the Kelvin–Voigt unit. ηVl is the viscosity of the Kelvin–Voigt unit and the ratio of ηVl/EVl is defined as the relaxation time τ, which is closely related to the movements of polymer chain segments.49 It is interesting that the τ values of all the samples are in the same order of magnitude. This suggests that the mobility of the PLA chain segments is not strongly restrained by the microsized spodumene powder and silica nanoparticles. Actually, this is already indicated by the nearly unchanged Tg of PLA in the presence of the particles, as can be seen in Fig. 5b. A similar observation has also been reported for PLA composites filled with graphene.25
It is noteworthy that the composites show higher ηVp values than the neat PLA, especially for the PLAC15 sample. ηVp is related to an unrecoverable creep strain contributed by the displacement of polymer chains or chain coils yielded in plastic deformation or flow processes.52 The increased ηVl values, therefore, indicate a strong retardation effect on the relaxation of local chain coils, rather than a confinement effect on the chain segments, by the presence of spodumene powder and silica particles. This was suggested using the increased relaxation time of the chain coils (Δλ) indicated in Fig. 8.
3.5. Degradation behavior of neat PLA and its composites
It is well known that PLA is degradable, and the presence of inorganic particles has an influence on the degradation of PLA.53 Fig. 14 shows the percentage of residual mass for the neat PLA and its composites during degradation in PBS. Clearly, the composite samples have higher loss levels compared with the neat PLA. A similar trend has also been reported for some other PLA composites containing inorganic particles with polyhydroxy surfaces.54–56 In a degradation process, water diffuses into the polymer until saturation occurs, firstly, and then degradation with a constant rate occurs, followed by accelerated hydrolysis as a result of the production of chain ends in the degradation medium.56 As indicated in Fig. 5b, the PLA used in this work is amorphous, and therefore, there are no issues with crystallization that should be taken into account. The difference in the degradation rate between neat PLA and its composites comes from the presence of filler particles.
 |
| | Fig. 14 Residual mass percentage against time for the neat PLA and its composites during degradation in PBS at 37.5 °C. | |
The presence of polyhydroxy slag particles and nanosilica, on the one hand, favors water diffusion and adsorption, and on the other hand, increases the saturation capacity for water. Both result in an increased degradation of the composite system. It is notable that PLAC15 has higher degradation rates than PLAC′15. This is reasonable because the former has a far higher volume filling ratio of filler particles than the latter, which is already shown in Fig. 6. This means that the former can provide much more sites for hydrolysis than the latter during degradation of PLA. Thus, evidently the presence of nanosilica favors PLA degradation more, relative to the microsized slag particles.
4. Conclusions
Spodumene slag is mainly composed of silicon and aluminium oxides, and calcium sulfate. As a powder with micro-sized particles it can enhance the modulus of PLA remarkably, from 1.6 GPa to 2.2 GPa, by about 37%, at a loading level of 15 wt%, while maintaining the normal strength level of PLA. Therefore, the slag powder could be used as a good inert filler in the polymeric material industry, with a desirable reduction in cost. Moreover, the slag powder can be further refined to nanosilica with an average diameter of 40 nm. The good dispersion and distribution of the nanosilica increase both the modulus and the strength of the polymer evidently. At a 15 wt% loading, the strength increases from 46 MPa to 57 MPa, by about 20%. As a result, the slag-yielded nanoparticles can be used as a good reinforcement material for polymer composites or as an active filler in the polymer additive industry. A modified Halpin–Tsai equation can be used to describe and predict the mechanical performance of the current composite system. Besides, both the slag particles and slag-yielded nanoparticles restrain the creep of PLA remarkably because the presence of these particles suppresses the relaxation of chain coils. Relative to the slag powder, the slag-yielded nanosilica has a much stronger suppression effect on the viscoplastic deformation of PLA because of its higher volume ratio in the composite at the same loading. This higher level of volume ratio of the nanosilica provides much more hydrolysis sites, and as a result, the composites with nanosilica particles show higher degradation rates than the one with spodumene slag powder. Within the experimental loading range, 15 wt% nanosilica or slag powder is the best composition to obtain PLA composites with optimal properties.
Acknowledgements
This work was supported by research grants from the National Natural Science Foundation of China (51573156), and the Prospective Joint Research Program of Jiangsu Province (BY2014117-01), as well as the Research Innovation Program for College Student (15-077X) and for Graduates of Jiangsu Province (SJLX15_0663).
References
- S. E. Kesler, P. W. Gruber, P. A. Medina, G. A. Keoleian, M. P. Everson and T. J. Wallington, Ore Geol. Rev., 2012, 48, 55–69 CrossRef.
- C. Grosjean, P. H. Miranda, M. Perrin and P. Poggi, Renewable Sustainable Energy Rev., 2012, 16, 1735–1744 CrossRef.
- A. Stamp, D. J. Lang and P. A. Wäger, J. Cleaner Prod., 2012, 23, 104–112 CrossRef CAS.
- P. Meshram, B. D. Pandey and T. R. Mankhand, Hydrometallurgy, 2014, 150, 192–208 CrossRef CAS.
- P. J. Koros, Metall. Mater. Trans. B, 2003, 34, 769–779 CrossRef.
- P. T. Teo, A. A. Seman, P. Basu and N. M. Sharif, Waste Manage., 2014, 34, 2697–2708 CrossRef CAS PubMed.
- A. Nazari and J. G. Sanjayan, J. Cleaner Prod., 2015, 99, 297–304 CrossRef CAS.
- H. Shen and E. Forssberg, Waste Manage., 2003, 23, 933–949 CrossRef CAS PubMed.
- S. N. M. Hairi, G. N. L. Jameson, J. J. Rogers and K. J. D. MacKenzie, J. Mater. Sci., 2015, 50, 7713–7724 CrossRef CAS.
- T. Du, X. Fang and X. P. Zhang, Adv. Mater. Res., 2014, 989–994, 3–6 CrossRef CAS.
- G. Pritchard, Plastics Additives, Chapman & Hall, London, 1998 Search PubMed.
- K. Snars and R. J. Gilkes, Appl. Clay Sci., 2009, 46, 13–20 CrossRef CAS.
- P. R. Pati and A. A. Sataphty, Adv. Polym. Technol., 2015, 34, 1–8 CrossRef.
- G. Cornacchia, S. Agnelli, M. Gelfi, G. Ramorino and R. Roberti, JOM, 2015, 67, 1370–1378 CrossRef CAS.
- C. Kantala, E. Wimolmala, C. Sirisinha and N. Sombatsompop, Polym. Adv. Technol., 2009, 20, 448–458 CrossRef CAS.
- L. J. Wang, J. P. Yu, K. C. Chou and S. Seetharaman, Metall. Mater. Trans. B, 2015, 46, 1802–1808 CrossRef CAS.
- S. I. Hussain, D. W. Blowes, C. J. Ptacek and D. Olding, Environ. Eng. Sci., 2014, 31, 631–642 CrossRef CAS.
- M. Bhattacharya and S. Chaudhry, Mater. Sci. Eng., C, 2013, 33, 2601–2610 CrossRef CAS PubMed.
- W. Zhang, A. A. Dehghani-Sanij and R. S. Blackburn, Prog. Nat. Sci., 2008, 18, 801–805 CrossRef CAS.
- Y. Chujo and T. Saegusa, Adv. Polym. Sci., 1992, 100, 11–30 CrossRef CAS.
- H. Barthel, M. Dreyer, T. Gottschalk-Gauding, V. Litvinov and E. Nikitina, Macromol. Symp., 2002, 187, 573–584 CrossRef CAS.
- D. F. Wu, L. Wu, L. F. Wu, B. Xu and M. Zhang, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 1100–1113 CrossRef CAS.
- L. DiMaio, E. Garofalo, P. Scarfato and L. Incarnato, Polym. Compos., 2015 DOI:10.1002/pc.23424.
- D. F. Wu, L. Wu, L. F. Wu, B. Xu and M. Zhang, J. Nanosci. Nanotechnol., 2008, 8, 1658–1668 CrossRef CAS PubMed.
- Y. Wang, Y. X. Cheng, J. X. Chen, D. F. Wu, Y. X. Qiu, X. Yao, Y. N. Zhou and C. Chen, Polymer, 2015, 67, 216–226 CrossRef CAS.
- K. H. Liao, S. Aoyama, A. A. Abdala and C. Macosko, Macromolecules, 2014, 47, 8311–8319 CrossRef CAS.
- I. M. Krieger, Adv. Colloid Interface Sci., 1972, 3, 111–136 CrossRef CAS.
- D. Quemada, Eur. Phys. J.: Appl. Phys., 1998, AP-1, 119–127 CrossRef.
- J. F. Brady, J. Chem. Phys., 1993, 99, 567–581 CrossRef CAS.
- D. R. Paul and C. B. Bucknall, Polymer Blends: Formulation and Performance, Wiley, New York, 2000 Search PubMed.
- J. Ferry, Viscoelastic Properties of Polymers, Wiley, New York, 1980 Search PubMed.
- P. H. Nam, M. Kaneko, N. Ninomiya, A. Fujimori and T. Masuko, Polymer, 2005, 46, 7403–7409 CrossRef CAS.
- D. F. Wu, L. Wu, L. F. Wu and M. Zhang, Polym. Degrad. Stab., 2006, 91, 3149–3155 CrossRef CAS.
- S. S. Ray, P. Maiti, M. Okamoto, K. Yamada and K. Ueda, Polymer, 2003, 44, 857–866 CrossRef.
- D. F. Wu, L. Wu, M. Zhang and Y. L. Zhao, Polym. Degrad. Stab., 2008, 93, 1577–1584 CrossRef CAS.
- D. F. Wu, Y. S. Zhang, M. Zhang and W. Yu, Biomacromolecules, 2009, 10, 417–424 CrossRef CAS PubMed.
- D. F. Wu, L. Wu, W. D. Zhou, Y. R. Sun and M. Zhang, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 479–489 CrossRef CAS.
- J. C. Halpin and J. L. Kardos, Polym. Eng. Sci., 1976, 16, 344–352 CAS.
- H. L. Cox, Br. J. Appl. Phys., 1952, 3, 72 CrossRef.
- H. Fukuda and K. Kawata, Fibre Sci. Technol., 1974, 7, 207–222 CrossRef.
- D. F. Wu, L. Wu and M. Zhang, J. Polym. Sci., Part B: Polym. Phys., 2007, 45, 2239–2251 CrossRef CAS.
- M. K. Yeh, N. H. Ta and J. H. Liu, Carbon, 2006, 44, 1–9 CrossRef CAS.
- E. H. Kerner, Proc. Phys. Soc., London, Sect. B, 1959, 69, 808–813 CrossRef.
- J. N. Gao, J. T. Li, S. Zhao, B. C. Benicewicz, H. Hillborg and L. S. Schadler, Polymer, 2013, 54, 3961–3973 CrossRef CAS.
- S. M. Dinh and R. C. Armstrong, J. Rheol., 1984, 28, 207–227 CrossRef CAS.
- T. Chatterjee and R. Krishnamoorti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 050403 CrossRef PubMed.
- T. Chatterjee, K. Yurekli, V. G. Hadjiev and R. Krishnamoorti, Adv. Funct. Mater., 2005, 15, 1832–1838 CrossRef CAS.
- T. Chatterjee and R. Krishnamoorti, Macromolecules, 2008, 41, 5333–5338 CrossRef CAS.
- Z. Yao, D. F. Wu, C. Chen and M. Zhang, Composites, Part A, 2013, 50, 65–72 CrossRef CAS.
- W. N. Findley and D. B. Peterson, Proc. ASTM, 1958, 58, 841–855 Search PubMed.
- C. J. Perez, V. A. Alvarez and A. Vazquez, Mater. Sci. Eng., A, 2008, 480, 259–265 CrossRef.
- L. S. Nielsen, R. F. Landel and L. L. Faulkner, Mechanical Properties of Polymers and Composites, Marcel Dekker Inc, New York, 1994 Search PubMed.
- J. M. Raquez, Y. Habibi, M. Murariu and P. Dubois, Prog. Polym. Sci., 2013, 38, 1504–1542 CrossRef CAS.
- F. Luzi, E. Fortunati, D. Puglia, R. Petrucci, J. M. Kenny and L. Torre, Polym. Degrad. Stab., 2015, 121, 105–115 CrossRef CAS.
- D. F. Wu, L. Wu, W. D. Zhou, M. Zhang and T. Yang, Polym. Eng. Sci., 2010, 50, 1721–1733 CAS.
- S. Rakmae, Y. Ruksakulpiwat, W. Sutapun and N. Suppakarn, Mater. Sci. Eng., C, 2012, 32, 1428–1436 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to 30
1 to 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Its number average molecular weight (Mn) and density are about 87
1. Its number average molecular weight (Mn) and density are about 87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 g mol−1 and 1.25 g cm−3, respectively. Spodumene slag, the residue after extraction of lithium minerals, was provided by Shandong Mingrui Chemical Engineering Co. Ltd., P. R. China. It is a kind of white powder with an average particle size of 31.2 μm with a standard deviation of 12.7, as shown in Fig. 1. The density of this kind of slag powder is about 1.95 g cm−3 (measured by drainage).
000 g mol−1 and 1.25 g cm−3, respectively. Spodumene slag, the residue after extraction of lithium minerals, was provided by Shandong Mingrui Chemical Engineering Co. Ltd., P. R. China. It is a kind of white powder with an average particle size of 31.2 μm with a standard deviation of 12.7, as shown in Fig. 1. The density of this kind of slag powder is about 1.95 g cm−3 (measured by drainage).




![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibration peak of PLAC′15 sample is nearly unchanged. However, this peak shifts from 1747 cm−1 to 1751 cm−1, by about 4 cm−1, in the presence of silica particles. This upshift is believed to be due to the weakening of the polymer–polymer hydrogen bonding19 because the presence of silica particles leads to a lowering of chain mobility and to a disordering of the chain arrangement due to dipole–dipole coupling or hydrogen bonding between the surface hydroxyl groups of silica and the carboxyl groups in the polyester chain.20,21 A similar ‘red shift’ observation has also been reported for PLA composites with clay.22–24 This confirms good affinity between the PLA chain and silica particles.
O stretching vibration peak of PLAC′15 sample is nearly unchanged. However, this peak shifts from 1747 cm−1 to 1751 cm−1, by about 4 cm−1, in the presence of silica particles. This upshift is believed to be due to the weakening of the polymer–polymer hydrogen bonding19 because the presence of silica particles leads to a lowering of chain mobility and to a disordering of the chain arrangement due to dipole–dipole coupling or hydrogen bonding between the surface hydroxyl groups of silica and the carboxyl groups in the polyester chain.20,21 A similar ‘red shift’ observation has also been reported for PLA composites with clay.22–24 This confirms good affinity between the PLA chain and silica particles.




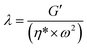






![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−aVf−b
e−aVf−b
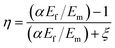
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) e−λeffVf
e−λeffVf






