Eight membered cyclic-borasiloxanes: synthesis, structural, photophysical, steric strain and DFT calculations

Abstract

Eight-membered cyclic borasiloxanes, Ph₂Si[OBArO]₂SiPh₂ [Ar = 4-EtC₆H₄ (1), 4-^tBuC₆H₄ (2), 2-PhC₆H₄ (3), 4-PhC₆H₄ (4) and β-C₁₀H₇ (Nap) (5); Ph = phenyl], were synthesized via the reaction of diphenylsilanediol with aryl boronic acid through a condensation reaction. The compounds were characterized using elemental analysis, FT-IR and NMR (¹H, ¹³C, ²⁹Si and ¹¹B). The compounds 1, 3 and 5 were further confirmed using single crystal X-ray diffraction studies. This showed the eight-membered ring (B₂O₄Si₂) configuration and that organic substituents occupied the axial and equatorial positions. Furthermore, non-covalent C–H⋯π and π⋯π interactions were observed in the crystal packing pattern. These borasiloxanes exhibited strong solid state fluorescence. The thermal behavior of the compounds 1–5 has been investigated using thermogravimetric analysis (TGA), which shows that the borasiloxanes 1 and 2 are thermally stable up to 220 °C and 180 °C respectively, whereas 3 and 4 are stable up to ∼120 °C and 5 is stable up to 230 °C. The band gap was calculated using the diffuse reflectance spectroscopic method. Compound 5 exhibits a low band gap (3.28 eV) which indicates that the naphthyl group shows more π-bonding delocalization within the molecule (strong intra-molecular charge transfer). The band gap decreases in the order of the compounds, 1 > 2 > 3 > 4 > 5. The theoretically computed band gap values were in good agreement with the experimentally observed trend. HOMO–LUMO analysis, TD-DFT, and the electrophilicity index, dipole moment and hyperpolarizability were computed using the B3LYP/6-31+G** method. The steric strain energies of the borasiloxanes and their degree of puckering conformation (O–Si–O, O–B–O and B–O–Si) were also analysed using DFT. This confirms that compound 3 has more strain, which is due to having a phenyl group in a sterically hindered ortho-position.

---

Introduction

Inorganic ring systems have been widely used not only owing to their aesthetic appeal but also due to potential applications arising out of their interesting magnetic and optical properties.^1–4 Among these, borasiloxane (B–O–Si) ring systems have attracted considerable attention due to their use as molecular building blocks and in materials science.^5,6 The cyclo-borasiloxane cage is well represented as six, eight and ten membered ring systems and the compounds involve a three-coordinate boron centre but there are also a few cases where the boron atoms are four-coordinate.⁷ These compounds are derived from conventional cyclo-siloxanes via the replacement of a skeletal silicon atom with one or more boron atoms.⁸ From a structural point of view, the eight-membered ring core assists as a junction for two extended π-systems and to form a linear fashion borasiloxane. From a functional point of view, the axial open coordination sites of boron in this design serve as recognition units capable of accepting electrons.^5,9,10 The first eight-membered borasiloxane (B₂Si₂O₄ ring) and its ring–ring transformation reactions were reported by Manners et al.¹⁰ Subsequently, Beckett et al. published the structural and Lewis acidity of bromo-substituted eight-membered borasiloxanes.¹¹ Lee et al. investigated a conjugated polymer sensor which contained an eight-membered borasiloxane.⁵ Severin et al. described macrocycles containing imine and borasiloxane links.¹² Recently, Baskar et al. demonstrated the synthesis and structural aspects of twelve-membered B₂Si₄O₆ borasiloxanes.¹³ Tri-substituted boron compounds in connection with p-conjugated systems gained interest because the vacant p-orbital enables effective pπ–pπ* conjugation to provide unique electronic and optical properties.¹⁴ It is concluded that they act as p-electron acceptors. Furthermore, boryl-functionalized chromophores have been promising functional materials in the fields of nonlinear optics, two-photon absorption, emissive systems, electronic devices and chemosensors.¹⁵ Moreover, the silicon-containing compounds have remarkably small HOMO–LUMO gaps, intrinsically high electron mobility, and high fluorescence efficiencies, as these materials are used for the manufacturing of high-performance electro-optical devices.¹⁶

On the other hand, cyclic compounds like trisiloxane, (RSiO)₃, and boroxine, (RBO)₃, rings possess a chemically significant amount of ring strain.¹⁷ The ring strain energies represent useful parameters for considering the electronic dispensation and thermodynamically instability in cyclic organic and inorganic systems. The compounds containing small organic substituents (–R) find applications as precursors for the preparation of high-molecular weight polymers via ring-opening polymerization (ROP).^5,18 This process exploits the relief of the ring strain energy as the thermodynamic driving force of the reaction. The transition from strained cyclic ring to ring opening polymerization would directly account for the entropy term of the Gibbs–Helmholtz equation (ΔG = ΔH − TΔS).^19–21 The entropic gain is attained from the conversion of the inflexible ring to a more flexible linear chain. The ring strain energy also depends on the ring member count, which atoms comprise the ring and the nature of the peripheral substituents. Beckmann et al. described six and eight-membered stannosiloxane ring strain and their puckered conformation.¹⁹ Khudobin et al. investigated cis and trans cyclosiloxane (RR′SiO)₃ ring strain energies.^15a To the best of our knowledge, there is no report in the literature about computational investigations of steric strain energies in cyclic borasiloxanes. Herein, we report the synthesis and spectral characterization of new eight-membered borasiloxanes 1–5, and the X-ray structure determination of three (1, 3 and 5) of these derivatives. We found that differences in ring strain due to steric hindrance and the degree of puckering were linked to the different substituents on the Si, O and B atoms. The HOMO and LUMO band gap values, hyperpolarizability (β₀), dipole moments and electrophilicity index were analysed using the DFT method. Furthermore, the luminescence properties were investigated.

Results and discussion

Synthesis and spectral characterization

The synthesis of eight-membered borasiloxanes involved the condensation reaction of equal molar amounts of arylboronic acid and diphenylsilanediol in toluene under reflux using a Dean–Stark trap to remove water molecules (Scheme 1), and the borasiloxanes were formed in good yield.

Scheme 1 Synthesis of borasiloxanes 1–5.

The eight-membered borasiloxanes, cyclo-Ph₂Si[OB(4-EtC₆H₄)O]₂SiPh₂ (1), cyclo-Ph₂Si[OB(4-^tBuC₆H₄)O]₂SiPh₂ (2), cyclo-Ph₂Si[OB(2-PhC₆H₄)O]₂SiPh₂ (3), cyclo-Ph₂Si[OB(4-PhC₆H₄)O]₂SiPh₂ (4) and cyclo-Ph₂Si[OB(Nap)O]₂SiPh₂ (5) were characterized using analytical and spectroscopic techniques. Compounds 1–5 are colourless crystalline solids and readily soluble in non-polar organic solvents. According to the ¹H NMR spectra, compounds 1–5 display well-resolved resonance. The aromatic proton signals appeared in the range of δ = 7.01–8.26 ppm for all compounds and these were compared with the reported literature.^11,22 The quartet at δ = 2.70 ppm, as well as triplet at δ = 1.26 ppm, corresponds to the ethyl group in compound 1, and the singlet appearing at δ = 1.35 ppm (2) can be assigned to the tert-butyl group in compound 2. The ¹³C NMR spectra show signals for the aromatic carbons in the ranges of 127.53–135.83 ppm (1), 124.88–135.60 ppm (2), 126.69–144.37 ppm (3), 126.31–135.33 ppm (4) and 114.96–137.93 ppm (5).¹⁰ The methylene carbon appears at 29.13 ppm and methyl carbon resonates at 15.44 ppm (Et) in 1. The aliphatic methyl terminal carbon resonates at 34.95 ppm and the ipso carbon at 31.23 ppm (^tBu) in 2; ¹¹B NMR spectra of the borasiloxanes show a broad singlet in range of 25–30 ppm which indicates the two boron atoms are in the same chemical environment. Similarly, the ²⁹Si chemical shift values show a singlet in the range of −45 to −48 ppm due to the similar coordination geometry around the Si atom, and these values are listed in Table 1. The NMR (¹H, ¹³C, ²⁹Si and ¹¹B) spectra of compounds 1–5 are shown in Fig. S9–S28.†

Table 1 ²⁹Si and ¹¹B chemical shift values in CDCl₃ solution; UV (λ_max) and emission (λ_ex) values for borasiloxanes 1–5

Compound	^29Si (ppm)	^11B (ppm)	UV (nm) CHCl3	Fluorescence (nm)
				CHCl3	Solid
1	−45.26	25.7	272	316	295
2	−45.52	31.0	246, 264	321	310
3	−44.80	30.2	260, 292	308	297
4	−47.72	29.9	267, 289	324	314
5	−44.48	25.0	266	353	305

---

FT-IR spectra obtained for all compounds showed strong absorptions in the regions of 1300–1440 cm⁻¹ and 1020–1110 cm⁻¹, due to B–O and Si–O stretching modes.²³ Additional strong signals were observed around 3000–3100 cm⁻¹ (ArC–H), 1261 cm⁻¹ (O–B–O stretching), 808 cm⁻¹ (O–Si–O bend), and 900–990 cm⁻¹ (O–Si–B).²⁴ Aliphatic C–H stretching appears at around 2900 cm⁻¹ for 1 and 2.

Crystal description of 1, 3 and 5

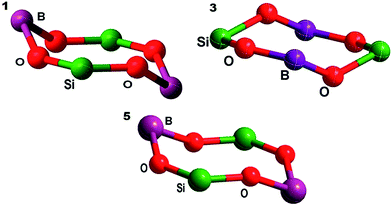
Borasiloxanes 1, 3 and 5 were crystallized in chloroform solution using a slow evaporation method. All display a triclinic crystal system (Z = 1) with the P1̄ space group (Fig. 1a–c).

Fig. 1 (a) Molecular structure of cyclo-Ph₂Si[OB(4-EtC₆H₄)O]₂SiPh₂ (1). (b) Molecular structure of cyclo-Ph₂Si[OB(2-PhC₆H₄)O]₂SiPh₂ (3). (c) Molecular structure of cyclo-Ph₂Si[OB(Nap)O]₂SiPh₂ (5).

Compounds 1, 3 and 5 show an eight-membered ring structure with four annular O atom bridges in alternate arrangement. The B atoms are three-coordinate and each is bound to two O atoms and one carbon atom with the angles O2–B1–C1 = 118.93(12)°, O1–B1–C1 = 118.90(13)° (2), O1–B1–C1 = 117.25(1)°, and O2–B1–C1 = 118.90(13)°, (3) and internal ring O–B–O angles of 122.17(13)° (1), 122.73(1)° (3) and 121.92(5)° (5) which confirms the trigonal planar geometry. The eight-membered ring B–O and Si–O bond lengths are 1.369(2) and 1.630(1) Å (1), 1.365(2) and 1.636(2) Å (3) and 1.361(2) and 1.621(2) Å (5), which are shorter than the covalent radii of literature compounds (B–O 1.54 Å, Si–O 1.91 Å and B–O 1.43 Å, Si–O 1.66 Å),^11,25 indicating π-bonding interactions within the ring.

Si shows slightly distorted tetrahedral geometry, and each atom is bound to two O atoms and two C atoms with angles of O2–Si1–C15 = 107.50(1)°, O1–Si1–C9 = 106.89(1)°, and C15–Si1–C9 = 113.51(1)° (1), O1–Si–C9 = 106.89(6)° and O2–Si–C9 = 107.71(6)° (3), and O2–Si–C17 = 109.43(3)°, O1–Si1–C11 = 107.68(4)°, and C17–Si1–C11 = 111.57(3)° (5), and with internal ring angles of O2–Si1–O1 = 112.52(1)° (1) and 112.52(6)°, (3) and O2–Si1–O1 = 107.84(4)° (5). The bond lengths and bond angles are comparable to the previously reported borasiloxane (PhBO)₂(Ph₂SiO).^10,25

The B–O–Si angles within the ring are 142.19(1) and 135.25(1)° (1), 148.06(2) and 138.02(2)° (3) and 133.08(5) and 139.14(5)° (5), which are shorter than for corresponding reported compounds (144.73(3) and 160.9(3)°)¹¹ due to the bulky substitution on the boron atom. Furthermore, it has been noted that the B–O–Si angles for borasiloxanes (1, 3 and 5) show considerable distortions on the O atoms in the annular ring, as shown in Fig. 2.^25,26

Fig. 2 B₂O₄Si₂ eight-membered ring conformation in 1, 3, and 5.

The crystal packing shows non-covalent interactions (π⋯π and C–H⋯π) were observed between {compound 1 [π⋯π = 4.053 Å], compound 3 [π⋯π = 3.649 Å; C20–H20⋯π = 2.655 Å; C22–H22⋯π = 2.682 Å; C23–H23⋯π = 2.702 Å] and compound 5 [π⋯π = 4.032 Å; C7–H7⋯π = 2.672 Å; C23–H23⋯π = 2.731 Å]}²⁷ the aromatic ring and hydrogen and ring to ring for adjacent molecules as shown in Fig. 3. Thus, the phenyl rings played phenomenologically important roles in the cooperation of CH–π and hydrogen-bonding interactions.

Fig. 3 Non-covalent π⋯π and C–H⋯π interactions in the crystal packing of compounds 1, 3 and 5; hydrogen atoms are omitted for clarity.

Photophysical properties

UV-vis absorption spectral data for compounds 1–5 are listed in Table 1. The UV-vis absorption spectra, measured in chloroform solution, show peaks in the range of 250 to 300 nm, as shown in Fig. S7.† The characteristic absorption patterns were attributed to π–π* electronic transitions of intra-molecular charge-transfer between the HOMO and LUMO.⁵ The absorptions show a bathochromic shift compared with phenylboronic acid (235 nm).²⁸ Compounds 2, 3 and 4 exhibited shoulder peaks at 264, 292 and 288 nm (Table 1), which is due to the Si and B being attached to different aromatic substituents. In order to calculate the optical band gap of borasiloxanes 1–5, diffuse reflectance spectroscopic methods were used. The absorption coefficient (α) was calculated using the Kubelka–Munk equation.²⁹

(α/S) = (1 − R)²/2R (1)

Here, S is the scattering coefficient and R is the diffused reflectance at a certain energy. The optical energy band gap (E_g) of the borasiloxanes was calculated using the following equation.³⁰

hν = A(hν − E_g) (2)

where A is the absorbance, h stands for Planck's constant and ν is the frequency of the incident photons. The energy band gap value was obtained from Tauc's graph [(αhν)² vs. hν]. The intersection of a line drawn from the maximum absorption end point of the curve with the photon energy axis was considered as the energy band gap of the compounds. We have measured the indirect band gap energy with this method. The band gap values were observed to be 5.73, 4.29, 4.15, 3.72 and 3.28 eV for compounds 1–5 respectively, as shown in Fig. S7.† Silicon or boron based compounds generally exhibit very small dispersion in the flat valence band (VB) and conduction band (CB).⁵ The band gap energies of borasiloxanes decrease with increasing π-electron interaction.¹⁶ The naphthyl substituted borasiloxane, 5, shows a low band gap (E_g = 3.28 eV) which is due to the strong π-bond interaction and high crystallinity. The band gap decreases in the order of the compounds 1 > 2 > 3 > 4 > 5. These band gap values are in good agreement with the theoretically computed trend.

In the photoluminescence spectra of 1–5, recorded in chloroform, the maximum emission wavelengths (λ_max) of the compounds are 316, 321, 308, 324 and 353 nm, respectively (Fig. S5†). The solid state emission spectra of compounds 1–5 are show in Fig. 4. The emission bands are fairly broad in the solid state compared with solution. Further, the solid state emission spectra of the compounds show a hypsochromic shift compared to the corresponding solution emission spectra, as shown in Fig. S5.† This may be caused by the solid-state packing between adjacent molecules. The maximum emission wavelength of compounds 1–5 is shown in the range of 290–350 nm. The conjugation of the aryl unit with the substituents of the eight-membered structures in 1–5 clearly has an impact on the emissions, as shown in Table 1.

Fig. 4 Solid state emission of borasiloxanes 1–5.

Thermal analysis

The thermal stabilities of borasiloxanes 1–5 were analysed using thermogravimetric analysis. Thermograms were obtained at a heating rate of 10 °C/10.0 K min⁻¹ up to 700 °C under an N₂ atmosphere. Typical TG curves for compounds 1–5 are represented in Fig. S5.† The TG curves of compounds 1–2 show a similar decomposition pattern. The decomposition occurred between 230 and 455 °C (77.66%) in 1, and 180–502 °C (75.46%) in 2, due to the removal of alkyl and aryl substituents and the final residue is 1/2B₂O₃·SiO₂ with carbon residue.³¹ After major weight loss it remains as 1/2B₂O₃·SiO₂ with carbon and the compounds 1 and 2 are stable up to 220 °C and 180 °C respectively. Compound 3's weight loss occurred between 122 and 366 °C (31.12%) and the major decomposition occurred at 530 °C (35.11%), indicating the removal of all aromatic substituents. This remains unchanged up to 720 °C. Compound 4 shows weight loss in the range of 112–182 °C (7.94%) and 183–475 °C (74.23%), indicating that aryl groups are decomposed to form residue of borosilicate with carbon.³¹ Compounds 3 and 4 start their decomposition at low temperatures compared with other borasiloxanes due to greater steric stain. Compound 5's weight loss starts around 220–442 °C (77.67%) indicating decomposition of phenyl and naphthyl substituents. Based on this study the borasiloxanes 3 and 4 are stable up to ∼120 °C whereas 5 is stable up to 240 °C.

DFT calculations

Energies and structures. In order to find the energy minimized geometries of all the borasiloxanes (1–5), energy optimization is carried out at the B3LYP/6-31+G** level of theory. The optimized structures of all the borasiloxanes are shown in Table S2.† The structural parameters of the optimized geometries of compounds 1, 3 and 5 are in good agreement with the crystal data as listed in Table 2. The other compounds, 2 and 4, have similar geometries to 1, 3 and 5. In the crystal structure, the ring adopts non-planar geometry with the planar phenyl group slightly rotated out of the plane of the eight-membered ring. This can be seen in the optimized geometries of ortho/para phenyl and naphthyl group substituents which make greater structural changes compared to the alkyl substituted compounds. The results show that the substituents act to increase the bond length of (B–O–Si) which indicates reduced eight-membered ring strain. The minimum energy geometries of all the borasiloxanes were used to calculate the molecular properties.

Table 2 Bond angle and bond length parameters between the crystal structure and optimized structure

	Crystal structure (optimized)
	1	3	5
Bond angle (°)
B–O–Si (1)	142.19 (150.90)	148.06 (157.69)	148.98 (152.05)
B–O–Si (2)	135.23 (149.34)	138.08 (138.61)	145.14 (151.30)
O–Si–O	112.52 (113.06)	112.07 (111.60)	119.72 (112.75)
O–B–O	121.68 (121.77)	119.98 (120.98)	111.59 (121.99)
Bond length (Å)
B1–O1	1.36 (1.36)	1.36 (1.36)	1.36 (1.36)
Si–O1	1.63 (1.65)	1.63 (1.65)	1.639 (1.65)
B1–C1	1.55 (1.56)	1.56 (1.57)	1.54 (1.57)
Si1–C9	1.84 (1.87)	1.84 (1.86)	1.85 (1.86)

---

HOMO–LUMO analysis. The energies of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) are computed at the B3LYP/6-31+G** level of theory. The HOMO represents the ability to donate an electron, and the LUMO acts as an electron acceptor representing the ability to accept an electron. These orbitals play an important role in the electrical and optical properties. The HOMO energy is directly related to the ionization potential and LUMO energy is directly related to the electron affinity. The frontier molecular orbitals (HOMO and LUMO) are mostly the π-anti-bonding type molecular orbitals in the structure. The frontier molecular orbital distributions and corresponding energy levels for all the borasiloxanes (1–5) are shown in Fig. 5.

Fig. 5 Energy gaps and the orbital composition distribution of the HOMO–LUMO for compounds 1–5.

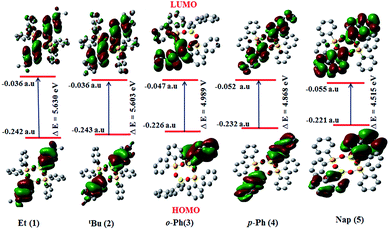
The band gap decreases in the order of the compounds 1 > 2 > 3 > 4 > 5 as shown in Fig. 5. The theoretically calculated band gaps follow similar trends to the experimental values. The variation in the HOMO and LUMO energy gap in all the borasiloxanes explains the eventual charge transfer process within the molecule.³²

TD-DFT calculations

In order to correlate the electronic properties of the borasiloxanes (1–5), we have carried out time-dependent DFT (TD-DFT) studies in the gas phase. The electronic structures of these compounds are used to study the orbitals involved in the electronic transitions and visualize the effect of the nature of the boron atom, the donor as well as the acceptor strength on the observed polarizability and related properties. The calculated energies using B3LYP/6-31+G** show a good association with the corresponding values from the UV-vis absorption data (Table 1). The chromophore energies of the set of HOMO and LUMO transitions are listed in Fig. S1–S3.† The associated frontier orbital energy level plot of the chromophores shows an interesting correlation between the electronic absorption properties. The HOMO, HOMO−1, HOMO−2 and HOMO−3 in 1 and 2 were predicted to be predominantly localized on the boron substituted phenyl core. The LUMO and LUMO+1 of borasiloxanes 1 and 2 are centered on the silicon attached phenyl core. TD-DFT calculations for 1 and 2 show that the S₀ → S₁ transition of the chromophores has large oscillator strengths at 257 nm (1) and 258 nm (2). It is dominated by the number of intra-molecular π → π* transitions in the HOMO−1 → LUMO (1) and HOMO−1 → LUMO (2) transitions. The HOMO, HOMO−1 and HOMO−2 in 3 and 4 have significant contributions from the biphenyl group. The transitions of these compounds are observed in HOMO−1 → LUMO (267 nm) in 3 and HOMO−1 → LUMO (276 nm) in 4 with good oscillator strengths. The HOMO, HOMO−1, HOMO−3, and HOMO−4 in 5 are mainly localized on the naphthyl group attached to the boron atom. The most intense transition in 5 is dominated by the HOMO−1 → LUMO electron transfer and is π → π* (305 nm). The results show that for all the borasiloxanes 1–5, the transitions S₀ → S₁ are predominately occupied by HOMO−1 → LUMO as shown in Table 3. The TD-DFT results clearly indicate the intra-molecular charge transfer (ICT) process in borasiloxanes 1–5.

Table 3 Selected transitions obtained from TD-DFT calculations at the B3LYP/6-31+G** level of theory

Entry	λ (nm)	Oscillator strength, f	Energy (eV)	Major contributions^a
a H = HOMO; L = LUMO; only contributions above 15% are included.
1	257	0.3789	5.21	H−1 → L (59%), H−2 → L+2 (14%)
	257	0.1069	5.22	H−1 → L (28%), H−4 → L+2 (−23%)
	257	0.066	3.31	H−4 → L (41%), H−1 → L+1 (26%), H−6 → L (21%)
2	258	0.629	5.22	H−1 → L (22%), H → L+2 (20%)
	244	0.016	5.21	H−4 → L+9 (22%), H−5 → L+8 (20%), H−6 → L+2 (20%)
	245	0.007	5.17	H−5 → L+3 (25%), H−4 → L+2 (−21%), H−6 → L+2 (20%)
3	267	0.191	4.63	H−1 → L (47%), H−1 → L+2 (27%), H → L+1 (−24%),
	253	0.088	4.89	H−1 → L+1 (45%), H → L+1 (−23%), H−2 → L (−22%)
	245	0.036	5.06	H → L+2 (55%), H → L+3 (−24%), H → L+4 (−25%)
	253	0.022	4.88	H → L+1 (46%), H−1 → L+1 (22%)
4	276	1.597	4.48	H−1 → L (55%), H → L (−42%)
	266	0.026	4.66	H → L +1 (55%), H−1 → L (43%)
	263	0.008	4.71	H−3 → L+1 (38%), H−2 → L (−37%), H−1 → L+12 (22%)
5	305	0.079	4.06	H−1 → L (47%), H → L+1 (36%)
	286	0.033	4.34	H−3 → L (31%), H−2 → L+1 (−30%), H → L+5 (−30%)
	263	0.005	4.70	H → L+2 (66%), H−1 → L+3 (16%)
	261	0.002	4.73	H−1 → L+3 (56%), H−1 → L+4 (−26%)

---

Electrophilicity index

To find out the reactivity of borasiloxanes 1–5 towards nucleophiles, it is necessary to study the electrophilicity index of the boron atom.³³ The electrophilicity index is calculated according to the following equation.³⁴

ω = μ²/2η (3)

where μ and η are the chemical potential and chemical hardness, respectively.³⁵

μ = (ε_LUMO + ε_HOMO)/2 and η = (ε_LUMO − ε_HOMO)/2

where ε_LUMO is the energy of the lowest unoccupied molecular orbital and ε_HOMO is the energy of the highest occupied molecular orbital. The HOMO and LUMO as main orbitals are responsible for the reactivity of compounds.³⁶ The main characteristics of Lewis acidity include high electrophilicity and a tendency to accept electrons in chemical reactions. Boron atom with Lewis acidity carry a partial positive charge, and can react with nucleophilic compounds bearing nitrogen, oxygen and sulphur atoms. Two important factors, the electron-accepting level and the vacancy of the orbital at the reaction site, have been included for the purpose of comparing the relative reactivity of the molecules. The electrophilicity indexes of all the borasiloxanes are given in Table 4. The calculated value for the boron center is lower in 1 and 2 (1.347, 1.349), suggesting that it should be less reactive toward nucleophiles compared with analogue borasiloxanes. Parr et al. demonstrated that ω shows the second-order energy of an electrophile when it gets saturated with electrons. The electrophilicity (ω) remains low although the system does not like to take electrons.³⁵ The electrophilicity of the borasiloxanes decreases in the order of 5 > 4 > 3 > 2 > 1 which follows the decreasing trend in the HOMO and LUMO energy gap (Fig. 5). The high electrophilicity of borasiloxane 5 is due to the low-lying unoccupied molecular orbital having a large amplitude on the boron centre. Brown et al. suggested that the delocalization of π-electrons in aromatic rings increases the electrophilicity of the boron center.³⁷ The borasiloxanes 1–5 examined in this study clearly indicate that the boron atom is in an sp² planar arrangement.

Table 4 The calculated electrophilicity index (ω), dipole moment (μ_tot), polarizability (α₀) and first hyperpolarizability (β₀) of borasiloxanes 1–5

Compound	μ	η	ω	μtotal	α0 × 10^−24 esu	β0 × 10^−32 esu
1	1.819	0.103	1.347	1.04	81.658	51.764
2	1.757	0.103	1.349	2.15	88.367	52.189
3	1.700	0.090	1.525	2.76	91.815	77.610
4	2.181	0.089	1.577	1.64	98.419	87.575
5	1.904	0.083	1.662	1.30	99.921	106.492

---

Table 5 Crystallographic data for compounds 1, 3 and 5

Parameter	1	3	5
Empirical formula	C40H38B2O4Si2	C48H38B2O4Si2	C44H34B2O4Si2
Formula weight	660.5	756.58	704.51
Temperature	110.15 K	110.15 K	150.15 K
Wavelength	0.71073 Å	0.71073 Å	0.71073 Å
Crystal system	Triclinic	Triclinic	Triclinic
Space group	P1̄	P1̄	P1̄
Unit cell dimensions	a = 9.342 Å	a = 9.912 Å	a = 9.266 Å
	b = 12.043 Å	b = 12.033 Å	b = 10.367 Å
	c = 16.083 Å	c = 17.304 Å	c = 19.142 Å
	α = 86.892°	α = 102.333°	α = 82.609°
	β = 82.972°	β = 92.103°	β = 87.097°
	γ = 83.982°	γ = 100.313°	γ = 83.429°
Volume	1785.1(7) Å^3	1978.9(8) Å^3	1810.6(19) Å^3
Z	2	2	2
Density (calculated)	1.229 mg m^−3	1.270 mg m^−3	1.292 mg m^−3
Absorption coefficient	0.140 mm^−1	0.135 mm^−1	0.143 mm^−1
F(000)	696	792	736
Crystal size	0.57 × 0.54 × 0.53 mm^3	0.54 × 0.53 × 0.5 mm^3	0.4 × 0.25 × 0.19 mm^3
Theta range for data collection	1.702 to 27.509°	1.765 to 27.488°	1.994 to 27.552°
Completeness to theta = 25.242°	99.70%	99.50%	99.40%
Max. and min. transmission	0.7456 and 0.6912	0.7456 and 0.4340	0.7456 and 0.6689
Refinement method	Full-matrix least-squares on F^2	Full-matrix least-squares on F^2	Full-matrix least-squares on F^2
Data/restraints/parameters	8092/584/510	8908/0/505	8155/760/590
Goodness-of-fit on F^2	1.024	1.029	1.062
Final R indices [I > 2sigma(I)]	R1 = 0.0432, wR2 = 0.1106	R1 = 0.0474, wR2 = 0.1215	R1 = 0.0652, wR2 = 0.1636
R indices (all data)	R1 = 0.0527, wR2 = 0.1174	R1 = 0.0602, wR2 = 0.1325	R1 = 0.0858, wR2 = 0.1744

---

Polarizability

The molecular polarizability of compounds depends on the efficiency of electronic communication between acceptor and donor groups. The results of calculating the polarizability, and the first hyperpolarizability at the B3LYP/6-31+G** level of theory are given in Table 4. The values of the first hyperpolarizability (β), dipole moment (μ) and polarizability (α) for the borasiloxanes are reported in atomic mass units (a.u) and electrostatic units (esu). The first hyperpolarizability is a third rank tensor that can be described using a 3 × 3 × 3 matrix. The components of β are defined as the coefficients in the Taylor series expansion of the energy in an external electric field. When the external electric field is weak and homogeneous, this expansion becomes

E = E⁰ − μ_αF_α − 1/2α_αβF_αF_β − 1/6β_αβ_γF_αF_βF_γ +… (4)

where E⁰ is the energy of the unperturbed molecule, F_α is the field at rigid μ_α, and α_αββ and β_αβγ are the components of the dipole moment, polarizability and first order hyperpolarizability respectively. To calculate the magnitude of the total static dipole moment (μ_tot), the mean polarizability (α₀) and the mean first hyperpolarizability (β₀) are followed as given in the literature.^38,39 The mean polarizability is defined using the following equation.

α₀ = (α_xx + α_yy + α_zz)/3 (5)

The components of the first hyperpolarizability can be calculated using the following equation.

β₀ = (β_x² + β_y² + β_z²)^1/2 (6)

where β_x = β_xxx + β_yyy + β_zzz; β_y = β_yyy + β_yzz + β_yxx; β_z = β_zzz + β_zxx + β_zyy, a complete equation for calculating the magnitude of β₀. The total dipole moment can be calculated using the following equation.

μ_t = (μ_x² + μ_y² + μ_z²)^1/2 (7)

Similar hyperpolarizability values were obtained in the pairs 1–2 and 3–4 due to similar aromatic π-delocalization in these compounds. The borasiloxane 5 exhibits maximum hyperpolarizability β₀ (106.49 × 10⁻³² esu), suggesting that it is strongly dependent on the relative arrangement and orientation of the π-conjugation of the naphthyl group.

Thus, only a small increase in conjugation, but a significant increase in the β₀ value is found. This can be interpreted as an intra-molecular charge distribution that leads to the weakening of the electron–nucleus interaction. The total dipole moment and hyperpolarizability of the borasiloxanes were compared to standard urea molecules (μ_tot and β₀ of urea are 1.669 debye and 158.39 × 10⁻³⁰ esu respectively).⁴⁰ The hyperpolarizability of compounds 1–5 was less than a standard urea molecule.

Steric strain analysis

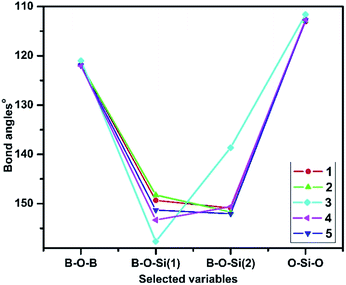
The optimized geometries of all the borasiloxanes show puckering in the ring due to different aromatic substituents. Strong evidence indicates predominantly polarized B–O–Si bonds and minor charge delocalization of electron density from O to B and O to Si in borasiloxanes. It should be possible to qualitatively assess the steric strain in the borasiloxanes by decomposing into its angular strain components.

The steric strain analysis methods were those followed by reported literature.^19,41 The bond angles of B–O–B, B–O–Si(1), B–O–Si(2) and O–Si–O in all the borasiloxanes are shown in Fig. 6. The highest level of steric strain is observed in compound 3. It reveals more steric strain than the other borasiloxane analogues, which indicates the phenyl moiety occupies the sterically hindered ortho-position. The equilibrium angles in 3 are larger than the other borasiloxanes, providing an explanation for the ring puckering, to reduce steric strain. Three-dimensional geometry requires that the sum of the endocyclic angles of any eight-membered ring should be less than or equal to 720°, where the maximum sum correlates to a planar ring. Puckering would therefore necessitate a reduction in the average endocyclic angle and enhance both the B–O–Si(1) and B–O–Si(2) linkages even further away from their preferred values. In addition, compound 3 is used to understand the steric strain energy.

Fig. 6 Steric strain of 1–5 with respect to their bond angles.

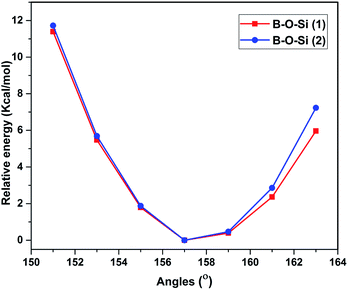
The potential energy surface of 3 is scanned by varying the bond angles of B–O–Si(1) and B–O–Si(2). A rigid potential energy scan is performed using relaxed optimized structures, by varying the B–O–Si(1) and B–O–Si(2) angles between 148 and 154° in 3. The average trigonal B–O–Si(1) bond angles and the mean B–O–Si(2) angles increase by 2° to 121.9(9) and 121.8(8)° respectively. The resulting potential energy surface is shown in Fig. 7 as the relative energy to the optimized geometry with a variation in bond angle. The steric strain energy surface clearly dictates how the delocalization is affected because of steric factors which lead to non-planar geometry. The results indicate the reason for more steric strain in 3 is the bulky substituent in the ortho-position which will facilitate the dissociation process.

Fig. 7 Energy profile of 3 with respect to the deformation of the B–O–Si(1) and B–O–Si(2) bonds.

Experimental

All the reactions were carried out under an inert atmosphere with dry nitrogen. Solvents were dried and distilled prior to use. Diphenylsilanediol and substituted aryl boronic acids were obtained from Aldrich Chemical and used as supplied. The melting points were measured using a JSGW melting point apparatus. Elemental analysis were carried out using a Thermo quest CE instruments model EA/110 CHNS-O elemental analyser. ¹H, ¹³C, ¹¹B and ²⁹Si NMR spectra were recorded on a Bruker AMX-400 MHz spectrometer using CDCl₃. Infrared spectra were collected as KBr discs on a Mattson galaxy 3000 spectrometer. UV-vis and DRS spectra were obtained on a Jasco-v-670 spectrophotometer, and fluorescence spectra were recorded using a Hitachi F7000 spectrophotometer. Thermal analysis were performed on a PerkinElmer STA 6000, Diamond TG thermal analyser.

General procedure

The eight-membered borasiloxanes 1–5 were synthesized using the following procedure.

A condensation reaction with equal molar ratios of diphenylsilanol (0.648 g, 3 mmol) and the corresponding aryl boronic acid (Et (1) = 0.450 g; ^tBu (2) = 0.534 g; o (3) and p-Ph (4) = 0.594 g; Nap (5): 0.516 g, 3 mmol) employing 50 mL of toluene as a solvent was carried out. The reaction mixture was heated to reflux for 12 h in a Dean–Stark apparatus. The H₂O layer which formed during the reflux was discarded using azeotropic distillation. The reaction solution was concentrated and allowed to cool to room temperature. The solvent was removed by reducing the pressure and the residual solid was recrystallized from chloroform.

4,8-Bis(4-ethylphenyl)-2,2,6,6-tetraphenyl-1,3,5,7,2,6,4,8-tetraoxadisiladiborocane (1). Yield: 88%. Melting point: 158–160 °C. Anal. calcd: C₄₀H₃₈B₂O₄Si₂ (M.W. 660.52): C, 72.73; H, 5.80%. Found: C, 72.51; H, 5.63%. ¹H NMR (400 MHz, CDCl₃, ppm, TMS): δ = 1.26 (t, 6H, J = 16 Hz), 2.70 (m, 4H), 7.23–7.42 (m, 12H), 7.47–7.497 (m, 8H), 7.72–7.79 (m, 4H), 8.01–8.17 (m, 4H); ¹³C NMR (400 MHz, CDCl₃, ppm, TMS): δ = 15.44 (2C); 29.13 (2C); 127.53 (8C); 127.9 (2C); 130.47 (4C). 133.59–135.83 (12C); 148.2 (2C). ¹¹B NMR (CDCl₃, TMS): 25.7 ppm. ²⁹Si NMR (CDCl₃, TMS): −45.26 ppm. FT-IR (cm⁻¹, KBr pellet): 3134 (m), 3068 (m), 3020 (m), 2966 (s), 2839 (m), 1608 (s), 1458 (m), 1429 (s), 1350 (s), 1311 (s), 1182 (s), 1311 (s), 1143 (s), 1126 (s), 835 (s), 719 (s), 700 (s), 651 (s). UV-vis (CHCl₃): 272 nm. Fluorescence (λ_ex = 270 nm): 316 nm.

4,8-Bis(4-(tert-butyl)phenyl)-2,2,6,6-tetraphenyl-1,3,5,7,2,6,4,8-tetraoxadisiladiborocane (2). Yield: 83%. Melting point: 154–156 °C. Anal. calcd: C₄₄H₄₆B₂O₄Si₂ (M.W. 716.63): C, 73.74; H, 6.47% Found: C, 73.41; H, 6.42%. ¹H NMR (400 MHz, CDCl₃, ppm, TMS): δ = 1.35 (s, 18H) 7.22–7.40 (m, 12H), 7.47–7.49 (d, 4H), 7.72 (t, 8H), 8.03 (d, 4H); ¹³C NMR (400 MHz, CDCl₃, ppm, TMS): δ = 31.2 (6C); 34.9 (2C); 124.8 (8C); 127.98 (8C); 130.46 (6C); 133.59–135.60 (12C); 154.95 (2C). ²⁹Si NMR (CDCl₃, TMS): −45.35 ppm. ¹¹B NMR (CDCl₃, TMS): 31.0 ppm. FT-IR (cm⁻¹, KBr pellet): 3136 (m), 3051 (m), 2958 (s), 2949 (s), 2899 (m), 1606 (s), 1475 (m), 1429 (s), 1394 (s), 1373 (s), 1348 (s), 1315 (s), 1269 (s), 1147 (s), 1130 (s), 1118 (s), 840 (s), 721 (s), 700 (s), 655 (s), 513 (s). UV-vis (CHCl₃): 246, 264 nm. Fluorescence (λ_ex = 293 nm): 321 nm.

4,8-Di([1,1′-biphenyl]-2-yl)-2,2,6,6-tetraphenyl-1,3,5,7,2,6,4,8-tetraoxadisiladiborocane (3). Yield: 84%. Melting point: 186–188 °C. Anal. calcd: C₄₈H₃₈B₂O₄Si₂ (M.W. 756.61): C, 76.20; H, 5.06%. Found: C, 76.11; H, 4.96%. ¹H NMR (400 MHz, CDCl₃, ppm, TMS): δ = 7.01–7.19 (m, 12H); 7.18–7.24 (m, 8H); 7.27–7.33 (m, 12H); 7.33–7.43 (m, 6H); ¹³C NMR (400 MHz, CDCl₃, ppm, TMS): δ = 127.6–127.9 (8C); 128.8–128.9 (12C); 130.6 (4C); 135–132 (12C); 143.15 (8C); 147.91 (4C); ²⁹Si NMR (CDCl₃, TMS): −48.92 ppm. ¹¹B NMR (CDCl₃, TMS): 30.2 ppm. FT-IR (cm⁻¹, KBr pellet) 3136 (m), 3081 (m), 3011 (m), 1605 (m), 1514 (m), 1482 (m), 1429 (s), 1392 (s), 1338 (s), 1304 (s), 1257 (s), 1182 (s), 1143 (s), 1132 (s), 834 (s), 736 (s), 725 (s), 694 (s), 652 (s), 649 (s), 583 (s), 511 (s). UV-vis (CHCl₃): 260, 292 nm. Fluorescence (λ_ex = 275 nm): 308 nm.

4,8-Di([1,1′-biphenyl]-4-yl)-2,2,6,6-tetraphenyl-1,3,5,7,2,6,4,8-tetraoxadisiladiborocane (4). Yield: 90%. Melting point: 178–180 °C. Anal. calc.: C₄₈H₃₈B₂O₄Si₂ (M.W. 756.61): C, 76.20; H, 5.06%. Found: C, 75.97; H, 5.13%. ¹H NMR (400 MHz, CDCl₃, ppm, TMS): δ = 7.31–7.39 (m, 12H), 7.41–7.48 (d, 8H), 7.64–7.76 (m, 12H), 8.14–8.16 (d, 6H); ¹³C NMR (400 MHz, CDCl₃, ppm, TMS): δ = 126.69–127.64 (8C); 128.07–128.82 (8C); 130.6 (4C); 133.39–134.12 (12C); 136.15 (8C); 141.01 (4C); 144.37 (4C); ²⁹Si NMR (CDCl₃, TMS): −44.80 ppm. ¹¹B NMR (CDCl₃, TMS): 29.9 ppm. FT-IR (cm⁻¹, KBr pellet): 3132 (m), 3072 (m), 3049 (m), 3018 (m), 1606 (s), 1517 (m), 1485 (m), 1427 (s), 1398 (s), 1348 (s), 1300 (s), 1263 (s), 1185 (s), 1141 (s), 1128 (s), 835 (s), 738 (s), 721 (s), 696 (s), 655 (s), 646 (s), 584 (s), 513 (s). UV-vis (CHCl₃): 267 and 289 nm. Fluorescence (λ_ex = 290 nm): 324 nm.

4,8-Di(naphthalen-2-yl)-2,2,6,6-tetraphenyl-1,3,5,7,2,6,4,8-tetraoxadisiladiborocane (5). Yield: 92%. Melting point: 175–176 °C. Anal. calc.: C₄₄H₃₄B₂O₄Si₂ (704.22): C, 75.01; H, 4.86%; Found: C, 74.96; H, 4.80%. ¹H NMR (400 MHz, CDCl₃, ppm, TMS): δ = 7.32–7.39 (m, 8H); 7.40–7.43 (m, 8H); 7.47–7.54 (m, 8H); 7.79–7.81 (m, 4H); 8.06–8.16 (m, 4H); ¹³C NMR (400 MHz, CDCl₃, ppm, TMS): δ = 127.27–128.18 (4C); 129.04 (4C); 131.21–130.73 (12C); 133.48 (4C); 137.44 (2C); 134.25 (4C); 135.15 (4C); ¹¹B NMR (CDCl₃, ppm, TMS): 25.0 ppm. ²⁹Si NMR (CDCl₃, TMS): −48.8 ppm. FT-IR (cm⁻¹, KBr pellet): 3070 (s), 3065 (s), 1625 (m), 1597 (s), 1504 (s), 1471 (s), 1357 (s), 1319 (s), 1319 (s), 1230 (s), 1130 (s), 1066 (s), 947 (m), 860 (s), 744 (s), 696 (s). UV-vis (CHCl₃): 266 nm. Fluorescence (λ_ex = 295 nm): 353 nm.

Single crystal X-ray solution and refinement

Single crystals of 1, 3 and 5 were obtained from chloroform. A Leica MZ 75 microscope was used to identify suitable colorless crystals. A BRUKER APEX 2 X-ray (three-circle) diffractometer was employed for crystal screening,⁴² unit cell determination and data collection at 150 K. Data were collected using graphite-monochromatic and 0.5 mm mono Cap-collimated Mo-K_α radiation (λ = 0.7107 Å) with the ω scan method. Integrated intensity information for each reflection was obtained through the reduction of the data frames with the program APEX2.⁴³ The integration method employed a three dimensional profiling algorithm and all data were corrected for Lorentz and polarization factors, as well as for crystal decay effects. Finally, the data was merged and scaled to produce a suitable data set. The absorption correction program SADABS⁴⁴ was employed to correct the data for absorption effects. A solution was obtained readily using XT/XS in APEX2.^43,44 Hydrogen atoms were placed in idealized positions and were set riding on the respective parent atoms. All non-hydrogen atoms were refined with anisotropic thermal parameters. The absence of additional symmetry and voids was confirmed using PLATON (ADDSYM).⁴⁵ The structure was refined (weighted least squares refinement on F²) to convergence.⁴⁶ Olex2 was employed for the final data presentation and structure plots.⁴⁷ The compounds 1, 3 and 5 crystal data and refinement details are listed in Table 5.

Computational calculation methods

The electronic structures and the molecular properties of compounds 1–5 were investigated in the gas phase using DFT methods to understand chemical bonding patterns, steric strain, electronic charge distributions, band gaps, electrophilicity indexes and non-linear optical properties. In order to find the energy minimized structures and predict the molecular properties of compounds 1–5, Becke's three-parameter and the Lee–Yang–Parr functional, as B3LYP,^47–50 was utilized in DFT and TD-DFT. The initial geometry of compounds 1, 3 and 5 were taken from the available crystal data and guessed structures of compounds 2 and 4 were obtained by replacing substituents in compound 1. The geometries of compounds 1–5 in the gas phase were optimized using the B3LYP functional combined with a 6-31+G** basis set. Inclusion of diffusion and polarization functions in the 6-31+G** basis set accounts for the electronic charge distributions in compounds 1–5 and the effects of polarization in atomic orbitals for all the cyclic borasiloxanes. The B3LYP/6-31+G** level of computational calculations was carried out using the G09 package⁵¹ for all cyclic borasiloxanes. In order to understand the role of steric effects on all the cyclic borasiloxanes, the energy minimized geometries of compounds 1–5 were used to analyse the degree of puckering in the ring with respect to the O–Si–O, O–B–O and B–O–Si bond angles. Further, the steric strain energies of compound 3 were computed by scanning the potential energy surface, varying the B–O–Si (1) and B–O–Si (2) bond angles. The HOMO–LUMO energy band gap values, dipole moments, polarizability and hyperpolarizability were also calculated. The electronic geometries and frontier molecular orbital structures were taken using the Gauss View 5.0 molecular visualization program.⁵²

Conclusions

We have synthesized and characterized a series of borasiloxanes, 1–5. They show good thermal stability, electron-transport and strong blue emission properties. The single crystal structures of three compounds (1, 3 and 5) and DFT level calculations of the electronic structures confirm the eight-membered ring geometry, bridged with four annular O atoms, and the crystal packing patterns show non-covalent interactions (C–H⋯π and π⋯π). Compound 5 has a low band gap which indicates the naphthyl group shows strong intra-molecular interactions. The TD-DFT results reveal that the various electronic transitions of the borasiloxanes are contributed to from π–π* orbitals. The ring contains two boron atoms that act as Lewis acid centres and the electrophilicity was analysed using HOMO–LUMO energy values. This shows that compound 5 has a maximum value, which is due to the naphthyl group in the borasiloxane producing an electric field that influences the B atom, which increases the electrophilicity. The hyperpolarizability of all compounds was analysed and 5 has a higher value than the other borasiloxanes, due to the effective π-delocalization on the naphthyl group. The steric strain energies of the compounds were investigated using the DFT method. It is confirmed that compound 3 has more steric strain, which is due to the steric hindrance of the o-phenyl substituent. The experimental and theoretical results suggest that the prepared borasiloxanes can be considered as precursors for the synthesis of inorganic polymers via ring opening polymerisation and as potential candidates for optical applications. To gain better understanding of the ring strain energy of borasiloxanes, homodesmotic reactions will be carried out, which are currently in progress.

Acknowledgements

We gratefully acknowledge the financial support from the Department of Science and Technology-Science & Engineering Research Board, Government of India (Grant No. SR/FT/CS-11/2011). NP and MGK thank DST-VIT-FIST for NMR and SIF-VIT University for the research facilities. The authors thank Dr S. Easwaramoorthi, CLRI-Chennai, for useful discussion and solid state fluorescence.

References

1. E. J. L. Mcinnes, S. Piligkos, G. A. Timco and R. E. P. Winpenny, Coord. Chem. Rev., 2005, 249, 2577–2590.
2. Z. M. Zhang and K. I. Haiduc, The Chemistry of Inorganic Ring Systems, 2, Wiley Interscience, New York, 1970.
3. O. Cador, D. Gatteschi, R. Sessoli, F. K. Larsen, J. Overgaard, A.-L. Barra, S. J. Teat, A. Timco and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2004, 43, 5196–5200.
4. Z. M. Zhang, Y. G. Li, S. Yao, E. B. Wang, Y. H. Wang and R. Clerac, Angew. Chem., Int. Ed., 2009, 48, 1581–1584.
5. W. Liu, M. Pink and D. Lee, J. Am. Chem. Soc., 2009, 131, 8703–8707.
6. (a) D. A. Foucher, A. J. Lough and I. Manners, J. Organomet. Chem., 1991, 414, C1–C4; (b) M. Liang and I. Manners, J. Am. Chem. Soc., 1991, 113, 4044–4045; (c) H. R. Allcock, J. A. Dodge, I. Manners and G. H. Riding, J. Am. Chem. Soc., 1991, 113, 9596–9603.
7. (a) F. B. J. Brisdon, M. F. Mahon, K. C. Molloy and P. J. Schofield, J. Organomet. Chem., 1992, 436, 11–22; (b) J. R. Hunt, C. J. Doonan, J. D. LeVangie, A. P. Cote and O. M. Yaghi, J. Am. Chem. Soc., 2008, 130, 11872–11873.
8. A. T. O'Dowd, T. R. Spalding, G. Ferguson, J. F. Gallagher and D. Reed, J. Chem. Soc., Chem. Commun., 1993, 1816–1817.
9. F. J. Feher, T. A. Budzichowski and J. W. Ziller, Inorg. Chem., 1992, 31, 5100–5105.
10. D. A. Foucher, A. J. Lough and I. Manners, Inorg. Chem., 1992, 31, 3034–3043.
11. M. A. Beckett, D. E. Hibbs, M. B. Hursthouse, K. M. Abdul Malik, P. Owen and K. S. Varma, J. Organomet. Chem., 2000, 595, 241–247.
12. M. Pascu, A. Ruggi, R. Scopelliti and K. Severin, Chem. Commun., 2013, 49, 45–47.
13. P. V. V. N. Kishore and V. Baskar, J. Organomet. Chem., 2013, 743, 83–86.
14. (a) W. Noll, Chemistry and Technology of the Silicones, Academic Press, New York, 1968; (b) E. E. Bostick, Ring-Opening Polym., 1969, 2, 327–430; (c) Siloxane Polymers, ed. E. E. Bostick, J. A. Semlyen and S. J. Clarson, Prentice-Hall, Englewood Cliffs, NJ, 1991.
15. (a) M. G. Voronkov, V. A. Klyuchnikov, E. V. Mironenko, G. N. Shvets, T. F. Danilova and Y. I. Khudobin, J. Organomet. Chem., 1991, 406, 91–100; (b) T. C. Kendrick, B. Parbhoo and J. W. White, Chem. Org. Silicon Compd., 1989, 2, 1289–1361.
16. (a) T. Kudo and S. Nagase, J. Am. Chem. Soc., 1985, 107, 2585–2589; (b) M. Cypryk and Y. Apeloig, Organometallics, 1997, 16, 5938–5949; (c) Y. Cai, K. Samedov, B. S. Dolinar, Z. Song, B. Z. Tang, C. Zhang and R. West, Organometallics, 2015, 34, 78–85.
17. (a) H. E. Goldbach and M. A. Wimmer, J. Plant Nutr. Soil Sci., 2007, 170, 39–48; (b) Z. M. Hudson and S. Wang, Acc. Chem. Res., 2009, 42, 1584–1596; (c) D. Li, H. Zhang and Y. Wang, Chem. Soc. Rev., 2013, 42, 8416–8433.
18. (a) M. Elbing and G. C. Bazan, Angew. Chem., Int. Ed., 2008, 47, 834–838; (b) E. Galbraitha and T. D. James, Chem. Soc. Rev., 2010, 39, 3831–3842; (c) S. J. Rowan, S. J. Cantrill, G. R. L. Cousins, J. K. M. Sanders and J. F. Stoddart, Angew. Chem., Int. Ed., 2002, 41, 898–952.
19. J. Beckmann, K. Jurkschat and M. Schurmann, Organometallics, 2001, 20, 5125–5133.
20. D. T. Hurd, R. C. Osthoff and M. L. Corrin, J. Am. Chem. Soc., 1954, 76, 249–252.
21. (a) Ring Opening Polymerization, ed. K. J. Ivin and T. Saegusa, Elsevier, New York, 1984; (b) Ring Opening Polymerization, ed. J. E. McGrath, ACS Symposium Series 266; (c) R. H. Grubbs and W. Tomas, Science, 1989, 243, 907–915.
22. A. G. A. Vent, S. E. Lawrence, M. M. Meehan, T. G. R. Ussell and T. R. Spalding, Collect. Czech. Chem. Commun., 2002, 67, 1051–1060.
23. S. G. Ferguson, S. E. Lawrence, L. A. Neville, B. J. O'Leary and T. R. Spalding, Polyhedron, 2007, 26, 2482–2492.
24. G. Wesela-Bauman, P. Ciećwierz, K. Durka, S. Luliński, J. Serwatowski and K. Woźniak, Inorg. Chem., 2013, 52, 10846–10859.
25. (a) A. T. O'Dowd, T. R. Spalding, G. Ferguson, J. F. Gallagher and D. Reed, J. Chem. Soc., Chem. Commun., 1993, 1816–1817; (b) J. G. Stark and H. G. Wallace, Chemistry Data Book, John Murray, London, 1975.
26. (a) P. Wei, D. A. Atwood and T. S. Keizer, Inorg. Chem., 1999, 38, 3914–3918; (b) L. A. Neville, T. R. Spalding and G. Ferguson, Angew. Chem., Int. Ed. Engl., 2000, 39, 3595–3598.
27. (a) M. Nishio, CrystEngComm, 2004, 6, 130–158; (b) Y. Umezawa, S. Tsuboyama, K. Honda and J. Uzawa, Bull. Chem. Soc. Jpn., 1998, 71, 1207–1213.
28. S. S. Patil, G. V. Muddapur, N. R. Patil, R. M. Melavanki and R. A. Kusanur, Spectrochim. Acta, Part A, 2015, 138, 85–91.
29. P. Kubelka and F. Z. Munk, Tech. Phys., 1931, 12, 593–601.
30. J. Tauc, R. Grigorovici and A. Vancu, Phys. Status Solidi B, 1966, 15, 627–637.
31. K. L. Fujdala, A. G. Oliver, F. J. Hollander and T. D. Tilley, Inorg. Chem., 2003, 42, 1140–1150.
32. L. Padmaja, C. Ravikumar, D. Sajan, I. Hubert Joe, V. S. Jayakumar, G. R. Pettit and O. Faurskov Nielsen, J. Raman Spectrosc., 2009, 40, 419–428.
33. (a) P. K. Chattaraj, U. Sarkar and D. R. Roy, Chem. Rev., 2006, 106, 2065–2091; (b) P. K. Chattaraj, S. Giri and S. Duley, Chem. Rev., 2011, 111, PR43–PR75.
34. R. G. Parr, L. V. Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924.
35. R. G. Parr and W. Yang, J. Am. Chem. Soc., 1984, 106, 4049–4050.
36. H. Saeidian and M. Sahandi, J. Mol. Struct., 2015, 1100, 486–495.
37. (a) H. C. Brown, U. S. Racherla and P. J. Pellechia, J. Org. Chem., 1990, 55, 1868–1874; (b) K. Omoto and H. Fujimoto, J. Org. Chem., 1998, 63, 8331–8336.
38. (a) O. Christiansen, J. Gauss and J. F. Stanton, J. Chem. Phys. Lett., 1999, 305, 147–155; (b) R. Zhang, B. Dub, G. Sun and Y. Sun, Spectrochim. Acta, Part A, 2010, 75, 1115–1124.
39. R. T. Lynch Jr, M. D. Levenson and N. Bloembergen, Phys. Lett. A, 1974, 50, 61–62.
40. D. A. Dixion and N. Matsuzawa, J. Phys. Chem., 1994, 98, 3967–3977.
41. (a) J. Beckmann, D. Dakternieks, A. Duthie, A. E. K. Lim and E. R. T. Tiekink, J. Organomet. Chem., 2011, 633, 149–156; (b) J. Beckmann, K. Jurkschat, D. Schollmeyer and M. Schurmann, J. Organomet. Chem., 1997, 543, 229–236.
42. APEX2 “Program for Data Collection on Area Detectors”, BRUKER AXS Inc., 5465 East Cheryl Parkway, Madison, WI, 53711–5373, USA.
43. SADABS, G. M. Sheldrick, “Program for absorption correction of area detector frames”, BRUKER AXS Inc., 5465 East cheryl parkway, Madison, WI 53711–5373 USA.
44. (a) G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122; (b) XT, XS, BRUKER AXS Inc., 5465 East Cheryl Parkway, Madison, WI 53711-5373 USA.
45. (a) A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13; (b) R. W. W. Hooft, L. H. Straver and A. L. Speak, J. Appl. Crystallogr., 2008, 41, 96–103.
46. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
47. R. G. Parr and Y. Weitao, Density-Functional Theory of Atoms and Molecules, Oxford University Press, 1994.
48. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
49. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
50. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
51. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
52. GaussView, Version 5.0.9, Dennington, Roy, Keith, Todd, Millam, John. Semichem Inc., Shawnee Mission, KS, 2009.

---

Footnote

† Electronic supplementary information (ESI) available: Optimized structures, UV-vis, fluorescence, DRS, Tauc's plot and TGA data, and all NMR (¹H, ¹³C, ²⁹Si and ¹¹B) spectra are available. CCDC 1046950–1046952. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ra02080a

---