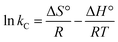DOI:
10.1039/C6RA00456C
(Paper)
RSC Adv., 2016,
6, 40354-40365
Fabrication of chitosan/silica nanofibrous adsorbent functionalized with amine groups for the removal of Ni(II), Cu(II) and Pb(II) from aqueous solutions: batch and column studies
Received
7th January 2016
, Accepted 31st March 2016
First published on 7th April 2016
Abstract
A chitosan/tetraethylorthosilicate/aminopropyl triethoxysilane (CS/TEOS/APTES) composite nanofibrous adsorbent was prepared via an electrospinning process. The performance of the prepared nanofibers was investigated for Ni(II), Cu(II) and Pb(II) ion sorption in single and ternary systems. The prepared nanofibers were characterized using FTIR, SEM and BET analysis. The effects of sorption parameters including pH, contact time, initial concentration and temperature were evaluated in a single system. The maximum sorption capacities for Ni(II), Cu(II) and Pb(II) ions onto the CS/TEOS/APTES nanofibrous adsorbent were found to be 696.2, 640.5 and 575.5 mg g−1 at an equilibrium time of 30 min and at 45 °C. The kinetic and equilibrium data were well described using pseudo-first-order kinetic and Langmuir isotherm models. The calculated thermodynamic parameters indicated a spontaneous and endothermic adsorption process. A Box–Behnken design was used to evaluate the effects of four parameters including pH and initial concentration of Ni(II), Cu(II) and Pb(II) ions on the sorption efficiency. The selectivity order of metal ions onto the CS/TEOS/APTES nanofibers was Ni(II) > Cu(II) > Pb(II) in a ternary system. In fixed bed column studies, the Ni(II), Cu(II) and Pb(II) sorption capacities were increased by increasing the flow rate up to 4 mL min−1. A Thomas model predicted well the adsorption capacity of metal ions in a fixed bed column. The removal efficiency of metal ions by the regenerated nanofibers did not significantly change in both batch and fixed-bed column studies.
1. Introduction
The removal of heavy metal ions from water and wastewater is of primary importance with respect to human health and environmental considerations. Several methods including chemical precipitation, membrane filtration, solvent extraction and adsorption have been used for the removal of heavy metal ions from aqueous solutions.1 The adsorption process, due to the low cost and higher efficiency, is commonly preferred.2,3 Nanofibers prepared using an electrospinning process, due to their unique properties including high specific surface area and high porosity with fine pores, have been widely applied in the adsorption process.4 In recent studies, nanofibrous adsorbents based on both synthetic and natural polymers such as polyvinyl alcohol (PVA),5–7 polyvinylpyrrolidone (PVP),8 polyacrylonitrile (PAN),9,10 cellulose11 and chitosan12–16 were used for the removal of heavy metal ions. Chitosan nanofibers, due to their higher surface area and ion exchange properties, have been used as an alternative adsorbent for metal ion sorption.14,15 The presence of hydroxyl and amino groups in the chitosan network allows for the uptake of heavy metal ions during chelation, electrostatic attraction or ion-exchange mechanisms. Furthermore, the chemical modification of chitosan nanofibers improves the removal efficiency towards metal ions.16,17 Functional groups such as Si–H, Si–OH and N–H groups in tetraethylorthosilicate (TEOS) as a silica precursor,6,18 and aminopropyl triethoxysilane (APTES) as an aminated silica precursor,6 have a significant effect on improving the adsorption efficiency. However, there is no study about the incorporation of TEOS and APTES into chitosan nanofibers and the subsequent investigation into the sorption behavior.
To investigate the simultaneous removal of metal ions onto the adsorbent, a statistical design of experiments was applied to reduce the number of experiments and allow consideration of the interactions in multivariable systems.19,20 Response surface methodology (RSM) is essentially a particular set of mathematical and statistical methods for developing, improving and optimizing processes. Recently, RSM was used for the optimization of the process conditions in the removal of heavy metal ions from aqueous solutions.21–23 RSM based on Central-Composite Design (CCD) and Box–Behnken Design (BBD) are commonly used as experimental design techniques.19,20 However, for a quadratic response surface model with three or more factors, the BBD technique is much more advantageous compared to CCD.20
In the present study, a CS/TEOS/APTES nanofibrous adsorbent was prepared via an electrospinning process and its application to the removal of Ni(II), Cu(II) and Pb(II) ions from aqueous solutions was investigated in batch and fixed bed column systems. The influence of pH, contact time, initial concentration and temperature on the adsorption process was evaluated in a single system. The nature of the adsorption process with respect to kinetics, isotherms and thermodynamic aspects was determined. The reusability of CS/TEOS/APTES was tested after five adsorption–desorption cycles. After the optimization of parameters for the maximum adsorption of metal ions, RSM based on BBD was used to evaluate the interaction effects of pH and the initial concentrations of Ni(II), Cu(II) and Pb(II) ions on the simultaneous adsorption of metal ions in a ternary system. The experimental data from the fixed bed column system were also fitted to the Thomas model. Desorption studies were carried out in both batch and fixed bed column systems.
2. Experimental
2.1. Materials
Chitosan (average Mw = 200 kD), TEOS (density = 940 kg m−3), APTES (99%), cetyltrimethylammonium bromide (CTAB), ethanol and HCl were purchased from Sigma-Aldrich. Deionized water was used throughout this work.
2.2. Preparation of CS/TEOS/APTES solution
A chitosan solution was prepared by dissolving chitosan in 0.5 M acetic acid under magnetic stirring conditions for 24 h at 30 °C. Then, TEOS and APTES were added to the chitosan solution.
The TEOS mixture was prepared by mixing CTAB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TEOS
TEOS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl
HCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O
H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol in the molar ratio of 1
ethanol in the molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1
0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50. For this, CTAB was mixed with water and ethanol for 10 min at 30 °C. Then, 20 wt% TEOS was added to the solution with stirring for a further 1 h. After that, HCl was dropped slowly into the solution to prepare the TEOS mixture. Then, 0.5 mL of APTES was added to the TEOS mixture and the stirring was continued for a further 1 h. Finally, the TEOS/APTES mixture was added to the chitosan solution with stirring for a further 6 h at 30 °C.
50. For this, CTAB was mixed with water and ethanol for 10 min at 30 °C. Then, 20 wt% TEOS was added to the solution with stirring for a further 1 h. After that, HCl was dropped slowly into the solution to prepare the TEOS mixture. Then, 0.5 mL of APTES was added to the TEOS mixture and the stirring was continued for a further 1 h. Finally, the TEOS/APTES mixture was added to the chitosan solution with stirring for a further 6 h at 30 °C.
2.3. Electrospinning process
In order to fabricate CS/TEOS/APTES nanofibers, the CS/TEOS/APTES solution was loaded into a 5 mL plastic syringe equipped with a syringe needle. After that, a high voltage was applied between the needle and the collector and CS/TEOS/APTES nanofibers were produced on the collector. A voltage of 25 kV, with a tip-collector distance of 12 cm, and a speed of 0.2 mL h−1 was applied to fabricate the nanofibers on the cylindrical collector. Then, 25% glutaraldehyde (GTA) vapor was used for the cross-linking of the CS/TEOS/APTES nanofibers. Finally, the nanofibers were dried at 30 °C for 24 h.
2.4. Characterization
The functional groups of the nanofibers were determined using Fourier transform infrared spectroscopy (Vector22-Bruker Company, Germany) in the range of 400–4000 cm−1.
The morphology of the nanofibers was determined using scanning electron microscopy (SEM, JEOL JSM-6380) after gold coating. The average diameter and diameter distribution of the nanofibers were obtained with an image analyzer (Image-Proplus, Media Cybernetics). From each image, at least 50 different fiber segments were randomly selected and their diameters were measured to generate an average fiber diameter.
The average pore diameter, specific surface area and pore volume of the prepared nanofibrous adsorbents were measured with nitrogen adsorption and the Brunauer–Emmett–Teller (BET) method on a Quantachrome Autosorb-1 instrument.
The final concentration of heavy metal ions in the adsorption medium was determined using an inductively coupled plasma atomic emission spectrophotometer (ICP-AES, Thermo Jarrel Ash, Model Trace Scan).
2.5. Adsorption experiments in a single system
Metal ion sorption onto the CS/TEOS/APTES nanofibers was carried out as a function of pH (2–7), contact time (0–60 min), initial concentration (20–1000 mg L−1) and temperature (25–45 °C) in a batch system. The sorption experiments were carried out in 250 mL flasks containing 50 mg of the adsorbent in 100 mL of metal ion solution (100 mg L−1) on a rotary shaker at 200 rpm for 1 h at different pH levels. For determining the effect of contact time on metal ion sorption, experiments were done by placing 50 mg of adsorbent in 100 mL of metal solution (100 mg L−1) at 25 °C and the optimum pH at definite time intervals. For examining the effect of the initial concentration of metal ions and temperature, 50 mg of nanofibrous sample was rinsed in 100 mL of metal ion solution with concentrations varying in the range of 20–1000 mg L−1 at three different temperatures (25, 35 and 45 °C) for 1 h.
For the regeneration of the nanofibrous adsorbents, the nanofibers were rapidly washed with 1 M HNO3 for 1 h and then were washed several times with deionized water. Desorption experiments were carried out with an initial metal concentration of 100 mg L−1 and an adsorbent dosage of 0.5 g L−1, at the optimum pH with a contact time of 1 h and at a temperature of 25 °C.
After that, the nanofibers were dried in an oven at 60 °C for 1 h. Each experiment was repeated in triplicate and the results are given as an average. The adsorption capacity (qe (mg g−1)) and removal percentage (R (%)) are calculated as follows:
| |
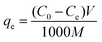 | (1) |
| |
 | (2) |
where
C0 and
Ce are the initial and equilibrium concentrations of metal ion solution in mg L
−1,
V is the volume of the solution in mL and
M is the weight of the adsorbent in g.
2.6. Design of experiments in a ternary system
The Box–Behnken design (BBD) is a class of rotatable second-order design based on three level incomplete factorial designs where the variable combinations are at the midpoints of the edges of the variable space and at the center. The number of experiments (N) needed for the development of BBD is defined as N = 2k(k − 1) + C0, where k is the factor number and C0 is the replicate number of the central point. In the current study, four factor three level BBD was used to determine the relation between variables containing pH (5–6) and the Ni(II), Cu(II) and Pb(II) initial concentration (20–100 mg L−1) on the removal of metal ions in a ternary system. A contact time of 30 min and a temperature of 45 °C were considered constants in the experiments. The polynomial model for the metal ion removal percentage is expressed as follows:| |
 | (3) |
where Y is the predicted response of the model and β0, βi, βii, βij are the constant regression coefficients of the model. Xi, Xii and Xij represent the linear, quadratic and interactive terms of the uncoded independent variables, respectively. The coefficient of determination (R2) was used to evaluate the accuracy of the full quadratic equation. The experimental design and results of the metal ion removal percentages onto the CS/TEOS/APTES nanofibrous adsorbent are presented in Table 1.
Table 1 Experimental design and results of metal ion sorption onto the CS/TEOS/APTES nanofibers
| Run number |
pH (X1) |
Ni(II) initial concentration (mg L−1) (X2) |
Cu(II) initial concentration (mg L−1) (X3) |
Pb(II) initial concentration (mg L−1) (X4) |
Ni(II) removal (%) |
Fitted value (%) |
Cu(II) removal (%) |
Fitted value (%) |
Pb(II) removal (II) |
Fitted value (%) |
| 1 |
5.0 |
20 |
60 |
60 |
93 ± 2 |
91 |
55 ± 2 |
56 |
50 ± 1 |
50 |
| 2 |
6.0 |
20 |
60 |
60 |
83 ± 3 |
87 |
59 ± 1 |
59 |
52 ± 2 |
52 |
| 3 |
5.0 |
100 |
60 |
60 |
61 ± 1 |
63 |
42 ± 2 |
43 |
37 ± 2 |
38 |
| 4 |
6.0 |
100 |
60 |
60 |
60 ± 2 |
60 |
48 ± 1 |
48 |
39 ± 2 |
40 |
| 5 |
5.5 |
60 |
20 |
20 |
68 ± 3 |
66 |
87 ± 2 |
86 |
82 ± 1 |
82 |
| 6 |
5.5 |
60 |
100 |
20 |
65 ± 2 |
65 |
37 ± 2 |
36 |
68 ± 2 |
68 |
| 7 |
5.5 |
60 |
20 |
100 |
66 ± 1 |
66 |
77 ± 1 |
78 |
32 ± 2 |
33 |
| 8 |
5.5 |
60 |
100 |
100 |
50 ± 2 |
51 |
30 ± 3 |
32 |
25 ± 2 |
26 |
| 9 |
5.0 |
60 |
60 |
20 |
66 ± 2 |
67 |
51 ± 2 |
53 |
69 ± 1 |
68 |
| 10 |
6.0 |
60 |
60 |
20 |
65 ± 1 |
64 |
55 ± 2 |
58 |
71 ± 1 |
70 |
| 11 |
5.0 |
60 |
60 |
100 |
59 ± 2 |
60 |
47 ± 3 |
48 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
23 |
| 12 |
6.0 |
60 |
60 |
100 |
56 ± 1 |
57 |
50 ± 2 |
51 |
26 ± 1 |
25 |
| 13 |
5.5 |
20 |
20 |
60 |
94 ± 2 |
93 |
86 ± 2 |
87 |
62 ± 2 |
61 |
| 14 |
5.5 |
100 |
20 |
60 |
62 ± 3 |
65 |
72 ± 3 |
74 |
52 ± 1 |
51 |
| 15 |
5.5 |
20 |
100 |
60 |
85 ± 2 |
85 |
37 ± 2 |
38 |
53 ± 2 |
52 |
| 16 |
5.5 |
100 |
100 |
60 |
59 ± 2 |
57 |
26 ± 1 |
28 |
39 ± 1 |
38 |
| 17 |
5.0 |
60 |
20 |
60 |
68 ± 2 |
68 |
81 ± 2 |
79 |
50 ± 2 |
51 |
| 18 |
6.0 |
60 |
20 |
60 |
66 ± 3 |
64 |
84 ± 3 |
82 |
52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ± ±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
53 |
| 19 |
5.0 |
60 |
100 |
60 |
58 ± 2 |
60 |
32 ± 2 |
30 |
40 ± 1 |
40 |
| 20 |
6.0 |
60 |
100 |
60 |
56 ± 1 |
56 |
37 ± 1 |
35 |
42 ± 1 |
42 |
| 21 |
5.5 |
20 |
60 |
20 |
92 ± 2 |
92 |
60 ± 2 |
59 |
81 ± 2 |
82 |
| 22 |
5.5 |
100 |
60 |
20 |
60 ± 3 |
64 |
55 ± 2 |
53 |
65 ± 1 |
65 |
| 23 |
5.5 |
20 |
60 |
100 |
86 ± 3 |
85 |
60 ± 3 |
58 |
30 ± 2 |
31 |
| 24 |
5.5 |
100 |
60 |
100 |
60 ± 2 |
58 |
45 ± 3 |
42 |
26 ± 1 |
25 |
| 25 |
5.5 |
60 |
60 |
60 |
64 ± 2 |
62 |
60 ± 1 |
60 |
50 ± 2 |
50 |
| 26 |
5.5 |
60 |
60 |
60 |
64 ± 2 |
62 |
59 ± 2 |
60 |
49 ± 3 |
50 |
| 27 |
5.5 |
60 |
60 |
60 |
63 ± 3 |
62 |
60 ± 1 |
60 |
50 ± 2 |
50 |
2.7. Adsorption experiments in fixed bed column
The fixed bed adsorption used in this study was performed in a glass column with a height of 100 mm and an internal diameter of 15 mm, filled with a known quantity (1 g) of the CS/TEOS/APTES nanofibrous adsorbent. The initial concentration of metal ions was held constant at 50 mg L−1 and the input flow rate was 1, 2, 4 and 6 mL min−1, controlled by a peristaltic pump. In order to investigate the desorption process, an experiment was carried out to desorb the previously adsorbed metal ions by passing 1 M HNO3 through the bed column containing the nanofibers.
3. Results and discussion
3.1. Characterization of the CS/TEOS/APTES nanofibers
The functional groups of the CS and CS/TEOS/APTES nanofibers were characterized using Fourier Transform Infrared (FTIR) spectroscopy. The results are shown in Fig. 1. The broad band in the 3200–3600 cm−1 region was assigned to O–H and N–H groups in the chitosan chain. The bands at 1650 and 1560 cm−1 correspond to the amino I and amino II functional groups of chitosan. The bands in the 1020–1100 cm−1 region are due to the presence of Si–O–Si and Si–O–C in the network of the CS/TEOS/APTES nanofibers. The peak at 780 cm−1 was assigned to the Si–C band in the CS/TEOS/APTES structure. The N–H stretching peak was observed at 1580 cm−1 which indicates that the APTES had been successfully added into the CS/TEOS/APTES structure.
 |
| | Fig. 1 FTIR spectra of pure chitosan and the CS/TEOS/APTES nanofibrous adsorbent. | |
SEM images of the pure CS and CS/TEOS/APTES nanofibers are shown in Fig. 2. As shown, homogeneous fibers with an average diameter of 90 nm were formed for pure CS, while an increase in fiber diameter was observed for the CS/TEOS/APTES nanofibers with an average diameter of 138 nm. This could be attributed to an increase in the viscosity of the solution resulting in the formation of thicker fibers compared with pure CS nanofibers. EDAX analysis of chitosan (Fig. 2c) and the CS/TEOS/APTES nanofibers (Fig. 2d) reveals the presence of silica and mercapto groups in the CS/TEOS/APTES structure.
 |
| | Fig. 2 SEM images of (a) chitosan and (b) the CS/TEOS/APTES nanofibrous adsorbent, and EDAX analysis of (c) chitosan and (d) the CS/TEOS/APTES nanofibers. | |
The SBET, pore volume and average pore diameter of pure CS and the CS/TEOS/APTES nanofibers were determined using the Brunauer–Emmett–Teller (BET) method. The results are shown in Table 2. Increasing the Si and N atoms of TEOS/APTES groups on the CS nanofibers causes a decrease in the adsorption of nitrogen molecules and results in a decrease in the SBET, pore volume and average pore diameter of CS/TEOS/APTES nanofibers compared with pure CS nanofibers.
Table 2 Physical properties of the prepared nanofibers
| Sample |
SBET (m2 g−1) |
Pore volume (cm3 g−1) |
Average diameter (nm) |
| CS |
310.2 |
0.482 |
3.98 |
| CS/TEOS/APTES |
272.3 |
0.431 |
3.52 |
Similar trends were reported by other researchers.25,26 They found that adding Si and N atoms into polymeric nanofibers led to a decrease in the SBET, pore volume and pore diameter of the nanofibers.
3.2. Batch adsorption experiments in a single mode
The effect of pH on Ni(II), Cu(II) and Pb(II) ion sorption on pure CS and CS/TEOS/APTES nanofibers is shown in Fig. 3. As shown, the adsorption capacities for metal ions onto the CS and CS/TEOS/APTES nanofibrous adsorbents reached maximum values at pH values of 5, 6 and 5.5 for Ni(II), Cu(II) and Pb(II) ion sorption, respectively. At lower pH values, the competition between hydrogen ions and metal ions in chelating with the anionic functional groups of the nanofibrous adsorbents leads to a decrease in the adsorption capacities for the metal ions onto both CS and the CS/TEOS/APTES nanofibers. At pH values above the optimum pH value, the formation of hydroxylated complexes of metal ions in the form of Ni(OH)2, Cu(OH)2 and Pb(OH)2 results in a decrease in the adsorption capacities for metal ions onto CS and the CS/TEOS/APTES nanofibers.18,24,25 Furthermore, metal ion sorption using the CS/TEOS/APTES nanofibrous adsorbent was higher than when using CS nanofibers. This behavior could be attributed to the incorporation of negative functional groups including siloxane, silanol and amine groups into the chitosan network which enhances the available active sites for the adsorption process. Also, the results showed that the adsorption capacity for different metal ions increased in the order of Pb(II) < Cu(II) < Ni(II). The ionic radius range of these ions are in the order of Ni(II) < Cu(II) < Pb(II). As the ionic radius increases due to a charge density decrease, the availability of active sites on the nanofibers for the adsorption process decreases; which results in a decrease in the adsorption capacity for different metal ions from an increase in the ionic radius.15 Therefore, pH values of 5, 6 and 5.5 were selected as optimum values for Ni(II), Cu(II) and Pb(II) ion sorption onto the CS/TEOS/APTES nanofibrous adsorbent for further experiments.
 |
| | Fig. 3 Effect of pH on the removal of metal ions using chitosan and CS/TEOS/APTES nanofibrous adsorbents. | |
The effect of contact time on the adsorption of Ni(II), Cu(II) and Pb(II) ions onto the CS/TEOS/APTES nanofibers is shown in Fig. 4. As shown, metal ion sorption onto the nanofibrous adsorbent reached equilibrium after only 30 min. Therefore, 30 min is selected as the equilibrium time for further experiments. Pseudo-first-order and pseudo-second-order kinetic models were used to describe the kinetic data from the metal ions using the CS/TEOS/APTES nanofibrous adsorbent. The kinetic equations are expressed as follows:27,28
| | |
Pseudo-first-order qt = qe(1 − exp(−k1t))
| (4) |
| |
 | (5) |
where
qt and
qe (mg g
−1) are the adsorption capacities for the metal ions at time
t and the equilibrium time, respectively.
k1 (min
−1) and
k2 (g mg
−1 min
−1) are the pseudo-first-order and pseudo-second-order rate constants, respectively. The results are presented in
Table 3. The results show that the pseudo-first-order kinetic model (
R2 > 0.994) well described the kinetic data for the metal ions on the CS/TEOS/APTES nanofibrous adsorbent.
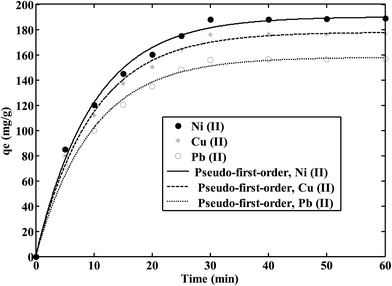 |
| | Fig. 4 Effect of contact time on metal ion sorption using the CS/TEOS/APTES nanofibrous adsorbent. | |
Table 3 Kinetic parameters of metal sorption onto the CS/TEOS/APTES nanofibrous adsorbent
| Metal ion |
Pseudo-first-order model |
Pseudo-second-order model |
| qeq (mg g−1) |
K1 (min−1) |
R2 |
qeq |
K2 (g mg−1 min−1) |
R2 |
| Ni2+ |
190.1 |
0.1025 |
0.994 |
223.0 |
0.000569 |
0.990 |
| Cu2+ |
177.9 |
0.1032 |
0.994 |
208.5 |
0.000615 |
0.989 |
| Pb2+ |
158.0 |
0.1039 |
0.995 |
185.0 |
0.000699 |
0.989 |
The effect of the initial concentration of metal ions on the adsorption capacity of the nanofibers at three different temperatures (25, 35 and 45 °C) is shown in Fig. 5. As shown, the metal ion sorption capacity was increased by increasing the temperature which indicates that the adsorption process onto the CS/TEOS/APTES nanofibrous adsorbent was favorable at higher temperatures. The known Freundlich and Langmuir isotherm models were used to describe the equilibrium data of metal ion sorption using CS/TEOS/APTES nanofibers.
 |
| | Fig. 5 Effect of the initial concentration of metal ions on the removal of (a) Ni(II), (b) Cu(II) and (c) Pb(II) onto the CS/TEOS/APTES nanofibrous adsorbent. | |
The isotherm equations are expressed as follows:29–31
| |
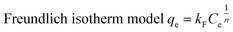 | (6) |
| |
 | (7) |
where
kF (mg g
−1) and
n are Freundlich parameters related to the sorption capacity and intensity of the sorbent, respectively.
qm (mg g
−1) and
b (mg
−1) are the Langmuir model constants.
qm is the maximum value of metal ion adsorption per unit weight of adsorbent that is related to the monolayer adsorption capacity and b is related to the enthalpy of adsorption. The parameters of the isotherm models were calculated using nonlinear regression of qe versus Ce using MATLAB software. The results are shown in Table 4. By comparing the correlation coefficients, it was found that the equilibrium data was best described using the Langmuir isotherm model (R2 > 0.984) compared with Freundlich (R2 > 0.911) isotherm model. This behavior indicated the monolayer reaction of metal ions when using the CS/TEOS/APTES nanofibers. Furthermore, the adsorption of metal ions increased slightly as the temperature increased from 25 to 45 °C at higher concentrations of Ni(II), Cu(II) and Pb(II) ions. This indicates that a high temperature favors the adsorption process when using the CS/TEOS/APTES nanofibrous adsorbent at higher initial concentrations of metal ions.
Table 4 Isotherm parameters for metal adsorption onto the CS/TEOS/APTES nanofibrous adsorbent
| Metal |
T (°C) |
Freundlich isotherm |
Langmuir isotherm |
| KF (mg g−1) |
n |
R2 |
qmax (mg g−1) |
KL (L mg−1) |
R2 |
| Ni2+ |
25 |
148.3 |
4.081 |
0.901 |
662.0 |
0.06451 |
0.998 |
| 35 |
167.2 |
4.273 |
0.909 |
684.9 |
0.08157 |
0.998 |
| 45 |
189.4 |
4.566 |
0.911 |
696.2 |
0.11420 |
0.997 |
| Cu2+ |
25 |
111.2 |
3.564 |
0.888 |
619.3 |
0.03870 |
0.997 |
| 35 |
123.8 |
3.817 |
0.892 |
630.0 |
0.04721 |
0.998 |
| 45 |
145.4 |
4.150 |
0.884 |
640.5 |
0.06173 |
0.992 |
| Pb2+ |
25 |
72.4 |
3.191 |
0.929 |
553.7 |
0.01964 |
0.995 |
| 35 |
77.8 |
3.248 |
0.940 |
570.0 |
0.02041 |
0.994 |
| 45 |
88.9 |
3.441 |
0.941 |
575.5 |
0.02356 |
0.990 |
The thermodynamic parameters including Gibbs free energy change (ΔG°), entropy change (ΔS°) and enthalpy change (ΔH°) for metal ions sorption using CS/TEOS/APTES nanofibrous adsorbents were evaluated using the following equations:
| |
 | (8) |
| |
ΔG° = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kC kC
| (9) |
| |
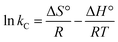 | (10) |
where
R (kJ mol
−1 K
−1) is the gas constant, and
T (K) is the temperature.
Ces and
Cel are the values of the solid and liquid phase concentration at equilibrium (mg L
−1) respectively. The thermodynamic parameters are summarized in
Table 5. The negative values of Δ
G° show the spontaneous nature of metal sorption using the CS/TEOS/APTES nanofibrous adsorbent. The positive values of Δ
H° indicate the endothermic nature of metal ion sorption using the nanofibrous adsorbent. The positive values of Δ
S° show that randomness was increased at the solid-solution interface.
Table 5 Thermodynamic parameters for metal adsorption onto the CS/TEOS/APTES nanofibrous adsorbent
| Metal |
KC |
ΔH° kJ mol−1 |
ΔS° kJ mol−1 K−1 |
ΔG° kJ mol−1 |
| 25 °C |
35 °C |
45 °C |
25 °C |
35 °C |
45 °C |
| Ni2+ |
73.07 |
121.57 |
156.21 |
30.03 |
0.1370 |
−10.632 |
−12.293 |
−13.355 |
| Cu2+ |
19.10 |
29.65 |
42.88 |
31.89 |
0.1315 |
−7.308 |
−8.680 |
−9.937 |
| Pb2+ |
11.66 |
19.33 |
31.89 |
39.62 |
0.1533 |
−6.0853 |
−7.584 |
−9.154 |
The result of five cycles of adsorption/desorption of metal ions onto the CS/TEOS/APTES nanofibrous adsorbent is shown in Fig. 6. The results show that the sorption capacities for metal ions using the CS/TEOS/APTES nanofibrous adsorbent were slightly decreased after five adsorption/desorption cycles. The reduction in the adsorption capacity of the nanofibers for metal ion sorption could be attributed to physically losing some functional groups from the CS/TEOS/APTES nanofibrous adsorbent (such as Si–H, Si–OH and N–H) through acid cleavage.
 |
| | Fig. 6 Five cycles of metal ion adsorption–desorption using the CS/TEOS/APTES nanofibrous adsorbent. | |
The maximum sorption capacities of metal ions onto the CS/TEOS/APTES nanofibrous adsorbent were compared with those of other nanofibrous adsorbents whose results are presented in Table 6. As shown, the sorption capacities for metal ions onto the CS/TEOS/APTES nanofibers were found to be comparable and moderately higher than those of many corresponding sorbents in the literature.10,11,14–17,32–34 The higher surface area and greater number of functional groups on the prepared nanofibers, including Si–H, Si–OH and N–H groups in the CS/TEOS/APTES structure, may be responsible for the higher sorption of metal ions using the CS/TEOS/APTES nanofibrous adsorbent.
Table 6 Comparison of the adsorption capacities (mg g−1) of synthesized CS/TEOS/APTES nanofibers for metal ions sorption with other nanofibrous adsorbents reported in the literature
| Adsorbent |
Adsorption capacity of Ni(II) (mg g−1) |
Adsorption capacity of Cu(II) (mg g−1) |
Adsorption capacity of Pb(II) (mg g−1) |
Reference |
| Amidoxime-PAN |
— |
52.70 |
263.45 |
10 |
| Aminated-PAN |
— |
116.20 |
— |
11 |
| Chitosan |
— |
485.44 |
263.15 |
14 |
| PEO/chitosan |
357.10 |
310.20 |
237.20 |
15 |
| Chitosan/hydroxyapatite |
180.20 |
— |
296.70 |
16 |
| Lead-chitosan |
— |
— |
577.00 |
17 |
| PVA/ZnO |
94.43 |
162.80 |
— |
31 |
| PAN/cellulose/thiol |
— |
— |
137.70 |
32 |
| Chitin |
135.00 |
— |
302.51 |
33 |
| CS/TEOS/APTES |
715.70 |
715.70 |
579.10 |
This study |
3.3. Batch adsorption experiments in a ternary system
Analysis of variance (ANOVA) was performed to estimate the significance of the model and terms. P values lower than 0.05 indicated the significance of the terms in the surface response analysis. The results are presented in Table 7. As shown, the linear terms as well as some quadratic and interaction terms exhibited a significant effect on the metal ion sorption efficiency using the CS/TEOS/APTES nanofibers (p < 0.05). Through the elimination of insignificant terms (p > 0.05) from the full quadratic model, the equations (11)–(13) for Ni(II) (R1), Cu(II) (R2) and Pb(II) (R3) removal percentages (%) were obtained, as follows:| | |
R1 = 62.067 − 1.833X1 − 13.667X2 − 3.917X3 − 3.417X4 + 12.933X22 − 3.250X3X4
| (11) |
| | |
R2 = 60.741 + 2.083X1 − 5.750X2 − 24.000X3 − 3.000X4 − 4.819X12 − 4.319X22 − 3.194X42 − 2.500X2X4
| (12) |
| | |
R3 = 49.481 + 1.000X1 − 5.833X2 − 5.250X3 − 22.750X4 − 4.389X12 + 1.236X32 + 1.486X42 + 3.000X2X4 + 1.750X3X4
| (13) |
Table 7 ANOVA results for (a) Ni(II), (b) Cu(II) and (c) Pb(II) ions sorption onto the CS/TEOS/APTES nanofibrous adsorbent
| (a) Source |
F |
P |
| Regression |
67.02 |
0.000 |
| Linear |
161.46 |
0.000 |
| X1 |
10.00 |
0.008 |
| X2 |
555.51 |
0.000 |
| X3 |
45.62 |
0.000 |
| X4 |
34.72 |
0.000 |
| Square |
69.76 |
0.000 |
| X12 |
1.11 |
0.313 |
| X22 |
201.07 |
0.000 |
| X32 |
2.21 |
0.163 |
| X42 |
0.83 |
0.381 |
| Interaction |
2.23 |
0.112 |
| X1X2 |
0.56 |
0.470 |
| X1X3 |
0.56 |
0.470 |
| X1X4 |
0.25 |
0.628 |
| X2X3 |
0.56 |
0.470 |
| X2X4 |
0.99 |
0.339 |
| X3X4 |
10.47 |
0.007 |
| Lack-of-fit |
14.32 |
0.067 |
| Total |
|
|
| (b) Source |
F |
P |
| Regression |
90.78 |
0.000 |
| Linear |
307.29 |
0.000 |
| X1 |
8.57 |
0.013 |
| X2 |
65.29 |
0.000 |
| X3 |
1137.52 |
0.000 |
| X4 |
17.77 |
0.001 |
| Square |
9.12 |
0.001 |
| X12 |
17.12 |
0.001 |
| X22 |
13.46 |
0.003 |
| X32 |
1.28 |
0.280 |
| X42 |
6.84 |
0.023 |
| Interaction |
0.87 |
0.543 |
| X1X2 |
0.16 |
0.692 |
| X1X3 |
0.16 |
0.692 |
| X1X4 |
0.04 |
0.843 |
| X2X3 |
0.37 |
0.554 |
| X2X4 |
4.11 |
0.049 |
| X3X4 |
0.37 |
0.554 |
| Lack-of-fit |
21.68 |
0.045 |
| Total |
|
|
| (c) Source |
F |
P |
| Regression |
371.87 |
0.000 |
| Linear |
1259.43 |
0.000 |
| X1 |
8.68 |
0.012 |
| X2 |
295.48 |
0.000 |
| X3 |
239.34 |
0.000 |
| X4 |
4494.21 |
0.000 |
| Square |
32.66 |
0.000 |
| X12 |
76.71 |
0.000 |
| X22 |
0.17 |
0.690 |
| X32 |
5.25 |
0.041 |
| X42 |
7.75 |
0.017 |
| Interaction |
6.30 |
0.003 |
| X1X2 |
0.00 |
1.000 |
| X1X3 |
0.00 |
1.000 |
| X1X4 |
0.00 |
1.000 |
| X2X3 |
2.89 |
0.115 |
| X2X4 |
26.05 |
0.000 |
| X3X4 |
8.86 |
0.012 |
| Lack-of-fit |
4.77 |
0.185 |
| Total |
|
|
The high values of R2 (R12 > 0.97, R22 > 0.96 and R32 > 0.99 for Ni(II), Cu(II) and Pb(II)) indicate the high reliability of the model in predicting the removal percentages of metal ions. The probability distribution plots of residuals (the difference between the model predictions and those derived experimentally) for the metal ion removal percentages (%) are shown in Fig. 7. As shown, for all of the results, the errors were normally distributed which indicates that the predicted models fit all the experimental data of metal ion removal percentages (%) well.
 |
| | Fig. 7 Probability distribution plot of residuals for (a) Ni(II), (b) and (c) Cu(II) and Pb(II) sorption onto the CS/TEOS/APTES nanofibrous adsorbent. | |
By solving the statistical models and optimizing the variables, the optimal uncoded values of pH (X1), initial Ni(II) concentration (X2), initial Cu(II) concentration (X3) and initial Pb(II) concentration (X4) were estimated to be an initial concentration of 20 mg L−1 at pH values of 5.0, 6.0 and 5.56 for Ni(II), Cu(II) and Pb(II) ions removal, respectively. The optimum predicted values for metal ion removal percentages were estimated to be 94.4, 90.8 and 85.7%, respectively. The experimental values for Ni(II), Cu(II) and Pb(II) removal percentages under optimum conditions were found to be 95, 90 and 85%, respectively. These values were in good agreement with the estimated values from the model under optimum conditions.
The simultaneous relation between the metal ion initial concentration and the adsorption capacity for metal ions is shown in Fig. 8. As shown, the effect of Ni(II) ions on the Cu(II) and Pb(II) removal percentages onto the CS/TEOS/APTES nanofibrous adsorbent was more than that of Cu(II) and Pb(II) ion effects on the Ni(II) removal percentage. Also, the sorption selectivity of Ni(II), Cu(II) and Pb(II) ions onto the CS/TEOS/APTES nanofibrous adsorbent was in order of Ni(II) > Cu(II) > Pb(II) in the ternary system. The lower ionic radius of Ni(II) ions (Ni(II) < Cu(II) ≪ Pb(II)) could be responsible for the easier availability of Ni(II) ions for chelating with the active sites of the nanofibrous adsorbent compared with Cu(II) and Pb(II) ions.
 |
| | Fig. 8 Surface plots of the simultaneous effect of initial concentration on the sorption efficiency of (a–c) Ni(II); (d–f) Cu(II) and (g–i) Pb(II) ions onto the CS/TEOS/APTES nanofibrous adsorbent. | |
3.4. Adsorption experiments in a fixed bed column
The breakthrough curves of metal ion sorption using the CS/TEOS/APTES nanofibrous adsorbent at different flow rates are illustrated in Fig. 9. As shown, the breakthrough time decreased with an enhancement in the flow rate. This behavior could be attributed to the insufficient residence time of the solute in the column, which caused the metal solutions to leave the column before equilibrium occurred. Also, the removal percentages of metal ions were lower in the fixed bed column compared with metal ion sorption in batch mode. This was because the metal ions flowing through the column did not reach equilibrium. Moreover, the metal ion sorption capacities were increased by increasing the flow rate up to 4 mL min−1. The results show that Ni(II), Cu(II) and Pb(II) ion sorption onto the nanofibrous adsorbent could be controlled by diffusion limitations of the solute into the pores of the sorbent. When the flow rate increased from 4 to 6 mL min−1, the liquid residence time in the column decreased and following this the sorption capacity decreased. Also, the time to reach the plateau of Ct/C0 was significantly higher for Pb(II) than Ni(II) and Cu(II).
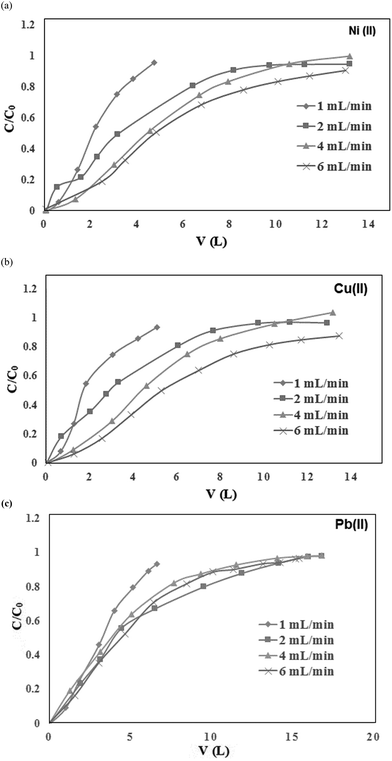 |
| | Fig. 9 Breakthrough curves of (a) Ni(II), (b) Cu(II) and (c) Pb(II) ion sorption onto the CS/TEOS/APTES nanofibers. | |
The known Thomas model predicted the adsorption capacity of Ni(II), Cu(II) and Pb(II) ions using CS/TEOS/APTES. The Thomas model assumes that the rate driving force obeys second order reversible reaction kinetics, and the adsorption equilibrium follows the Langmuir model.35 The Thomas model is expressed as follows:
| |
 | (14) |
where
C0 (mg L
−1) and
Ct (mg L
−1) are the initial concentration and final concentration at time
t, respectively;
M is the mass of adsorbent (g) and
Q is the filtration flow rate.
kTh is the Thomas rate constant (l min
−1 g
−1) and
q0 is the maximum uptake capacity (mg g
−1). The model parameters
kTh and
q0 can be estimated by non-linear fitting to the experimental data of the breakthrough curves. The model constants (
kTh and
q0) and correlation coefficients are presented in
Table 8 (figure is not shown). As shown, a decrease in
kTh and increase in
q0 was obtained by increasing the flow rate up to 4 mL min
−1. Based on the obtained results of the correlation coefficients (
R2 > 0.98), it was found that the Thomas model was able to describe the complete breakthrough curves. Furthermore, the Thomas model predicted that the adsorption capacities (
Table 8) follow the same order as the batch Langmuir adsorption capacities (
Table 4) for the different metal ions using the CS/TEOS/APTES nanofibers.
Table 8 Parameters obtained from the non-linear fit of the breakthrough data to the Thomas model
| Metal |
Q (mL min−1) |
Thomas model |
| kTh (l g−1 min−1) |
q0 (mg g−1) |
R2 |
| Pb(II) |
1 |
0.0278 |
453.21 |
0.981 |
| 2 |
0.0234 |
490.45 |
0.983 |
| 4 |
0.0205 |
504.53 |
0.990 |
| 6 |
0.0223 |
518.23 |
0.982 |
| Ni(II) |
1 |
0.0218 |
510.11 |
0.990 |
| 2 |
0.0204 |
530.75 |
0.992 |
| 4 |
0.0196 |
560.11 |
0.986 |
| 6 |
0.0205 |
580.39 |
0.980 |
| Cu(II) |
1 |
0.0268 |
500.19 |
0.993 |
| 2 |
0.0244 |
518.17 |
0.994 |
| 4 |
0.0209 |
540.98 |
0.990 |
| 6 |
0.0218 |
555.63 |
0.989 |
Five cycles of adsorption–desorption of metal ions onto the CS/TEOS/APTES nanofibrous adsorbent were carried out at the initial Ni(II), Cu(II) and Pb(II) concentration of 60 mg L−1. Desorption of metal ions from the nanofibrous adsorbent occurred when it was treated with 1 M HNO3, the results of which are illustrated in Fig. 10. As shown, the lack of change in nanofibers efficiency for metal ions removal was observed after five adsorption–desorption cycles.
 |
| | Fig. 10 Five cycles of adsorption–desorption of Ni(II), Cu(II) and Pb(II) ions onto the nanofibrous adsorbent in a fixed bed column system. | |
4. Conclusion
In the present study, the performance of a CS/TEOS/APTES nanofibrous adsorbent was investigated for the removal of Ni(II), Cu(II) and Pb(II) metal ions. The pH values of 5, 6 and 5.5 resulted in the maximum sorption capacities for Ni(II), Cu(II) and Pb(II) ions onto the CS/TEOS/APTES nanofibrous adsorbent at an equilibrium time of 30 min and temperature of 45 °C. The kinetic data for the Ni(II), Cu(II) and Pb(II) ions were well fitted using a pseudo-first-order kinetic model, while the equilibrium data were well described using the Langmuir isotherm model. Then, 27 experiments based on BBD for four factors at three levels were used to determine the effects of pH and initial concentration of metal ion on the removal efficiency of the CS/TEOS/APTES nanofibrous adsorbent. The results showed the selectivity order of metal ions onto the CS/TEOS/APTES nanofibers was Ni(II) > Cu(II) > Pb(II) in a ternary system. The inhibitory effect was increased by an increase in the initial concentration of metal ion. This study showed the CS/TEOS/APTES nanofibers as a promising adsorbent with high efficiency for the adsorption process. In fixed bed column studies, the efficiency increased with an increasing flow rate up to 4 mL min−1. The removal efficiencies of Ni(II), Cu(II) and Pb(II) ions, using the regenerated CS/TEOS/APTES nanofibers, did not remarkably change in both batch and fixed-bed column systems.
References
- M. Nourbakhsh, S. Illhan and H. Ozdag, Chem. Eng. J., 2002, 85, 351 CrossRef.
- M. Irani, M. Amjadi and M. A. Mousavian, Chem. Eng. J., 2011, 178, 317 CrossRef CAS.
- A. Sari, M. Tuzen and M. Soylak, J. Hazard. Mater., 2007, 144, 41 CrossRef CAS PubMed.
- C. S. Ki, E. H. Gang, I. C. Um and Y. H. Park, J. Membr. Sci., 2007, 302, 20 CrossRef CAS.
- L. Roshanfekr Rad, A. Momeni, B. Farshi Ghazani, M. Irani, M. Mahmoudi and B. Noghreh, Chem. Eng. J., 2014, 256, 119 CrossRef.
- M. Irani, A. R. Keshtkar and M. A. Moosavian, Chem. Eng. J., 2012, 200–202, 192 CrossRef CAS.
- A. R. Keshtkar, M. Irani and M. A. Moosavian, J. Radioanal. Nucl. Chem., 2013, 295, 563 CrossRef CAS.
- M. Teng, H. Wang, F. Li and B. Zhang, J. Colloid Interface Sci., 2011, 355, 23 CrossRef CAS PubMed.
- A. Dastbaz and A. R. Keshtkar, Appl. Surf. Sci., 2014, 293, 336 CrossRef CAS.
- K. Saeed, S. Haider, T. J. Oh and S. Y. Park, J. Membr. Sci., 2008, 322, 400 CrossRef CAS.
- X. He, L. Cheng, Y. Wang, J. Zhao, W. Zhang and C. Lu, Carbohydr. Polym., 2014, 111, 683 CrossRef CAS PubMed.
- A. Razzaz, S. Ghorban, L. Hosayni, M. Irani and M. Aliabadi, J. Taiwan Inst. Chem. Eng., 2016, 58, 333 CrossRef CAS.
- H. Beheshti, M. Irani, L. Hosseini, A. Rahimi and M. Aliabadi, Chem. Eng. J., 2016, 284, 557 CrossRef CAS.
- H. H. Najafabadi, M. Irani, L. R. Rad, A. H. Haratameh and I. Haririan, RSC Adv., 2015, 5, 16532 RSC.
- M. Aliabadi, M. Irani, J. Ismaeili, H. Piri and M. J. Parnian, Chem. Eng. J., 2013, 220, 237 CrossRef CAS.
- M. Aliabadi, M. Irani, J. Ismaeili and S. Najafzadeh, J. Taiwan Inst. Chem. Eng., 2014, 45, 518 CrossRef CAS.
- Y. Li, T. Qiu and X. Xu, Eur. Polym. J., 2013, 49, 1487 CrossRef CAS.
- M. Irani, A. R. Keshtkar and M. A. Mousavian, Chem. Eng. J., 2011, 175, 251 CrossRef CAS.
- R. H. Myers, D. C. Montgomery and C. M. Anderson-Cook, Response surface methodology: process and product optimization using designed experiments, New York (NY), Wiley, 2009 Search PubMed.
- M. D. Mobarake, P. Jafari and M. Irani, Microporous Mesoporous Mater., 2016 DOI:10.1016/j.micromeso.
- Y. Zheng and A. Wang, Chem. Eng. J., 2010, 162, 186 CrossRef CAS.
- J. Landaburu-Aguirre, E. Pongrácz, P. Perämäki and R. L. Keiski, J. Hazard. Mater., 2010, 180, 524 CrossRef CAS PubMed.
- F. Gönena and Z. Aksu, J. Hazard. Mater., 2009, 172, 1512 CrossRef PubMed.
- A. R. Keshtkar, M. Irani and M. A. Moosavian, J. Taiwan Inst. Chem. Eng., 2013, 44, 279 CrossRef CAS.
- X. Xue and F. Li, Microporous Mesoporous Mater., 2008, 116, 116 CrossRef CAS.
- M. Irani, A. R. Keshtkar and M. A. Mousavian, Korean J. Chem. Eng., 2012, 29, 1459 CrossRef CAS.
- S. Lagergren, K. Sven. Vetenskapsakad. Handl., 1898, 24, 1 Search PubMed.
- Y. S. Ho and G. McKay, Process Biochem., 1999, 34, 451 CrossRef CAS.
- H. M. F. Freundlich, J. Am. Chem. Soc., 1906, 57, 385 CAS.
- I. Langmuir, J. Am. Chem. Soc., 1916, 38, 2221 CrossRef CAS.
- O. Redlich and D. I. Peterson, J. Phys. Chem., 1959, 63, 1024 CrossRef CAS.
- H. Hallaji, A. R. Keshtkar and M. A. Moosavian, J. Taiwan Inst. Chem. Eng., 2015, 46, 109 CrossRef CAS.
- R. Yang, K. B. Aubrecht, H. Ma, R. Wang, R. B. Grubbs, B. S. Hsiao and B. Chu, Polymer, 2014, 55, 1167 CrossRef CAS.
- D. Liu, Y. Zhu, Z. Li, D. Tian, L. Chen and P. Chen, Carbohydr. Polym., 2013, 98, 483 CrossRef CAS PubMed.
- H. C. Thomas, Ann. N. Y. Acad. Sci., 1948, 49, 161 CrossRef CAS PubMed.
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) TEOS
TEOS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl
HCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O
H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethanol in the molar ratio of 1
ethanol in the molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1
0.1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200
200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50. For this, CTAB was mixed with water and ethanol for 10 min at 30 °C. Then, 20 wt% TEOS was added to the solution with stirring for a further 1 h. After that, HCl was dropped slowly into the solution to prepare the TEOS mixture. Then, 0.5 mL of APTES was added to the TEOS mixture and the stirring was continued for a further 1 h. Finally, the TEOS/APTES mixture was added to the chitosan solution with stirring for a further 6 h at 30 °C.
50. For this, CTAB was mixed with water and ethanol for 10 min at 30 °C. Then, 20 wt% TEOS was added to the solution with stirring for a further 1 h. After that, HCl was dropped slowly into the solution to prepare the TEOS mixture. Then, 0.5 mL of APTES was added to the TEOS mixture and the stirring was continued for a further 1 h. Finally, the TEOS/APTES mixture was added to the chitosan solution with stirring for a further 6 h at 30 °C.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1



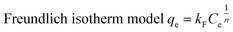


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kC
kC