Enhanced piezoelectric properties and constricted hysteresis behaviour in PZT ceramics induced by Li⁺–Al³⁺ ionic pairs

Abstract

Recently, we proposed a new approach (Li⁺–Al³⁺ ionic pairs doping) to enhance the piezoelectric properties of BaTiO₃ ceramic. Here we sequentially prove that Li⁺ and Al³⁺ can also enhance the piezoelectric properties of PbZr_0.52Ti_0.48O₃ (PZT) ceramic. The X-ray diffraction results demonstrate the optimized distribution of Li⁺–Al³⁺ ionic pairs parallel to the [001] direction in the doped ceramics, as same as the results in BaTiO₃-based ceramic. The doped ceramics exhibit constricted hysteresis loops, which is associated with the restoring force of Li⁺–Al³⁺ ionic pairs as a result of the Coulomb force between Li⁺ and Al³⁺ ions. The results show that the piezoelectric properties and corresponding temperature stability of the doped ceramics were enhanced significantly. The analysis and conclusion indicate that the piezoelectric mechanism coming from ionic pairs applies equally well to the PZT ceramic. Co-doping Li⁺ and Al³⁺ into the A-site is a preferable approach for the piezoelectric property enhancement of ABO₃ ferroelectric ceramics.

---

Introduction

Piezoelectric materials are used in sensor and actuator technologies because of their ability to couple electrical and mechanical displacement, resulting in electrical polarization changes in response to applied mechanical stress and/or strain that can generate an electric field.^1,2 Actuator applications require a high piezoelectric constant and electromechanical coupling providing high strain with high force, for example ultrasonic motors.^1,2 It is well known that phase instabilities are responsible for optimizing the piezoelectric and dielectric properties of ferroelectric ceramics, and have thus been of great interest to the ferroelectric community for more than half a century. Usually, there are two kinds of methods to obtain high piezoelectric properties in the ABO₃-type piezoelectric ceramic.

One is to design a morphotropic phase boundary (MPB) in the ABO₃ systems, as in the case for PbZrO₃–PbTiO₃ (PZT).³ It is well known that Jaffe et al. introduced the concept of MPB from the PZT system in an unlimited range solid solution of PbTiO₃ and PbZrO₃.³ The enhancement of the piezoelectric properties in PZT occurs near the boundary of the composition–temperature phase diagram where crystal structure changes from tetragonal (T) to rhombohedral (R).⁴ This boundary is known as the MPB which is nearly vertical along the temperature scale.⁵ According to the large piezoelectric mechanism found in the PZT, researchers began to investigate the possibility of MPB in the lead-free piezoelectric ceramic by doping various ABO₃-type perovskite, such as (Bi_1/2Na_1/2)TiO₃–BaTiO₃ and Ba(Zr_0.2Ti_0.8)O₃–(Ba_0.7Ca_0.3)TiO₃ systems. (Bi_1/2Na_1/2)TiO₃–BaTiO₃ (BNT–BT) system has been of great interest since the discovery of an MPB, where a rhombohedral and a tetragonal symmetry coexist.^6–8 The interest has arisen largely because the MPB was reported to separate the rhombohedral BNT and the tetragonal BT as in PZT, accompanied by a significant enhancement in the dielectric permittivity and electromechanical coupling factor as well as piezoelectric properties. Another important lead-free piezoelectric system that includes MPB was found and developed in Ba(Zr_0.2Ti_0.8)O₃–(Ba_0.7Ca_0.3)TiO₃ (BZT–BCT) system, where high piezoelectricity starts from a point of a paraelectric cubic phase (C), ferroelectric rhombohedral (R), and tetragonal (T) phases.^9–11 This point was further proved to be a tricritical point by the vanishing thermal hysteresis and highest transition permittivity peak at the point. In the vicinity of triple critical point, the system has a flattened energy landscape and consequently a low energy barrier for polarization rotation. In terms of previous studies, several essential characteristics which a MPB should possess can be recapitulated as follows. Firstly, two different end members with almost the same type of structure could form an unlimited solid solution and in the MPB region it has the characteristic of compositional homogeneity.^4,6 Secondly, although a MPB was initially defined as a boundary with equal amounts of two separated phases with similar structure, in fact, the exact composition location of the MPB was hardly determined. Therefore, in fact, the MPB represents a narrow composition region with the coexistence of two different phases or a transitional phase with lower symmetry.^5,12,13

Another method to obtain high piezoelectric properties is to design polymorphic phase transition (PPT) in a composition system. A typical PPT was found in K_0.5Na_0.5NbO₃ (KNN) solid solution.^14–17 The enhanced properties of the KNN-based piezoelectric ceramics are related to the process of PPT, which also known as the orthorhombic-tetragonal ferroelectric phase transition. By shifting the phase transition temperature T_O–T downward, it leads to the coexistence of the orthorhombic phase and the tetragonal phase at room temperature, and exhibits the analogous effect of a morphotropic phase boundary in the PZT system.¹⁸ Considering previous studies, several essential characteristics which a PPT should possess can be recapitulated as follows. On the one hand, two ferroelectric phases should coexist at room temperature, which is beneficial to polarization rotation and piezoelectric effect. On the other hand, the high piezoelectric properties induced by PPT are very sensitive to temperature since the coexistence stage of two ferroelectric phases will disappear with the temperature increasing.^17,19

Recently, an easy and novel method (neither the MPB nor the PPT) is proposed to achieve high piezoelectric properties in the ABO₃ ferroelectrics.^20–22 Our recent work indicates that the replacement of Ba²⁺ by the smaller Li⁺ and Al³⁺ ions in the A-sites can form Li⁺–Al³⁺ ionic pairs and greatly improve the piezoelectric properties of BaTiO₃-based ceramics.²⁰ The reason why we choose the Li⁺ and Al³⁺ is discussed in ESI.† XRD results proved precisely the optimized distribution of Li⁺–Al³⁺ ionic pairs parallel to the [001] direction in the lattice. After the comprehensive analysis, we proposed a new approach to obtain large piezoelectric effect, which is associated with appropriate ionic pairs doping. In this study, similar research process has been applied for the PZT system. The XRD patterns demonstrate the same distribution of Li⁺–Al³⁺ ionic pairs compared with BaTiO₃ ceramic doped by Li⁺–Al³⁺ ionic pairs. Above all, we discovered a kind of dipole polarization existing in the doped PZT ceramic, which resulted in constricted hysteresis loops. Through comparing the hysteresis loops measured after different thermal treatment, the effect of dipole polarization (P_D) caused by Li⁺–Al³⁺ ionic pairs on the spontaneous polarization was researched. For the piezoelectric properties, the results finally confirm that doping Li⁺–Al³⁺ ionic pairs can enhance the piezoelectric constant and electromechanical coupling factor, as well as the thermal stability of piezoelectric properties. In a word, the enhanced effect of Li⁺–Al³⁺ ionic pairs on the piezoelectric properties in PZT-based ceramic is identical to that in BaTiO₃-based ceramic. The results and analysis in the PZT-based ceramics justify the validity of Li⁺–Al³⁺ ionic pairs again. Compared with MPB, researcher can easily take advantage of ionic pairs doping to obtain large piezoelectric properties in ceramics instead of finding narrow MPB region. In addition, the temperature stability testing reveals that the depolarization temperature of these doped ceramics are greatly improved, even close to their Curie temperatures, which can't be acquired by designing PPT. The mechanism (Li⁺–Al³⁺ ionic pairs) will provide a new method to achieve large and stable piezoelectric response in a wide range of ABO₃-type perovskite systems.

Experimental

Materials and methods

Pb_1−2xLi_xAl_xZr_0.52Ti_0.48O₃ ceramics with Li⁺ and Al³⁺ contents of 0, 0.5, 1, 1.5, and 2 mol% were prepared by conventional ceramic processing techniques using the following reagent-grade raw materials: Pb₂O₃ (99.9%), TiO₂ (99.9%), ZrO₂ (99.9%), Li₂O (99.9%) and Al₂O₃ (99.9%). The doped ceramics including Li⁺ and Al³⁺ will be called PLAZT for short in present study. All chemicals were purchased from Aladdin Industrial Corporation. An excess of 3 mol% Pb₂O₃ was included to compensate for Pb loss during sintering. The starting reagents were ball milled in ethanol for 15 h. After ball-milling, the resulting slurries were dried at 80 °C for 12 h, then calcined in an alumina crucible at 800 °C for 2 h. The calcined powders were then ball milled in ethanol for 15 h using ZrO₂ ball-milling media, followed by drying the slurries at 80 °C for 12 h. The dried powders were pressed into pellets of 10 mm in diameter and 1 mm in thickness using a few drops of 5 wt% polyvinyl alcohol (PVA) as a binder. After burning off the PVA, the PLAZT pellets embedded in remaining powders were sintered at 1200 °C for 2 h at a rate of 5°C min⁻¹ in covered alumina crucibles.

Characterization

The crystalline structure of each sample were collected using a Philips X'Pert diffractometer with Cu Kα radiation, operating at 40 kV and 40 mA, in the 2θ ranges of 20–80° with a step size of 0.05°and 0.5 s per step. The fine scan XRD patterns were carried out with a step size of 0.02°and 5 s per step. The morphology and grain size were examined on a FEI Nanolab 600i scanning electron microscopy (SEM). Platinum electrodes were evaporated onto the ceramic surfaces and then annealed at 500 °C for 30 min to allow for electrical properties characterization.

The polarization vs. electric field (P–E) hysteresis loops were determined using a Radiant Technologies Precision work station. There are two groups of loops are carried out after different treatment: thermal annealing and thermal quenching. Thermal annealing experiments were heating the samples to 500 °C (above the Curie temperature of PZT ceramics) for 30 min, followed by a subsequent furnace cooling to room temperature. Thermal quenching experiments were performed by holding the samples at 500 °C for 30 min, and subsequent air cooling on a cold metallic plate to room temperature.

For the piezoelectric properties, samples were poled at 120 °C in a silicone oil bath under a DC field of 3 kV mm⁻¹ for 30 min. The piezoelectric constant (d₃₃) was measured employing a quasi-static piezoelectric constant testing meter (ZJ-4AN, Institute of Acoustics, Chinese Academy of Science). The electromechanical coupling factor (k_p) of every poled samples were calculated via a resonance–antiresonance method using an Agilent 4294A impedance analyzer. The thermal stability of d₃₃ was measured via separate ex situ thermal depoling measurements. The measurements were completed in which the samples were annealed at a set temperature for 30 min in a furnace, after which they were removed and the d₃₃ was measured when the sample reached room temperature. Each reported reading was an average of several readings at different positions on the face of the pellet. The set temperature was progressively increased until the samples exhibited a near-zero d₃₃ value.

Results and discussion

Phase and microstructure characterization

Fig. 1(a) shows the XRD patterns of PZT and PLAZT ceramic powders with different Li⁺ and Al³⁺ contents in the 2θ range of 20–80° measured at room temperature. All diffraction peaks match well with the ABO₃-type perovskite phases. The diffraction data confirms that both PZT and PLAZT powders exhibit tetragonal symmetry (PDF no. 33-0784), as evidenced by the relative intensity ratios of the 002/200 and the existence of a single 111 peak at 2θ = 38.9°.

Fig. 1 XRD patterns of PZT and PLAZT ceramic powders measured at room temperature (a), fine-scan XRD patterns in the 2θ ranges of (b) 37.75–38.75° and (c) 43–45.6°, (d) (I₀₀₂/I₂₀₀)^x/(I₀₀₂/I₂₀₀)⁰ intensity ratio and (e) schematic illustration of the preferential distribution of Li⁺–Al³⁺ ionic pairs parallel to the [001] direction.

In order to obtain the location of Li⁺ and Al³⁺ ions in the PLAZT lattice, fine scan XRD patterns measured at room temperature in the range of 27.5–28.5° and 43–45.5°, corresponding to the 111 and 200 peaks were shown in Fig. 1(b) and (c), respectively. In the Fig. 1(b), the right shift of 111 peak is observed with Li⁺ and Al³⁺ content increasing, which indicates that both ions are incorporated into lattice because the radius of Li⁺ and Al³⁺ is far smaller than radius of Pb²⁺. After the introduction of Li⁺ and Al³⁺, however, a distinct change in the relative intensity ratio of 002/200 peaks (here after referred to as I₀₀₂/I₂₀₀) was observed for the PLAZT ceramic powders in the Fig. 1(c). Fig. 1(d) shows that the (I₀₀₂/I₂₀₀)^x/(I₀₀₂/I₂₀₀)⁰ value (where the superscripts 0 and x denote PZT and PLAZT ceramic powders, respectively) tends to decrease firstly, and then increase with Li⁺ and Al³⁺ content increasing. This result is attributed to the preferential distribution of Li⁺–Al³⁺ ionic pairs parallel to c axis ([001] direction) as explained in our previous papers and ESI.† ^20,23 Fig. 1(e) presents a diagram of the lattice distortion induced by the preferential distribution of Li⁺–Al³⁺ ionic pairs parallel to the [001] direction. As Li⁺–Al³⁺ content increasing (0–1 mol%), the lattice distortion induced by Li⁺–Al³⁺ ionic pairs parallel to the [001] direction mainly impact the diffraction intensity of the 002 peak rather than 200 peak, which brings on reduced (I₀₀₂/I₂₀₀)^x/(I₀₀₂/I₂₀₀)⁰. When the Li⁺ and Al³⁺ are further added (≥1 mol%), the number of [100] and [010]-oriented Li⁺–Al³⁺ ionic pairs begins to increase as a result of elastic energy limitations, resulting in the uptrend of the (I₀₀₂/I₂₀₀)^x/(I₀₀₂/I₂₀₀)⁰.

Fig. 2 exhibits the scanning electron micrographs of the Pb_1−2xLi_xAl_xZr_0.52Ti_0.48O₃ (where x = 0, 0.5, 1.5 and 2 mol%, respectively) ceramics. In general, the PZT and PLAZT ceramics show dense and homogeneous microstructures. The effect of the Li⁺ and Al³⁺ on the microstructure of the ceramics is obvious. Inhomogeneous and irregular shape grains whose size is in the range of 10–20 μm are found on the surface of PZT ceramic, as shown in Fig. 2(a).

Fig. 2 Surface SEM micrographs of PLAZT ceramics: (a) x = 0 mol%, (b) x = 0.5 mol%, (c) x = 1.5 mol% and (d) x = 2 mol%.

However, the grain of ceramics doped by 0.5, 1.5 and 2 mol% Li⁺ and Al³⁺ (Fig. 2(b)–(d)) are comparatively uniform, whose size in the range of 2–10 μm. In addition, the grains in the PLAZT ceramics exhibit obviously sphere shape and smaller size than that of pure PZT ceramic. Evidently, the Li⁺ and Al³⁺ doping plays a role in grain refinement.

Constricted hysteresis behaviour

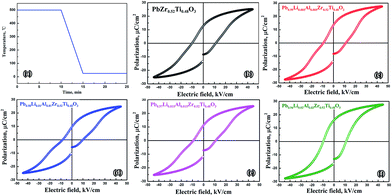
Lowered temperature curve during the annealing (cooling down from 500 °C to room temperature slowly) is shown in Fig. 3(a). The P–E hysteresis loops for the ceramics at room temperature measured after thermal annealing are shown in Fig. 3(b)–(f). PZT ceramic shows a typical ferroelectric behaviour that is distinct in terms of both significant saturated polarization (2P_S = 41.7 μC cm⁻²) and remnant polarization (2P_r = 25.6 μC cm⁻²). There are constricted hysteresis loop observed in Fig. 3(c)–(e), corresponding to the PLAZT ceramics doped by 0.5, 1 and 1.5 mol%, respectively. The constricted hysteresis loop should not be attributed to antiferroelectric phase of PbZrO₃ because the ratio of Zr/Ti is only 52/48 rather than larger value. Hence, the constricted behaviour in hysteresis loops gradually come out in the Li⁺–Al³⁺ content range of 0–1 mol%, and then slowly disappear when Li⁺–Al³⁺ content is further added. Interestingly, the most obvious constricted hysteresis loop is discovered in the Pb_0.98Li_0.01Al_0.01Zr_0.52Ti_0.48O₃ (1 mol%) ceramic, in which I₀₀₂/I₂₀₀ is relatively low compared with other ceramics. Through a comparative analysis on the hysteresis loops between PZT and Pb_0.98Li_0.01Al_0.01Zr_0.52Ti_0.48O₃, we found that the saturated polarization in both ceramics is almost identical, but remnant polarization of Pb_0.98Li_0.01Al_0.01Zr_0.52Ti_0.48O₃ is smaller than that of PZT. The analysis above indicates that when the electrical field is applied on the two sides of both ceramics, the domain switching behaviours in above both ceramics are almost identical. The difference is that a part of domains possibly return to original state in the Pb_0.98Li_0.01Al_0.01Zr_0.52Ti_0.48O₃ ceramic after the electrical field is removed, resulting in the lower remnant polarization. We thought this constricted behaviour should be attributed to certain restoring force existing in the lattice.^24–26 Considering the distribution and effect of Li⁺–Al³⁺ ionic pairs, the restoring force is possibly caused by dipole polarization (P_D) of Li⁺–Al³⁺ ionic pairs accompanied by Coulomb force between Li⁺ and Al⁺ ions.

Fig. 3 Lowered temperature curve during the annealing (a) and hysteresis loops of PLAZT ceramics measured after thermal annealing (b) x = 0 mol%, (c) 0.5 mol%, (d) 1 mol%, (e) 1.5 mol% and (f) 2 mol%.

To further investigate the formation process of constricted hysteresis loop in the PLAZT ceramics, the P–E hysteresis loop for all the ceramics at room temperature measured after thermal quenching (cooling down from 500 °C to room temperature quickly) are carried out again and P–E loops are shown in Fig. 4. Lowered temperature curve during the quenching is shown in Fig. 4(a). All PLAZT ceramics show typical ferroelectric behaviour as well as PZT ceramic. After above thermal treatment, the constricted hysteresis loops in PLAZT ceramics disappear, which demonstrates that there is no restoring force helping the domains return to original state when the temperature cools down just below Curie temperature.

Fig. 4 Lowered temperature curve during the quenching (a) and hysteresis loops of PLAZT ceramics measured after thermal quenching (b) x = 0 mol%, (c) 0.5 mol%, (d) 1 mol%, (e) 1.5 mol% and (f) 2 mol%.

By contrasting the hysteresis loops measured after various treatments (Fig. 3 and 4), the formation mechanism of constricted hysteresis loops, in what follows, are described in detailed. As shown in Fig. 5, the preferential distribution of Li⁺–Al³⁺ ionic pairs along the [001] direction possibly comes from the emergence of spontaneous polarization (P_S) after C–T phase transition. Above the phase transition point T_C, the crystal of PLAZT ceramic is in the paraelectric state and has a cubic symmetry. When the temperature is just below T_C, the crystal of PLAZT ceramic changes to ferroelectric state with a spontaneous polarization P_S along the [001] direction. In particular, the paraelectric–ferroelectric phase transition of PZT ceramics with ABO₃-type perovskite structure belongs to a first order transition, which includes two processes-nucleation and growth of tetragonal ferroelectric phase. The c-axis orientation of tetragonal ferroelectric phase is determined by the nucleus orientation. The nucleation process can be affected by the local electric field, and it is actively favorable for the spontaneous polarization (P_S) parallel to electric field. The Li⁺–Al³⁺ pair can create an electric dipole moment P_D as mentioned above, the local electric fields (E_D) formed by the dipole at the head and the tail of the pairs are nearly parallel to P_D, and the E_D in the middle and at the sides around the dipole are nearly antiparallel to P_D (see Fig. 5(a)). The former E_D can lead to ferroelectric phase nucleus with P_S nearly parallel to P_D and the latter E_D can induce ferroelectric phase nucleus with P_S nearly antiparallel to P_D. Therefore, the nucleation of tetragonal phase in the vicinity of Li⁺–Al³⁺ dipole causes the coexistence of P_S nearly parallel (P_S∥P_D) and nearly antiparallel to P_D(−P_S∥P_D) in the PZT ceramics (see Fig. 5(b)).^20,22

Fig. 5 Influence of P_D and Li⁺–Al³⁺ ionic pairs on the P_S in PLAZT ceramics through various thermal treatments. (a) Cubic paraelectric crystal above T_C. (b) The direction of P_S around ionic pairs is impacted by the local electric fields (E_D) when the temperature is just below T_C. (c) The state of the P_S around ionic pairs after thermal quenching. (d) The state of the P_S around ionic pairs after thermal annealing. (e) The normal hysteresis loop observed in the (c). (f) The constricted hysteresis loop observed in the (d).

Through the thermal quenching (cooling down from 500 °C to room temperature quickly) as shown in Fig. 5(c), it is too rapid for the tetragonal ferroelectric phase to grow because of short time. At this moment, most of P_S around ionic pairs remains the original state similar to the state in Fig. 5(b).

Through the thermal annealing (cooling down from 500 °C to room temperature slowly) as shown in Fig. 5(d), growth processes of tetragonal ferroelectric phase are ongoing owing to the enough time and higher temperature. The P_S in region 1 and 3 possess the same direction, but there is opposite direction P_S existing in the region 2 (see Fig. 5(b)). Compared with region 1 and 3, the region 2 is obviously small, because the Li⁺ ion is quite close with Al³⁺ ion. The area of region 2 in Fig. 5(b) will be easily reduced due to the growth processes of region 1 and 3. Consequently, regions 1, 2 and 3 will integrated into one domain with same direction as shown in Fig. 5(d). The changing of spontaneous polarization in region 2 will finish during the temperature cooling down from T_C to room temperature (RT) in the furnace. Finally, there are two kinds of polarizations with same direction coexisting in that domain: one is the spontaneous polarization P_S, another is the dipole polarization P_D(P_D∥P_S).

It is noteworthy that there is no constricted hysteresis loops observed in PLAZT ceramic through the thermal quenching (see Fig. 4(d)) and LiAlSiO₄/BaTiO₃ (BT/LAS) ceramics in our previous study.²⁰ This can be attributed to the following two reasons. For the PLAZT ceramic through the thermal quenching, the nucleation of tetragonal phase in the vicinity of Li⁺–Al³⁺ dipole causes the coexistence of P_S nearly parallel (P_S∥P_D) and nearly anti-parallel to P_D(−P_S∥P_D). Consequently, P_D is distributed randomly in space and the total net electric field from P_D is zero, giving rise to the relatively symmetric. In addition, the Li⁺ and Al³⁺ ions locate either near the domain boundary or in the different domains, so the P_D can't act as the source of restoring force. For the doped BaTiO₃ ceramics, the Curie temperature is far lower (∼120 °C) than that of PZT ceramics. There is no enough time or high temperature for tetragonal phase to grow in the cooling process of 120 °C-RT. In other words, domain state around the ionic pairs at RT is similar to that of PLAZT ceramic after thermal quenching: coexistence of P_D∥P_S and P_D∥−P_S; marginalized location of Li⁺ and Al³⁺ ions.

For the PLAZT ceramics through the thermal annealing, there are, however, two kinds of polarizations with same direction coexisting in one domain. The type of situation is similar to that in the ceramics including defect dipoles. According to the principle of symmetry conforming defect provided by Ren, the reason of constricted hysteresis loops and detailed discussions are as follows.^26–31 If the ionic pair symmetry in each domain follows the tetragonal crystal symmetry, and exhibits a dipole polarization P_D aligning along the direction of P_S(P_D∥P_S), as shown in Fig. 6(a), every domain containing P_D is in its stable state. The tetragonal crystal symmetry is represented by the large rectangle, while P_S is represented by the thick arrow as shown in Fig. 6. The ionic pair symmetry is represented by the small rectangle, while P_D is represented by the thin arrow. The stable and unstable states of the domains including ionic pair are also schematically illustrated by the symbol shown in Fig. 6.

Fig. 6 Mechanism of constricted hysteresis loop by reversible domain switching in the PLAZT ceramic due to the restoring force of Li⁺–Al³⁺ ionic pair. (a) Multi-domain tetragonal ferroelectric crystal and ionic pair symmetry. (b) 90° domain switching under electric field E, but this state is unstable owing to the existence of ionic pair symmetry. (c) 90° domain switching return to (d) due to restoring force resulted from P_D. (d) constricted hysteresis loop in the PLAZT ceramic.

When electric field is applied along other direction perpendicular to P_S, domain switching occurs abruptly with spontaneous polarization following the field direction (90° domain switching) (see Fig. 6(b)). It is noted that the direction of P_D cannot be rotated immediately in such a diffusion less domain-switching process. Once electric field is removed, this ionic pair symmetry and the P_D will provide a restoring force or a reverse internal field causing a reverse domain switching (Fig. 6(b) to Fig. 6(c)) because the state of switched domain is unstable (−P_D∥P_S or P_D⊥P_S). As a consequence, crystal symmetry will follow the ionic pair symmetry in every domain so that the domain pattern will try best to restore original state. Constricted hysteresis loops in the polarization–electric field (P–E) relation for the PLAZT ceramics (Fig. 6(d)) are obtained, as a result of the restoration of initial multi-domain pattern (which has zero macroscopic/averaged polarization) when the electric field is back to zero. Besides, we notice that the constricted hysteresis loop disappears gradually during the Li⁺–Al³⁺ content further increasing (>1 mol%), which is due to the emergence of [100] and [010]-oriented Li⁺–Al³⁺ ionic pairs, which is proved at previous XRD analysis. At this moment, parts of P_D caused by Li⁺–Al³⁺ ionic pairs is vertical to P_S(P_D⊥P_S), thus P_D can't deservedly provide the restoring force for 90° domain-switching after removing electric field. Consequently, the constricted hysteresis loops gradually disappears when the Li⁺ and Al³⁺ contents are greater than 1 mol% as shown in Fig. 3(d) and (e). The P–E loops of the poled PZT ceramic after prolonged storage measured under different electric field and at different frequencies are shown in Fig. S1 and S2,† respectively. The comparison between ionic pair and defect dipole has been discussed in ESI.†

Effect of ionic pairs on the piezoelectric properties

The variation of piezoelectric constant (d₃₃) and electromechanical coupling factor (k_p) with different Li⁺ and Al³⁺ contents are shown in Fig. 7(a). It is observed that Li⁺ and Al³⁺ substitutions have enhanced the values of piezoelectric constant and electromechanical coupling factor of PZT ceramic significantly. With the Li⁺ and Al³⁺ content increasing (0–1 mol%), the d₃₃ and k_p increase from 160 to 309 pC N⁻¹ and from 0.36 to 0.51, respectively. As the Li⁺ and Al³⁺ content added continuously, both d₃₃ and k_p fall. The d₃₃ and k_p both reach maximum value at 1 mol%, where the constricted behaviour in hysteresis loops is most obvious and massive Li⁺–Al³⁺ ionic pairs is parallel to the [001] direction. It is noticed that the enhanced piezoelectric properties of PLAZT ceramic are caused from doping Li⁺ and Al³⁺ ionic pairs in the lattice rather than MPB or PPT. The effect of Li⁺–Al³⁺ ionic pairs on the piezoelectric properties in the PZT ceramic is identical to that in the BT ceramic. On the one hand, smaller Li⁺ and Al³⁺ can respond immediately to the electrical field, which as a series of dipole contributes to the piezoelectric properties of PLAZT ceramics. On the other hand, the radii of Li⁺ and Al³⁺ is far smaller than that of Pb²⁺, the distortion induced by substitution is larger, which is proved at previous analysis in Fig. 1(c). There are local lattice distortion and lower symmetry than tetragonal symmetry existing in the PLAZT ceramics. It is well known that low symmetry always is connected with high piezoelectric properties.^4,32

Fig. 7 (a) Piezoelectric constant (d₃₃) and electromechanical coupling factor (k_p) (b) temperature dependence of the normalized d₃₃ values of the poled PLAZT ceramics measured ex situ.

Fig. 7(b) shows the temperature dependence of the normalized d₃₃ values of the poled ceramics measured ex situ after annealing the poled samples at various temperatures for 30 min. It is clear that the temperature stability of d₃₃ in PLAZT ceramics is more excellent than PZT ceramic. With the temperature increasing, the d₃₃ of PZT ceramic gradually decreases. However, for the PLAZT ceramics, d₃₃ of all ceramics exhibits high temperature stability until the temperature is close to 370 °C (near their Curie temperature). The phenomenon confirms that the depolarization temperature T_d of PLAZT ceramics is quiet high (close to T_C), which implies that their stability and reliability are improved. Because the high piezoelectricity in PLAZT ceramics possible originates from the dipole re-orientation of ionic pairs and distortion of lattice induced by Li⁺–Al³⁺ ionic pairs, it is too hard to make Li⁺ and Al³⁺ return to original site under temperature field.³¹

Above all, the effect of Li⁺ and Al³⁺ on the enhanced piezoelectric properties of PZT ceramic is mainly reflected in two aspects: the enhanced value and thermal stability of d₃₃. The influence of Li⁺–Al³⁺ ionic pairs in the PZT ceramic is the same as that in the BT ceramic. We speculate that the approach in the present study is different from any known large piezoelectric mechanism, which includes the PPT and MPB. Our work also indicates that the piezoelectric properties should reach a higher level by doping ionic pairs in ether lead ceramic or lead-free ceramic systems.

Conclusions

Pb_1−2xLi_xAl_xZr_0.52Ti_0.48O₃ ceramics with Li⁺ and Al³⁺ contents of 0, 0.5, 1, 1.5, and 2 mol% were prepared by conventional ceramic processing techniques. The preferential [001]-distributed Li⁺–Al³⁺ ionic pairs were proved in the PLAZT ceramics through XRD patterns analysis. There is obvious restoring force inducing constricted hysteresis loops in the PLAZT ceramics, which is due to the existence of independent dipole polarization. The dipole polarization evidently comes from the Coulomb force between Li⁺ and Al³⁺ ions. The formation mechanism of constricted hysteresis loops in the PLAZT ceramics are proposed experimentally and theoretically. Li⁺–Al³⁺ ionic pairs in PLAZT ceramics can play a significant role in the enhancement of piezoelectric properties and their thermal stability. This approach and technique (doping ionic pairs) efficiently improves the piezoelectric properties of the ABO₃-type perovskite systems, which can be a new guideline for further fabrication of piezoelectric ceramic.

Acknowledgements

This work was financially supported by the National Nature Science Foundation of China (Grant No. 11272102, and 51471057).

Notes and references

1. G. H. Haertling, J. Am. Ceram. Soc., 1999, 82, 797–818.
2. D. Damjanovic, Rep. Prog. Phys., 1998, 61, 1267–1324.
3. B. Jaffe, R. S. Roth and S. Marzullo, J. Appl. Phys., 1954, 25, 809–810.
4. D. Damjanovic, Appl. Phys. Lett., 2010, 97, 062906.
5. X. H. Du, J. H. Zheng, U. Belegundu and K. Uchino, Appl. Phys. Lett., 1998, 72, 2421–2423.
6. W. Jo, J. E. Daniels, J. L. Jones, X. L. Tan, P. A. Thomas, D. Damjanovic and J. Rodel, J. Appl. Phys., 2011, 109, 014110.
7. R. Z. Zuo, X. S. Fang, C. Ye and L. T. Li, J. Am. Ceram. Soc., 2007, 90, 2424–2428.
8. H. D. Li, C. D. Feng and W. L. Yao, Mater. Lett., 2004, 58, 1194–1198.
9. W. F. Liu and X. B. Ren, Phys. Rev. Lett., 2009, 103, 257602.
10. B. Z. Li, J. E. Blendell and K. J. Bowman, J. Am. Ceram. Soc., 2011, 94, 3192–3194.
11. D. Z. Xue, Y. M. Zhou, H. X. Bao, J. H. Gao, C. Zhou and X. B. Ren, Appl. Phys. Lett., 2011, 99, 122901.
12. J. A. Gallagher, J. Tian and C. S. Lynch, Acta Mater., 2014, 81, 512–523.
13. M. Kumar, S. Shankar, O. Parkash and O. P. Thakur, J. Mater. Sci.: Mater. Electron., 2014, 25, 888–896.
14. B. Peng, Z. X. Yue and L. T. Li, J. Appl. Phys., 2011, 109, 054107.
15. Y. Saito, H. Takao, T. Tani, T. Nonoyama, K. Takatori, T. Homma, T. Nagaya and M. Nakamura, Nature, 2004, 432, 84–87.
16. J. L. Zhang, X. J. Zong, L. Wu, Y. Gao, P. Zheng and S. F. Shao, Appl. Phys. Lett., 2009, 95, 022909.
17. R. Z. Zuo, J. A. Fu, D. Y. Lv and Y. Liu, J. Am. Ceram. Soc., 2010, 93, 2783–2787.
18. Y. P. Guo, K. Kakimoto and H. Ohsato, Appl. Phys. Lett., 2004, 85, 4121–4123.
19. X. P. Wang, J. G. Wu, X. J. Cheng, B. Y. Zhang, D. Q. Xiao, J. G. Zhu, X. J. Wang and X. J. Lou, J. Phys. D: Appl. Phys., 2013, 46, 495305.
20. D. Xu, W. L. Li, L. D. Wang, W. Wang, W. P. Cao and W. D. Fei, Acta Mater., 2014, 79, 84–92.
21. D. Xu, W. L. Li, L. D. Wang, W. Wang and W. D. Fei, RSC Adv., 2014, 4, 34008–34013.
22. D. Xu, L. D. Wang, W. L. Li, W. Wang, Y. F. Hou, W. P. Cao, Y. Feng and W. D. Fei, Phys. Chem. Chem. Phys., 2014, 16, 13078–13085.
23. Y. M. Wang, X-ray Diffraction of noncrystal and crystal with defects, Science Press, Beijing, 1st edn, 1988, in Chinese.
24. X. B. Ren, Nat. Mater., 2004, 3, 91–94.
25. L. X. Zhang and X. Ren, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 174108.
26. S. M. Ke, H. T. Huang, H. Q. Fan, H. K. Lee, L. M. Zhou and Y. W. Mai, Appl. Phys. Lett., 2012, 101, 082901.
27. L. X. Zhang, W. Chen and X. Ren, Appl. Phys. Lett., 2004, 85, 5658–5660.
28. D. M. Lin, K. W. Kwok and H. L. W. Chan, Appl. Phys. Lett., 2007, 90, 232903.
29. R. A. Eichel, P. Erhart, P. Traskelin, K. Albe, H. Kungl and M. J. Hoffmann, Phys. Rev. Lett., 2008, 100, 095504.
30. L. X. Zhang and X. Ren, Mater. Sci. Eng., A, 2006, 438, 354–359.
31. U. Robels and G. Arlt, J. Appl. Phys., 1993, 73, 3454–3460.
32. R. Guo, L. E. Cross, S. E. Park, B. Noheda, D. E. Cox and G. Shirane, Phys. Rev. Lett., 2000, 84, 5423–5426.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra00152a

---